Optics and Photonics Journal
Vol. 3 No. 2 (2013) , Article ID: 32625 , 6 pages DOI:10.4236/opj.2013.32023
Numerical Study on Optical Solitons Transmission System with 40 Gbit/s in the Photonic Crystal Fiber*
Institution of Information Science and Engineering, Ocean University of China, Qingdao, China
Email: #wjing@ouc.edu.cn
Copyright © 2013 Jing Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received December 25, 2012; revised February 15, 2013; accepted February 24, 2013
Keywords: Maximum Transmission Distance; Eye Pattern; Photonic Crystal Fiber; Polarization Mode Dispersion; High Order Nonlinear
ABSTRACT
The 40 Gbit/s optical solitons transmission system in photonic crystal fiber was investigated by fast Fourier transform method, and the maximum transmission distance of system was calculated numerically. By the eye pattern of system, the transmission performances of system were studied. Results show that when polarization mode dispersion coefficient Dp is smaller than 0.5 , the influence of the PMD on the transmission distance was neglectable. When the dispersion coefficient D is larger than 1.5 ps/km/nm, the transmission distance decreases rapidly. The positive or negative of three order group-velocity dispersion makes no differences on the system transmission.
, the influence of the PMD on the transmission distance was neglectable. When the dispersion coefficient D is larger than 1.5 ps/km/nm, the transmission distance decreases rapidly. The positive or negative of three order group-velocity dispersion makes no differences on the system transmission.
1. Introduction
Optical solitons are generated when group velocity dispersion (GVD) effects and self-phase modulation (SPM) effects reach balance in the fiber. Of course, there are strong demands for the properties of the fiber. The photonic crystal fiber (PCF) becomes the ideal medium for producing solitons due to its controllable dispersion property and strong nonlinear effects.
Solitons with low peak power are launched into highly nonlinear the PCF to generate high-order solitons easily, here the PCF is used as the compressor with high-solitons effect and fiber optical solitons laser to provide highrepetition-rate ultrashort solitons pulse sequence [1-3]. The potential applications of the PCF include generation and transmission of short-wavelength optical solitons, ultrashort-pulse laser, laser with high-power PCF [4-9], solitons generator with the nonlinear effects [10] and so on. Recently, H. Hasegawa studied the 10 Gbit/s solitons transmission system in the PCF [11-13]. It’s noticed that photonic band gap of PCF can be used to support the transmission of high power solitons because of the feebleness nonlinear effects of the empty core [14-16]. The solitons with peak power of 2 mw can be supported in air core photonic band gap PCF, and the solitons with peak power of 5 mw can be supported after filling PCF with nitrogen, which means that the solitons power transmitted in fiber can be raised by two orders.
In this paper, optical solitons transmission system was designed at 40 Gbit/s, and all factors which may influence on transmission system are analyzed. Such as the GVD and the SPM, three order group-velocity dispersion (TOD), polarization mode dispersion (PMD) and high order nonlinear effects. The longest transmission distances of system are calculated and system eye patterns are plotted by numerical algorithm in the PCF.
2. Solitons Transmission Equation
Considering the fiber loss, GVD, TOD, PMD and high order nonlinear effect, the generalized propagation equation of unity soliton takes the following forms:
 (1-a)
(1-a)
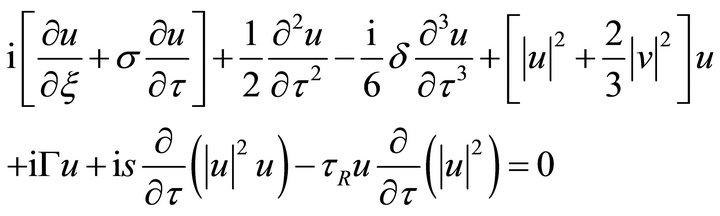 (1-b)
(1-b)
In the equation, u and v are unitary amplitude along the x and y coordinates, τ is unitary time, ![]() is unitary length, and t0 is the initial pulse width. The term proportional to σ includes polarization mode dispersion. The parameter σ is given by
is unitary length, and t0 is the initial pulse width. The term proportional to σ includes polarization mode dispersion. The parameter σ is given by . The second term and third term stand for GVD and TOD. The fourth term are self-phase modulation and cross-phase modulation. The term proportional to
. The second term and third term stand for GVD and TOD. The fourth term are self-phase modulation and cross-phase modulation. The term proportional to ![]() express fiber loss, and
express fiber loss, and
![]() is given by
is given by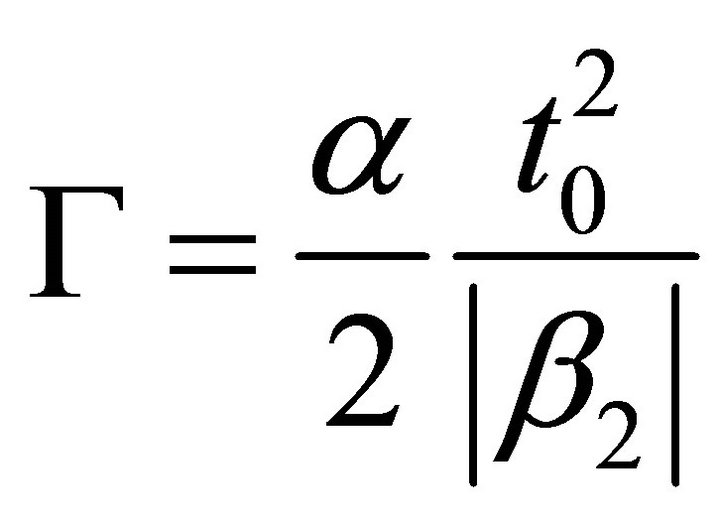 . The term proportional to s is responsible for self-steepening of the pulse edge, which is a phenomenon that has attracted considerable attention, and s is the self-steepening parameter. The last terms has its origin in the delayed nonlinear response, and is responsible for the self-frequency shift. τR is the Raman dispersion parameter.
. The term proportional to s is responsible for self-steepening of the pulse edge, which is a phenomenon that has attracted considerable attention, and s is the self-steepening parameter. The last terms has its origin in the delayed nonlinear response, and is responsible for the self-frequency shift. τR is the Raman dispersion parameter.
Because the random polarization model coupling is sensitive to the fluctuation of surrounding temperature and wavelength of light, the difference of group velocity delay is a statistic value which follows Maxwell distributing. The average value is linear to square root of distance.
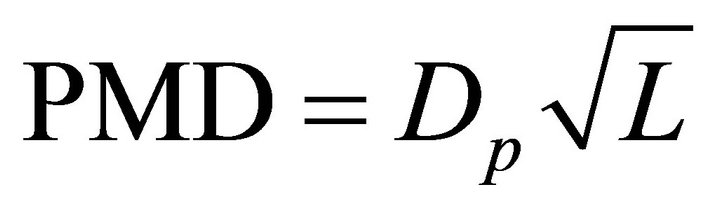 (2)
(2)
In this equation, the unit of the PMD, Dp, and L are ps, 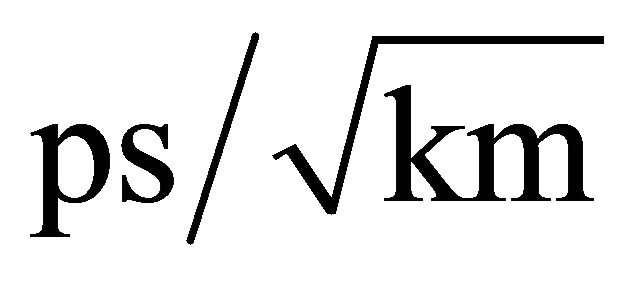 , and km, respectively. In order to solve the randomicity of polarization model coupling, we use a usual model of a randomly varying birefringent fiber that is a cascade of many short fibers with constant birefringence. And in every piece, it has the same length Zh and invariable double refraction
, and km, respectively. In order to solve the randomicity of polarization model coupling, we use a usual model of a randomly varying birefringent fiber that is a cascade of many short fibers with constant birefringence. And in every piece, it has the same length Zh and invariable double refraction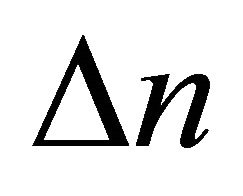 . Transmission of pulse in every piece follows Equation (1). At the two pieces connections
. Transmission of pulse in every piece follows Equation (1). At the two pieces connections 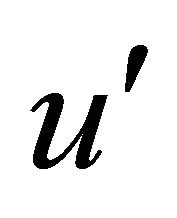 and
and  are two polarization parameters after random rotation of polarization axis and u and v are parameters before rotation and satisfy:
are two polarization parameters after random rotation of polarization axis and u and v are parameters before rotation and satisfy:
 (3)
(3)
where  is the rotation angle of the two polarization models and
is the rotation angle of the two polarization models and ![]() is the adjunctive phase factor. In this model, the PMD coefficient Dp is given by [17]
is the adjunctive phase factor. In this model, the PMD coefficient Dp is given by [17]
 (4)
(4)
This is the theoretical model we used.
The transmission of solitons in a random double refraction is calculated by fast Fourier transform method. The 64-bit fake random codes transmit in double refraction fiber at 40 Gbit/s and the figures of pulse are hyperbolic secant, Gauss and super Gauss type. One pulse is divided into 4096 points to calculate. In this model, it is assumed that the length of one fiber sect Zh is 0.025 km. By Q judgment method, the relationship of maximum transmission distance, GVD, TOD, PMD and high order nonlinear effects in the PCF are calculated. The transmission performance is evaluated by eye pattern of system. Because of PMD effect, the maximum distance changes randomly depending on random changes of optics axis of double refraction and phase. Under the same conditions, we calculated the PMD for 20 times and mean them to get the average value as the statistical result.
In the calculation, parameters of the PCF are n2 = 3.0 × 10−20 m2/w, Aeff = 3.14 μm2, λ = 800 nm, β3 = 0.082385 ps3/km, γ = 75 w−1/km, α = 0.37 dB/km, R = 40 Gbit/bit, and c = 2.998 × 108 m/s.
3. Calculation Result and Discussion
3.1. Effect of the PMD on the Maximum Transmission Distance of the System
In Figure 1, relationship between maximum transmission distances by different model pulses and PMD are shown under the condition of positive TOD. It is assumed that dispersion coefficient D is 1.6 ps/nm/km, and the PMD coefficient Dp are 0.2, 0.4, 0.6, 0.8, 1.0, and , respectively. The width of pulse is 60 fs. Results show that for all types of code, the maximum transmission distance of all three types of code decrease as PMD coefficient increases, which means that transmission performance get worse as PMD increases. But changes of three types code have great differences. The maximum distance of solitons is much larger than the other two (Gauss and super Gauss). When
, respectively. The width of pulse is 60 fs. Results show that for all types of code, the maximum transmission distance of all three types of code decrease as PMD coefficient increases, which means that transmission performance get worse as PMD increases. But changes of three types code have great differences. The maximum distance of solitons is much larger than the other two (Gauss and super Gauss). When , the distance of solitons changes slowly, and the distance of super Gauss decreases dramatically. When Dp > 0.5
, the distance of solitons changes slowly, and the distance of super Gauss decreases dramatically. When Dp > 0.5 , the maximum distance of solitons decreases dramatically and the other two decrease very slowly.
, the maximum distance of solitons decreases dramatically and the other two decrease very slowly.
In Figure 2, the TOD is negative and other parameters are the same as those used in Figure 1. The maximum distance of solitons is still the biggest, and the distance of super Gauss is the shortest. When , the maximum distance of solitons changes slowly and the distance of super Gauss and Gauss decreases rapidly. When
, the maximum distance of solitons changes slowly and the distance of super Gauss and Gauss decreases rapidly. When , the maximum distance of solitons decrease dramatically as PMD increases.
, the maximum distance of solitons decrease dramatically as PMD increases.
Results show that when the PMD is slight, it can be strongly restrained by solitons. When PMD is relatively large, Gauss and super Gauss type strongly restrain PMD. Because of the PMD effect, two polarization parts of solitons separate gradually, and the center location and center frequency of solitons are changed. By optimizing fiber parameters, the separation of the two polarization parts can be compensated. And at the same time, cross phase modulation causes frequency shift that make the
 (a) (b) (c)
(a) (b) (c)
Figure 1. The change of the maximum transmission distance with polarization mode dispersion under the TOD is positive. (a) Solitons; (b) Gauss pulse; (c) Super gauss pulse.
 (a) (b) (c)
(a) (b) (c)
Figure 2. The change of the maximum transmission distance with the PMD and the TOD is negative. (a) Solitons; (b) Gauss pulse; (c) Super gauss pulse.
two polarization parameters astricted each other. Thus separation of the two polarization parts was weakened and PMD is restrained. So transmission performance is the best.
3.2. Effect of the GVD on the Maximum Transmission Distance of the System
When the TOD parameter 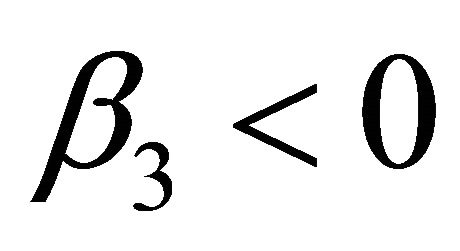 and
and , the maximum transmission distance of solitons, Gauss and super Gauss are calculated as dispersion changes.
, the maximum transmission distance of solitons, Gauss and super Gauss are calculated as dispersion changes.
In Figure 3, the average maximum transmission distance of solitons is shown with the coactions of the second order, third order dispersion and the PMD when the TOD is negative. We assume that , dispersion coefficient D are 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 ps/nm/km, respectively. As the GVD increases, the maximum distance of all three types pulse decrease. When D < 1.5 ps/nm/km, the maximum distance of solitons changes slightly. If GVD is larger, the distance decreases rapidly. When D = 3.0 ps/nm/km, the maximum distance is 51 km only.
, dispersion coefficient D are 0.5, 1.0, 1.5, 2.0, 2.5, and 3.0 ps/nm/km, respectively. As the GVD increases, the maximum distance of all three types pulse decrease. When D < 1.5 ps/nm/km, the maximum distance of solitons changes slightly. If GVD is larger, the distance decreases rapidly. When D = 3.0 ps/nm/km, the maximum distance is 51 km only.
Figure 4 shows the average maximum transmission distance of solitons under the coaction of second, third order dispersion and PMD when . For solitons and Gauss type, changes of
. For solitons and Gauss type, changes of  are the same as the changes of
are the same as the changes of . However, when
. However, when  is affirmative, the distance of super Gauss type decreases faster compared to the distance with
is affirmative, the distance of super Gauss type decreases faster compared to the distance with .
.
Comparing Figures 3 and 4, it is evident that the distance has slight difference, which indicates that the TOD does affect solitons transmission, and as a result transmission distance decreases. Whatever the TOD is affirmative or not, according to the same GVD and PMD, the maximum transmission distance of solitons changes slightly, and trend of change is similar. It is found that whatever the TOD is affirmative or not, the dispersion causes osillations at the foreside and tail of pulse and dispersion wave. Thus the transmission distance is limited.
In conclusion, the appearance of TOD breaks the balance between the GVD and the SPM effects. As a result, solitons can’t transmit steadily and maximum transmission distance decreases. On the other hand, the center shift and oscillations in pulse caused by the TOD make the coaction of general dispersion (including PMD, GVD, and high order dispersion) and nonlinear effects changing slightly. As a result, the PMD is restrained and sometimes the maximum distance increases but not decreases as the PMD increases.
3.3. Eye Pattern of the System
For further investigation of the effect of dispersion, PMD
 (a) (b) (c)
(a) (b) (c)
Figure 3. The change of the maximum transmission distance with GVD when β3 < 0. (a) Solitons; (b) Gauss pulse; (c) Super gauss pulse.
 (a) (b) (c)
(a) (b) (c)
Figure 4. The change of the biggest transmission distance with GVD when β3 > 0. (a) Solitons; (b) Gauss pulse; (c) Super gauss pulse.
 (a)
(a) (b)
(b)
Figure 5. Eye pattern of solitons transmission in 40 Gbit/s system. (a) 180 km; (b) 150 km; (c) 120 km; (d) 90 km.
and nonlinearity, eye patterns of the system were simulated at different transmitting location in the PCF. The PMD coefficient Dp is 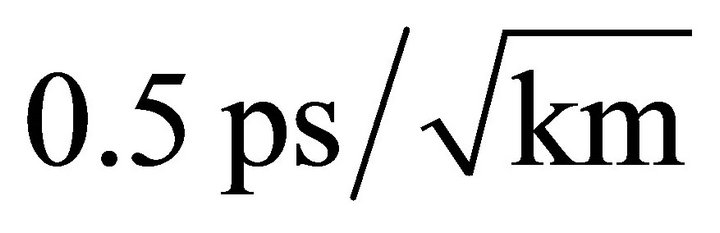 and the GVD coefficient D is 1.6 ps/nm/km. Eye patterns of solitons are calculated numerically.
and the GVD coefficient D is 1.6 ps/nm/km. Eye patterns of solitons are calculated numerically.
Figure 5 shows the eye pattern of solitons in the PCF with transmission distance of 180 km, 150 km, 120 km and 90 km, respectively. Compared four eye patterns, we conclude that the eye pattern of 90 km is very clear, which indicates the perfect performance of system. When the transmission distance increases to 120 km, splaying of eye pattern decreases and error dropping phenomena happens. With the further increasing transmission distance, eye pattern tends to be more and more faint. At 180 km, the eye pattern is messy and closed which ms that performance of system is poor.
4. Conclusions
In one word, as transmission speed is faster and faster, the width of pulse is more and more narrow. And the effect of the TOD and high nonlinear is more and more evident. For the system, it is essential to reduce the effect of PMD. Because PMD is randomicity, it is difficult to get a method of conquered PMD. So the numerical calculated could have helped to design transmission system. The results are given by:
When 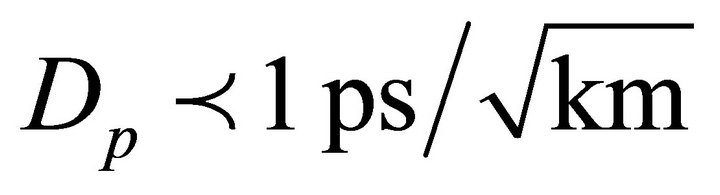 the maximum transmission distance of the system could exceed 100 km. The maximum transmission distance of the system is the more decrease as PMD effects increase for
the maximum transmission distance of the system could exceed 100 km. The maximum transmission distance of the system is the more decrease as PMD effects increase for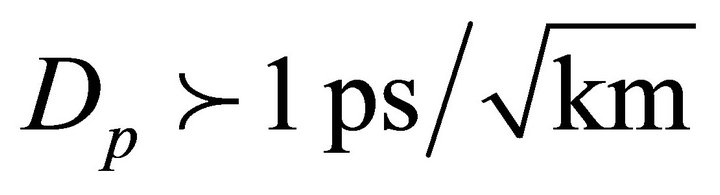 . The stronger nonlinear could control PMD and increase the distance in the PCF. The transmission distance was independent of the TOD sign.
. The stronger nonlinear could control PMD and increase the distance in the PCF. The transmission distance was independent of the TOD sign.
The transmission distance has uniform varitional current for three codes. The transmited distances of solitons did not have more superiority. So the system of other two codes pulse could have more communication performance in the PCF.
The results of eye pattern of system were accorded with the calculated maximum transmission distance by Q judgment method. Thus the simulated method was viable.
5. Acknowledgements
We would like to thank financial supports from the Natural Science Foundation of China (No. 61171161), the Fundamental Research Funds for the Central Universities (No. 201113011) and the Fundamental Research Project of Qingdao (No. 12-1-4-1-(26)-jch).
REFERENCES
- N. Nishizawa, Y. Ito and T. Goto, “0.78 - 0.90-μm Wavelength-Tunable Femtosecond Soliton Pulse Generation Using Photonic Crystal Fiber,” IEEE Photonics Technology Letters, Vol. 14, No. 7, 2002, pp. 986-988. doi:10.1109/LPT.2002.1012407
- F. Luan, J. C. Knight, et al., “Femtosecond Soliton Pulse Delivery at 800 nm Wavelength in Hollow-Core Photonic Bandgap Fibers,” Optics Express, Vol. 12, No. 5, 2004, pp. 835-840. doi:10.1364/OPEX.12.000835
- W. Gobel, A. Nimmerjahn, F. Helmchem, et al., “Distortion-Free Delivery of Nanojoule Femtosecond Pulses from a Ti:Sapphire Laser through a Hollow-Core Photonic Crystal Fiber,” Optics Letters, Vol. 29, No. 11, 2004, pp. 1285-1287. doi:10.1364/OL.29.001285
- K. L. Duan, J. M. Wang, J. F. Li, et al., “Experimental Study of Phase-Locking of Two Photonic Crystal Fiber Lasers,” Optics Communications, Vol. 281, No. 9, 2008, pp. 2557-2560. doi:10.1016/j.optcom.2007.12.086
- G. Bonati, H. Voelckel, T. Gabler, et al., “Photonics West,” Late Breaking Developments, San Jose, 2005.
- R. Cherif, M. Zghal, L. Tartara and V. Degiorgio, “Supercontinuum Generation by Higher-Order Mode Excitation in a Photonic Crystal Fiber,” Optics Express, Vol. 16, No. 3, 2008, pp. 2147-2152. doi:10.1364/OE.16.002147
- A. S. Y. Hsieh, S. G. Murdoch, S. Coen, et al., “Influence of Raman Susceptibility on Optical Parametric Amplification in Optical Fibers,” Optics Letters, Vol. 32, No. 5, 2007, pp. 521-523. doi:10.1364/OL.32.000521
- S. Wabnitz, “Broadband Parametric Amplification in Photonic Crystal Fibers with Two Zero-Dispersion Wavelengths,” Journal of Lightwave Technology, Vol. 24, No. 4, 2006, pp. 1732-1739. doi:10.1109/JLT.2006.871068
- W.-H. Liu, X.-Z. Song, Y.-S. Wang, et al., “Experimental Research of Supercontinuum Generation by Femtosecond Pulse in Highly Nonlinear Photonic Crystal Fiber,” Acta Physica Sinica, Vol. 57, No. 2, 2008, pp. 917-922.
- P. Petropoulos, H. Ebendorff-Heidepriem, V. Finazzi, et al., “Highly Nonlinear and Anomalously Dispersive Lead Silicate Glass Holey Fibers,” Optics Express, Vol. 11, No. 26, 2003, pp. 3668-3673. doi:10.1364/OE.11.003568
- H. Hasegawa, Y. Oikawa and M. Nakazawa, “10 Gbit/s 2 km Photonic Crystal Fiber Transmission over 850 nm with a Directly Modulated Single-Mode VCSEL H,” IEEE Electronics Letters, Vol. 43, No. 2, 2007, pp. 119-121.
- Y. Xu, X. Ren, Z. Wang, X. Zhang and Y. Huang, “Flatly Broadened Supercontinuum Generation at 10 Gbit/s Using Dispersion-Flattened Photonic Crystal Fibre with Small Normal Dispersion,” IEEE Electronics Letters, Vol. 43, No. 2, 2007, pp. 87-88. doi:10.1049/el:20073303
- C. H. Kwok, S. H. Lee, K. K. Chow, et al., “Photonic Crystal Fiber Based All-Optical Modulation Format Conversions between NRZ and RZ with Hybrid Clock Recovery from a PRZ Signal,” Opt-Electronics, Vol. 1, No. 1, 2007, pp. 47-53.
- D. G. Ouzounov, F. R. Ahmad, D. Müller, N. Venkataraman, M. T. Gallagher, M. G. Thomas, J. Silcox, K. W. Koch and A. L. Gaeta, “Generation of Megawatt Optical Solitons in Hollow-Core Photonic Band-Gap Fibers,” Science, Vol. 301, No. 5640, 2003, pp. 1702-1704. doi:10.1126/science.1088387
- M. Ballav and A. R. Chowdhury, “Raman Perturbation and Surface Core Soliton in Hollow Photonic Crystal Fiber,” Physics Letters A, Vol. 372, No. 14, 2008, pp. 2391- 2399. doi:10.1016/j.physleta.2007.11.052
- J. Atai, B. A. Malomed and I. M. Merhasin, “Stability and Collisions of Gap Solitons in a Model of a Hollow Optical Fiber,” Optics Communications, Vol. 265, No. 1, 2006, pp. 342-348. doi:10.1016/j.optcom.2006.03.037
- M. Matsumoto, Y. Akagi and A. Hasegawa, “Propagation of Solitons in Fibers with Randomly Varying Birefringence: Effects of Soliton Transmission Control,” Journal of Lightwave Technology, Vol. 15, No. 4, 1997, pp. 584- 589. doi:10.1109/50.566679
NOTES
*Supports from the Natural Science Foundation of China (No. 6117- 1161), the Fundamental Research Funds for the Central Universities (No. 201113011) and the Fundamental Research Project of Qingdao (No. 12-1-4-1-(26)-jch).
#Corresponding author.

