Geomaterials
Vol.04 No.04(2014), Article ID:49830,11 pages
10.4236/gm.2014.44012
Experimental Study of Induced Polarization Effect in Unconventional Reservoir Rocks
Vladimir Burtman1,2*, Haiyan Fu1, Michael S. Zhdanov1,2,3
1Geology and Geophysics Department, University of Utah, Salt Lake City, USA
2TechnoImaging LLC, Salt Lake City, USA
3Moscow Institute of Physics and Technology, Moscow, Russia
Email: *vlad.burtman@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 July 2014; revised 10 August 2014; accepted 8 September 2014
ABSTRACT
Unconventional hydrocarbon reserves substantially surpass those of conventional resources and therefore are extremely economically attractive. However, exploration and production of unconventional reserves is challenging. This paper demonstrates that one can observe significant induced polarization effects in shale reservoir rocks, which can be used in exploration for unconventional reserves. The generalized effective-medium theory of induced polarization (GEMTIP) was used to model the complex resistivity of shale rocks. We demonstrate that GEMTIP modeling provides an evaluation of mineral composition and volume fractions in rock samples. We have conducted spectral induced polarization (IP) measurements using different types of shale rocks to test the feasibility of the IP method and GEMTIP modeling for studying unconventional hydrocarbon (HC) reservoir rocks.
Keywords:
Unconventional Energy Resources, EM Exploration, Induced Polarization, Effective Medium

1. Introduction
The development of innovative methods for discovering and monitoring of unconventional reserves represents an important task of geophysics. This paper investigates the possibility of using the IP effect in studying the unconventional reservoir rocks, e.g., oil- and gas-shale and tight sands. We demonstrate that, one can observe significant induced polarization (IP) effects in shale reservoir rocks, which can be used in exploration for unconventional reserves.
The IP method is used in different geological applications: mineral exploration [1] [2] , hydrology [3] , and bio-geophysics [4] . The IP measurements are also used to study physical properties of soils and sediments. The hydraulic conductivity using the IP method was analyzed [5] - [9] and IP study of the pore or grain size distribution was conducted [10] [11] . It was demonstrated recently [12] [13] that the content and grain size of disseminated sulfide minerals can be obtained through deconvolution of CR spectra of sulfide samples. The application of the IP method to hydrocarbon exploration has been discussed in a number of publications, as well [14] - [20] .
Shale rocks with a percentage of total organic carbon (TOC) above 3% are usually considered as organic-rich shales. These shales may be deposited over a wide range of depositional environments ranging from terrestrial to marine. They may have a wide geographic distribution, and they occur in sediments of all ages, from modern to Precambrian. The geochemical variations within black shales may reflect depositional conditions, including water-column conditions and those within the sediment, sediment provenance, variations in the source of organic matter, diagenetic alteration including hydrothermal alteration, and even weathering processes [21] . For these reasons, shales can be classified by their composition (carbonate minerals such as calcite or detrital minerals such as quartz and clays) or by their depositional environment (large lakes, shallow marine, lagoon/small lake, and terrestrial settings).
This study is based on application of the generalized effective medium theory of induced polarization (GEMTIP) to the analysis of the complex resistivity (CR) of oil- and gas-shale rocks. GEMTIP modeling provides a basis for remote petrophysical analysis of shale rocks, which we compare with actual structural analysis of shale rocks using a Quantitative Evaluation of Minerals by Scanning Electron Microscopy (QEMSCan) and core analysis. Based on this analysis we have found that, GEMTIP modeling provides a useful evaluation of the mineral composition and volume fractions in the shale rock samples.
2. Modeling the IP Response in Reservoir Rocks
2.1. Empirical Conductivity Relaxation Models
Over the last 40 years several resistivity relaxation models have been developed, which provided quantitative characterization of the electric charging phenomena, including the empirical Cole-Cole model [22] - [27] , electrochemical model [2] [28] , the GEMTIP model [29] - [31] , based on generalized effective-medium theory of induced polarization.
One of the most widely used models is the Cole-Cole resistivity relaxation model introduced in the pioneering work of Pelton et al. [23] . According to this model, the complex resistivity can be presented as following:
 (1)
(1)
where 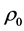 is the DC resistivity (ohm-m), ω is the frequency (rad/sec), τ is the time constant, C is the relaxation parameter, and
is the DC resistivity (ohm-m), ω is the frequency (rad/sec), τ is the time constant, C is the relaxation parameter, and 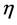 is the intrinsic chargeability [32] .
is the intrinsic chargeability [32] .
We should note that, the Cole-Cole model uses empirical parameters, while the GEMTIP model uses the effective medium theory to describe the complex resistivity of heterogeneous rocks. At the same time, it was shown by Zhdanov [29] - [31] that, in the case of spherical inclusions, the GEMTIP model reduces exactly to the Cole-Cole model. The GEMTIP resistivity model incorporates the physical and electrical characteristics of rocks at the porous/grain scale and translates them into an analytic expression for the effective complex resistivity. These characteristics include grain size, porous space shape, fluid and host rock conductivities, porosity, anisotropy, polaizability, etc. [29] - [31] . Note that, in a simple case of spherical grains in the homogeneous host medium, GEMTIP model reduces to the Cole-Cole model [29] .
2.2. Effective-Medium Model for Analysis of Complex Resistivity in Hydrocarbon-Saturated Rocks and Inversion for the GEMTIP Model Parameters
In the framework of the GEMTIP model, we represent a complex heterogeneous rock formation as a composite model formed by a homogeneous host medium of a volume V with a complex conductivity tensor  (where r is an observation point) filled with grains of arbitrary shape and conductivity. In a general case, the rock is composed of a set of N different types of grains, the lth grain type having complex tensor conductivity
(where r is an observation point) filled with grains of arbitrary shape and conductivity. In a general case, the rock is composed of a set of N different types of grains, the lth grain type having complex tensor conductivity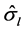 . The grains of the lth type have a volume fraction fl in the medium and a particular shape and orientation. Following [29] - [31] , we can write the following expression for the effective conductivity of the polarized inhomogeneous medium:
. The grains of the lth type have a volume fraction fl in the medium and a particular shape and orientation. Following [29] - [31] , we can write the following expression for the effective conductivity of the polarized inhomogeneous medium:
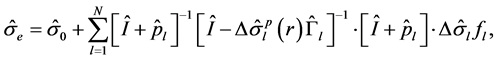 (2)
(2)
where  is an effective-medium conductivity tensor;
is an effective-medium conductivity tensor; 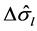 is an anomalous conductivity tensor;
is an anomalous conductivity tensor;  is the polarized anomalous conductivity;
is the polarized anomalous conductivity; 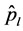 is a surface polarizability tensor;
is a surface polarizability tensor; 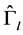 is a volume depolarization tensor; and index l corresponds to the grain of the lth type. The last formula provides a general solution of the effective conductivity problem for an arbitrary multiphase composite polarized medium. This formula allows us to find the effective conductivity for inclusions with arbitrary shape and electrical properties. That is why the new composite geoelectrical model of the IP effect may be used to construct the effective conductivity for realistic rock formations typical for mineralization zones and/or HC reservoirs.
is a volume depolarization tensor; and index l corresponds to the grain of the lth type. The last formula provides a general solution of the effective conductivity problem for an arbitrary multiphase composite polarized medium. This formula allows us to find the effective conductivity for inclusions with arbitrary shape and electrical properties. That is why the new composite geoelectrical model of the IP effect may be used to construct the effective conductivity for realistic rock formations typical for mineralization zones and/or HC reservoirs.
For this study, we have developed the three-phase ellipsoidal GEMTIP model for a medium with randomly oriented ellipsoidal inclusions. The expression for GEMTIP model in this case takes the following form:
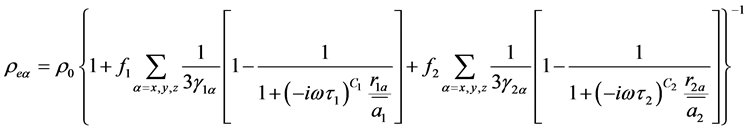 (3)
(3)
where

The  [Ohm-m] is the resulting effective resistivity,
[Ohm-m] is the resulting effective resistivity,  [Ohm-m] is the matrix resistivity of the rock being modeled,
[Ohm-m] is the matrix resistivity of the rock being modeled,  is a volume fraction of the l-th grain,
is a volume fraction of the l-th grain, 





The terms “two-phase” and “three-phase” model are related to structural model, which is characterized by one type of inclusions in the host medium or two types of inclusions, respectively. In the first case, for example, we may have pyrite in the host rock, while in the second case we may have the pyrite grains and pores in the host reservoir rock. The classic Cole-Cole model corresponds to a two-phase system with the host rock and one type of grains (e.g. pyrite). Equation (3) describes a three-phase model, which represents the host rock and two types of inclusions—grains of pyrite and pores filled with HC. Note that,a three-phase Cole-Cole model [26] was proposed as well.
GEMTIP model, Equation (3), can be formed by more than three phases as well. The exact choice of thenumber of phases depends on the structure and composition of the rock sample. Each phase should produce the IP effect, observable in the resistivity relaxation curve. It was demonstrated [29] that a two phase GEMTIP model can be reduced to the two-phase empiric Cole-Cole model, if the inclusions have a spherical shape. Following the same derivations [29] [30] , it can be shown that three phase GEMTIP model (Equation (3)) can be reduced to three phase Cole-Cole model for spherical inclusions. We should note that, the GEMTIP theory and model are based on a direct solution of Maxwell’s equations for EM field propagation in the complex model of reservoir rocks, which accounts for the relaxation of the resistivity with the frequency caused by the IP effect. In a general case, GEMTIP model can be simplified in order to reduce the number of unknown parameters, shown in Equation (1). For example three-phase GEMTIP model of Equation (3) is characterized by seven parameters only. The geoelectrical parameters of the GEMTIP model are determined by the intrinsic petrophysical and geometrical characteristics of the composite medium. Therefore, effective resistivity can serve as a basis for determining the intrinsic characteristics of the reservoir rock (the porosity, hydrocarbon saturation, etc.).
We introduce a vector, m, of the unknown model parameters:


where AIP is a forward modeling operator described by the corresponding analytical equations of GEMTIP model, Equation (3).
We can solve the inverse problem described by Equation (4) by using the regularized conjugate gradient method as follows [34] :

where 

3. Experimental Study of the IP Effect in Shale Reservoir Rocks
3.1. Rock Samples Description
The viability of the GEMTIP conductivity model was tested with multifrequency EM measurements acquired for shale-oil, laminated shale gas, and shale gas samples. Shale-oil, laminated shale gas, and shale gas samples (#8, #33, and #45) were provided by TerraTek. The shale samples and their thin sections are shown in Figure 1. All of the samples are rich in clay minerals, and they also contain disseminated pyrite. The samples were cut along less fragile direction, which were along the core axis for sample #8 and orthogonal to the core axis for samples 45 and 33. The X-ray diffraction data for whole rock, clay mineralogy by weight (%), and their core analysis were provided by TerraTek as well.
Figure 1. The left panels: photos of three shale samples. The right panels: thin sections of the same rock samples prepared for QEMSC an analysis.
The shale samples were examined using Quantitative Evaluation of Minerals by Scanning Electron Microscopy (QEMSCan) for structural analysis and phase evaluation [35] . The color-coded maps of mineral composition were created as well as a quantitative measurement of mineral abundance and inclusion size was conducted using QEMSCan 4300. Energy-dispersive X-ray spectral analysis (EDX) involves interpretation of secondary X-ray spectra to determine elemental composition and, ultimately, mineralogy. The rock samples were prepared as standard thin polished sections, then carbon coated and submitted for the QEMSCan measurement and analysis. The right panels in Figure 1 show samples of the thin sections, prepared for the QEMSCan measurement.
We have conducted complex resistivity measurements for each sample at 27 frequencies over a range from 0.005 Hz to 1000 Hz using the TechnoImaging’s experimental lab. The details of CR measurement system were reported [16] . The CR system is operating in frequency domain in order to avoid errors related to the conversion from time to frequency domain. The statistical standard error (SE) for the CR measurement was defined by measuring the artificial rock samples [32] and the SE does not exceed 1.2% for any frequency. The phase error at the 5 kHz was within 1 mrad for RC circuit, which had impedance of about 10 kΩ [36] .
3.2. Results of the QEMSCAN and GEMTIP Analysis of the Shale Reservoir Rocks
Figures 2-4 present the results of QEMSCan analysis for shale samples. Note that, according to the QEMSCan results, sample #8 contains 6.64% of the disseminated pyrite, sample #33 has 1.47% of the pyrite, and sample #45contains 3.53% of the pyrite, respectively.
Figure 2. A QEMSCan image of the shale rock sample #8 with a phase analysis shown on the right. The pyrite is designated by yellow color in this image.
Figure 3. A QEMSCan image of the shale rock sample #33 with a phase analysis shown on the right. The pyrite is designated by yellow color in this image.
Figure 4. A QEMSCan image of the shale rock sample #45 with a phase analysis shown on the right. The pyrite is designated by yellow color in this image.
Figures 5-7 show imaginary parts of the complex resistivity spectra measured for samples # 8, # 33, and # 45, respectively. We have inverted the observed complex resistivity data for the parameters of the GEMTIP models using two-phase and three-phase models. Both two- and three-phase models produce good misfits, which were 5% for two-phase and 3.2% for three-phase models, respectively, for sample #8; 5% and 3.5% for sample #33; and 7% and 6.2% for sample #45, respectively.
Figures 8-10 show the maps of the misfit functional for three-phase models for samples #8, #33, and #45, respectively, plotted as a function of the relaxation parameter (C) and the time constant (τ). The shaded isolines in this plot signify the direction of decreasing misfit. The paths of the conjugate gradient inversions are shown by the red lines. The final models are represented by red triangles. One can see that, for all three rock samples, the inversion converges rapidly to the specific parameters of the GEMTIP models. The corresponding GEMTIP parameters, produced by the inversion, are shown in the tables provided below.
Table 1 summarizes the results of GEMTIP inversion for rock sample #8. The recovered values of the volume fraction of inclusions with different electrical properties for both the two-phase and three-phase models are about 10%, which corresponds approximately to the combined volume fraction of pyrite (6.64%), determined by QEMSCan analysis, and gas-filled porosity (pgas = 6.34%) determined by the core analysis.
Table 2 presents similar results for rock sample # 33. The recovered values of the volume fraction of inclusions with different electrical properties for both the two-phase and three-phase models are about 13%, which corresponds approximately to the combined volume fraction of pyrite (2.4%), determined by QEMSCan analysis, and gas-filled porosity (pgas = 8.11%) determined by the core analysis.
Table 3 presents similar results for rock sample #45. The recovered values of the volume fraction of inclusions with different electrical properties for both the two-phase and three-phase models are about 13%, which corresponds approximately to the combined volume fraction of pyrite (4.4%), determined by QEMSCan analysis, and gas-filled porosity (pgas = 1%) determined by the core analysis.
3.3. Analysis of Experimental Results
It is important to note that, the three-phase inversion makes it possible to estimate separately the volume fraction of one phase in the GEMTIP model representing the polarization caused by disseminated pyrite, and that of another phase representing induced polarization caused by the presence of HC in the porous space of the sample. For example in sample #8 the dissiminated pyrite show a volume fraction 6.35% and 4% corresponds to the HC in the porous space. The time constant of pyrite is larger than the time constant of HC, because the capacitance of the mineral carrying the charge is much stronger than that of the HC.
We should note that, the pgas value in turn is directly associated with TOC in shale gas deposits. It was demonstrated [37] that in core shale samples the ratio between TOC and pgas is in 0.5 - 1 range. It was also reported close to 0.5 ratio between TOC and pgas in shale gas deposits [38] . This ratio was equal to 0.5 for shale samples used in our study, according to TerraTek core analysis. The same analysis between the internal structure of the
Figure 5. Imaginary part of the observed complex resistivity spectrum (red lines) and the data predicted based on the GEMTIP model (blue lines) for shale sample #8. The top panel presents the result for the two-phase GEMTIP model; the bottom panel shows the result for the three-phase GEMTIP model.
Figure 6. Imaginary part of the observed complex resistivity spectrum (red lines) and the data predicted based on the GEMTIP model (blue lines) for shale sample #33. The top panel presents the result for the two-phase GEMTIP model; the bottom panel shows the result for the three-phase GEMTIP model.
Figure 7. Imaginary part of the observed complex resistivity spectrum (red lines) and the data predicted based on the GEMTIP model (blue lines) for shale sample #45. The top panel presents the result for the two-phase GEMTIP model; the bottom panel shows the result for the three-phase GEMTIP model.
Figure 8. The map of the misfit functional as a function of relaxation parameter (C) and time constant (τ) for shale sample #8.
Figure 9. The map of the misfit functional as a function of relaxation parameter (C) and time constant (τ) for shale sample #33.
Figure 10. The map of the misfit functional as a function of relaxation parameter (C) and time constant (τ) for shale sample #45.
Table 1. Parameters of GEMTIP models used for sample #8.
Table 2. Parameters of GEMTIP models used for sample #33.
Table 3. Parameters of GEMTIP models used for sample #45.
samples and their complex resistivity spectra was conducted for the shale-gas and laminated shale-gas samples. The results of the study for all three samples are summarized in Table 4.
The result of QEMSCan analysis have demonstrated that the shale rock samples have very complex mineral composition. For example, Figure 2 and Figure 4 show that, the percentage of the clay minerals (kaolinite and chloride) reaches 4.5% for sample #8 and 1.43% for sample #45. It is known that the clay minerals may cause a non-linearity in CR spectra, especially at higher frequencies (or lower time constants). The question may arise if the IP effect in the shale samples could be caused by these clay minerals. In addressing this question we should note that, according to published data, a significant IP effect in clay-containing samples has been observed at
Table 4. Volume fraction of pyrite and porosity determined by QEMSCan and core analysis vs. GEMTIP three phases model parameters of shale samples, respectively.
high frequency only (>1 kHz) [39] - [41] . The low frequency IP effect in clays was not observed or it was caused by other factors than the presence of the pure clay minerals [6] [10] [19] [42] -[49] . In addition, in our study the kaolinite and chloride minerals appear in two samples only (#8, Figure 2, and #45, Figure 4). Sample #33 (Figure 3) does not contain any of these clay minerals, however we observe a strong frequency variations of the resistivity in this sample and GEMTIP modeling recovers rather accurately the shale porosity for this sample. Thus, the results of GEMTIP modeling of sample #33, which does not contain any clay minerals, confirm that the IP effect in our experiments is attributed to pyrite and HC fractions.
4. Conclusion
An important result of this study is that one can observe significant induced polarization effects in shale reservoir rocks. This observation opens a possibility of direct application of the spectral IP method for exploration and monitoring of traditional and unconventional (shale gas, shale oil, tar sands etc.) energy resources. This paper also shows that the GEMTIP modeling can be used for an evaluation of the mineral composition and HC fractions in the rock samples comparable with the direct core analysis. A proper modeling and inversion with the three-phase GEMTIP model, used in our experimental study, recovers the true characteristics and structural composition of the reservoir rocks. In summary, this paper demonstrates that, the GEMTIP modeling and inversion provides a solid foundation for an application of the spectral IP method in exploration and monitoring of hydrocarbon reservoirs.
Acknowledgements
The authors acknowledge the support of the University of Utah Consortium for Electromagnetic Modeling and Inversion (CEMI) and TechnoImaging. We are thankful to TerraTek for providing the shale rock samples and core analysis.
References
- Vanhala, H. and Peltoniemi, M. (1992) Spectral IP Studies of Finnish Ore Prospects. Geophysics, 57, 1545-1555. http://dx.doi.org/10.1190/1.1443222
- Ostrander, A.G. and Zonge, K.L. (1978) Complex Resistivity Measurements of Sulfide-Bearing Synthetic Rocks. SEG Technical Program Extended Abstract.
- Slater, L.D. and Lesmes, D. (2002) IP Interpretation in Environmental Investigations. Geophysics, 67, 77-88.
- Abdel Aal, G.Z., Atekwana, E.A. and Atekwana, E.A. (2010) Effect of Biocloggingin Porous Media on Complex Conductivity Signatures. Journal of Geophysical Research, 115, G00-G07. http://dx.doi.org/10.1029/2009JG001159
- Börner, F.D., Schopper, J.R. and Weller, A. (1996) Evaluation of Transport and Storage Properties in the Soil and Groundwater Zone from Induced Polarization Measurements. Geophysical Prospecting, 44, 583-601. http://dx.doi.org/10.1111/j.1365-2478.1996.tb00167.x
- Binley, A., Slater, L.D., Fukes, M. and Cassiani, G. (2005) The Relationship between Spectral Induced Polarization and Hydraulic Properties of Saturated and Unsaturated Sandstone. Water Resources Research, 41, Article ID: W12417. http://dx.doi.org/10.1029/2005WR004202
- Weller, A., Slater, L., Nordsiek, S. and Ntarlagiannis, D. (2010) On the Estimation of Specific Surface per Unit Pore Volume from Induced Polarization: A Robust Empirical Relation Fits Multiple Datasets. Geophysics, 75, WA105- WA112. http://dx.doi.org/10.1190/1.3471577
- Weller, A., Breede, K., Slater, L. and Nordsiek, S. (2011) Effect of Changing Water Salinity on Complex Conductivity Spectra. Geophysics, 76, F315-F327. http://dx.doi.org/10.1190/geo2011-0072.1
- Zisser, N., Kemna, A. and Nover, G. (2010) Relationship between Low Frequency Electrical Properties and Hydraulic Permeability of Low Permeability Sandstones. Geophysics, 75, 131-141. http://dx.doi.org/10.1190/1.3413260
- Scott, J.B. and Barker, R.D. (2003) Determining Pore-Throat Size in Permo-Triassic Sandstones from Low-Frequency Electrical Spectroscopy. Geophysical Research Letters, 30, 1450. http://dx.doi.org/10.1029/2003GL016951
- Revil, A. and Florsch, N. (2010) Determination of Permeability from Spectral Induced Polarization Data in Granular Media. Geophysical Journal International, 181, 1480-1498. http://dx.doi.org/10.1111/j.1365-246X.2010.04573.x
- Zhdanov, M.S., Burtman, V., Endo, M. and Wilson, G.A. (2012) Laboratory-Based GEMTIP Analysis of Spectral IP Data for Mineral Discrimination. SEG Technical Program Extended Abstract, 1-5. http://dx.doi.org/10.1190/segam2012-1268.1
- Gurin, G., Tarasov, A., Ilyin, Yu. and Titov, K. (2013) Spectral’naia kharakteristika vyzvannoi poliarizatsii vkraplennykh rud. (Spectral Induced Polarization Characteristics of Disseminated Ores). Vestnik Sankt-Peterburgskogo Universiteta, 7, 14-30.
- Veeken, P., Legeydo, P.J., Davidenko, Y., Kudryavceva, E., Ivanov, S. and Chuvaev, A. (2009) Benefits of the Induced Polarization Geoelectric Method to Hydrocarbon Exploration. Geophysics, 74, B47-B59. http://dx.doi.org/10.1190/1.3076607
- Schmutz, M., Revil, A., Vaudelet, P., Batzle, M., Viñao, P.F. and Werkema, D.D. (2010) Influence of Oil Saturation upon Spectral Induced Polarization of Oil-Bearing Sands. Geophysical Journal International, 183, 211-224. http://dx.doi.org/10.1111/j.1365-246X.2010.04751.x
- Zhdanov, M.S., Burtman, V. and Marsala, A. (2013) Carbonate Reservoir Rocks Show Induced Polarization Effects, Based on Generalized Effective Medium Theory. EAGE International Exposition and Annual Meeting, London, 10-13 June 2013.
- Olhoeft, G.R. (1985) Low-Frequency Electrical Properties. Geophysics, 50, 2492-2503. http://dx.doi.org/10.1190/1.1441880
- Zonge, K.L. (1983) Case Histories of an Electromagnetic Method. In: Hughes, L., Ed., Proprietary Data Sale, Vol. 10, 315-330.
- Vinegar, H.J. and Waxman, M.H. (1984) Induced Polarization of Shaly Sands. Geophysics, 49, 1267-1287. http://dx.doi.org/10.1190/1.1441755
- Davydycheva, S., Rykhlinski, N. and Legeido, P. (2006) Electrical-Prospecting Method for Hydrocarbon Search Using the Induced-Polarization Effect. Geophysics, 71, G179-G189. http://dx.doi.org/10.1190/1.2217367
- Altun, N.E., Hicyilmaz, C. and Hwang, J. (2006) Oil Shales in the World and Turkey; Reserves, Current Situation and Future Prospects. A Scientific-Technical Journal, 23, 211-227.
- Cole, K.S. and Cole, R.H. (1941) Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. Journal of Chemical Physics, 9, 341-351. http://dx.doi.org/10.1063/1.1750906
- Pelton, W.H., Ward, S.H., Hallof, P.G., Sills, W.R. and Nelson, P.H. (1978) Mineral Discrimination and Removal of Inductive Coupling with Multifrequency IP. Geophysics, 43, 588-609. http://dx.doi.org/10.1190/1.1440839
- Kemna, A. (2000) Tomographic Inversion of Complex Resistivity—Theory and Application. Der Andere Verlag, Osnabruck. http://www2.geo.uni-bonn.de/members/kemna/Kemna_2000_PhD_thesis.pdf
- Nordsiek, S. and Weller, A. (2008) A New Approach to Fitting Induced-Polarization Spectra. Geophysics, 73, F235- F245. http://dx.doi.org/10.1190/1.2987412
- Kavian, M., Slob, E.C. and Mulder, W.A. (2012) A New Empirical Complex Electrical Resistivity Model. Geophysics, 77, E185-E191. http://dx.doi.org/10.1190/geo2011-0315.1
- Tarasov, A. and Titov, K. (2013) On the Use of the Cole-Cole Equations in Spectral Induced Polarization. Geophysical Journal International, 195, 352-356. http://dx.doi.org/10.1093/gji/ggt251
- Revil, A., Woodruff, W.F., Torres-Verdín, C. and Prasad, M. (2013) Complex Conductivity Tensor of Anisotropic Hydrocarbon-Bearing Shales and Mudrocks. Geophysics, 78, D403-D418. http://dx.doi.org/10.1190/geo2013-0100.1
- Zhdanov, M.S. (2008) Generalized Effective-Medium Theory of Induced Polarization. Geophysics, 73, F197-F211. http://dx.doi.org/10.1190/1.2973462
- Zhdanov, M.S. (2006) Generalized Effective-Medium Theory of Induced Polarization. SEG Technical Program Expanded Abstracts, 21, 805-809.
- Zhdanov, M.S. (2008) Geophysical Technique for Mineral Exploration and Discrimination Based on Electromagnetic Methods and Associated Systems. US Patent No. 7324899 B2.
- Siegel, H.O. (1959) Mathematical Formulation and Type Curves for Induced Polarization. Geophysics, 43, 588-609.
- Burtman, V., Gribenko, A. and Zhdanov, M.S. (2010) Advances in Experimental Research of Induced Polarization Effect in Reservoir Rock. SEG Technical Program Extended Abstract, 2475-2479. http://dx.doi.org/10.1190/1.3513351
- Zhdanov, M.S. (2002) Geophysical Inverse Theory and Regularization Problems. Elsevier, Amsterdam.
- Rollinson, G.K., Andersen, J.C.Ø., Sticklanda, R.J., Boni, M. and Fairhurst, R. (2011) Characterization of Non-Sulphide Zinc Deposits Using QEMSCAN. Minerals Engineering, 24, 778-787. http://dx.doi.org/10.1016/j.mineng.2011.02.004
- Burtman, V., Endo, M. and Zhdanov, M.S. (2011) High-Frequency Induced Polarization Measurements of Hydrocarbon-Bearing Rocks. SEG Technical Program Extended Abstract, 30, 4.
- Boyer, C., Kieschnick, J., Suares-Rivera, R., Lewis, R.E. and Waters, G. (2006) Producing Gas from Its Source. Oilfield Review, 36-49. http://water.slb.com/~/media/Files/resources/oilfield_review/ors06/aut06/producing_gas.pdf
- Passey, Q.R., Bohacs, K.M., Esch, W.L., Klimentidis, R. and Sinha, S. (2010) From Oil-Prone Source Rock to Gas- Producing Shale Reservoir-Geologic and Petrophysical Characterization of Shale-Gas Reservoirs. Society of Petroleum Engineers: The International Oil and Gas Conference and Exhibition in China, Beijing, 8-10 June 2010, 29. http://dx.doi.org/10.2118/131350-MS
- Buist, S.I. (2009) Induced Polarization Effect in Land and Marine CSEM Data: Application for Hydrocarbon Exploration. Master of Science Thesis, The University of Utah, Salt Lake City.
- Jougnot, D., Ghorbani, A., Revil, A., Leroy, P. and Cosenza, P. (2010) Spectral Induced Polarization of Partially Saturated Clay-Rocks: A Mechanistic Approach. Geophysical Journal International, 180, 210-224. http://dx.doi.org/10.1111/j.1365-246X.2009.04426.x
- Slater, L., Ntarlagiannis, D. and Wishart, D. (2006) On the Relationship between Induced Polarization and Surface Area in Metal-Sand and Clay-Sand Mixtures. Geophysics, 71, A1-A5. http://dx.doi.org/10.1190/1.2187707
- Slater, L.D. and Glaser, D.R. (2003) Controls on Induced Polarization in Sandy Unconsolidated Sediments and Application to Aquifer Characterization. Geophysics, 68, 1547-1558. http://dx.doi.org/10.1190/1.1620628
- Revil, A. (2012) Spectral Induced Polarization of Shaly Sands: Influence of the Electrical Double Layer. Water Resources Research, 48, Article ID: W02517. http://dx.doi.org/10.1029/2011WR011260
- Hyslip, J.P. and Vallejo, L.E. (1997) Fractal Analysis of the Roughness and Size Distribution of Granular Materials. Engineering Geology, 48, 231-244. http://dx.doi.org/10.1016/S0013-7952(97)00046-X
- Drolon, H., Hoyez, B., Druaux, F. and Faure, A. (2003) Multiscale Roughness Analysis of Particles: Application to the Classification of Detrital Sediments. Mathematical Geology, 35, 805-817. http://dx.doi.org/10.1023/B:MATG.0000007780.52861.57
- Le Mehaute, A. and Crepy, G. (1983) Introduction to Transfer and Motion in Fractal Media: The Geometry of Kinetics. Solid State Ionics, 9-10, 17-30.
- Wong, P.Z. (1987) Fractal Surfaces in Porous Media. Physics and Chemistry of Porous Media, 2, 304-318.
- Titov, K., Tarasov, A., Ilyin, Y., Seleznev, N. and Boyd, A. (2010) Relationships between Induced Polarization Relaxation Time and Hydraulic Properties of Sandstone. Geophysical Journal International, 180, 1095-1106. http://dx.doi.org/10.1111/j.1365-246X.2009.04465.x
- Zisser, N., Kemna, A. and Nover, G. (2010) Dependence of Spectral-Induced Polarization Response of Sandstone on Temperature and Its Relevance to Permeability Estimation. Journal of Geophysical Research, 115, Article ID: B09214. http://dx.doi.org/10.1029/2010JB007526
NOTES
*Corresponding author.













