Geomaterials
Vol.2 No.2(2012), Article ID:18695,8 pages DOI:10.4236/gm.2012.22005
Effect of Compaction on Soil Hydraulic Parameters of Vegetative Landfill Covers
Osnabrueck University of Applied Sciences, Osnabrueck, Germany
Email: r.anlauf@hs-osnabrueck.de
Received February 14, 2012; revised March 28, 2012; accepted March 29, 2012
Keywords: Water Balance; Available Water Capacity; Air Capacity; Pedo-Transfer Function; Pore Structure
ABSTRACT
Parameters of water retention and air capacity are important factors for the evaluation of soil material that will be used for vegetative covers or evapotranspiration (ET) covers of landfills. These values are often measured in the laboratory (usually on disturbed samples), but are also estimated from texture, organic matter content and dry bulk density. The standard basis for the estimation in Germany is the German Soil Classification Handbook (KA5). This estimation implicitly assumes that the data in the KA5 compiled from naturally developed soils are also valid for artificially compacted materials. In the present study, 25 materials were evaluated in the laboratory for the available water capacity, air capacity and permanent wilting point at 85%, 90% and 95% of Proctor density. The data were compared with parameter estimations from the KA5 and the program ROSETTA. Both estimation methods show significant deviations from the measured values; specifically, the change in the available water capacity in compressed samples is not estimated correctly. A possible explanation is a change in pore structure at different compaction levels of build in soil material in comparison with naturally developed soils of different bulk densities.
1. Introduction
Water retention parameters are important and necessary information to evaluate materials used for landfill vegetative covers. Above all, available water capacity (AWC) as a measure of water storage and air capacity (AC) are important parameters for plant’s growth. These parameters depend on soil texture, bulk density and organic matter content.
The guideline for the properties of material used to cover landfills in Germany is the Landfill Ordinance [1]. Soil material to be used as landfill vegetative covers must have a minimum thickness of 1 m, so that the function of the underlying system components is not impaired by subsequent land use, drying, freezing or root exposure [1]. Similar thicknesses are given in international guidelines for landfill covers [2,3].
Furthermore, according to German guidelines, an available water capacity (AWC) of at least 140 mm for the total thickness of the vegetative cover must be ensured. If the landfill cover should be function as an evapotranspiration (ET) layer, a minimum thickness of 1.50 m and an AWC of 220 mm are required, so that the maximum seepage will not exceed 60 mm per year [4]. In addition, an air capacity of at least 8% vol is recommended in the entire vegetative layer [5]. International guidelines postulate either similar values or, at least, a high available water capacity [3,6].
Literature states that the AWC primarily depends on soil texture and that an increase in organic matter increases the AWC. The bulk density has a major impact on AC and AWC in the sense that a higher bulk density reduces AC and AWC [5].
These important soil hydraulic characteristics are usually measured in the laboratory before installation on a landfill, or are estimated based on texture, organic matter content, and bulk density, e.g. from the official German Soil Classification Handbook (KA5) [7]. Prerequisite and implicit assumption is that the estimated values, which are based on naturally developed soils, can be applied to artificially compacted materials.
In accordance to studies on naturally developed soils, a decline of the AWC and AC is expected with increasing compaction of soil material. This is usually also assumed for landfill cover layers [5]. However, there are some hints that for artificially compacted materials, at least the AWC does not always depend on the compaction [5,8].
Other studies report a regular decrease of the pore volume (PV) and air capacity (AC) with increasing compaction, while the AWC remained the same or even increased [8,9]. One conclusion is that the estimated values of AC and AWC based on data from naturally developed soils are not necessarily valid for artificially compacted materials and should be checked regularly with analytical methods [9].
The aim of the work presented in this study was to investigate the transferability of air capacity and available water capacity values based on usual estimation methods to artificially compacted materials.
2. Materials and Methods
2.1. Estimation of Soil Hydraulic Parameters
Two different estimation methods were applied: the tables of the German Soil Classification Handbook KA5 [7] and values calculated with the program ROSETTA [10,11].
The German Soil Classification Handbook (KA5) is the standard in Germany, which is also used to evaluate materials used for landfill covers. The data is also used in the German version of the simulation model HELP (Hydrologic Evaluation of Landfill Performance) [12,13] which is often used to evaluate water balances in landfill caps.
The KA5 tables for the estimation of soil physical parameters, such as field capacity, available water capacity and air capacity as a function of texture, soil organic matter content and bulk density, were developed based on more than 6000 records from various places in Germany with empirical regression relationships [14].
The program ROSETTA is available as a standalone program and also part of the simulation model HYDRUS- 1D [15], which is often used to simulate soil water balances. ROSETTA calculates pedo-transfer functions with the method of neural networks and a hierarchical method based on 2134 data sets mainly from temperate and subtropical regions of North America and Europe [10]. Input data for ROSETTA are clay, silt and sand content and bulk density. ROSETTA estimates the course of the entire water retention curve. The air capacity was determined as the difference of the water content at saturation (pF 0) and the water content at field capacity (pF 1.8; 68 hPa). The available water capacity was calculated as the difference of the water content at field capacity and at the permanent wilting point (at pF 4.2).
2.2. Measurement of the Soil Hydraulic Parameters
Various materials were each examined in 3 different densities (Table 1). All the materials selected with Proctor densities of 0.97 g·cm–3 to 1.88 g·cm–3 can generally be used for vegetative cover layers (e.g. mixtures of different mineral soil, clay and organic material, mixtures of mineral soil and rubble, and dredged material). After determining the maximum Proctor density according to DIN 18127 [16] the samples were packed layer wise [17]
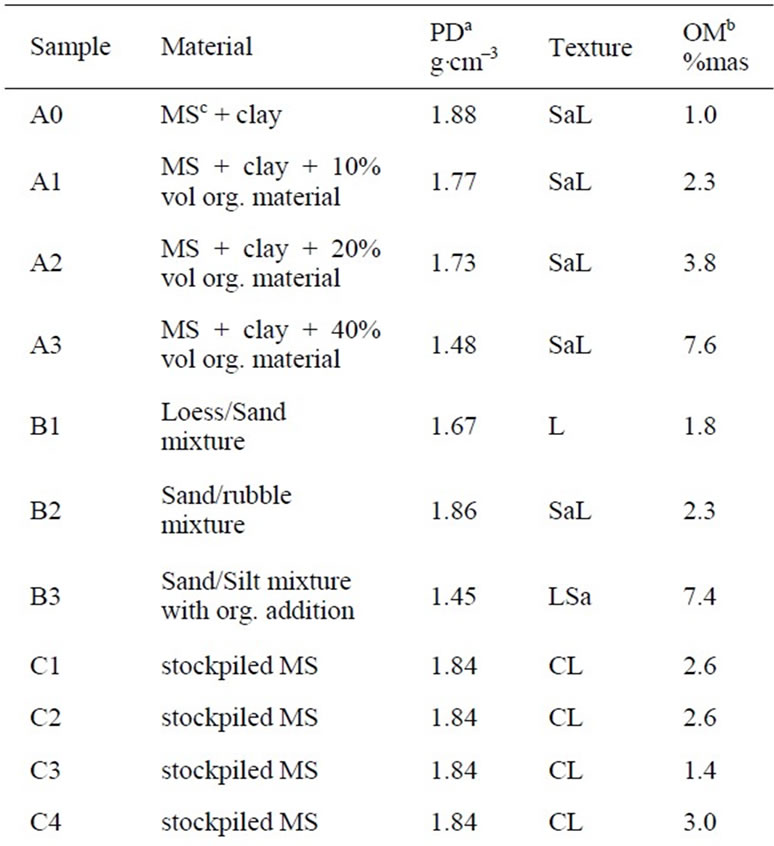

Table 1. Investigated materials.
in a metal cylinder (100 cm3) at 85%, 90% and 95% Proctor density.
Water content at pF 1.8 and pF 2.5 were determined using a standard sand box apparatus [18] and at pF 4.2 on a pressure plate apparatus [19].
2.3. Comparison of Measurement and Estimation
To evaluate the quality of the estimation methods, different quality measures were applied. For a quick overview of the estimation quality, graphs of the measured values against the simulated values were drawn together with the linear regression, the correlation coefficient and the 1:1 line. Without any estimation error, the measured and estimated simulated values are identical and all points should lie on the 1:1 line. The points of good quality estimations should lie close to the 1:1 line, the slope of the linear regression should be close to one and the coefficient of determination (r2) should also be close to one.
In addition, numerical measures of agreement between the measured and estimated values were used as follows: A simple method to quantify the average difference between the measured and estimated values is the bias [20]:
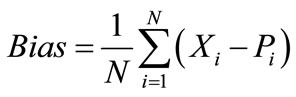
where N is the number of observations, Xi are the measured values and Pi are the estimated values. There should be no bias, i.e. no overor under-prediction of the values on an average. However, a bias close to zero is not sufficient to quantify estimation quality, because this could be a result of a good prediction, or large overand under-prediction may simply cancel each other. A measure which avoids compensation between overand underprediction is the mean absolute error (MAE) [20]:
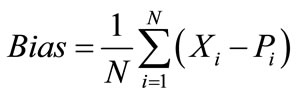
The MAE should be close to zero.
A widely used measure of agreement between measured and estimated values is the root mean squared error (RMSE) [20]:
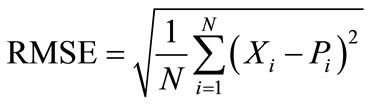
RMSE weighs large differences much higher than small differences between measured and estimated values.
3. Results and Discussion
3.1. Changes of the Estimated Soil Hydraulic Parameters with Compaction
To illustrate the changes of air capacity (AC) and available water capacity (AWC) with increasing compaction, results according to KA5 are shown for the 7 cohesive USDA soil textural classes [21] loamy sand (LSa), sandy loam (SaL), loam (L), silty loam (SiL), clay loam (CL), silty clay loam (SiCL), and sandy clay (SaC) (Figure 1). These textures are commonly used for vegetative landfill covers. Obviously, AWC strongly depends on texture and decreases with compaction by about 3 to

Figure 1. Soil hydraulic parameters for the textural classes LSa, SaL, L, SiL, CL, SiCL, and SaC according to KA5 for the density classes loose, medium and compacted.
7% vol. The same is true for the AC, which also strongly depends on texture and decreases with increasing density by about 2% to 8% vol. Also, the water content at the permanent wilting point (PWP) decreases significantly with increasing compaction. A strong decrease of the AWC with increasing compaction is also reported by several other authors who used data from naturally compacted soils as basis for their measurements and estimations [22-25].
A comparison of the values estimated with KA5 and ROSETTA as average values of the 7 textural classes is shown in Figure 2. The decrease in AWC is as pronounced in the ROSETTA as in the KA5 estimation, but the values are by about 5% vol higher than the estimates of KA5. The ROSETTA air capacity values are significantly lower and decrease less with compaction than the KA5 estimates, and are all below the specified limit for vegetative covers of 8% vol.
The PWP values of ROSETTA are significantly lower than those of KA5 and are almost independent of soil density. Obviously, two widely accepted estimation methods yield very different values for important soil physical parameters.
3.2. Measured Soil Hydraulic Parameters
The results of the measurements of air capacity (AC), available water capacity (AWC), permanent wilting point (PWP) and pore volume (PV) are shown in Table 2 and Figure 3. The PV of all mixtures containing mineral soil are 40% - 50% vol at a compaction level of 85% Proctor density, which corresponds to usual values in natural soils. Only the dredged material has a PV of more than 60% vol at 85% of Proctor density. The PV decrease on an average by –7% to –12% at 90% and 95% of Proctor density compaction levels. This reduction in PV with compaction corresponds to the reduction of the PV as estimated by KA5 and ROSETTA.
The measured AC values strongly decrease on average by –44% to –78% with compaction from 85% to 95%
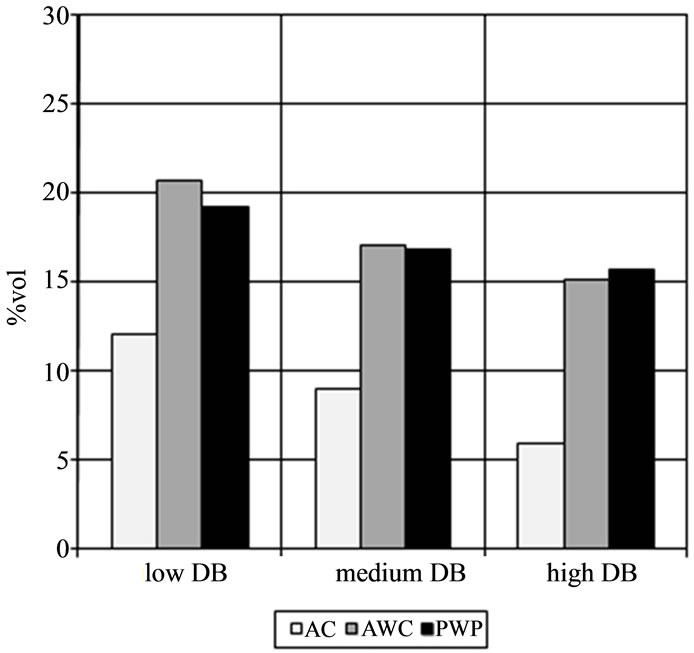

Figure 2. Soil hydraulic parameters (averages for the textural classes LSa, SaL, L, SiL, CL, SiCL, and SaC) according to KA5 (left) and ROSETTA (right).

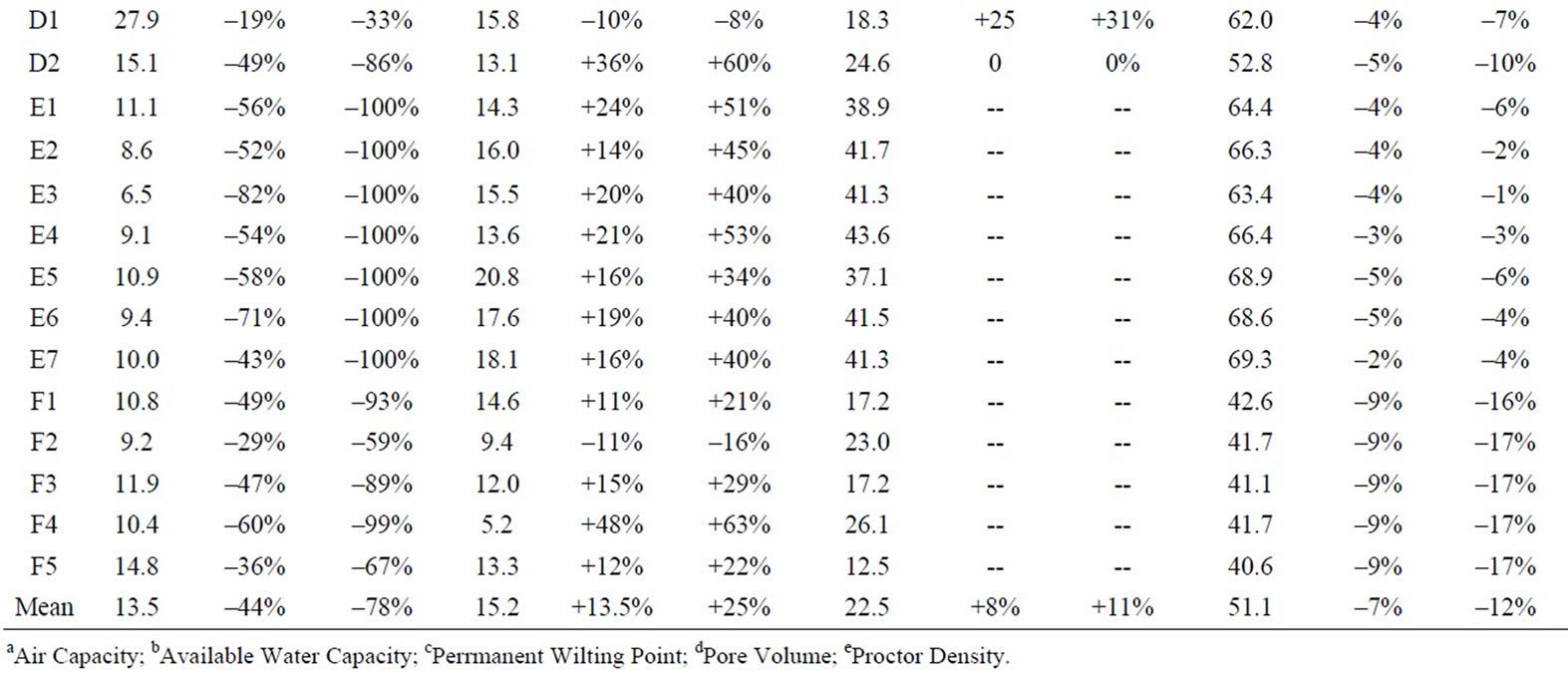
Table 2. Measured AC, AWC, PWP and PV of the materials investigated.

Figure 3. Soil hydraulic parameters of the materials investtigated (averages).
Proctor density. This strong reduction in AC basically corresponds with the KA5 estimates, while ROSETTA indicates a rather small reduction of AC with compacttion.
The measured water content at PWP increases slightly with compaction by an average of 8% to 11%. This rather small increase in water content at PWP corresponds to the estimates with ROSETTA, while the KA5 estimates indicate a reduction of the water content at PWP.
The available water capacity increases on average by 13% to 25% with compaction from 85% to 95% Proctor density. This measured increase in AWC with compacttion is in clear contrast to the estimates with KA5 and ROSETTA.
3.3. Comparison of Measurement and Estimation
Figure 4 shows the comparison of measured and estimated values for the KA5 estimation. The relationship between measurement and estimation for AC and PWP is very poor with a coefficient of determination (r2) below 0.20. The AWC estimation quality is only slightly better with r2 = 0.38. Only the estimation of the PV shows a better relation with the measured values (r2 = 0.78). An even worse relation between measured and estimated values is obtained with ROSETTA (not shown). Here also, only the PV estimates show a good correlation (r2 = 0.83).
The estimation error of the PV is about 6% - 8% vol for all quality measures studied (Table 3), where the KA5 systematically overestimates and ROSETTA systematically underestimates the PV (bias). The AWC is systematically overestimated (on average 5% vol bias with KA5
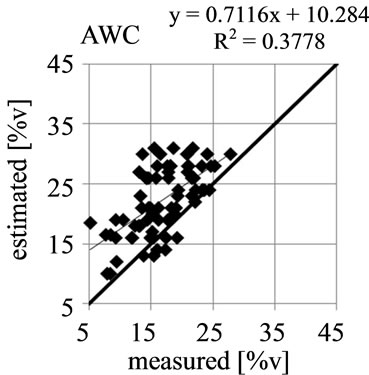
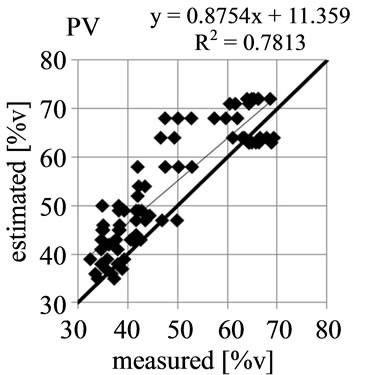
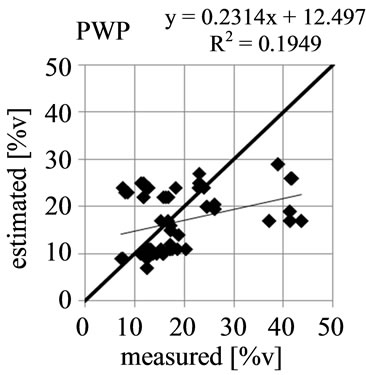

Figure 4. Comparison of measurement and estimation according to KA5.
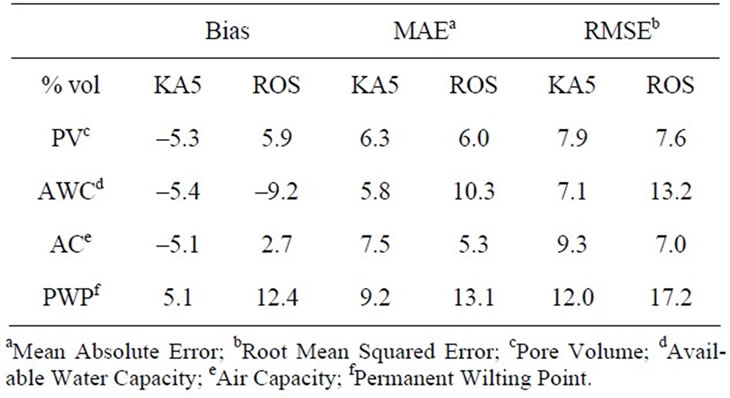
Table 3. Quality of the estimation methods in relation to the measurements.
and 9% vol bias with the ROSETTA estimation). The magnitude of the errors is similar for the estimations of AC and PWP.
A deviation of the available water capacity (AWC) of 5% - 9% vol means that there is a deviation of 50 - 90 mm AWC for 1 m thickness of vegetative cover layer. For a given minimum value of 140 mm according to the German Landfill Ordinance [1], this may account for more than 50% of the total storage capacity. Consequently, planning a landfill vegetative cover based on KA5 or ROSETTA estimations would need an additional safety margin of 50 and 90 mm AWC, respectively.
3.4. Reasons for Differences between Naturally Developed and Artificially Compacted Soils
A major difference between naturally developed soils and artificially compacted soil material is the very long period, in which pore systems develop in soils. Soil pores are usually divided into coarse pores (equivalent to air capacity), medium pores (equivalent to available water capacity) and fine pores (equivalent to permanent wilting point). Under certain assumptions (no compaction of the solid soil material), the change of the PV can be calculated from the change in bulk density. The percentage change of different pore sizes during compaction can be calculated from the pore size distribution (AC, AWC and PWP) at different bulk densities. These calculations show that with increasing compaction of natural soils, the pore size shares (average of the 7 soil textures LSa, SaL, L, SiL, CL, SiCL, and SaC) are reduced according to the KA5 data in a similar magnitude (30% at the expense of coarse pores, 37% at the expense of the medium pores and 33% at the expense of the fine pores).
Results of measurements of the 25 artificially compacted materials, however, show that the reduction of pore size shares with increasing compaction (from 85% to 95% Proctor density) is almost exclusively at the expense of large pores (95%) and only 2% at the expense of medium pores and 3% at the expense of the fine pores. Similar results about artificial compaction have been reported [26].
These differences between the results of artificial compaction (measurement) and natural bulk density (KA5) indicate fundamentally different mechanisms of pore system changes.
A reduction of the pores almost exclusively at the expense of coarse pores must result in an increase in AWC and PWP with increasing density. Figure 5 shows the example of a low density soil with 11.2% vol fine pores (PWP), 12.4% vol medium pores (AWC) and 15.7% vol coarse pores (AC).
The left part of the figure shows the change in pore
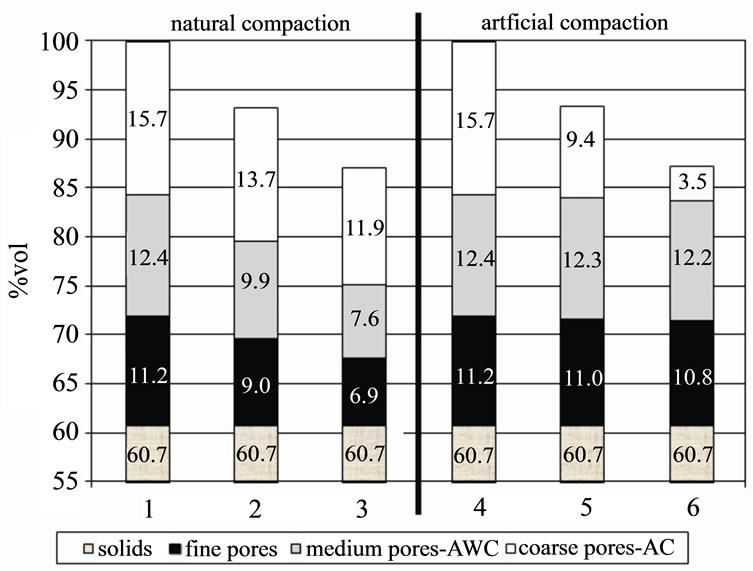
Figure 5. Example for the change of AC, AWC and PWP with compaction of soil material (natural soil compaction— derived from KA5 estimates [left] and artificial compaction—derived from measurements [right]).
size distribution with natural compaction from loose to dense according to KA5 (30% at the expense of coarse pores, 37% at the expense of medium pores and 33% at the expense of the fine pores). The right part of the figure shows the change in the pore size distribution due to artificial compaction according to the measurements (95% at the expense of coarse pores, 2% at the expense of medium pores and 3% at the expense of fine pores). The amount of solid material remains the same as long as the total amount of soil will not change.
The soil hydraulic parameters, however, are based on 100% of the soil and, therefore, these values must be converted accordingly (Figure 6).
With natural soil compaction from loose to dense; according to KA5, with an assumed change of bulk density from 1.35 to 1.50 to 1.65 g·cm–3, the AWC will decrease from 12.4% vol to 10.6% vol to 8.7% vol. Similar is true for the fine pores which reduce from 11.2 % vol to 9.6% vol to 8.0% vol. The AC is reduced to a relatively small extent from 15.7% vol to 14.7% vol to 13.6% vol (Figure 6, left).
If the same soil is compacted artificially, the changes behave completely different. Artificially compacting the soil from 1.35 to 1.50 to 1.65 g·cm–3 results in a slight increase of the AWC from 12.4% vol to 13.2% vol to 14.0 % vol. Also the fine pores will be slightly increased from 11.2% vol to 11.8% vol to 12.4 % vol. The AC, however, is significantly reduced from 15.7% vol to 10.0% vol to only 4.4% vol (Figure 6, right).
4. Conclusions
The results made clear that estimates of the soil hydraulic parameters of artificially compacted soil materials based
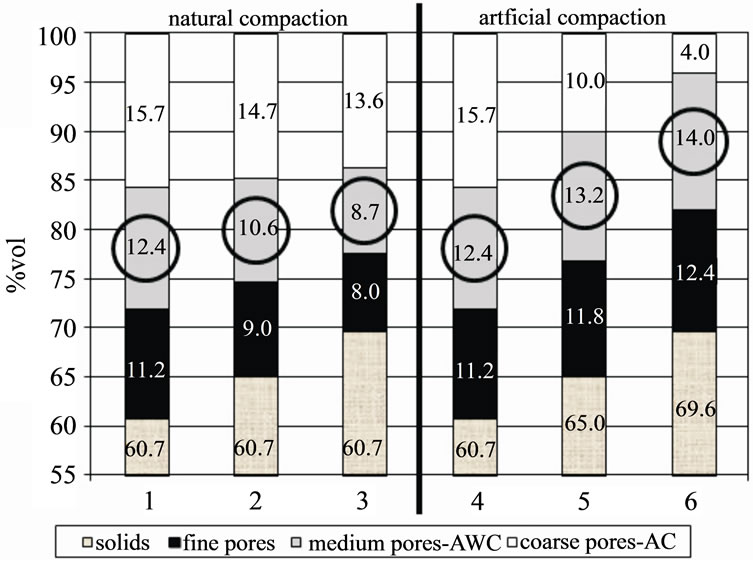
Figure 6. Example for the changes of AC, AWC and PWP due to compaction of soil material (natural soil compaction —derived from KA5 estimates [left] and artificial compaction—derived from measurements [right]), recalculated to 100% soil volume. The circles denote the changes in AWC (decrease: left, increase: right).
on KA5 or the ROSETTA program is associated with considerable uncertainties. The measurements also showed that with increasing compaction, the air capacity considerably decreases, while available water capacity and water content at permanent wilting point slightly increase. The reason is the almost exclusive reduction of coarse pores in artificially compacted soil material.
This is in contradiction to the results of usual estimation methods based on the German standard KA5 and also on ROSETTA. The estimates of KA5 and ROSETTA in terms of changes of the hydraulic parameters with increasing density, which were developed based on naturally developed soils, cannot be transferred readily (or only with large uncertainties) to landfill vegetative cover layers.
There is no need for a frequently demanded loose installation of vegetative cover material to ensure a high available water capacity (AWC). On the contrary, a high AWC, i.e., a large proportion of medium pores in the entire layer, can be realized with increasing compaction. However, a loose installation is essentially to achieve the required high air capacity, which is necessary for optimum plant growth and maximum transpiration.
In the course of time, the properties of artificially installed soil material will approach those of natural soils and, thus, the values based on estimation methods should eventually be correct. The time frame will depend on many factors, such as the biological activity at the landfill site, bulk density, aggregate stability, soil chemical properties, and others. Short-term soil subsidence is frequently observed (e.g., increasing the density by 11% within 6 months [27]). Measurements of long-term changes at different bulk densities due to different installation methods suggest that the soil physical properties will become similar with time (5 years) [27]. Other authors report that the topsoil soil density of a landfill cap has been reduced significantly within 3 years due to biological activity, whereas no changes occurred in the subsoil [28]. Thus, there are many uncertainties, and considerable study and research is still necessary.
Consequently, materials to be used for landfill vegetative covers should be regularly examined analytically with the planned installation bulk densities. Using estimates based on procedures developed for natural soils, adequate safety margins should be provided for air capacity and available water capacity due to uncertainties of the estimations.
5. Acknowledgements
We wish to thank our former students Christian Schroeder and Tobias Nagel for conducting part of the analyses in the framework of their Diploma and Master thesis. We also thank Alicia Jacquemin for proof reading the English manuscript.
REFERENCES
- T. A. Abfall, “Technical Instructions on Waste Management (in German),” Gemeinsames Ministerialblatt, Vol. 42, No. 8, 1991, pp. 139-214.
- EC Directive, “Council Directive 1999/31/EC of 26 April 1999 on the Landfill of Waste,” Official Journal, L 182, 1999, pp. 1-19.
- R. Bonaparte, B. A. Gross, D. E. Daniel, R. M. Koerner, and S. Dwyer, “Draft Technical Guidance for RCRA/ CERCLA Final Covers,” US Environmental Protection Agency, Office of Solid Waste and Emergency Response, Washington DC, 2002.
- DepV, “Ordinance Concerning Dumps and Long-Term Storage Facilities,” 2009. http://www.gesetze-im-internet.de/bundesrecht/depv_2009/gesamt.pdf
- GDA, “E 2-31 Recultivation Layers (in German),” Rekultivierungsschichten, 2006. http://www.gdaonline.de/download/E2-31.pdf
- ITRC, “Technical and Regulatory Guidance for Design, Installation, and Monitoring of Alternative Final Landfill Covers,” Alternative Landfill Technologies, Interstate Technology & Regulatory Council, Washington DC, 2003. http://www.itrcweb.org
- A. G. Boden, “German Soil Classification Handbook (in German),” 5th Edition, Hannover, 2005.
- J. R. Archer and P. D. Smith, “The Relation between Bulk Density, Available Water Capacity, and Air Capacity of Soils,” Journal of Soil Science, Vol. 23, No. 4, 1972, pp. 475-480. doi:10.1111/j.1365-2389.1972.tb01678.x
- S. Melchior, “Recultivation Layers (in German): Rekultivierungsschichten—Geltende Anforderungen, Stand der Technik und Praxiserfahrungen,” In: J. Gebert and E. M. Pfeiffer, Eds., Hamburger Bodenkundliche Arbeiten, Vol. 63, 2010, pp. 25-42.
- M. G. Schaap, F. J. Leij and M. Th. van Genuchten, “Rosetta: A Computer Program for Estimating Soil Hydraulic Parameters with Hierarchical Pedotransfer Functions,” Journal of Hydrology, Vol. 251, No. 3-4, 2001, pp. 163-176. doi:10.1016/S0022-1694(01)00466-8
- United States Department of Agriculture, “Rosetta Model,” 2011. http://www.ars.usda.gov/Services/docs.htm?docid=8953
- GDA, “Modelling the Water Balance of Landfill Capping Systems (in German),” 2003. http://www.gdaonline.de/download/E2-31.pdf
- K. Berger and P. R. Schroeder, “The Hydrologic Evaluation of Landfill Performance (HELP) Model (German Version) HELP 3.80 D. CD,” Institute of Soil Science, Hamburg University, Hamburg, 2004.
- U. Krahmer, V. Hennings, U. Müller and H. P. Schrey, “Determination of Soil Physical Characteristics as a Function of Soil Type, Compaction and Organic Matter Content (in German),” Journal of Plant Nutrition and Soil Science, Vol. 158, No. 4, 1995, pp. 323-331. doi:10.1002/jpln.19951580403
- J. Simunek, M. Sejna, H. Saito, M. Sakai and M. Th. van Genuchten, “The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media, Version 4.0, HYDRUS Software Series 3,” Department of Environmental Sciences, University of California Riverside, Riverside, 2008, p. 315.
- DIN 18127, “Soil, Investigation and Testing—Proctor Test,” Beuth, Berlin/Cologne, 1997.
- A. Klute, “Water Retention: Laboratory Methods,” In: A. Klute, Ed., Methods of Soil Analysis: Part I—Physical and Minerological Methods: Soil Science Society of America Book Series No. 5, Soil Science Society of America, Madison, 1986, pp. 635-660.
- DIN EN 13041, “Soil Improvers and Growing Media— Determination of Physical Properties—Dry Bulk Density, Air Volume, Water Volume, Shrinkage Value and Total Pore Space,” Beuth, Berlin/Cologne, 2012.
- DIN 11274, “Soil Quality—Determination of the Water Retention Characteristics—Laboratory Methods,” Beuth, Berlin/Cologne, 2011.
- D. Wallach, “Evaluating Crop Models,” In: D. Wallach, D. Makowski and J. W. Jones, Eds., Working with Dynamic Crop Models, Elsevier, Amsterdam, 2006:
- Soil Survey Division Staff, “Soil Survey Manual,” Soil Conservation Service, US Department of Agriculture Handbook 18, 1993.
- K. E. Saxton, W. J. Rawls, J. S. Romberger and R. I. Papendick, “Estimating Generalized Soil Water Characteristics from Texture,” Soil Science Society of America Journal, Vol. 50, No. 4, 1986, pp. 1031-1035. doi:10.2136/sssaj1986.03615995005000040039x
- P. R. Schroeder, N. M. Aziz, C. M. Lloyd and P. A. Zappi, “The Hydrologic Evaluation of Landfill Performance (HELP) Model: User’s Guide for Version 3, EPA/600/ R-94/168a,” US Environmental Protection Agency Office of Research and Development, Washington DC, 1994.
- M. Acutis and M. Donatelli, “SOILPAR 2.00: Software to Estimate Soil Hydrological Parameters and Functions,” European Journal of Agronomy, Vol. 18, No. 3-4, 2002, pp. 373-377. doi:10.1016/S1161-0301(02)00128-4
- K. E. Saxton and W. J. Rawls, “Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions,” Soil Science Society of America Journal, Vol. 70, No. 5, 2006, pp. 1569-1578. doi:10.2136/sssaj2005.0117
- D. Dec, J. Dörner, O. Becker-Fazekas and R. Horn, “Effect of Bulk Density on Hydraulic Properties of Homogenized and Structured Soils,” Journal of Soil Science and Plant Nutrition, Vol. 8, No. 1, 2008, pp. 1-13.
- Th. Egloffstein, D. Sturm and H. Brackelmann, “Experience in the Construction of ET Covers and Recultivation Layers (in German),” Expertengespräch zum Thema: Wasserhaushaltsschichten im Deponiebau, LUGV Brandenburg, Potsdam, 2009.
- W. Konold, P. Wattendorf, O. Ehrmann, A. Bieberstein, H. Reith, G. Bönecke and H. Schack-Kirchner, “Water Balance and Soil Development of Rehabilitation Layers (in German),” Institut für Landespflege, Albert-LudwigsUniversität Freiburg, Freiburg im Breisgau, 2004.

