American Journal of Computational Mathematics
Vol.08 No.04(2018), Article ID:89018,17 pages
10.4236/ajcm.2018.84023
Algorithms of the Femtoscope: KeV X-Rays Cure Cancer While MeV X-Rays Only Burn the Cells
Edward Jiménez Calderon
Faculty of Chemistry Engineering, Central University of Ecuador, Quito, Ecuador

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0).
http://creativecommons.org/licenses/by-nc/4.0/



Received: September 13, 2018; Accepted: December 4, 2018; Published: December 7, 2018
ABSTRACT
The study of cancer with the Femtoscope shows us that the information of the cell nucleus is correlated with the atomic nucleus. Femtoscope and entropy algorithms monitor the time and energy of x-rays that transform cancer cells into healthy cells and vice versa. Curing cancer means recovering the information lost from a cancer cell, leading to a minimum entropy. The efficient treatment of cancer presents resonance frequencies in the production and elimination of cancerous cells, asymmetrically. The cure asymmetry of cancer is due to the support of DNA repair genes, allowing the stability of a race or species, and prioritizing life to death. Using the Femtoscope and Spectroscopy, we experimentally validate the resonance frequencies, which effectively cure the cancer and find the optimal times and doses of treatment. In this way, we minimize collateral effects and unnecessary economic costs. In addition, the phosphorus resonance demonstrates why the low energies of x-rays cure cancer and high x-ray energies only burn cancer cells.
Keywords:
Cancer, Femtoscope, Spectroscopy

1. Introduction
If there is already a cure for certain types of cancer, why has not this treatment been generalized to other cancers? The answer lies in the use of low energy. The cancers treated with low energy are cured, because resonances are created in the atom of phosphorus, component of the DNA. The other DNA atoms, such as: H, C, N and O, do not have resonances giving stability to the DNA. Phosphorus-containing molecules, proteins, and cells inherit the atomic resonance properties.
At the biochemical level, the generation of ATP in the nucleus and not in the mitochondria is a fundamental discovery in the cure of the cancer and is in total concordance with other investigations [1] [2] [3] .
Of the different types of cancer, prostate and breast cancer have a cure rate and remission greater than 99%, demonstrating that there is an optimal treatment with low energy radiotherapy. When we speak of low energy, we refer to ionizing radiation (electrons or Rx) with an energy lower than 0.05 MeV. At the atomic and molecular level, the low energies produce resonances in the internal molecular layers, and between nuclear surface and K shell.
Globally, the most common cancers in 2016 were breast cancer, lung and bronchial cancer, prostate cancer, colon and rectum cancer, bladder cancer, skin melanoma, non-Hodgkin’s lymphoma, thyroid cancer, kidney and renal pelvis cancer, leukemia, endometrial cancer and pancreatic cancer. By 2017, in USA, the number of new cancer cases (cancer incidence) is 454.8 per 100,000 men and women per year (based on cases from 2008 to 2012).
Radiotherapy for cancer treatment is a phenomenon of resonance of ionizing radiation with matter in its atomic and molecular form. Cancer is a form of memory loss and/or DNA damage of cells. DNA composed essentially of atoms of H, C, N, O and P inherits the characteristics and resonances of its constituent atoms. It is evident that the hydrogen by its ease of movement to the interior of the alive matter is constituted in an information conveyor through the hydrogen bridges, see Figure 1. This ability of the hydrogen bridges allows us a greater knowledge of the dynamic interactions of the cancer, to biological and chemical level [3] [4] [5] [6] .
Normally, the cells get their energy in the mitochondria, energy centers that are in the cytoplasm and whose work allows healthy cells to grow and carry out the chemical reactions that allow them to be alive. But in an exceptional investigation 1, it was discovered that the tumor cells can also produce energy and ATP in the nucleus, in order to use them to change the way the genes are read and benefit the growth of the tumor. This requires completely changing the placement of the genes, and that consumes a lot of energy. The fundamental chemical element of ATP is phosphorus, which causally presents resonance sections, which represents a key element in the treatment of cancer with x rays [1] [6] [7] .
The protagonist of this little cell drama is an enzyme, NUDIX5. It is capable of producing ATP in the nucleus when the damage has occurred and without it, wounded tumor cells would have less resilience. That’s why NUDIX5 could be a perfect target for new drugs. These results place NUDIX5 as a key player in the synthesis of ATP in the nucleus used to remodel the chromatin. Because NUDIX5 is ove expressed (i.e., present in greater amounts) in various types of cancer (leukemia, lung and breast cancer), this finding may contribute to improved cancer therapies [1] [2] [8] [9] .
The current target group of the Spanish biochemistry says “We are looking at how to inhibit the synthesis of ATP in the nucleus to selectively attack tumor cells”. We have shown that it is possible to achieve the mitochondria to generate ATP, through the phosphorus resonance.
Figure 1. Correlation of information between cell and atomic nucleus. It indicates that the information of the cell nucleus represented by the DNA is correlated with the information of the atomic nucleus measured with the femtoscope. Cancer shows that there are chromosomal and phosphorus metabolism abnormalities. On the other hand, the atomic nucleus presents low energy x-ray resonances with the atomic nucleus, according to the NIST public information and GEANT 4 simulations. These resonances appear in all the atoms of the periodic table with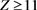 , that is, they do not exist for N,C,H,O but for phosphorus resonance is very high, to K-edge level. The femtoscope determines characteristics of the nuclear surface.
, that is, they do not exist for N,C,H,O but for phosphorus resonance is very high, to K-edge level. The femtoscope determines characteristics of the nuclear surface.
There will be some theoretical and experimental elements of the variables that affect the cure of cancer:
・ Prostate and breast cancer has a cure close to 100% only if we use low energies, while certain cancers such as the pancreas have rates below 30%.
・ The resonances at low energies of atoms and molecules that make up the DNA of the human body: H, O, N, C and P have an impact on the treatment of cancer. After intensively reviewing the NIST information of their English and German equivalents and performing the relevant simulations in Geant 4 10, 11, 12 we conclude that only the phosphor has big x-ray resonances, a threshold energy of 2146 eV according to NIST and 1992 eV according to Geant 4 (Figure 1).
・ The ionization of atoms, molecules, cells with X. rays does not necessarily imply the death of cancer cells rather it is both a side effect of resonance and a direct effect of the interaction of radiation with matter. Resonance of waves already were used efficiently as a fundamental tool in the treatment of kidney stones, to revive patients of heart attacks, NMR to know the functioning of the brain, among others [10] [11] [12] .
・ The cause of cancer cell death is the direct resonance of atoms, molecules and cells with ionizing radiation at specific frequencies. Using an analogy, a heart attack can result in death of the person and therefore cell death. There is an exact resonance frequency through which a patient is revived. Similarly, a cancer cell is out of systemic functioning which means the same or worse than a dead cell. Therefore, we must give a resonance frequency to the cancer cell so that it returns to the systemic functioning [13] [14] [15] .
・ The cross section is directly related to ionization efficiency, therefore, it is related to resonance, according to theorems 1, 2.
・ Hydrogen bridges are information handlers between normal and cancerous cells. The fundamental postulates of new advances in the treatment of cancer could be:
・ Phosphorus manages the recovery of memory from cancer cells (equilibrium). At the biological level phosphorus is fundamental in cellular metabolism [1] [2] [3] [16] [17] [18] .
・ The regeneration of DNA and specifically the phosphorus bonds of a cancer cell occurs only when irradiated with the resonance frequency, corresponding to an energy of 1992 eV [17] [18] [19] [20] .
・ Cancer healing processes involve resonance and therefore minimal entropy in the human body. Theorems 1, 2.
・ The implementation of the Minimal Entropy translates into maximum useful information, administered in the human body and in the atomic, molecular and cellular system.
The main results of this investigation are:
The efficiency of the radiotherapy of ionizing radiation at high energies is suboptimal and produces maximum entropy in the system. For high energies, only secondary radiation that has lost enough energy to reach the limits of low energy produces resonance and cure of cancer.
The efficiency of low energy radiation therapy is maximal for resonance frequencies. Logically, for frequencies outside the resonance value is lower.
The femtoscope allows to study the nuclear dynamics and the biological processes that are related to the electronic clouds directly and indirectly with the atomic nucleus.
This paper will be structured in a coherent way to give a comprehensive vision of the work. Section 2 describes the mathematical model and the physical implications of implementing an X-ray femtoscope for the first time. Section 3 explains the outstanding results of the investigation. Section 4, performs an analysis of each of the results to establish the limits of application. Section 5 is the conclusions. Sections 6 and 7 respectively represent the bibliography and the annexes.
2. Model
There are resonances in the inner and outer layers of the atoms in the periodic table. These resonances can be of three types: atomic resonances with the atom as a whole, resonances in the outer layer, resonances in the inner layers. From the resonance of x-rays in the K-layer, we have found the radius of electrons, protons, neutrons and nucleus, according to theorem 1. These atomic and molecular radius have an error of less than 5%, so we can say that the construction of the Femtoscope is close. Of course we used Geant 4 and NIST public information.
Resonance is the maximum transfer of energy and information due to constructive interference, of incident photon waves, when interacting with matter.
It is demonstrated experimentally and theoretically in Theorems 1 and 2, that resonances exist in atoms, molecules, cellules and DNA.
・ The resonance frequencies of the atoms are maintained in simple and complex molecules.
・ The cell is the union of atoms and molecules therefore inherits the resonance frequencies of the atoms and molecules that constitute it.
The hydrogen bond is a very strong fixed dipole-dipole electrostatic force when many molecules are bound, since it gives great stability, but weaker than the covalent bond or the ionic bond. The strength of the hydrogen bond lies somewhere in between a covalent bond and a Van der Waals force (dispersion force). This type of binding occurs in both inorganic molecules such as water, and in organic molecules such as DNA.
Correlation of DNA with the Atomic Nucleus through the Resonance of Phosphorus
The energy of resonance with photons corresponds to a wavelength that is equal to Bohr radius.
The main equations of the femtoscope allow to determine uniquely an atomic nucleus . From the perspective of the information, it shows that the correlation term between Z protons, Z electrons and N neutrons is the femtoscope constant for all atoms, and that it is similar to the Rydberg constant .
The equations that allow the calculation of the excess of cross section are the following:
(1)
where average radius of proton and neutron. X-ray wavelenght and resonance cross sections.
Equation (1), with a was demonstrated and constructed using the elements of the solution of the Navier Stokes equations, in special the golden
ratio (Figure 2).
(2)
Equation (2), was obtained with a , and indicates that the ratio of the effective sections fully explain each element of the periodic table (Figure 3).
Figure 2. Golden ratio Vs atomic number, one of the most important equation of femtoscope.
Figure 3. Nuclear stability probability as a function of golden ratio.
(3)
Equation (3), obtained for a , complements the system of equations that allow to know the simulation (experimental) values as a function of Z for and .
Theorem 1 Resonance region and golden ratio. The resonance cross section is produced by interference between the atomic nucleus and the incoming X-rays inside the resonance region, where the boundaries are the surface of the atomic nucleus and K-shell.
Proof. In order to have a clear understanding of how this process occurs, we are going to explain each one of the events. Those events are ordered and optimized naturally, in such a way, that a maximum value of the cross section is obtained for every atom of the periodic table.
First, interaction of matter with radiation: The X-rays have a wavelength , and interact constructively with a given material, and as a result of this, a resonance is produced.
Second, constructive interference: There is constructive interference among the X-rays and later on with the atomic nucleus or electron. This occurs only if , where is the atomic radius, the electron radius and is the nucleus radius.
Third, the resonance maximizes the total atomic cross section of the system. This resonance comes mainly from the nucleus since it has the largest interaction probability when compared to the electron.
Fourth, the optimal cross section of the atomic nucleus depends on the nucleon radius . The nucleon radius will be measured indirectly through the atomic total cross section, which is a result of the interference between the nucleus (but always with a specific nucleon), X-rays and the electron. See Appendix: Navier Stokes equations. The cross section of the atomic nucleus is given by:
(4)
The photon cross section at K-shell depends on the wave length and the shape of the atomic nucleus:
(5)
Subtracting the cross sections (4) and (5), we have:
(6)
The resonance is produced by interactions between the X-rays, the K-shell electrons and the atomic nucleus. The cross sections corresponding to the nucleus is weighted by a specific function and should have a simple dependence of an interference term , because for large atomic number . Where a could be understood as an interference magnitude, . This last Equation (6) depends on the nucleon radius or the difference between the nucleus and nucleon radius ( ). According to
Beltramis Theory (ratios, ) and Navier Stokes (resonance term, ), we obtain the following relation
(7)
We note that left hand side of Equations (6) and (7) should have a factor larger than one due to resonance, . The unique factor that holds this requirement
is the golden ratio . Where are constants.
(8)
After performing Geant 4 simulations, it is shown that therm a is related to the dimensionless Rydberg constant, where . Similarly, the equivalence of effective cross section and Navier Stokes equations is established using equation: , Figure 4 and Table 1.
(9)
Using data of Figure 2, we can get the average nucleon radius fm. In the other way, the radius of the neutron can be obtained using Equation (9) as follows.
Using the latest proton radius measurement given fm, for the Max Plank Institute.
Theorem 2 X-ray resonance affects cross section and intensity, in DNA atoms, mainly in phosphorus, stores energy at the atomic level, up to a threshold. After the threshold gives this energy to recover the cellular equilibrium.
Figure 4. The term a, shows the existence of a generalized Rydberg constant, valid for elements of periodic table.
Table 1. Phosphorus resonance. Some chemical elements that are part of the human body.
Proof. We will use the Mean Value Theorem, to write.
(10)
where . The theorem does not specify how to determine , but it turns out that it matches the average value of the function in the interval . That is, Equation (10) can be written as:
(11)
This last equation greatly facilitates the calculation of the area of the resonance peaks. Let E be the total energy of radiation with x-rays, in the interval . is the start of the spectrum and is the end of the right tail. We define resonance efficiency as:
(12)
In DNA molecules, only phosphorus has a resonance of about 800%, so it is directly responsible for curing cancer with low energy. Well, for high energies the efficiencies decrease. And in the case of the other DNA forming atoms such as H, C, O, N the resonances are undetectable below 200% or they do not exist.
Of all x-rays or photons with an initial intensity ( photons) that are launched as projectiles towards the phosphorus atoms only a fraction less than 1% interact with the atoms. Of this 1%, a fraction inferior to 0.5% produces resonance as evidenced by the Monte Carlo simulation, through Geant 4 software
Thus two efficiencies are defined, called ionization efficiency and resonance efficiency . Respectively, it is calculated as:
(13)
(14)
where indicates the intensity of photons entering the interaction zone and in the area of resonance and II the intensity of photons entering the interaction zone, but in the resonance zone and fail to produce resonance.
Theorem 3 The resonance-efficient section in ionization of matter by photons, or the attenuation coefficient in ionization of matter by electrons are responsible for large and/or abnormal variations in the absorbed radiation .
Proof. Let us rewrite the quadratic equation of attenuation, depending on the effective section.
(15)
In the resonance zone, the resonance energy is clearly defined. If, in addition, we define a constant value for the thickness of irradiated material r, then experimentally and theoretically the only variable that can change is the cross section , allowing us to write the value of the intensities before and after the resonance:
(16)
(17)
We can find the value of the elasticity of the intensity with respect to the effective section, .
(18)
The previous value of the elasticity is calculated with finite differences. If we calculate the elasticity analytically, using the function (16).
(19)
Replacing the average value of Equations (18) in (19).
(20)
Similarly, we can obtain the elasticity for ionization with low energy electrons:
(21)
The average values of the terms and vary slowly, so that large
variations in effective sections or mass absorption coefficients, sometimes large variations in absorbed energy. According to Equations (20) and (21) very large variations of photon radiation or electron absorption coefficients cause large variations in the absorbed dose which is proportional to the variation in radiation intensity . See Table 1.
3. Results
The success of Medical Physics and Oncology in the treatment of prostate and breast cancer, with an efficiency greater than 99%, shows us that the resonance produced by the equality of the wavelength of Rx and the Bohr radius at low energies is a sufficient condition for an efficient cancer radiation treatment, while ionization is the necessary condition. Biochemistry and Biophysics converge to demonstrate that the fundamental goal for cancer cure is to inhibit the synthesis of ATP in the cell nucleus and selectively attack tumor cells. We propose that it is possible to achieve a regeneration of ATP at the mitochondria through a resonance of the phosphorus bonds. A resonance region is created in a natural way at the K-shell between the nucleus and the electrons at S-level. The condition for the photons to enter into the resonance region is given by . The efficiency of radiotherapy is a function of resonance, ionization and the effective cross-section of phosphorus within the ATP, in terms of correcting cellular metabolism in mitochondria. In addition, resonance is one of the causes of ionization and allows us to measure the efficiency of radiotherapy, which was corroborated with Monte Carlo simulation performed with Geant 4. The cancers treated with low energy are cured, because resonances are created in the atom of phosphorus which is a component of the DNA. The other DNA atoms such as: H, C, N and O do not have resonances giving this way stability to the DNA. The phosphorus atom has larger X-ray resonances among the DNA components [17] [18] [19] [20] , having an energy threshold of 2146 eV according to NIST and 1992 eV according to Geant 4. We then conclude that radiation cancer treatment using X-rays is efficient only when they produce resonances. We have also coined the term femtoscope which measures dimensions and interactions in the range of femtometers.
The main results of this research are related to the resonance wavelengths for the efficient treatment of cancer. Moreover, only low energy x-rays are efficient in the treatment of cancer. The effectiveness of the treatment of cancer is related to phosphorus by its huge cross section, constituting the phosphorus in the fundamental element of DNA from the perspective of radiation. The other chemical elements that make up the DNA have small resonances in comparison with the phosphorus, enabling the stability of the DNA against mutations due to unwanted radiation.
An investigation of the journal Nature 1, 2, showed that from the biological perspective phosphorus is the main element in the evolution and in the treatment of cancer. In this sense, our research demonstrates the strategic complementarity of radiation treatment of cancer, as we show in the following figures.
Figures 1-3. Show us that:
The efficiency in the creation of resonances in each of the elements that make up DNA (Figure 1), clearly indicates resonance peaks, using two rigorous information and simulation systems worldwide, NIST and GEANT 4.
It is clearly observed that the resonance efficiency values greater than 50%, is given at low energies to values below 10,000 eV. While for high energy the efficiency drops to 0.001%. The relevant result of this table is the reduction of the time of cancer treatment by radiotherapy.
4. Discussion
Photons of Resonance Vs Treatment Doses.
The dose of absorbed radiation that cures the cancer is only the one that produces resonance and as a side effect appears ionization. The efficient dose is much lower than the absorbed dose, we have shown that for the resonance of atoms and molecules forming the DNA the efficiency dose is less than 1% of the absorbed dose. In this way the dose required depends on each type of cancer and treatment. But in general the optimal irradiation time is proportional to the resonance dose.
The absorbed dose is consumed essentially in ionizing atoms, while resonance photons can produce changes in the DNA of cancer cells. Theorem 4.
Efficiency in the treatment of cancer.
We will perform Monte Carlo simulation through the Geant 4 Software, to generate ionization and resonance efficiency indices. To later correlate them with the efficiency in the treatment of cancer.
Current experiences demonstrate that low energy efficiently cures cancer. The classic solution has been to give greater amount of energy and therefore greater amount of ionization, in a random manner and with maximum entropy, doesn’t produce efficient results. But in this case we have an opposite effect Low energies and resonance that are negatively correlated. For what must exist, a strategic variable that is positively correlated with low energies. The strategic variable corresponds to the resonance efficiency index, by two reasons:
・ Resonance maximizes information and transmits it to mitochondria specifically to ATP, efficiently and with minimal entropy. This result is consistent with Science Journal research 1.
・ High energy is inefficient in the treatment of cancer because it is based exclusively on ionization, which is a totally random phenomenon of high entropy and minimal transmitted information. Current successful drugs are based on maximum information transfer, achieving specific goals. Radiation therapy cannot be the opposite, when prioritizing high energies.
Use of Geant 4 to low energies.
The great computing power of Geant 4, is tested in low energy and medical problem solving as the efficiency of resonance and ionization in the treatment of cancer. In a definitive way Geant 4, shows us through 109 simulations, for each range of energies that resonance is positively correlated with low energy and gives us the threshold values of resonance in the fundamental chemical element of cancer treatment: phosphorus. In addition, it confirms the NIST information about the absence of resonance big peaks for the other elements of the DNA, these are: H, O, C and N. See Figure 5.
This research is a verification of the intrinsic protection of DNA, against ionizing radiation. Well, if all elements of DNA would resonate the risk of damage would multiply exponentially. Life is guaranteed by the absence of these resonances in all atoms of DNA. Now our work has been simplified by focusing on the phosphorus resonance from the perspective of medical physics. Medical physics is in total agreement with the phosphorus biochemistry.
Figure 5. Phosphorus resonance. The other elements of DNA such us N, O, C, H not have resonances.
For example, for Leukemia it is possible to measure the amount of Philadelphia chromosomes before and after the resonance radiation. While for healthy cells we measure the minimum time capable of creating Philadelphia chromosomes.
5. Conclusions
First implementation of the femtoscope through mathematical modeling and experimentation in order to study cancer and nuclear dynamics.
Cancer is a problem of information lost in the cell nucleus. Therefore, DNA has translocation problems as in the Philadelphia chromosome. The recovery of lost information can only occur with the minimization of the entropy (Shanons entropy).
The progression of cancer depends on the ability of tumor cells to produce ATP in their nucleus. Therefore, blocking the production of ATP in the cell nucleus is equivalent to recovering ATP production in the mitochondria, through atomic-nuclear resonance in K-Shell. From two fields of knowledge: Physics-Medical and Biochemistry, we have the same proposal to efficiently face the treatment of cancer.
In general, we propose to re-train the mitochondria to produce ATP. In a certain way, it would be a vaccine that recovers the lost memory, with the use of phosphorus resonance. Treatment of cancer with x-ray or electron radiation is efficient only when they produce resonances. At high energies, there is a great deal of energy loss and only a low resonance index. So, treatment with high energy is not optimal.
The efficiency in cancer treatment at high energies is minimal.
The fundamental equations of the low energy x-ray femtoscope are 1, 2, 3, A1, A2 and A3.
Acknowledgements
To Teachers and Students of the Chemical Engineering, Faculty of the Central University of Ecuador. To the participants of the congress 3rd Edition of International Conference on Advanced Spectroscopy, Crystallography and Applications in Modern Chemistry during 4-5 June 2018, London, UK. To the participants of the congress CIPANP 2018―“Thirteenth Conference on the Intersections of Particle and Nuclear Physics” from 29 May 2018 to 3 June 2018, Berkeley, USA.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Calderon, E.J. (2018) Algorithms of the Femtoscope: KeV X-Rays Cure Cancer While MeV X-Rays Only Burn the Cells. American Journal of Computational Mathematics, 8, 279-295. https://doi.org/10.4236/ajcm.2018.84023
References
- 1. Aditya, K.A., Praveen, K. and Ransinchung, R.N. (2013) Use of Various Agricultural and Industrial Waste Materials in Road Construction. Procedia, Social and Behavioral Sciences, 104, 264-273.
- 2. Hossain, K.M.A., Lachemi, M. and Easa, S. (2007) Stabilized Soils for Construction Applications Incorporating Natural Resources of Papua New Guinea. Resources, Conservation and Recycling, 51, 711-731. http://dx.doi.org/10.1016/j.resconrec.2006.12.003
- 3. Hossain, K.M.A. and Mol, L. (2011) Some Engineering Properties of Stabilized Clayey Soils Incorporating Natural Pozzolans and Industrial Wastes. Construction and Building Materials, 25, 3495-3501. http://dx.doi.org/10.1016/j.conbuildmat.2011.03.042
- 4. Gungat, L., Putri, E.E. and Makinda, J. (2013) Effects of Oil Palm Shell and Curing Time to the Load-Bearing Capacity of Clay Subgrade. Procedia Engineering, 54, 690-697. http://dx.doi.org/10.1016/j.proeng.2013.03.063
- 5. Zaimoglu, A.S. (2010) Freezing-Thawing Behavior of Fine-Grained Soils Reinforced with Polypropylene Fibers. Cold Regions Science and Technology, 60, 63-65. http://dx.doi.org/10.1016/j.coldregions.2009.07.001
- 6. Mahipal, S.C., Satyendra, M. and Bijayananda, M. (2008) Performance Evaluation of Silty sand Subgrade Reinforced with Fly Ash and Fiber. Geotextiles and Geomembranes, 26, 429-435. http://dx.doi.org/10.1016/j.geotexmem.2008.02.001
- 7. Ghazavi, M. and Roustaie, M. (2010) The Influence of Freeze-Thaw Cycles on the Unconfined Compressive Strength of Fiber-Reinforced Clay. Cold Regions Science and Technology, 61, 125-131. http://dx.doi.org/10.1016/j.coldregions.2009.12.005
- 8. Miqueleiz, L., Ramírez, F., Seco, A., Nidzam, R.M., Kinuthia, J.M., Tair, A.A. and Garcia, R. (2012) The Use of Stabilized Spanish Clay Soil for Sustainable Construction Materials. Engineering Geology, 133-134, 9-15. http://dx.doi.org/10.1016/j.enggeo.2012.02.010
- 9. Fauzi, A., Rahmanb, W. and Jauhari, Z. (2013) Utilization Waste Material as Stabilizer on Kuantan Clayey Soil Stabilization. Procedia Engineering, 53, 42-47. http://dx.doi.org/10.1016/j.proeng.2013.02.007
- 10. Qi, J., Ma, W. and Song, C. (2008) Influence of Freeze-Thaw on Engineering Properties of a Silty Soil. Cold Regions Science and Technology, 53, 397-404. http://dx.doi.org/10.1016/j.coldregions.2007.05.010
- 11. Zaimoglu, A.S. (2010) Freezing-Thawing Behavior of Fine-Grained Soils Reinforced with Polypropylene Fibers. Journal of Cold Regions Science and Technology, 60, 63-65. http://dx.doi.org/10.1016/j.coldregions.2009.07.001
- 12. Jafari, M. and Esna-Ashari, M. (2012) Effect of Waste Tire Cord Reinforcement on Unconfined Compressive Strength of Lime Stabilized Clayey Soil under Freeze-Thaw Condition. Cold Regions Science and Technology, 82, 21-29. http://dx.doi.org/10.1016/j.coldregions.2012.05.012
- 13. Kuity, A. and Roy, T.K. (2013) Utilization of Geogrid Mesh for Improving the Soft Subgrade Layer with Waste Material Mix Compositions. Procedia, Social and Behavioral Sciences, 104, 255-263.
- 14. Hejazi, S.M., Sheikhzadeh, M., Abtahi, S.M. and Zadhoush, A. (2008) A Simple Review of Soil Reinforcement by Using Natural and Synthetic Fibers. Construction and Building Materials, 30, 100-116. http://dx.doi.org/10.1016/j.conbuildmat.2011.11.045
- 15. Zhu, Z.D. and Liu, S.Y. (2008) Utilization of a New Soil Stabilizer for Silt Subgrade. Engineering Geology, 97, 192-198. http://dx.doi.org/10.1016/j.enggeo.2008.01.003
- 16. Singh, S.P., Tripathy, D.P. and Ranjith, P.G. (2008) Performance Evaluation of Cement Stabilized Fly Ash-GBFS Mixes as a Highway Construction Material. Waste Management, 28, 1331-1337. http://dx.doi.org/10.1016/j.wasman.2007.09.017
- 17. Zhang, Z. and Tao, M. (2008) Durability of Cement Stabilized Low Plasticity Soils. Journal of Geotechnical and Geo-environmental Engineering, 134, 203-213. http://dx.doi.org/10.1061/(ASCE)1090-0241(2008)134:2(203)
- 18. Parker, J.W. (2008) Evaluation of Laboratory Durability Tests For Stabilized Subgrade Soils. M.Sc. Thesis, Department of Civil and Environmental Engineering, Brigham Young University, Provo.
- 19. Jones, D., Rahim, A., Saadeh, S. and Harvey, J.T. (2010) Guidelines for Stabilization of Subgrade Soils in California. Partnered Pavement Research Center (PPRC) Contract Strategic Plan Element.
- 20. ASTM D 560-03. Test Methods for Freezing and Thawing Compacted Soil Cement Mixtures. American Society for Testing and Materials, West Conshohocken.
- 21. Egyptian Code of Practice for Urban and Rural Roads, ECP-2008.
- 22. Chamberlain, E.J., Iskveer, I. and Hunsiker, S.E. (1990) Effect of Freeze-Thaw on the Permeability and Macrostructure of Soils. Proceedings International Symposium on Frozen Soil Impacts on Agricultural, Range, and Forest Lands, Spokane, 21-22 March 1990, 145-155.
- 23. Hassini, S. (1992) Some Aspects of Landfill Design. Mediterranean Conference on Environmental Geotechnology, Cesme, 25-27 May 1992, 137-144.
- 24. Prasad, D.S., Kumar, M.A., Raju, G.V. and Kondayya, V. (2011) A Study on Flexible Pavement Performance with Reinforcement Flyash Subbase. International Journal of Earth Sciences and Engineering, 4, 94-99.
- 25. Davidovic, N., Zoran, B. and Prolovic, V. (2012) Waste Glass as Additive to Clay Material in Subgrade and Embankment of Road Pavement. Architecture and Civil Engineering, 10, 215-222.
- 26. Rao, G.V. and Pothal, G.K. (2009) Geosynthetic Reinforced Pond Ash Subgrade for Rural Roads. Geosynthetics in Civil Environmental Engineering. Proceedings of the 4th Asian Regional Conference on Geosynthetics, Shanghai, 349-354.
- 27. Saltan, M., Kavlak, Y. and Ertem, F. (2011) Utilization of Pumice Waste for Clays Subgrade of Pavements. Journal of Material in Civil Engineering, 23, 1616-1623. http://dx.doi.org/10.1061/(ASCE)MT.1943-5533.0000336
- 28. Wright, R.H.G., et al. (2016) ADP-Ribose-Derived Nuclear ATP Synthesis by NUDIX5 Is Required for Chromatin Remodeling. Science, 352, 1221-1225. https://doi.org/10.1126/science.aad9335
- 29. Distinct Structural Transitions of Chromatin Topological Domains Correlate with Coordinated Hormone-Induced Gene Regulation Genes Dev.
- 30. Zhang, J. (2012) Are Poly(ADP-ribosyl)ation by PARP-1 and Deacetylation by Sir2 Linked? The Journal of Biological Chemistry, 287, 12405-12416.
- 31. Ning, C. and Gu, H.M. (2018) Weak Galerkin Finite Element Method for the Unsteady Navier-Stokes Equation. American Journal of Computational Mathematics, 8, 108-119.
- 32. Hasnain, S., Saqib, M. and Mashat, D.S. (2017) Numerical Study of One Dimensional Fishers KPP Equation with Finite Difference Schemes. American Journal of Computational Mathematics, 7, 70-83.
- 33. Ducomet, B. (2000) Global Existence for a Simplified Model of Nuclear Fluid in One Dimension. Journal of Mathematical Fluid Mechanics, 2, 1-15. https://doi.org/10.1007/s000210050017
- 34. O’Connor, J.J. (1974) Rydberg’s Discovery of the Spectral Laws. Proceedings of the Rydberg Centennial Conference on Atomic Spectroscopy, Acta Universitatis lundensis, 50, 15-21.
- 35. Henke, B.L., Gullikson, E.M. and Davis, J.C. (1993) X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50 - 30,000 eV, Z = 1 - 92. Atomic Data and Nuclear Data Tables, 54, No. 2.
- 36. Auerbach, Y. (1975) Nuclear Viscosity and Widths of Giant Resonances. Annals of Physics, 95, No. 1.
- 37. Oganessian and Utyonkov (2015) Superheavy Nuclei from 48Ca-Induced Reactions. Nuclear Physics A, 944, 62-98. https://doi.org/10.1016/j.nuclphysa.2015.07.003
- 38. (2004) Introductory to Nuclear Physics. WILEY-VCH Verlag Gmbl I & Co. KGaA, Weinheim.
- 39. Straub, H.C., et al. (1996) Absolute Partial Cross Sections for Electron-Impact Ionization of H2, N2, and O2 from Threshold to 1000 eV. Physical Review A, 54, 2146-2153.
- 40. S.M. X-Ray Mass Attenuation Coefficients, Radiation Division, PML, NIST, 2017. https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients
- 41. Database.(2017) https://dbshino.nifs.ac.jp/index-j.html
- 42. Leray. (1934) Sur le mouvement d’un liquide visquex emplissent l’espace. Acta Mathematica, 63, 193-248.
- 43. Geant 4. (2016) Geant 4 User’s Guide for Application Developers Version: Geant 4 10.3. Publication date 9 December 2016.
- 44. Ingall, E.D., et al. (2011) Phosphorus K-Edge XANES Spectroscopy of Mineral Standards. Journal of Synchrotron Radiation, 18, 189-197.
- 45. Czapla-Masztafiak, J., et al. (2016) Investigating DNA Radiation Damage Using X-Ray Absorption Spectroscopy. Biophysical Journal, 110, 1304-1311. https://doi.org/10.1016/j.bpj.2016.01.031
- 46. Nashed, A.L. (2003) Clinical Applications of BCR-ABL Molecular Testing in Acute Leukemia. The Journal of Molecular Diagnostics, 5, 63-72. https://doi.org/10.1016/S1525-1578(10)60454-0
- 47. (2017) An Unsuspected Finding of t(9;22): A Rare Case of Philadelphia Chromosome-Positive B-Lymphoblastic Lymphoma. Case Reports in Hematology.
Appendix 1: Navier Stokes Equations and Golden Ratio ( )
The speed needs to be defined as , where is the logistic probability function , defined in This P is the general solution of the Navier Stokes 3D equations, which satisfies the conditions (A1) and (A2), allowing to analyze the dynamics of an incompressible fluid.
(A1)
where, an known velocity vector, constant density of fluid and pressure .
With speed and pressure dependent on r and t. We will write the condition of incompressibility as follows.
(A2)
Theorem 4. The velocity of the fluid given by: , where is the logistic probability function , defined in is the general solution of the Navier Stokes equations, which satisfies conditions (A1) and (A2).
Proof. Firstly, we will make the equivalence and replace it in Equation (A1). Taking into account that is irrotational, , we have.
We can write,
It is equivalent to,
where is the difference between the actual pressure p and certain reference pressure . Now, replacing , Navier Stokes equation becomes.
(A3)
The external force is zero, so that there is only a constant force F due to the variation of the pressure on a cross section . Where 3c3 is the total cross section of all events that occurs in nuclear the surface including: scattering, absorption, or transformation to another species.
(A4)
putting (A3) in (A4) we have
(A5)
In order to verify Equation (A2), , we need to obtain , .
(A6)
Replacing the respective values for the terms: and of Equation (A6). The Laplacian of P can be written as follows.
(A7)
Using gradient , modulus and in (A7).
(A8)
Replacing Equations (A6) and (A7) in (A8) we obtain the main result of the Navier Stokes equations, the solution represents a fixed point of an implicit
function where .
(A9)







