American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:58917,3 pages
10.4236/ajcm.2015.53020
Levenberg-Marquardt Method for Mathematical Programs with Linearly Complementarity Constraints
Cong Zhang1*, Limin Sun1, Zhibin Zhu2, Minglei Fang3
1Department of Mathematics and Computer Science, Huarui College, Xinyang Normal University, Xinyang, China
2School of Mathematics & Computational Science, Guilin University of Electronic Technology, Guilin, China
3College of Science, Anhui University of Science and Technology, Huainan, China
Email: *zhcopt@126.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 June 2015; accepted 17 August 2015; published 20 August 2015
ABSTRACT
In this paper, a new method for solving a mathematical programming problem with linearly complementarity constraints (MPLCC) is introduced, which applies the Levenberg-Marquardt (L-M) method to solve the B-stationary condition of original problem. Under the MPEC-LICQ, the proposed method is proved convergent to B-stationary point of MPLCC.
Keywords:
Mathematical Programs with Linear Complementarity Constraints, MPEC-LICQ, B-Stationarity, Levenberg-Marquardt Method

1. Introduction
The mathematical program with equibrium constraints (MPEC) has extensive application in area engineering design and economic model [1] . It has been an active research topic in recent years. In this paper, we consider the mathematical programming problem with linearly complementarity constraints (MPLCC), which is a special case of the MPEC:
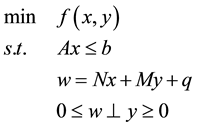 (1.1)
(1.1)
where  is twice continuously differential real-valued function;
is twice continuously differential real-valued function; ,
, 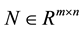 and
and 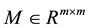 are given matrices;
are given matrices; 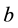 and
and 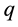 are given p, m dimensional vectors, respectively.
are given p, m dimensional vectors, respectively.
Complementarity constraints in MPEC are known to be difficult to treat. Research work on the MPEC includes the monograph of Luo et al. [1] in which Bouligand stationary condition is introduced that provides a comprehensive study on MPEC. Based on different formulations, there are many algorithms such as Fukushima [2] , Zhu [3] , Zhang [4] [5] , Jiang [6] , Tao [7] , and Jian [8] . Notice that B-stationary condition is a stronger stationary point. Differing from the approaches mentioned above, we directly introduce L-M technique, without any reformulation or relax form, to solve the B-stationary condition of MPLCC (1.1).
The plan of the paper is as follows: in Section 2, some preliminaries and model we used are presented; in Sec- tion 3, the algorithm is proposed.
2. Preliminaries
For reader’s convenience, we use following notation throughout this paper:
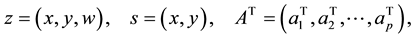
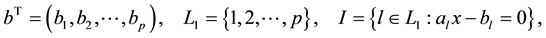
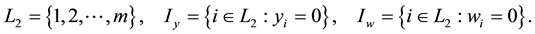
Let F denote the feasible set of problem (1.1).
Now we give two definitions as follow.
Definition 2.1. Let 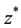 be a feasible point of MPLCC (1.1), we say that MPEC linear independence constraint qualification is satisfied at
be a feasible point of MPLCC (1.1), we say that MPEC linear independence constraint qualification is satisfied at 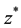 if the gradient vectors
if the gradient vectors
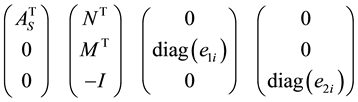
is linearly independent, where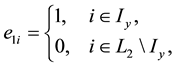 ,
, 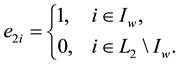
Definition 2.2. Under the MPEC-LICQ, a feasible point z is a B-stationary of problem (1.1) if there exist multiplier vectors ,
, 






As we know, most of the works on MPLCC want to get the B-stationary point of problem (1.1), so we also put emphasis on trying to construct a method to obtain the B-stationary of MPLCC (1.1). Now we rewrite the conditions (2.1)-(2.5) in term of lagrange multipliers as follow:

subject to:

and

where

Remark: In (2.7) we replace 

3. The Description of Algorithm
Without any reformulation and relaxing techniques, we now use L-M method to solve the nonlinear systems (2.6). Firstly, let J be the Jacobian of 



where

Lemma 3.1. The coefficient matrix of (L − M) is positive definite, and furthermore, (L − M) method has unique solution.
According to the constraint conditions, we now find a step length for current iterated point. First, we consider computing the step length of



where 



As to calculating the step length for the constraint 




so
Secondly, we will consider the step length of




In this paper, we take 
Lemma 3.2. Let 
Proof. In view of Equation (3.1) and the positive definition of matrix
Now we present the algorithm.
Algorithm A:
Step 0: Given a feasible initial point

Step 1: If

Step 2: Compute the step length
Step 3:

Theorem 3.1. Suppose that 


many k, let the MPEC-LICQ hold on

Proof. From the construction of the algorithm, we have 



Funding
This work was supported in part by the National Natural Science Foundation (No. 11361018), the Natural Science Foundation of Guangxi Province (No. 2014GXNSFFA118001), Key Program for Science and Technology in Henan Education Institution (No. 15B110008) and Huarui College Science Foundation (No. 2014qn35) of China.
Cite this paper
CongZhang,LiminSun,ZhibinZhu,MingleiFang, (2015) Levenberg-Marquardt Method for Mathematical Programs with Linearly Complementarity Constraints. American Journal of Computational Mathematics,05,239-242. doi: 10.4236/ajcm.2015.53020
References
- 1. Luo, Z.Q., Pang, J.S. and Ralph, D. (1996) Mathmetical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511983658 - 2. Fukushima, M., Luo, Z.Q. and Pang, J.S. (1998) A Globally Convergent Sequential Quadratic Programming Algorithm for Mathematical Programs with Linear Complementarity Constraints. Computational Optimization and Application, 10, 5-34.
http://dx.doi.org/10.1023/A:1018359900133 - 3. Zhu, Z.B. and Zhang, K.C. (2006) A Superlinearly Convergent SQP Algorithm for Mathematical Programs with Linear Complementarity Constraints. Application and Computation, 172, 222-244.
http://dx.doi.org/10.1016/j.amc.2005.01.141 - 4. Zhang, C., Zhu, Z.B., Chen, F.H. and Fang, M.L. (2010) Sequential System of Linear Equations Algorithm for Optimization with Complementary Constraints. Mathematics Modelling and Applied Computing, 1, 71-80.
- 5. Zhang, C., Zhu, Z.B. and Fang, M.L. (2010) A Superlinearly Convergent SSLE Algorithm for Optimization Problems with Linear Complementarity Constraints. Journal of Mathematical Science: Advance and Application, 6, 149-164.
- 6. Jiang, H. (2000) Smooth SQP Methods for Mathematical Programs with Nonlinear Complementarity Constraints. SIAM Journal of Optimization, 10, 779-808.
http://dx.doi.org/10.1137/S1052623497332329 - 7. Tao, Y. (2006) Newton-Type Method for a Class of Mathematical Programs with Complementarity Constrains. Computers and Mathematics with Applications, 52, 1627-1638.
http://dx.doi.org/10.1016/j.camwa.2006.09.002 - 8. Jian, J.B. (2005) A Superlinearly Convergent Implicit Smooth SQP Algorithm for Mathematical Programs with Nonlinear Complemetarity Constraints. Computational Optimization and Applications, 31, 335-361.
http://dx.doi.org/10.1007/s10589-005-3230-5
NOTES
*Corresponding author.








