Received 9 September 2014; revised 10 October 2014; accepted 20 October 2014

ABSTRACT

Trummer’s problem is the problem of multiplication of an n × n Cauchy matrix C by a vector. It serves as the basis for the solution of several problems in scientific computing and engineering [1] . The straightforward algorithm solves Trummer’s problem in O(n²) flops. The fast algorithm solves the problem in O(nlog²n) flops [2] but has poor numerical stability. The algorithm we discuss here in this paper is the celebrated multipoint algorithm [3] which has been studied by Pan et al. The algorithm approximates the solution in O(nlogn) flops in terms of n but its cost estimate depends on the bound of the approximation error and also depends on the correlation between the entries of the pair of n-dimensional vectors defining the input matrix C.

Keywords:

Cauchy Matrix, Mulipoint Algorithm, Structure Matrices, Displacement Operators

1. Introduction

Computations with dense structured matrices have many applications in sciences, communications and engineering. The structure enables dramatic acceleration of the computations and major decrease in memory space but sometimes leads to numerical stability problems. The best well-known classes of structured matrices are Toeplitz, Hankel, Cauchy and Vandermonde matrices.

The computations with such matrices are widely applied in the areas of algebraic coding, control, signal processing, solution of partial differential equations and algebraic computing. For example, Toeplitz matrices arise in some major signal processing computations and the problem of multiplying Vandermonde matrix by a vector is equivalent to polynomial evaluation, whereas solving a Vandermonde system is equivalent to polynomial interpolation. Moreover, Cauchy matrices appear in the study of integral equations and conformal mappings. The complexity of computations with n × n dense structured matrices dramatically decreases in comparison with the general n × n matrices, that is, from the order of n² words of storage space and 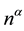arithmetic operations (ops) with 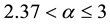in the best algorithms, to 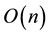words of storage space and 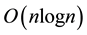ops (see Table 1 below for more details).

2. Some Basic Definitions

Throughout this paper, we use the following notations; 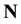denotes the set of nonnegative integers, 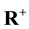is the set of positive real numbers, Z⁺ denotes the set of positive integers, and R denotes the set of real numbers.

Definition 2.1. A matrix 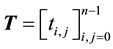is a Toeplitz matrix if 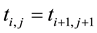for every pair of its entries 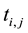and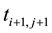. A matrix 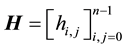is a Hankel matrix if 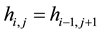for every pair of its entries and.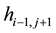

Definition 2.2. For a given vector, the matrix of the form is called a Vandermonde matrix.

Definition 2.3. Given two vectors s and t such that for all i and j, the n × n matrix is a Cauchy (generalized Hilbert) where

For more details regarding the four classes of structured matrices, see Table 2 below.

Remark 2.1. It is quite easy to verify that TJ and JT are Hankel matrices if T is a Toeplitz matrix, and HJ and JH are Toeplitz matrices if H is a Hankel matrix where J is the following reflection matrix,

.

3. The Displacement Operators of Dense Structured Matrices

The concept of displacement operators and displacement rank which was introduced by T. Kailath, S. Y. Kung, and M. Morf in 1979 and studied by Pan, Bini, and other authors is one of the powerful tools for studying and dealing with matrices that have structure. The displacement rank approach, when it was initially introduced, was intended for more restricted use [4] , namely, to measure how “close” to Toeplitz a given matrix is. Then the idea turned out to be even more powerful, thus it was developed, generalized and extended to other structured matrices. In this section, we consider the most general and modern interpretation of the displacement of a matrix.

The main idea is, for a given structured matrix A, we need to find an operator L that transforms the matrix into a low rank matrix such that one can easily recover A from its image and operate with low rank matrices instead. Such operators that shift and scale the entries of the structured matrices turn out to be appropriate tools for introducing and defining the matrices of Toeplitz-like, Hankel-like, Vandermonde-like, and Cauchy-like types [5] .

Definition 3.1. For any fixed field such as the complex field and a fixed pair of operator matrices, we define the linear displacement operators of Sylvester type,

and Stein type,

.

The image of the operator L is called the displacement of the matrix A. The operators of Sylvester and Stein types can be transformed easily into one another if at least one of the two associated operator matrices is non-singular. The following theorem explains this fact.

Theorem 3.1. if the operator matrix M is non-singular, and if the op-

erator matrix N is non-singular.

Proof:

The operator matrices that we will be using are the matrices Z_f, , and where Z_f, is the unit f-circulant matrix,

f is any scalar, is the transpose of Z_f, and is a diagonal matrix with diagonal entries,

We may use the operator matrices Z₁ and Z₀ in the case of Toeplitz matrices, Z₁ and in the case of Hankel matrices, Z₀ and in the case of Vandermonde matrices, and and in the case of Cauchy matrices. However, there are other choices of operator matrices that can transform these matrices to low rank.

4. The Correlation of Structured Matrices to Polynomials

The product

(1)

represents the vector of the values of the polynomial on a node set

If is the vector of the n^th roots of unity,

,

then the matrix and multipoint evaluation turns into discrete Fourier transform which takes only

ops and allows numerically stable implementation according to [6] . If we express in Equation (1) via Cauchy matrices we will get

(2)

Here, for denotes n × n diagonal matrix with diagonal entries.

Note that the numerical stability is very important in approximation algorithm for multipoint polynomial evaluation. It relies on expressing in terms of Cauchy matrices as in Equation (2). Clearly in Equation (2), the product by a vector has been reduced to ones with Cauchy, which brings us to Trummer’s problem, that is, the problem of multiplication of Cauchy matrix by a vector. Its solution by multipoint algorithm ([6] , pp. 261-262) leads to multipoint polynomial evaluation based on Equation (2) which is fast in terms of ops and numerically stable as it was proved by Pan.

We may vary the vector x by linearly mapping it to the vector where we can take and and b are any scalars.

5. New Transformation of Cauchy Matrices

As we mentioned earlier, Trummer’s problem is the problem of multiplication of an n × n Cauchy matrix C by a vector which is the basis for the solution of many important problems of scientific computing and engineering. The straightforward algorithm solves Trummer’s problem in flops. The fast algorithm solves the problem in flops but has poor numerical stability.

The algorithm we presenting in this paper approximates the solution in flops in terms of n. However, its cost estimate depends on the bound of the approximation error and on the correlation between the entries of the pair of n-dimensional vectors defining the input matrix C. This algorithm is numerically stable as we will see throughout this section and the next section.

The main goal in this paper is to enrich the power of the multipoint algorithm by introducing and proving some new expressions for Cauchy matrix via other Cauchy matrices [7] , which we may vary by changing one of their basis vectors. Under a certain choice of such a vector, the solution of Trummer’s problem will be simplified; thus, the power of the multipoint algorithm can be developed as we will see in the next section.

Therefore, we will achieve our goal by using a simple transformation of the useful basic formula of [8] , and the resulting expressions for C will give us further algorithmic opportunities.

Definition 5.1. For a pair of n-dimensional vectors, let,

, , for, for, denote the asso-

ciated n × n Cauchy, Vandermonde, and triangular Hankel matrices, respectively. For a vector with

for a Cauchy degenerate matrix has the diagonal entries zeros and the entry

for. Furthermore, denote the polynomial and its derivative

. Lastly,

and

denote a pair of n × n diagonal matrices, defined by the vectors a and b.

Theorem 5.1. (See [8] ) Let,. Then

(3)

(4)

The main idea of the transformation of the basic vectors defining the problem is taken from [9] , where this idea was used for multipoint polynomial evaluation and interpolation.

Definition 5.2. Trummer’s problem is the problem of computing the vector for three given vectors

, and where for all pairs i, j. Trummer’s degenerate problem is

the problem of computing the vector for two given vectors and where for.

Definition 5.3., where, is a primitive root of 1, , for.

Lemma 5.1. for.

Approximate solution of Trummer’s degenerate problem can be reduced to Trummer’s problem due to the next simple result.

Lemma 5.2. as, where is the vector filled with the values one and is a scalar parameter.

Proof: due to Lem-

ma 5.1.

6. Transformations of Cauchy Matrices and Trummer’s Problem

Theorem 6.1. For a triple of n-dimensional vector, , where, , for we have the following matrix equations:

(5)

(6)

(7)

(8)

Proof Theorem 6.1:

1) Proof of Equation (5):

From Equation (3), we obtain This is done by taking the inverse of Equation (3) and replacing the vectors c, d by b, d. Then substitute the equation

and Equation (3) for into the following matrix identity

.

This gives:

Clearly, the last one is just Equation (5).

2) Proof of Equation (6):

From Equation (4); replace the vector d by b, then we will get:

.

Then solve for;

.

Now substitute the last expression into Equation (5) and obtain the following:

which is obviously Equation (6).

3) Proof of Equation (7):

From Equation (4); first solve for to get:

,

replace to get:

.

Now, replace the vector d by b and obtain

. (9)

Since we have also.

Start with Equation (4) which is and replace the vector to

obtain, then use the equation to get:

Now replace in the last equation by (that is, use the identity)

.

This implies that which is Equation (7).

4) Proof of Equation (8):

From Equation (4): solve for and obtain

Expand Equation (4), and change and to get the equation: and take the transpose of both side of the last equation to get:

. (10)

Substitute Equation (10) and the matrix equation into Equation (7):

(this is from Equation (10))

which is Equation (8).

7. Approximate Stable Solutions of Trummer’s Problems

The algorithm we are studying and presenting in this section depends on the multipoint algorithm which approximates the solution of Trummer’s problem in ops in terms of n, and works efficiently for a large classes of input vectors but sometimes has problems with some of the input vectors, especially if the ratio of the input vectors is close to 1.

Recall, the power series expansion: this series converges whenever and has a sum.

The basis for the algorithm is the following expressions:

(11)

where and. Clearly this series converges whenever. Now for large M the expression approximates On the other hand can be also written as

(12)

Once again for large M the expression approximate.

The product of Cauchy matrix by a vector is. This is just Trummer’s problem. If we simplify this expression, we get the following approximations:

where.

For any n × n Cauchy matrix, the approximation requires ops for all i and it is numerically stable.

If either of the ratios or is small, then the approximate error will be small for large M. However, there will be a problem whenever one of the ratios is close to 1, in this case, the error will be large.

8. Discussions and Conclusions

Recall the following two formulas from Section 5:

, (13)

. (14)

Equations (13) and (14) are Vandermonde-free and Hankel-free, but they enable us to transform the basis vectors s and t for into the two pairs of basis vectors s, q and q, t for any choice of the vector, , ,. Then Trummer’s problem is reduced to the evaluation of the diagonal matrices, and/or for, , , , and/or and also reduced to recursive multiplication of the above matrices and and by vectors.

To compute the matrices, and for given in general, we first compute the coefficients of the polynomial and then

And,. We compute the coefficients by simply pairwise multiply the linear factors first and then, recursively, the computed products. The computation is numerically stable and uses ops. Multipoint polynomial evaluation can be computed in arithmetic operations (ops), but it is not numerically stable; therefore the fast and numerically stable approximation techniques of [10] can be used instead. If we choose any vector, we will simplify the evaluation of the matrices

For example, if

(15)

is the scaled n^th roots of unity for a scalar a and, where Then

and the matrices and can be immediately evaluated in flops. In addition, any polynomial of degree n can be evaluated at the scaled n^th roots of 1 in ops by means of Fast Fourier Transform (FFT). Trummer’s problem is the multiplication of by a vector or by a vector. Its solution can be simplified under appropriate choice of the vector q. One way to do it is to restrict q to the above choice in Equation (15). Even with this particular choice, yet the scalar a allows faster convergence of the power series of the Multipole Algorithm presented in Section 7. This can be extended to the Equations (5) and (7). On the other hand, one can linearly map the vector q into, where, and and b are any scalars. In addition, the computations of the diagonal matrices will be simplified if our choice of the vector q is the scaled nth root of unity.

Remark 8.1. Trummer’s problem frequently arises for Cauchy degenerate matrices that are defined as fol-

lows:, , for all pairs of distinct i and j.

We have

where, , is a scalar parameter. Hence,

because for.

Acknowledgements

We thank the Editor and referees for their valuable comments.

References