American Journal of Computational Mathematics
Vol.04 No.02(2014), Article ID:43953,7 pages
10.4236/ajcm.2014.42005
Numerical solutions of second Order initial value Problems of Bratu-Type via optimal homotopy Asymptotic Method
Mohamed Abdalla Darwish, Bothayna S. Kashkari
Department of Mathematics, Sciences Faculty for Girls, King Abdulaziz University, Jeddah, KSA
Email: dr.madarwish@gmail.com, bkashkari@kau.edu.sa
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 December 2013; revised 26 January 2014; accepted 1 February 2014
ABSTRACT
We present the optimal homotopy asymptotic method (OHAM) to find the numerical solution of the second order initial value problems of Bratu-type. We solve some examples to illustrate the validity and efficiency of the method.
Keywords:
Initial-value Problem; Bratu; Numerical solution; optimal Homotopy Asymptotic method

1. Introduction
Herişanu et al. [1] proposed a new technique called the optimal homotopy asymptotic method (OHAM). The main advantage of OHAM is that it is reliable and straight forward. Also, the OHAM does not need to worry about 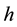 curves as homotopy asymptotic method (HAM). Moreover, the OHAM provides controls the convergence of the series solution and its solution agrees with the exact one at large domains, for more infor- mation see [2] - [6] .
curves as homotopy asymptotic method (HAM). Moreover, the OHAM provides controls the convergence of the series solution and its solution agrees with the exact one at large domains, for more infor- mation see [2] - [6] .
On the other hand, the standard Bratu problem is used in a large variety of applications, such as the fuel ignition model of the theory of thermal combustion, the thermal reaction process model, the Chandrasekhar model of the expansion of the universe, radiative heat transfer, nanotechnology and theory of chemical reaction, for more information see [7] [8] and references therein.
The Bratu initial value problems have been studied extensively because of its mathematical and physical properties. In [9] , Batiha studied a numerical solution of Bratu-type equations by the variational iteration method; Feng et al. [10] considered Bratu’s problems by means of modified homotopy perturbation method; Rashidinia et al. [11] applied Sinc-Galerkin method for numerical solution of the Bratu’s problems; Syam and Hamdan [12] used variational iteration method for numerical solutions of the Bratu-type problems; Wazwaz [13] applied Adomian decomposition method to study the Bratu-type equations.
The main goal of this paper is to extend OHAM method to solve the initial value problems of second order differential equations of Bratu-type. The OHAM is very useful to get an approximate solution of the initial value problems of second order differential equations of Bratu-type. Our numerical examples of OHAM are compared with exact ones.
2. Analysis of OHAM
In this section we start by describing the basic formulation of OHAM, see for example [1] [3] - [5] . Consider the boundary value problem
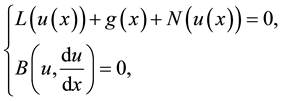 (2.1)
(2.1)
where 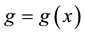 is a given function and
is a given function and 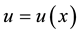 is an unknown function. Here,
is an unknown function. Here, 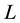 ,
, 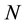 and
and 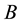 represent a linear operator, a nonlinear operator and a boundary operator, respectively.
represent a linear operator, a nonlinear operator and a boundary operator, respectively.
By means of OHAM one constructs a homotopy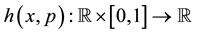 , which satisfies the following fa- mily of equations
, which satisfies the following fa- mily of equations
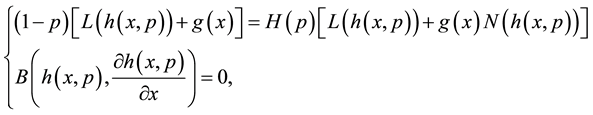 (2.2)
(2.2)
where 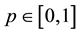 is an embedding parameter,
is an embedding parameter,  is a non-zero auxiliary function for
is a non-zero auxiliary function for 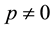 and
and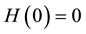 . It is easy to see that when
. It is easy to see that when  and
and  we have
we have 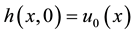 and
and


Therefore, the unknown function 





In the sequel, we choose auxiliary function 

where

In order to obtain an approximate solution, we expand



Now, substituting by Equation (2.5) into Equation (2.2) and equating the coefficients of like powers of 




and

respectively. Also, the general governing problems of 

where 




where

Observe that the convergence of the series (2.5) depends upon the auxiliary constants



The m-th order approximations are given by

By substituting Equation (2.11) into Equation (2.1), we get the following expression for residual

If




where 


After knowing those constants, the approximate solution of order 
3. Numerical Examples
Example 1 Consider the second order initial value problem of Bratu type

The initial value problem (3.1) has 
Next, we apply the OHAM method to the initial value problem (3.1). We have



we have
Problem of zero order:

which has a solution
Problem of first order:

Problem (3.3) has a solution

The problem of second order

The solution of Problem (3.5) is given by

Third order problem is

and its solution is given in the form

Finally, fourth order problem is

which has a solution in the form

Now, by using equations (3.4), (3.6), (3.8) and (3.10), the fourth order approximate solution, using OHAM with

Next, we follow the procedure presented in Section 2, we obtain the following values of




Table 1. Absolute error between the exact solution and approximation solution.
Example 2 In this example, let us consider the Bratu initial value problem

which has

Now, we apply the OHAM method presented in previous section. In this example, we have



Problem of zero order:

Problem (3.13) has a solution
Problem of first order:

The solution of Problem (3.14) is given by

The problem of second order

and its solution is given by

Third order problem is

The solution of Problem (3.18) is given by

In the end, the fourth order problem is given by

which has a solution in the form
Table 2. Absolute error between the exact solution and approximation solution.

Now, by using equations (3.4), (3.6), (3.8) and (3.10), the fourth order approximate solution, using OHAM with

Next, we follow the procedure presented in Section 0.2, we obtain the following values of




4. Final Remarks
Throughout this paper, an technique for obtaining a numerical solution for second order initial value problems of Bratu-type, is optimal homotopy asymptotic method (OHAM). The main advantage of the used technique is achieving high accurate approximate solutions. In the numerical tables and graphics, our numerical results are compared with the exact ones.
Cite this paper
Mohamed AbdallaDarwish,Bothayna S.Kashkari, (2014) Numerical solutions of second order initial value problems of Bratu-type via optimal homotopy asymptotic method. American Journal of Computational Mathematics,04,47-54. doi: 10.4236/ajcm.2014.42005
References
- 1. Herisanu, N., Marinca, V., Dordea T. and Madescu, G. (2008) A New Analytical Approach to Nonlinear Vibration of an Electrical Machine. Proceedings of the Romanian Academy, Series A, 9, 229-236.
- 2. Ali, J., Islam, S., Islam, S. and Zamand, G. (2010) The Solution of Multipoint Boundary Value Problems by the Optimal Homotopy Asymptotic Method. Computers & Mathematics with Applications, 59, 2000-2006.
http://dx.doi.org/10.1016/j.camwa.2009.12.002 - 3. Ene, R.D., Marinca, V., Negrea, R. and Caruntu, B. (2012) Optimal Homotopy Asymptotic Method for Solving a Nonlinear Problem in Elasticity. Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), 14th International Symposium, Timisoara, 26-29 September 2012, 98-102.
- 4. Esmaeilpour, M. and Ganji, D.D. (2010) Solution of the Jeffery-Hamel Flow Problem by Optimal Homotopy Asymptotic Method. Computers & Mathematics with Applications, 59, 3405-3411.
http://dx.doi.org/10.1016/j.camwa.2010.03.024 - 5. Hashmi, M.S., Khan, N. and Iqbal, S. (2012) Optimal Homotopy Asymptotic Method for Solving Nonlinear Fredholm Integral Equations of Second Kind. Applied Mathematics and Computation, 218, 10982-10989.
http://dx.doi.org/10.1016/j.amc.2012.04.059 - 6. Marinca, V., Herisanu, N., Bota, C. and Marinca, B. (2009) An Optimal Homotopy Asymptotic Method Applied to the Steady Flow of a Fourth-Grade Fluid Past a Porous Plate. Applied Mathematics Letters, 22, 245-251.
http://dx.doi.org/10.1016/j.aml.2008.03.019 - 7. Abukhaled, M., Khuri, S. and Sayfy, A. (2012) Spline-Based Numerical Treatments of Bratu-Type Equations. Palestine Journal of Mathematics, 1, 63-70.
- 8. Wazwaz, A. (2012) A Reliable Study for Extensions of the Bratu Problem with Boundary Conditions. Mathematical Methods in the Applied Sciences, 35, 845-856. http://dx.doi.org/10.1002/mma.1616
- 9. Batiha, B. (2010) Numerical Solution of Bratu-Type Equations by the Variational Iteration Method. Hacettepe Journal of Mathematics and Statistics, 39, 23-29.
- 10. Feng, X., He, Y. and Meng, J. (2008) Application of Homotopy Perturbation Method to the Bratu-Type Equations. Topological Methods in Nonlinear Analysis, 31, 243-252.
- 11. Rashidinia, J., Maleknejad, K. and Taheri, N. (2013) Sinc-Galerkin Method for Numerical Solution of the Bratu’s Problems. Numerical Algorithms, 62, 1-11. http://dx.doi.org/10.1007/s11075-012-9560-3
- 12. Syam, M.I. and Hamdan, A. (2006) An Efficient Method for Solving Bratu Equations. Applied Mathematics and Computation, 176, 704-713. http://dx.doi.org/10.1016/j.amc.2005.10.021
- 13. Wazwaz, A. (2005) Adomian Decomposition Method for a Reliable Treatment of the Bratu-Type Equations. Applied Mathematics and Computation, 166, 652-663. http://dx.doi.org/10.1016/j.amc.2004.06.059




