American Journal of Computational Mathematics
Vol.04 No.03(2014), Article ID:44899,7 pages
10.4236/ajcm.2014.43011
A Five-Step P-Stable Method for the Numerical Integration of Third Order Ordinary Differential Equations
D. O. Awoyemi1, S. J. Kayode2, L. O. Adoghe3
1Department of Mathematics, Landmark University, Umuaru, Nigeria
2Department of Mathematical Sciences, Federal University of Technology, Akure, Nigeria
3Department of Mathematics, Ambrose Alli University, Ekpoma, Nigeria
Email: adoghelarry@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 December 2013; revised 26 February 2014; accepted 6 March 2014
ABSTRACT
In this paper we derived a continuous linear multistep method (LMM) with step number k = 5 through collocation and interpolation techniques using power series as basis function for approximate solution. An order nine p-stable scheme is developed which was used to solve the third order initial value problems in ordinary differential equation without first reducing to a system of first order equations. Taylor’s series algorithm of the same order was developed to implement our method. The result obtained compared favourably with existing methods.
Keywords:
continuous Collocation, Multistep Methods, Interpolation, Third Order, Power Series, approximate Solution

1. Introduction
Linear multistep methods (LMM) for solving first order initial value problems (ivps) is of the form
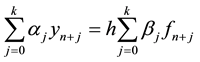 (1)
(1)
where  and
and 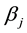 are uniquely determined and
are uniquely determined and 
Conventionally, they are used to solve higher order ordinary differential equations by first reducing them to a system of first order. This approach has been extensively discussed in [1] -[5] . However the method of reducing to a system first order has some serious drawback which includes wastage of human effort and computer time [6] .
The LMM in (1) generates discrete schemes which are used to solve first order odes. Various forms of this LMM have been developed [1] -[4] . Other researchers have introduced the continuous LMM using the continuous collocation and interpolation technique. This has led to the development of continuous LMM of form
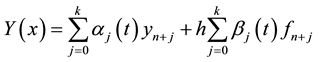 (2)
(2)
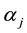 and
and  are expressed as continuous functions of t and are at least differentiable once.
are expressed as continuous functions of t and are at least differentiable once.
The introduction of continuous collocation methods as against the discrete schemes enhances better global error estimation and ability to approximate solution at all interior points [6] - [10] . In this study, we shall develop continuous multistep collocation method for the solution of third order ordinary differential equations using power series as the basis function.
Power Series Collocation
In [6] [8] [9] , some continuous LMM of Type (2) were developed using power series of form
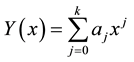 : (3)
: (3)
In [10] Chebyshev polynomial function of the form
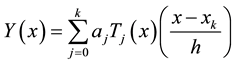 (4)
(4)
where  are some Chebyshev function used to develop continuous LMM.
are some Chebyshev function used to develop continuous LMM.
The use power series as basis function for derivation of continuous LMM are based on the property of analytic function that given the Taylor’s polynomial of the form
 (5)
(5)
The approximate function 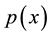 reduces to
reduces to 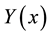 as
as 
In this study we proposed the polynomial function of the form in [7] :
 (6)
(6)
which is of Type (3) to develop a continuous LMM for the solution of initial value problem of the form:
 (7)
(7)
This paper is organized as follows: Section 1 consists of introduction and background of study; Section 2, we derive a continuous approximation to 

2. Derivation of the Method
Consider the third order differential Equation (7), we proposed an approximate solution of the form:

where
The derivative of (8) up to the third order yield

And 


Collocating (10) at 

of equations given below


The above equations are solved to obtain the values of 

The continuous polynomial obtained when the values of 

Evaluating (14) at 

3. Analysis and Implementation of the Method
3.1. Basic properties of the Method
The method (15) is a specific member of the conventional LMM which can expressed as

Following [1] [2] , we define the local truncation error associated with (16) by the difference operator

where 


where the 

In the sense of [1] , we say that the method (20) is of order p and error constant 
Using the concept above, the method (19) has order 
3.2. Zero-stability of the 5-Step Method
Considering the first characteristics polynomial of the method of Equation (15) given as
Putting 





3.3. Region of absolute Stability of the 5-Step scheme
Applying the boundary locus method, we have that
In the spirit of Lambert (1973),
By letting 
At 




3.4. Implementattion
Single step method can be used to solve higher order ordinary differential equations directly without the need to first reducing it to an equivalent system of first order.
Consider the initial value problem in (7). For our method of order


Then the known values of 

where


3.5. Numerical Experiments
Our methods of order 
The following initial value problems were used as our test problems:
3.6. Problem 1
Exact solution:
3.7. Problem 2
Exact solution:
3.8. Problem 3

Exact solution:
Table 1. showing the result of test problem 1.
Table 2. Showing the result of test problem 2.
Table 3. showing the result of test problem 3.
4. Discussion of Result
We have developed and implemented our methods using Taylor series of the same order as the schemes that we developed. Some special and general third order initial value problems (ivps) were used to test the efficiency of our methods. Our method was found to be zero stable, consistent and convergent. The better accuracy of our method can be shown from the numerical examples.
Cite this paper
D. O.Awoyemi,S. J.Kayode,L. O.Adoghe, (2014) A Five-Step P-Stable Method for the Numerical Integration of Third Order Ordinary Differential Equations. American Journal of Computational Mathematics,04,119-126. doi: 10.4236/ajcm.2014.43011
References
- 1. Lambert, J.D. (1973) Computional Methods in ODEs. John Wiley & Sons, New York.
- 2. Fatunla, S.O. (1988) Numerical Methods for Initial Value Problems in Ordinary Differential Equations. Academic Press Inc., Harcourt Brace, Jovanovich Publishers, New York.
- 3. Butcher, S.C. (2003) Numerical Methods for Ordinary Differential Equations. John Wiley & Sons, New York.
http://dx.doi.org/10.1002/0470868279 - 4. Henrici, P. (1962) Discrete Variable Method in Ordinary Differential Equations. John Wiley & Sons, New York.
http://dx.doi.org/10.1002/zamm.19660460521 - 5. Bruguano, L. and Trigiante. D. (1998) Solving Differential Problems by Multistep Initial and Boundary Value Methods. Gordon and Breach Science Publishers, Amsterdam, 280-299.
- 6. Awoyemi, D.O. (2003) A P-Stable Linear Multistep Method for Solving General Third Order Ordinary Differential Equations. International Journal of computer Mathematics, 80, 987-993.
http://dx.doi.org/10.1080/0020716031000079572 - 7. Okunuga, S.A. and Ehijie, J. (2009) New Derivation of Continuous Multistep Methods Using Power Series as Basis Function. Journal of Modern Mathematics and Statistics, 3, 43-55.
- 8. Adesanya, A.O. (2011) Block Methods for Direct Solutions of General Higher Order Initial Value Problems of Ordinary Differential Equations. Ph.D. Thesis, the Department of Mathematical Sciences, Federal University of Technology, Akure.
- 9. Adeniyi, R.B. and Alabi, M.O. (2006) Derivation of Continuous Multistep Methods Using Chebyshev Polynomial Basis Functions. Abacus, 33, 351-361.
- 10. Onumanyi, P., Oladele, J.O., Adeniyi, R.B. and Awoyemi, D.O. (1993) Derivation of Finite Difference Method by Collocation. Abacus, 23, 2-83.
- 11. Olabode, B.T (2007) Some Linear Multistep Methods for Special and General Third Order Initial Value Problems in Ordinary Differential Equations. Ph.D. Thesis, the Department of Mathematical Sciences, The Federal University of Technology, Akure.




















