American Journal of Computational Mathematics
Vol.04 No.01(2014), Article ID:42295,4 pages
10.4236/ajcm.2014.41001
Logarithm of a Function, a Well-posed Inverse Problem
Silvia Reyes Mora, Víctor A. Cruz Barriguete, Denisse Guzmán Aguilar
Instituto de Física y Matemáticas, Universidad Tecnológica de la Mixteca, Huajuapan de León, Oax, México
Email: sreyes@mixteco.utm.mx
Copyright © 2014 Silvia Reyes Mora et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Silvia Reyes Mora et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Received November 13, 2013; revised December 13, 2013; accepted December 20, 2013
It poses the inverse problem that consists in finding the logarithm of a function. It shows that when the function is holomorphic in a simply connected domain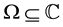 , the solution at the inverse problem exists and is unique if a branch of the logarithm is fixed. In addition, it’s demonstrated that when the function is continuous in a domain
, the solution at the inverse problem exists and is unique if a branch of the logarithm is fixed. In addition, it’s demonstrated that when the function is continuous in a domain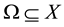 , where
, where
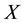 is Hausdorff space and connected by paths. The solution of the problem exists and is unique if a branch of the logarithm is fixed and is stable; for what in this case, the inverse problem turns out to be well-posed.
is Hausdorff space and connected by paths. The solution of the problem exists and is unique if a branch of the logarithm is fixed and is stable; for what in this case, the inverse problem turns out to be well-posed.
Keywords:
Logarithm function; Inverse problem; Stability
1. Introduction
The inverse problems generally are ill-posed in Hadamard sense. These words lead us to think that there exist inverse problems that are well-posed and which are possible to be solved analytically [1].
The ill-posed problems do not fulfill with at least one of the conditions of existence, uniqueness or stability of the solution. Nevertheless, if a problem does not have a solution, or the solution is not unique, it is possible to correct in spite of doing considerations on the domain and the co-domain of the operator who represents the problem.
Unlike a complex number different from zero for which, it is always possible to find his logarithm. The functions need certain conditions on his domain to guarantee the existence of his logarithm [2]. It appears that one of these conditions is that the domain is simply connected. To assure the uniqueness of the logarithm of a function, it is es- sential to take a branch of the logarithm.
In this paper, there appears the problem of finding the logarithm of a given function, by different techniques. It is demonstrated that the above-mentioned problem is an inverse stable problem in Hadamard sense [3]. Therefore, the problem of existence and uniqueness is solved. In addition, it is demonstrated that it is stable, which transforms it into a well-posed inverse problem. It is realized the analysis of the solution of the inverse problem for when the do- main of the inverse operator, it corresponds to the functions that are not annulled and in addition they are holomor- phic in some region [4]. It is demonstrated that when
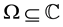 is a simply connected domain, the solution of the in- verse problem exists and is unique. In a similar way, when the space
is a simply connected domain, the solution of the in- verse problem exists and is unique. In a similar way, when the space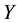 , it corresponds to the space of the conti- nuous functions that are not annulled on a region
, it corresponds to the space of the conti- nuous functions that are not annulled on a region
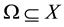 simply connected and where Z is a Hausdorff’s space and connected for paths, the solution of the inverse problem exists, is unique and is stable [5].
simply connected and where Z is a Hausdorff’s space and connected for paths, the solution of the inverse problem exists, is unique and is stable [5].
2. Exposition of the problem
It’s known that not all the real numbers have logarithm, nevertheless, all complex numbers have it.
The natural question that arises is under what conditions a function has logarithm. To answer to the previous question, an operator
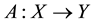 is considered, if
is considered, if , and
, and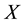 ,
,
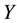 are spaces of functions, it is possible to pose the direct problem: From a function on
are spaces of functions, it is possible to pose the direct problem: From a function on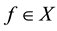 , find to a function
, find to a function
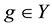 such that
such that . The corresponding inverse problem is given a function
. The corresponding inverse problem is given a function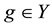 , to find to a function
, to find to a function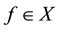 , such that
, such that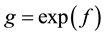 . It’s known that the inverse of the operator
. It’s known that the inverse of the operator
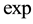 is the operator
is the operator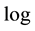 , so the inverse problem can be seen as the search of the logarithm of a given function. Notice that as is considered the operator
, so the inverse problem can be seen as the search of the logarithm of a given function. Notice that as is considered the operator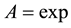 , it has felt to take as space
, it has felt to take as space
 to the functions that are not annulled and in addition be continuous or holomorphic on some region; nevertheless they must determine the conditions that the region must fulfill to demonstrate the existence, uni- queness and stability of the inverse problem.
to the functions that are not annulled and in addition be continuous or holomorphic on some region; nevertheless they must determine the conditions that the region must fulfill to demonstrate the existence, uni- queness and stability of the inverse problem.
3. Holomorphic logarithm
In this section, it is considered that
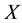 corresponds to the holomorphic functions and
corresponds to the holomorphic functions and
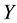 to the holomorphic functions that are not annulled on any region. There’s demonstrated that when Ω is a simply connected domain, the solution of the inverse problem exists and is unique when a branch of the logarithm is fixed. The problem consists of knowing if given a function holomorphic f can be a function
to the holomorphic functions that are not annulled on any region. There’s demonstrated that when Ω is a simply connected domain, the solution of the inverse problem exists and is unique when a branch of the logarithm is fixed. The problem consists of knowing if given a function holomorphic f can be a function , such that
, such that .
.
Definition: Given a domain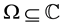 , and be
, and be
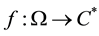 and
and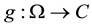 . It is said that
. It is said that
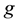 is a loga- rithm of
is a loga- rithm of
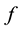 if
if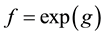 . If the functions
. If the functions
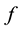 and
and
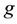 are holomorphic in Ω, it is said that
are holomorphic in Ω, it is said that
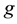 is a ho- lomorphic logarithm of
is a ho- lomorphic logarithm of
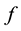 [6].
[6].
Theorem 1: Let
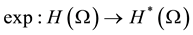 be, where Ω is a simply connected set of the plane, then the so- lution of the inverse problem exists and is unique.
be, where Ω is a simply connected set of the plane, then the so- lution of the inverse problem exists and is unique.
Proof: If it thinks that Ω it is a simply connected domain, by theorem of the Riemann application, the simply connected domains of the flat sound of two types: the conformal equivalent to the plane
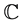 and the conformal equivalent to the unitary disc D. For such a motive, the existence of the solution of the inverse problem, are obtained as a consequence of the propositions 1, 2 and 3. As for the uniqueness, it is essential to take a branch of the logarithm.
and the conformal equivalent to the unitary disc D. For such a motive, the existence of the solution of the inverse problem, are obtained as a consequence of the propositions 1, 2 and 3. As for the uniqueness, it is essential to take a branch of the logarithm.
Proposition 1: Every function
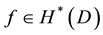 admits a holomorphic logarithm.
admits a holomorphic logarithm.
Proof: It is known that
 for every
for every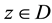 . Let
. Let
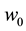 be a point such that
be a point such that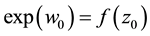 . It’s de- fined by:
. It’s de- fined by:
 , (1)
, (1)
where
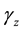 is the curve that joins to
is the curve that joins to
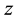 with
with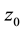 .
.
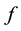 it’s holomorphic and is not annulled on
it’s holomorphic and is not annulled on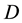 , then
, then
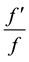 is holomorphic on
is holomorphic on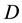 . Then,
. Then,
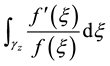 it´s definite as well. This way,
it´s definite as well. This way,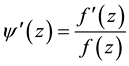 . Consider
. Consider
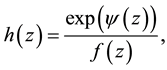 then
then

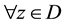 . Then,
. Then,
 it is constant on
it is constant on . So,
. So,
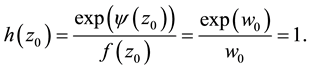
Then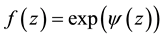 .
.
Let
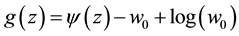 be, then
be, then
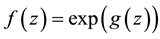 and the proof it is complete.
and the proof it is complete.
Proposition 2: Let Ω be a simply connected domain own of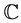 , admits a holomorphic logarithm.
, admits a holomorphic logarithm.
Proof: Consider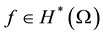 , since Ω be a simply connected domain own of
, since Ω be a simply connected domain own of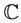 , there is an conformal function
, there is an conformal function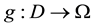 , such that
, such that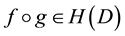 . Since
. Since , follows that
, follows that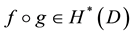 . By the propo- sition 1, the function
. By the propo- sition 1, the function
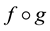 admits a holomorphic logarithm in
admits a holomorphic logarithm in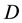 . That is, there exists
. That is, there exists
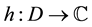 such that
such that
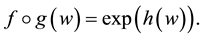
Hereby
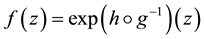 and therefore
and therefore
 admits a holomorphic logarithm in Ω.
admits a holomorphic logarithm in Ω.
Proposition 3: Every function
 admits a holomorphic logarithm.
admits a holomorphic logarithm.
Proof: Since
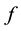 it is not annulled in
it is not annulled in
 and
and . Then
. Then , that is, there exist a function
, that is, there exist a function
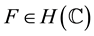 such that is the primitive of
such that is the primitive of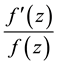 , that is to say,
, that is to say,
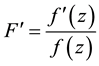 for everything
for everything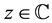 . Notice that
. Notice that
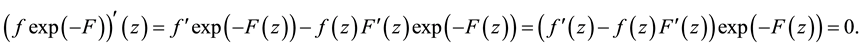
Then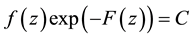 , if
, if
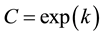 it follows that
it follows that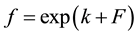 .
.
4. Continuous logarithm
In this section, the inverse problem it’s studied, when the condition weakens of being a holomorphic function to being a continuous function. Nevertheless, on having asked him only continuity to the functions and hav- ing tried to solve the inverse problem, it is needed to do more restrictions on the domain of the above men- tioned functions.
It is considered to be that
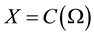 and the space
and the space
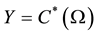 that correspond to the spaces of conti- nuous and continuous that are not annulled function respectively. There is demonstrated that when
that correspond to the spaces of conti- nuous and continuous that are not annulled function respectively. There is demonstrated that when
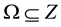 it’s a simply connected domain and
it’s a simply connected domain and
 is Hausdorff space and connected by paths, the solution of the inverse problem exists, is unique if a branch of the logarithm is fixed adapted and is stable.
is Hausdorff space and connected by paths, the solution of the inverse problem exists, is unique if a branch of the logarithm is fixed adapted and is stable.
Theorem 2 Let
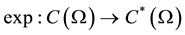 be, where
be, where
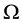 a simply connected set is (not necessarily it is a subset of the plane) content in Hausdorff space and connected by paths; then the solution of the inverse problem exists, is unique and is stable.
a simply connected set is (not necessarily it is a subset of the plane) content in Hausdorff space and connected by paths; then the solution of the inverse problem exists, is unique and is stable.
Proof: The existence of the solution of the inverse problem, it’s demonstrated in the proposition 3 and the ex- istence in the proposition 4.
Since , where
, where
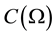 and
and
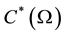 are Banach spaces, in addition, the operator is continuous; then, by the open mapping theorem, the inverse operator is continuous and therefore, the solution of the inverse problem is stable.
are Banach spaces, in addition, the operator is continuous; then, by the open mapping theorem, the inverse operator is continuous and therefore, the solution of the inverse problem is stable.
Definition: Let
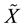 and
and
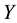 be topological spaces. Consider to
be topological spaces. Consider to
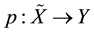 a continuous function. Is say that
a continuous function. Is say that
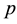 is a covering map if
is a covering map if
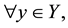 it exists a neighborhood
it exists a neighborhood
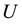 for
for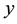 , with following properties:
, with following properties:
1)
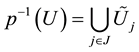 with
with

2)
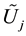 is a neighborhood for
is a neighborhood for
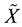 such that
such that
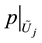 is a homeomorphism on
is a homeomorphism on ,
, .
.
Proposition 4: The
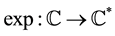 function is a covering map.
function is a covering map.
Definition: Let
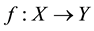 be a continuous function and let
be a continuous function and let
 be a covering map. The
be a covering map. The
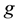 ap- plication is a lifting for
ap- plication is a lifting for
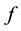 (in respect of
(in respect of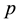 ) if
) if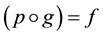 .
.
Note that if it is known that the exp function is a covering map, then to define the lifting, and under the condi- tions for the existence and uniqueness of the lifting, it will be had that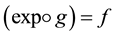 ; and therefore on having demonstrated the existence and uniqueness of the lifting, there will be demonstrated the existence and unique- ness of the logarithm of a continuous function .
; and therefore on having demonstrated the existence and uniqueness of the lifting, there will be demonstrated the existence and unique- ness of the logarithm of a continuous function .
4.1. Uniqueness of the lifting
For the uniqueness of the lifting it is necessary that the
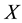 topological space be connected and Hausdorff.
topological space be connected and Hausdorff.
Theorem 3 Let
 be a local homeomorphism, let
be a local homeomorphism, let
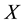 be a connected and Hausdorff space and let
be a connected and Hausdorff space and let
 be a continuous application. Suppose that
be a continuous application. Suppose that
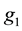 and
and
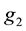 are lifting of
are lifting of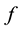 . Then, if
. Then, if
 exists, such that
exists, such that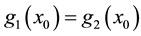 , it follows that
, it follows that
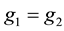 in
in .
.
Proof: The set
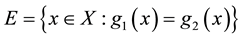 is defined. Note that
is defined. Note that
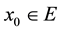 and therefore
and therefore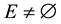 . If it is shown that
. If it is shown that
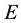 is open and closed it follow that
is open and closed it follow that . To show that
. To show that
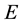 is a closed set, enough to prove that
is a closed set, enough to prove that
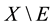 is an open set. Let
is an open set. Let
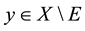 be, clearly
be, clearly
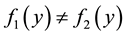 and since
and since
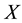 is a Hausdorff space, exist
is a Hausdorff space, exist
neighborhoods
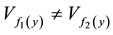 for
for
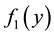 and
and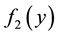 , respectively such that
, respectively such that . Consider that
. Consider that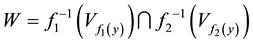 , note that
, note that
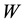 isn’t an empty set, then
isn’t an empty set, then
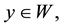 so,
so,
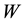 is open set since is a
is open set since is a
finite intersection of open sets. Let
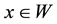 be, then
be, then
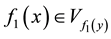 and
and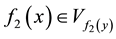 . What implies that
. What implies that . Therefore
. Therefore
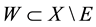 and so, the
and so, the
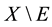 open set and then the
open set and then the
 set is closed. To show that
set is closed. To show that
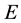 is an open set. Let
is an open set. Let
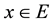 be and
be and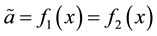 . By hypothesis, there is a neighborhood
. By hypothesis, there is a neighborhood
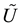 for
for
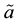 such that
such that
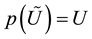 is open set and
is open set and
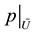 is an homeomorphism. Since
is an homeomorphism. Since
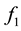 and
and
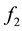 are continuous func- tion, there is
are continuous func- tion, there is
 an neighborhood for
an neighborhood for
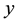 such that
such that
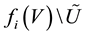 and
and . Since
. Since
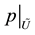 is an injective function, it follows that
is an injective function, it follows that
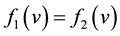 so,
so,
 it’s a closed set and then the
it’s a closed set and then the
 set is open. Since
set is open. Since
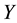 is connected space and
is connected space and
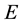 is a non-empty, open and closed set, it follows that
is a non-empty, open and closed set, it follows that .
.
4.2. Existence of the lifting
The study of the existence of the lifting needs of the study of the fundamental group.
Let
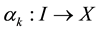 be, where
be, where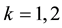 , curves that begin and end in
, curves that begin and end in , it is to say, they are closed curves. Is said that
, it is to say, they are closed curves. Is said that
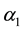 it is related with
it is related with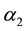 ,
,
 , if it exists
, if it exists
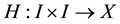 a continuous function such that
a continuous function such that
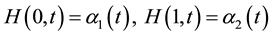 ,
,
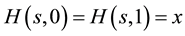
The
 function is called continuous homotopy.
function is called continuous homotopy.
It is easy to see that the relation
 is an equivalence relation. Since it is known well, everything equivalence relation induces a partition. In this case the classes
is an equivalence relation. Since it is known well, everything equivalence relation induces a partition. In this case the classes
 are formed by the set of curves
are formed by the set of curves
 that are homotopic to
that are homotopic to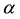 . Intuitively it is possible to define the operation join curved and the above mentioned operation gives a structure of group.
. Intuitively it is possible to define the operation join curved and the above mentioned operation gives a structure of group.
Definition: The first group of homotopy of
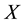 is defined, with basis
is defined, with basis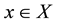 :
:
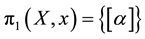 ,
,
where
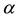 is a closed curve.
is a closed curve.
We noted that
 is the curve
is the curve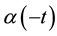 .
.
The following result gives necessary and sufficient conditions for the existence of the lifting.
Theorem 4: Let
 be a covering map and let
be a covering map and let
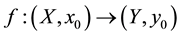 be a continuous function, with
be a continuous function, with
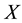 a connected by paths set. Then they are equivalent:
a connected by paths set. Then they are equivalent:
1) A lifting
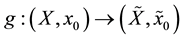 there exists for
there exists for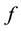 ;
;
2)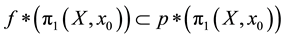 .
.
Where
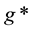 is the induced mapping of fundamental groups.
is the induced mapping of fundamental groups.
Proof: The demonstration
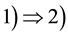 obviously, because
obviously, because .
.
There will be demonstrated that . Let
. Let
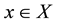 be and let
be and let
 be a curve in
be a curve in
 from
from
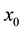 to
to . The curve
. The curve
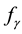 in
in
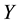 that it begins in
that it begins in
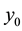 it has a unique lifting
it has a unique lifting
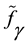 that it begins
that it begins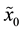 .
.
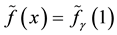 is defined. It is demonstrated that it is definite as well, independently of the choice of
is defined. It is demonstrated that it is definite as well, independently of the choice of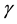 , let
, let
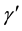 be another curve from
be another curve from
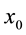 to
to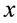 . Then
. Then
 is a closed curve of
is a closed curve of
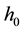 to
to
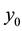 with:
with:
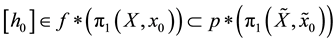 .
.
This means that there is a homotopy
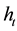 from
from
 to a closed curve
to a closed curve
 that gets up to a closed curve
that gets up to a closed curve
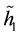 in
in
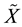 based in
based in . Property homotopy covering is applied to
. Property homotopy covering is applied to
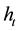 to obtain a lifting
to obtain a lifting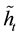 . Since
. Since
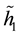 is a closed curve to
is a closed curve to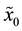 ,
,
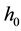 it’s too. By the uniqueness of the lift curve, the first half of
it’s too. By the uniqueness of the lift curve, the first half of
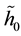 is
is
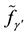 and the second half is
and the second half is
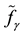 route the other way around, with the common midpoint
route the other way around, with the common midpoint . This shows that
. This shows that
 it´s definite as well. Need to show that
it´s definite as well. Need to show that
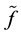 is a continuous function. Let
is a continuous function. Let
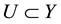 be a neighborhood of
be a neighborhood of
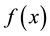 that it has a lifting
that it has a lifting
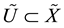 containing to
containing to
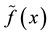 such that
such that
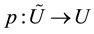 is an homeomorphism. A connected by path neighborhood
is an homeomorphism. A connected by path neighborhood
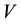 is chosen for
is chosen for
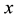 with
with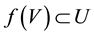 . The curves from
. The curves from
 to
to
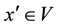 points, it is possible to take a given fixed curve
points, it is possible to take a given fixed curve
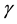 from
from
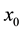 to
to
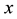 follow by curves
follow by curves
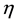 in
in
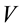 from y to the points
from y to the points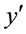 . Then, the curves
. Then, the curves
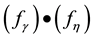 in
in
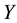 it has lifting
it has lifting
 where
where
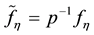 and
and
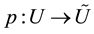 is the inverse of
is the inverse of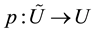 . So,
. So,
 and
and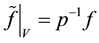 , therefore
, therefore
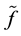 is continuous in
is continuous in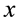 .
.
References
- C. W. Groetsch, “Inverse Problems: Activities for Undergraduates,” The Mathematical Association of America, Ohio, 1999.
- A. Browder, “Topology in the Complex Plane,” The American Mathematical Monthly, Vol. 107 No. 10, 2006, pp. 393-401. https://getinfo.de/app/Topology-in-the-Complex-Plane/id/BLSE%3ARN079983226
- A. Hatcher, “Algebraic Topology,” Cambridge University Press, Cambridge, 2009.
- L. V. Ahlfors, “Complex Analysis,” McGraw-Hill, New York, 1979.
- A. Kirsch, “An Introduction to the Mathematical Theory of Inverse Problems,” 2nd Edition, Springer, Berlin, 2011. http://dx.doi.org/10.1007/978-1-4419-8474-6
- E. Stein and R. Shakarchi, “Complex Analysis,” Princeton University Press, Princeton, 2009.

