American Journal of Computational Mathematics
Vol.3 No.1(2013), Article ID:28988,5 pages DOI:10.4236/ajcm.2013.31001
Numerical Solution of Singularly Perturbed Two-Point Boundary Value Problem via Liouville-Green Transform
Department of Mathematics, Jaypee University of Engineering & Technology, Guna, India
Email: hk.mishra@juet.ac.in, sonali.saini1386@gmail.com
Received October 17, 2012; revised November 21, 2012; accepted December 7, 2012
Keywords: Singular Perturbation; Ordinary Differential Equation; Boundary Layer; Two-Point Boundary Value Problem; Liouville-Green Transform
ABSTRACT
In this paper, author describes a Liouville-Green transform to solve a singularly perturbed two-point boundary value problem with right end boundary layer in the interval [0,1]. They reply Liouville-Green transform into original given problem and finds the numerical solution. Then they implemented this method on two linear examples with right end boundary layer which nicely approximate the exact solution.
1. Introduction
Singular perturbation problems are of common occurrence in fluid mechanics, quantum mechanics, optimal control, chemical reactor theory, aerodynamics, reaction-diffusion processes, geophysics. It is a well known fact that the singularly perturbed two-point boundary value problem posses boundary or interior layers i.e. regions of rapid change in the solution near the end points or some interior points with width O(1) as . In recent years, a large number of special methods have been developed to provide accurate numerical solutions. For details one may refer to the books of [1-5] and the references [6-11]. Many of these methods consist of: 1) dividing the problem into an inner region (boundary layer) problem and an outer region problem; 2) expressing the inner and outer solutions as asymptotic expansions; 3) equating various terms in the inner and outer expressions to determine the constants in these expressions; and 4) combining the inner and outer solutions in some fashion to obtain a uniformly valid solution. Typically, the inner region problems are obtained from the original problem by rescaling the independent variable. These techniques and their variations have been used successfully on a variety of linear and nonlinear singular perturbation problems. However, there can be difficulties in applying these methods, such as the matching of the coefficients of the inner and outer expansions. Success may depend on finding the proper scaling or the proper transformation to express the dependent and independent variables.
. In recent years, a large number of special methods have been developed to provide accurate numerical solutions. For details one may refer to the books of [1-5] and the references [6-11]. Many of these methods consist of: 1) dividing the problem into an inner region (boundary layer) problem and an outer region problem; 2) expressing the inner and outer solutions as asymptotic expansions; 3) equating various terms in the inner and outer expressions to determine the constants in these expressions; and 4) combining the inner and outer solutions in some fashion to obtain a uniformly valid solution. Typically, the inner region problems are obtained from the original problem by rescaling the independent variable. These techniques and their variations have been used successfully on a variety of linear and nonlinear singular perturbation problems. However, there can be difficulties in applying these methods, such as the matching of the coefficients of the inner and outer expansions. Success may depend on finding the proper scaling or the proper transformation to express the dependent and independent variables.
A non-asymptotic method, also called boundary-value technique, has been introduced by Roberts [12-14] to solve certain classes of singular perturbation problems. He also discussed the analytical and approximate solutions of several numerical examples. To the best of our knowledge, very few asymptotic solutions were established for boundary value problems [15,16]. In this paper, author studies the second order singularly perturbed twopoint boundary value problem with right end boundary layer via Liouville-Green transform and obtain asymptotic and numerical solutions. Few examples are also demonstrated for the applicability of the method.
2. Liouville-Green Transforms
Now, we discuss our method for singularly perturbed two-point boundary value problems with right-end boundary layer of the underlying interval. To be specific, we consider a class of singular perturbation problem of the form
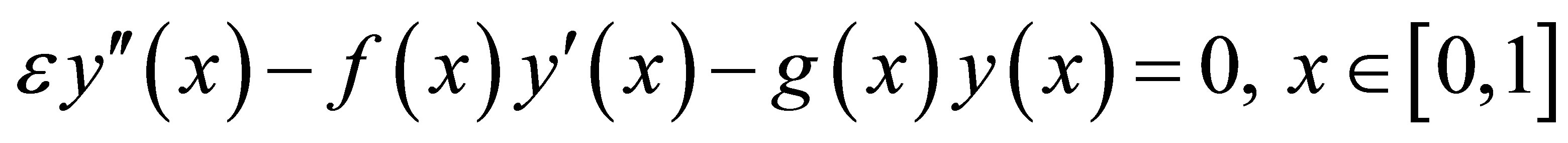 (1)
(1)
with boundary conditions
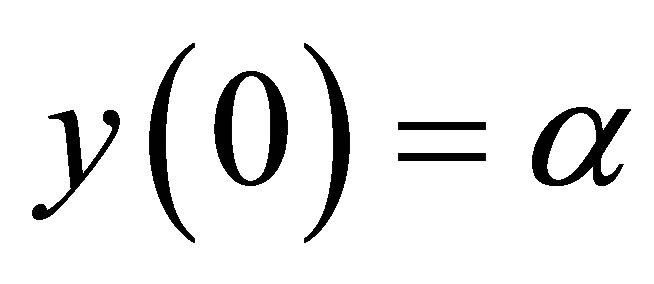 and
and 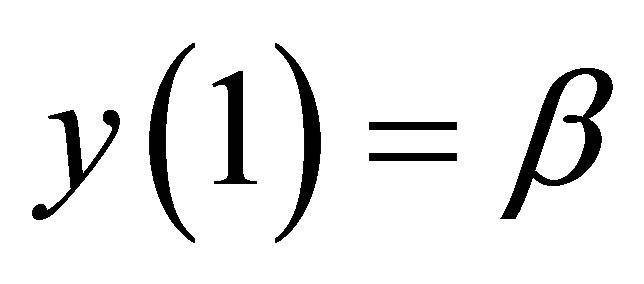 (2)
(2)
where 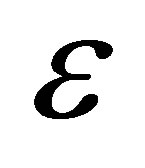 is a small positive parameter
is a small positive parameter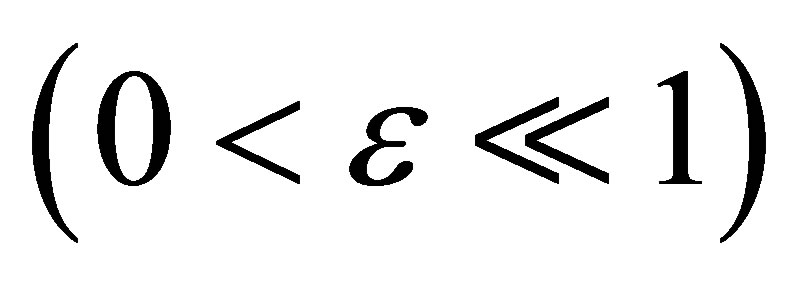 ;
;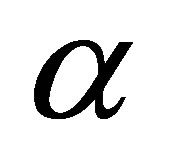 ,
,  are known constants; we assume that
are known constants; we assume that ,
,  are assumed to be sufficiently continuously differentiable function in [0,1]. Furthermore, since the coefficient of
are assumed to be sufficiently continuously differentiable function in [0,1]. Furthermore, since the coefficient of 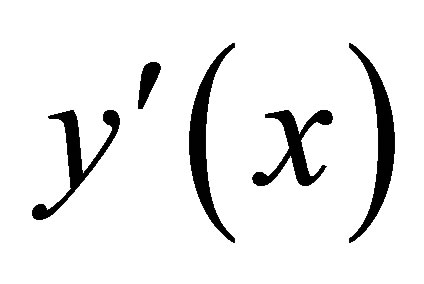 is negative and non zero throughout the interval [0,1]. This assumption merely implies that the boundary layer will be in the neighborhood of x = 1.
is negative and non zero throughout the interval [0,1]. This assumption merely implies that the boundary layer will be in the neighborhood of x = 1.
Rewrite the Equation (1) as below:
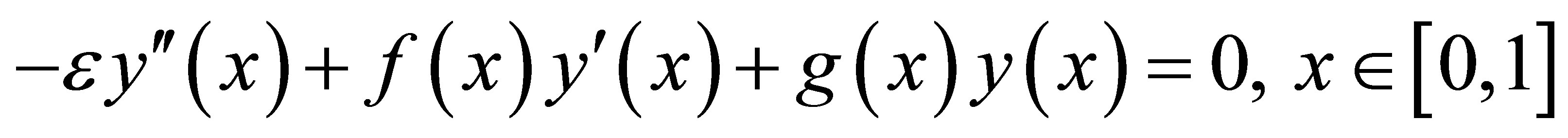 (3)
(3)
Let the new Liouville-Green transforms 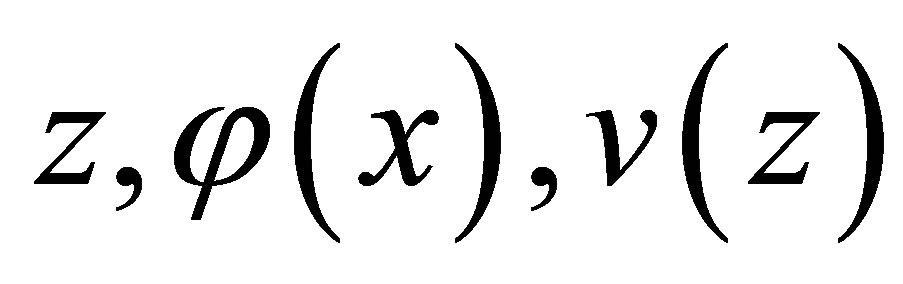 be
be
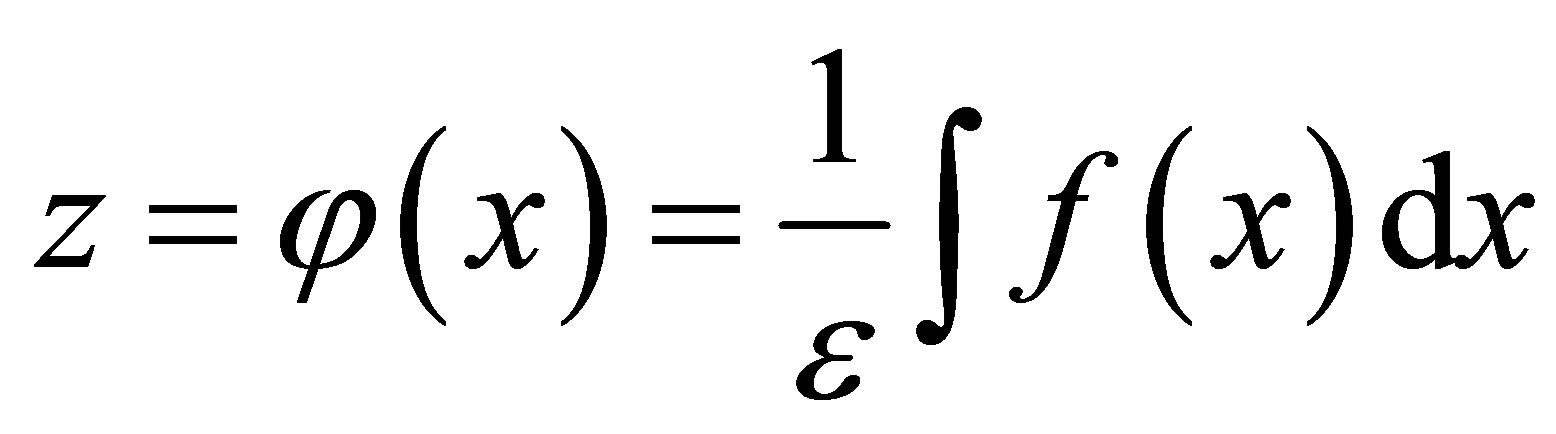 (4)
(4)
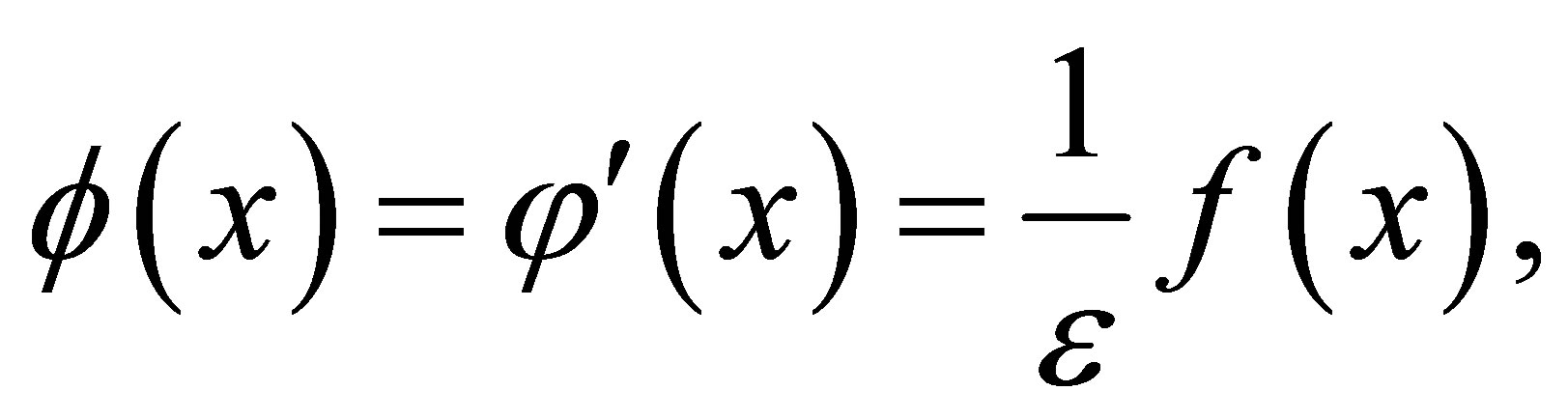 (5)
(5)
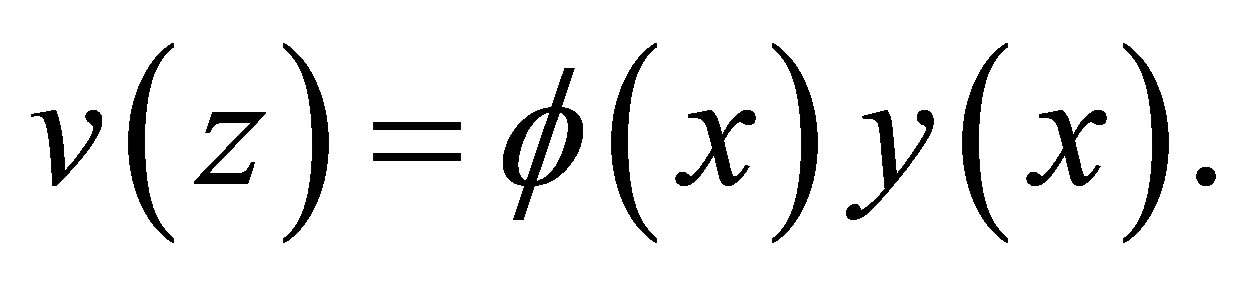 (6)
(6)
According to (6), we have
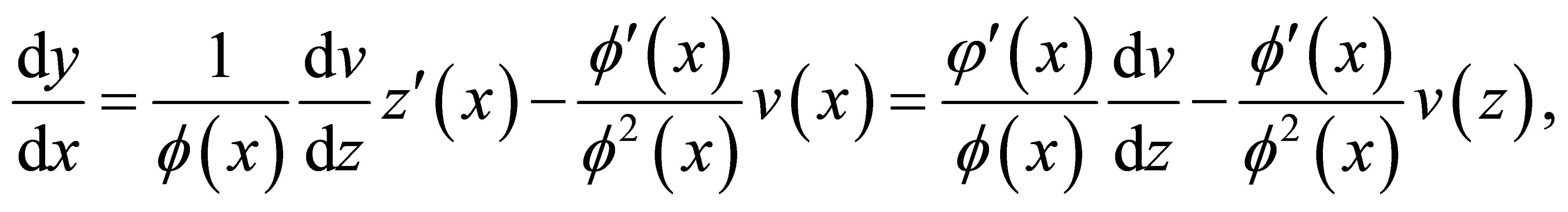 (7)
(7)
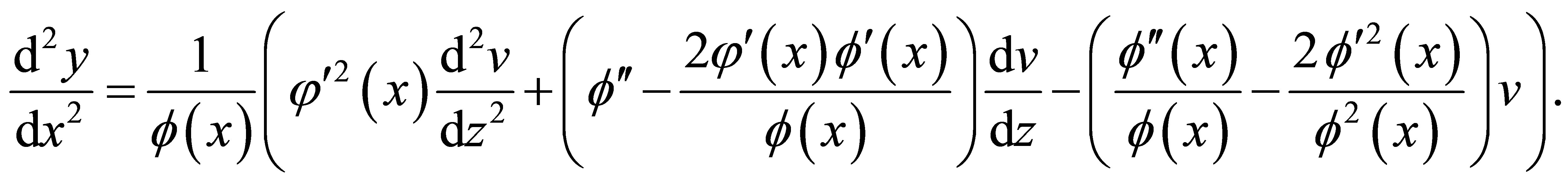 (8)
(8)
From (3), (7) and (8), we obtain
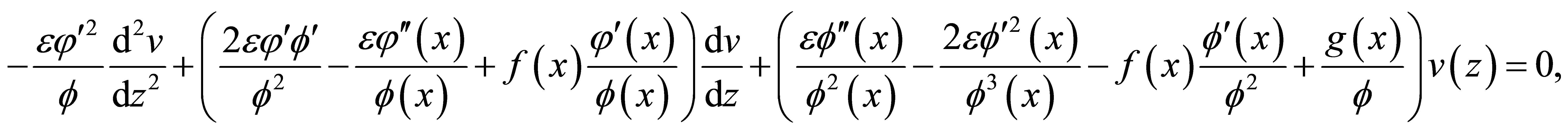
i.e.

From (4), we have
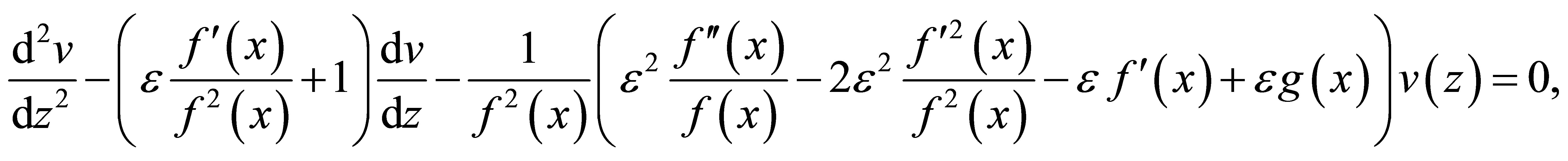
i.e.
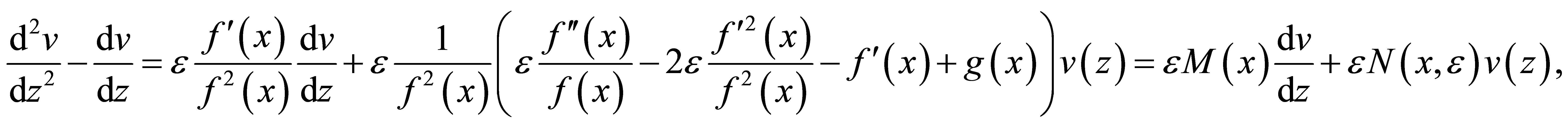 (9)
(9)
where
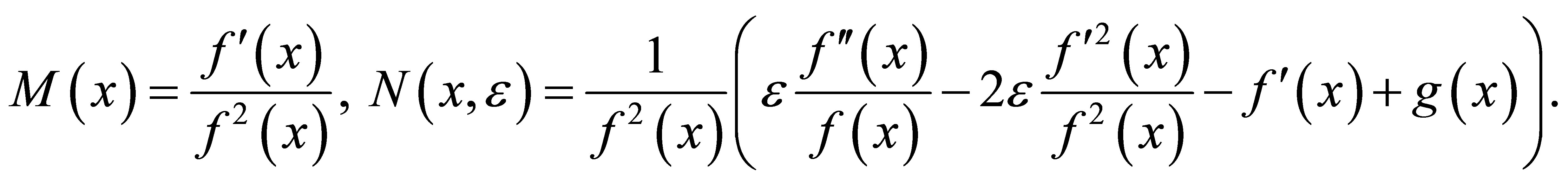
Since 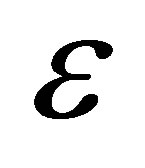 is a small parameter
is a small parameter ,
, 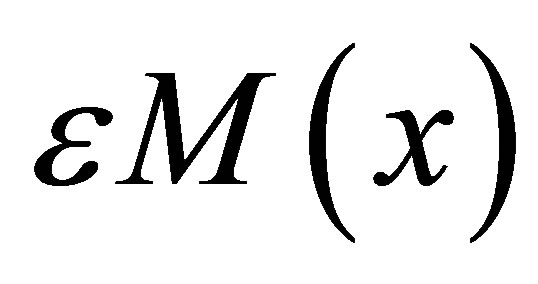 and
and 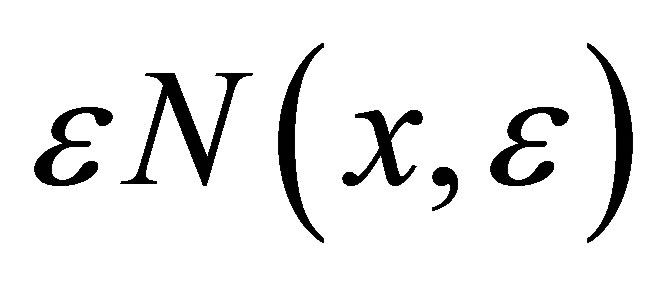 are sufficiently small on [0,1]. So, as
are sufficiently small on [0,1]. So, as , the right hand side of Equation (9) vanishes. Therefore, we have
, the right hand side of Equation (9) vanishes. Therefore, we have
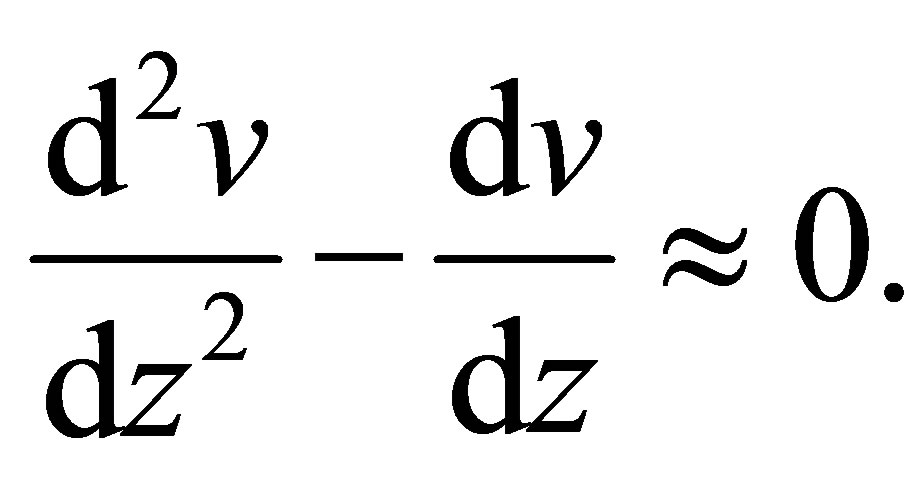 (10)
(10)
Therefore, the approximate solutions 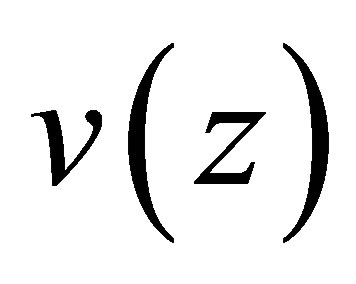 of (10) are
of (10) are
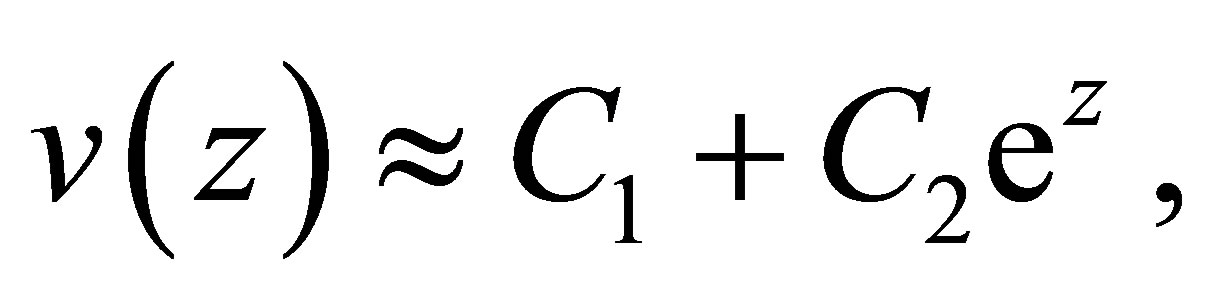 (11)
(11)
where 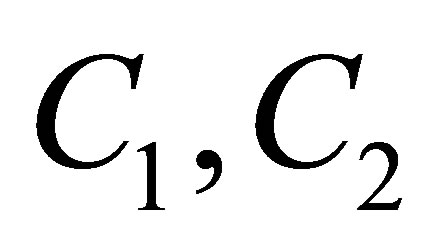 are two arbitrary constants. From (4)-(6), one has the asymptotic solutions of differential equations
are two arbitrary constants. From (4)-(6), one has the asymptotic solutions of differential equations
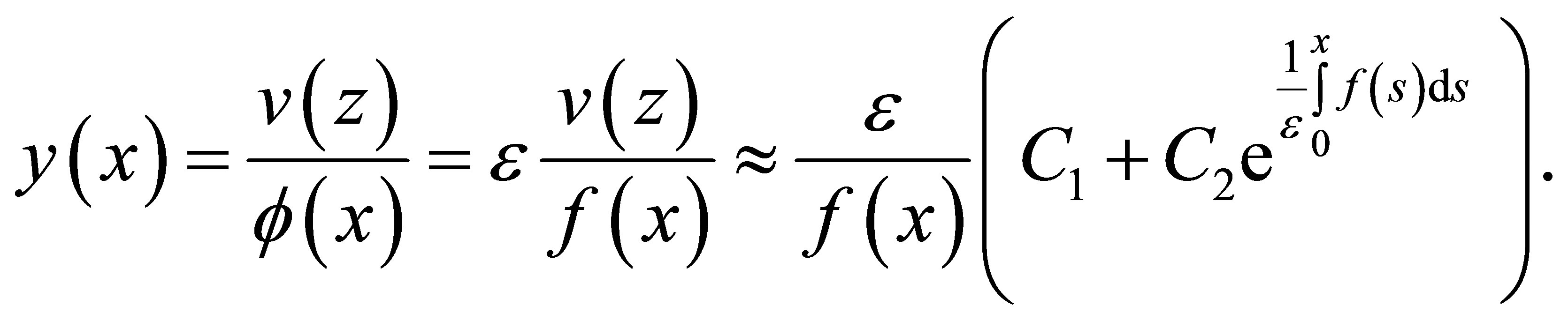 (12)
(12)
where 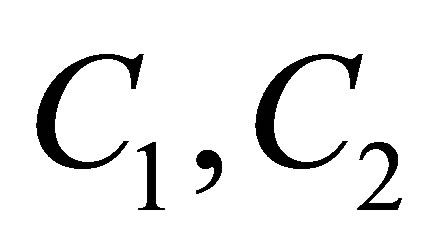 are two arbitrary constants.
are two arbitrary constants.
3. Application to Two Point Boundary Value Problems
As an application, we consider the following secondorder two-point boundary value problem
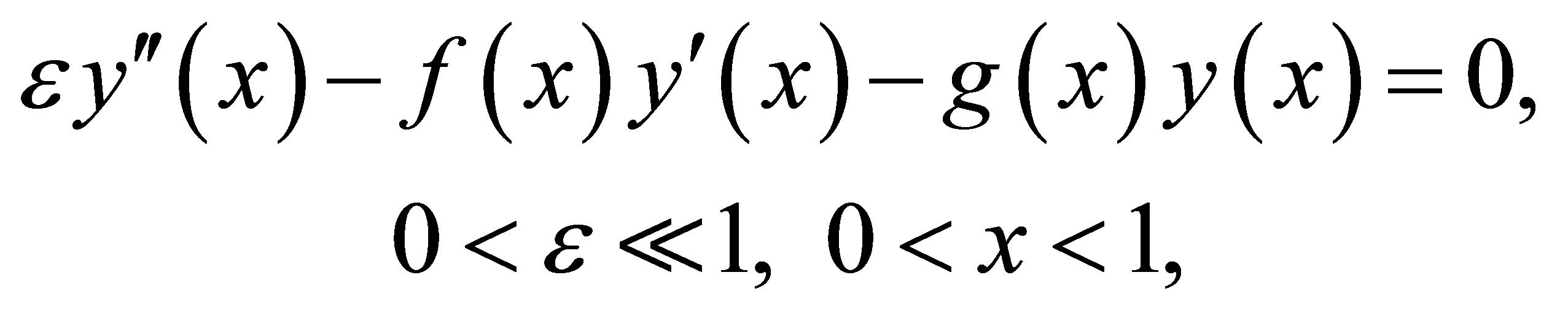 (13)
(13)
Which is equivalent to
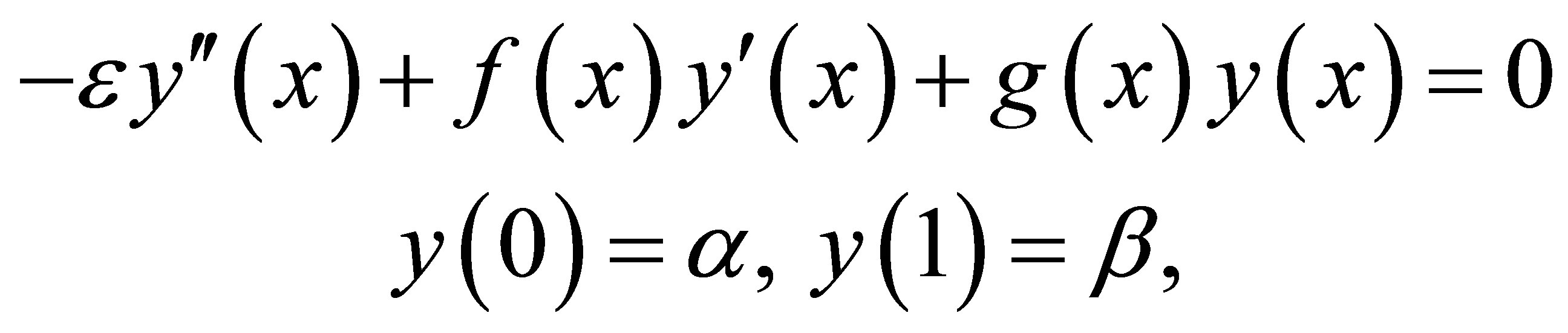
where 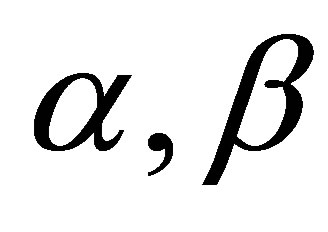 are constants.
are constants.
Applying the boundary conditions of (13), in (12), we have
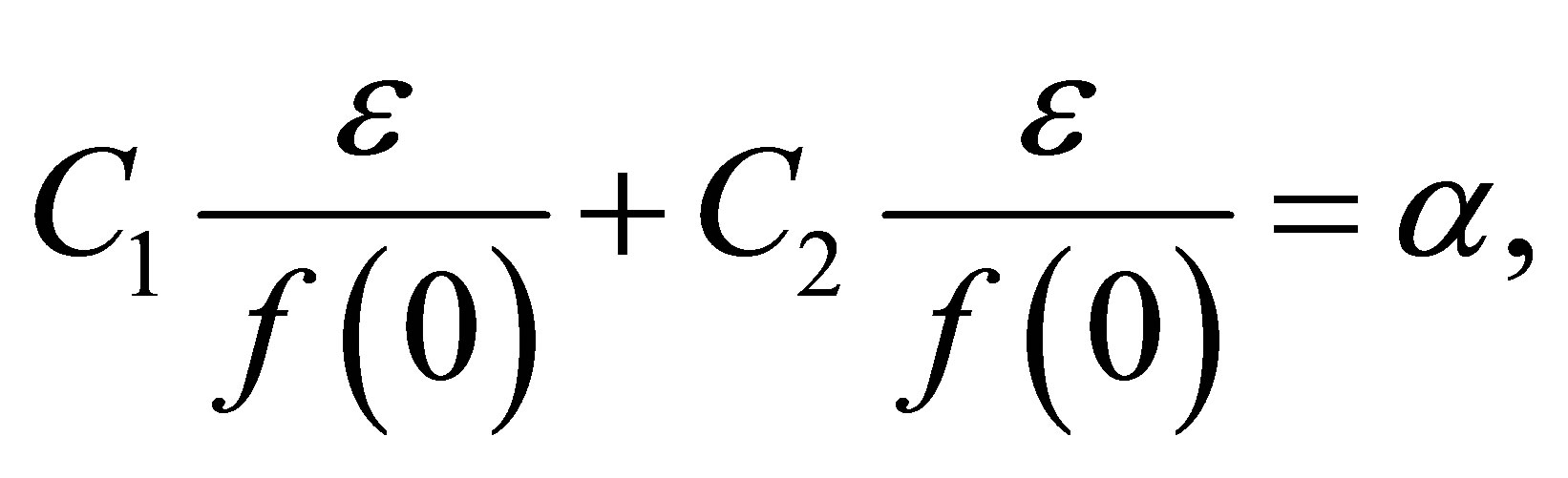
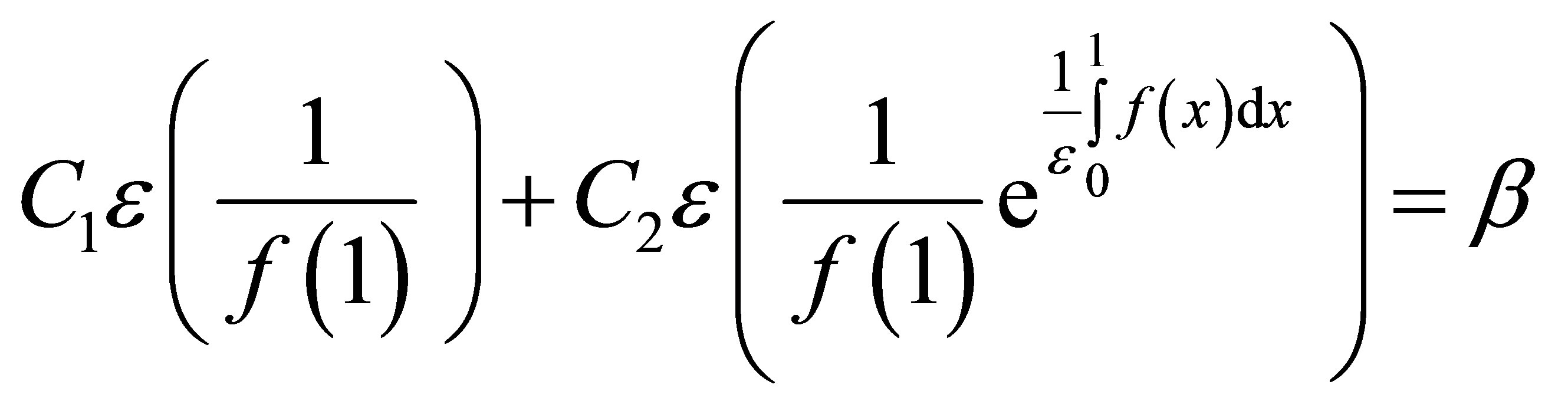
One has
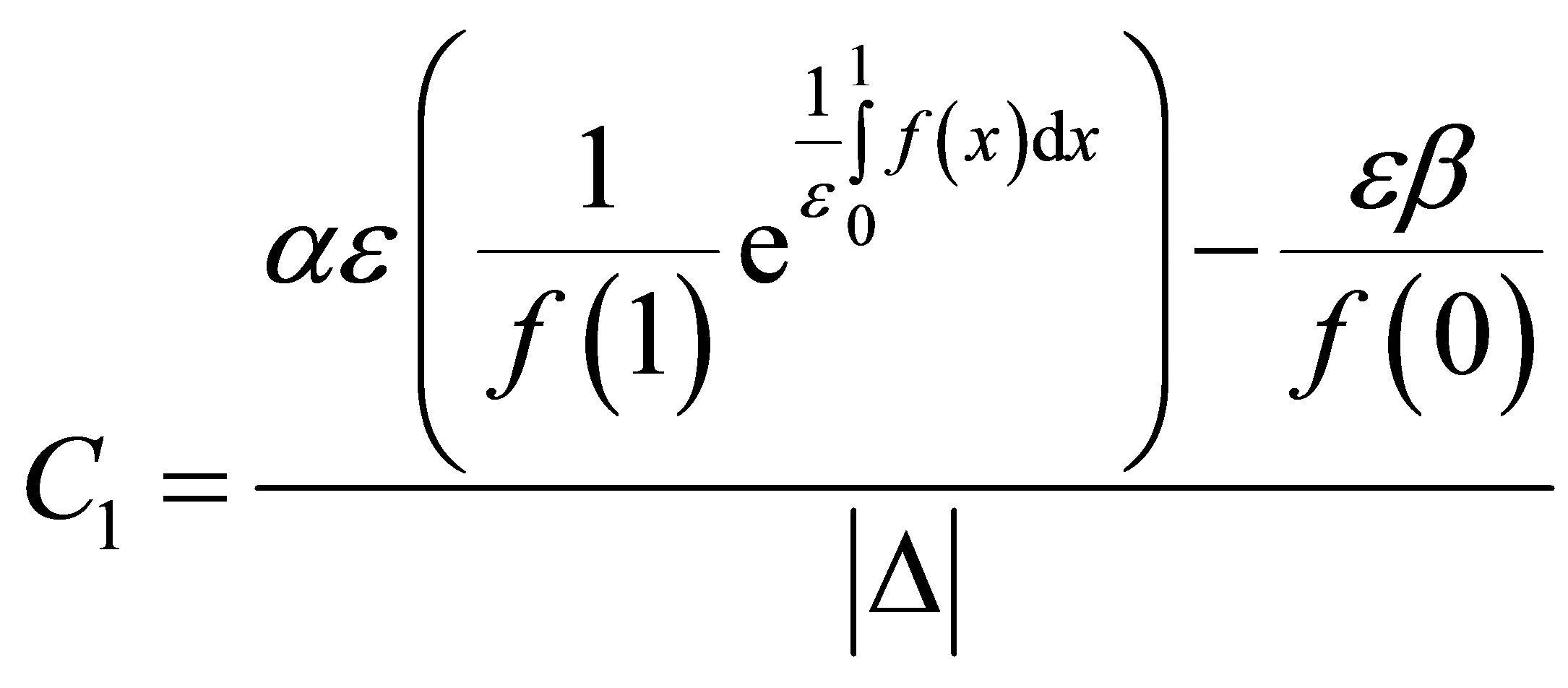 (14)
(14)
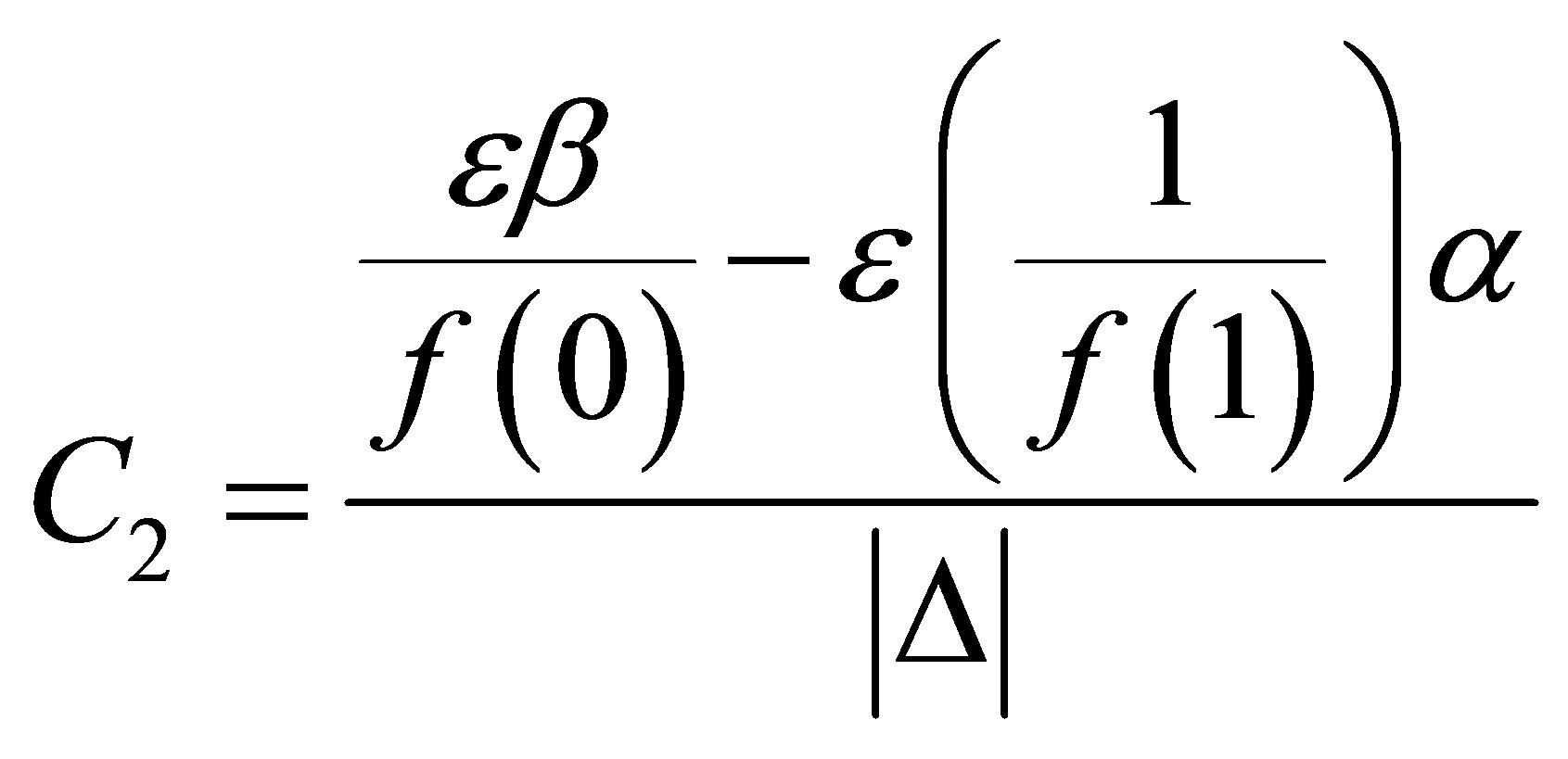 (15)
(15)
where
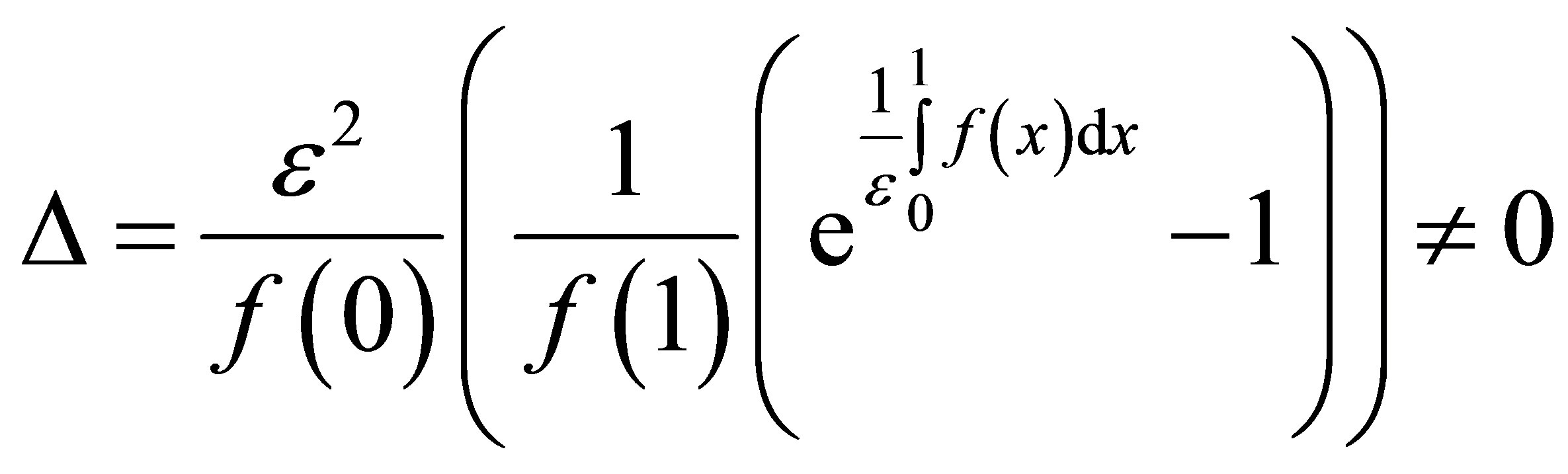
Then BVP (13) has the following asymptotic solution:
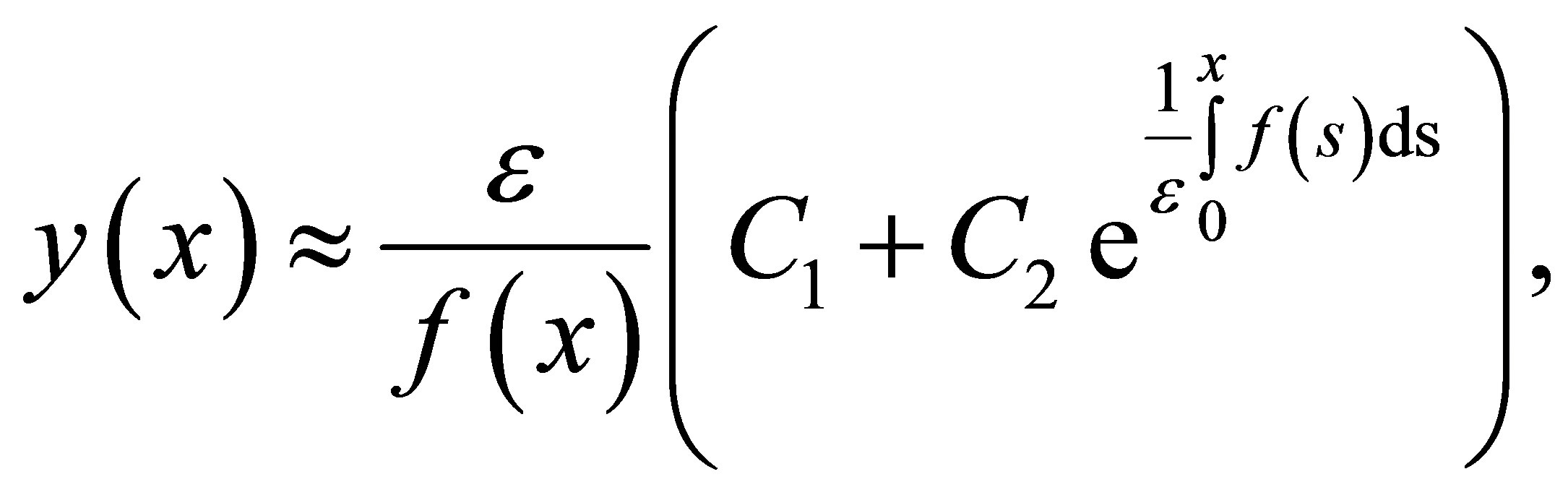 (16)
(16)
where 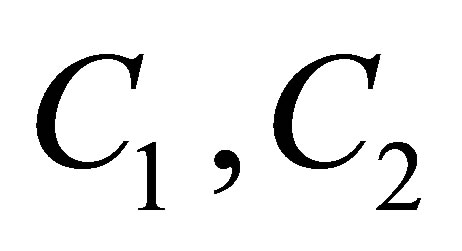 are given by (14), (15) respectively.
are given by (14), (15) respectively.
Example 3.1. Consider the following singular perturbation problem
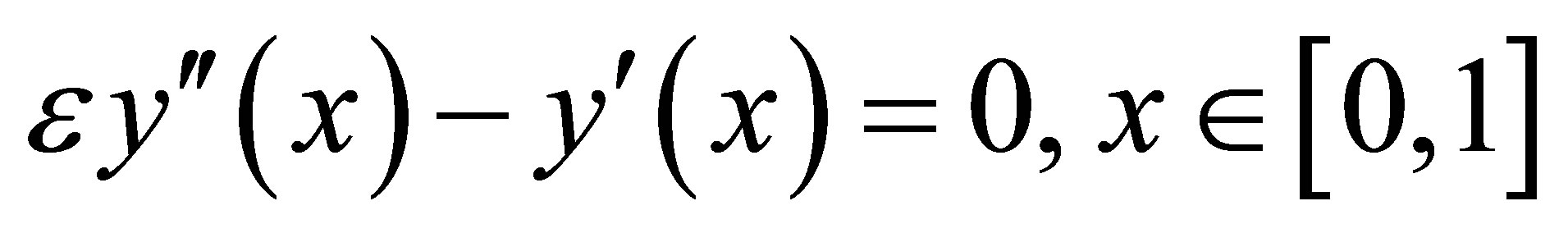 (17)
(17)
with 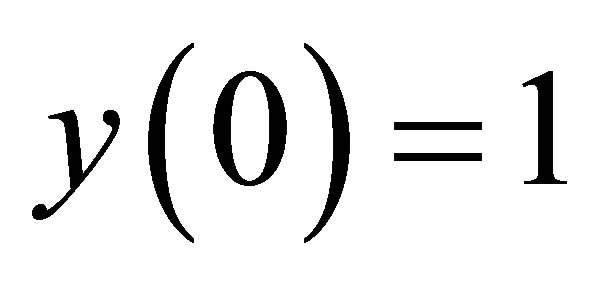 and
and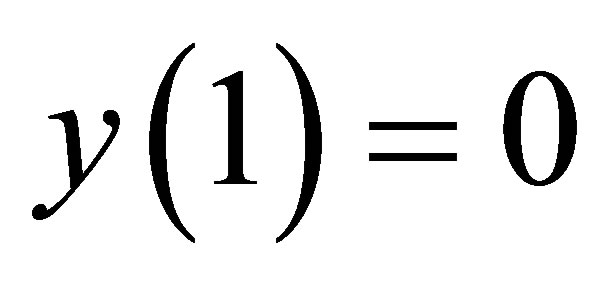 . (18)
. (18)
Clearly this problem has a boundary layer at x = 1. i.e.; at the right-end of the underlying interval. The exact solution is given by
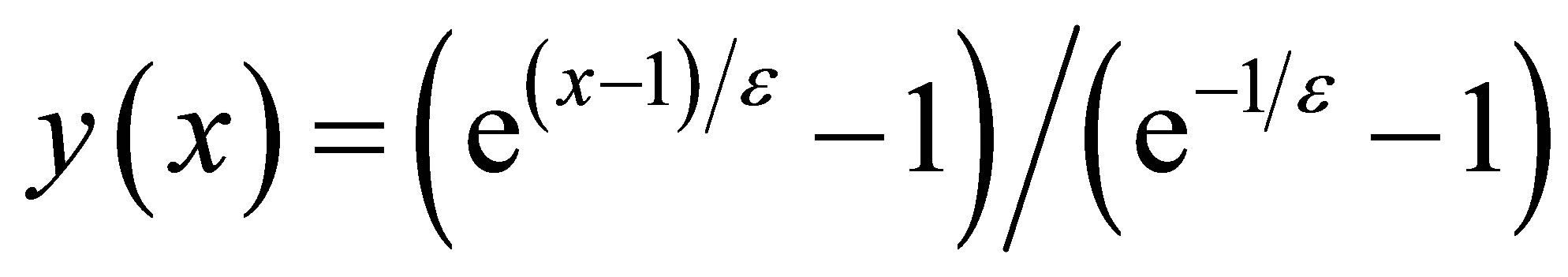
Comparing (17) with (13), we have
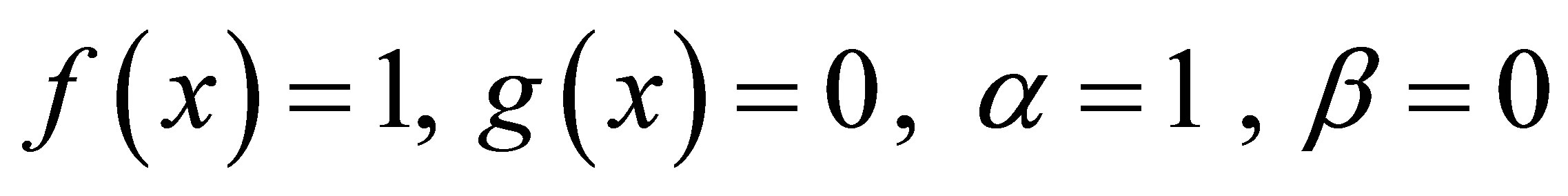
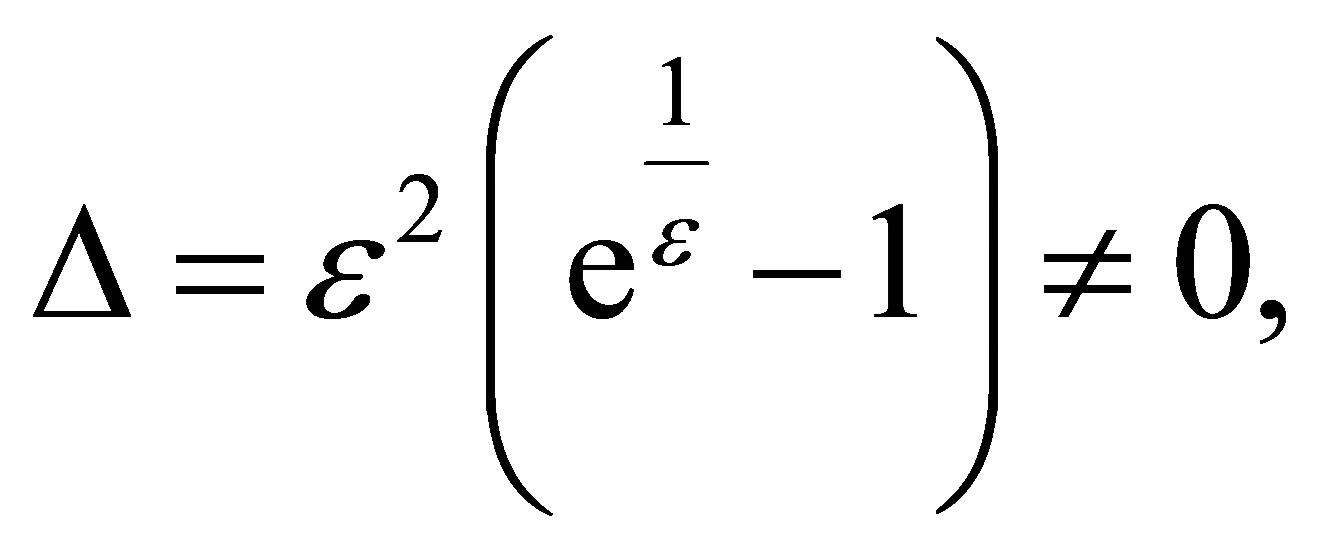
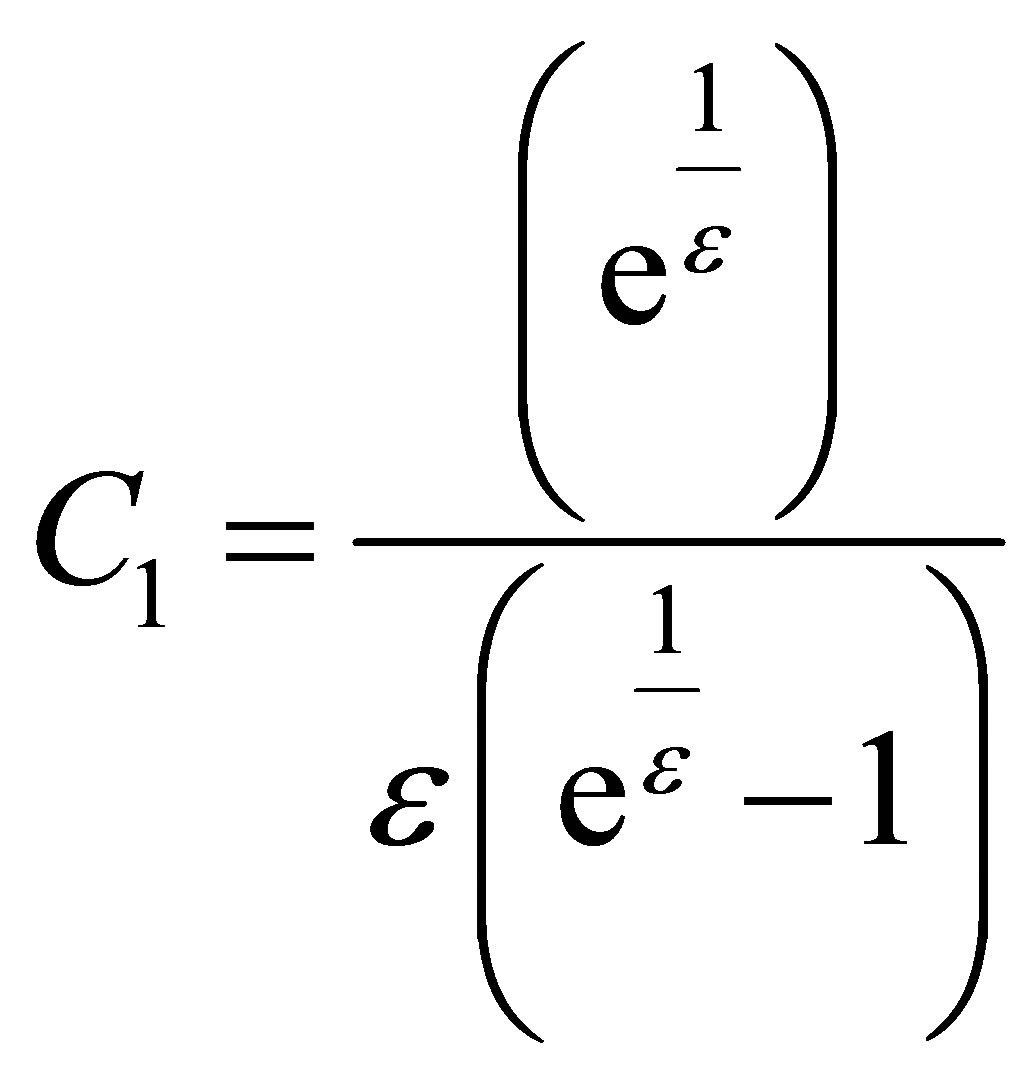
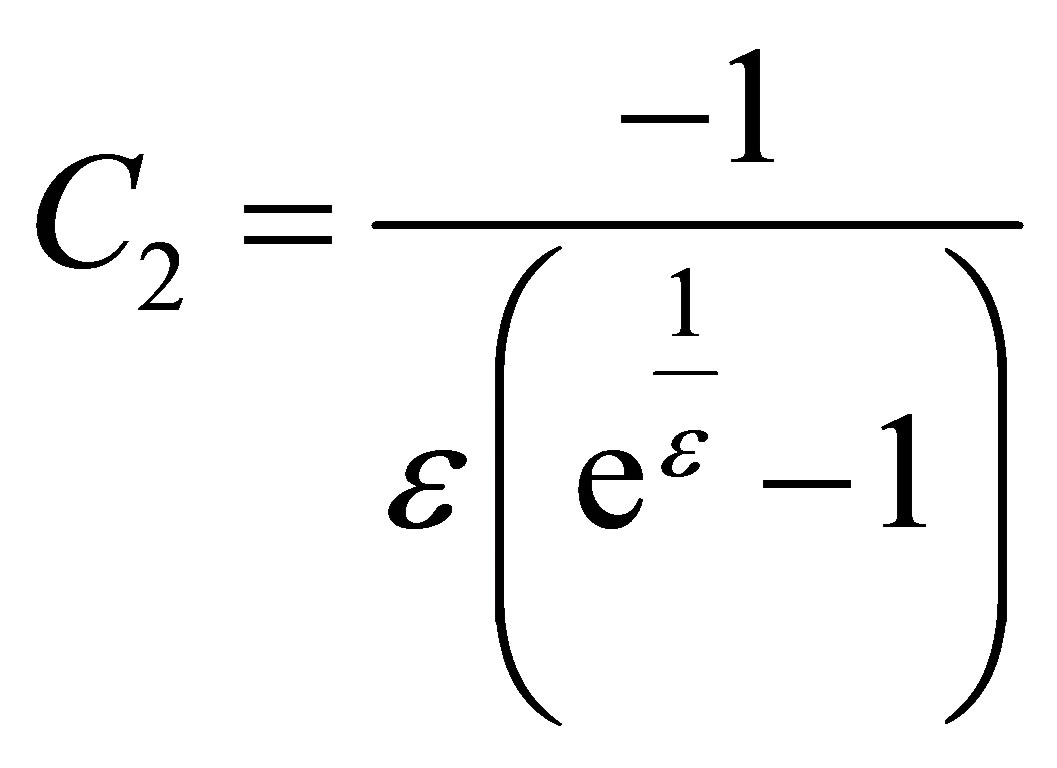
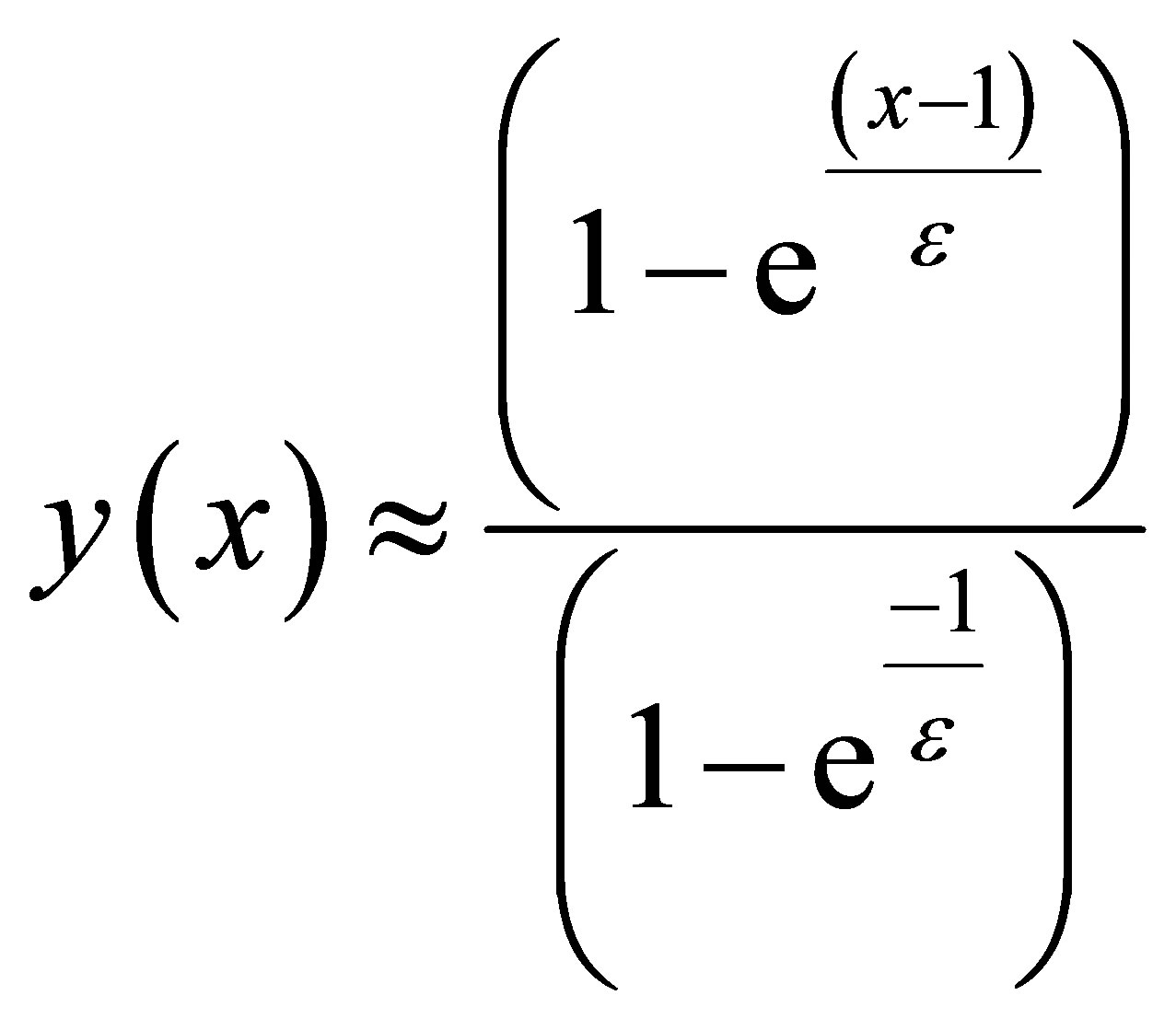 (19)
(19)
The computational results are presented in Tables 1 and 2 for 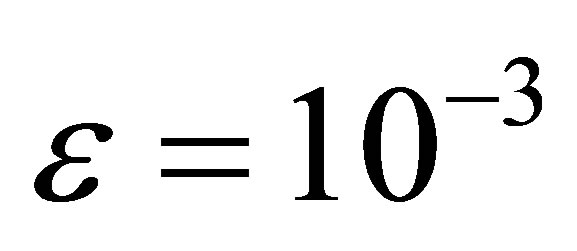 and 10−4, respectively. Figures 1 and 2 show our solution and exact solution for different values of x.
and 10−4, respectively. Figures 1 and 2 show our solution and exact solution for different values of x.
Example 3.2. We consider the following variable coefficient singular perturbation problem from Kevorkian and Cole [2, p. 33, Equations (2.3.26) and (2.3.27) with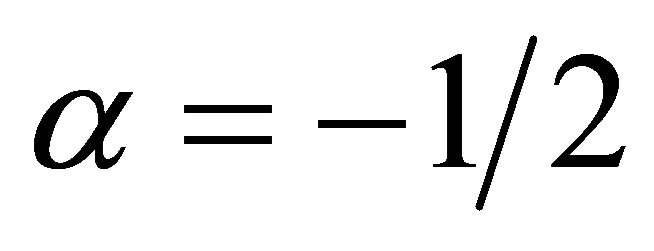 ].
].
Table 1. Numerical results of example 3.1 with ε = 10−3, h = 10−3.
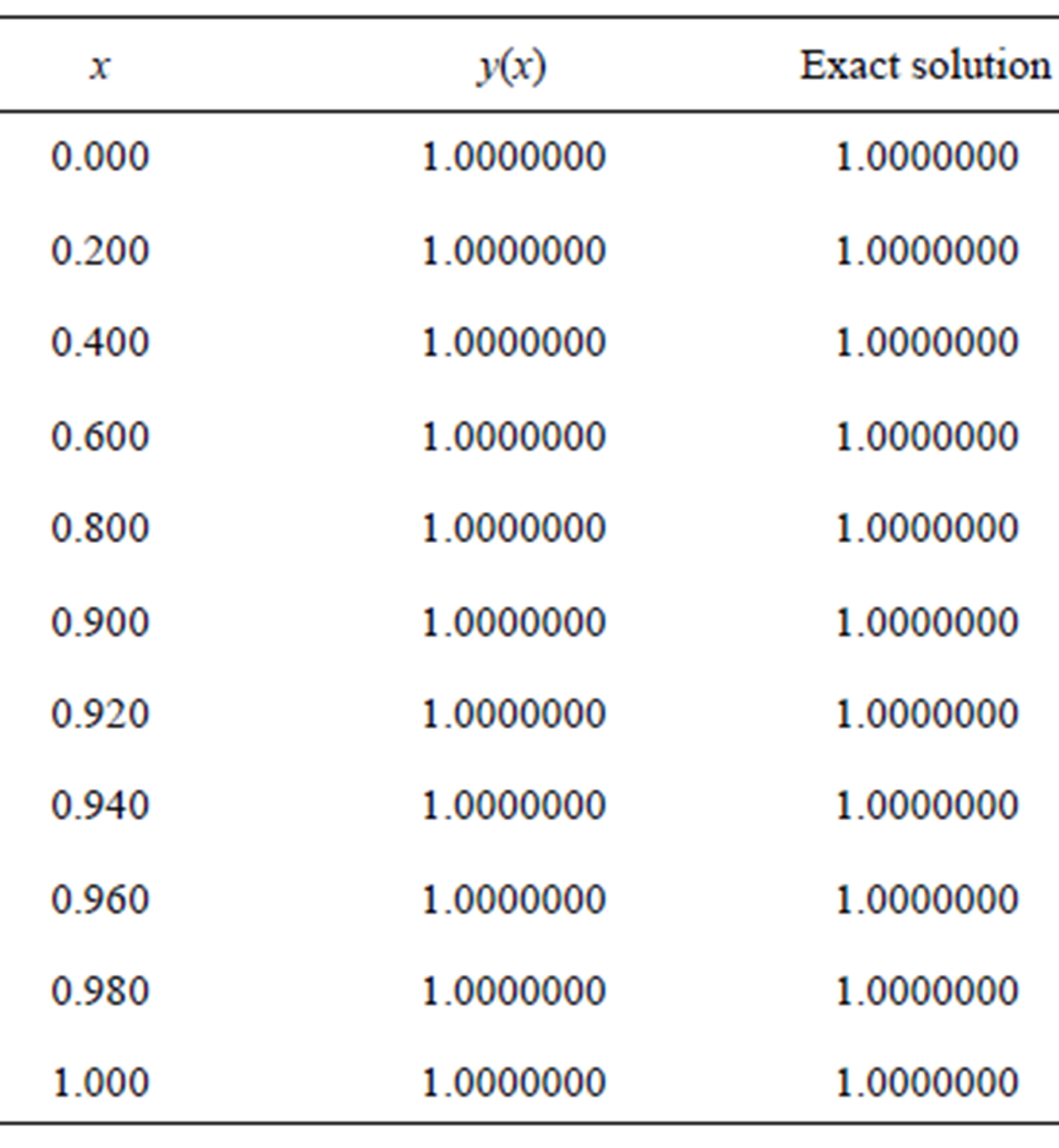
Table 2. Numerical results of example 3.1 with ε = 10−4, h = 10−4.

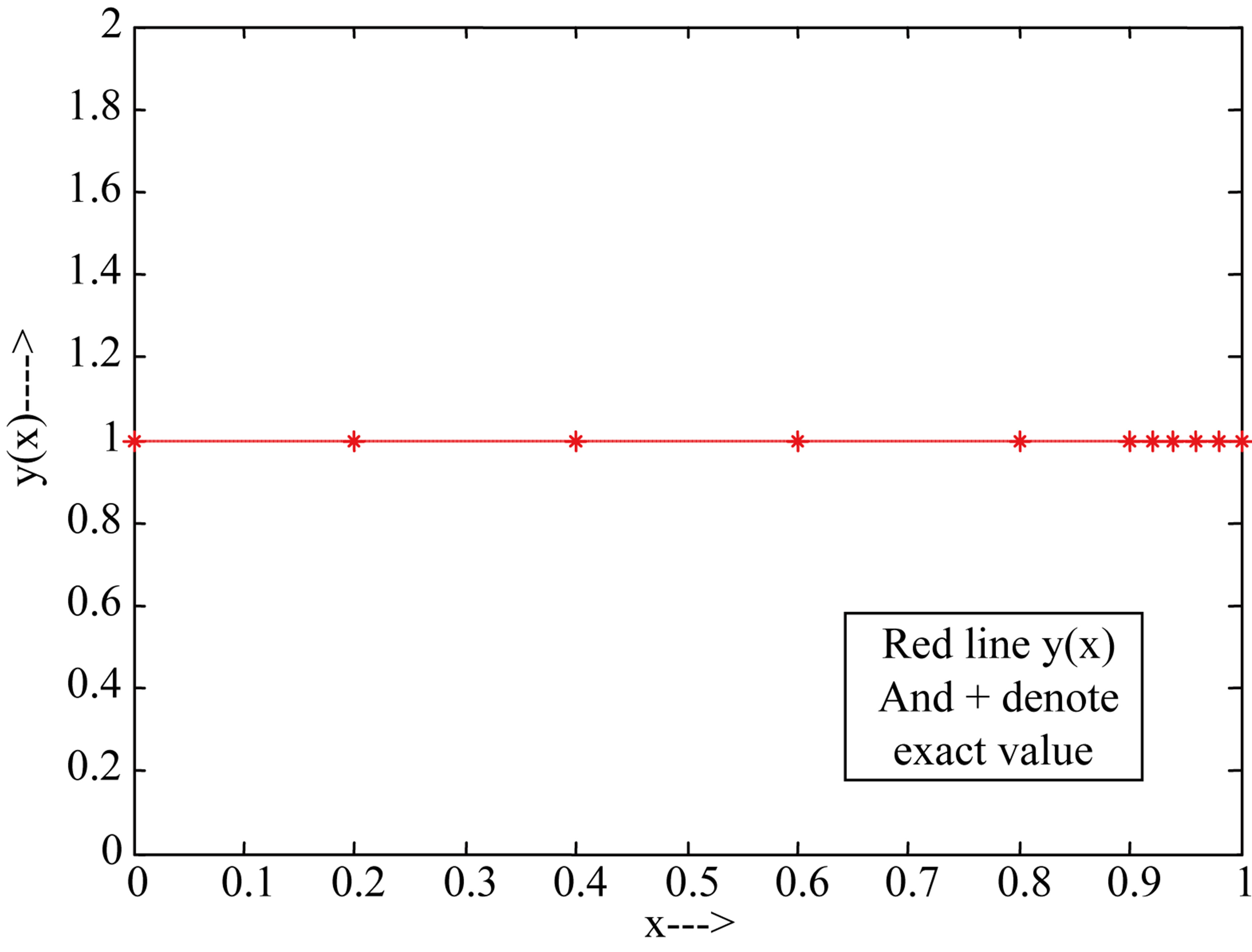
Figure 1. x versus y(x) and exact solution for example 3.1 at ε = 10−3, h = 10−3.

Figure 2. x versus y(x) and exact solution for example 3.1 at ε = 10−4, h = 10−4.
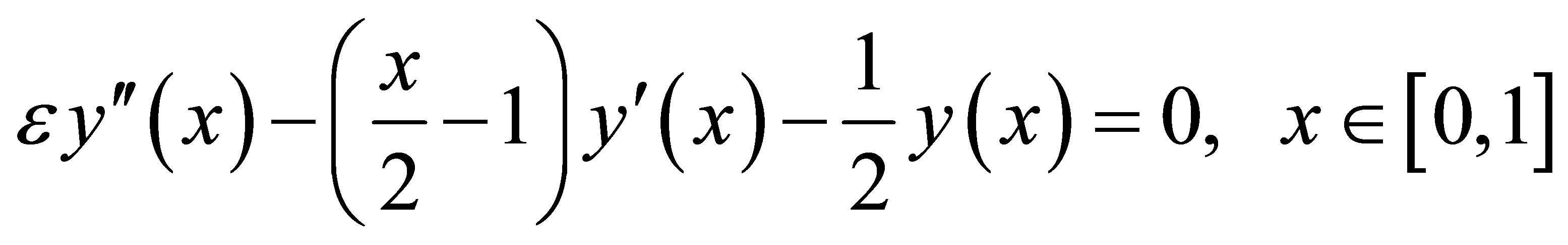 (20)
(20)
 . (21)
. (21)
He has chosen to use uniformly valid approximation (which is obtained by the method given by Nayfeh [12, p. 148, Equation (4.2.32)] as our “exact” solution;
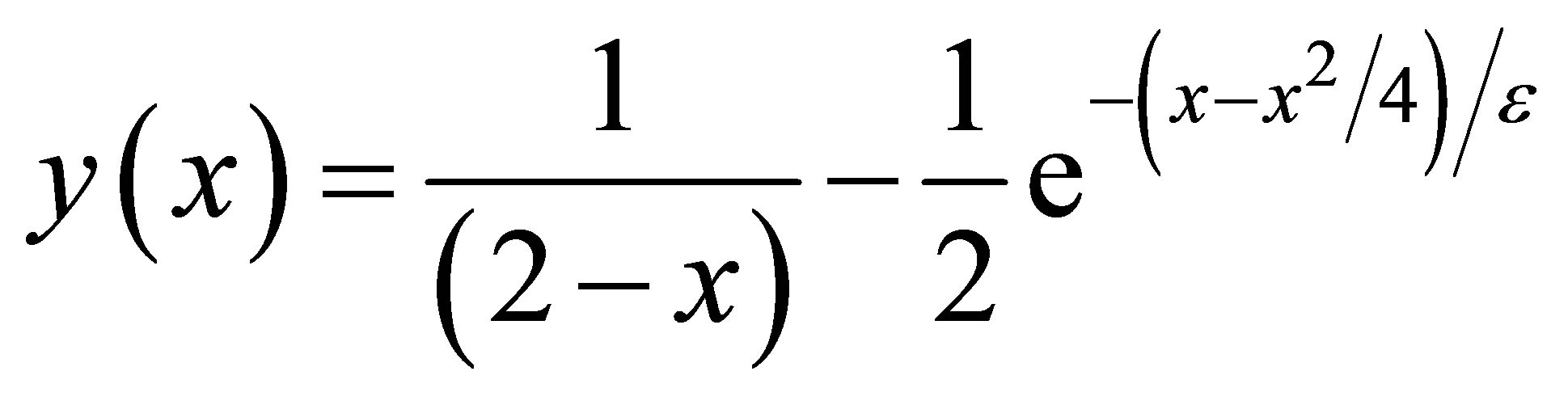
The numerical results are given in Tables 3 and 4 for 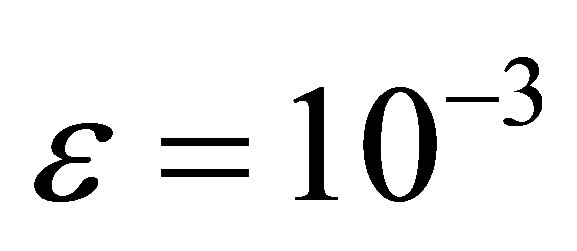 and
and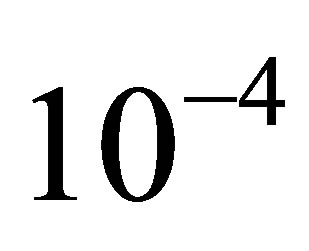 , respectively.
, respectively.
Comparing (20) with (13), we have
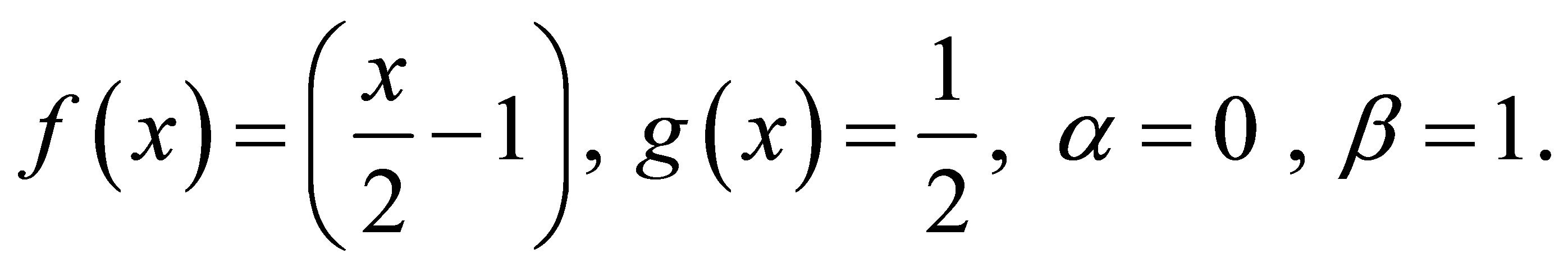
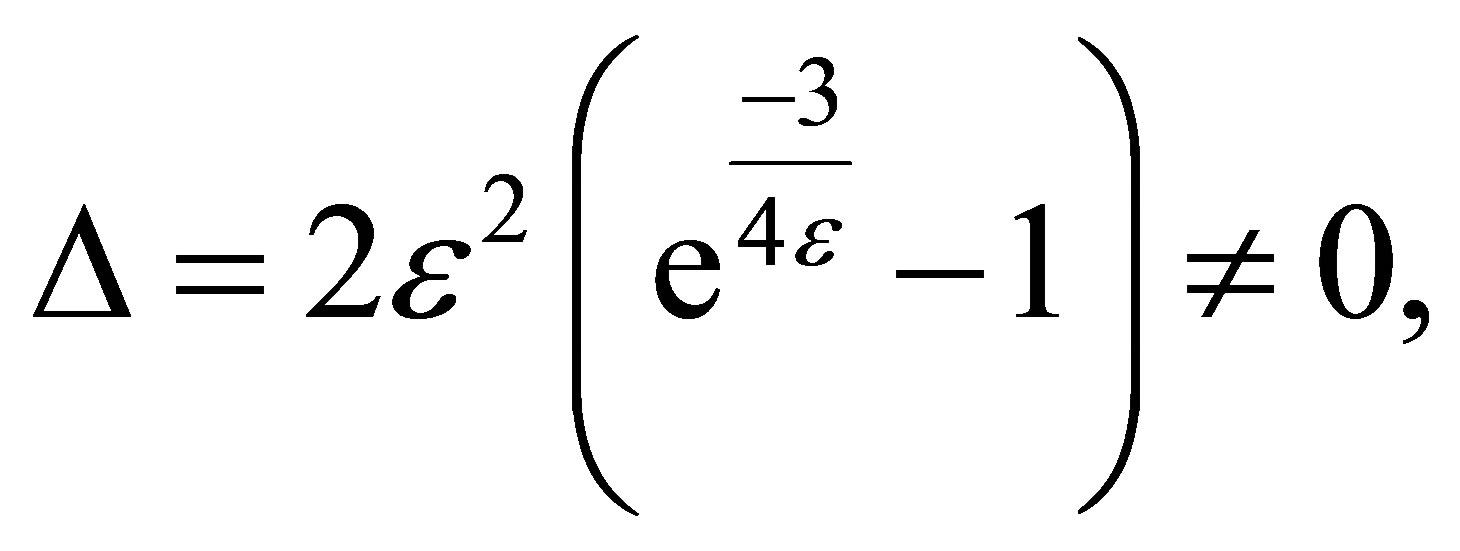
Table 3. Numerical results of example 3.2 with ε = 10−3, h = 10−3.

Table 4. Numerical results of example 3.2 with ε = 10−4, h = 10−4.

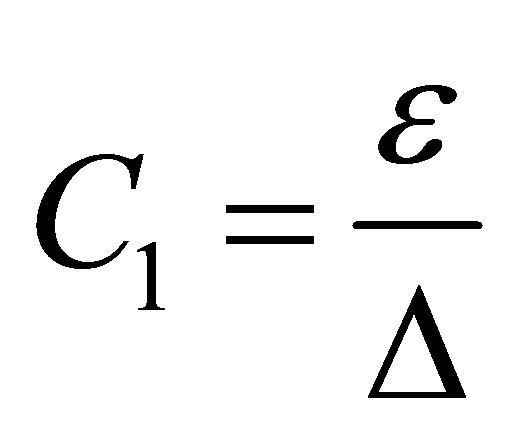
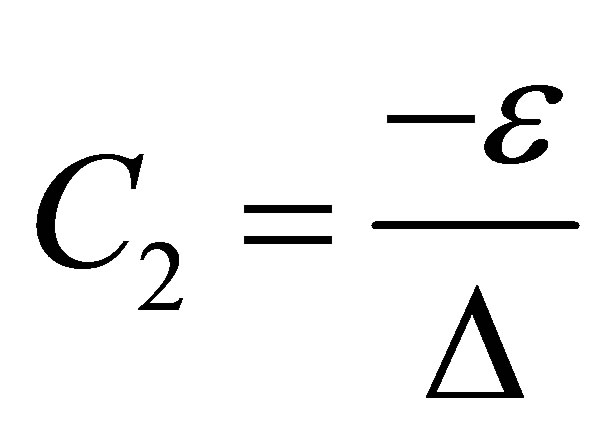
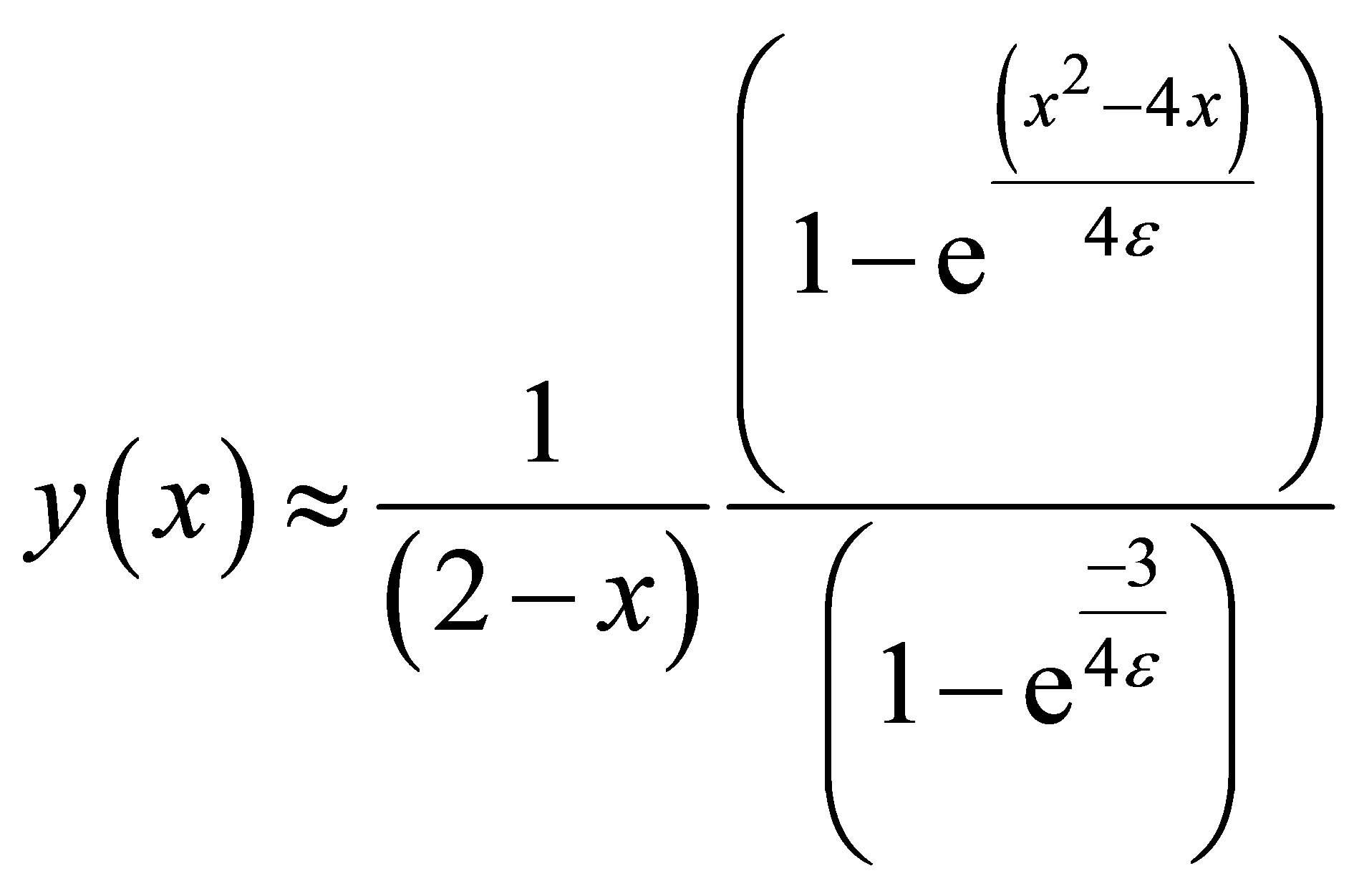 (22)
(22)
The computational results are presented in Tables 3 and 4 for 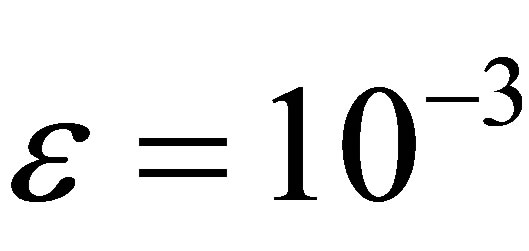 and 10−4, respectively. Figures 3 and 4 show our solution and exact solution for different values of x.
and 10−4, respectively. Figures 3 and 4 show our solution and exact solution for different values of x.
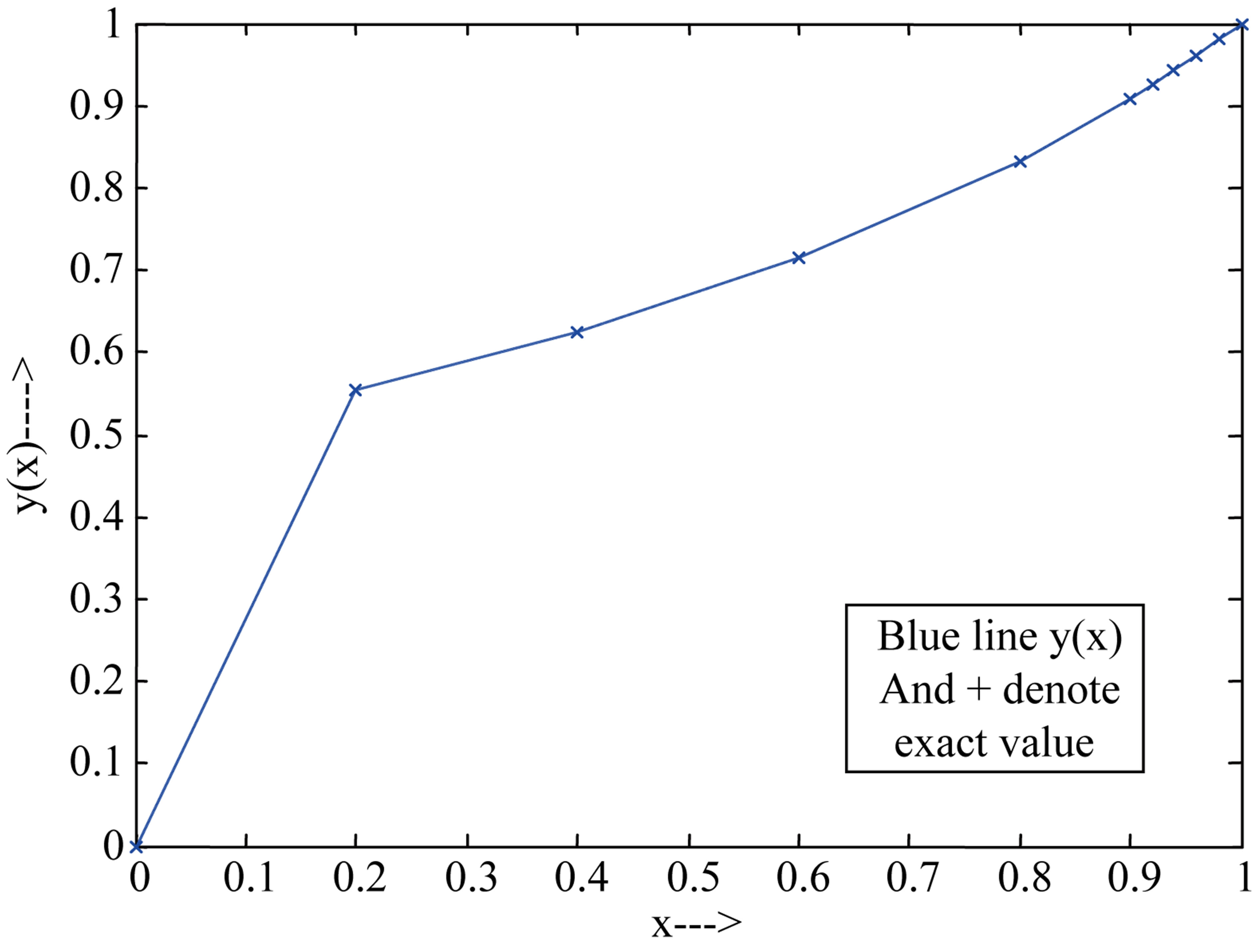
Figure 3. x versus y(x) and exact solution for example 3.2 at ε = 10−3, h = 10−3.
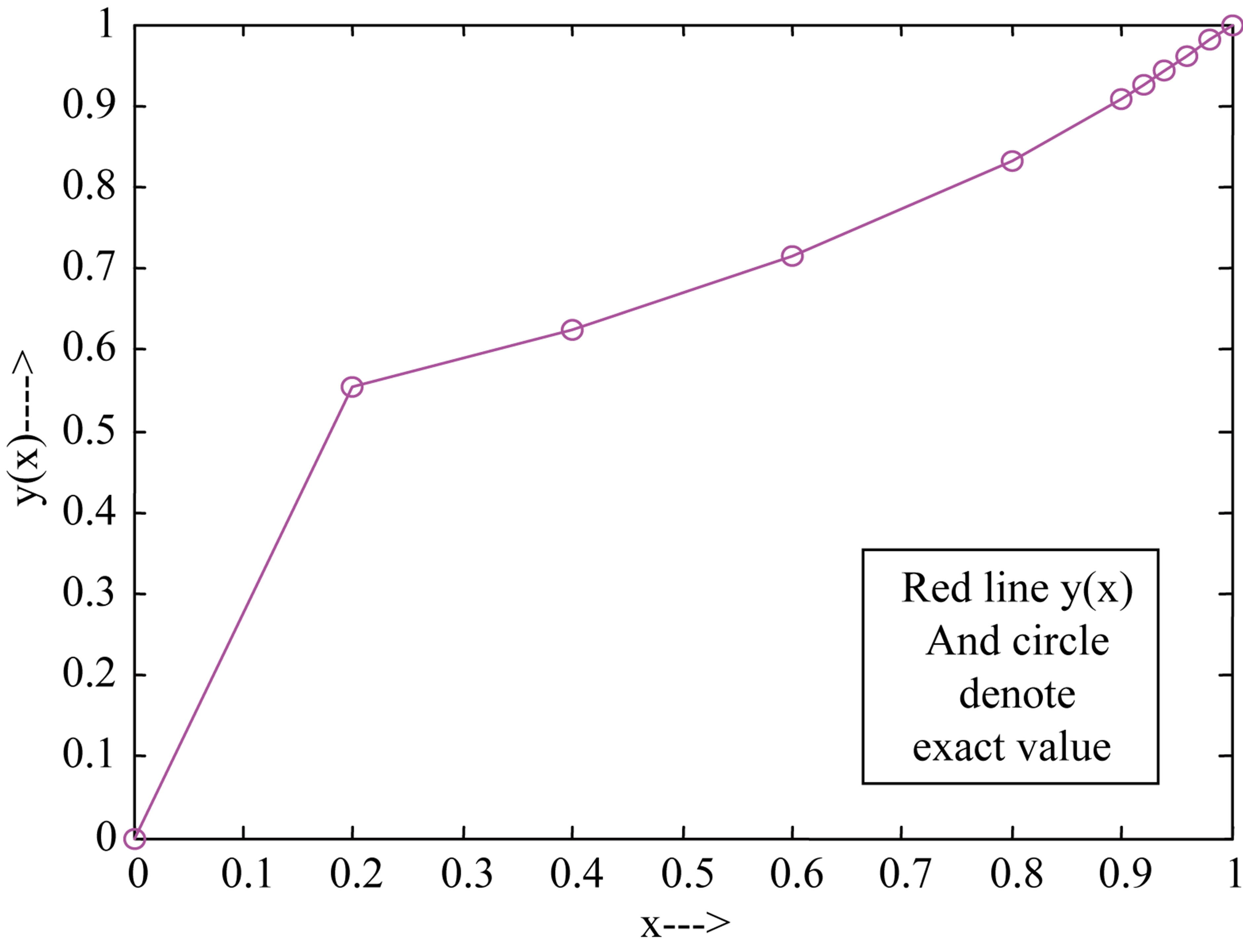
Figure 4. x versus y(x) and exact solution for example 3.2 at ε = 10−4, h = 10−4.
4. Conclusion
In this paper, authors concerned with the numerical solutions of singularly perturbed two-point boundary value problems with right end boundary layer. Here they take the assumption that 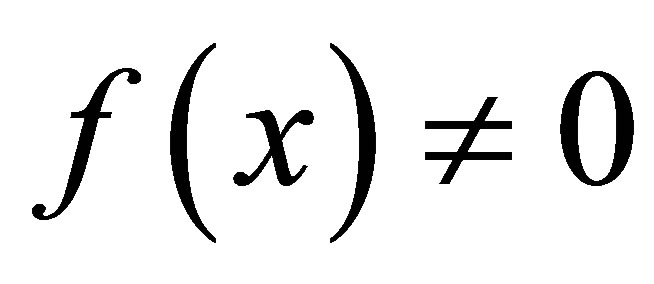 on the whole interval [0, 1], i.e. the function
on the whole interval [0, 1], i.e. the function 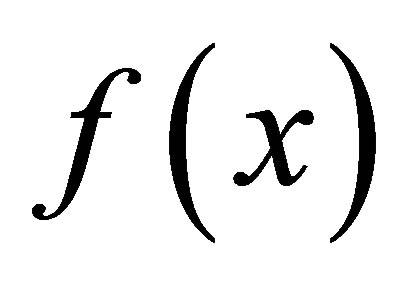 has same sign on the whole interval [0,1]. Our method is good on computer implementation. But this method is not valid if the equation is changed into
has same sign on the whole interval [0,1]. Our method is good on computer implementation. But this method is not valid if the equation is changed into
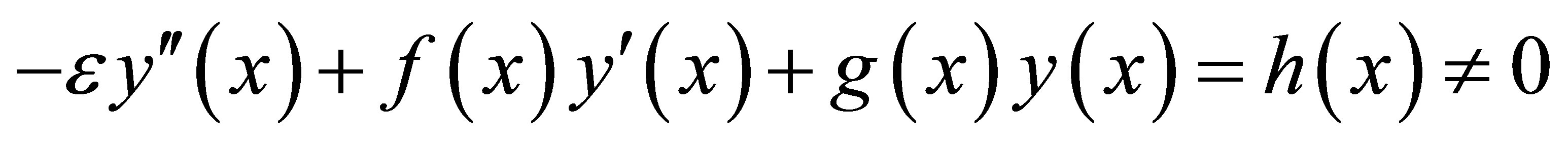
i.e. in no-homogeneous form.
REFERENCES
- C. M. Bender and S. A. Orszag, “Advanced Mathematical Methods for Scientists and Engineers,” McGraw-Hill, New York, 1978.
- J. Kevorkian and J. D. Cole, “Perturbation Methods in Applied Mathematics,” Springer-Verlag, New York, 1981. doi:10.1007/978-1-4757-4213-8
- R. E. O’Malley, “Singular Perturbation Methods for Ordinary Differential Equations,” Springer-Verlag, New York, 1991. doi:10.1007/978-1-4612-0977-5
- J. J. H. Miller, E. O’Riordan and G. I. Shishkin, “Fitted Numerical Methods for Singular Perturbation Problems,” World Scientific, Singapore City, 1996.
- A. H. Nayfeh, “Perturbation Methods,” Wiley, New York, 1973.
- M. K. Kadalbajoo and Y. N. Reddy, “Approximate Method for the Numerical Solution of Singular Perturbation Problems,” Applied Mathematics and Computation, Vol. 21, No. 3, 1987, pp. 185-199. doi:10.1016/0096-3003(87)90001-4
- M. Kumar, H. K. Mishra and P. Singh, “Numerical Treatment of Singularly Perturbed Two-Point Boundary Value Problems Using Initial Value Method,” Journal of Applied Mathematics and Computation, Vol. 29, No. 1-2, 2009, pp. 229-246. doi:10.1007/s12190-008-0127-3
- M. Kumar, H. K. Mishra and P. Singh, “Initial Value Technique for Self-Adjoint Singular Perturbation Boundary Value Problems,” Computational Mathematics and Modeling, Vol. 20, No. 2, 2009, pp. 207-217. doi:10.1007/s10598-009-9029-y
- Z. C. Lin and M. R. Zhou, “Singular Perturbations in Applied Mathematics,” Jiangsu Education Press, Nanjing, 1995.
- H. K. Mishra, “An Order Reduction Method of Second Order Singular Perturbation Boundary Value Problems,” Jnanabha, Vol. 40, 2010, pp. 49-62.
- Y. N. Reddy and P. Pramod Chakravarthy, “Method of Reduction of Order for Solving Singularly Perturbed Two-Point Boundary Value Problems,” Applied Mathematics and Computation, Vol. 136, No. 1, 2003, pp. 27- 45. doi:10.1016/S0096-3003(02)00015-2
- S. M. Roberts, “A Boundary-Value Technique for Singular Perturbation Problems,” Journal of Mathematical Analysis and Applications, Vol. 87, No. 2, 1982, pp. 489-503. doi:10.1016/0022-247X(82)90139-1
- S. M. Roberts, “The Analytical and Approximate Solutions of
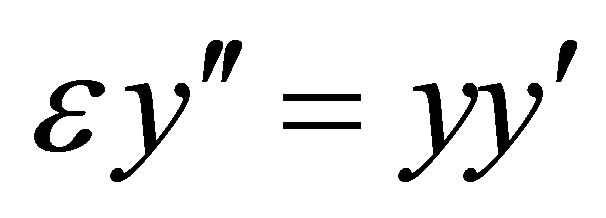 ,” Journal of Mathematical Analysis and Applications, Vol. 97, No. 1, 1983, pp.245-265. doi:10.1016/0022-247X(83)90249-4
,” Journal of Mathematical Analysis and Applications, Vol. 97, No. 1, 1983, pp.245-265. doi:10.1016/0022-247X(83)90249-4 - S. M. Roberts, “Solution of
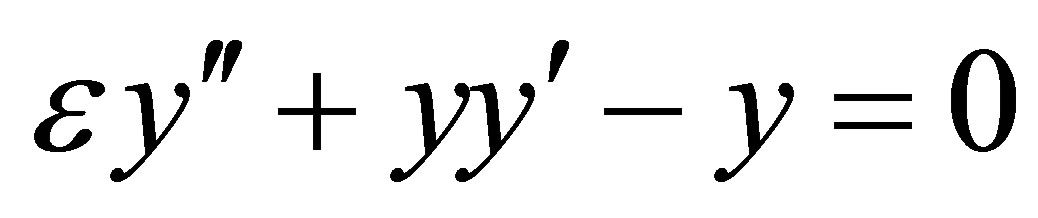 by a NonAsymptotic Method,” Journal of Optimization Theory and Applications, Vol. 44, No. 2, 1984, pp. 303-332. doi:10.1007/BF00935440
by a NonAsymptotic Method,” Journal of Optimization Theory and Applications, Vol. 44, No. 2, 1984, pp. 303-332. doi:10.1007/BF00935440 - Z. Du and Z. Bai, “Asymptotic Solution for a SecondOrder Differential Equation with Three-Point Boundary Conditions,” Applied Mathematics and Computation, Vol. 186, No. 1, 2007, pp. 469-473. doi:10.1016/j.amc.2006.07.110
- Z. Du and L. Kong, “Asymptotic Solution of Singularly Perturbed Second-Order Differential Equations and Application to Multi-Point Boundary Value Problems,” Applied Mathematics Letters, Vol. 23, No. 9, 2010, pp. 980-983. doi:10.1016/j.aml.2010.04.021

