World Journal of Nuclear Science and Technology
Vol.2 No.3(2012), Article ID:21242,9 pages DOI:10.4236/wjnst.2012.23011
Determination of Full Energy Peak Efficiency of NaI(Tl) Detector Depending on Efficiency Transfer Principle for Conversion Form Experimental Values
1Department of Basic and Applied Science, Faculty of Engineering, Arab Academy for Science, Technology and Maritime Transport, Alexandria, Egypt
2Physics Department, Faculty of Science, Alexandria University, Alexandria, Egypt
Email: *mohzaher400@hotmail.com
Received March 18, 2012; revised April 22, 2012; accepted May 11, 2012
Keywords: Full Energy Peak Efficiency; NaI(Tl) Scintillation; Efficiency Transfer
ABSTRACT
In this work we calibrated the NaI(Tl) scintillation detectors (5.08 × 5.08 cm2 and 7.62 × 7.62 cm2) and the Full Energy Peak Efficiency (FEPE) for these detectors have been calculated for point sources placed at different positions on the detector axis using the analytical approach of the effective solid angle ratio. This approach is based on the direct mathematical method reported by Selim and Abbas [1,2] and has been used successfully before to calibrate the cylindrical, parallelepiped, and 4π NaI(Tl) detectors by using point, plane and volumetric sources. In addition, the present method is free of some major inconveniences of the conventional methods.
1. Introduction
Determination of detector efficiency is very important in various scientific and industrial fields. Because the experimental work is tedious and even difficult for extended sources, many researches have been focused on the development of computational techniques to determine these efficiencies. There are three famous methods used in this field, the semi-empirical, the Monte Carlo, and the direct mathematical methods. One of these computational techniques is the efficiency transfer method in which the computation of the detector efficiency for various geometrical conditions is derived from the known efficiency for a reference source-detector geometry. The main advantage of the Efficiency Transfer approach with a point calibration source located at a sufficient distance from the detector is that one may neglect coincidence summing effects and obtain a coincidence free efficiency curve [3]. The efficiency transfer method is particularly useful due to its insensitivity to the inaccuracy of the input data, e.g. to the uncertainty of the detector characterization [4,5].
Change in efficiency under conditions of measurement different from those of calibration can be determined on the basis of variation of the geometrical parameters of the source-detector arrangement. By calculation, it is possible to determine the efficiency corresponding to non-point samples and/or different distances. The basic case corresponds to calibration with known efficiency for a point source located at position, Pο, at energy, E, the efficiency can be expressed as:
 (1)
(1)
where,  , represents the intrinsic efficiency of the detector for energy, E, and, Ωeff(Po), is the solid angle subtended by point, Pο, and the active surface of the detector, this geometrical factor must include absorbing factors, taking into account the attenuation effects in the materials between the source and the active part of the crystal [6].
, represents the intrinsic efficiency of the detector for energy, E, and, Ωeff(Po), is the solid angle subtended by point, Pο, and the active surface of the detector, this geometrical factor must include absorbing factors, taking into account the attenuation effects in the materials between the source and the active part of the crystal [6].
For a point source located at a different distance, P, the efficiency can be written, in a similar manner, as:
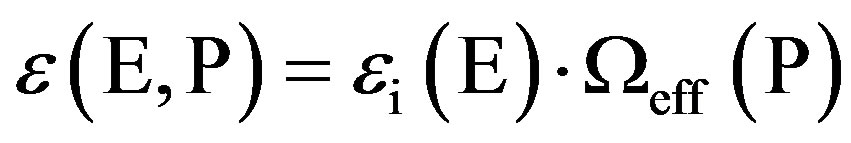 (2)
(2)
So we can establish the basic relationship which makes it possible to express the efficiency as a function of the reference efficiency, known at the same energy, E:
 (3)
(3)
In general, by knowing the source-detector geometry, we can compute the detector efficiency for different positions using the principle of efficiency transfer by computing the relevant solid angle and absorbing factors [7].
2. Mathematical Treatment
Selim and co-workers using the spherical coordinate system derived direct analytical elliptic integrals to calculate the detector efficiencies (total and full-energy peak) for any source-detector configuration [8].
The solid angle, (Ω), subtended by the detector at the source point has been given by Abbas [9], and it is defined as
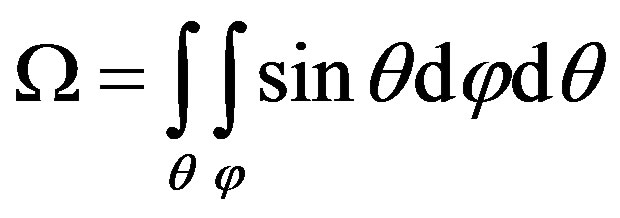 (4)
(4)
The effective solid angle is defined as:
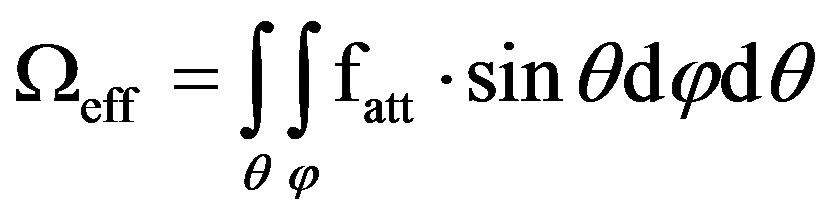 (5)
(5)
where, fatt, factor determins the photon attenuation by all absorbers between source and detector and it is expressed as:
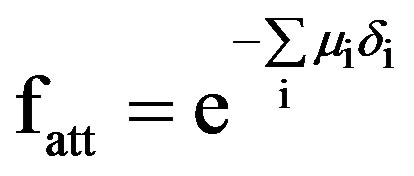 (6)
(6)
where, μi, is the attenuation coefficient of the ith, absorber for a gamma-ray photon with energy, Eγ, and, δi, is the average gamma photon path length through the ith absorber.
The location of an arbitrarily positioned axial point source is specified by, (h, θ, φ) where, h, is the sourcedetector distance, see Figure 1, and the polar, θ, and the azimuthal, φ, angles at the point of entrance of the considered surface define the direction of the incidence of a gamma-ray photon. Where, the polar angles can be expressed as, Abbas [9]
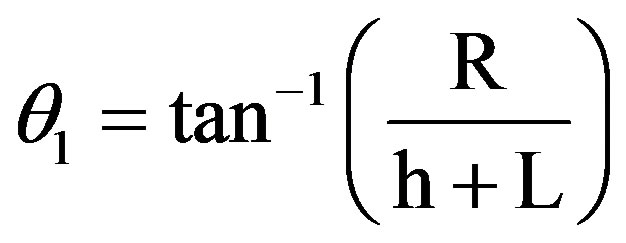 &
&  (7)
(7)
And the azimuthal angles (j) will be from 0 to 2π, therefore the effective solid angle can be expressed as:
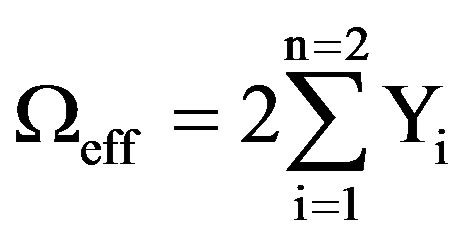 (8)
(8)
where:
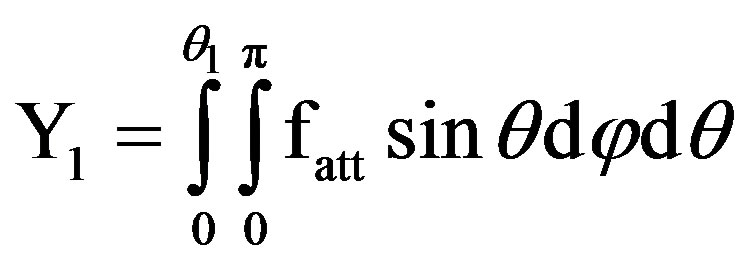 ,
,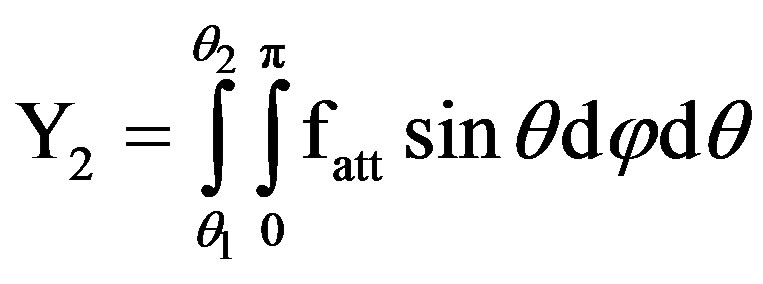 (9)
(9)
The previous integrations calculated numerically by using the trapezoidal rule in a BASIC program.
3. Experimental Setup
The Full Energy Peak Efficiency values will determined for NaI(Tl) Scintillation Detector Model number 802- made by Canberra USA in this work two NaI (Tl) scin-
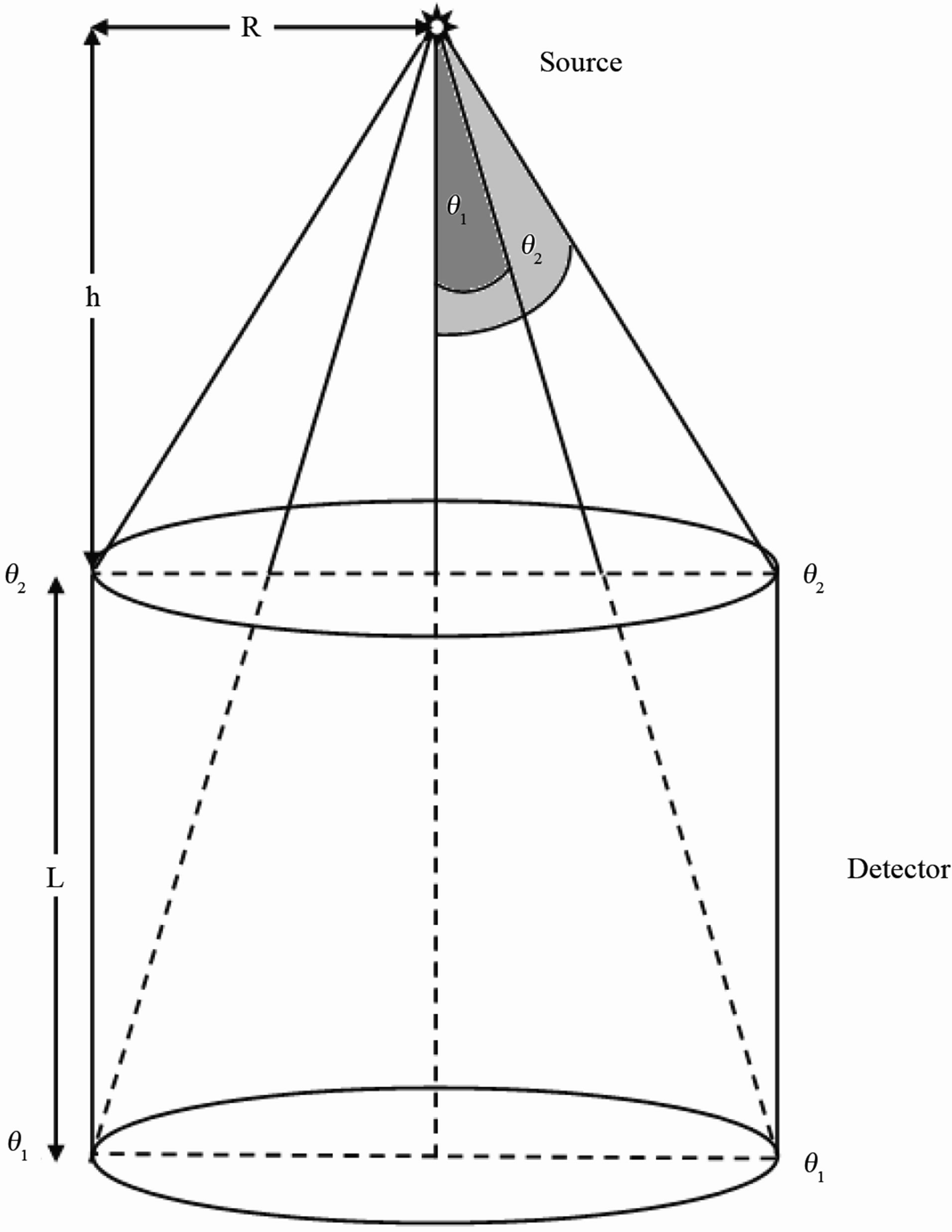
Figure 1. An axial point source with cylindrical detector.
tillation detectors (5.08 × 5.08 cm2) detector (D1) with resolution 8.5% which specified at the 661 keV, and (7.62 × 7.62 cm2) detector (D2) with resolution 7.5% which also specified at the 661 keV were used. The details of these detectors setup parameters with acquisition electronics specifications are listed in Table 1 supported by the (serial & model) number.
In these measurements, the standard point sources 241Am, 133Ba, 152Eu, 137Cs and 60Co where used (these point sources were purchased from The PhysikalischTechnische Bundesanstalt (PTB) in Braunschweig and Berlin). The certificates give the sources activities and their uncertainties for (PTB) sources are listed in Table 2. The data sheet states values of half lives, photon energies and photon emission probabilities per decay for the all radionuclides used in the calibration process are listed in Table 3, which available from the National Nuclear Data Center Web Page or on the IAEA website.
The calibration process was done by using (PTB) point sources, measured these sources at seven different axial distances starts from 20 cm up to 50 cm by step 5 cm each time from the detectors surface, using the homemade Plexiglas holder which placed directly on the detector entrance window as an absorber to avoid the effect of β- and x-rays and to protect the detector heads, so there is no correction was made for x-gamma coincidences, since in most cases the accompanying x-ray were

Table 1. Detectors setup parameters with acquisition electronics specifications for Detector (D1) and Detector (D2).
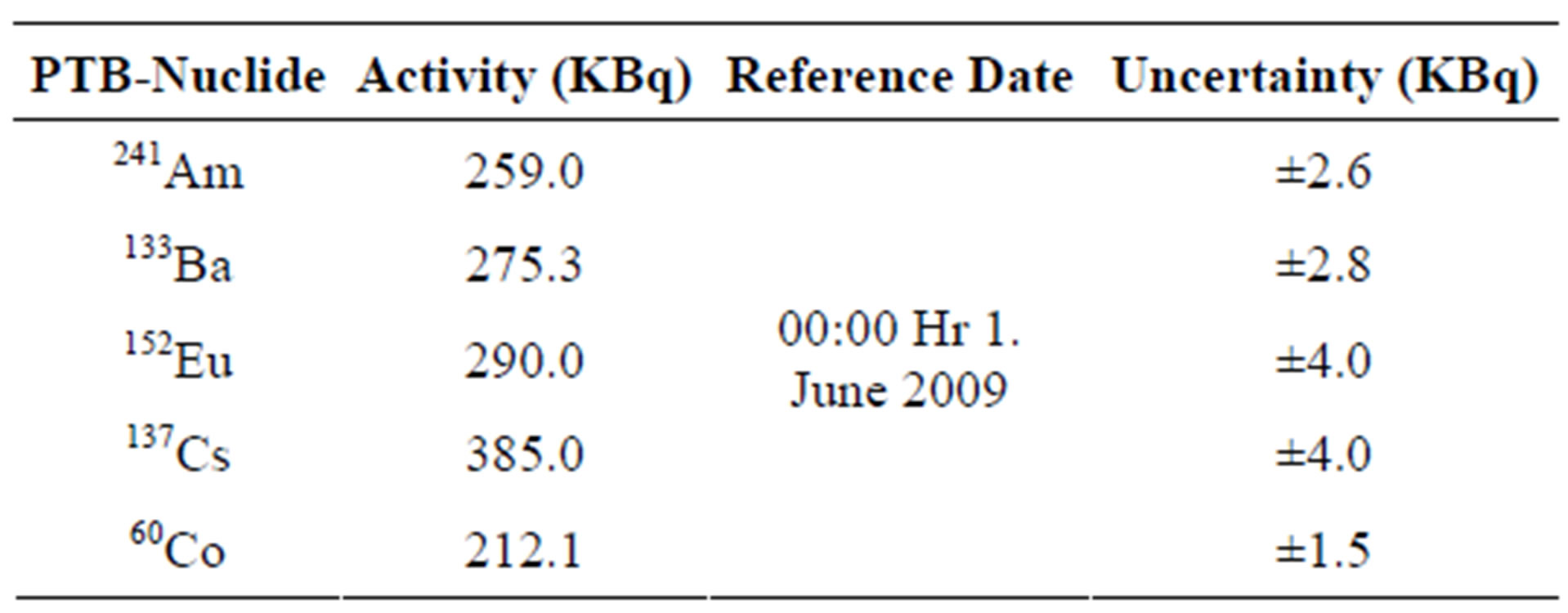
Table 2. PTB point sources activities and their uncertainties.
soft enough to be absorbed completely before entering the detector [10]. The source-detector separations start from 20 cm to neglect the coincidence summing correction.
The spectrum was recorded as example P4D1, where, P, refers to the source type (point) measured on detector (D1) at the distance number (4), which means (h = 20 cm).
The spectrum acquired with winTMCA32 software made by ICx Technologies, were analyzed with (Genie 2000 data acquisition and analysis software) made by Canberra using its automatic peak search and peak area calculations, along with changes in the peak fit using the interactive peak fit interface when necessary to reduce
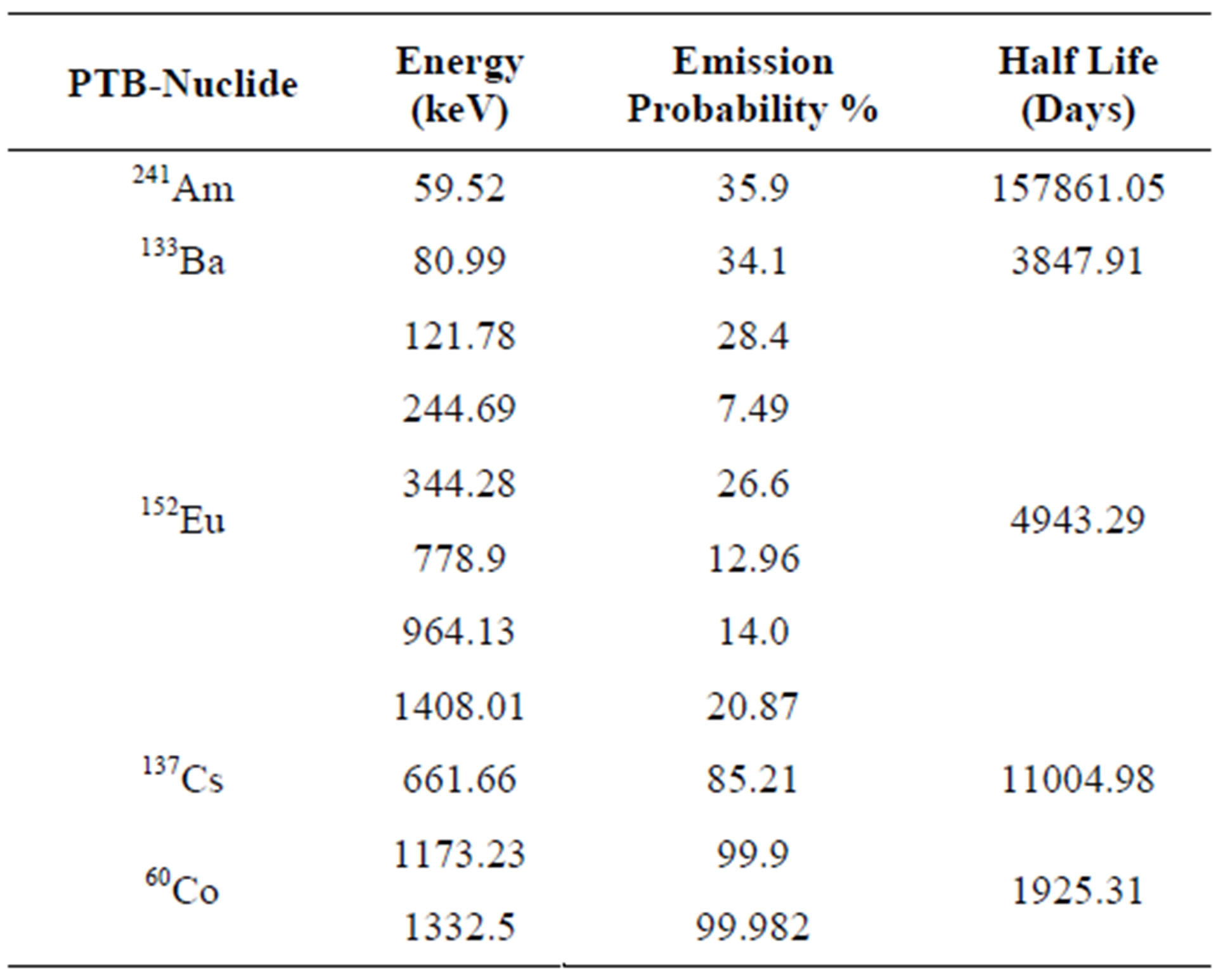
Table 3. Half lives, photon energies and photon emission probabilities per decay for the all radionuclide’s used in this work.
the residuals and error in the peak area values. The live time, the run time and the start time for each spectrum were entered in the spread sheets. Those sheets were used to perform the calculations necessary to generate the experimental full energy peak efficiency (FEPE) curves with their associated uncertainties as a function of the photon energy for all cylindrical NaI(Tl) detectors listed in Table 1 and with different point sources positions.
The ETNA program used to convert the Full Energy Peak Efficiency (FEPE) curve from point sources at position (P4) to the FEPE at positions (P5, P6, P7, P8, P9 and P10). These calculations extended for two cylindrical NaI(Tl) detectors (D1 & D2).
4. Results and Discussion
This part shows the comparisons between the efficiency transfer theoretical method (ETTM) with the experimental work which is done at Younis S. Selim Laboratory for Radiation Physics, Faculty of Science, Alexandria University. This laboratory uses several coaxial NaI(Tl) scintillation detectors (5.08 × 5.08 cm2 and 7.62 × 7.62 cm2) which used in the present work. The detectors were calibrated by measuring low activity point sources, which previously described. The theoretical Full Energy Peak Efficiency (FEPE) can obtain as described in Equation (3).
Another method of calibration is by using ETNA program (an acronym standing for Efficiency Transfer for Nuclide Activity measurements) developed in the Laboratoire National Henri Becquerel (BNM/LNHB) CEA/ Saclay, France by Marie Christine [11]. The percentage error between the measured and the calculated efficiencies is given by:
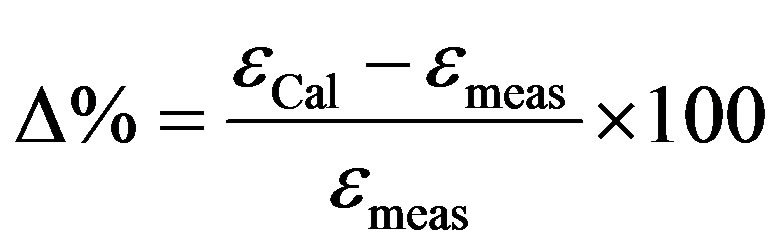 (10)
(10)
where, εCal and εmeas, are the calculated and experimentally measured efficiencies, respectively.
The measured efficiency values as a function of the photon energy, ε(E), for all NaI(Tl) scintillation detectors were calculated by:
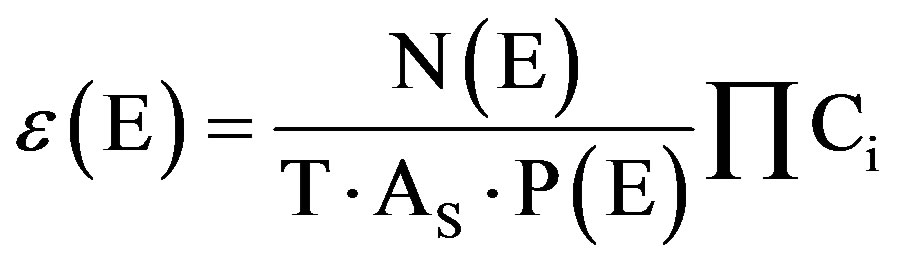 (11)
(11)
where, N(E), is the number of counts in the full-energy peak which can be obtained using Genie 2000 software, T, is the measuring time (in second), P(E), is the photon emission probability at energy, E, AS, is the radionuclide activity and, Ci, are the correction factors due to dead time, radionuclide decay.
In these measurements of low activity sources, the dead time always less than 3%, so the corresponding factor was obtained simply using ADC live time. The statistical uncertainties of the net peak areas were smaller than 1.0% since the acquisition time was long enough to get number of counts at least 10,000 counts. The background subtraction was done. The decay correction, Cd, for the calibration source from the reference time to the run time was given by:
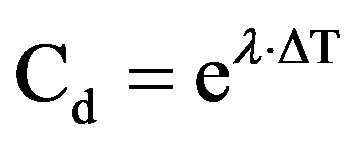 (12)
(12)
where, λ, is the decay constant and, ΔT, is the time interval over which the source decays corresponding to the run time. The main source of uncertainty in the efficiency calculations was the uncertainties of the activities of the standard source solutions. Coincidence summing effects were negligible in the reference measurement geometries.
The uncertainty in the full-energy peak efficiency, σε, was given by:
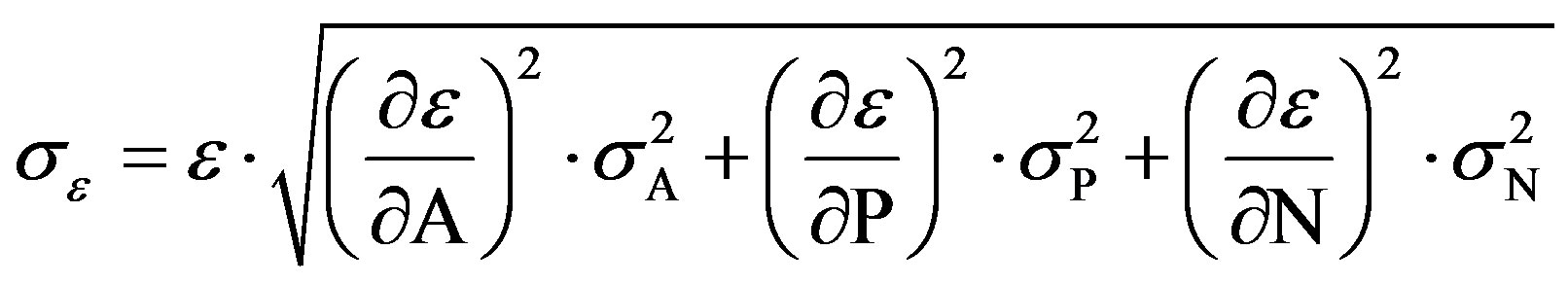 (13)
(13)
where, σA, σP, and, σN, are the uncertainties associated with the quantities, AS, P(E), and, N(E), respectively, assuming that the only correction made is due to the source activity decay.
In order to study the effect of the detector volume, and the source-to-detector distance on the full-energy peak efficiency of NaI(Tl) detectors (D1 and D2), comparing the measured efficiency for different source detector arrangement were done.
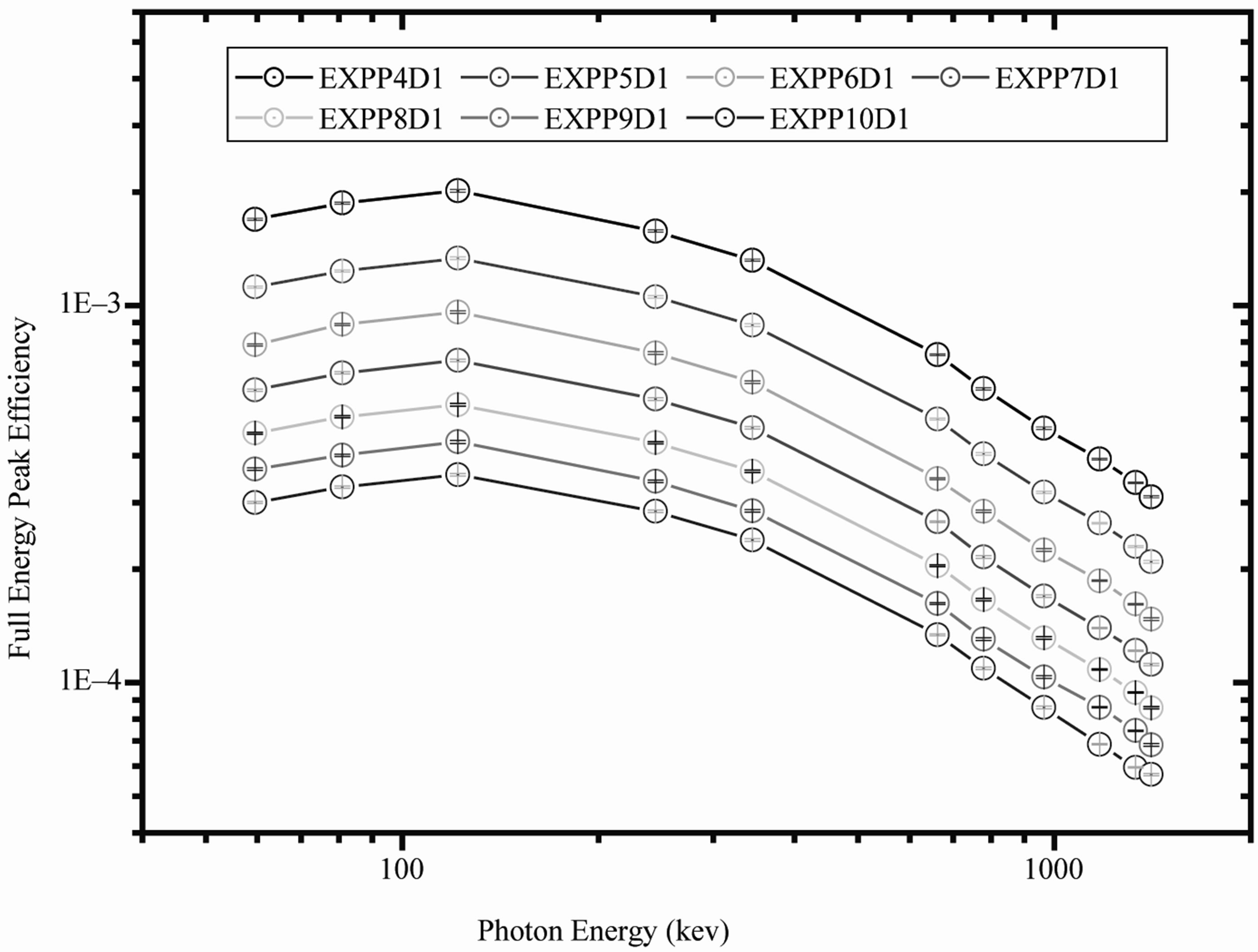
For D1 the maximum measured FEPE value of detector measured with point sources placed at P4 and the minimum one which measured at P10. Also we found that D2 obey the same behavior, by comparison between D1 and D2 results we found that D2 FEPE is greater than it for D1, P4D2 has the maximum FEPE and P10D1 has the minimum one as shown in Figure 2. This phenomenon related to that, the gamma-ray intensity emanating from a source falls off with the distance according to the inverse square law. In addition to the larger detector in dimensions is the more efficient one.
The full-energy peak efficiency calculated by the pre-
 (a)
(a) (b)
(b)
Figure 2. Comparison between various experimental (FEPE) efficiency results for measured point sources at different positions (P4 up to P10) by using detectors (D1 and D2). (a) Detector (D1) Experimental results; (b) Detector (D2) Experimental results.

Figure 3. Comparison between ETNA, ETTM, and experimental (FEPE) efficiencies for conversion from point sources at (P4 up to P10) using (D1) detector.
sent ETTM and ETNA program over a wide energy range and have been tested against various data sets obtained by the experimental method using point sources measured from position P4 up to P10 by (D1 and D2), respectively, and good agreement was obtained from the comparisons, see Figures 3 and 4.
The efficiency of the detectors is higher at low source energies (absorption coefficient is very high) and decreases as the energy increases (fall off in the absorption coefficient) because the photoelectric is dominant below 100 keV, which mean in other words that it is higher for the bigger detector than the smaller one and it is higher for lower source energy than higher source energy because of the dominance of the photoelectric at lower source energies.
The present work provides a great understanding to several aspects of gamma-ray spectroscopy and will provide us with useful tools ETTM for efficiency calculation for detectors (D1 and D2). This method constitute good approach for the efficiency computation for laboratory routine measurements and can save time in avoiding experimental calibration for different position geometries, where the values of the efficiency calculations using ETTM was compared with the measured ones Tables 4 and 5.
5. Conclusion
This work show the way to a simple method (ETTM) to compute the full-energy peak efficiency over a wide energy range, which deal with different detector types using isotropic axial point sources. The present work can be extensive to calculate the FEPE for more complicated geometries. The discrepancies in wide-ranging for all the measurements were found to be less (8%) in case of ETNA program and our ETTM expressions with the

Table 4. Point sources theoretical full energy peak efficiency for D1 (ETTM), and the Discrepancy percentage (Δ%) with experimental values.
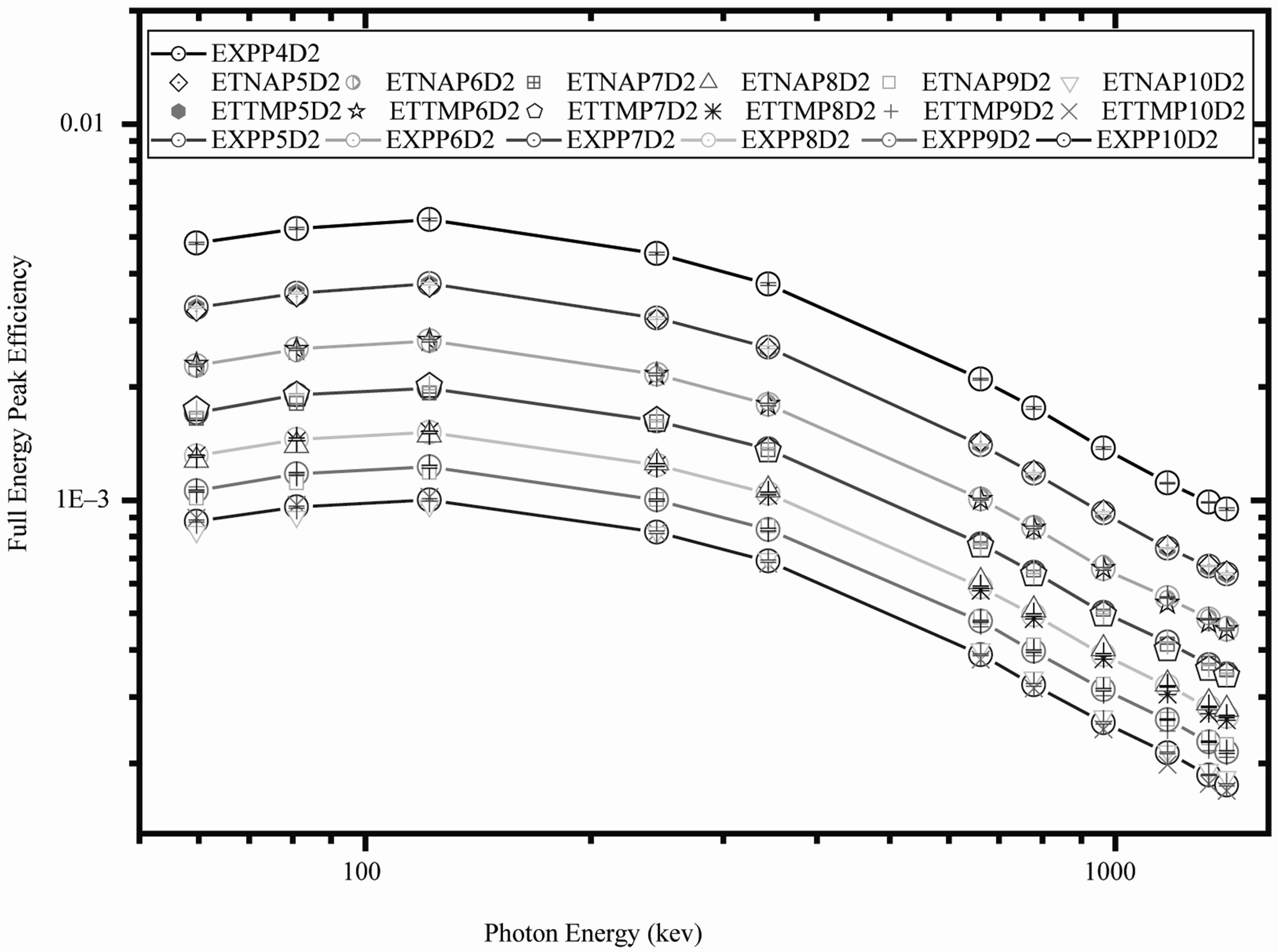
Figure 4. Comparison between ETNA, ETTM, and experimental (FEPE) efficiencies for conversion from point sources at (P4 up to P10) using (D2) detector.
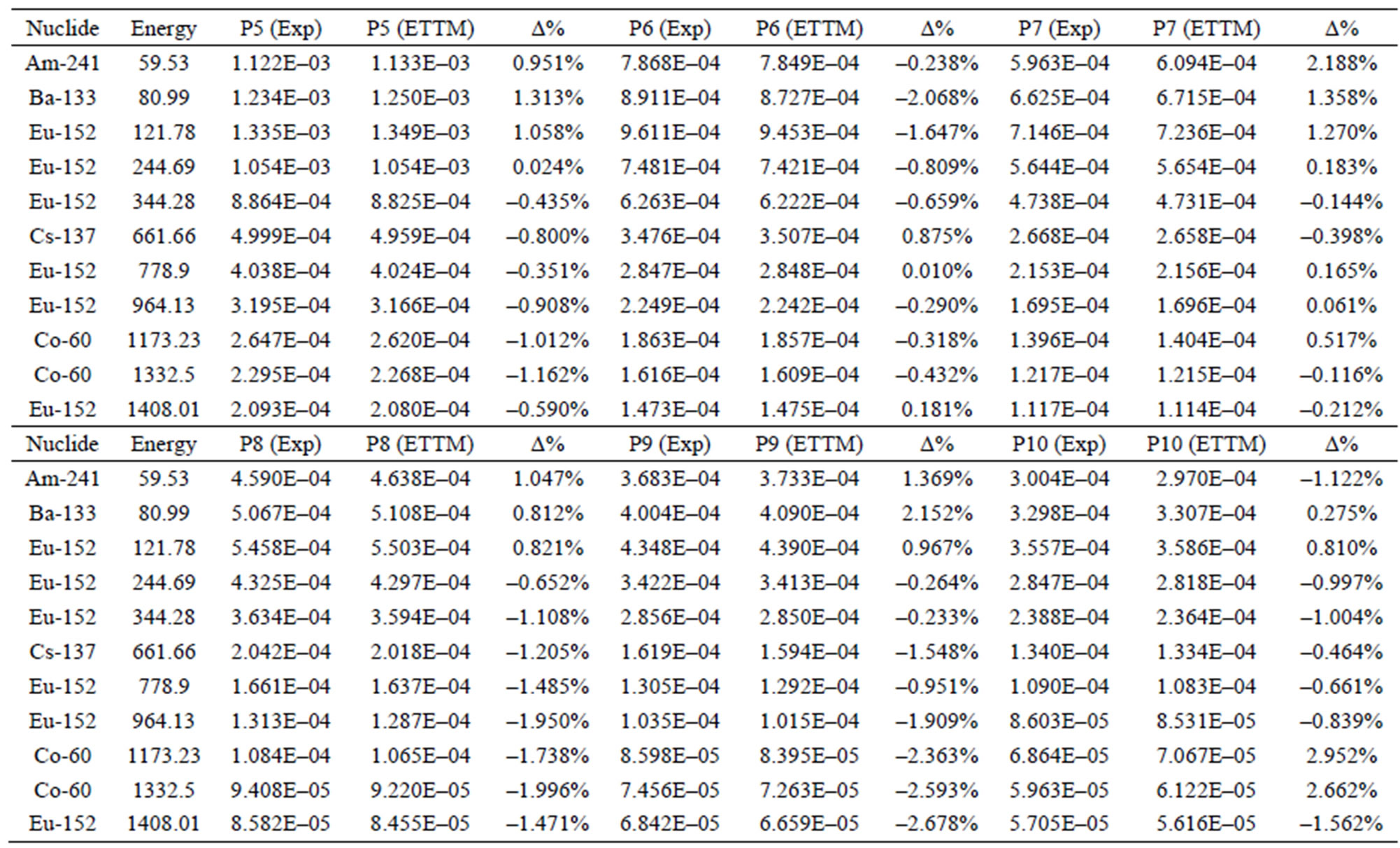
Table 5. Point sources theoretical full energy peak efficiency for D2 (ETTM), and the Discrepancy percentage (Δ%) with experimental values.
experimental values at all energy region.
6. Acknowledgements
The authors would like to introduce a special thanks to Prof. Mahmoud I. Abbas, Faculty of Science, Alexandria University, for fruitful help.
REFERENCES
- Y. S. Selim and M. I. Abbas, “Source-Detector Geometrical Efficiency,” Radiation Physics and Chemistry, Vol. 44, No. 1-2, 1994, pp. 1-4. doi:10.1016/0969-806X(94)90093-0
- Y. S. Selim and M. I. Abbas, “Direct Calculation of the Total Efficiency Cylindrical Scintillation Detectors for Extended Circular Sources,” Radiation Physics and Chemistry, Vol. 48, No. 1, 1996, pp. 23-27. doi:10.1016/0969-806X(95)00047-2
- V. Tim, B. Vodenik and M. Necemer, “Efficiency Transfer between Extended Sources,” Applied Radiation and Isotopes, Vol. 68, No. 12, 2010, pp. 2352-2354. doi:10.1016/j.apradiso.2010.05.010
- M. C. Lepy, et al., “Intercomparison of Efficiency Transfer Software for Gamma-Ray Spectrometry,” Applied Radiation and Isotopes, Vol. 55, No. 4, 2001, pp. 493-503.
- T. Vidmar, et al., “An Intercomparison of Monte Carlo Codes Used in Gamma-Ray Spectrometry,” Applied Radiation and Isotopes, Vol. 66, No. 6-7, 2008, pp. 764-768. doi:10.1016/j.apradiso.2008.02.015
- F. Piton, et al., “Efficiency Transfer and Coincidence Summing Corrections for Gamma-Ray Spectrometry,” Applied Radiation and Isotopes, Vol. 52, No. 3, 2000, pp. 791-795. doi:10.1016/S0969-8043(99)00246-8
- S. Jovanovic, et al., “ANGLE: A PC-Code for Semiconductor Detector Efficiency Calculations,” Radiation Physics and Chemistry, Vol. 218, No. 1, 1997, pp. 13-20.
- M. S. Badawi, “Faculty of Science,” Ph.D. Thesis, Alexandria University, Alexandria, 2009.
- M. I. Abbas, “HPGe Detector Absolute Full-Energy Peak Efficiency Calibration including Coincidence Correction for Circular Disc Sources,” Journal of Physics D: Applied Physics, Vol. 39, No. 18, 2006, pp. 3952-3958. doi:10.1088/0022-3727/39/18/005
- K. Debertin and U. Schotzig, “Coincidence Summing Corrections in Ge(Li)-Spectrometry at Low Source-to-Detector Distances,” Nuclear Instruments and Methods, Vol. 158, 1979, pp. 471-477.
- M.-C. Lépy, M.-M. Bé and F. Piton, “ETNA (Efficiency Transfer for Nuclide Activity measurements) Software for Efficiency Transfer and Coincidence Summing Corrections in Gamma-Ray Spectrometry,” CEA-SACLAY, DA-MRI-LNHB, Bât.602, 91191 GIF-SUR-YVETTE CEDEX, France, 2004.
NOTES
*Corresponding author.

