World Journal of Nuclear Science and Technology
Vol.2 No.1(2012), Article ID:16556,5 pages DOI:10.4236/wjnst.2012.21001
Reduction of Systematic Error in Radiopharmaceutical Activity by Entropy Based Mutual Information
Research Institute of Nuclear Engineering, University of Fukui, Fukui-shi, Japan
Email: gstptk@gmail.com, t_takeda@u-fukui.ac.jp
Received August 21, 2011; revised September 21, 2011; accepted October 18, 2011
Keywords: Random and Systematic Errors; Covariance Matrix; Limits for Correlated Elements by Determinant Inequalities; Mutual Information; Reduction of Systematic Errors by Maximizing Mutual Information
ABSTRACT
The quality of the radiation dose depends upon the gamma count rate of the radionuclide used. Any reduction in error in the count rate is reflected in the reduction in error in the activity and consequently on the quality of dose. All the efforts so far have been directed only to minimize the random errors in count rate by repetition. In the absence of probability distribution for the systematic errors, we propose to minimize these errors by estimating the upper and lower limits by the technique of determinant in equalities developed by us. Using the algorithm we have developed based on the technique of determinant inequalities and the concept of maximization of mutual information (MI); we show how to process element by element of the covariance matrix to minimize the correlated systematic errors in the count rate of 113mIn. The element wise processing of covariance matrix is so unique by our technique that it gives experimentalists enough maneuverability to mitigate different factors causing systematic errors in the count rate and consequently the activity of 113mIn.
1. Introduction
Radiopharmaceuticals are used in nuclear medicine to study the functioning of organs and tissues. One of the major objectives of these radiopharmaceuticals in radio therapy is to ensure precise delivery of dose to a tumour. As radiation dose is proportional to the radioactivity, any error in measured activity will affect the dose deposited to the organ. Hence, it is important to estimate the amount of radiation delivered by these radiopharmaceuticals both for optimization of image quality and for radiation protection purposes.
The quality of the dose depends upon the gamma count rate of the radionuclide used [1]. The error in the number of counts at the gamma camera is a measure of the error in dose deposited at the human body tissues, which is a cumulative effect of the errors due to instrumentation and nuclear characteristics of the radiopharmaceuticals. Thus, any reduction in error in the count rate is reflected in the reduction in error in the activity and consequently on the quality of dose. The total error in the count rate estimate should include both the random and the systematic errors. To quantify the errors, covariance matrix has been identified as the error matrix as per international recommendation [2]. The diagonal and off diagonal elements of the covariance matrix represent uncorrelated random and the correlated systematic errors respectively. To our knowledge, so far many attempts have been made only to minimize the random error by repetition as it decreases by 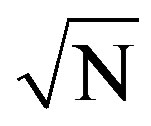 if a measurement is repeated N times. On the contrary, the systematic error can never be reduced by repetition and is the main cause of correlation [3].
if a measurement is repeated N times. On the contrary, the systematic error can never be reduced by repetition and is the main cause of correlation [3].
All the attempts made so far on systematic errors of SPECT imaging, either neglected them [4] or randomized them [5]. The only approach suggested to mitigate the systematic errors is to assume a statistical distribution for them like in Linearized Bayesian Update Procedure (LBUP) [6]. Assuming a statistical distribution for the systematic error requires knowledge of the second central moment or the variance. In the case of the systematic errors, the initial estimate is taken as the mean or the first moment of the probability density function. The estimate of the corresponding variance or the second central moment depends strongly on the availability of supplementary knowledge. As variance is seldom available for the systematic errors, their probability density function cannot be assumed and hence, LBUP cannot be applied in principle.
To circumvent the lack of knowledge of variance, we propose in this paper, estimation of limits for the systematic errors. Accordingly, if the upper and lower limit of the systematic error can be estimated and no additional information exists, then one can assume a constant probability density within these limits [2]. We have developed an algorithm based on the Technique of Determinant Inequalities (TDI) to estimate these limits. These limits are used to maximize the information theoretic concept of Mutual information (MI) to reduce the systematic errors. We demonstrate the utilization of our approach in reducing the systematic errors and consequently the total error in the gamma count rate of 113mIn.
2. Generation of Covariance Matrices from the Neutron Activation Analysis of 113mIn
113mIn is a diagnostic nuclear medicine agent for internal radiotherapy and is also used as a tracer in experimental studies [7]. In our laboratory, 113mIn is produced by neutron activation analysis in a standard neutron field of 252Cf, by the reaction 113In (n, n’) 113mIn. 113In foils with thickness 2.0 cm were irradiated for about 15 hours at a distance of 6 cm from the 252Cf source. The californium 252Cf is a needle type source, containing about 500 µg of 252Cf encapsulated in a stainless steel cylinder having 5 mm diameter and 17 mm height. Induced gamma activities due to 113mIn were measured by a Ge (Li) detector having intrinsic efficiency ε and let the gamma count rate be C. The induced activity A of 113mIn depends upon its neutron absorption cross-section Σ, its atom density N and the induced neutron flux density φ of the 252Cf. If m is the tissue mass, so that (A/m) is the activeity per unit mass, the absorbed dose rate D = k (A/m) E, where k is a constant whose value depends on the units used for other factors in the equation and E is the average energy released per transformation. Since, E is a constant for each radionuclide, k and E can be combined into a single constant Ω, hence, D = Ω (A/m). For a particular tissue mass and specific γ radiation, D = Δ A, where Δ = (Ω/m). Thus,
 (1)
(1)
Thus, as activity A and count rate C are proportional, any reduction in the error of the count rate will lead to the reduction in error in the activity as per law of error propagation [8]. In the gamma count rate measurements of 113mIn, several measurement systematic errors like back scattering from the room walls, geometrical factors are introduced during its formation and attenuation of the gamma ray and gamma ray intensity are introduced during its decay, requiring corrections. Applying the correction factors f to the count rate,

Here,  is the correction factor for each of the
is the correction factor for each of the  systematic errors. For generality, the above equation is rewritten for any element i as
systematic errors. For generality, the above equation is rewritten for any element i as
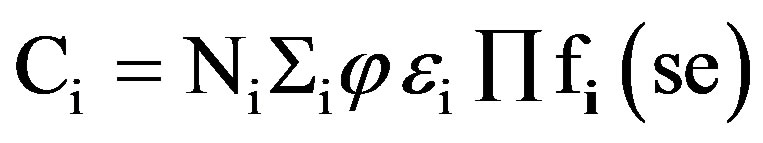 (2)
(2)
In Equation (2), both Σ and φ are unknown. An unknown cross-section is often determined by means of reaction rate ratio measurement relative to a well-known cross-section. The principle behind such relative measurements is the parallel irradiation of two different foils in the same neutron field of 252Cf and subsequently counting their induced activities. Hence, by ratio measurement, unknown neutron flux density φ is eliminated,

In our analysis, we consider formation of 113mIn by two sets of ratio measurement, i.e. 113In (n, n’) relative to 27Al (n, α) and 115In (n, n’) respectively in the standard neutron field of 252Cf.
Differentiating Equation (2) and writing dC/C = δC, one can obtain
 (3)
(3)
The relative covariance MC between the count rate Ci and Cj with its various components as in Equation (2) with their respective correlation coefficient ρij is obtained as follows,
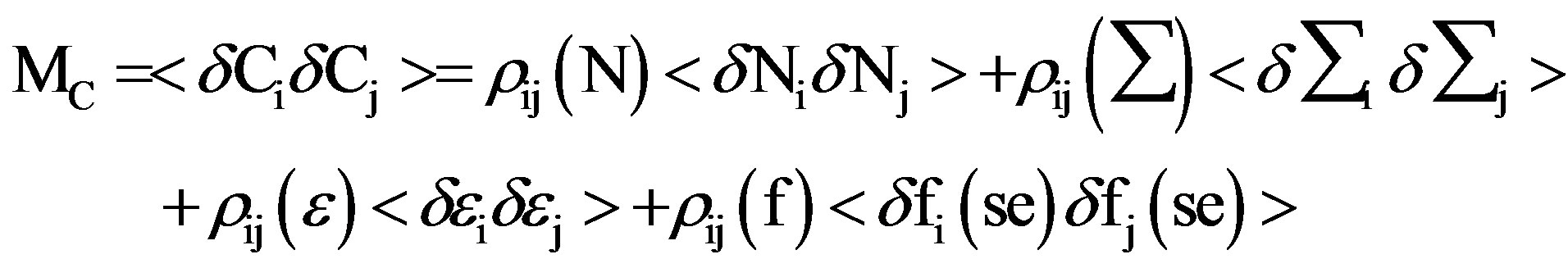
The Determinant of MC is designated as G. i.e. G = Det. MC.
The complete list of all the error contributions with their magnitude and the correlation coefficients depicted in curly braces are given is Table 1. The two 113In foils used for the relative measurements have same correction factors for mass N and hence the errors are fully correlated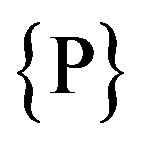 . The correction for geometrical factor
. The correction for geometrical factor  is the same for all measurements and so the corresponding errors show full correlation {Q}. 113mIn is the product nucleus in both the sets of relative measurement and hence the correction factors for half lives
is the same for all measurements and so the corresponding errors show full correlation {Q}. 113mIn is the product nucleus in both the sets of relative measurement and hence the correction factors for half lives  of 113mIn are fully correlated {R}. Similarly since 113mIn is a γ emitter, the correction factors for gamma ray attenuation
of 113mIn are fully correlated {R}. Similarly since 113mIn is a γ emitter, the correction factors for gamma ray attenuation  and intensity
and intensity 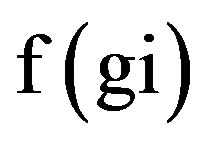 are fully correlated
are fully correlated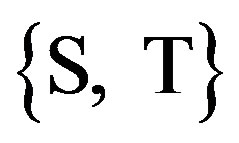 . The sources of back scattering are the room walls and the correction factors
. The sources of back scattering are the room walls and the correction factors  are fully correlated
are fully correlated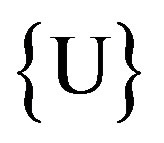 . The details of constructing the covariance matrix given the various correlation coefficients for the above activation measurement is described in detail in [8].
. The details of constructing the covariance matrix given the various correlation coefficients for the above activation measurement is described in detail in [8].
3. Reduction of Systematic Error by Entropy Based Mutual Information
The fundamental property of systematic error is that they vary between a lower limit L and an upper limit U. If a probability distribution of the error over these limits is

Table 1. Errors and their magnitudes and their correlation in 113In activation measurement.
known, then it can be used to describe the error. However, in most of the cases, such a distribution is not known, and it seems reasonable to choose a maximally uncertain density function. The appropriate measure of uncertainty for a distribution is a positive quantity called entropy H, given by,

The larger the entropy, the greater the uncertainty and hence we should choose a density function 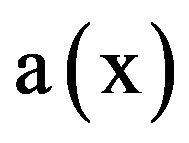 that maximizes the entropy subject to the following constraints,
that maximizes the entropy subject to the following constraints,  for all values of x
for all values of x
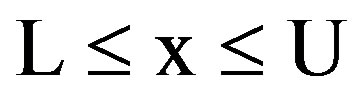
 between the Upper and lower limits.
between the Upper and lower limits.
When data on known standards are available, then, the standard techniques for estimating the end points of a uniform distribution can be used to estimate the limits L and U. But, where no such standards are available, the value of end points should be estimated using the knowledge of the measurement process. Further, in our case, systematic error in cross-section dominates over the statistical and hence conventional central limit theorem fails [9] making it necessary to use information theory approach [10]. A novel property of entropy principle is that it remains valid even if one of the sources of errors is highly correlated and dominant [10]. Further, entropy principle does not make assumptions about the distribution of data thereby belonging to the non-parametric family of statistics. According to information theory, MI is a measure of statistical correlation between the variables, A and C [11]. We show below, how in maximizing the MI, the systematic errors are reduced.
The MI between A and C is expressed as [12]

or
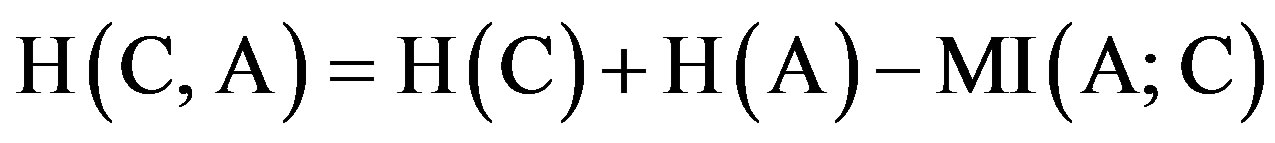
where  and
and 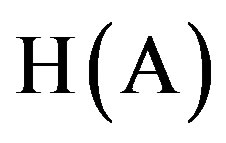 are the entropies or the uncertainty of C and A respectively and
are the entropies or the uncertainty of C and A respectively and  is the joint entropy of C and A.
is the joint entropy of C and A.
1) When,  , then,
, then,  , i.e. joint entropy or uncertainty is the sum of individual uncertainty of C and A.
, i.e. joint entropy or uncertainty is the sum of individual uncertainty of C and A.
2) When,  , then
, then  i.e. joint entropy or uncertainty is less than the sum of individual uncertainty of C and A. Thus, maximizing, MI implies, minimizing the total uncertainty in both C and A.
i.e. joint entropy or uncertainty is less than the sum of individual uncertainty of C and A. Thus, maximizing, MI implies, minimizing the total uncertainty in both C and A.
When, C is having Gaussian distribution, MI is given by [12],
 (4)
(4)
MI thus depends on the determinant of the covariance matrix MC and is always positive and maximizing MI is equivalent maximizing the determinant of the covariance matrix MC.
As an illustration, let us consider a simple case of just two count rates,
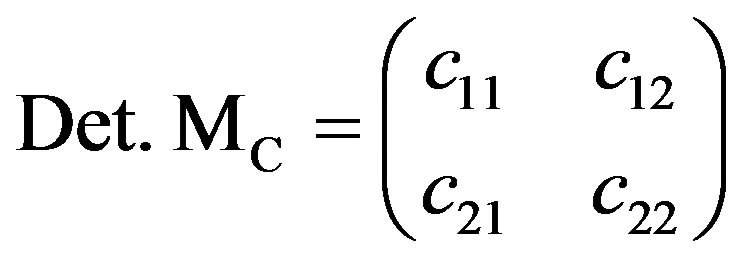
The elements of the covariance matrix can be written as the variances of C1 and C2
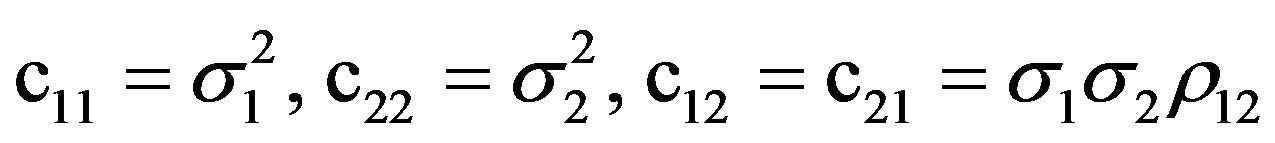 where ρ12 is the correlation coefficient between C1 and C2.
where ρ12 is the correlation coefficient between C1 and C2.
 (5)
(5)
From Equation (5), the maximum value of G is 
 when ρ12 = 0 and minimum value of G is 0, when ρ12 = ±1.
when ρ12 = 0 and minimum value of G is 0, when ρ12 = ±1.
Thus, G depends upon, ρ12 in addition to 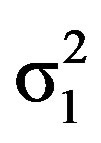 and
and . As mentioned earlier, MI quantifies the amount of correlation between the variables A and C and G can be maximized by minimizing ρ12. Minimization of ρ12 by estimating its limits leads to minimization of correlated systematic errors. Hence, an index of minimization correlated systematic errors is the maximization of MI by the estimation of upper and lower limits for the correlated elements of M. The technique of determinant Inequalities (TDI) to obtain these upper and lower limits [13] and the algorithm [14] based on TDI is described elsewhere and would not be repeated here. The total error (TE) in the count rate, is given by the sum of Uncorrelated Statistical Error (UCSTE) and the Correlated Systematic Error (CSYE).
. As mentioned earlier, MI quantifies the amount of correlation between the variables A and C and G can be maximized by minimizing ρ12. Minimization of ρ12 by estimating its limits leads to minimization of correlated systematic errors. Hence, an index of minimization correlated systematic errors is the maximization of MI by the estimation of upper and lower limits for the correlated elements of M. The technique of determinant Inequalities (TDI) to obtain these upper and lower limits [13] and the algorithm [14] based on TDI is described elsewhere and would not be repeated here. The total error (TE) in the count rate, is given by the sum of Uncorrelated Statistical Error (UCSTE) and the Correlated Systematic Error (CSYE).
 (6)
(6)
where  and
and
 (7)
(7)
Hence lesser the value of ρ12, the lesser is the CSYE and consequently decreases the TE in the count rates.
4. Robustness of the Analysis
According to Hadamard’s inequality [11],
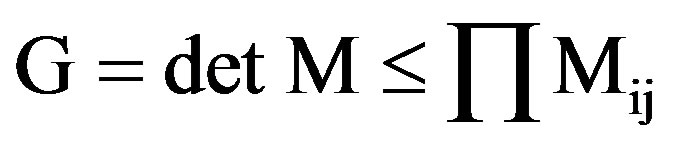 (8)
(8)
The equality is achieved if and only if ρij = 0. The maximum value of the determinant is the product of the diagonal elements and the least positive value is zero, when ρij is either +1 or –1. Since, MI cannot be negative, the value of either the upper or the lower limit of ρij which maximizes G is the robust value which maximizes the MI.
5. Results
The complete covariance matrix MC generated with the contributions due to uncorrelated and correlated errors mentioned in Table 1 is depicted in Table 2. As we have to minimize the correlated systematic error, we focused our attention on the correlated non-diagonal elements in the Matrix MC. The values of the upper and lower limits for these elements are determined by TDI and are tabulated in Table 3 along with the corresponding values of G.
6. Discussion
Systematic errors pervade in all types of physical measurements and affected by errors due to instrumentation, environment and personnel. The best investment is therefore to spend the maximum possible effort on identification and minimization of systematic errors. According to Table 3, the maximum value of G is 465303 for the ideal case of ρij = 0. Only the values of lower limit of matrix MC yield the second largest value of 424657 as compared to both the upper limits and the existing element values of matrix MC. Further, it is apparent that the value of correlation coefficient is also less for the these lower limits and consequently, the corresponding correlated systematic errors is also less according to Equation (7). Since the systematic error is reduced by the lower limits, the total error in count rate is also reduces according to Equation (6). As activity and dose are proportional to the count rate as per Equation (1), any reduction in error in the count rate is reflected in the reduced errors of dose and activity.
From Table 3, it is evident that in using our TDI, element wise processing to minimize the systematic error is feasible by using the concept of MI where the entire structure of the covariance matrix is taken and not by the

Table 2. Covariance Matrix MC for the 113In Activation Measurement.
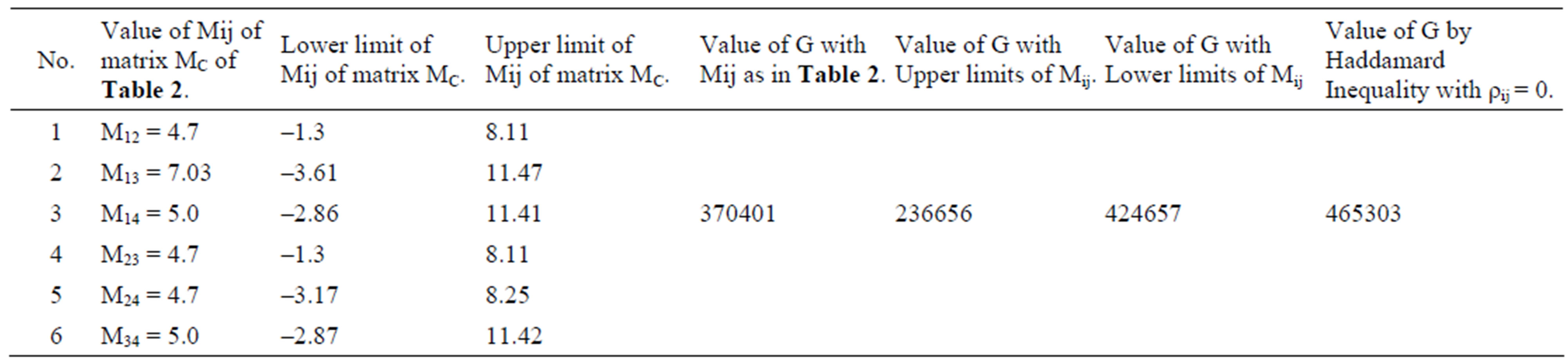
Table 3. Upper and lower limits of the non-diagonal elements of the Matrix MC of Table 2 and the corresponding values of G where G = Det. MC.
Principal Component Analysis (PCA) and Factor analysis methods where the covariance matrix is only decorrelated and factored into dominant eigen values. The element wise processing of covariance matrix is a boon to experimentalists as it gives them enough maneuverability to improve the different factors causing systematic errors by way of improving either the quality of measurement or the associated instrumentation. Hence in our case, upper and lower limits have been given for all the correlated elements as an aid for the experimentalists to venture and such flexibility exists only by method of MI and not by PCA and other methods.
REFERENCES
- L. Carole, C. Claude, E. Paul, F. Nuno, B. Bernard and T. Regine, “Optimization of Injected Dose Based on Noise Equivalent Count Rates for 2- and 3-Dimensional WholeBody PET,” Journal of Nuclear Medicine, Vol. 43, No. 9, 2002, pp. 1268-1278.
- K. Weise and W. Woger, “A Bayesian Theory of Measurement Uncertainty,” Measurement Science and Technology, Vol. 4, No. 1, 1993, pp. 1-11. doi:10.1088/0957-0233/4/1/001
- D. L. Smith, “Probability, Statistics and Data Uncertainties in Nuclear Science and Technology,” American Nuclear Society, Inc., La Grange Park, Illinois, 1991.
- H. J. Kim, B. Zeeberg and R. C. Reba, “Evaluation of Reconstruction Algorithms in SPECT Neuroimaging II: Computation of Deterministic and Statistical Error Components,” Physics in Medicine and Biology, Vol. 38, No. 7, 1993, pp. 881-895.
- D. J. Kadarmas, E. V. R. Di Bella, R. H. Huesman and G. T. Gullberg, “Analytical Propagation of Errors in Dynamic SPECT: Estimators, Degrading Factors, Bias and Noise,” Physics in Medicine and Biology, Vol. 44, No. 8, 1999, p. 1997.
- P. Talou, et al., “Covariance Matrices for ENDF/B-VII235, 238U and 239Pu Evaluated Files in the Fast Energy Range,” Proceedings of the International Conference on Nuclear Data for Science and Technology, 22-27 April 2007, Nice, France.
- M. Neves, A. Kling and A. Oliveira, “Radionuclides Used for Therapy and Suggestion for New Candidates,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 266, No. 3, 2005, pp. 377-384. doi:10.1007/s10967-005-0920-5
- D. L. Smith, “Covariance Matrices and Applications to the Field of Nuclear Data,” ANL/NDM-62, 1981.
- P. Meyer, “Introductory Probability and Statistical Applications,” Addison-Wesley, Reading, MA, 1970.
- F. H. Frohner, “Evaluation of Data with Systematic Errors,” Nuclear Science and Engineering, Vol. 145, No. 8, 2003, pp. 342-353.
- G. Deco and D. Obradovic, “An Information—Theoretic Approach to Neural Computing,” Springer, New York, 1996.
- T. Cover and J. Thomas, “Elements of Information Theory,” Wiley, New York, 1991.
- P. T. K. Kumar, “Estimation of Bounds for Monte Carlo Uncertainty Analysis,” Annals of Nuclear Energy, Vol. 17, No. 9, 1990, pp. 483-486. doi:10.1016/0306-4549(90)90002-U
- P. T. Krishna Kumar, “Algorithm for Evaluation of Bounds for Covariance Based Uncertainty Analysis,” Annals of Nuclear Energy, Vol. 18, No. 8, 1991, pp. 479-481. doi:10.1016/0306-4549(91)90091-B

