World Journal of Nuclear Science and Technology
Vol.2 No.2(2012), Article ID:18578,5 pages DOI:10.4236/wjnst.2012.22008
Nuclear Fuel Cell Calculation Using Collision Probability Method with Linear Non Flat Flux Approach
1Nuclear and Biophysics Research Group, Faculty of Mathematics and Natural Sciences,
Bandung Institute of Technology, Bandung, Indonesia
2Department of Physics, Faculty of Mathematics and Natural Sciences,
Andalas University, Padang, Indonesia
Email: mashafii@fmipa.unand.ac.id
Received May 11, 2011; revised October 27, 2011; accepted December 26, 2011
Keywords: Nuclear Fuel Cell Calculation; Neutron Flux; Linear NFF Approximation
ABSTRACT
Nuclear fuel cell calculation is one of the most complicated steps of neutron transport problems in the reactor core. A few numerical methods use neutron flat flux (FF) approximation to solve this problem. In this approach, neutron flux spectrum is assumed constant in each region. The solution of neutron transport equation using collision probability (CP) method based on non flat flux (NFF) approximation by introducing linear spatial distribution function implemented to a simple cylindrical annular cell has been carried out. In this concept, neutron flux spectrum in each region is different each other because of an existing of the spatial function. Numerical calculation of the neutron flux in each region of the cell using NFF approach shows a fairly good agreement compared to those calculated using existing SRAC code and FF approach. Moreover, calculation of the neutron flux in each region of the nuclear fuel cell using NFF approach needs only 6 meshes which give equivalent result when it is calculated using 24 meshes in FF approach. This result indicates that NFF approach is more efficient to be used to calculate the neutron flux in the regions of the cell than FF approach.
1. Introduction
Collision probability (CP) method has advantage that for relatively simple geometry, more over by its symmetrical feature such as cylindrical cell, due to the angular integration is possible to do analytically. CP method starts from the integral neutron transport equation which is usually used to calculate the flux fine structure in a heterogeneous medium or sub region of the reactor. It is assumed that the cell is a part of a repeating pattern of cells as a net of leakage into or out of the cell. The cell is divided into a number of regions within each of which the source of neutron (resulting from fission or scattering reaction) is treated as uniform and isotropic. The problem of treatment of heterogeneity exists in two parts; that is how to calculate the cell flux and how to produce equivalent homogeneous cross section [1,2]. It has two alternatives to be taken regarding the starting neutron distribution. First, use a flat source distribution within a small volume element which leads to a simple expression from collision probabilities. Second, use the non flat source distribution within a small volume element by introducing a spatial function which can improve the linear approximation of source distribution.
In the previous works [3,4], a conceptually simple numerical method to calculate cell homogenization using neutron first flight collision probabilities have been carried out. The integral transport equation is solved using CP method with the flat flux (FF) approximation. This approach explains that neutron flux spectrum is assumed constant in each region. Now, the new approach of the collision probabilities is considered. In this concept, collision probabilities can be performed using a spatial function distribution that describes a real condition inside the cell. Neutron flux spectrum in each region is different each other because of an existing of the spatial function. This assumption is called as non flat flux (NFF) approximation, so the CP matrix is performed not only by the optical path length as an exponential parameter, but also the shape of the function that describe the behavior of neutron flux spectrum in each region.
In this paper, a mathematical argument to support the new approach has been offered to solve neutron transport equation based on NFF approximation by introducing linear spatial distribution function. The computer program to calculate the neutron flux spectrum distribution in a simple cylindrical annular cell is developed by using library of SLAROM JFS-3-J33 for 70 groups.
2. Materials and Method
The infinitely long cylinder cell model is divided into several annular shells with the outer radius of the shell i is 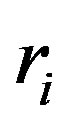 and the outer radius of shell j is
and the outer radius of shell j is  is shown in Figure 1.
is shown in Figure 1.
The probability of neutron born or travelling in region i of cell will have its next collision either in the same region i or in some other region j is defined by [5]
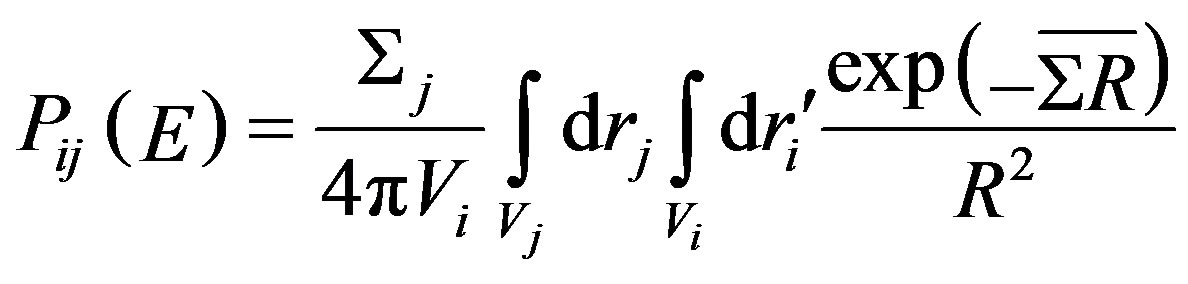 (1)
(1)
If size of each cell is small compared with a neutron mean free path, exponential part in Equation (1), and the total cross section is constant then it is reasonable to assume that the neutron flux is flat therefore the neutrons are distributed uniformly in each regions of the cell [6]. In such situation the flat flux approximation is applied and the neutron transport equation for volume Vj is [5]
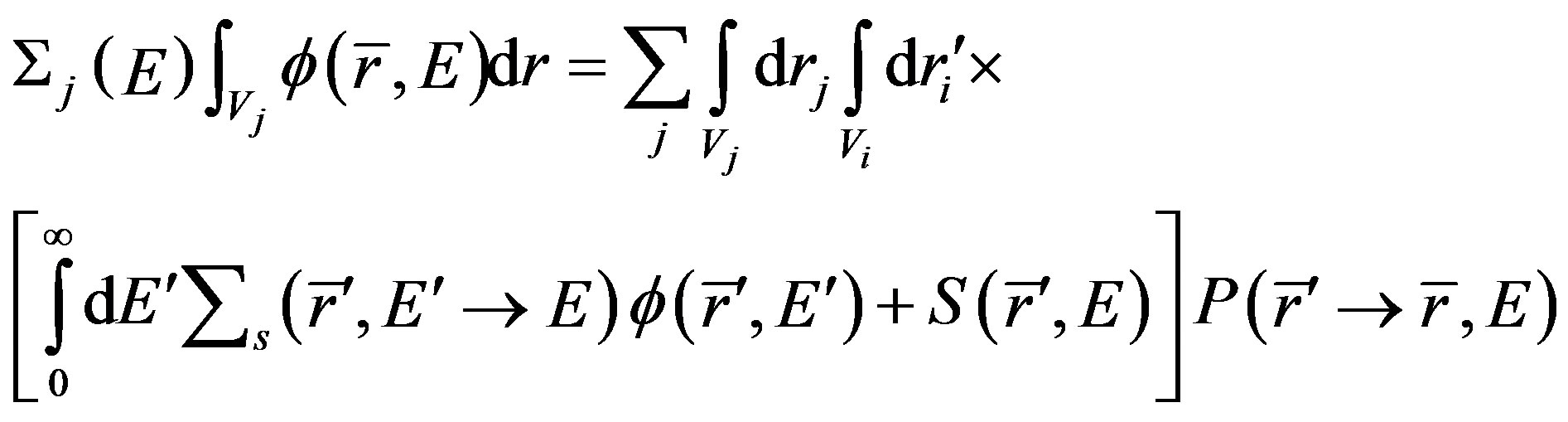 (2)
(2)
Subscript i or j denotes the space dependent of regions, 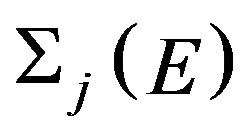 is cross sections associated to j region with energy E,
is cross sections associated to j region with energy E, 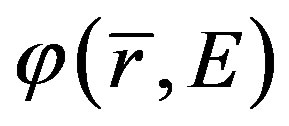 is flux neutron that is assumed constant in each region,
is flux neutron that is assumed constant in each region, 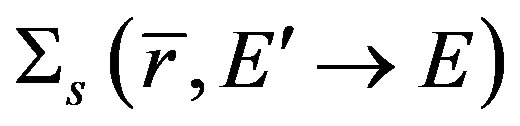 is scattering cross section at point
is scattering cross section at point 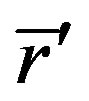 at energy E’ to E,
at energy E’ to E,  is neutron source at the point
is neutron source at the point 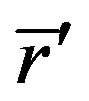 with the energy E.
with the energy E.
If neutron flux is not flat in each region, the neutron flux is defined as
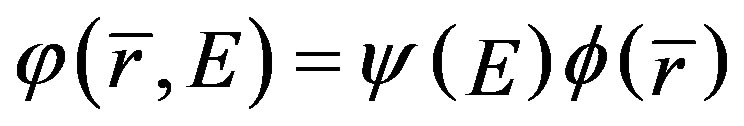 (3)
(3)
Substituting Equation (3) to (2) leads to
 (4)
(4)
Integrating left side of (4) over volume V equal to sum of each region volume Vj.The neutron flux in each region is remain non-flat due to the region distribution function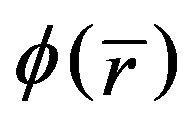 . For 1D case the variation of neutron flux in each region has liniear relationship, read
. For 1D case the variation of neutron flux in each region has liniear relationship, read
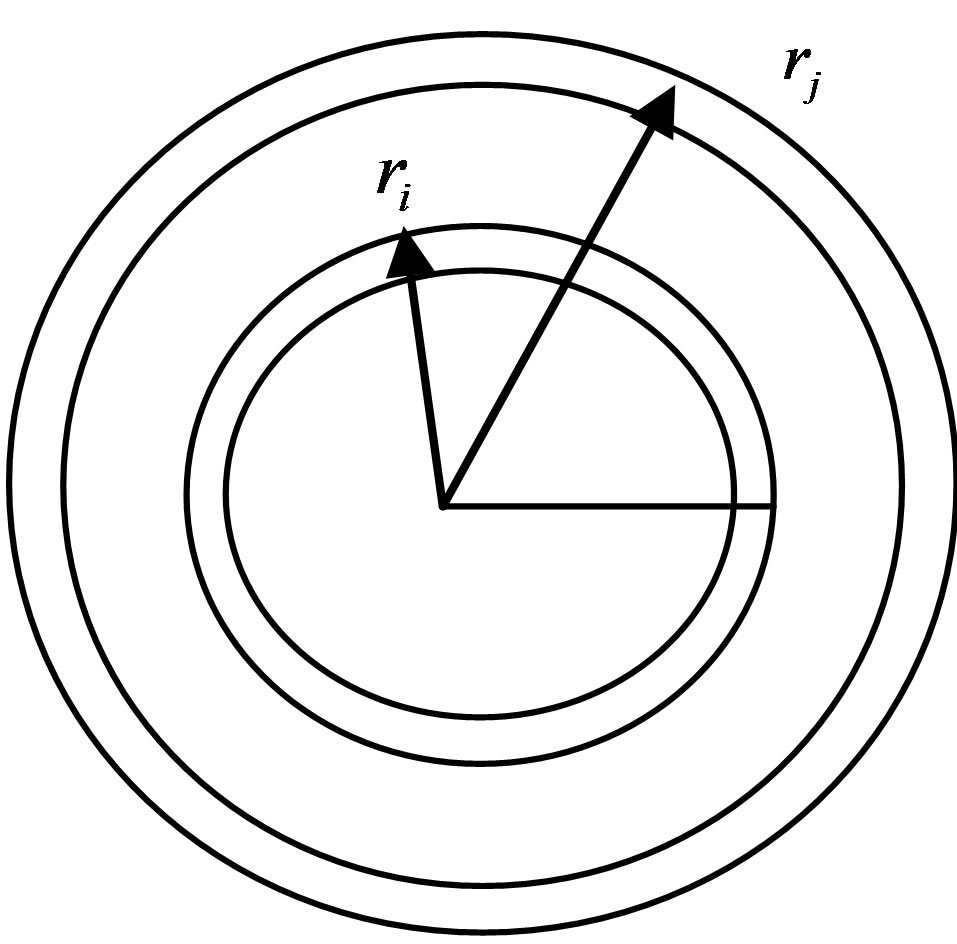
Figure 1. Modeled nuclear fuel cell.
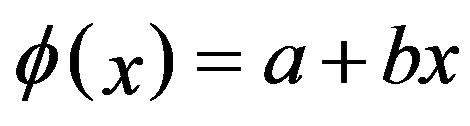 (5)
(5)
Coefficients a and b are determined by using linier interpolation scheme at two adjacent nodes of the region as shown in Figure 2 [7].
By using nodal boundary condition, the neutron flux at nodal are
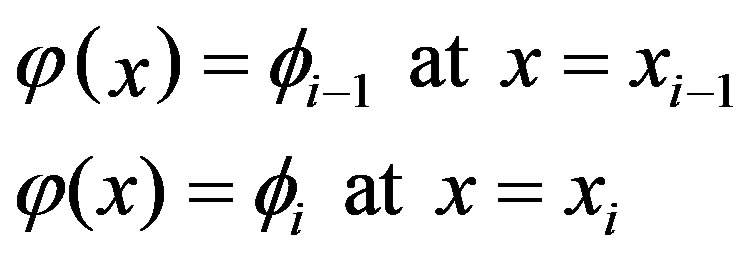
then (5) becomes to
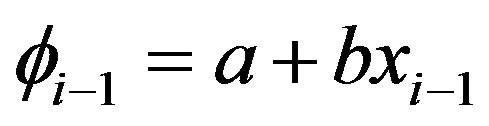 and
and  (6)
(6)
where 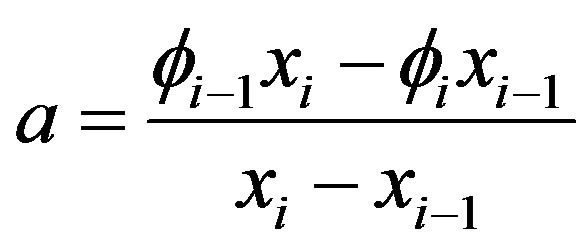 and
and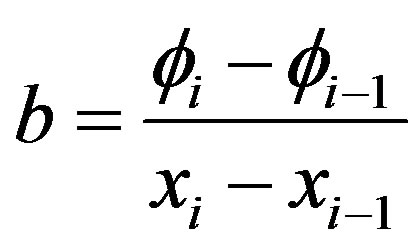 .
.
Substituting (6) into (5) yields
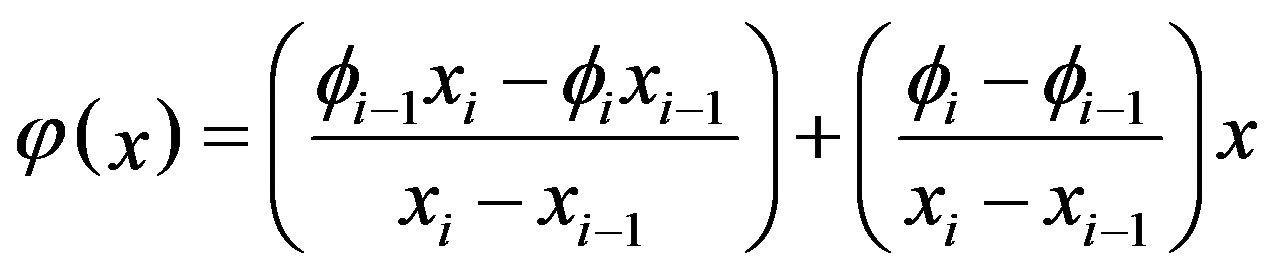 (7)
(7)
In the x direction, neutron flux leads to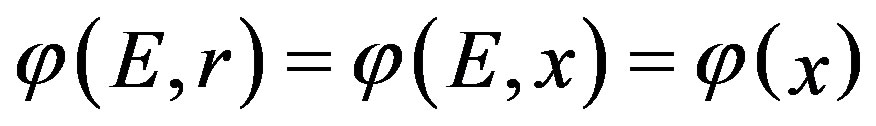 , that independent of energy.
, that independent of energy.
Because the energy width in the group g and g’ is same, therefore the neutron flux in each region in the energy grup g and g’ also same accordingly. In such situation (4) can be rewritten as follows
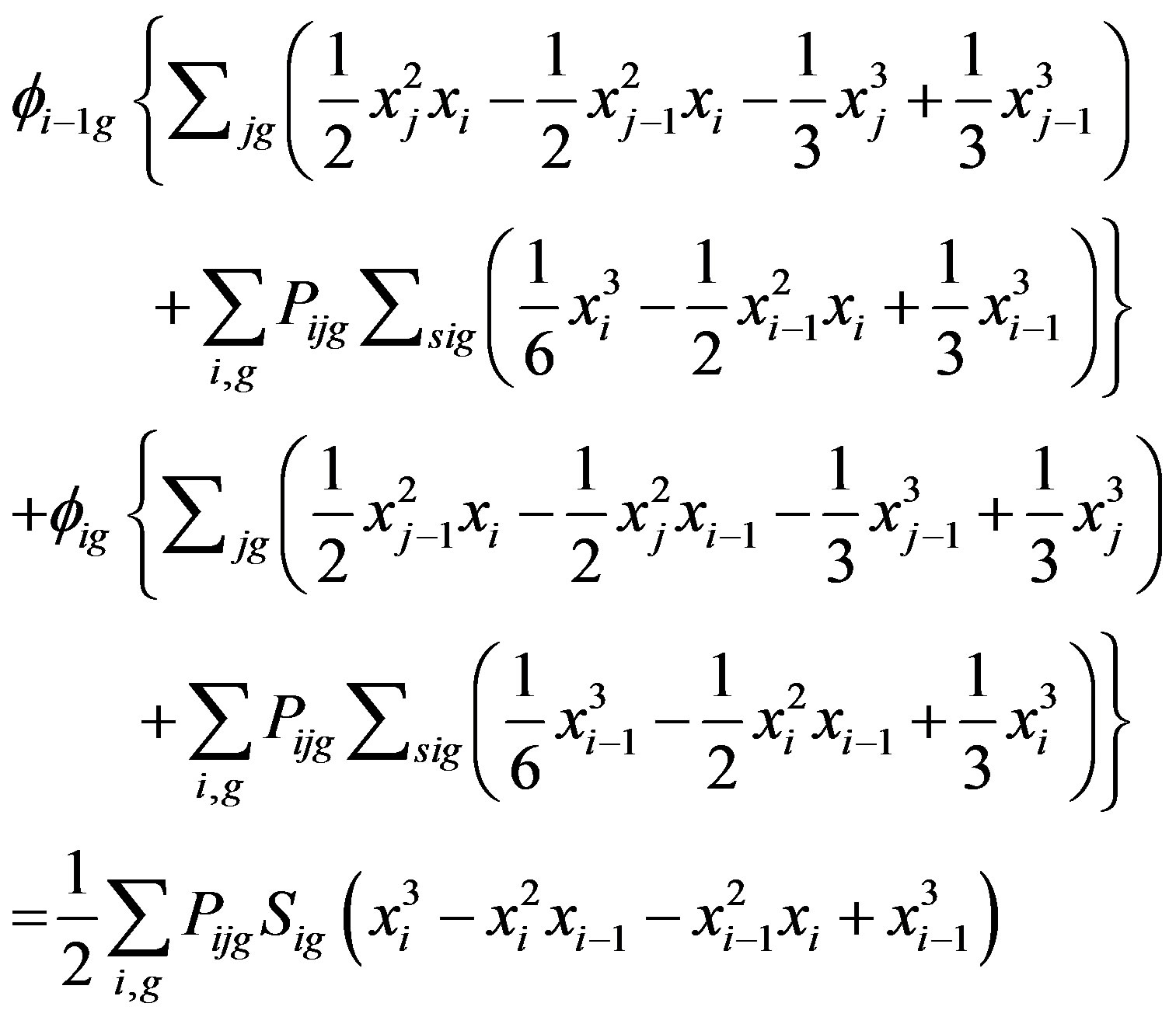 (8)
(8)
Equation (8) can be simplified to the form of matrix equation
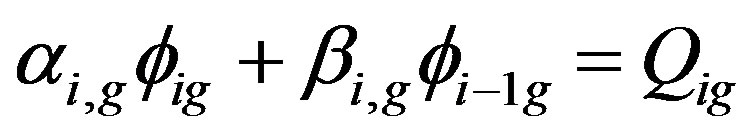 (9)
(9)
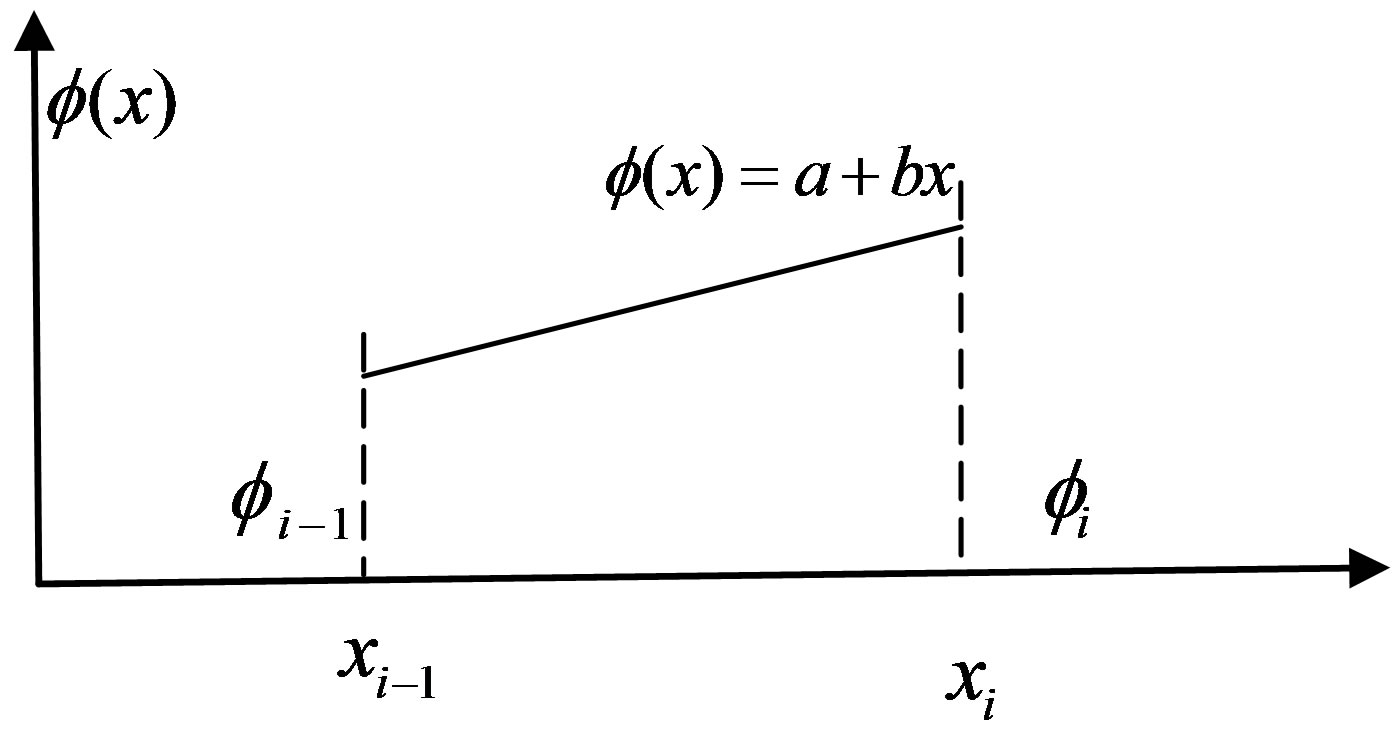
Figure 2. Element of neutron flux with the linear interpolation between two nodes.
where
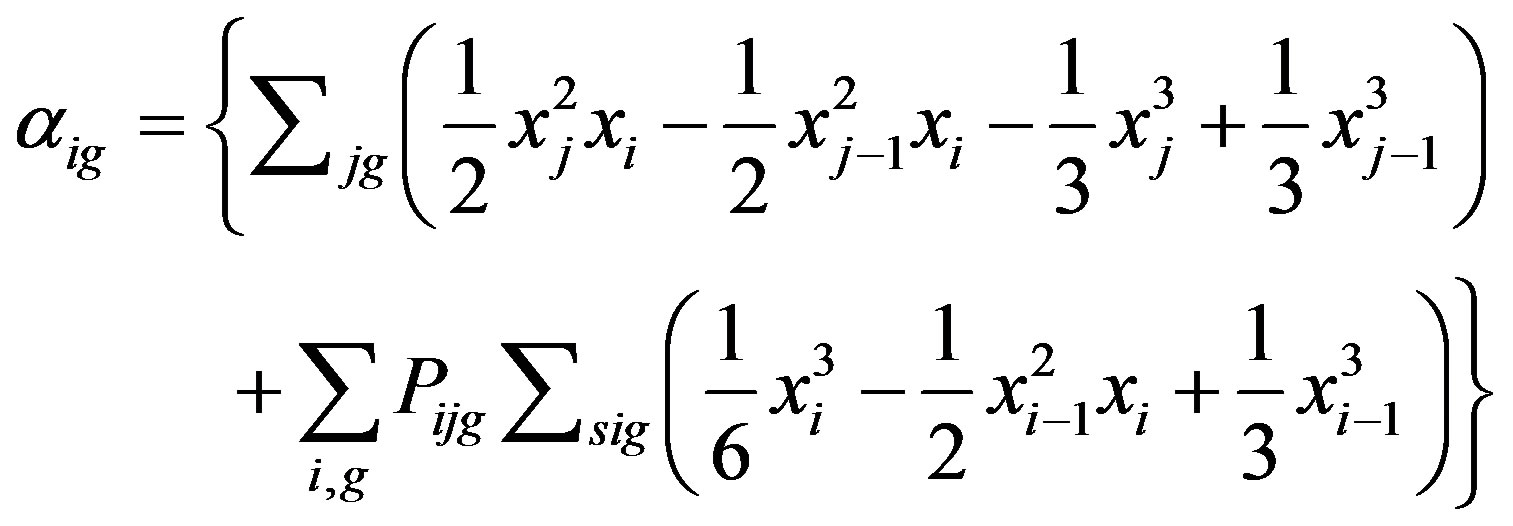
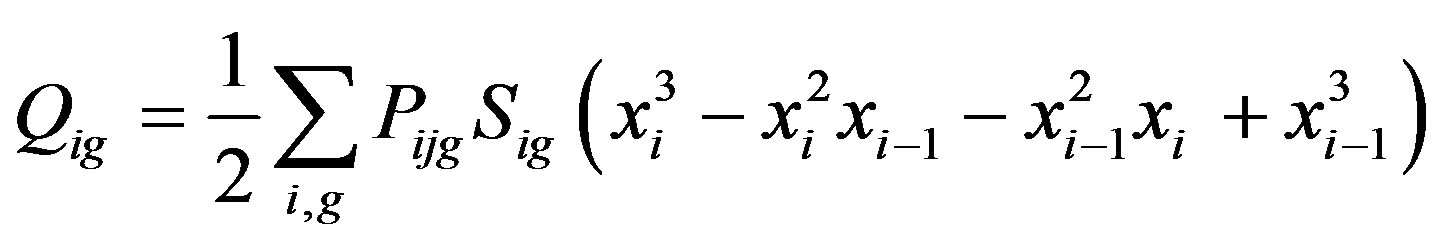
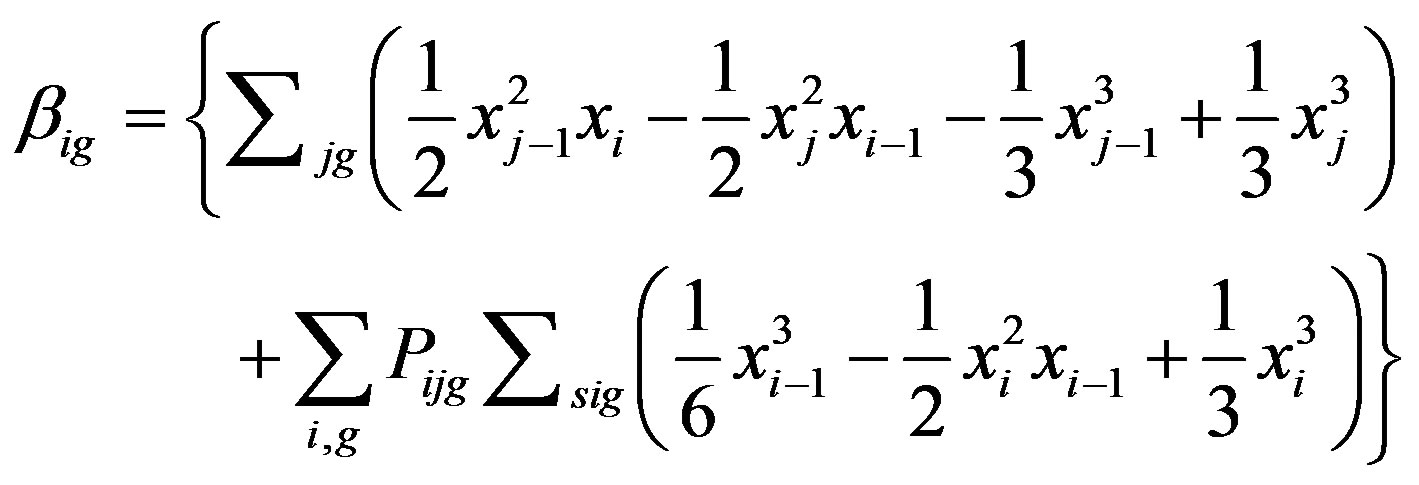
Gauss elimination is used to solve (9) to explain that neutron flux in each region i on the energy group g which valid for two-diagonals matrix
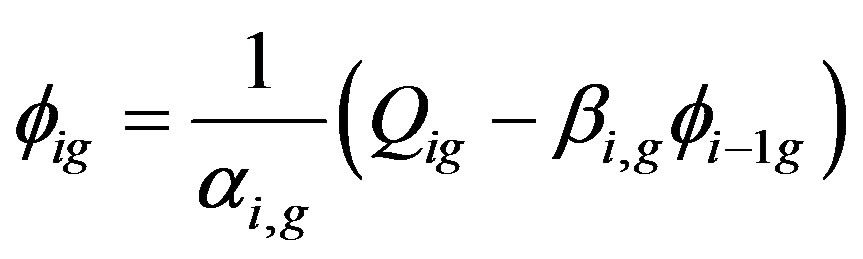 (10)
(10)
Equation (10) is used to calculate the multiplication factor as an eigen value [3]
 (11)
(11)
Collision probability is solved using Bickley-Naylor function [5]
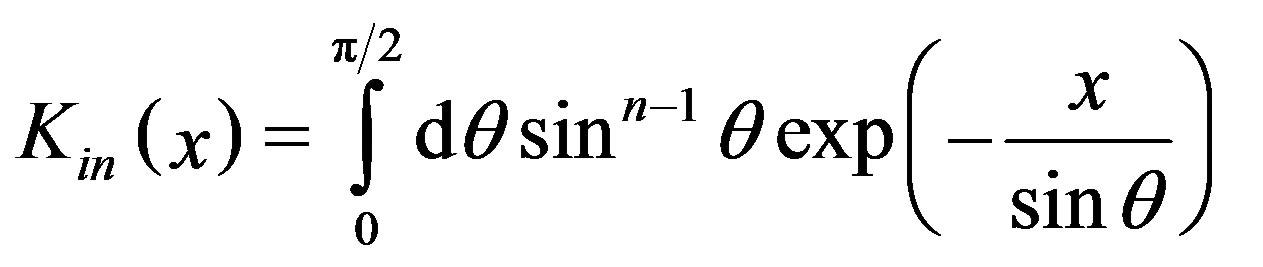 (12)
(12)
For the case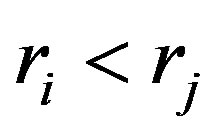 , collision probability becomes [5]
, collision probability becomes [5]
 (13)
(13)
where
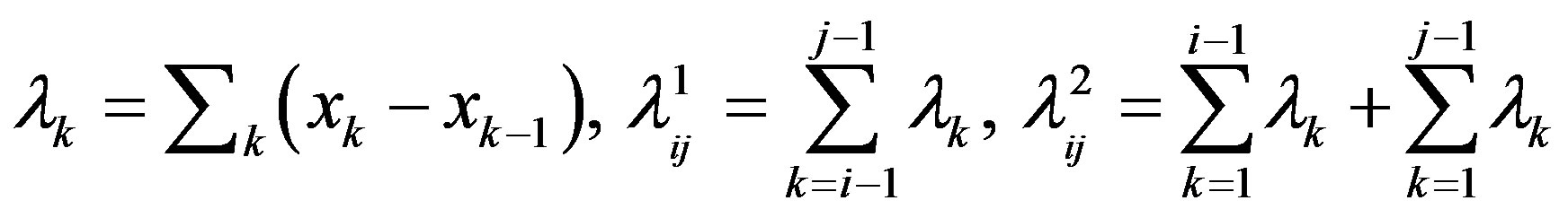
For the case of the shell i coincides with the shell j, the self collision probability can be written as [5]
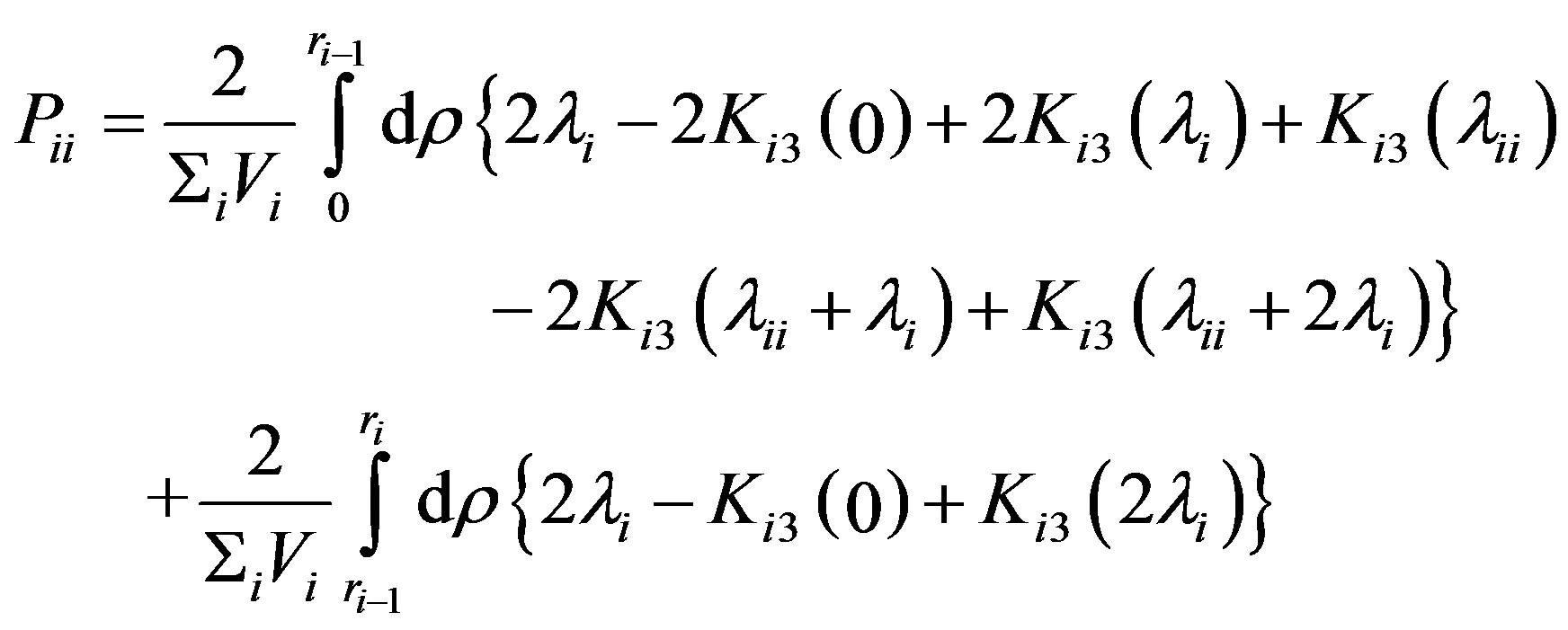 (14)
(14)
Equations (9) to (14) become a starting point for calculating the neutron spectrum and multiplication factor in the nuclear fuel cells. These are a basic formulation to obtain the solving of integral transport equation using NFF approximation.
The development of the computational program to explore the fuel cell calculation using CP method has been written in Delphi. It was written for determining the effective multiplication factor k-eff, neutron flux spectrum and CP matrix using NFF approach. The computer program in Delphi software package has been written to determine the effective multiplication factor k-eff, neutron flux spectrum and CP matrix using NFF approach. The method for calculation of the NFF collision probabilities was solved for a variety of parameter such as effective group constant and volume of cell variables. In the previous study, the calculation of neutron flux spectrum for 39 nuclides and CP matrix for 70 energy groups by using library of JFS-3-J32 have been carried out [4]. In the present work, the JFS-3-J33 library [8] provides group constants for the SLAROM code in 70 energy group structure for 383 nuclides and 8 lumped fission products is used to calculate neutron spectrum in all regions and the effective multiplication factor (k-eff) for cell homogenization. As a sample input of calculation, a nuclear fuel cell is divided in three regions; region 1 is fuel, region 2 is cladding and region 3 is coolant as shown at Figure 3. The fuel cell is a mixture of U-Pu nuclides. The material structure of cladding is stainless steel and Pb-Bi is as a coolant. The radii of three regions of fuel cell, cladding and coolant are 0.35, 0.46 and 0.567 cm, respectively.
In practical calculation, the cell region is composed of several sub regions, called mesh, for which the averages flux is computed. The computation was carried out for 6 meshes in a radial axis of cell. The detail of mesh composition, the radius of each region cell and number of nuclide in each region are shown in Table 1. In this work, 24 nuclides are used from the library with the distribution as follows; 10 nuclides in the fuel, 10 nuclides in the cladding and 4 nuclides in the coolant region.
The accuracy of the program has been examined with SRAC code for the same input sample under substantial simplified problem.
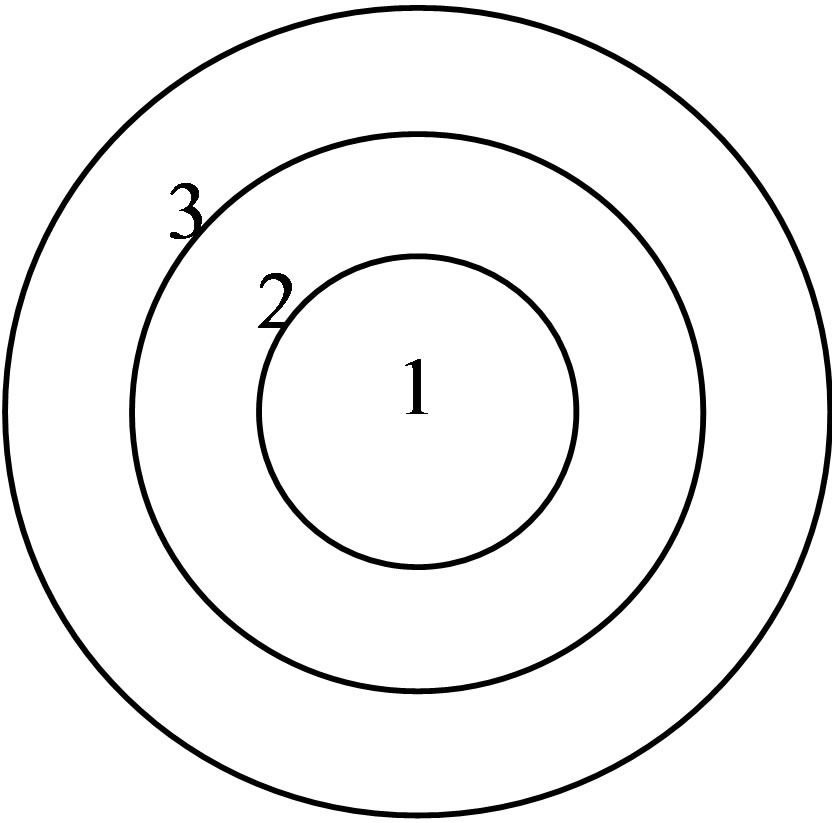
Figure 3. Three region of fuel cell, region 1 for fuel, region 2 for cladding, region 3 for coolant.
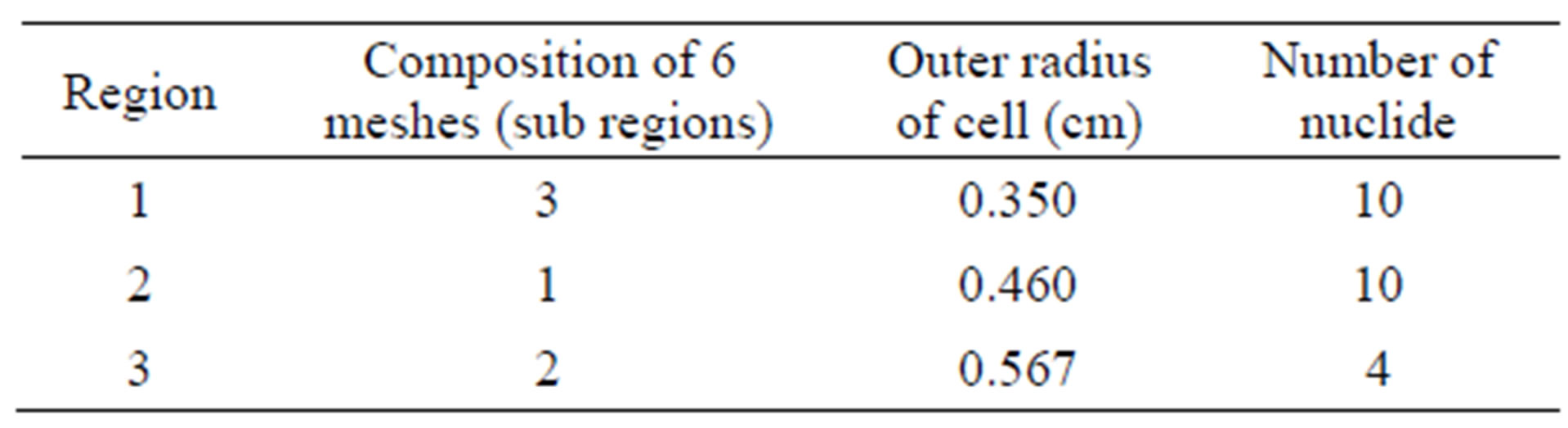
Table 1. Composition of meshes in each region of cell.
3. Result and Discussion
Comparison of effective multiplication factor k-eff calculated by FF and NFF approach of the CP method and by the SRAC code is shown in Table 2.
As can be seen in Table 2 that the k-eff calculated using FF and NFF approaches is not very much different when it calculated using SRAC code which difference is down to about 0.0078% only. In other words, k-eff calculated by the two approaches is in good agreement with those calculated by SRAC code.
Energy group increase to right, but the energy decreases. The fast neutron energy groups covers the cross section data for neutron energy range from 0.11109 to 10 MeV, while the thermal neutron energy group cover the neutron energy range from 0.32242 eV to 86.517 keV [9]. Comparison of the neutron spectrum for 6 meshes in the three region of cell and the energy group calculated using FF and NFF approach is shown in Figure 4. In the FF approach, the peak of neutron spectrum profile in a fast region (group 1 to 30) is higher than the peak in NFF approach. In the thermal region (start from group 37), however, both spectrum tend to stable. This is understood because type of reactor chosen is a fast reactor. The spectrum difference is caused by the selection of the method which assumed that neutron flux at adjacent two mesh node is no longer flat but rather follows the shape of the linear interpolation. Neutron fluxes in the three regions of cell are close each other. This suggests that the neutron distribution in each region was homogeneous in fuel, cladding and coolant.
Figure 5 shows neutron spectrum in the areas of fuel, cladding and coolant region which are reviewed using the FF approach for different mesh size. As can be seen, mesh changes have no effect in the neutron spectrum.
Different result is shown in Figure 6 for NFF ap-

Table 2. Effective multiplication factor calculated using FF, NFF and SRAC.
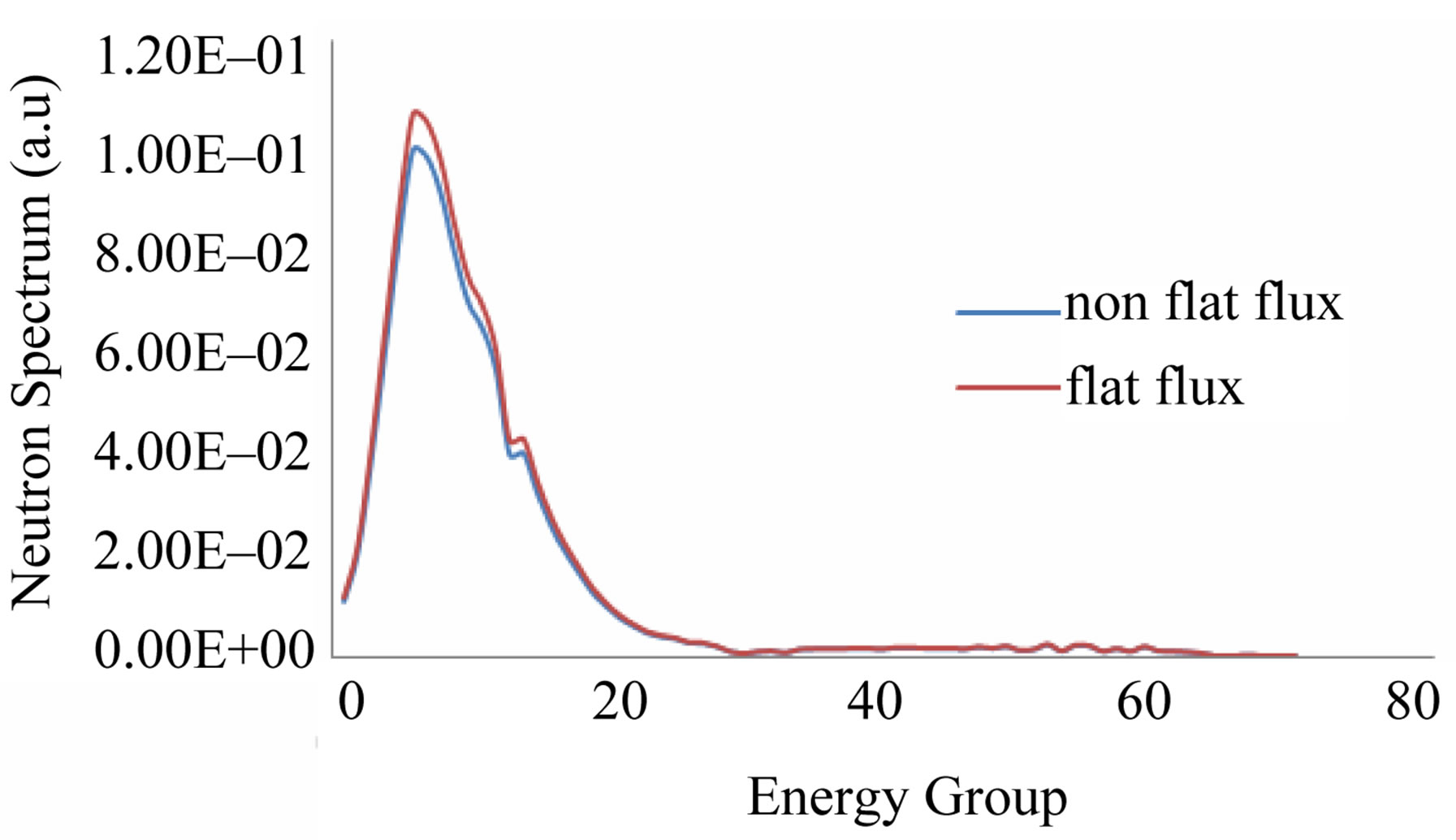
Figure 4. Neutron spectrum calculated using FF and NFF approach.

Figure 5. Neutron spectrum with variation of mesh using FF approach.
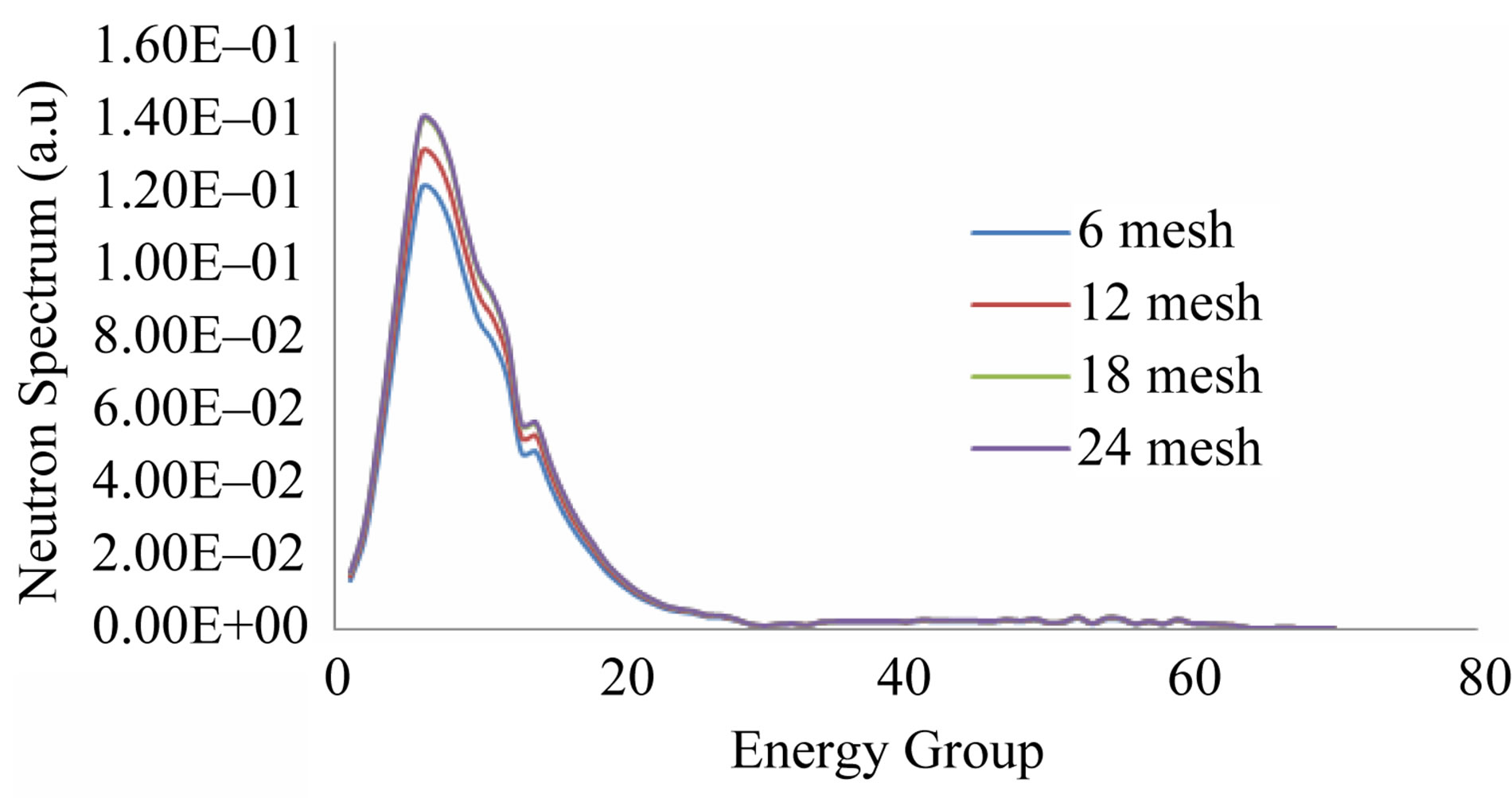
Figure 6. Neutron spectrum with variation of mesh using NFF approach.
proach. The variation of mesh affects the neutron spectrum. This event indicates that the process of nuclear fuel cell calculations with NFF approach is similar to the neutron transport processes conducted without homogenization of cells. As it is known that the heterogeneity factors are very influential in determining an anisotropic
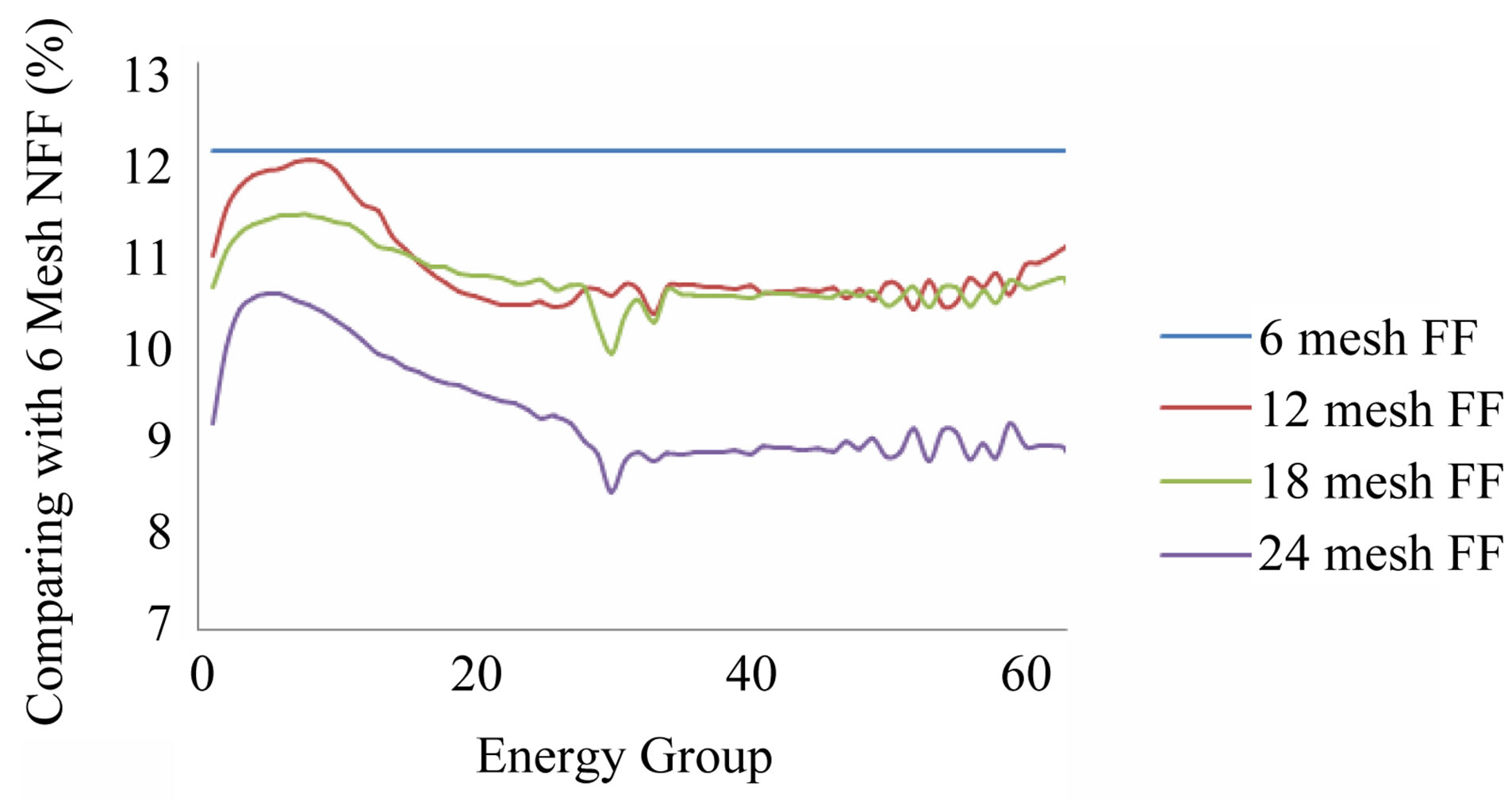
Figure 7. Difference percentage of 6 meshes using NFF approach with variation of mesh using FF approach.
scattering cross section in the nuclear fission process.
The accuracy of FF approach in term of its appropriate number of mesh used is performed by calculating the neutron flux distribution and compared it with using 6 meshes of NFF approach as the reference. To do this, the neutron flux distribution has been evaluated using 6, 12, 18 and 24 meshes of FF approach respectively which the result of the examination is shown in Figure 7.
Refer to Figure 7, it can be shown that the best accuracy is obtained when the neutron flux distribution is examined using 24 meshes of FF approach with maximum error account of 9% compared to those evaluated by 6 meshes of NFF approach. This comparison concludes that NFF approach is more effective and efficient in term of number of mesh used than FF approach for calculation of neutron flux distribution in each region within the cylindrical nuclear fuel cell. It is understood that for fast reactor the neutron flux is fluctuated in the fast energy region whereas in the thermal region the neutron flux is stable.
4. Conclusion
From this study it is concluded that solution of neutron transport equation using NFF approach is in good agreement with FF approach and SRAC code. Moreover, in term of number of mesh used, calculation of neutron flux distribution in each region of cylindrical nuclear fuel cell using 6 meshes of NFF approach gives an equivalent result when those is calculated using 24 meshes FF approach meaning that the NFF approach is more efficient in using of mesh number.
5. Acknowledgements
The first author wishes to thank Prof. T. Hazama from JAEA Japan for his deeply discussion and attention concerning this topic.
REFERENCES
- Z. Su’ud, “Computer Code for Homogenization of Nuclear Fuel Cell in the Fast Reactor,” Proceeding of a Workshop in Computational Science and Nuclear Technology, Bandung, 24-25 February 1998, pp. 110-115.
- Z. Su’ud, Y. K. Rustandi and R. Kurniadi, “Parallel Computing in the Calculation of a Constant Group of Nuclear,” Proceeding of the seventh seminar of Technology and Safety of NPP and Nuclear Facilities, Bandung, 19 February 2002, pp. 17-22.
- M. A. Shafii and Z. Su’ud, “Development of Cell Homogenization Code Using General Geometry Approach,” International Conference on Advances in Nuclear Science and Engineering, Bandung, 13-14 November 2007, pp. 403-406.
- M. A. Shafii, Z. Su’ud, A. Waris and N. Kurniasih, “Development of Cell Homogenization Code with Collision Probability Method,” International Conference of Mathematics and Natural Science, Bandung, 28-30 October 2008, pp. 169-175.
- K. Okumura, T. Kugo, K. Kaneko and K. Tsuchihashi, “SRAC 2006: A Comprehensive Neutronics Calculation Code System,” Japan Atomic Energy Agency, Ibaraki, 2007.
- M. Nakagawa and K. Tsuchihashi, “SLAROM: A Code for Cell Calculation of Fast Reactor,” Japan Atomic Energy Research Institute, Ibaraki, 1984.
- S. S. Rao, “Finite Element Method in Engineering,” Pergamon Press, New York, 1983.
- T. Hazama, “Private communication,” 2008.
- T. Hazama, G. Chiba and K. Sugino, “Development of a Fine and Ultra-Fine Group Cell Calculation Code SLAROM-UF for Fast Reactor Analyses,” Journal of Nuclear Science and Technology, Vol. 43, No. 8, 2006, pp. 908- 918. doi:10.3327/jnst.43.908

