Journal of Encapsulation and Adsorption Sciences
Vol.2 No.4(2012), Article ID:25976,8 pages DOI:10.4236/jeas.2012.24009
Natural Convection Flow of Heat Generating/Absorbing Fluid near a Vertical Plate with Ramped Temperature
Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria
Email: basant777@yahoo.co.uk, *askamba2003@yahoo.co.uk, olubadey2k@yahoo.com
Received August 4, 2012; revised September 4, 2012; accepted October 21, 2012
Keywords: Heat Generating/Absorbing; Natural Convection; Ramped Temperature
ABSTRACT
This study considers a theoretical analysis of natural convection flow of heat generating/absorbing fluid near an infinite vertical plate with ramped temperature. It is assumed that the bounding plate has a ramped temperature profile. Exact solutions of energy and momentum equations are obtained using the Laplace transform techniques. Solutions are obtained for different values of the Prandtl number (Pr) and the heat sink parameter (S). Results of the ramped and isothermal temperature and velocity as well as Nusselt number and skin friction have been compared and presented with the help of graphs.
1. Introduction
Several aspects of unsteady laminar free or natural convection flow have been studied extensively over the past 40 years. The interest in such problems stems from their important applications, such as the early stages of melting and in transient heating of insulating air gap by heat input at the start-up of furnaces. Also, time dependent laminar natural convection is likely to find wider use as it could provide the flow mechanism in some types of solar heating and ventilating passive systems. In modern electronic equipment, the vertical circuit boards include heat generating elements, and this situation can be modelled by parallel heated plates with upward flow in the intervening space [1].
Heat generation/absorption plays significant role in various physical phenomena such as convection in earth’s mantle [2], application in the field of nuclear energy and fire combustion modeling [3].
Natural convection flow of heat generating/absorbing fluid was studied by [4-6], and [7]. Vajravelu [8] concluded that the heat source/ sink play an important role in delaying the velocity and the temperature to reach the steady state condition. Several interests have been built in the study of flow of heat generating/absorbing fluid because as the temperature differences are increased appreciably, the volumetric heat generation/absorbing term may exert strong influence on the heat transfer and transitively on the flow [9]. Jha [9] discusses and analyze the flow behaviour of transient free convective flow of viscous incompressible fluid in a vertical channel due to asymmetric heating of the channel walls in the presence of temperature dependent heat sink. He concluded that an increase in heat sink parameter (S) decreases both skin friction (τ) and Nusselt number (Nu).
Unsteady flow formation in vertical channel due to symmetric and asymmetric heating has been studied by Jha et al. [10], and Singh et al. [11]. Paul et al. [12] presented analytical solutions for transient natural convection flow in a vertical channel by considering isofluxisothermal and isoflux-adiabetic boundary conditions respectively.
Chandran et al. [13] studied natural convection near a vertical plate with ramped temperature and obtained two different solutions, one valid for the fluid of Prandtl numbers different from unity and the other for which the Prandtl number is unity. They obtained analytical solutions under the assumption that the velocity and temperature conditions on the wall are continuous and welldefined. They concluded that the solutions for the nondimensional velocity and temperature variables depend upon the Prandtl number of the fluid, and the expression of the fluid velocity is not uniformly valid for all values of Pr. In their work, heat source or sink is absent. However, when the temperature differences are appreciably large, the volumetric heat generation (absorption) term may exert strong influence on the heat transfer and as a consequence, on the fluid flow as well.
The present work considers natural convection flow of heat generation/absorption fluid near a vertical plate with ramped temperature. The organization of the paper is as follows: The problem is formulated in Section 2. Two cases are considered under this section. First case discusses plate with continuous ramped temperature and second case considers plate with isothermal temperature. Results and discussion is presented in Section 3. Section 4 contains the concluding remarks
2. Mathematical Formulations
The flow considers unsteady natural convective flow of a viscous incompressible fluid of arbitrary Prandtl number near a vertical plate. Figure 1 shows the physical configuration. An arbitrary Origin O on the wall is chosen, the axis Ox' is taken along the wall in the upward direction and Oy' axis is taken perpendicular to it into the fluid. For time t' ≤ 0 both the fluid and the plate are at rest and at the constant temperature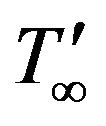 . When the time is greater than zero i.e. t' > 0 the temperature of the plate is increased or decreased to
. When the time is greater than zero i.e. t' > 0 the temperature of the plate is increased or decreased to  when t' ≤ t0 and thereafter, for t' > t0 is maintained at the constant temperature
when t' ≤ t0 and thereafter, for t' > t0 is maintained at the constant temperature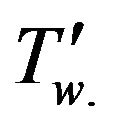 . The objective here is to analyze the unsteady natural convective flow of heat generating/absorbing fluid with ramped temperature. The flow is assumed to be laminar and therefore, the effects of the convective and pressure gradient terms in the momentum and energy equations are neglected. Here the physical variables become functions of the time variable t' and the space variable y' only as a result of the boundary layer approximations By the use of Boussinesq’s approximation, the governing equations for the flow problem in dimensional form are:
. The objective here is to analyze the unsteady natural convective flow of heat generating/absorbing fluid with ramped temperature. The flow is assumed to be laminar and therefore, the effects of the convective and pressure gradient terms in the momentum and energy equations are neglected. Here the physical variables become functions of the time variable t' and the space variable y' only as a result of the boundary layer approximations By the use of Boussinesq’s approximation, the governing equations for the flow problem in dimensional form are:
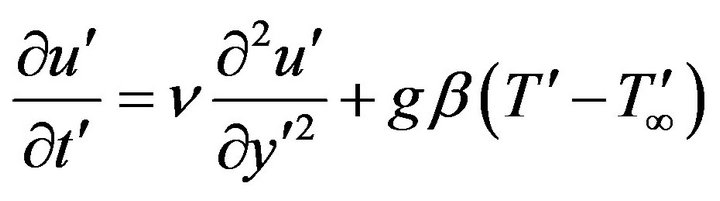 (1)
(1)
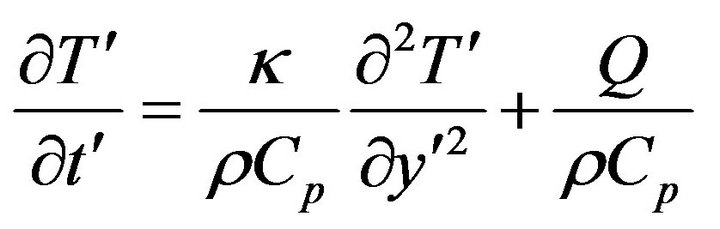 (2)
(2)
In the present analysis we have considered the heat generation (absorption) of the type Vajravelu and Sastri, [7]; Foraboschi and Federico, [3]
 (3)
(3)
The initial and boundary conditions to be satisfied are:
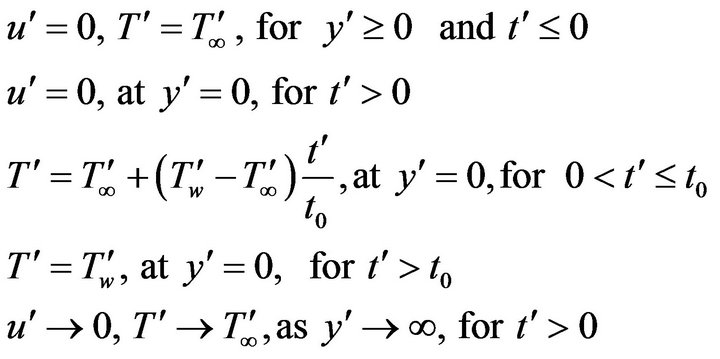 (4)
(4)
Solutions of (1) and (2) can be obtained subject to the condition (4) in non-dimensional form and as such the non-dimensional quantities are introduced as follows
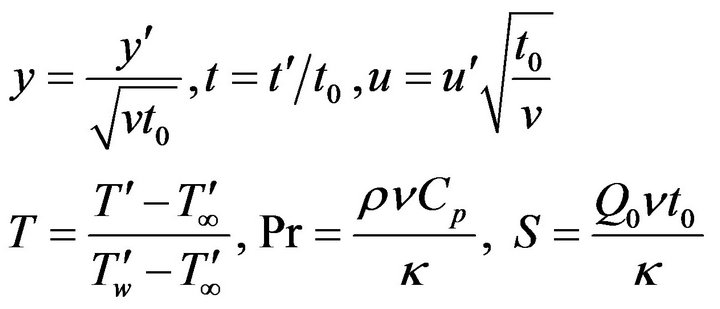 (5)
(5)
Using Equation (5) in (1) and (2), the momentum and energy equations are presented in dimensionless form as
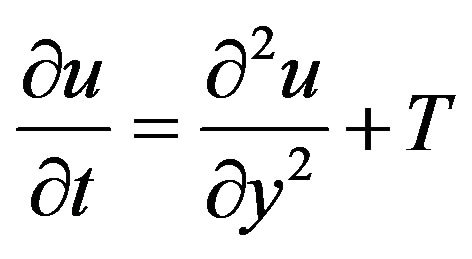 (6)
(6)
According to the above non-dimensional process, the characteristic time ![]() can be defined as
can be defined as
 (7)
(7)
The initial and boundary conditions given by equations (4) now become
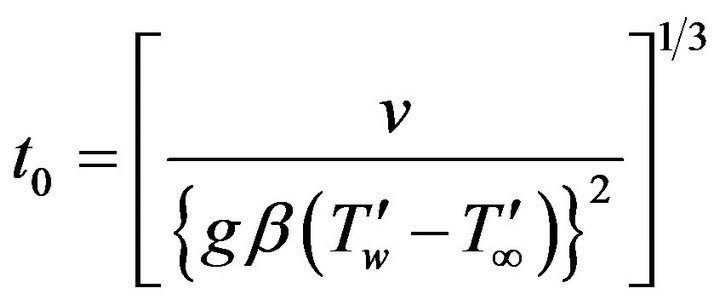 (8)
(8)
The solutions of Equations (6) and (7) under condition (9) were obtained using Laplace transform techniques
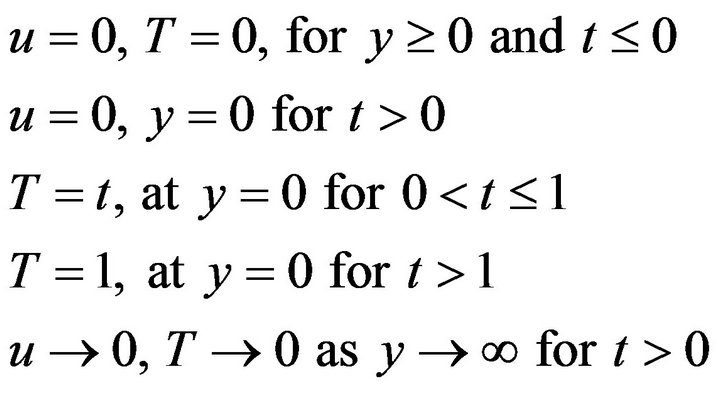 (9)
(9)

Figure 1. Physical configuration.
2.1. Case 1. Plate with Continuous Ramped Temperature
Using partial fraction with detailed simplifications and shifting on the t-axis, the solution can be written as
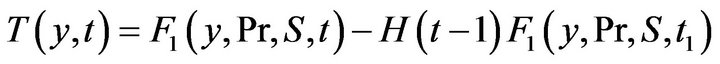 (10)
(10)
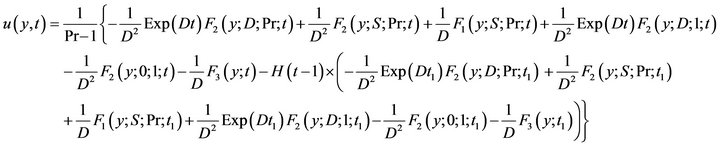 (11)
(11)
where
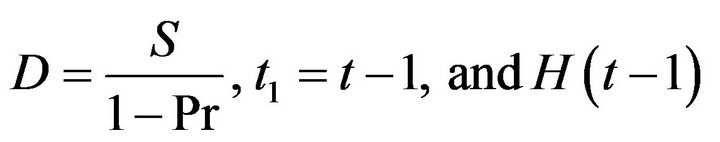
is the unit step function.
The Nusselt number (Nu) and Skin friction (τ) which are respectively measures of the heat transfer rate and shear stress at the boundary are expressed as follows
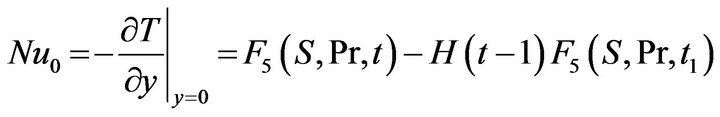 (12)
(12)
 (13)
(13)
2.2. Case 2. Plate with Isothermal Temperature
Analytical expressions for the temperature and velocity variables are given in Equations (10) and (11) for fluid flows with heat generating/absorbing near a vertical plate with ramped temperature.
To show the effect of the ramped temperature distribution of the boundary on the flow, it may be interesting to compare such a flow with the one near a plate with isothermal temperature. Under the same assumptions considered in this article, the temperature and velocity field for the fluid flow with heat generating/absorbing near an isothermal, plate can be written as follows
 (14)
(14)
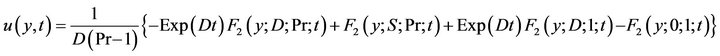 (15)
(15)
The rate of heat transfer on the wall and the skin friction are given as follows
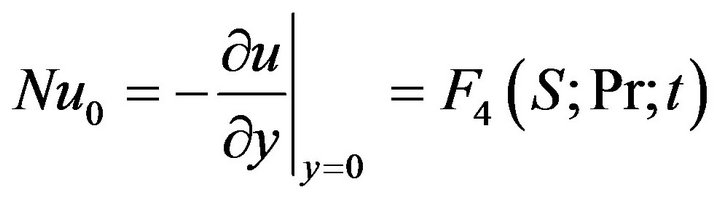 (16)
(16)
 (17)
(17)
where 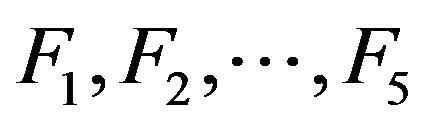 are defined in the appendix.
are defined in the appendix.
3. Results and Discussion
For the numerical validation of our results, we have chosen physically meaningful values of the parameters entering the problem. In Figures 2-12, the variations of the physical variables of interest have been plotted. Temperature profile for ramped and isothermal boundary conditions for different values of time is presented in Figure 2 while keeping the heat sink parameter S and the Prandtl number constant. It shows that as time t increases the temperature increases. In Figure 3 the temperature presents an inversely proportional relationship with Pr. Also the temperature decays with distance. For fluid with large Pr, the temperature decays faster with distance which makes thermal boundary layer to decrease. This is expected since fluid with large Pr has low thermal diffusivity and hence heat penetration is less when Pr is large. For fluid with low Pr the temperature increases and thereby increasing the thermal boundary layer. Figure 4 shows temperature profile for ramped and isothermal temperature boundary conditions. As the heat sink parameter (S) increases the temperature decreases for both ramped and isothermal case. It is seen from Figure 4 that the fluid temperature is greater in the case of isothermal plate than in the case of ramped temperature at the plate. This should be expected since in the latter case, the heating of the fluid takes place gradually than in the isothermal case.
Figure 5 shows variation of velocity due to ramped
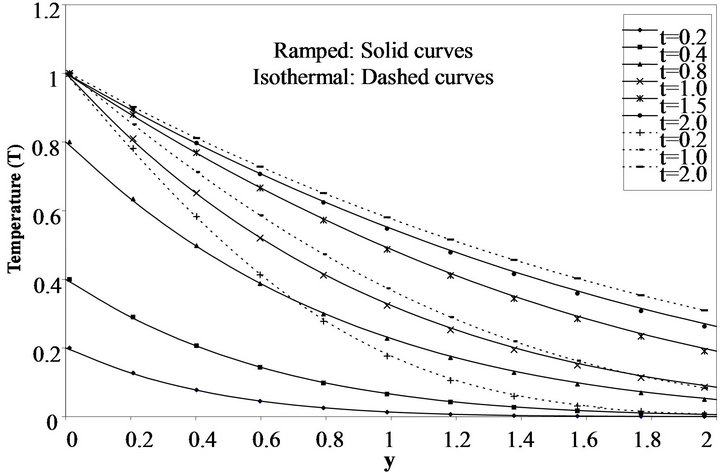
Figure 2. Temperature Profile for ramped temperature and isothermal boundary conditions for different values of t (S = 0.2 and Pr = 0.71).
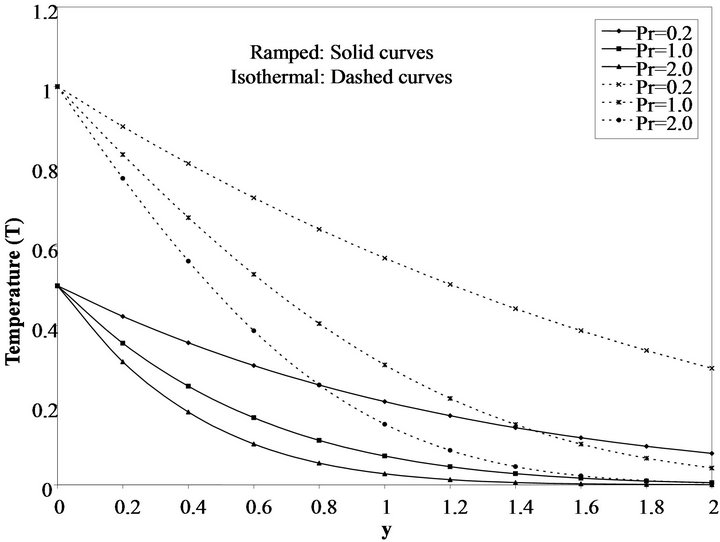
Figure 3. Temperature Profile for ramped temperature and isothermal boundary conditions for different values of Pr (S = 0.2 and t = 0.5).

Figure 4. Temperature profile for ramped temperature and isothermal boundary conditions for different values of S (Pr = 0.71 and t = 0.5).

Figure 5. Ramped velocity profile for different values of t (S = 0.2 and Pr = 0.71).
plate temperature for different values of time (t). As time increases the velocity increases. Figure 6 shows velocity profile for different values of the heat sink (S). From Figure 6, it is clear that velocity decreases with increase of heat sink parameter (S) for thermal boundary conditions (i.e. ramped as well as isothermal). Figures 7 and 8 show two profiles corresponding to ramped velocity and isothermal boundary conditions. In Figure 7 for 0 < t < 1, the velocity increases after which it starts descending. It was observed that the presence of heat sink S reduces the velocity profile for both ramped and isothermal cases. In Figure 8, it is observed that for very small values of time, the velocity profiles are nearly flat, but assume parabolic shapes near the plate as t increases. Moreover, the points of maxima on the curves get shifted to the right, as time increase. It is also seen that the velocity increases monotonically with the temporal variable t. The same observation is made, that the velocity on the ramped temperature plate is always less than that of the flow induced by a plate of isothermal temperature and this agrees with earlier observation made with regards to the temperature variation.
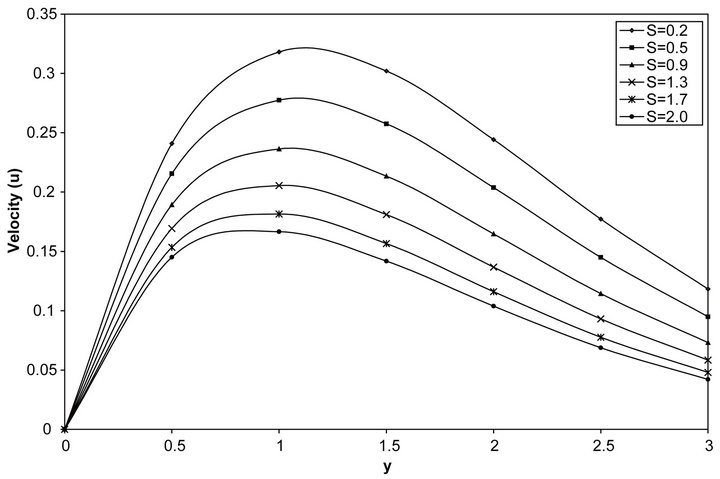
Figure 6. Ramped velocity profile for different values of S (t = 0.5 and Pr = 0.71).
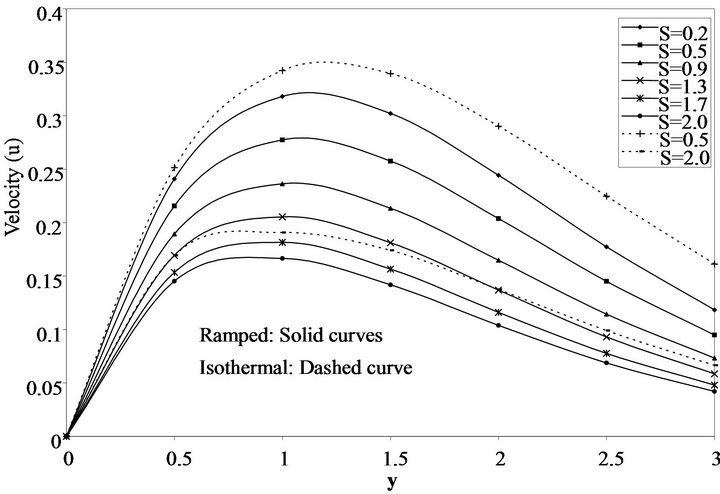
Figure 7. Variation of velocity (![]() ). Two profiles corresponding to ramped and isothermal boundary conditions for different values of S (t = 0.5 and Pr = 0.71).
). Two profiles corresponding to ramped and isothermal boundary conditions for different values of S (t = 0.5 and Pr = 0.71).
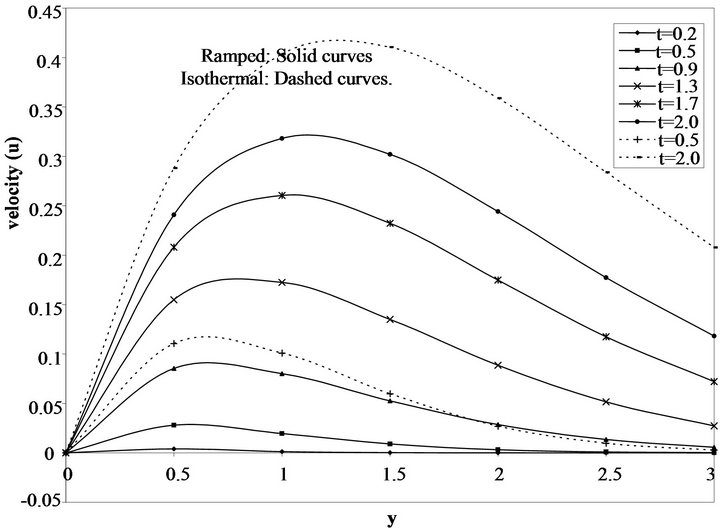
Figure 8. Variation of velocity profile (![]() ) corresponding to ramped and isothermal boundary conditions for different t (S= 0.2 and Pr = 0.71).
) corresponding to ramped and isothermal boundary conditions for different t (S= 0.2 and Pr = 0.71).
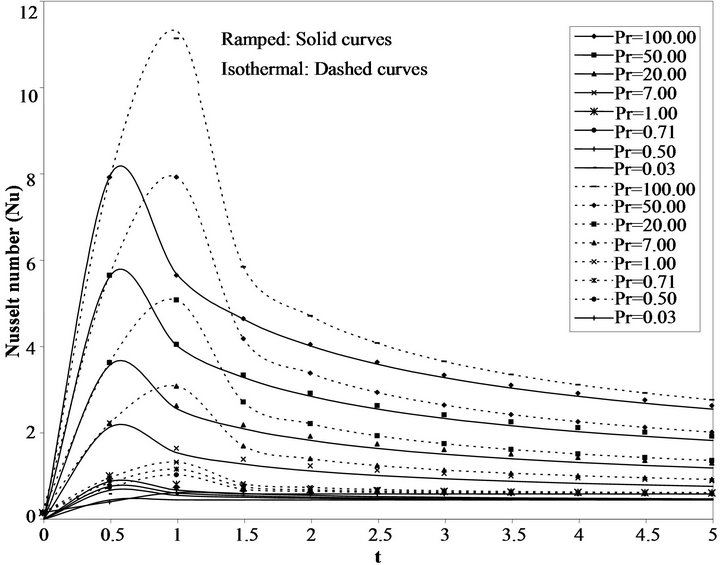
Figure 9. Variation of the Nusselt number (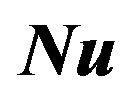 ) for different Pr corresponding to ramped and isothermal boundary conditions and
) for different Pr corresponding to ramped and isothermal boundary conditions and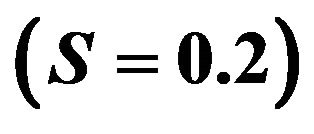 .
.
Figure 9 shows variation of the Nusselt number (Nu) corresponding to ramped and isothermal boundary conditions. For t < 1, the Nusselt number increase with time. There is a sharp decrease for isothermal case between 1 < t < 1.5 and 0 < t ≤ 0.5 for the ramped case. The Nusselt number increases as Pr increases because temperature reduces with increasing Pr thereby increasing the temperature gradient between the wall and the fluid and hence an increase in the rate of heat transfer is achieved. In Figure 10, as the Prandtl number increases the Nusselt number increases for both ramped and isothermal cases. It is observed that for 0 < S < 0.5 the Nusselt number is increasing and for 0.5 < S < 1 it is decreasing while it assumed constant value for S > 1 It is also seen that for

Figure 10. Variation of the Nusselt number ( ) corresponding to ramped and isothermal boundary condition for different Pr and (t = 0.5).
) corresponding to ramped and isothermal boundary condition for different Pr and (t = 0.5).
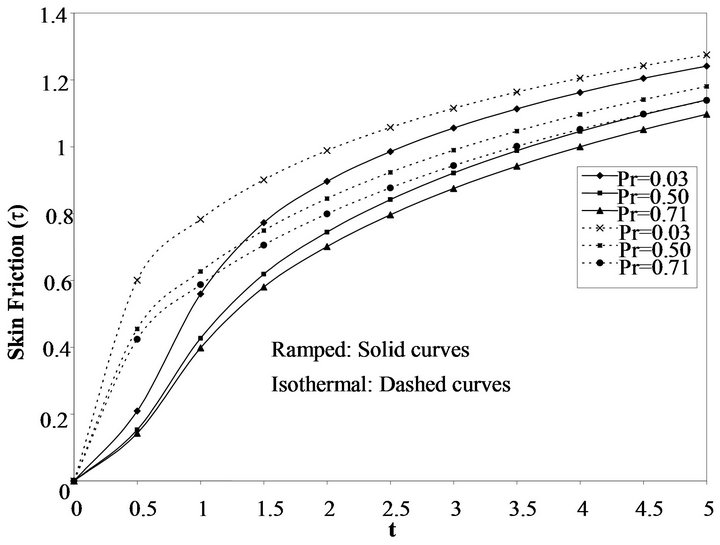
Figure 11. Variation of skin friction (τ) corresponding to ramped and isothermal boundary condition (S = 0.2).
Pr > 1 the Nusselt number for isothermal case coincide with that of the ramped case when S ≤ 0.5. For small Pr i.e. 0 < Pr < 1 the Nusselt number increases with the heat sink parameter S. Also for large values of the heat sink parameter S and large Pr the Nusselt number in the isothermal case converges to that of ramped, while for small Pr, the isothermal case diverges away from the ramped case when S is large. In Figure 11 as the value of the Prandtl number Pr increases, the skin friction increases with respect to time. It is observed that as , both the ramped and isothermal skin friction coincide. Figure
, both the ramped and isothermal skin friction coincide. Figure
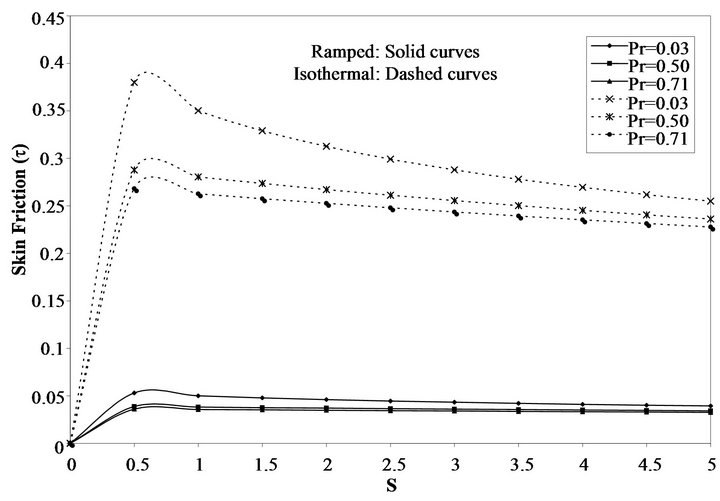
Figure 12. Variation of the skin friction for ramped and isothermal boundary conditions for different values of Pr (t = 0.5).
12 shows variation of the skin friction for ramped and isothermal boundary conditions for different values of Pr. There is an increase of the skin friction for ramped and isothermal cases between 0 < S < 1.5, after which both ramped and isothermal skin friction decrease.
4. Conclusion
This work investigates the Natural convection flow of heat generating/absorbing fluid near a vertical plate with ramped temperature. Results for temperature and velocity profiles as well as Nusselt number and skin friction are presented graphically. The result shows that isothermal case is always high than the ramped case. It is concluded that the presence of the heat sink parameter (S), reduces temperature and velocity profile as well as the skin friction for both ramped and isothermal cases.
5. Acknowledgements
The author Ahmad K. Samaila is thankful to Usmanu Danfodiyo University, Sokoto for financial support.
REFERENCES
- M. A. Al-Nimr, “Analytical Solution for Transient Laminar Fully Developed Free-Convection in Vertical Concentric Annuli,” Heat Mass Transfer, Vol. 36, No. 9, 1993, pp. 2385-2395. doi:10.1016/S0017-9310(05)80122-X
- D. P. McKenzie, J. M. Roberts and N. O. Weiss, “Convection in the Earth’s Mantle: Towards a Numerical Simulation,” Journal of Fluid Mechanics, Vol. 62, No. 3, 1974, pp. 465-538. doi:10.1017/S0022112074000784
- F. P. Foraboschi and I. D. Federico, “Heat Transfer in Laminar Flow of Non-Newtonian Heat Generating Fluids,” International Journal of Heat and Mass Transfer, Vol. 7, No. 3, 1964, pp. 315-318. doi:10.1016/0017-9310(64)90107-3
- J. C. Crepeau and R. Clerksean, “Similarity Solutions of Natural Convection with Internal Heat Generation,” Journal of Heat Transfer, 1997, pp. 119-183.
- J. A. Chamkha, “Hydromagnetic Three Dimensional Free Convection on a Vertical Stretching Surface with Heat Generation or Absorption,” International Journal of Heat and Fluid Flow, Vol. 20, No. 1, 1999, pp. 84-92. doi:10.1016/S0142-727X(98)10032-2
- A. K. Singh, “Stokes Problem for a Porous Vertical Plate with Heat Sinks by Finite Difference Method,” Astrphysics and Space Science, Vol. 103, No. 2, 1984, pp. 241- 248.
- K. Vajravelu and K. S. Sastri, “Laminar Free Convection Heat Transfer of a Viscous Incompressible Heat Generating Fluid Flow Past a Vertical Porous Plate in the Presence of Free-Stream Oscillations. II,” Acta Mechanica, Vol. 31, No. 1-2, 1978, pp. 80-100.
- K. Vajravelu, “Natural Convection at a Heated Semi-Infinite Vertical Plate with Temperature Dependent Heat Sources or Sinks,” Indian Academic Science, Vol. 88A, No. 4, 1979, pp. 369-376. doi:10.1007/BF02842483
- B. K. Jha, “Transient Free Convective Flow in a Vertical Channel with Heat Sinks,” International Journal of Applied Mechanics and Engineering, Vol. 6, No. 2, 2001, pp. 279-286
- B. K. Jha, A. K. Singh and H. S. Takhar, “Transient Free Convective Flow in a Vertical Channel Due to Asymmetric Heating,” International Journal Applied Mechanical Engineering, Vol. 8, No. 3, 2003, pp. 497-502.
- A. K. Singh, H. R. Gholami and V. M. Soundalgeker, “Transient Free Convective flow between Two Vertical Parallel Plates,” Heat Mass Transfer, Vol. 31, No. 5, 1996, pp. 329-331. doi:10.1007/BF02184046
- T. Paul, B. K. Jha and A. K. Singh, “Transient Free Convective Flow in a Vertical Channel with Constant Temperature and Constant Heat Flux,” Heat Mass Transfer, Vol. 32, No. 1-2, 1996, pp. 61-63. doi:10.1007/s002310050092
- P. Chandran, N. C. Sacheti and K. A. Singh, “Natural Convection near a Vertical Plate with Ramped Wall Temperature,” Heat Mass Transfer, Vol. 41, No. 5, 2005, pp. 459-464. doi:10.1007/s00231-004-0568-7
Appendix

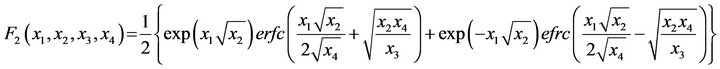
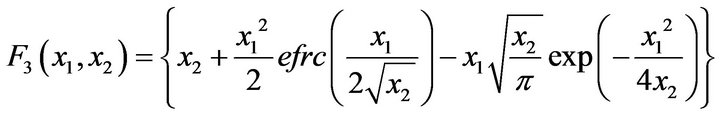
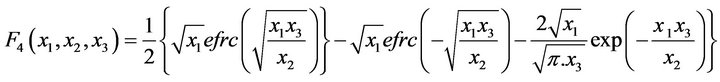
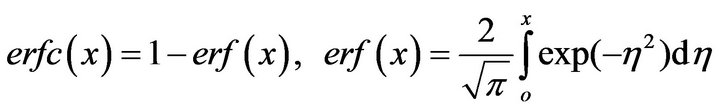
Nomenclature
 specific heat of the fluid at constant pressure;
specific heat of the fluid at constant pressure;
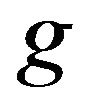 acceleration due to gravity;
acceleration due to gravity;
 Nusselt number;
Nusselt number;
 Prandtl number;
Prandtl number;
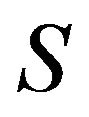 dimensionless heat sink parameter;
dimensionless heat sink parameter;
![]() dimensional time;
dimensional time;
 dimensionless time;
dimensionless time;
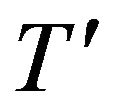 dimensional temperature of the fluid;
dimensional temperature of the fluid;
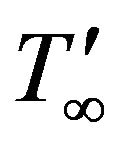 initial temperature;
initial temperature;
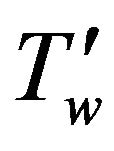 wall temperature;
wall temperature;
 dimensionless temperature;
dimensionless temperature;
 dimensional velocity of the fluid;
dimensional velocity of the fluid;
![]() dimensionless velocity of the fluid;
dimensionless velocity of the fluid;
 vertical axis;
vertical axis;
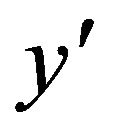 horizontal axis;
horizontal axis;
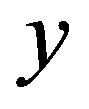 dimensionless co-ordinate perpendicular to the plate;
dimensionless co-ordinate perpendicular to the plate;
 dimensional heat generation term;
dimensional heat generation term;
 coefficient of heat generation.
coefficient of heat generation.
Greek letters
 volumetric coefficient of thermal expansion;
volumetric coefficient of thermal expansion;
![]() thermal conductivity of the fluid;
thermal conductivity of the fluid;
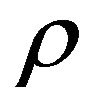 density of the fluid;
density of the fluid;
![]() dimensionless skin friction of the wall;
dimensionless skin friction of the wall;
![]() kinematic viscosity.
kinematic viscosity.
NOTES
*Corresponding author.

