American Journal of Operations Research
Vol.08 No.05(2018), Article ID:87138,20 pages
10.4236/ajor.2018.85019
Fast Computation of Pareto Set for Bicriteria Linear Programs with Application to a Diet Formulation Problem
F. Dubeau, M. E. Ntigura Habingabwa
Département de Mathématiques, Université de Sherbrooke, Sherbrooke, Canada
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 26, 2018; Accepted: September 2, 2018; Published: September 5, 2018
ABSTRACT
In case of mathematical programming problems with conflicting criteria, the Pareto set is a useful tool for a decision maker. Based on the geometric properties of the Pareto set for a bicriteria linear programming problem, we present a simple and fast method to compute this set in the criterion space using only an elementary linear program solver. We illustrate the method by solving the pig diet formulation problem which takes into account not only the cost of the diet but also nitrogen or phosphorus excretions.
Keywords:
Bicriteria Linear Program, Pareto Set, Criterion Space, Weighted-Sum, Diet Formulation, Taxation System

1. Introduction
Animal diet formulation is a very important problem from an economic and environmental point of view, so it is an interesting example in operations research. Many modern animal diet formulation methods tend to take into account nitrogen and phosphorus excretions that are detrimental from an environmental point of view. Following [1] , it is appropriate to apply a tax on excretions so as to change the behavior of the producers in the swine industry. These changes in behavior are studied using a formulation of the problem as a bicriteria problem and are obtained by the determination of the Pareto set of the problem. For linear models, this Pareto set is a simple polygonal line. This fact implies that changes in behavior of the producers are abrupt and correspond to particular values of the tax. In other words even in increasing the tax it can happen that there is no change in behavior. Behavior changes happend only at very particular values of the tax. We will see that these behaviors correspond to efficient extreme points of the Pareto set, and to every extreme point corresponds a tax interval so that any value of the tax in this interval leads to the behavior given by that extreme point.
The computation and visualization of the Pareto set, also known as the efficiency set, for bicriteria linear programming problems is a useful tool for decision makers. We could try to compute this set in the decision space [2] - [10] , but due to the high dimension of this space, it can be a quite large and complicated set. Methods to obtain this set are also complicated, see for example [11] . Fortunately, the geometric aspect of the Pareto set in the criterion (or outcome) space for bicriteria linear program is quite simple [12] .
The outline of the paper is the following. The bicriteria problem is presented in Section 2. We will see in Section 3, that the Pareto set of a bicriteria linear problem is a simple polygonal line with L + 1 extreme points joined by L adjacent segments. Then in Section 4 we presents the link between the geometric structure of the Pareto set and the weighted-sums approach. Then an elementary algorithm to determine the Pareto set in the criterion space is suggested and its complexity is analyzed. Let us point out that this method uses only elementary result from a linear program solver, that is to say the optimal solution (values of the decision variables). This fact is an interesting property of the method.
Few methods exist for computing the Pareto set in the criteria space. One such method is presented in [13] . The method requires information about the dual, assume the feasible set is compact, and determine the Pareto set with at most 2L + 4 calls to a linear program solver. Another simple method for bi-criteria problems is presented in [12] to obtain the Pareto set in the criterion space. The algorithm is based on information about the reduced costs of all nonbasic variables, which is equivalent to have information about the solution of the dual problem. For bi-criteria linear problems we could also use a parametric analysis to obtain the Pareto set [11] [14] . The last two methods require that the software used to solve a linear program send information about the dual, reduced cost or postoptimal analysis, which is not always possible for a simple linear program solver. Unfortunately, even if it seems that those two methods require around 2L iterations, their complexities are nowhere analyzed. Moreover they can cycle as explained in [15] (pages 281-282), and [16] (pages 162-166).
Finally, in Section 5, we compute the Pareto sets for least cost diet formulation problems for pig, or any monogastric animal, taking into account the nitrogen and/or phosphorus excretions. Tax systems related to efficient extreme points of this problem are described.
2. Bicriteria Linear Programming Problem
Let us consider the standard form of the bicriteria linear programming problem [11]
where x is a column vector in , and the 's ( ) are two row vectors in . The feasible set in is defined by , where A is a -matrix, and b is a column vector in . Let C be the -matrix given by
The feasible set in the criterion space is then . It is well-known that and are polyhedral sets in and respectively. Throughout this paper we will suppose that the two criteria are lower bounded on which means that for we have
3. Structure of the Pareto Set
3.1. Efficiency Set
A feasible solution is an efficient solution if and only if it does not exist any other feasible solution such that 1) for , and 2) for at least one . The set of all efficient solutions is called the efficiency set noted , also called Pareto set. The corresponding set in the criterion space is the set .
3.2. Geometric Structure
Under the assumption that the two cost vectors and are linearly independant, Using weighted-sums, we can replace the bicriteria linear programming problem by a single criterion linear programming problem. We consider and the weighted-sum function is
and we consider the single criteria problem for
The value function of is defined by
From [11] we have
Hence the efficiency set in the decision space is a connected set and is the union of faces, edges and vertices of . This set may be quite complex due to the high dimension of the decision space. On the other side , which is the image in of by a linear transform, is a much simpler set.
Since we have assumed that both criteria are lower bounded on , it follows that is a simple compact polygonal line. Indeed in that case is the union of a finite number L of segments
where
and such that
with
To each segment is associated a weight such that the vector is orthogonal to the segment in . To each point Q of is associated an interval defined by
where
with for .
3.3. Weak Efficiency Set
We will call weak efficiency set, or weak Pareto set, the set defined by
Obviously . In the criteria space we will have . Geometrically in the criterion space , this means we add to possibly a vertical segment or a ray from in the positive direction of , ,
and/or a horizontal segment or a ray from in the positive direction of , ,
where and are nonnegative finite or infinite values. They are the maximal values of such that and are both subsets of . To these points on we set
3.4. Link to Parametric Analysis
The parametric analysis is based on the weighted-sum given by
for , and the value function in this case is defined by
Instead of , we could consider the single criteria problem for
Since and are related by the formulae
to the efficient extreme points on the efficiency set correspond also the following intervals for the parameter
where
In many applications, the parameter is in fact a tax over the the second criteria (for a minimization problem). Interesting enough is to observe that the behavior change (extreme point) only for the critical values of the parameter . Indeed when increases and its value passes through , the optimal point, extreme point, move from to . Thus, any level of taxes strictly between the values and causes the same behavior described by .
4. Computation of the Pareto Set
4.1. Preliminaries
Let us associate to any the weighted-sum function given by
Then the value function associated to is such that
Hence we have the following results.
Theorem 4.1. [12] Let , we have if and only if .
Theorem 4.2. [12] Let and . Then and if and only if . It follows that Q is one of the ( ).
Theorem 4.3. [17] The function is continuous, piecewise linear and concave. The abscissae of slope changes are the increasing values for .
Let us observe that the slope associated to strictly decreases for Q going from to on , since increases and decreases steadily. We deduce the next results.
Theorem 4.4. [12] Let and be two distinct points on . For , is orthogonal to the segment if and only if .
Theorem 4.5. Let and be two distinct points on and , such that is orthogonal to the segment . For a fixed , the function is constant as a function of Q on the segment . Let us note this constant value by . Moreover
1) if then , and ;
2) if then .
Theorem 4.6. Let and be two distinct points on . If is such that then . Moreover there exists such that and .
Theorem 4.7. Let and be two distinct points on . Let and , and consider the following two lines
and
(A) If , the point of intersection of and is where
so
and
(B) If , then which contains the segment .
4.2. Algorithm
In this section we consider both criteria upper bounded on . In the forthcoming algorithm we initialize the process with the two points and on . Then we gradually obtain a sequence of points on , and
a sequence of intervals associated to these points such that and
At the end of the process and we have with
for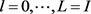 .
.
Algorithm (Pareto bicriteria)
STEP 0. Initialization.
(A) Enter the data of the problem.
(B) Determine 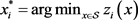 for
for  and set
and set . For
. For 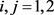 and
and 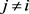 set
set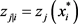 . We get the initial point
. We get the initial point 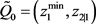 which as the same first coordinate as
which as the same first coordinate as , and
, and 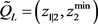 which as the same second coordinate as
which as the same second coordinate as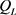 . Those two points might not be on
. Those two points might not be on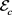 , but are on
, but are on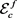 .
.
(C) Set 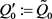 and
and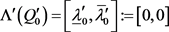 ;
;
(D) Set 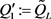 and
and ;
;
(E) Set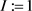 .
.
STEP 1. As long that there exists an index i such that
(A) Find 




(B) Solve


(C) Update the list of points 

I) Modification of the intervals. If 




We modify as follow:
a) for

b) for

In the sequel no more point will be generated on
II) Point insertion and interval modification. If 

a) Insert 



b) Set
c) If





d) If





STEP 2. For any i such that


STEP 3. End of the process (and

Let us observe that this process use only optimal solutions of
Remark 4.8. This algorithm produces at each iteration an inner and an outer approximation. The inner approximation is the polygonal line joining the 













4.3. Complexity
In this section we are going to determine the maximum number of calls to a linear program solver to completely determine the Pareto set, or equivalently its 




We will use the following ordering on
















Theorem 4.9. The algorithm generates at most 3 points on 



Proof. Let us remark that the algorithm will eventually find a point in 









1) 







2) 







3) 


Let 





1) 








2) 








Two points of 














1) We have only one extreme point










2) We already have two extreme points 









In the sequel, the algorithm generate no more point on 








Theorem 4.10. If



Proof. When 







Theorem 4.11. The algorithm generates the extreme points 

Proof. The initialization STEP 0 requires 2 calls. For STEP 1, as we generate the 





5. A Real World Application: Pig Diet Formulation
To illustrate our method of computation of the Pareto set we consider the pig diet formulation problem taking into account not only the cost of the diet but also environmental considerations, such as the reduction of nitrogen or phosphorus excretions. One way to analyze this problem is to rewrite the problem as bicriteria problem. Hence the Pareto set indicates the effect of the reduction of excretions, nitrogen or phosphorus, on the cost of the diet. This information is certainly useful for a decision maker which have to choose a diet which decrease the excretions without being too expensive [1] . Even if in thispaper we describe the problem for the swine industry, the method could be applied to any monogastric animal: pig, rabbit, chicken, etc.
5.1. Classical Model
The least cost diet problem, introduced in [18] , is a classical linear programming problem [19] [20] [21] . A decision variable 






The constraints impose some bounds on the quantity of the different ingredients in the diet. For example a unit of feed is produced (a 1 kg mix), expressed by the constraint
where 


where 
5.2. Modelling of Nitrogen and Phosphorus Excretions
Nitrogen and phosphorus excretions are directly related to the excess of amounts of protein (amino acids) and phosphorus in the diet. Hence, we have to establish the protein and the phosphorus contents of the diet and take into account the parts that are actually assimilated.
The protein content of a diet 




Hence decreasing the total excretion 


As for the nitrogen, the amount of phosphorus of a unit weight diet 




Hence, decreasing the phosphorus excretion 


5.3. Data
The ingredients and their corresponding variables are described in Table 1. Table 2 contains the entire model together with the values of the technical coefficients of the model.
5.4. Software
The algorithm was programmed in MATLAB, which includes in its standard library the linear program solver called Linprog. This software can use the simplex method or an interior point method.
5.5. Two Criteria Models and Results
At first we analyse the relation between the cost of the diet and the two different excretions (nitrogen and phosphorus). As a curiosity, we also consider the interactions between the two kind of excretions: nitrogen and phosphorus.
Table 1. List of available ingredients.
5.5.1. Cost and Excretions
We have considered two separate bicriteria models. We look for least cost diets while taking into account the nitrogen excretion for the first model and the phosphorus excretion for the second model. For each of these two bicriteria problems, the Pareto curve indicates the diet cost increase caused by an excretion decrease.
While considering the nitrogen excretion, the problem is :
Table 3 presents the set of efficient extreme points of the Pareto set in the criterion space, and the Pareto curve is sketched in Figure 1. For this problem, the algorithm detects 
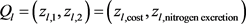
for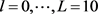 . A total of 22 calls to the linear program solver was required (the predicted maximum is
. A total of 22 calls to the linear program solver was required (the predicted maximum is ).
).
From its associated weighted-sum model given by
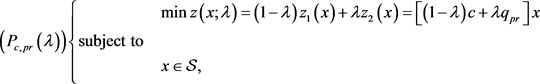
Table 3. Efficient extreme points in the criterion space  and the corresponding taxes for
and the corresponding taxes for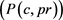 . and the corresponding taxes.
. and the corresponding taxes.
Table 3. Efficient extreme points in the criterion space  and the corresponding taxes for
and the corresponding taxes for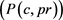 . and the corresponding taxes.
. and the corresponding taxes.
Figure 1. Pareto curve: nitrogen excretion vs diet cost.
we get the following expression for its value function

defined for



For the parametric model given by
we get the following expression for its value function 

defined for



So we see that for any tax value in 





A similar analysis holds for the second bicriteria problem with phosphorus excretion. Indeed, for the phosphorus excretion problem, the model is:


for

From its associated weighted-sum model given by
Table 4. Efficient extreme points in the criterion space 

Figure 2. Pareto curve: phosphorus excretion vs diet cost.
we get the following expression for its value function 

defined for



For the parametric model given by
we get the following expression for its value function 

defined for for



So we see that for any tax value in 





These problems of taxation are nice examples of abrupt (discrete) changes in behavior depending on the level of taxation of one criterion.
5.5.2. The Two Kinds of Excretion as Criteria
As a curiosity, we have computed the Pareto set for the bicriteria problem where the two kinds of excretions are considered. This bicriteria problem is given by
Table 5 presents the set of efficient extreme points of the Pareto set in the criteria space. Its corresponding Pareto curve is sketched in Figure 3. This table shows the opposite effect of trying to reduce simultaneously both excretions. Minimizing one excretion leads to an increse in the other excretion. For this problem, the algorithm detects 

For each
Figure 3. Pareto curve: phosphorus excretion vs nitrogen excretion.
Table 5. Efficient extreme points in the criterion space 


for







Let us observe that the last line of Table 3 (



6. Conclusion
In this paper we have considered bicriteria linear programming problems and have presented an elementary and efficient algorithm to compute the Pareto set in the criterion space. We have illustrated the method on a real important application. This application also suggests that it could be interresting to extend the method to three-criteria problems. Moreover it could be interesting to compare our method to other methods to find the Pareto set in the criterion space, but it is out of the scope of this paper and could be a nice subject for a future research.
Acknowledgements
This work has been supported in part by the Natural Sciences and Engineering Research Council of Canada and by the canadian corporation Swine Innovation Porc.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Dubeau, F. and Habingabwa, M.E.N. (2018) Fast Computation of Pareto Set for Bicriteria Linear Programs with Application to a Diet Formulation Problem. American Journal of Operations Research, 8, 323-342. https://doi.org/10.4236/ajor.2018.85019
References
- 1. Dubeau, F., Julien, P.-O. and Pomar, C. (2011) Formulating Diets for Growing Pigs: Economic and Environmental Considerations. Annals of Operations Research, 190, 239-269. https://doi.org/10.1007/s10479-009-0633-1
- 2. Adulbhan, P. and Tabucanon, M.T. (1977) Bicriterion Linear Programming. Computers & Operations Research, 4, 147-153. https://doi.org/10.1016/0305-0548(77)90036-3
- 3. Benson, H.P. (1979) Vector Maximization with Two Objective Functions. Journal of Optimization Theory and Applications, 28, 253-258. https://doi.org/10.1007/BF00933245
- 4. Cohon, J.L., Church, R.L. and Sheer, D.P. (1979) Generating Multiobjective Trade-Offs. Water Resources Research, 15, 1001-1010. https://doi.org/10.1029/WR015i005p01001
- 5. Gearhart, W.B. (1979) On the Characterization of Pareto-Optimal Solutions in Bicriteria Optimization. Journal of Optimization Theory and Applications, 27, 301-307. https://doi.org/10.1007/BF00933233
- 6. Geoffrion, A.M. (1967) Solving Bicriterion Mathematical Programs. Operations Research, 15, 39-54. https://doi.org/10.1287/opre.15.1.39
- 7. Kiziltan, G. and Yucaoglu, E. (1982) An Algorithm for Bicriterion Linear Programming. European Journal of Operationl Research, 10, 406-411. https://doi.org/10.1016/0377-2217(82)90091-1
- 8. Prasad, S.Y. and Karwan, M.H. (1992) A Note on Solving Bicriteria Linear Programming Problems Using Single Criteria Software. Computers & Operations Research, 19, 169-173. https://doi.org/10.1016/0305-0548(92)90090-R
- 9. Sadagan, S. and Ravindran, A. (1982) Interactive Solution of Bicriteria Mathematical Programs. Naval Research Logistics Quarterly, 29, 443-459. https://doi.org/10.1002/nav.3800290307
- 10. Walker, J. (1978) An Interactive Method as an Aid in Solving Bicriteria Mathematical Programming Problems. Journal of the Operational Research Society, 29, 915-922. https://doi.org/10.1057/jors.1978.195
- 11. Steuer, R.E. (1986) Multiple Criteria Optimization. Wiley, New York.
- 12. Dubeau, F. and Kadri, A. (2012) Computation and Visualization of the Pareto Set in the Criterion Space for the Bicriteria Linear Programming Problem. International Journal of Mathematics and Computation, 15, 1-15.
- 13. Benson, H.P. (1997) Generating the Efficient Outcome Set in Multiple Objective Linear Programs: The Bi-Criteria Case. Acta Mathematica Vietnamica, 22, 29-51.
- 14. Bertsimas, D. and Tsitsiklis, J.N. (1997) Introduction to Linear Optimization. Athenas Scientific and Dynamic Ideas, Belmont.
- 15. Murty, K.G. (1983) Linear Programming. Wiley, New York.
- 16. Chvatal, V. (1983) Linear Programming. W.H. Freeman and Company, New York.
- 17. Ferris, M.C., Mangasarian, O.L. and Wright, S.J. (2007) Linear Programming with MATLAB, MPS-SIAM Series on Optimization, Philadelphia.
- 18. Stigler, G.J. (1945) The Cost of Subsistance. Journal of Farm Economics, 27, 303-314. https://doi.org/10.2307/1231810
- 19. Dantzig, G.B. (1963) Linear Programming and Extensions. Princeton Press, Princeton.
- 20. Dantzig, G.B. (1990) The Diet Problem. Interfaces, 20, 43-47. https://doi.org/10.1287/inte.20.4.43
- 21. Garille, S.G. and Gass, S.I. (2001) Stigler’s Diet Problem Revisited. Operations Research, 49, 1-13. https://doi.org/10.1287/opre.49.1.1.11187























