ABSTRACT

Our research focuses on the development of two cooperative approaches for resolution of the multi-item capacitated lot-sizing problems with time windows and setup times (MICLSP-TW-ST). In this paper we combine variable neighborhood search and accurate mixed integer programming (VNS-MIP) to solve MICLSP-TW-ST. It concerns so a particularly important and difficult problem in production planning. This problem is NP-hard in the strong sense. Moreover, it is very difficult to solve with an exact method; it is for that reason we have made use of the approximate methods. We improved the variable neighborhood search (VNS) algorithm, which is efficient for solving hard combinatorial optimization problems. This problem can be viewed as an optimization problem with mixed variables (binary variables and real variables). The new VNS algorithm was tested against 540 benchmark problems. The performance of most of our approaches was satisfactory and performed better than the algorithms already proposed in the literature.

Keywords:

Variable Neighborhood Decomposition Search, Formatting, Metaheuristics, Production Planning, Capacitated Lot Sizing, Mixed Integer Programming, Matheuristics, Production Time Windows

1. Introduction and Motivations

The multi-item capacitated lot-sizing problem with time windows and setup times (MICLSP-TW-ST) has been an important part of material requirement planning (MRP) system. This problem is both complex and very important. Wherein, we seek to minimize the total cost of production, preparation and inventory. It comes to determine a production plan of a set of N products, for a time horizon consisting of T periods. This plan is finite capacity and must consider a set of additional constraints. Indeed, the manufacture of a unit of product i to the period t engenders a production cost pit and requires a manufacture time of $t{f}_i$ units of the capacity of the resource ( $C_t$ ). The cost of preparation ${\text{cpr}}_{it}$ is generated at each period. A storage cost of a unit of the product $i$ at the end of period t is $h_{it}$ . All these costs are deterministic. Each request must be produced before a deadline $D_i$ and of the same it becomes even available at a period $r_i$ “availability period” before which she cannot be produced.

The decision variables are $X{}_{it}$ which represents the product quantity $i$ manufactured in the period $t$ and $Y_{it}$ , the preparation variable that is equals 1 if $X_{it}>0$ . We need also to define Y_it as a binary variable equal to 1 if item i is produced at period t and 0 otherwise (i.e. if X_it > 0 only if Y_it = 1).

・ For this problem we dispose a set of command during a time horizons consisting of T periods in seek to satisfy the customer following delays taking into account the capacity constraint and fixed charge and variable launch of each product. Several extensions have been presented for this problem. We can therefore, classify those problems of the lot sizing at a level by Kuik and Solmon [1] and several production levels by Brahimi et al. [2] . Similarly, for the problem at a single level, they can be classified into problems to several products or to a single product. Several extensions have been proposed, and one finds the problem of several products with the re-fabrication (Richter and Sonbrutzki [3] ), preparation time (Trigeiro et al. [4] ), and with common preparations (Suerie and Stadtler [5] ). One finds these same extensions with the problems to a single product, in particular the case without capacity (Wagner and Whitin [6] ), and the products of re-fabrication (Golany, Yan, and Yu [7] ). One also finds the case with time windows on the demand (Lee, Cetinkaya, and Wagelmans [8] ). It has always been considered that the requests can be prepared early in the planning horizon.

However, there are several constraints that do than this hypothesis is not true. This is the case, for example, when the raw material is supplied to us at different periods. That is why we made recourse to the time window constraint and its importance in modeling and solving production planning problems, and in this case one should consider for each request an availability date in addition to her delivery date.

In the particular case with time windows for non-specific customers, products arriving at a period $s$ are used to satisfy the demands for which the due period expired is t ( $s\le t$ ) and which are not yet covered by products arriving before (First-In-First-Out).

The time window constraint signifies that there is a time interval where the customer demand can be satisfied without inventory and backlogging costs. Under this constraint, two cases may be presented: The specific customer case means that each specific demand should be satisfied within a given time interval. Therefore, the production between two periods’ $t_1$ and $t_2$ can only satisfy the specific demand available before $t_2$ . On the other hand, the non-specific customer case means that time windows are not inclusive, i.e. for any pair of time windows ( $s_1;t_1$ ) and ( $s_2;t_2$ ), it holds that $s_1\le s_2$ and $t_1\le t_2$ .

In the literature, Dauzère-Pérès et al. [9] are the first ones who presented the production time windows constraint in the LSP context. They have treated the customer specific case with single item. Wosley [10] considered the LSP with time windows under non-specific customer case. The LSP with non customer specific model is equivalent to the single item problem with stock upper bounds by Wosley [10] , whereas, in other study, Van den Heuvel and Wagelmans [11] have showed that this model is equivalent to the lot-sizing model with a remanufacturing option and the lot-sizing model with cumulative capacities.

In the literature, the first exact algorithm was presented by Wagner & Whitin [6] denoted (WW), is polynomial (initially resolved in O (T²)). It’s of a dynamic programming algorithm which explores the solution space of a problem for find the optimum. Recently, the complexity of dynamic algorithm of the lot sizing problem at a product and without capacity constraints has been improved at O (TlogT).

Pochet & Wolsey [12] , there are also several variations of the basic problem: the stock shortage, the preparation time and refabrication. For states of the recent art on the problem (see Brahimi & Nordli [2] ). Karimi et al. [13] and Dauzère-Pérès & Nordli [9] have proven that the algorithmic complexity for the lot sizing problem to a product as well as without capacity constraint with non- customer specific is NP-complete.

Lee & Wagelmans [8] imposed some assumptions on costs and have studied two cases: with and without the out of stock. For the case, with no stock shortage, an algorithm in O (T²) time has been proposed. When stock shortage is permitted the problem is solved in O (T³) time.

Our particular contribution relative to this subject is the introduction of a new model with constraints of time window. For which, we have developed two algorithm based mainly on two new formulations mathematical and analysis of methods of solving several classes of problems.

The choice of this problematic has relied on the reasons following: First of all we will exploit nature of the problem for propose a new resolution approach based on decomposition. In the second place, this algorithm of metaheuristic has proven its performance in solving of mixed-variable optimization problems.

Finally, this algorithm has never been applied to resolve the problems of multi-item capacitated lot-sizing problems with time windows and setup times.

In our study, we have focused on the problems at one level but at several products under capacity constraint with time windows and setup times. Let LSP denotes the lot sizing problem, as is shown in Figure 1.

The remaining of the paper is organized as follows: Section 2 describes an MIP formulation of the MICLSP-TW-ST problem, computational experiments are described in Section 3, and the conclusions and future researches are presented in Section 4.

2. Mathematical Formulation and Resolution

I will pass now to describe the mathematical model from lot sizing problem at several products that consists of determining a production plan for a set of N

products over a time horizon consisted of T periods. The objective is determined the periods of productions and the quantities to produce, in order to minimize the total production, setup and holding costs to satisfy all requests.

In this model, N and T stand for the number of items and the number of periods in the planning horizon respectively. The following notations are used in order to describe the mathematical model of the MICLSP-TW-ST problem:

Parameters for the MICLSP-TW-ST

The decision variables are as follows:

・ Model MICLSP-TW-ST

$\text{Min}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{t=1}^T\left(s_{it}{Y}_{it}+p_{it}{X}_{it}+h_{it}{I}_{it}\right)}}$ (1)

Subject to:

$I_{i,t-1}+X_{it}-I_{it}=D_{it}\forall i,t$ (2)

${\displaystyle \sum _{k=1}^t{X}_{ik}}\le {\displaystyle \sum _{k=1}^t{\displaystyle \sum _{s=k}^T{d}_{iks}}}\forall i,t$ (3)

${\displaystyle \sum _{k=t_1}^{t_2}{X}_{ik}}\ge {\displaystyle \sum _{k=t_1}^{t_2}{\displaystyle \sum _{l=k}^{t_2}{d}_{ikl}}}\forall i,t_1,t_2\left(t_1\le t_2\right)$ (4)

${\displaystyle \sum _{i=1}^N\left({\sigma }_i{X}_{it}+r_i{Y}_{it}\right)}\le C_t\forall t$ (5)

$X_{it}\le \left({\displaystyle \sum _{l=t}^T{d}_{il}}\right)Y_{it}\forall i,t$ (6)

$Y_{it}\in \{0,1\}\forall i,t$ (7)

$X_{it},I_{it}\ge 0\forall i,t$ (8)

The objective (1) is to minimize total setup, production and holding costs. Constraints (2) are the inventory balance equations. Constraints (3) state that the cumulative production in the first t periods does not exceed the cumulative quantity available from periods 1 to t. Constraints (4) guarantees that the constraints of time windows are satisfied. This constraints warrant that the production which is to be performed between two periods $t_1$ and $t_2$ .

The capacity constraints are represented by (5). Constraints (6) relate the binary setup variables $Y_{it}$ to the continuous variables $X_{it}$ . Finally, the integrality and non-negativity constraints are Constraints (7) and (8).

This problem may be seen as an optimization problem with variables mixed combined with binary variables and variable real.

2.1. Solving Multi-Item Capacitated Lot-Sizing Problems

Our idea for the approach proposed consists in decomposing the problem into two subproblems. The first one is composed of binary variables that will be resolved by an approximated method for the determination of days of production for each product during the time horizon. The second includes continuous variables that will be resolved by an exact method based on mathematical programming to determine the amounts of production and storage for each item during each period.

The general principle is to isolate the difficult part of the easy part of the problem and subsequently resolve the difficult part by an approached method and the easy part by an exact algorithm. We have developed two based algorithm principally on two new mathematical formulations to satisfy the capacity constraints.

We propose a procedure approached based on local search for the improvement of that solution. After creating an initial solution (shown in Figure 2), a phase of improvement is introduced by performing movements in the preparation sequence, because any changes in this sequence leads to a new solution (Y is a binary matrix). The vicinity of such a solution can be defined by the solution obtained in changing one or more components same time.

2.2. A Local Search Algorithm Based on Mathematical Programming (Algorithm 1)

For the first algorithm we proposed solve the problem with binary variables using a local search algorithm that will allow us to generate solutions in two neighboring structures.

The first is to be introduced or reviewed eliminate one day of production whereas second will allow us to change a day of production by another.

Whenever a new solution is generated, a new mathematical program will take place taking into account the partial solution obtained by the local search method, which going to make being an exact resolution for the definition of quantities to be produced for each product during each period.

・ A new mathematical formulation of the first algorithm

A new formulation of the MICLSP-TW-ST may be presented by a linear mixed integer program as follows:

Let $E_i$ denotes the set of periods where $y_{it}$ takes the value of 1. ( ∀ i )

and let F_t denotes the set of items produced in period t ( $\forall t$ ).

$\text{Min}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{t\in E_i}{p}_{it}{X}_{it}}}+{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{t=1}^T\left(h_{it}{I}_{it}+{\gamma }_{it}{Z}_{it}\right)}}$ (9)

Subject to:

$I_{i,t-1}+X_{it}+Z_{it}-I_{it}=D_{it}\forall i,t\in E_i$ (10)

$I_{i,t-1}+Z_{it}-I_{it}=D_{it}\forall i,t\in \{1,2,\cdots ,T\}/\left\{E_i\right\}$ (11)

${\displaystyle \sum _{k=1}^t{X}_{ik}}\le {\displaystyle \sum _{k=1}^t{\displaystyle \sum _{l=k}^T{d}_{ikl}}}\forall i,t\in E_i$ (12)

${\displaystyle \sum _{i\in F_t}^N\left({\tau }_i{X}_{it}+s{t}_i{Y}_{it}\right)}\le C_t\forall t$ (13)

$X_{it},I_{it},Z_{it}\ge 0\forall i,t$ (14)

In this new formulation, we introduced a new decision variable denoted $Z_{it}$ who means the quantity demand breaking than one item $i$ at period t and ${\gamma }_{it}$ is the cost associated with this variable. The new variable $Z_{it}$ , is used to create a feasible solution of the problem in order to calculate the value of the objective function. In addition, this new decision variable $Z_{it}$ measures the distance between region admissible and inadmissible of the search space. Indeed, the acceptance of a non-feasible solution will be penalized by a very high cost ${\gamma }_{it}$ .

According to basic math, this problem is a problem in whole numbers, including binary variables such as the configuration of each item for each period and continuous variables such as production quantities and stocks.

The complexity of the problem increases according to the numbers of items. In addition the size of the neighborhood is very wide which leads excessive execution times. We propose a procedure approach based on local search for improving this solution.

After you create an initial solution, a phase of improvement is introduced by performing movements in the preparation sequence, because any changes in this sequence led to a new solution.

First of all, all the elements of the matrix $Y_{it}$ are initialized to 1 for all items and all periods and the mathematical program will be resolved. In the solution obtained, the quantities produced are determined. On the basis of this modification within the matrix Y, the problem will be reformulated and solved.

These stages will be repeated until there is no quantity $X_{it}=0$ which corresponds to a preparation $Y_{it}$ different from zero. We used two structures of neighborhood to guide the local search to converge less rapidly to a local optimum.

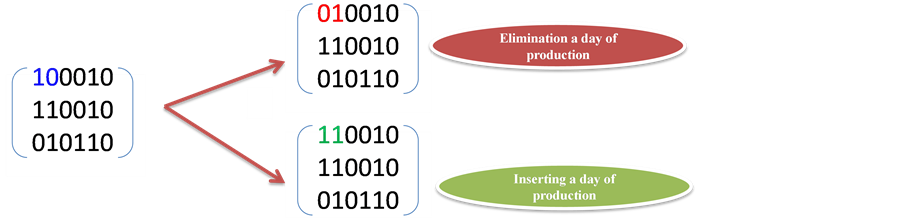
The first structure of used neighborhood is based on a single movement i.e. a single component of Y will be changed with every movement, as is shown in Figure 3. This structure consists in introducing or in eliminating a day of production. This stage will be repeated until the absence of the possible improvements, if a local optimum was found, the second structure of neighborhood will be realized, as is shown in Figure 4.

In this structure, the movement to base to two-segment is used. Two components will be changed. For each item $i$ , for each period t, all possible movements of permutation are used. A permutation movement consists in permute the values of two distinct periods for only one items i in the matrix Y. This step will be repeated up the absence of possible improvements. The choice of the change of the structure of a single item instead of two items is based on an extensive experiment. This second neighborhood structure will allow us to change a day of production by another.

An every time a new solution is generated, a new mathematical program will take place by taking into account the partial solution obtained by the method of local search. The algorithm will stop when the local optimum of the second procedure and the first procedure is the same.

2.3. Variable Neighborhood Search Based on a Local Search Algorithm (AL2)

In order to reduce the computing time engendered by the resolution of the mathematical program, we have developed a second algorithm based on a decomposition scheme which consists in transforming the problem of a problem multi-produced in a mono-produced problem; this procedure consists in considering the production item by item. Every time one seeks to optimize the days of production of one item, we consider that the quantities to produce other products during the horizon of time are fixed to the values of the best solution already obtained.

・ New mathematical formulation of the second algorithm

Based on the results of AL1, it is shown that the phase of the resolution of the mathematical programming is relatively slow. Therefore, we have proposed a decomposition scheme of the problem for reducing its size i.e. the number of constraints and the number of variables.

For each item; after performing the move, we evaluate this move according to the single item LSP by considering the remaining items as fixed. So, the multi-item LSP is transformed to the single-item LSP by performing the moves to the setup sequence of an item $i^{*}$ and assuming that the setup sequence for all remaining items are known. Therefore, in each iteration, a new mathematical formulation of the problem is developed and solved:

$\text{Min}\left(X,I,Z\right)={\displaystyle \sum _{t\in E_{i*}}\left(p_{i^{\ast }}{X}_{i^{\ast }t}\right)}+{\displaystyle \sum _{t=1}^T\left(h_{i^{\ast }t}{I}_{i^{\ast }t}+{\gamma }_{i^{\ast }t}{Z}_{i^{\ast }t}\right)}$ (15)

$\text{s}\text{.t}\text{.}{I}_{i^{*},t-1}+X_{i^{*}t}+Z_{i^{\ast }t}=D_{i^{\ast }t}+I_{i^{\ast }t}t\in E_{i*},$ (16)

$I_{i^{\ast },t-1}+Z_{i^{\ast }t}=D_{i^{\ast }t}+I_{i^{\ast }t}t\in \left\{1,2,\cdots ,T\right\}/E_{i*},$ (17)

${\displaystyle \sum _{K=1}^t{X}_{i^{\ast }k}}\le {\displaystyle \sum _{k=1}^t{\displaystyle \sum _{l=k}^T{d}_{i^{\ast }kl}t\in E_{i^{*}}}}$ (18)

${\delta }_{i^{\ast }}{X}_{i^{\ast }t}\le C_t-{\displaystyle \sum _{i^{\ast }=1}^N{\tau }_{i^{\ast }}{Y}_{i^{\ast }t}-{\displaystyle \sum _{\begin{array}{l}i\text{'}=1\\ i\text{'}\ne i^{\ast }\end{array}}^N{\delta }_{i\text{'}}{X}_{i\text{'}t}}}t=1,2,\cdots ,T,$ (19)

$X_{i*t}\le \left({\displaystyle \sum _{l=t}^T{D}_{i*l}}\right)t\in E_{i*},$ (20)

$I_{t*t},X_{i*t},Z_{i*t}\ge 0t=1,\cdots ,T$ (21)

where $E_{i*}$ the set of periods whose $Y_{it}=1\forall i*=1,2,\cdots ,N,$

The objective function (15) minimizes the total cost induced by the production plan that is production costs, inventory costs and penalty for the demand shortage costs for the item $i*$ .

The constraints capacity (19) is modified while taking into account the known production of the items other than $i*$ .

The evaluation of each move is computed according to the resolution of the mathematical programming presented above.

Indeed, if one reduces our mathematical program we will accelerate the resolution of the problem, it’s going to enable us to use a decomposition scheme which permutes from moving a local optimum and explore a larger region of the space search. The evaluation of motions with AL2 seems faster than that of AL1 since the reduction in the size of the mathematical program.

This second algorithm based on a decomposition scheme which consists in transforms the lot sizing problem multi products to a lot sizing problem to a finite capacity to single product. Our idea is to propose a new procedure for improvement using local search algorithm to variable neighborhood see Hansen [14] and Mladenović [15] .

The initialization of this algorithm follows the same way as in the algorithm 1. Our idea is to propose a new improvement procedure by using the Iterated Local Search algorithm (ILS) proposed by Lourenço et al. [16] .

This algorithm consists of two main steps: local search and perturbation. The first step leads to perform some moves to the current solution. The local optima found will be subject to the perturbation by applying random moves. These steps will be repeated until reaching a given stopping criterion.

The ILS algorithm has the advantage to explore regions far from the current region of the search space. So, once the best solution is found in a large region, it is necessary to go quite far to get better solutions. Therefore, this algorithm employs the concept of perturbation to move from one region to another which can be more profitable.

In our application, the neighbourhood structures used here are also the same used in algorithm1. However, within the local search, the way of solution’s evaluation of each move is based on the decomposition scheme described above.

3. Computational Experiments

This section reports computational experiments that evaluate the effectiveness of our algorithms and evaluate the performances against the proposed algorithms in the literature of the CLSP with time windows and set up times.

Our algorithms are implemented in the C++ programming language. We use the callable Cplex 9.0 library to solve the MILP problems. Computational experiments were performed on an Intel Core 2 CPU 2.67 GHz PC with 3.25 GB RAM.

The data sets used in our experiments are generated by Brahimi et al. [17] . These instance problems are based on the data sets of Trigeiro et al. [4] and extended by adding the time windows. More detailed information about these test problems is available in Brahimi et al. [17] .

3.1. Data Sets

The data sets used in our experiments are generated by Brahimi et al. [17] . These instance problems are based on the data sets of Trigeiro et al. [4] and extended by adding the time windows. More detailed information about these test problems is available in Brahimi et al. [18] .

The comparison was conducted after classifying the instances into 13 classes. For a time horizon will fixed at T = 20 periods and three values are used for the number of products N: 10, 20 and 30 products. We compared our approaches to resolution and we proposed several policies research local and procedures for improvement.

This extensive experimental study performed on 540 instances. For each product, the demand is uniformly randomly generated with a mean of 100 and a Coefficient of Variation (CV) is used to define the range of the uniform probability distribution. CV of the demand is set to 0.35 and 0.59 Moreover. 25% of the demands in each of the first four periods were randomly chosen and set to zero.

The utilization rate of total capacity is 75%, 85% and 95%. The time between two successive orders (TBO) is 1, 2 and 4. The average value of setup times over all products is 11 and 43 capacity unit. Finally, the production cost pit is set to 0 for all products and all periods.

3.2. Experimental Results

The Competing approaches used in our comparative study are the approaches developed by Brahimi et al. [17] . The first approach designated by (LR) is a lagrangian relaxation based heuristic.

The second one is an exact mixed integer programming approach based on a new reformulation of the problem and solved with a commercial software and denoted (MIPX). The last one is a mixed integer approach based on the original formulation of the problem and denoted by (MIPB).

To perform different quality measures by calculating the distances between lower and upper bounds of the same solution approach and between upper bounds (lower bounds) of different approaches. The distance or gap between two values $a$ and $b$ , where $a$ ≥ $b$ , is calculated as follows:

$\text{Gap}\left(a,b\right)=200\times \frac{a-b}{a+b}$ (22)

The formula $\text{Gap}\left(a,b\right)=200\times \frac{a-b}{a+b}$ is used instead of

( $\text{Gap}\left(a,b\right)=100\times \frac{a-b}{a}$ ) which overestimates the gap and

( $\text{Gap}\left(a,b\right)=100\times \frac{a-b}{b}$ ) which underestimates it. This approach was used. For

example, by Millar and Yang [19] and Brahimi et al. [18] .

In order to evaluate our results depending of the competing approaches of literature. We began our analysis by counting the number of feasible solutions found on the 540 tested problems.

Our first experiment, reported in Tables 1-4, involves running the Variable Neighborhood Search based on a local search algorithm approach for at most 500 iterations, stopping earlier if optimality is proven. The CPU time given to Lagrangian relaxation was at least 1 s longer than that required by AL2 (see columns 10 - 12 of Table 2).

As shown on Table 1. It can be seen that AL1 and AL2 are able to find 535 feasible solutions i.e. five instances remains unsolved as in LR algorithm.

The Lagrangian heuristic finds feasible solutions for most problems (99.1%). i.e. 5 problems were unsolved. In addition, to these 5 problems, the MIPX approach didn’t solve 6 more problems (feasible solutions were found for 98% of problems). Finally, the MIPB approach found feasible solutions for only 86.3% of the problems.

Table 2 summarizes the average gaps between upper bounds and lower bounds of each solution approach (columns 3 - 7) and the corresponding CPU times (columns 8 - 12). We note that these gaps are computed according to the feasible solutions provided by each approach. The best gaps are shown in boldface.

The first observation is that the MIPB approach always generates larger gaps (21.94% on average) than the four other approaches. It can be seen that the AL2 have provided the best gaps in average for 10 classes of instances among 13 whereas the LR algorithm have provided 2 best gaps.

The last line of Table 2 also shows that the average gaps of MIPX, LR, AL1 and AL2 are 1.84%, 1.46%, 2.13% and 1.17%, respectively. AL2 outperforms all the other approaches with 1. 17%. Concerning our proposed approaches, we notice that AL2 is the best algorithm.

Gaps increase with tighter capacities, and setup times and increasing TBO; and decrease with increasing demand variability and with number of products. Though the gaps of AL2 are better than those of LR, we notice that all lower bounds from LR are at least as good as those from AL2 and in most cases are better (larger).

From Table 2, we can notice that the CPU time for the approaches in each class of instances. We can see that AL2 has the smallest CPU time (4.11) according to AL1, MIPB and MIPX. This is due to the decomposion scheme used in this algorithm, where, at each iteration, a single item problem is solved. On the other hand, the AL1 algorithm appears to be the slowest algorithm. Besides, the CPU time and the gaps of the proposed algorithms increase when the number of items and TBO increase, and when the capacity is tightly constrained. In comparison with Brahimi et al. [17] approaches, the average CPU time values of our algorithms are relatively higher.

Table 3 shows the comparative study between the two proposed approaches in our paper. We compare the gap between the upper bound values provided by AL1 and AL2 according to Equation (22). It can be seen that AL2 is better than AL1 both in terms of average percentage deviations (0.26% in favour of AL1 and 1.76% in favour of AL2) and the number of better values of upper bounds. When AL2 is better than AL1, we find that the number of better upper bounds is large than the opposite case (31 upper bounds in favour of AL1 and 451 in favour of AL2). This is proving the contribution of the decomposition scheme introduced in AL2 for improving the results. However, in some cases AL1 is better than AL2 because AL1 explores more the depth of the space search.

Table 4 provides a comparative study between the upper bounds of AL2, MIPX and LR. It is shown that the proposed algorithm outperforms the two compared approaches. In average, for all classes, the percentage gap between AL2 and MIPX is equal 1.93% where AL2 is better than MIPX and is equal to 0.54% in the opposite case. The number of better upper bounds in favour of AL2 according to MIPX algorithm is 219. Regarding the LR algorithm, we see that AL2 is better in terms of average percentage deviations whereas the former is better in terms of number of improved upper bounds. However, as shown on Table 4, the LR upper bounds were better than those of AL2 in 34% of the problems and the bounds UB (AL2) were better for 33% of the test problems.

4. Conclusions

In our work, two cooperative approaches were proposed for solving multi-item capacitated lot-sizing problem with time windows and setup times where the non-customer specific demand is considered.

The problem is decomposed into two sub-problems: binary variables problem and continuous variables problem. Based on the complexity of each one of them, an exact approach using the mathematical programming is proposed for solving the problem with binary variables. On the other hand, the variable neighborhood search based on a local search algorithm, when applied to our efficient reformulations quickly finds good lower bounds and takes longer time to find and improve feasible solutions. However, its steady state is reached after almost 2 h thus yielding better results if it is given “enough” time.

The numerical results showed that the variable neighborhood search based on a local search algorithm quickly finds good feasible solutions. The comparative study is performed according to the representative approaches of the literature. The results have shown the efficiency of the proposed approaches.

Cite this paper

Erromdhani, R. and Rebaï, A. (2017) MIP Formulations and Metaheuristics for Multi-Item Capacitated Lot-Sizing Problem with Non-Customer Specific Production Time Windows and Setup Times. American Journal of Operations Research, 7, 83-98. https://doi.org/10.4236/ajor.2017.72006

References