American Journal of Operations Research
Vol.06 No.05(2016), Article ID:69644,7 pages
10.4236/ajor.2016.65034
Reliability Measures for Tele-Communication System with Redundant Transferring Machine by Using Algebraic Method
Pawan Kumar Sharma1, Ganesh Kumar Thakur1, Bandana Priya2
1Department of Applied Science, Krishna Engineering College, Mohan Nagar, India
2Department of Applied Science, G. L. Bajaj Institute of Technology & Management, Greater Noida, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 30, 2016; Accepted: August 8, 2016; Published: August 11, 2016
ABSTRACT
There are so many existing methods to obtain system reliability like re-generating point function technique, supplementary variables technique etc., but all these techniques are full of complicated calculations. Keeping above these facts in mind, the authors in this paper have evaluated some reliability parameters for tele-communica- tion system by using Boolean functions technique and algebraic method. Reliability of considered tele-communication system has been evaluated by considering the fact that failures follow arbitrary time distribution. In particular, the reliability expression has also been calculated for Exponential and Weibull distributions. Further, an important reliability parameter namely M.T.T.F. (mean time to failure) has also been calculated. A numerical example with graphical illustrations has been appended at the end to highlight the important results and practical utility of the model.
Keywords:
Boolean Function Technique, Algebra of Logics, Weibull Distribution, Exponential Distribution

1. Introduction
The whole tele-communication system has been divided into three parts, e.g., telephone instrument, main exchange and radar. The work of telephone instrument is to convert the human voice into radio waves and vice-versa. The main exchange receives these waves and transfers to their respective destinations (dialed by instrument) through the function of transferring machine and radar. In this paper, the author has assumed that, there are two identical transferring machines in both the main exchanges and working in parallel redundancy. The system configuration has been shown in Figure 1. The author has been used algebra of logics and method of Boolean functions to obtain some important reliability parameters under the following assumptions:
1. Initially, all components are in operable condition.
2. The state of each component and of the whole system is either good or fail.
3. There is no repair facility.
4. The states of all components of the system are statistically independent.
5. The reliability of every component of the system is known in advance.
6. The failure times of all components are arbitrary.
7. Supply between any two components of the system is fully reliable.
8. On failure of any one transferring machine, the system can work with the help of other.
The notations used for this study are as follows:
2. Material and Methods
This study was conducted at Department of Mathematics, K.E.C., Sahibabad, Ghaziabad, India during April 2015. The results obtained are studied there during June 2015.
In this study, the authors have been used Boolean function technique [1] to formulate mathematical model of the considered system. Various paths of successful operations of the system have been found. The reliability of considered system and MTTF [2] has been evaluated. These results can also be used to get various reliability parameters for the system having similar configurations.
Using algebra of logics, the conditions of capability for the successful operation of the considered system in terms of logical matrix has given as below:
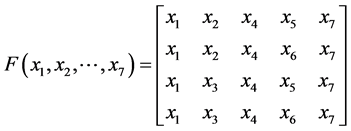 (1)
(1)
Figure 1. System configuration.
Using algebra of logics, Equation (1) can be written as
 (2)
(2)
where,
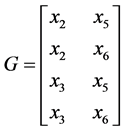 (3)
(3)
Now, substituting
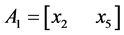 (4)
(4)
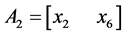 (5)
(5)
 (6)
(6)
and
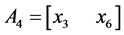 (7)
(7)
in Equation (3), we obtain
 (8)
(8)
Now using the theorem of summation of probabilities of compatible events, viz;
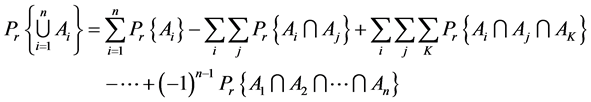
or,
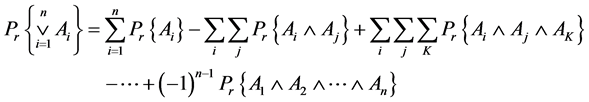 (9)
(9)
The probability of successful operation of the function G is given by
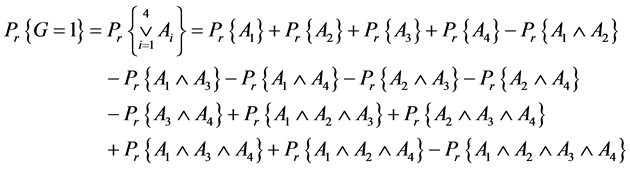 [By (9)] (10)
[By (9)] (10)
Now, we have

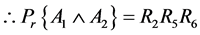
Similarly, we obtain the values of other terms appear in Equation (10) and get the following expression:
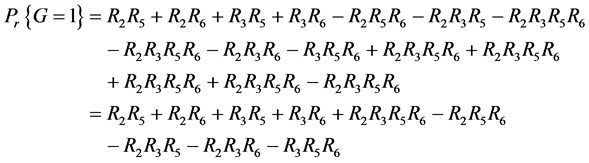 (11)
(11)
From Equation (2), we obtain
or,

3. Some Particular Cases
Case I: If the reliability of each unit of system is R
In this case, Equation (12) yields

Case II: When failures follow Weibull time distribution
For this, let 


where, p is a real positive parameter and
and
Case III: When failures follow exponential time distribution
Exponential time distribution is nothing but a particular case of Weibull distribution for

Also, an important reliability parameter viz; mean time to failure for the considered system, in this case, is given by

where, 

4. Numerical Computation
For a numerical computation, let us consider:
1) 


and

Now putting 
2)

Now putting 
Figure 2. Represent the way in which reliability of considered system decreases with time in case; failures follow Weibull and Exponential time distributions.
Figure 3. Represent the way in which mean time to failure of considered system decreases with increase in failure rate.
5. Results and Discussion
In this paper, we have evaluated reliability and mean time to failure [3] for the considered diesel tele-communication system by employing Boolean function technique [1] . Also, we have computed some particular cases to improve practical utility of the system. Gupta, P.P. et al. have done the reliability analysis of complex system but no care was given to structural redundancy [1] . On failure of main working unit, the whole system can also fail. So, for the better analysis we must have to consider the concept of structural redundancy. Thus we have done some better analysis of considered system of practical utility.
Figure 2 shows the values of reliability functions, when failures follow Weibull and exponential time distributions. Analysis of Figure 2 yields that as we make increase in time t, the values of 

Figure 3 gives the values of M.T.T.F. of considered system for different failure rates

6. Conclusion
In conclusion, author observes that we could improve system’s overall performance by using the concept of redundancy. The main objective of the study was to obtain continuous reliability of the system, and there should be no sudden jumps in the value of reliability of the system, and at the end authors were successful to do so. Boolean function technique is easier [4] as compared with the other techniques to obtain reliability parameters. We have compared the values of reliability function, in case; failures follow Weibull and Exponential time distributions. By using the structural redundancy, we obtain the better values of reliability and mean time to failure by taking the system with parallel redundant transferring machine.
Cite this paper
Sharma, P.K., Thakur, G.K. and Priya, B. (2016) Reliability Measures for Tele-Communication System with Redundant Transferring Machine by Using Algebraic Method. American Journal of Operations Research, 6, 371-377. http://dx.doi.org/10.4236/ajor.2016.65034
References
- 1. Gupta, P.P. and Agarwal, S.C. (1983) A Boolean Algebra Method for Reliability Calculations. Microelectronics Reliability, 23, 863-865.
http://dx.doi.org/10.1016/0026-2714(83)91014-4 - 2. He, Z.M., Han, T.L. and Eng, H.O. (2005) A Probabilistic Approach to Evaluate the Reliability of Piezoelectric Micro-Actuators. IEEE Transactions on Reliability, 54, 44-49.
- 3. Pandey, D. and Jacob, M. (1995) Cost Analysis, Availability and MTTF of a Three State Standby Complex System under Common-Cause and Human Failures. Microelectronics Reliability, 35, 91-95.
- 4. Cluzeau, T., Keller, J. and Schneeweiss, W. (2008) An Efficient Algorithm for Computing the Reliability of Consecutive-k-Out-Of-n:F Systems. IEEE Transactions on Reliability, 57, 84-87.
















