American Journal of Operations Research
Vol.05 No.03(2015), Article ID:55724,16 pages
10.4236/ajor.2015.53009
Applying Network Flow Optimization Techniques to Improve Relief Goods Transport Strategies under Emergency Situation
Novia Budi Parwanto1,2, Hozumi Morohosi1, Tatsuo Oyama1
1National Graduate Institute for Policy Studies (GRIPS), Tokyo, Japan
2Institute of Statistics (STIS), Jakarta, Indonesia
Email: oyamat@grips.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2015; accepted 15 April 2015; published 16 April 2015
ABSTRACT
Given the seriously damaged emergency situation occurring after a large-scale natural disaster, a critical and important problem that needs to be solved urgently is how to distribute the necessary relief goods, such as drinking water, food, and medicine, to the damaged area and how to transport them corresponding to the actual supply and demand situation as quickly as possible. The existing infrastructure, such as traffic roads, bridges, buildings, and other facilities, may suffer from severe damage. Assuming uncertainty related with each road segment’s availability, we formulate a transshipment network flow optimization problem under various types of uncertain situations. In order to express the uncertainty regarding the availability of each road segment, we apply the Monte Carlo simulation technique to generate random networks following certain probability distribution conditions. Then, we solve the model to obtain an optimal transport strategy for the relief goods. Thus, we try to implement a necessary and desirable response strategy for managing emergency cases caused by, for example, various natural disasters. Our modeling approach was then applied to the actual road network in Sumatra Island in Indonesia in 2009, when a disastrous earthquake occurred to develop effective and efficient public policies for emergency situations.
Keywords:
Natural Disaster, Emergency, Uncertainty, Transshipment Network Flow Optimization Problem, Monte Carlo Simulation, Relief Goods, Transport Strategy

1. Introduction
Emergencies occur from unexpected, serious, and often dangerous situations, such as natural disasters, human- caused accidents, and major terrorist attacks, and require immediate action. Large-scale emergencies may result in the loss of a large number of lives and/or severe property damage even though such emergencies may not occur so frequently. However, once a large-scale emergency occurred, as we experienced during the Great East Japan Earthquake in March 11, 2011, an enormous amount of confusion and damage to our society resulted.
Regarding disasters caused by nature, according to the International Disaster Database [1] , the incidence of natural disasters has risen dramatically over the last four decades. Natural disasters often cause a large number of fatalities and massive property damage, including those to infrastructure and transportation networks. Large natural disasters, such as earthquakes, hurricanes, and volcanic eruptions, have caused many casualties and/or severe damage to our infrastructure. These disasters include the Haiyuan Earthquake (1920), Tangshan Earthquake (1976), Hanshin-Awaji Great Earthquake (1995), Gujarat Earthquake (2001), Indian Ocean Earthquake and Tsunami (2004), Pakistan Earthquake (2005), Haiti Earthquake (2010), Great East Japan Earthquake and Tsunami (2011), New Zealand Earthquake (2011), the Bhola Cyclone (1970), Nevado del Ruiz Volcano Eruption (1985), Hurricane Andrew (1993), Hurricane Katrina (2005), and Cyclone Nargis (2008). Regarding the Great East Japan Earthquake and Tsunami in 2011, Parwan to and Oyama [2] have discussed details of the occurrence, causes, and damage by investigating the statistical data comparing natural disasters in Japan and Indonesia.
Shortly after a natural disaster occurs, many injured victims need to be immediately taken to hospitals, and survivors need some vital items for survival such as clean drinking water, food, and medicine. Some residents may not have any reserves of such vital items, while others may have them, though only in limited amounts. Unfortunately, the situation sometimes becomes worse, that is, when a large natural disaster occurs, severe damage to the existing infrastructure, such as traffic roads, buildings, bridges and other facilities, may happen. This condition will certainly complicate the process of delivering relief goods to the victims, even though a sufficient amount of goods may be available. Thus, the distribution of relief vital goods under large-scale emergencies, also known as logistics in an emergency, should be undertaken as quickly as possible, so that the victims can have an increased chance of survival. The planning strategy for the distribution of aid by considering all possibilities that occur is very important to implement. As pointed by Jiang et al. [3] , some specific characteristics of large-scale emergencies differ, depending on the type, for logistics in an emergency in the aftermath of a disaster. This condition makes the knowledge of aid logistics and supply chain management immensely important for humanitarian operations. One of the most highly recommended methods and the one often used for humanitarian operations is the operations research (OR) technique, since it has been proven to be beneficial for different planning situations (see Kovacs and Spens [4] ). However, given that the application of OR methods in emergency situations under uncertainty is still scarce, this study will investigate this issue, particularly proposing an optimization model regarding how to distribute necessary relief goods to the affected areas as soon as possible using the ground transportation.
We apply our model to the Indonesian case, where a M7.9 earthquake struck West Sumatra Province on September 30, 2009 at 17:16 pm local time and resulted in about 1197 dead and missing, 1798 people injured, and about 249,800 houses damaged. The West Sumatra Earthquake also caused damage to roads and bridges, which in turn disrupted the transportation network. In general, the earthquake caused damage in 13 regions (cities/re- gencies) out of 19 regions. These regions are Padang city, Pariaman city, Solok city, Padang Panjang city, Padang Pariaman regency, Bukittinggi city, Agam regency, Solok regency, Pasaman regency, Pasaman Barat regency, Pesisir Selatan regency, Tanah Datar regency and Mentawai Island regency, in which the last one is an archipelago regency separated from West Sumatra, with the only transportation to Mentawai Islandis by ship or aircraft.
In most cases of large-scale emergencies or large-scale disasters, the amount of relief supplies is limited while the demand is great. Liu et al. [5] argues that the key factor in an effective response under a large-scale emergency is the prompt availability of supplies at emergency sites. Hence, an efficient emergency transportation network becomes important in addressing and optimizing the complex distribution process.
In this paper firstly and generally we formulate a multi-commodity transshipment network flow optimization problem under various types of uncertain situations. Then by solving the network flow optimization problem, we try to find an optimal transport schedule for various kinds of relief goods including cases where all necessary demands are not met. Thus, under two different criteria, i.e. minimizing the total transport distance and minimizing the supply-demand gap, we investigate the characteristics of how the optimal transport schedule would be changed. Also, we take the uncertainty regarding the availability of each traffic road segment into consideration by giving the probability that each traffic road segment would be “blocked”. In order to deal with the quantitatively assumed probabilities, we apply the Monte Carlo simulation technique. Thus, we can determine the optimal transport schedule of various relief goods under emergency situations occurring just after natural disasters such as earthquakes and typhoons.
Van Wassen hove [6] describes as follows: disaster relief is about 80% logistics, therefore it would follow then that the only way to achieve this is through slick, efficient and effective logistics operations and more precisely, supply chain management. This condition renders the knowledge of aid logistics and supply chain management immensely important for humanitarian operations. Altay and Green [7] have summarized various applications of OR methods in disaster operations management. Delivery planning in disaster relief operations has also been studied rather extensively. Ozdamar et al. [8] proposed a logistics planning model in emergency situations that involves dispatching commodities to distribution centers in affected areas. Their model addresses the dynamic time-dependent transportation problems that need to be solved repetitively at given time intervals during ongoing aid delivery. Haghani and Oh [9] developed a multi-commodity, multi-modal network flow model for disaster relief operations in which they used penalty costs for unsatisfied demand.
On the other hand, Fiedrich et al. [10] proposed a dynamic optimization model to find the best assignment of available resources to affected areas after an earthquake. In addition, Lin et al. [11] developed a logistics model for disaster relief operations. They argue that the geographic location of the depot is very important as they have shown that they can improve the performance. Also they add that reduction in the number of clusters does not guarantee an improvement in the logistics of humanitarian relief by increasing the number of vehicles.
Meanwhile, Tzeng et al. [12] propose a multi-objective model for the optimal distribution of relief commodities, taking into account cost minimization, travel time minimization, and satisfied demand maximization. Vitoriano et al. also suggest a goal programming approach to support humanitarian organizations in aid distribution decisions [13] . Yi and Ozdamar [14] propose different transportation and network flow models in which they have also taken into account uncertainty, multiple aid items, and multiple time-periods (see also Ozdamar et al. [8] , and Barbarosoglu and Arda [15] ).
In most of the above-mentioned studies, the preparation phase or the immediate response of disaster relief has been addressed, in which most of the problems fall into the transportation problem category, namely allowing only shipments that go directly from a supply point to a demand point. However, in many situations, shipments should be allowed between supply points or between demand points, in which there may also be some points (called transshipment points) through which goods can be transshipped on their journey from a supply point to a demand point. Shipping problems with these kinds of characteristics are known as transshipment problems (see e.g. Winston [16] ). Fortunately, the optimal solution to a transshipment problem can be found by solving a transportation problem, although few studies have been conducted in this field. Herer et al. [17] developed a transshipment model in a supply chain, which consists of several retailers and one supplier. Rootkemper et al. [18] developed a mixed-integer programming model to minimize the unsatisfied demand as well as the operational costs by imposing penalty costs for unsatisfied uncertain demand.
We know there are more references dealing with emergency management issues such as the IJISCRAM1 and the IEEE International Conference on Emergency Management even though we could not include them in this paper. We believe these references could be very useful for our future research.
2. Transshipment Network Flow Optimization Model Analyses
2.1. Objectives of the Network Flow Optimization Model
We consider a case where an emergency situation, caused by, for example, a relatively large scale natural disaster, has just occurred in a particular area consisting of several regions/cities and has rendered significant damage to property and inflicted human casualties, both deaths and injuries. Some regions have experienced damage and losses more severely than other regions. These regions should immediately get help, in the form of consumable and durable commodities. Some emergency supplies must be transported from several supply centers/depots (airport/harbor or central inventory) to locations with demand (e.g. affected regions). In addition, it is given that, in general, every region has a supply/stockpile of emergency vital needs, albeit for a relatively short time and in limited quantities. Thus, for a relatively short time (i.e. a few days), the need of relief goods vital for survival, such as medicine/drugs, drinking water/clean water, and food, can be supplied by the affected regions of the natural disaster itself; in other words, the affected regions become both demand and supply regions.
We consider the following problem. Suppose we are given a set of regions, e.g. cities, and a set of commodities, e.g. drinking water, food and medicine, and moreover suppose we know that each city has a certain amount of each commodity it can supply, as well as some demand. Then if each city’s supply of each commodity is not less than its demand, then we do not need to transport any commodity from one city to another. However, as this case may occur generally, we want to find an optimal transport scheduling strategy so that all the demand for commodities for all cities can be met. Otherwise, namely in the case where all cities’ demands for commodities are not necessarily met, we want to find some desirable transport scheduling strategy. We denote regions with excess supply, namely regions where the supply for the commodity is larger than the demand, as RES. Similarly, other affected regions might not be able to satisfy their own demand. We denote such regions with excess demand, namely regions where the demand for the commodity is larger than the supply, as RED. Of course, affected regions that experience excess demand (RED) are regions that should immediately get help in order to minimize the number of casualties as a result of the disaster. The necessary goods for survival must be immediately sent to this region. Thus, logistics in an emergency can be defined as the distribution of relief vital needs commodities under (large-scale) emergencies, which is also known as humanitarian logistics or relief operations, carried out in the second phase of disaster management, i.e. the response phase. The following formulation of a multi-commodity transshipment network flow optimization model provides a solution to the problem described above.
Common practices follow that the available relief aid to be sent immediately should come from the neighboring regions that are less affected (RES) to the regions that are severely affected (RED). However, the immediate relief consignments may not be able to satisfy all the demands. Subsequently, we need to transport the relief logistics from, e.g. the supply center (SC) once they become available. Hence, these problems will be solved by a technique whereby we calculate the maximum demand gap and transport relief aid by using the shortest path technique.
In general, depending on the time when the SC can be established and operated, we consider the stage to deliver relief aid to the affected regions. Firstly, we consider how RES can deliver their surplus to RED, and if there still remains a demand gap in RED, then we consider how the SC can deliver relief aid to meet all the remaining demand “shortage” gap in RED.
2.2. General Formulation and Computational Procedures
We denote the network by
 where N is a set of vertices corresponding to regions/cities and E is a set of edges corresponding to road segments. We assume that each region is represented by the capital city, thus in order to measure the distance between two regions we define the distance between these capital cities. Set E
where N is a set of vertices corresponding to regions/cities and E is a set of edges corresponding to road segments. We assume that each region is represented by the capital city, thus in order to measure the distance between two regions we define the distance between these capital cities. Set E
consists of the edge
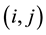 from region i to j defined by
from region i to j defined by . K is the set of relief vital com-
. K is the set of relief vital com-
modities such as drinking water, food, medicine/drugs, etc. We formulate a network flow optimization problem, which we call a network flow optimization model (NFOM). We denote input data as follows (i)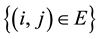
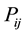 : probability that the edge (roadsegment) between region i and j is broken; (ii)
: probability that the edge (roadsegment) between region i and j is broken; (ii)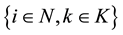
 : supply for commodity k in region i; (iii)
: supply for commodity k in region i; (iii)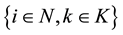
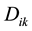 : demand for commodity k in region i; (iv)
: demand for commodity k in region i; (iv)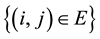
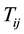 : transportation cost (distance or travel time) for road segment
: transportation cost (distance or travel time) for road segment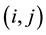 ; (v)
; (v)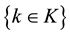
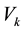 : maximum load capacity of the vehicle for commodity k; (vi)
: maximum load capacity of the vehicle for commodity k; (vi)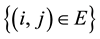
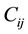 : road capacity for road segment
: road capacity for road segment

We define the decision variables, constraints and objective function of the NFOM as follows:
i) Decision variables




ii) Constraints
As the model is based on a network flow formulation, we need to formulate continuity and conservation conditions. The constraints are stated and explained as follows:




Constraint (1) expresses the flow conservation condition satisfying the demand for commodity k in region j. In addition, in constraint (1) the amount of commodity k transported to region j from all other region i may not satisfy the demand needed in region j, then, we assume that the amount of commodity k transported to region j should meet the demand for commodity k in region j by taking a positive value for the variable
iii) Objective function
Our linear programming model has two objectives, namely to minimize the transportation cost (i.e. distance or time travel) and the total demand gap. The objective function of the model is stated in the following:

where

To incorporate the uncertainty condition, we modify one of the constraints namely constraint (2), by adding the probability of broken road segment

Constraint (6) indicates that a road segment


We can summarize our computational procedures as follows:
A flow chart of the Iterative computational procedure is given in Figure 1.
The network flow optimization model, NFOM, described above gives an optimal allocation of supplying relief goods from some region in RES to another region in the RED. Then we consider how we can meet the remaining excess demand of relief aid in RED. We formulate a network flow optimization model to solve this problem for the emergency situation, which we call the demand shortage clearance model (DSCM). Our assumption follows that all the remaining demand of relief commodities in RED will be met by providing commodities from the SC, i.e. a certain designated region in the network, to each region in RED. In order to attain an optimal transportation schedule we formulate the following network flow optimization model.
We define the input data for the network flow optimization model as follows: I: set of destination regions,











Typically



scheduling problem. Decision variables, constraints and the objective function are stated as follows:
i) Decision variables


ii) Constraints



Figure 1. Flow chart of the iterative computational procedure.
Constraint (7) is on the minimum number of vehicles necessary for the delivery to destination i. The summation is taken for all the batches to calculate the total number of vehicles necessary for destination i. Constraint (8) limits the total number of vehicles used at every hour. Incidentally, this constraint (8) becomes redundant for some t values as they give the same constraint, so we need to delete those redundant constraints even though the application software FICO Express 7.4 (Fair Isaac Corporation) ignoredthis redundancy. Constraint (9) is the road capacity constraint.
iii) Objective function

We assume the shortest path is used in order to deliver the goods to any destination region. Our objective function aims at minimizing the number of vehicles necessary for the delivery from SC to the destination region in RED in the sense that we try to minimize the criterion given by (10). In the objective Function (10), the coefficient

3. Application to the Indonesian Sumatra Earthquake Case
3.1. Data and Assumptions
We apply the network flow optimization model described above to the case of the 2009 West Sumatra earthquake in Indonesia. We know that Sumatra Island is an area included in a zone of high seismic activity, the so- called “Pacific Ring of Fire”. Thus, earthquakes are one of the natural hazards that can hit the island at any time. Thus, a disaster management plan that includes emergency response preparations should be done as carefully and quickly as possible, with the principle of “hope for the best but prepare for the worst”.
Two earthquakes of 7.6 and 6.2-moment magnitude struck off the coast of West Sumatra, Indonesia on September 30, 2009. The first earthquake occurred at 17:16 p.m. and the second one followed 22 minutes later. The epicenter was 45 km west-northwest of the port city of Padang, the capital of West Sumatra, and it had recorded a depth of 71 km. A third earthquake of 6.8 magnitude struck an inland area, 225 km southeast of Padang, early the next morning (BNPB, 2009). The cumulative impact of these events left a broad swath of destruction. The earthquakes caused serious damage to housing and infrastructure in the communities in 13 regencies/cities2, destroying livelihoods, and disrupting economic activity and social conditions, causing extensive psychological trauma [19] [20] . Landslides in West Sumatra left scores of houses and several villages buried; i.e., three villages in the path of the disaster in Padang Pariaman regency appeared to have been completely leveled, and most of their inhabitants appear to have been buried due to subsequent landslides. Macro data for the casualties and property damages are given in Table 1, while the corresponding detailed data for the West Sumatra Provinces are shown in Table 2.
Furthermore, to deliver some relief commodities to the affected regions, we need to know the road transportation network system of West Sumatra Province. It should be noted that the entire transportation road network system in West Sumatra province is large as it comprises of state roads, provincial roads, and district roads. Since we only deliver relief aid from SC, located in the provincial capital, Padang city, to the capital of the district/city or to the depot in each district/city, we assume that we only deliver the relief aid up to the SC of each affected region, mostly located in the capital of each regency/city rather than delivering the relief aid directly to the beneficiaries. Thus, we simplify the entire network system by simply taking the main roads linking the capital of the affected district/city, which consists of state roads and provincial roads. Figure 2 shows the road transportation network system with 12 vertices and 22 edges in West Sumatra province as a whole.
In Figure 2, there are 7 regions affected by the disaster, which can be divided into two groups, namely severely affected and less affected regions. Regions that belong to the former group are 1, 2, 5, and 6, while regions 3, 4, and 7 belong to the latter group. Regions in the latter group may be able to satisfy their own demand, and they may have supply surplus for some relief commodities, which then makes them suppliers, and we define these regions as regions with supply surplus or RES. On the other hand, regions in the former group cannot satisfy their own demand, thus creating a demand shortage. We define these regions as regions with demand
Table 1. Casualties and property damage caused by the West Sumatra earthquake.
Source: National Disaster Management Board (BNPB) of Indonesia. H: Heavily; M: Moderately; L: Lightly.
Table 2. Number of population, households, casualties and property damage by affected region.
Source: National Disaster Management Board (BNPB) of Indonesia.
Figure 2. Illustration of road network system and flow commodity to/from a region.
shortage or RED. In most cases, when there is a disaster, the relief consignments from the supply center, which come from the central government or other parties, usually do not come immediately due to some difficulties. Therefore, common practices follow that the available relief aids to be sent immediately should come from the neighboring regions of less affected RES to those of severely affected RED. However, the immediate relief consignments may not be able to satisfy all the demands too. Subsequently, we need to transport the relief logistics from the SC once they become available. Thus, these problems will be solved by calculating the maximum demand gap and transporting relief aid by using the shortest path technique.
3.2. Numerical Results by the Deterministic Approach
Firstly we consider the case that all road segments are available (survive), i.e.




Table 3 gives the demand and supply for the commodity, i.e. drinking water for 7 days (one week). The supply and demand columns describe the stockpile/reserve and the need for each commodity in each affected region. In Table 3, the negative value of Gap indicates that the region is in a Region with Excess Demand (RED), while a positive value of Gap indicates that the region is in a Region with Excess Supply (RES). The Total Excess Demand (TED) from RED is the summation of all the negative values of Gap, which is 823.12 for drinking water from Table 1. The Total Excess Supply (TES) from RES is the summation of all positive values of Gap, which is 71.15 for drinking water from Table 1. As mentioned in Section 2, just after the natural disaster occurs, the affected region should try to satisfy the demands using existing reserves in each region. However, as this can only last for a few days, not long after, the increased demand and the diminishing supplies lead to gaps between supply and demand in some affected regions, especially in regions that have experienced the relatively severe impact of the natural disaster. Of course, this gap should be filled as soon as possible by sending the commodity from the neighboring region and/or the SC. Data sources for the supply for aid commodities are several governmental institutions. Data for drinking water are taken from the regional enterprise of drinking water (PDAM). Furthermore, the estimated relief commodity, drinking water for one week, available in the SC Padang city is 1058.76 (m3). The number of trucks for transporting food and medicine is estimated to be 56 vehicles with the maximum capacity per vehicle being 14 tons, while the number of tanker trucks for transporting drinking water is estimated to be 39 with the maximum capacity per vehicle being 6 m3.
Table 3. Demand and supply for drinking water to the affected area for one week by region.
From Table 3, we see that all the commodities have larger total demand than total supply, which leads to “demand gaps” interpreted as “shortages” for each commodity. Furthermore, we can also see that the situation is different for each commodity in each region. Figure 3 illustrates the condition of supply and demand of drinking water by region. For instance, as depicted in Figure 3, regions 1, 2, 3, 4, 5, 10, 11, and 12 encountered excess demand for drinking water denoted by RED, where region 11 has the largest (maximum) demand gap (282.49); while regions 6, 7, 8, and 9 denoted by RES experienced excess supply (71.15). Then by assuming that the main SC takes some times to be established and/or start operating, RES can deliver their excess supply to their neighboring RED.
Our objective function given in (5) consists of two terms in which the first one aims at minimizing the transportation cost (i.e. distance or time travel), while the second one corresponds to minimizing the maximum demand gap. Even though we are aiming at minimizing both the transportation cost and the maximum demand gap simultaneously, the optimal solution obtained from the model depends upon the values of coefficients K1 and K2 indicating the relative “importance” of the above two terms. A general computational procedure of the model analysis implies that after estimating the gap, we try to deliver supplying commodities from RES to RED with minimum transportation cost taking the maximum demand gap minimization into consideration.
Table 4 shows the change of optimal solution for water delivery corresponding to the gradual increase of coefficient value













Figure 3. Supply and demand of drinking water (m3) by region. Note: S: Supply; D: Demand; Number in brackets { } represent the gap; + indicate excess supply; − indicate excess demand; RES: Region with excess supply; RED: Region with excess demand.
Table 4. Optimal solutions for delivering drinking water (m3).
gap to be filled as 37.94 m3 corresponding to the available delivery of drinking water from region 9 given by
“turning” coefficient value appears between




We see no change for our optimal solution after we increase the value of

4. When
have been delivered to RED (i.e. region 11), resulting in a decrease in



The results in Table 4 and Figure 4 show that there still remain demand gaps for the commodity of drinking water in each region with demand shortage (RED). All of these remaining demand gaps in the RED need to be met by delivering additional relief goods from the SC to each destination. The problem then will be how to deliver the relief goods from the SC to the RED as quickly as possible. We try to solve this problem for the emergency situation using what we call DSCM, described in Section 2.2.
From the solutions shown in Figure 4 we see that the maximum excess demand gap in region 11 was reduced from 282.49 to 211.34. However, we know that still there remain excess demand gaps in regions 1, 2, 3, 4, 5, 10 and 12 also with 751.95 in total as shown in Table 3. We try to fill these excess demand gaps by sending vehicles to all regions needed carrying the relief commodity drinking water with the minimum number of batches for sending vehicles. In order to apply the optimization model given in (7)-(10), we use the following data. The number of simultaneously available vehicles, capacity of vehicle, velocity of vehicle, maximum number of batches and maximum time horizon of delivery are given as









Furthermore, as our objective is to deliver the vehicles from the SC, which is at the provincial capital i.e. Padang city, to the RED as quickly as possible, in solving this shortest path problem we exclude region 1. In addi-
tion, we also assign the following assumptions: vehicle velocity




Figure 4. Illustration for delivering drinking water from RES to RED (K2 = 210).
Table 5. Minimum number of vehicles necessary for delivering drinking water.
We define input data for the model DSCM given by (7)-(10) in order to meet all the demands for the relief
good, i.e. drinking water, in the RED as follows:





given in Table 5. Delivery routes for the relief good of drinking water from SC to RED are shown in Figure 5.
3.3. Numerical Results by the Probabilistic Approach
The probabilistic approach considers the probability


route for delivering aid commodity as well as the amount of aid commodity to be changed. Following the algorithm shown in Figure 1, we apply conducting

Table 6 presents the computational results giving the mean values of the max-gap, total distance to deliver the relief goods drinking water from RES to RED corresponding to various values of probability of broken road segments. In Table 6, we can see that the available drinking water is delivered from RES to region 11 with the highest demand gap. Figure 6 shows the total distance for delivering the drinking water from SC to RED and the value of the max-gap corresponding to various probability values. From Figure 6, we find that as the probability of broken road segments increases, the total distance for delivering the drinking water from SC to RED region 11 decreases while the max-gap increases. Figure 7 shows the amount of the drinking water from SC to RED corresponding to various probability values. We see that as the probability of broken road segments increases, the amount of the drinking water delivered from SC to region 11 decreases, reaching zero when all road segments were broken with probability 100%.
The higher possibility of broken road segments also suggests alarger remaining demand gap. As we can see from the column of max-gap which represents the amount of remaining maximum demand gap in Table 7, when all the road segments are available
4. Summary and Conclusions
Given that disasters are prominent throughout the world, the importance of disaster management is undeniable, and a large amount of human losses and unnecessary demolition of infrastructure can be avoided with very responsive Disaster Management Action, and thus humanitarian logistics or logistics in an emergency should be
Figure 5. Delivery routes for the drinking water from SC to RED (K2 = 210).
Figure 6. Total distance for delivering drinking water from SC to RED and the max gap.
Figure 7. Amount of the drinking water delivered from SC to RED.
Table 6. Mean of max gap, total distance and delivery of drinking water from RES to RED.
Note: Transshipment from RES to RED: positive value = imported; negative value = exported.
Table 7. Mean of the transshipment flow of drinking water to region 11.
well planned in advance. In such a situation, an optimal strategy on how to distribute necessary relief commodities to the damaged areas and transport them corresponding to their supply and demand condition as quickly as possible is vitally needed. As part of the action taken in the response phase, our optimization models have tried to address this issue.
In this study, an approach for logistics in emergency under uncertainty has been presented, which can be applied in the occurrence of seriously emergency situations. In such a situation, we try to find an optimal strategy on how to distribute necessary relief commodities to the damaged area and transport them corresponding to their supply and demand condition as quickly as possible. The optimal strategy should take into account two objectives: minimizing the transportation cost (i.e. distance or travel time) and the total demand gap.
In order to solve this problem, we build a multi-commodity transshipment network flow optimization model (NFOM) for making decisions under uncertainty. To evaluate the model and the solution method, we apply the NFOM to the case of the 2009 West Sumatra earthquake in Indonesia. The resulting planning problem consists of the distribution of the relief commodities and the number of vehicles necessary to deliver the relief commodities. Both the NFOM and the demand shortage clearance model (DSCM), including the simulation, and the solution analyses, are applicable to other planning situations such as air transportation and water transportation of various types of relief goods, which have similar characteristics.
The optimal strategy obtained from the NFOM should take into account two objectives, namely, minimizing the transportation cost (i.e. total distance or travel time) and minimizing the maximum demand gap. By assuming a fixed value of the coefficient


Both NFOM and DSCM are necessary, useful, and important, even though they have their own shortcomings and limitations in the sense that neither can solve the total and comprehensive relief goods transport problem completely. However, we believe that under conditions of uncertainty such as after the occurrence of natural disasters, and given that the amount of damage and casualties may not be known, our model results can give us new insights and findings regarding how we should handle relief goods transport problems under emergency situations.
In this regard, we can say from the viewpoint of public policy that the government must carefully plan the humanitarian logistics in advance. More specifically, the government should always keep an inventory of the supply of relief commodities and update it in terms of both quantity and quality, and keep track of the transportation modes.
Acknowledgements
The authors would like to express our sincere thanks to the reviewerswho have given us insightful,invaluable and useful comments. Their comments led us to a significant improvements of the paper.
References
- EM-DAT (2014) The OFDA/CRED International Disaster Database. Universite catholique de Louvain, Brussels. www.emdat.be
- Parwanto, N.B. and Oyama, T. (2014) A Statistical Analysis and Comparison of Historical Earthquake and Tsunami Disasters in Japan and Indonesia. International Journal of Disaster Risk Reduction, 7, 122-141. http://dx.doi.org/10.1016/j.ijdrr.2013.10.003
- Jiang, Y., Yuan, Y, Huang, K. and Zhao, L. (2012) Logistics for Large-Scale Disaster Response: Achievements and Challenges. 45th Hawaii International Conference on System Sciences, Maui, 4-7 January 2012, 1277-1285. http://dx.doi.org/10.1109/HICSS.2012.418
- Kovacs, G. and Spens, K.M. (2007) Humanitarian Logistics in Disaster Relief Operations. International Journal of Physical Distribution & Logistics Management, 37, 99-114. http://dx.doi.org/10.1108/09600030710734820
- Liu, D., Han, J.Y. and Zhu, J.M. (2007) Vehicle Routing for Medical Supplies in Large-Scale Emergencies. The First International Symposium on Optimization and Systems Biology (OSB2007), Beijing, 8-10 August 2007, 412-419. http://www.aporc.org/LNOR/7/OSB2007F47.pdf
- Van Wassenhove, L.N. (2006) Humanitarian Aid Logistics: Supply Chain Management in High Gear. Journal of Operational Research Society, 57, 475-489. http://dx.doi.org/10.1057/palgrave.jors.2602125
- Altay, N. and Green, W.G. (2006) OR/MS Research in Disaster Operations Management. European Journal of Operational Research, 175, 475-493. http://dx.doi.org/10.1016/j.ejor.2005.05.016
- Ozdamar, L., Ediz, E. and Beste, K. (2004) Emergency Logistics Planning in Natural Disasters. Annals of Operations Research, 129, 217-245. http://dx.doi.org/10.1023/B:ANOR.0000030690.27939.39
- Haghani, A. and Oh, S.C. (1996) Formulation and Solution of a Multi-Commodity Multi-Modal Network Flow for Disaster Relief Operations. Transportation Research Part A: Policy and Practice, 30, 231-250. http://dx.doi.org/10.1016/0965-8564(95)00020-8
- Fiedrich, F., Gehbauer, F. and Rickers, U. (2000) Optimized Resource Allocation for Emergency Response after Earthquake Disasters. Safety Science, 35, 41-57. http://dx.doi.org/10.1016/S0925-7535(00)00021-7
- Lin, Y.H., Batta, R., Rogerson, P.A., Blatt, A. and Flanigan, M. (2009) Application of a Humanitarian Relief Logistics Model to an Earthquake Disaster. http://www.acsu.buffalo.edu/~batta/TRB_Updated.pdf
- Tzeng, G.H., Cheng, H.J. and Huang, T.D. (2007) Multi-Objective Optimal Planning for Designing Relief Delivery Systems. Transportation Research Part E, 43, 673-686. http://dx.doi.org/10.1016/j.tre.2006.10.012
- Vitoriano, B., Ortuno, M.T., Tirado, G. and Montero, J. (2011) A Multi-Criteria Optimization Model for Humanitarian Aid Distribution. Journal of Global Optimization, 51, 189-208. http://dx.doi.org/10.1007/s10898-010-9603-z
- Yi, W. and Ozdamar, L. (2007) A Dynamic Logistics Coordination Model for Evacuation and Support in Disaster Response Activities. European Journal of Operational Research, 179, 1177-1193. http://dx.doi.org/10.1016/j.ejor.2005.03.077
- Barbarosoglu, G. and Arda, Y. (2004) A Two-Stage Stochastic Programming Framework for Transportation Planning in Disaster Response. Journal of the Operational Research Society, 55, 43-53. http://dx.doi.org/10.1057/palgrave.jors.2601652
- Winston, W.L. (2003) Operations Research Applications and Algorithms. 4th Edition, Duxbury Press, California.
- Herer, Y.T., Tzur, M. and Yuecesan, E. (2006) The Multilocation Transshipment Problem. IIE Transactions, 38, 185- 200. http://dx.doi.org/10.1080/07408170500434539
- Rottkemper, B., Fischer, K. and Blecken, A. (2012) A Transshipment Model for Distribution and Inventory Relocation under Uncertainty in Humanitarian Operations. Socio-Economic Planning Sciences, 46, 98-109. http://dx.doi.org/10.1016/j.seps.2011.09.003
- West Sumatra and Jambi Natural Disasters: Damage, Loss and Preliminary Needs Assessment. 2009. A Joint Report by the BPNB, Bappenas, and the Provincial and District/City Governments of West Sumatra and Jambi and International Partners.
- Sugimin, P. (2011) Lesson Learned: Rehabilitation and Reconstruction West Sumatra September 30th, 2009 Earthquake, Building Back Better. Gramedia Ltd. Printing Group, Jakarta.
NOTES
1International Journal of Information Systems for Crisis Response and Management. http://www.igi-global.com/journal/international-journal-information-systems-crisis/1119
2Since our study is only focused on the transportation network using land vehicles, we will exclude Mentawai Island regency from our analysis. Available transportation from/to Mentawai Island are air and/or water transportation.

















