Received 28 August 2014; revised 22 September 2014; accepted 6 October 2014

ABSTRACT

In this paper, we present an algorithm to solve the inequality constrained multi-objective programming (MP) by using a penalty function with objective parameters and constraint penalty parameter. First, the penalty function with objective parameters and constraint penalty parameter for MP and the corresponding unconstraint penalty optimization problem (UPOP) is defined. Under some conditions, a Pareto efficient solution (or a weakly-efficient solution) to UPOP is proved to be a Pareto efficient solution (or a weakly-efficient solution) to MP. The penalty function is proved to be exact under a stable condition. Then, we design an algorithm to solve MP and prove its convergence. Finally, numerical examples show that the algorithm may help decision makers to find a satisfactory solution to MP.

Keywords:

Multi-objective programming, penalty function, objective parameters, constraint penalty parameter, Pareto weakly-efficient solution

1. Introduction

Multi-objective programming is an important model in solving vector optimization problems. Many methods had been given to find solutions to multiobjective programming [1] . It is well-known that the penalty function is one of efficient methods in studying multiobjective programming. For example, in 1984, White [2] presented an exact penalty function for multiobjective programming. Sunaga, Mazeed and Kondo [3] applied penalty function formulation to interactive multiobjective programming problems. Ruan and Huang [4] studied weak calmness and weak stability of exact penalty functions for multiobjective programming. By penalty function, Liu [5] derived necessary and sufficient conditions without a constraint qualification for e-Pareto optimality of multi- objective programming, and the generalized e-saddle point for Pareto optimality of the vector Lagrangian. Huang and Yang [6] gave nonlinear Lagrangian for multiobjective optimization to duality and exact penalization. Chang and Lin [7] solved interval goal programming by using S-shaped penalty function. Antczak [8] studied the vector exact 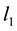penalty method for nondifferentiable convex multiobjective programming problems. Huang, Teo and Yang [9] discussed calmness of exact penalization in vector optimization with cone constraints. Huang [10] proved calmness of exact penalization in constrained scalar set-valued optimization. Meng, Shen and Jiang [11] defined an objective penalty function based on objective weight for multiobjective optimization problem and presented an interactive algorithm. This paper defines a penalty function with objective parameters and constraint penalty parameter which differs from an objective penalty function in [11] .

Because it is almost not possible for decision makers (DMs) to obtain all efficient solutions to MP, it is significant to present an efficient algorithm of MP so that DMs finds an easy and satisfactory solution to the MP. Luque, Ruiz and Steuer pointed out that an efficient algorithms not only help decision makers learn more about efficient solutions, but also navigate to a final solution as quickly as possible [12] . This paper presents an algorithm by modifying every objective parameter of penalty function so that a final solution is easily and quickly obtained. In Section 2, we introduce a penalty function with the objective parameters and constraint penalty parameter, and its algorithm. In Section 3, we give numerical results to show that the proposed algorithm is efficient.

2. Penalty Function with Objective Parameters and Constraint Penalty Parameter

In this paper we consider the following inequality constrained multi-objective programming:

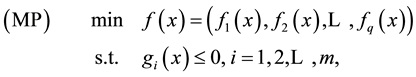(1)

where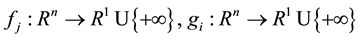, for.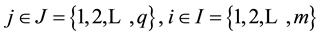

We denote the feasible set of MP (1) by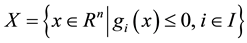. As usual, is called a Pareto

weakly-efficient solution if there is no 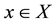such that 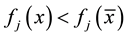for all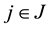, i.e..

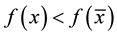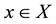is called a Pareto efficient solution if there is no such that 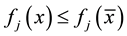for all 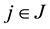and

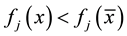for at least one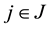, i.e..

Let functions and satisfy

where and

Let

where is an objective parameter and is the constraint penalty parameter. Let

and the penalty function of (1) be defined as:

Consider the following unconstraint penalty optimization problem:

For, let index set

We have.

Theorem 1. Suppose that for given, is a Pareto weakly-efficient solution to.

Then the following three assertions hold:

1) If, then is a feasible solution to (MP), for all

and for all.

2) If ( i.e.), then there is no such that.

3) If and is a feasible solution to (MP), then is a Pareto weakly-efficient

solution to (MP).

Proof. 1) The conclusion is obvious from the definitions of and.

2) Suppose that there be an such that. When for some, we

have

When for some, we have

Hence, , then is not a Pareto weakly-efficient solution to.

3) According to 2), the conclusion holds.

Theorem 2. Suppose that for a given, is a Pareto efficient solution to. Then the

following three assertions hold:

1) If, then is a feasible solution to (MP), for all

and for all.

2) If ( i.e.), then there is no such that.

3) If and is a feasible solution to (MP), then is a Pareto efficient solution to

(MP).

Proof. 1) The conclusion is obvious from the definitions of and.

2) Suppose that there be an such that. When for some, we

have

When for some, we have

Hence, , then is not a Pareto efficient solution to.

3) According to 2), the conclusion holds.

Based on Theorem 1, we develop an algorithm to compute an efficient solution to (MP). The algorithm solves the problem sequentially, and is called Multiobjective Penalty Function Algorithm (MPFA for short).

MPFA Algorithm:

Step 1: Choose, , and for each. Let, and

.

Step 2: Solve, where. Let be a Pareto weakly-efficient solution.

Step 3: If, for each, let, and go to Step 2. Otherwise, , go to Step 4.

Step 4: If is not feasible to (MP), for each, let, and go to Step 2. Otherwise, stop and is a Pareto weakly-efficient solution to (MP).

In the MPFA algorithm, it is assumed that for each can always be obtained .

The convergence of the MPFA algorithm is proved in the following theorem. For some, let

which is called a Q-level set. is bounded if, for any given and a convergent sequence

, is bounded.

Theorem 3. Suppose that, and are continuous on, and the Q-level set

is bounded for all. Let be the sequence generated by the MPFA algorithm.

1) If is a finite sequence (i.e., the MPFA algorithm stops at the -th iteration), then

is a Pareto weakly-efficient solution to (MP).

2) If is an infinite sequence, then is bounded and any limit point of it is a Pareto weakly-

efficient solution to (MP).

Proof. For all, it is clear that the sequence decreases with

(2)

Therefore, converges to for all.

1) If the MPFA algorithm terminates at the iteration and the second situation of Step 4 occurs, by Theorem 1, is a Pareto weakly-efficient solution to (MP).

2) We first show that the sequence is bounded. From the MPFA algorithm, we have for

all. Since converges to for all, there is a such that for all

and all. If for each, we have for all. Hence, we

have for all. By Theorem 1, there is a such that

So,

Therefore, there is an such that

Since is bounded, the sequence is bounded. Without loss of generality, we assume

. Since is a Pareto weakly-efficient solution to, for some, there are infinite

such that

We have

When, we have. Hence,. If is not a Pareto weakly-efficient

solution to (MP), there is an such that. Let. From, there is some such that

So, we have, which by Theorem 1 is a contradiction. Hence, is a Pareto weakly-efficient

solution to (MP).

Theorem 3 means that the MPFA algorithm is convergent in theory. Now, we discuss the exactness of the penalty function for (MP). If there are an and such that a Pareto weakly-efficient solution to

(MP) is also a Pareto weakly-efficient solution to for and, then

is called an exact penalty function.

Let (MP(s)) be a perturbed problem of (MP) given by

(3)

where. Similar to that for a constrained penalty function in [12] , we define stability.

Definition 1. Let be any feasible solution to (MP) and any feasible solution to (MP(s)) for each. If there is an such that for

where, then (MP) is stable.

We have an exact result of the penalty function.

Theorem 4. Let be an optimal solution to (MP). If (MP) is stable, is an exact penalty

function.

Proof. Suppose that is not an exact penalty function. Let a Pareto weakly-efficient solution

to (MP(s)). According to the definition of stability, we obtain that there is an satisfying

(4)

This implies that there is some such that for. Then, there always exists

some such that is not a Pareto weakly-efficient solution to (MP(M)), i.e. there is some such that

Thus,

Suppose that is a feasible solution to (MP). If for, we have.

Otherwise if for, from, , which

shows that is not a Pareto weakly-efficient solution to (MP). A contradiction occurs. Hence, is not a

feasible solution to (MP) and.

Let with, , and be a Pareto weakly-efficient solution to

(P(s')). Then, there is some such that and. Thus,

Therefore,

which shows that

where. This inequality contradicts to (4). Hence, (MP) is stable which yields a contradiction

with the assumption and proves that is an exact penalty function.

3. Numerical Examples

In the MPFA algorithm, it is not easy to solve multiobjective problem Let

It is easily known that an optimal solution to the problem is a Pareto weakly-efficient

solutions to the problem Hence, we replace the problem in the Step 2

of the MPFA algorithm with the problem. Let for. When,

we have

Hence, when decreases, the j-th objective will decrease too. For fixed

,

So, we may obtain different Pareto weakly-efficient solutions at given different. By

controlling, we can control the j-th objective value.

We have applied the MPFA algorithm to several examples programmed by Matlab 6.5. The aim of numerical examples is to check the convergence of the algorithm and to control changes in objectives.

Example 1. Consider the following problem:

Let penalty function

Let the starting point, , and constraint error

Clearly, if, is a feasible solution. We take different parameters in the MPFA

algorithm, the results are shown in Table 1.

In Table 1, when or decreases, the first objective value or decrease too.

Objective parameter can control change of each objective function. It helps decision makers learn about the change of each objective function and choose a satisfactory solution as quickly as possible.

Example 2. Consider the problem:

We want to find a solution that three objectives are as small as possible with the first and second objective value less than −2 and the third objective value less than −5.

Let penalty function

Let the starting point, , and constraint error

We take different parameters in the MPFA algorithm and get the results shown in Table 2.

In Table 2, we find a satisfactory solution when taking different

.

4. Conclusion

In this paper, we define a penalty function with objective parameters and constraint penalty parameter for MP and the corresponding unconstraint penalty optimization problem. Under some conditions, we prove that a Pareto efficient solution (or a weakly-efficient solution) to UPOP is a Pareto efficient solution (or a weakly- efficient solution) to MP, and the penalty function is exact under a stable condition. We present the MPFA algorithm to solve the multi-objective programming with inequality constraints by using the nonlinear penalty function with objective parameters. With this algorithm, we may find a satisfactory solution.

Acknowledgments

We thank the Editor and the referee for their comments. The research is supported by the National Natural Science Foundation of China under grunt 11271329 and 10971193.

References