American Journal of Operations Research
Vol.4 No.5(2014), Article
ID:48996,12
pages
DOI:10.4236/ajor.2014.45027
Novel Analytical Approach of Non Conventional Mapping Scheme with Discrete Hartley Transform in OFDM System
Shilpi Gupta1, Upena Dalal1, Vishnu Narayan Mishra2,3
1Electronics Engineering Department, Sardar Vallabhbhai National Institute of Technology, Surat, India
2Applied Mathematics & Humanities Department, Sardar Vallabhbhai National Institute of Technology, Surat, India
3L. 1627 Awadh Puri Colony Beniganj, Faizabad, Uttar Pradesh, India
Email: shilpi_ec@yahoo.com, udd@eced.svnit.ac.in, vishnu_narayanmishra@yahoo.co.in, vishnunarayanmishra@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received N samples in the ith OFDM symbol are
ABSTRACT
The system performance has been analyzed for π/4 DQPSK mapping scheme, which is differential in nature and hence adding additional advantage. Performance evaluation with random data as well as some images has been taken. Channel modeling has been performed in multipath fading environment. For elaboration of the concept mathematical modeling has been implemented using computer simulation. In this paper, an attempt is made to know the capabilities of DHT-OFDM with non conventional mapping technique π/4 DQPSK.
Keywords:DHT-OFDM, FFT-OFDM, Rayleigh, π/4 DQPSK, BER

1. Introduction
The ultimate requirement of the 4th generation communication system is efficient implementation of wireless system with high signal dynamics, which is highly expected to be provided by OFDM. OFDM is a multicarrier modulation technique being considered for many wireless applications [1] . High spectrum utilization and robustness against multipath fading are attractive features of OFDM system for high rate wireless communication [2] . Many applications like Digital Subscriber Loops (ADSL, VDSL), Digital Audio Broadcasting (DAB), Wireless LAN, Wireless Broadband (WiBro), LTE, LTE-Advanced, and WiMAX are based on OFDM technique. Despite of its number of features there are some challenging issues like sensitivity to frequency and phase offset and peak to average power ratio (PAPR) on which a lot of research work is going on for more & more improvements [3] -[6] .
In OFDM system the modulated data are mapped on subcarrier and summed up by means of inverse fast fourier transform (IFFT), and then transmitted. At the receiver end carriers are separated out and data are retrieved back using fast fourier transform (FFT) [7] . IDFT/DFT has complex exponential basis function so involving complex multiplications. Each complex multiplication requires four real multiplications and two real additions. Such a great complexity can be reduced if transform based on complex basis function could be replaced by real transforms. At the same time fast algorithms like FFT can still be applied [8] .
For multicarrier modulation orthogonal basis functions are the prime requirement. DFT is one of such functions used in OFDM because complex exponential functions are orthogonal. Besides that co-sinusoidal functions can also be the choice for orthogonal basis. Hence discrete cosine transform (DCT) and discrete sine transform (DST) both can be incorporated in OFDM [9] . A lot of research work has been done by considering DCT as a transform scheme in OFDM due to its high spectral efficiency and less complex arithmetic [10] -[12] . Discrete Hartley Transform (DHT) can also synthesize sinusoidal/co-sinusoidal orthogonal functions to be an OFDM signal [13] . DHT and its inverse can be one of the good choices for replacing its pre-existing counterpart-FFT/ IFFT, in OFDM. Mathematically, DHT and its inverse are represented in the same way, reducing its implementation cost. FFT/IFFT coefficients and DHT/IDHT coefficients can be derived from each other while knowing about the one. DHT has been established as a potential tool for signal processing applications. It has a real valued and symmetric transform kernel [14] .
Although there is a similarity between DHT and DFT but some DHT characteristics are different from DFT as no tracking of imaginary terms is required and only real arithmetic operation is involved, which makes it free form managing separate storage for real and imaginary part [15] [16] . The Fast Hartley Transform (FHT) requires only real arithmetic computations as compared to complex arithmetic operations in any standard FFT. Performance improvement in terms of speed is twice than FFT [17] . Various algorithms have been developed for optimization of the simulation timings.
A very useful performance measurement in digital communication is bit error rate. Precise symbol error rate analysis of an OFDM system with various modulation formats in presence of frequency offsets has been reported in [18] -[20] .
Gaussian approximation analysis for calculation of BER in OFDM system with BPSK over frequency selective channel and its improved analysis using QPSK & QAM have been done in [21] and [22] respectively. In all above analysis channel has been considered constant over one OFDM symbol. Frequency non-selective fast Rayleigh fading channel was considered for BPSK-OFDM system in [23] . All modulation techniques discussed till that were non-differential in nature. Differential technique can be an alternative option due to its low cost designing because of no requirement of channel estimation at the receiver side. Along with that due to non-zero crossing characteristic envelope of this modulation has less variation than that of QPSK.
Bit error rate analysis for π/4 DQPSK has been done in [24] . Precise bit error rate analysis has been done for π/4 DQPSK OFDM with carrier frequency offset over frequency selective fast fading channels in reference [25] .
In this paper the performance comparison of FFT with DHT has been presented with differential modulation technique. In comparison with QPSK, π/4 DQPSK can be detected coherently and non-coherently. Differential detection (one type of non-coherent detection) technique has been used for implementation. Channel modelings selected are AWGN and Rayleigh fading.
This paper has been organized as follows: Mathematical model of OFDM system has been represented using π/4 DQPSK mapping scheme in Section 2. In Section 3, performance comparisons among all the described schemes have been reported. Finally, conclusion has been drawn in Section 4.
2. System Model
Figure 1 shows the basic block diagram of OFDM System. OFDM is a multi carrier system which allows parallel processing and transmission of data on closely spaced sub-carriers, which are orthogonal to each other. The IFFT/IDHT is used at the transmission end to multiplex the data and encode it before transmission. The FFT/ DHT is used at the receiving end to decode and demultiplex the received data.
Each subcarrier can be modulated independently by a complex modulation symbol Dn,k, where subscript n & k represents time interval and no. of subcarriers respectively in the considered OFDM block. This complex value
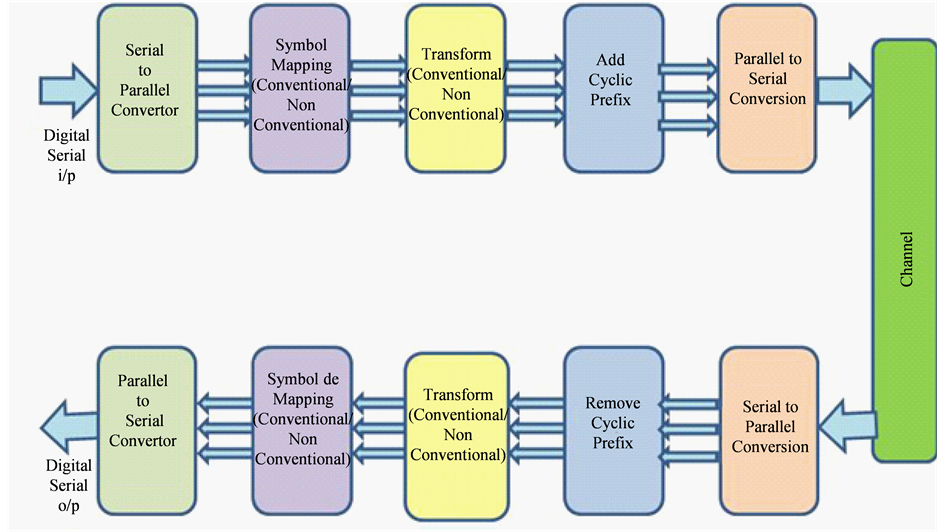
Figure 1. Basic block diagram of OFDM system.
is generated by mapping a sequence of m bits to one out of M = 2m points in the constellation diagram of applied modulation scheme. So, within symbol duration, the following signal of the nth OFDM block is formed [26] :
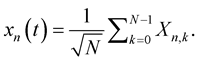 (1)
(1)
Total continuous time signal consisting all OFDM blocks is given by
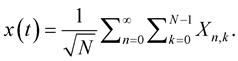 (2)
(2)
In the case of differential modulation the data bits to be transmitted are mapped to the quotient Bn,k of two successively transmitted modulation symbols instead of direct mapping on modulation symbols Dn,k. The operation of differential encoding in time domain can be described as below:
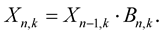 (3)
(3)
Here it is important that coherence time of channel be large compared to symbol duration to ensure that the channel transfer function Hn‒1,k and Hn,k are approximately equal.
In π/4 DQPSK one of four differential phases Δθn to be added to carrier phase are selected on the basis of each two successive bits of data {cn, dn}, here Δθn = ±π/4, ±3π/4, for every symbol period Ts [24] . The carrier phase is updated using following relation for signal when its power (prior to any signal processing) is P
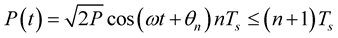
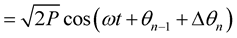
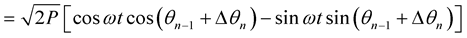
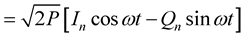 (4)
(4)
where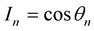 ,
, . The selection of differential phase values is made according to convention below:
. The selection of differential phase values is made according to convention below: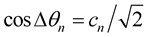 ,
, . Data bits cn and dn take values ±1.
. Data bits cn and dn take values ±1.
The possible changes in the carrier phase of Δθn is {±π/4, ±3π/4}, means offset by 45˚ from that of previous bit pair. That is the reason that π/4 DQPSK can be looked as superposition of two QPSK signal constellation offset by 45˚ relative to each other. The signal ready for transmission is given by:
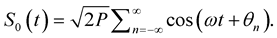 (5)
(5)
The received power will be different from transmitted power. The received signal is,
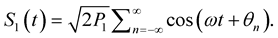 (6)
(6)
In non-coherent demodulation method of π/4 DQPSK, two cross correlators are used to extract estimates of  &
& 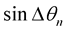 using In-phase & Quadrature correlation. The bit values cn and dn has been obtained by comparing these estimates to zero threshold.
using In-phase & Quadrature correlation. The bit values cn and dn has been obtained by comparing these estimates to zero threshold.
Let the B.W. of an OFDM system is W, here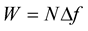 , then signals must be sampled with sampling time
, then signals must be sampled with sampling time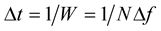 . The samples of the signals are written as sn,k,
. The samples of the signals are written as sn,k, 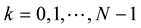 , symbols are mapped onto the subcarrier and then summed up which makes one OFDM symbol. In each OFDM symbol cyclic prefix of duration Tc is included. T is the useful period. FFT based OFDM has been discussed in literatures. Here we will do mathematical analysis for DHT based OFDM system.
, symbols are mapped onto the subcarrier and then summed up which makes one OFDM symbol. In each OFDM symbol cyclic prefix of duration Tc is included. T is the useful period. FFT based OFDM has been discussed in literatures. Here we will do mathematical analysis for DHT based OFDM system.
2.1. DHT Based OFDM System
Just like the IFFT/FFT, OFDM can be implemented using real valued arithmetic’s by means of DHT/IDHT. It is interesting to note that N real values of the DHT can substitute for the N complex values of the DFT, a total of 2N real numbers. It is justified on the basis of Hermitian property of the DFT that is redundancy by a factor of 2. N/2 real numbers that suffice to specify the cosine transform combine with N/2 needed for the sine transform to form a total of N DHT coefficients containing no degeneracy that is due to symmetry. The function cas(θ), can be considered as a sine wave shifted by 45˚ which automatically responds to cosine and sine components equally.
Mathematical analysis—OFDM will be done as follows. The basis function used in DHT is cas(θ). Where cas(θ) = cos(θ) + sin(θ).
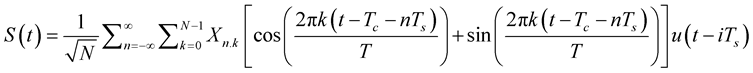 (7)
(7)
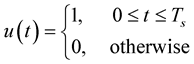
For frequency domain differential modulation π/4 DQPSK, the complex symbol  can be written as
can be written as
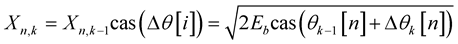 (8)
(8)
where 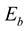 is the average energy per bit,
is the average energy per bit, 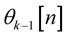 is the phase of symbol modulated on the (k ‒ 1)th subcarrier of the nth OFDM symbol, and
is the phase of symbol modulated on the (k ‒ 1)th subcarrier of the nth OFDM symbol, and 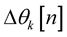 {±π/4, ±3π/4} is the differential phase carrying information bits. The differential encoding is performed in frequency domain subcarrier by subcarrier. The data modulated on the nth OFDM symbol can be written as vector
{±π/4, ±3π/4} is the differential phase carrying information bits. The differential encoding is performed in frequency domain subcarrier by subcarrier. The data modulated on the nth OFDM symbol can be written as vector
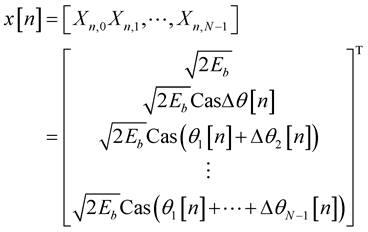 (9)
(9)
where 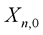 in each OFDM symbol is always assumed to be
in each OFDM symbol is always assumed to be 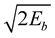 as reference for differential detection at receiver side. Although the channel variations can be within one OFDM symbol or adjacent OFDM symbols, the differential detection of DQPSK is effective provided there are no significant variations between two neighbouring subcarriers for frequency domain differential modulation.
as reference for differential detection at receiver side. Although the channel variations can be within one OFDM symbol or adjacent OFDM symbols, the differential detection of DQPSK is effective provided there are no significant variations between two neighbouring subcarriers for frequency domain differential modulation.
This signal is transmitted over a channel and at the receiver side reverse process will occur. FFT- & DHTOFDM systems differ in the inverse transform process. In the case of FFT-OFDM forward and inverse transform are represented by different basis function while in DHT-OFDM both forward and inverse transform are same. This feature of DHT makes it more favorable in comparison to FFT by reducing its complexity and cost.
The channel impulse response of the time varying L-path fading channel is given by
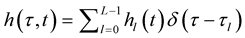 (10)
(10)
where 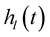 is complex amplitude and
is complex amplitude and 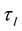 is propagation delay of the lth path. Time varying transfer function of channel is
is propagation delay of the lth path. Time varying transfer function of channel is
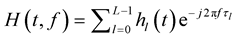 (11)
(11)
Cyclic prefix 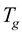 is much larger than the maximum channel delay. For simplicity it has been assumed that there is no carrier frequency offset. Hence the received signal is then represented by
is much larger than the maximum channel delay. For simplicity it has been assumed that there is no carrier frequency offset. Hence the received signal is then represented by
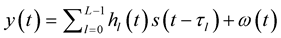 (12)
(12)
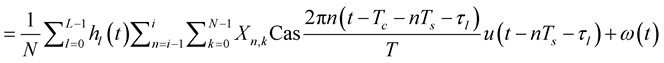 (13)
(13)
where 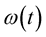 is a zero mean, complex Gaussian noise process with variance
is a zero mean, complex Gaussian noise process with variance  per dimension.
per dimension.
It is assumed here that the receiver is synchronized to the 0th path with delay 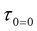 and sampled at the instants
and sampled at the instants
 (14)
(14)
Received N samples in the ith OFDM symbol are
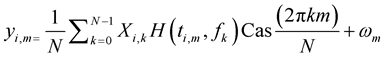 (15)
(15)
where 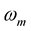 is a zero mean, complex Gaussian random variables with variance
is a zero mean, complex Gaussian random variables with variance 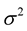 per dimension. The channel response
per dimension. The channel response 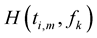 at different times and frequencies are zero mean jointly complex Gaussian random variables and correlation of these variables are given by
at different times and frequencies are zero mean jointly complex Gaussian random variables and correlation of these variables are given by
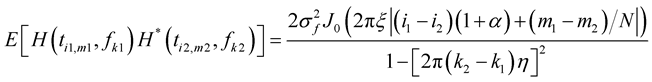 (16)
(16)
E[H] is the mean of random variable.  is Bessel function of first kind & order 0.
is Bessel function of first kind & order 0. 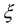 is normalized maximum Doppler spread.
is normalized maximum Doppler spread.
A DHT is performed on 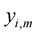
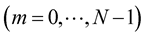 which gives data sequence in the ith OFDM symbol rd[i],
which gives data sequence in the ith OFDM symbol rd[i], 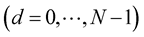 as
as
 (17)
(17)
where  is represented as
is represented as
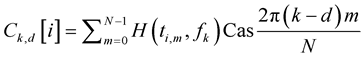 (18)
(18)
where 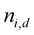 is a zero mean, complex Gaussian random variables with variance
is a zero mean, complex Gaussian random variables with variance 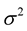 per dimension. By defining the 1 ´ N vector
per dimension. By defining the 1 ´ N vector 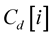
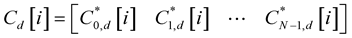
rd[i] can be written as
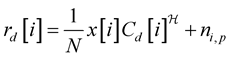 (19)
(19)
where 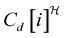 denotes the hermitian of the vector
denotes the hermitian of the vector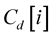 .
.
2.2. BER Analysis for Frequency Domain Differential Modulation
BER will be derived for the frequency domain differential modulation. The decision statistics can be written as
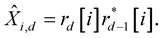 (20)
(20)
For π/4 DQPSK demodulation, the two bits can be decided independently by the real part and the imaginary part of . For frequency domain differential detection only operations for neighbouring subcarriers of the same OFDM symbol are performed, so symbol index [i] can be omitted for simplicity.
. For frequency domain differential detection only operations for neighbouring subcarriers of the same OFDM symbol are performed, so symbol index [i] can be omitted for simplicity.
The decision statistics for the I-bit and the Q-bit of symbol 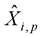 are
are
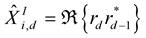 (21)
(21)
and
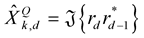 (22)
(22)
where real & imaginary part of  are denoted by
are denoted by 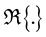 and
and 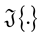 respectively. The received signal
respectively. The received signal 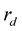 is a conditional complex Gaussian random variable, which is conditioned on a given data sequence xl or a given phase sequence
is a conditional complex Gaussian random variable, which is conditioned on a given data sequence xl or a given phase sequence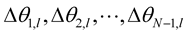 . For a given data sequence or differential phase sequence,
. For a given data sequence or differential phase sequence, 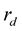 is sum of several jointly complex Gaussian random variables with zero mean and variance
is sum of several jointly complex Gaussian random variables with zero mean and variance
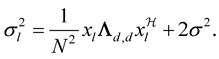 (23)
(23)
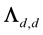 is N ´ N correlation matrix.
is N ´ N correlation matrix.
Unconditional PDF of the received signal 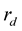 can be written as the sum of several conditional PDFs, i.e.
can be written as the sum of several conditional PDFs, i.e.
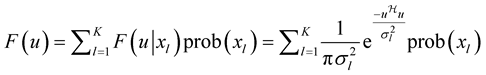 (24)
(24)
where u is complex variable. K is the no. of all possible data sequences or phase sequences.
Rewriting the 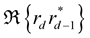 and
and 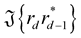
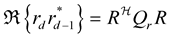 (25)
(25)
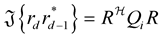
where, 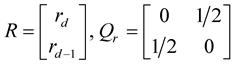 and
and 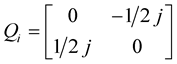
Characteristic function of  conditioned on
conditioned on 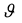 and Δθd is given by
and Δθd is given by
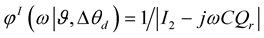 (26)
(26)
C is the covariance matrix and I2 is 2 ´ 2 identity matrix.
 (27)
(27)
where,
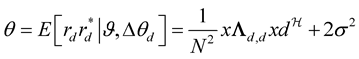
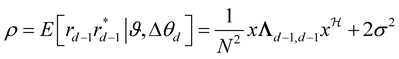
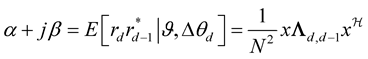
Similarly, characteristic function can be find for . The decision rules for both I & Q bit can be written as
. The decision rules for both I & Q bit can be written as
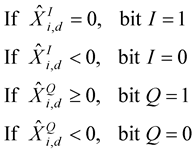
I-bit error probability of dth subcarrier conditioned on a phase sequence
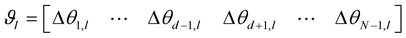
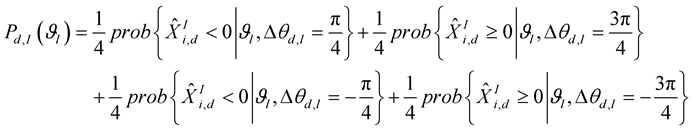
By doing extensive calculation of bit error probability for I-bit the I-bit error probability conditioned on 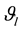
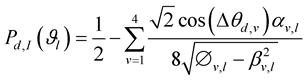
where, 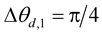 ,
, 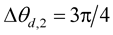 ,
, 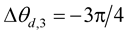 ,
,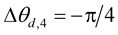 .
.
In a similar manner Q-bit error probability is obtained as
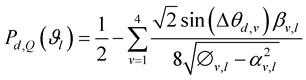
averaging over N ‒ 1 subcarriers except subcarrier 0 (since used as a reference) the conditional BER is:
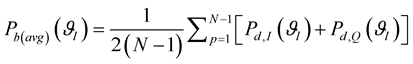
As for the case of π/4 DQPSK, total possibilities for phase sequence 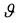 are four. While averaging overall possible sequences, average BER is represented as [25] .
are four. While averaging overall possible sequences, average BER is represented as [25] .
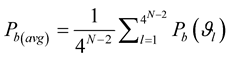
where 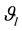 is the phase sequence as described above.
is the phase sequence as described above.
3. Simulation Results
In this section, we have compared the bit error rate vs. SNR performances of DFT-OFDM system and DHTOFDM system using analytical approach. Results have been obtained in previous section by considering π/4 DQPSK as a mapping scheme, which has been calculated numerically. As a reference, for differentially encoding of other subcarriers, the amplitude and phase of the π/4 DQPSK data symbols at the 0th subcarriers of each OFDM symbol is fixed to (Eb)1/2 and 0, respectively. Simulation parameters are summarized in Table1
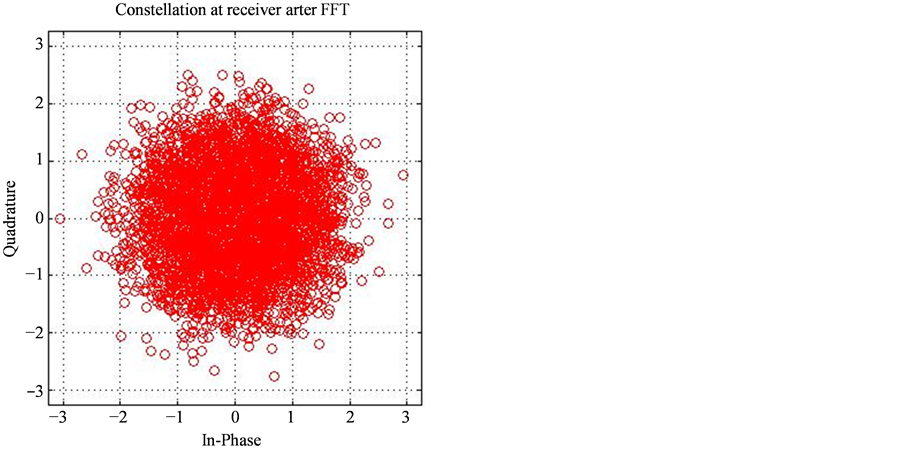
Constellation diagram for FFT & DHT-OFDM using π/4-DQPSK has been given in Figure 2. It can be observed that for the same SNR (=20 dB) DHT-OFDM gives better constellation than FFT-OFDM.
 (a)
(a)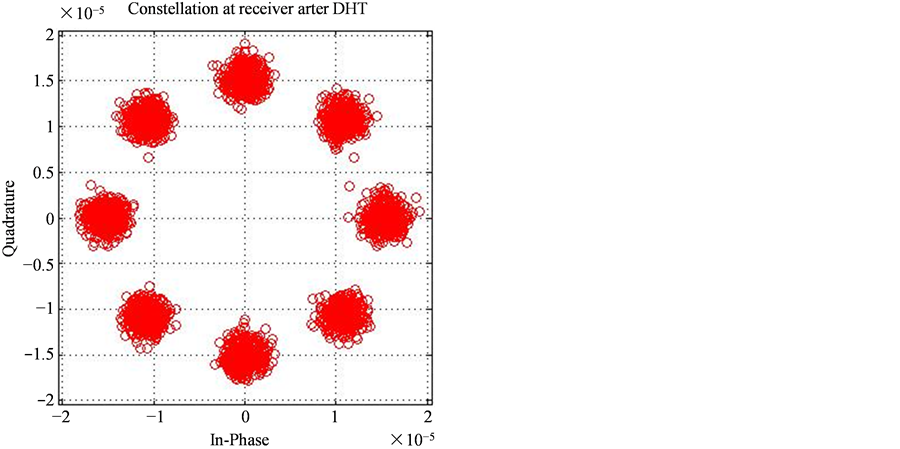 (b)
(b)
Figure 2. Constellation of π/4-DQPSK using (a) FFT, (b) DHT.
Figure 3 and Figure 4 show the bit error rate performance (BER) of a FFT-OFDM system and DHT-OFDM system both with BPSK, QPSK and π/4 DQPSK modulations in AWGN environment. These results clearly show that DHT-OFDM outperforms FFT-OFDM. From the results it can be observed that for FFT with BPSK scheme, at a bit error rate of 10−2 SNR value is 22 dB while for DHT it is 7 db keeping bit error rate constant i.e. 15 dB improvements can be achieved by using DHT-OFDM.
Similar analysis has been done by applying QPSK modulation in FFT and DHT. Here also, the same 15 dB improvement has been noticed at the bit error rate of 10−2. Further, for DHT-OFDM it can also be observed that up to 15 dB SNR bit error rate is gradually decreasing but after that it remains constant so this scheme may be

Figure 3. BER performances of FFT-OFDM with BPSK, QPSK, and π/4 DQPSK modulation over AWGN channel.
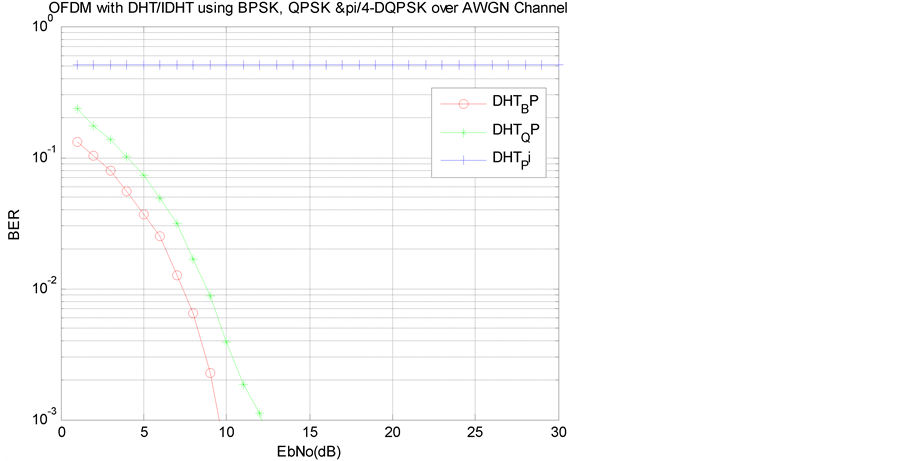
Figure 4. BER performances of DHT-OFDM with BPSK, QPSK, and π/4 DQPSK modulation over AWGN channel.
good where the requirement of SNR is up to 15 dB. π/4 DQPSK is a differential technique in which subsequent results are based on difference between current and just previous information. Since final output is the result of cumulative process, hence noise will also be cumulative which may lead to less bit error improvement in comparison to BPSK & QPSK.
BER performance comparison for DHT-OFDM & FFT-OFDM with π/4 DQPSK for AWGN & rayleigh channel has been shown in Figure 5 and Figure 6 respectively. It is clearly shown in Figure 6 that bit error rate is approaching up to 10−1 at SNR = 30 dB while for FFT-OFDM at same SNR bit error rate is 10−0.5.
Simulation result has also been generated by taking an image into consideration. Figure 7 shows the transmitted and received image of FFT- & DHT-OFDM using π/4 DQPSK modulation. It is observed that DHTOFDM provide better resolution of image in comparison of FFT-OFDM.
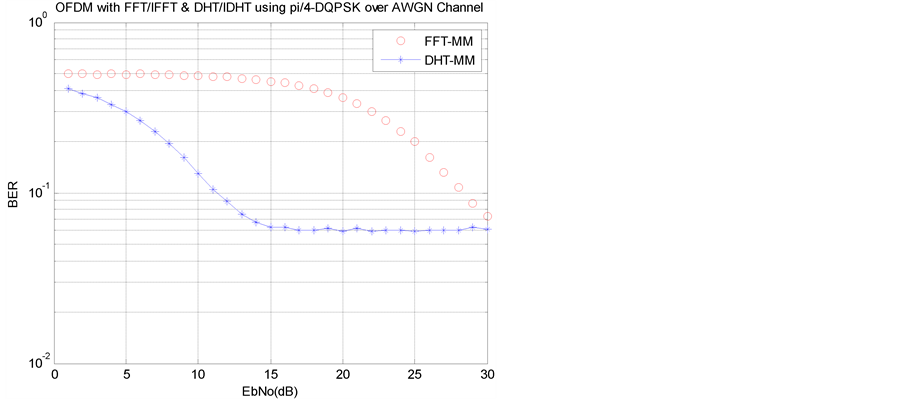
Figure 5. BER performances of DHT-OFDM & FFT-OFDM with π/4 DQPSK modulation over AWGN channel.
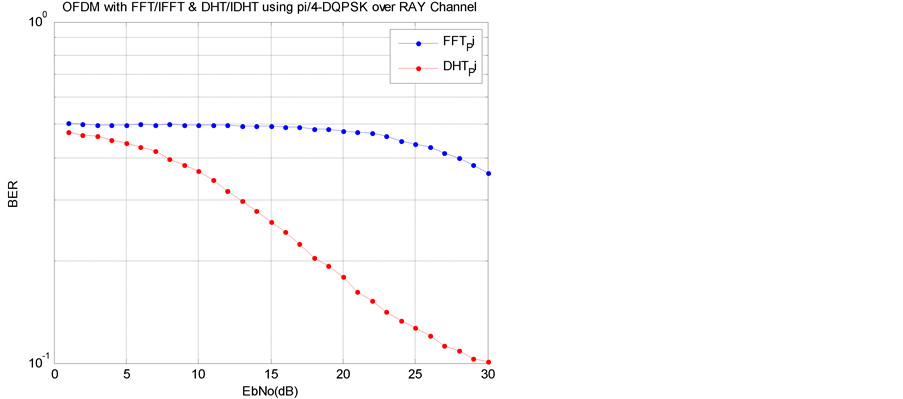
Figure 6. BER performances of DHT-OFDM & FFT-OFDM with π/4 DQPSK modulation over Rayleigh channel.

Figure 7. Transmitted & received images for FFT & DHT-OFDM using π/4 DQPSK over Rayleigh channel.
4. Conclusions
In conclusion, an analytical approach with lower BER of DHT-OFDM with π/4 DQPSK mapping scheme has been achieved in comparison to conventional technique. It has been found that DHT based OFDM system outperforms FFT based OFDM system while observing over AWGN channel. Even for π/4 DQPSK modulation it gives the improved result in combination with DHT. However this technique can be used for the conditions where signal SNR requirement is up to 15 dB, because after that error rate becomes constant. It can be considered as a great achievement because implementation complexity will be greatly reduced due to two factors— one is similar hardware required for forward & reverse basis function of DHT and another is no channel estimation required due to differential modulation technique applied. One more advantage of using π/4 DQPSK is that its data bit rate is increased in comparison to BPSK & QPSK modulation, hence spectral efficiency increases.
Furthermore, analysis has also been done for Rayleigh fading channel. Here again DHT-OFDM gives better results in comparison to FFT-OFDM with π/4 DQPSK modulation. In the entire scenario no channel coding has been applied, more favorable results can be found if such techniques would be applied. Same analysis has been done on image over Rayleigh channel which is also in agreement of the above conclusion by showing much better resolution in comparison of FFT-OFDM.
References
- Nee, R.V. and Prashad, R. (2000) OFDM Wireless Multimedia Communication. Artech House, Boston, 119-151.
- Cimini Jr., L.J. (1985) Analysis and Simulation of a Mobile Radio Channel Using Orthogonal Frequency Division Multiplexing. IEEE Transactions on Communications, 33, 665-675. http://dx.doi.org/10.1109/TCOM.1985.1096357
- Kim, D.-H., Kang, K.-M. and Lee, C. (2012) A Frequency Offset Estimation and Compensation Scheme for MB-OFDM UWB Modem. IEICE Transactions on Communications, 95B, 1015-1018.http://dx.doi.org/10.1587/transcom.E95.B.1015
- Mandai, T., Oka, I., Fossorier, M.P.C., Ata, S. and Fujiwara, C. (2004) A Practical Approach for Coded OFDM with Partial Transmit Sequence. IEICE Transactions on Communications, E87-B, 1273-1275.
- Han, S.H., et al. (2005) Modulation, Coding and Signal Processing for Wireless Communications—An Overview of Peak-to-Average Power Ratio Reduction Techniques for Multicarrier Transmission. IEEE Transactions on Wireless Communications, 12, 56-65. http://dx.doi.org/10.1109/MWC.2005.1421929
- Dan, L., Li, T., Xiao, Y. and Li, S. (2008) Performance of Peak Cacellation for PAPR Reduction in OFDM System. Proceedings of Communications, Circuits and Systems, 283-287.
- Bingham, J.A.C. (1990) Multicarrier Modulation for Data Transmission: An Idea Whose Time Has Come. IEEE Communications Magazine, 28, 5-14. http://dx.doi.org/10.1109/35.54342
- Wang, C.-L., Chang, C.-H., Fan, J.L. and Cioffi, J.M. (2000) Discrete Hartley Transform Based Multicarrier Modulation. Proceedings of ICASSP, 5, 2513-2516.
- Elhaded, M., El-Dolil, S.A. and Albagory, Y.A. (2009) Application of Trigonometric Transforms in Discretemultitone Systems. International Conference on Computer Engineering & Systems, 171-176.
- Peng, T. and Beaulieu, N.C. (2005) Precise Bit Error Probability Analysis of DCT OFDM in the Presence of Carrier Frequency Offset on AWGN Channels. Proceeding on IEEE GLOBECOM, 1429-1434.
- Tan, J. and Stiiber, G.L. (2002) Constant Envelope Multi-Carrier Modulation. Proceedings of 2002 IEEE MILCOM, 1, 607-611.
- Soliman, N.F., Shaalan, A.A., et al. (2009) Peak Power Reduction of OFDM Signals Using Trigonometric Transforms. International Conference on Computer Engineering & Systems, Cario, 14-16 December 2009, 333-337.
- Jao, C.-K., Long, S.-S. and Shiue, M.-T. (2010) DHT-Based OFDM System for Passband Transmission over Frequency-Selective Channel. IEEE Signal Processing Letters, 17, 699-702.
- Sembiring, Z. and Syahruddin, M. (2012) Performance Analysis of Discrete Hartley Transform Based OFDM Modulator and Demodulator. 3rd International Conference on Intelligent System, Modelling and Simulation (ISMS), Kota Kinabalu, 8-10 February 2012, 674-679.
- Bracewell, R.N. (1983) Discrete Hartley Transform. Journal of the Optical Society of America, 73, 1832-1835.http://dx.doi.org/10.1364/JOSA.73.001832
- Bracewell, R.N. (1994) Aspects of the Hartley Transform. Proceedings of the IEEE, 82, 381-387.
- Hou, H.S. (1987) The Fast Hartley Transform Algorithm. IEEE Transactions on Computers, 36, 147-156.
- Sathananthan, K. and Tellambura, C. (2001) Probability of Error Calculation of OFDM Systems with Frequency Offset. IEEE Transactions on Communications, 49, 1884-1888. http://dx.doi.org/10.1109/26.966051
- Beaulieu, N.C. (1990) An Infinite Series for the Computation of the Complementary Probability Distribution Function of a Sum of Independent Random Variables and Its Application to the Sum of Rayleigh Random Variables. IEEE Transactions on Communications, 38, 1463-1474. http://dx.doi.org/10.1109/26.61387
- Beaulieu, N.C. (1991) The Evaluation of Error Probabilities for Intersymbol and Cochannel Interference. IEEE Transactions on Communications, 39, 1740-1749. http://dx.doi.org/10.1109/26.120161
- Narasimhan, R. (2002) Performance of Diversity Schemes for OFDM Systems with Frequency Offset, Phase Noise, and Channel Estimation Errors. IEEE Transactions on Communications, 50, 1561-1565.http://dx.doi.org/10.1109/TCOMM.2002.803977
- Rugini, L. and Banelli, P. (2005) BER of OFDM Systems Impaired by Carrier Frequency Offset in Multipath Fading Channels. IEEE Transactions on Wireless Communications, 4, 2279-2288.http://dx.doi.org/10.1109/TWC.2005.853884
- Wan, L. and Dubey, V.K. (2000) Bit Error Probability of OFDM System over Frequency Nonselective Fast Rayleigh Fading Channels. Electronics Letters, 36, 1306-1307. http://dx.doi.org/10.1049/el:20000944
- Miller, L.E. and Lee, J.S. (1998) BER Expressions for Differentially Detected π/4 DQPSK Modulation. IEEE Transactions on Communications, 46, 71-81. http://dx.doi.org/10.1109/26.655405
- Tan, P. and Beaulieu, N.C. (2007) Precise BER Analysis of π/4-DQPSK OFDM with Carrier Frequency Offset over Frequency Selective Fast Fading Channels. IEEE Transactions on Wireless Communications, 6, 3770-3780.
- Molisch, A.F. (2000) Wideband Wireless Digital Communications. Prentice Hall PTR, Upper Saddle River.


