Received 5 December 2013; revised 5 January 2014; accepted 12 January 2014

ABSTRACT

In this paper we have considered a non convex optimal control problem and presented the weak, strong and converse duality theorems. The optimality conditions and duality theorems for fractional generalized minimax programming problem are established. With a parametric approach, the functions are assumed to be pseudo-invex and v-invex.

Keywords:

Non convex programming; pseudo-invex functions; v-invex functions; fractional minimax programming

1. Introduction

Parametric nonlinear programming problems are important in optimal control and design optimization problems. The objective functions are usually multi objective. The constraints are convex, concave or non convex in nature. In [1] -[3] , the authors have established both theoretical and applied results involving such functions. Here we have considered a generalized non-convex programming problem where the objective and/or constraints are non-convex in nature. Under non-convexity assumption [4] on the functions involved, the weak, strong and converse duality theorems are proved. Mond and Hanson [5] [6] extended the Wolfe-duality results of mathematical programming to a class of functions subsequently called invex functions. Many results in mathematical programming previously established for convex functions also hold for invex functions. Jeyakumar and Mond [7] introduced v-invex functions and established the sufficient optimality criteria and duality results in multi objective problem [8] in the static case. In [9] under v-invexity assumptions and continuity, the sufficient optimality and duality results for a class of multi objective variational problems are established. Here we extend some of these results to generalized minimax fractional programming problems. The parametric approach is also used in [10] by Baotic et al.

2. Preliminaries

Consider the real scalar function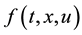, where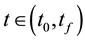, 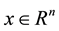and. Here 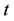is the independent variable, 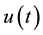is the control variable and is the state variable. is related to 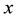by the state equations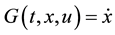, Where 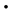denotes the derivative with respect to .

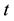If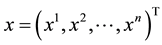, the gradient vector 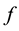with respect to is denoted by

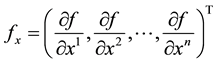where denotes the transpose of a matrix.

For a r-dimensional vector function ` the gradient with respect to x is

.

Gradient with respect to is defined similarly. It is assumed that and have continuous second derivatives with the arguments. The control problem is to transfer the state variable from an initial state at to a final state at so as to optimize (maximize or minimize) a given functional subject to constraints on the control and state variables.

Definition 1. A vector function is said to be v-invex [8] if there exist differentiable vector

functions with such that for each and to ,

Definition 2. We define the vector function to be v-pseudo invex if there exist functions with for each [4] [9] [11] [12] .

Definition 3. Let S be a non-empty subset of a normed linear space . The positive dual or positive conjugate

core of S (denoted S⁺) is defined by (where denotes the space of all continuous linear functionals on , and ) is the value of the functional at .

3. The Optimal control Problem

Problem P (Primal):

Minimize

subject to

(1)

(2)

(3)

The corresponding dual problem is given by:

Problem D (Dual):

Maximize

subject to

, ,

where and e

and are required to be piecewise smooth functions on , their derivatives are continuous except perhaps at points of discontinuity of , which has piecewise continuous first and second derivatives. [13] [14].

4. Previous Results

Theorem 1: (Weak Duality)

If , for any and with , is pseudo invex with respect

to then [3] [6] [9] [11] .

Theorem 2: (Strong Duality)

Under the pseudo invexity condition of theorem 1, if is an optimal solution of (P) then there exist

and such that is optimal for (D) and corresponding objective values are equal.

[1] [2] [5] [6] .

Theorem 3: (Converse duality)

If is optimal for (D) , and if is non-singular

for all then is optimal for (P) , and the corresponding objective values are equal [1] [2] [5] [6] .

Sufficiency:

It can be shown that, pseudo-convex functions together with positive dual conditions are sufficient for optimality [11] [12] .

5. Main Result

Optimality conditions and duality for generalized fractional minimax programming problem:

We consider the following generalized fractional minimax programming problem:

, , where

1) is non empty and complete set in.

2) be differentiable functions.

3) .

4) If is not affine then for all and .

Consider the following minimax nonlinear parametric programming problem.

.

Lemma 1: If has an optimal solution with an optimal value of -objective function as , then . Conversely, if at and , then and have some optimal solution.

Lemma 2: In relation to we have an equivalent programming problem for given

Minimize

subject to, .

Lemma 3: If is -feasible, then is (GP)-feasible. If is (GP)-feasible

then there exist and such that is -feasible.

Lemma 4: is -optimal with corresponding optimal value of the -objective equal to if and only if is -optimal with corresponding optimal value of the -objective

equal to zero i.e. .

Theorem 4: (Necessary conditions)

Let be an optimal solution of with an optimal value of -objective equal to . Let the conditions of lemma 1 be satisfied i.e. be a feasible solution for and be the set of

binding constraints. i.e. if and only if

Then for

(4)

and for

(5)

Hence from (4) and (5)

Then there exist , , , such that satisfy

(6)

Theorem 5: (Sufficient conditions)

For some , , , let be proper v-pseudo invex. At

and let be finite and conditions (6) be

satisfied. Then is an optimal solution for with corresponding value of the objective function.

Two duals are introduced Wolfe-type dual.

Max

subject to

,

, , , , , ,

Weir and Mond type dual.

Max

subject to

,;,

, , , , , ,

Proof of the corresponding duality results for the above two duals follow the same lines as the proofs of the theorems 2, 3, 4.

7. Conclusion

Here in this presentation we have considered a non convex optimal control problem in parametric form and established the weak duality theorem, the strong duality theorem and the converse duality theorem. The results which are available in literature for v-invex functions are hereby extended to v-pseudo invex functions in a minimax fractional non convex optimal control problem.

Acknowledgements

The authors are thankful to the reviewers for their valuable suggestions in the improvisation of this paper.

References