American Journal of Operations Research
Vol.3 No.2(2013), Article ID:29230,9 pages DOI:10.4236/ajor.2013.32023
Forecasting on Crude Palm Oil Prices Using Artificial Intelligence Approaches
1Arshad Ayub Graduate Business School, MARA University of Technology, Shah Alam, Malaysia
2Faculty of Business Management, Kota Kinabalu Campus, MARA University of Technology, Kota Kinabalu, Malaysia
3Faculty of Business Management, MARA University of Technology, Shah Alam, Malaysia
Email: azizkaria@gmail.com
Received December 17, 2012; revised January 19, 2013; accepted January 31, 2013
Keywords: Crude Palm Oil Prices; Neuro Fuzzy; Neural Networks; Fractionally Integrated; Forecast
ABSTRACT
An accurate prediction of crude palm oil (CPO) prices is important especially when investors deal with ever-increasing risks and uncertainties in the future. Therefore, the applicability of the forecasting approaches in predicting the CPO prices is becoming the matter into concerns. In this study, two artificial intelligence approaches, has been used namely artificial neural network (ANN) and adaptive neuro fuzzy inference system (ANFIS). We employed in-sample forecasting on daily free-on-board CPO prices in Malaysia and the series data stretching from a period of January first, 2004 to the end of December 2011. The predictability power of the artificial intelligence approaches was also made in regard with the statistical forecasting approach such as the autoregressive fractionally integrated moving average (ARFIMA) model. The general findings demonstrated that the ANN model is superior compared to the ANFIS and ARFIMA models in predicting the CPO prices.
1. Introduction
An accurate forecasting on CPO prices is considered critical especially in dealing with risks and uncertainties for the oil palm business. The most widely used model to forecast CPO prices is the Box and Jenkins model. This model presents the parsimony and produces the rational results for linear time series data. In recent years, the use of statistical forecasting approaches has been challenged by the artificial intelligence approaches [1-5]. All the studies reviewed so far, there are limits to how far the statistical forecasting approaches can be applied. This due to predictability of those statistical forecasting approaches to predict the CPO prices is still remaining an innermost depth questions among the researchers in the econometrics modelling literature.
Due to the common factor of level of risks and uncertainties, we are trying to fulfil the gap of which models are appropriate to forecast the CPO prices in Malaysia. In this case, we applied the previous empirical evidence of two artificial intelligence approaches, namely artificial neural network (ANN) and adaptive neuro fuzzy inference system (ANFIS). A review of the artificial intelligence forecasting on CPO prices is beyond the scope of this paper since only one relevant study available, such Karia and Bujang [6], which applied the ANN to forecast the CPO prices. Looking into different field of time series forecasting, the adaptation of artificial intelligence is snowballing [7-16].
The artificial intelligence based forecasting approaches is an increasingly important area for the time series forecasting. Therefore, it is difficult to ignore the use of ANN model to predict the reliable forecast. Duy, Sato and Inoguchi [17] found the ANN is a stable model for prediction with a surprisingly low overhead. Additionally, the ANN found by Hamzacebi [18] provides a better forecast output with the lower RMSE in a strong seasonality time series data. If the seasonality is weak, adjusting the network structure would be better. Consistent to the previous study, it is found by Rojas, Valenzuela, Rojas, Guillen, Herrera, Pomares, Marquez and Pasadas [19] and Sallehuddin, Shamsuddin, Hashim, and Abraham [20] the ANN is superior to predict nonlinear time series data. However, if we compared with the ANFIS, it has the ability to deal with linear and nonlinear time series data [21].
The evidence found by Maier and Dandy [22] which recommends that the ANN model is better for the long term forecasting. For this reason, the ANN model needs the large number of sample data and parameters [6,23]. Furthermore, it is considered as one of the efforts to reduce the risk of overfitting [21,24]. However, Kim, Oh, Kim and Do [25] viewed that, the overfitting behaviour by ANN model seems not to be a serious problem since it would be beneficial for the complex financial time series analysis. In one hand, the model of ANFIS does not require large number of sample data and parameters [1,6, 26,27]. The possible explanation for this due to it characteristic that combine the ability of ANN model and the fuzzy “IF-THEN” rules. However, the ANFIS model has been identified by Wang, Chau, Cheng and Qiu [5] to create the potencies of numerical problem since it is the combination of the ANN and FIS. Consistent to previous study, Vairappan, Tamura, Gao and Tang [27] revealed that ANFIS model ignore the correlation among the inputs data which might produce inefficient and affecting the robustness of forecasting modelling techniques. Additionally, Chang and Chang [28] draw our attention that the ANFIS model is time demanded for defining parameters and training construction. Worst come to worst, tuning the membership function (MF) can lead into utterly complex alteration of human intelligence of fuzzy inference system (FIS).
Wang, Chau, Cheng and Qiu [5] pointed out that the ANFIS model displaying the standard of forecasting and produce the lowermost errors compared to ANN model. This finding was supported by the previous empirical evidence since the ANFIS model assembles the human thinking process and learning strategy [28-31]. More recently, literature has emerged that offers contradictory findings about the effectiveness between the ANN and ANFIS models. The performance of the ANN and ANFIS models found to be almost similar and they displays decent result [32,33]. The finding of Wei, Bai, Sung, Liu, Wang and Cather [34] is consistent with the previous study. The ANN and ANFIS recognized with their effectiveness in overcome with the complex problems. However, between ANN and ANFIS which of these both models are effective to overcome this complex problem? The empirical evidence proved by Yunos, Shamsuddin and Sallehuddin [11], found that the ANFIS model is more effective than the ANN model. This shows that ANFIS is superior and efficient to forecast the KLCI.
Relating to the above matters, the objective of this study is to compare the predictability power for the listed forecasting models in predicting the CPO prices in Malaysia. Therefore, we are trying to fulfil the gap by applying the previous empirical evidence on two artificial intelligence approaches, namely the ANN and ANFIS. In this present study, we also put an effort toward projecting the reliable forecast by considering the statistical approach namely autoregressive fractionally integrated moving average (ARFIMA) models.
This paper consists four main sections. Section 2 provides materials and method that applied to forecast the daily CPO prices in Malaysia followed by Section 3 which present the empirical results and discussion on artificial intelligence and statistical approach. Finally, Section 4 is conclusion of this study.
2. Material and Methods
The present study focuses on daily CPO prices (free-onboard Ringgit Malaysia U$/Tonne) in Malaysia during the period of time covered between the 1st of January 2004 and 31st of December 2011. The data sample obtained from DataStream consist of 2087 observations of CPO prices records. Figure 1 display daily CPO prices movement in Malaysia.
2.1. Artificial Neural Network (ANN)
The ANN is the abbreviation of artificial neural network. The application of ANN is found in the operation of the biological neural networks, but adopted in the extremely critical artificial intelligence forecasting technique. Even though the application of forecasting these days is truly advanced, but there are certain task that existing forecasting application is incapable to perform. The ANN consist the interconnecting neurons. Basically, each neurons or node are interconnected independently which shows in the Figure 2. Refer Bishop [35] for detail on ANN model.
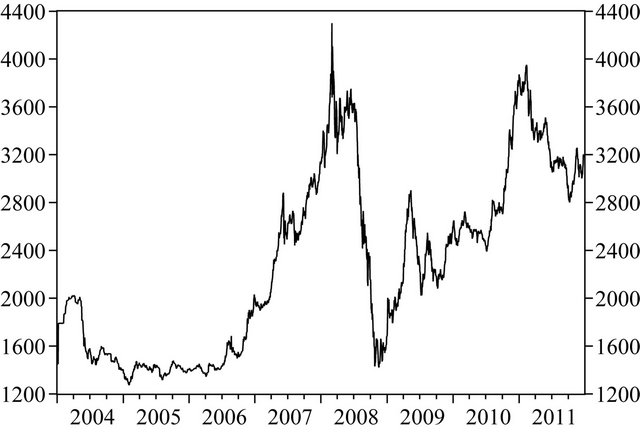
Figure 1. The CPO prices from 1st of January 2004 to end of December 2011.
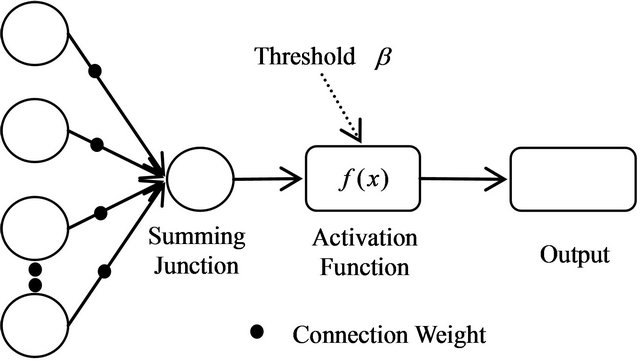
Figure 2. The basic artificial neural network architecture.
 (1)
(1)
The output from the neuron denoted as Y. Meanwhile, the inputs value presents by xt. The connection weights and the bias value (threshold) presented by wt and  respectively. The f present the transfer function which typically known as the sigmoidal function
respectively. The f present the transfer function which typically known as the sigmoidal function 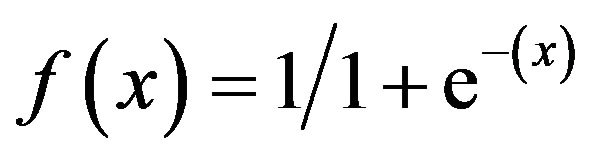 .
.
In this study, we applied the feed-forward neural network based from nonlinear autoregressive (NAR) which shows in Figure 3. The NAR is the system identification or dynamic modelling which build a physical system of the ANN. This dynamic modelling is vital for system analysis, simulation, monitoring and control for the ANN model. There are numerous numbers of dynamic modelling of the ANN, such as nonlinear autoregressive with external (NARX), nonlinear autoregressive (NAR), and the nonlinear input-output. In this study, the use of NAR as the dynamic modelling is already tolerable. The possible explanation for this is because of the NAR characteristics itself. It is utilizing the univariate time series data in which attracting our attention.
2.2. Adaptive Neuro Fuzzy Inference System (ANFIS)
The ANFIS model seems to be a good approach to stun and undertake the limitations of the ANN model and statistical forecasting approaches. The rudimentary learning law of ANFIS founded from the chain rule and gradient decent by Werbos [36]. However Werbos failed to obtain attention for his invention due to limitation of ANN investigation at that time. As an effort to recover the Werbos perspective, Jang [37] developed the ANFIS. The recommended ANFIS optimizing the power of ANN and its capabilities in nonlinear learning, meanwhile it is also absorbing in the rules of fuzzy logic which is applied the linguistic value in prediction which worth the higher precision and very powerful in prediction.
In this study, we applied the previous empirical evidence on Takagi-Sugeno-Kang fuzzy inference system. For the straightforwardness, the basic architecture of the ANFIS exposed in Figure 4 and assuming the model comprise five layers adaptive network which has two inputs namely x and, y and one output z. The TakagiSugeno-Kang set of rules FIS showed as follows
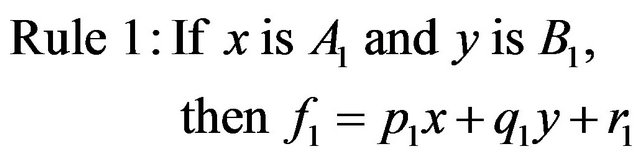 (2)
(2)
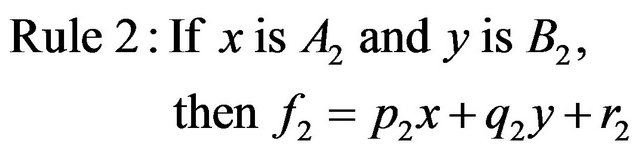 (3)
(3)
In this forecasting system, the inputs and output is in the linear combination and constant term. The final output produces in the last layer estimates the overall of the
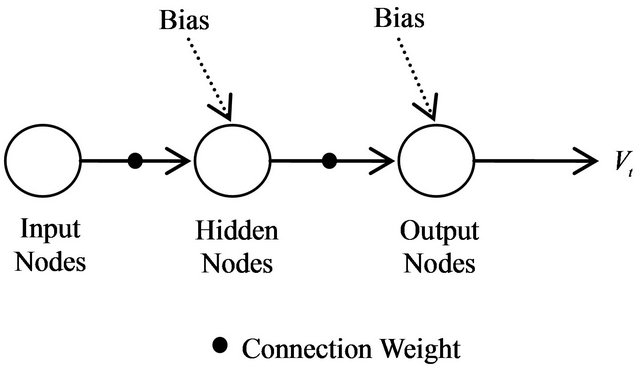
Figure 3. Nonlinear autoregressive network (NAR).
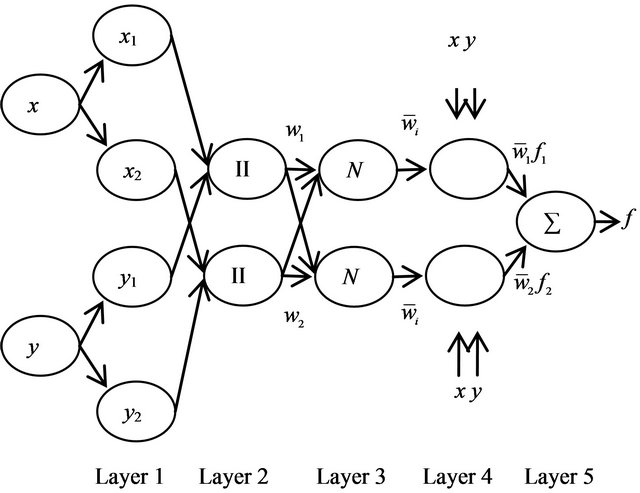
Figure 4. The basic architecture of the ANFIS model.
summation inbound signals.
Layer 1: It is also known as the input node. Each node in this layer generates membership characters which own by the Fuzzy groups in membership function. Every single node i is an adaptive to the node function of:
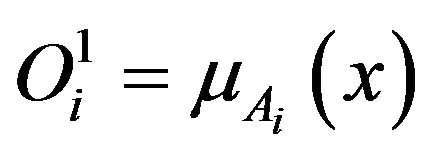 , which
, which 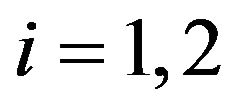 (4)
(4)
 , which
, which  (5)
(5)
where the input node i represented by x and y. Meanwhile, the linguistic variables signified by  and
and 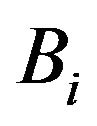 to a membership function of
to a membership function of  and
and 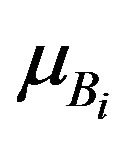 correspondingly. The used of Triangular, Trapezoidal, Gaussian, Two Gaussian, Generalized Bell, and Pi-shaped membership function progressively widespread due to its smoothness and succinct construction.
correspondingly. The used of Triangular, Trapezoidal, Gaussian, Two Gaussian, Generalized Bell, and Pi-shaped membership function progressively widespread due to its smoothness and succinct construction.
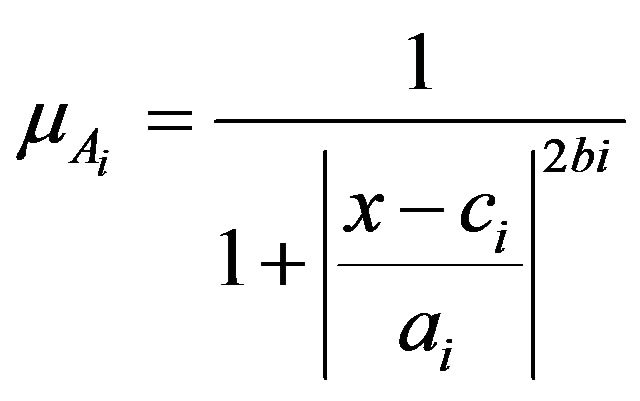 (6)
(6)
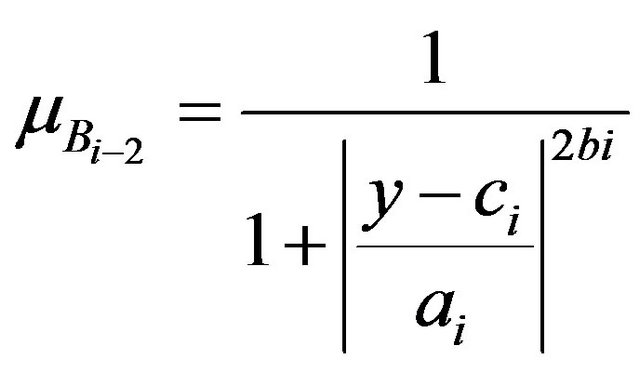 (7)
(7)
The ai, bi and ci is the premise parameters set change the membership function. Premise parameter is also one of the applications of ANFIS to search for optimum performance by updating its parameters. It is work by defining the membership function parameters. The ANFIS implements gradient descent to tune them until to its best performance.
Layer 2: The entire node in this layer will be represented by “II” label which is the multiplication of the inbound signal from output  display the characteristic of corresponding in the degree of first layer. This means in the node of “II”, it is the situation where the fuzzy “IF THEN” rule is satisfied and tailored with the output function for the rule. It is given by
display the characteristic of corresponding in the degree of first layer. This means in the node of “II”, it is the situation where the fuzzy “IF THEN” rule is satisfied and tailored with the output function for the rule. It is given by
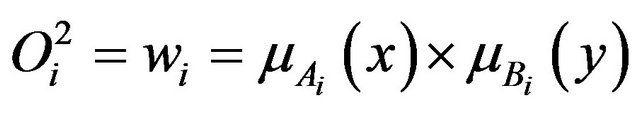 , which
, which  (8)
(8)
Layer 3: The third layer labelled with “N”. The entire node in this layer is the static node. The i-Th node estimate the proportion of the i-Th rules of firing strength divided to the sum of firing strength of all the rules. This output of the “N” layer also known as normalized firing strengths. It is shown as follows
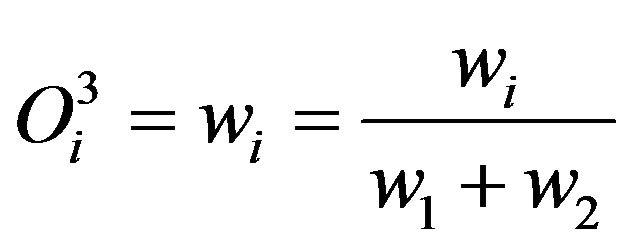 , which
, which  (9)
(9)
Layer 4: An adaptive node in this layer has the following i-Th node function
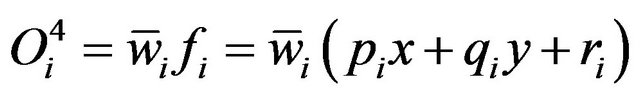 (10)
(10)
where  is the output created from the third layer, meanwhile the
is the output created from the third layer, meanwhile the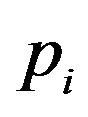 ,
, 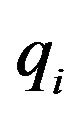 and
and  is not the premise parameters, but it is a consequent parameters. The consequent parameters are other options of ANFIS to achieve its ideal performance. The coefficient of consequent parameters explain every of the output equation. In this application, the ANFIS employ least-square technique to identify them.
is not the premise parameters, but it is a consequent parameters. The consequent parameters are other options of ANFIS to achieve its ideal performance. The coefficient of consequent parameters explain every of the output equation. In this application, the ANFIS employ least-square technique to identify them.
Layer 5: In this final layer, the static single node labelled with “∑” estimates the overall of the summation inbound signals
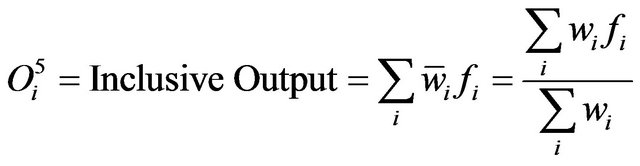 (11)
(11)
2.3. Autoregressive Fractionally Integrated Moving Average (ARFIMA)
As we know, most of the high frequency time series data present the long memory. For this reason, we applied the ARFIMA model since it is very good model to forecast the time series that consist the long memory. The ARFIMA model is the higher level of the ARMA family which generalize the integrated value of ARIMA model by permitting non integer values of integrated. In this study, we give special attention towards the ARFIMA package introduced by Doornik and Ooms [38], which the ARFIMA that possible for MLE for long memory time series data. It is said by the previous empirical evidence on ARFIMA model which consist the elements of fractionally difference d for the ranging of (0.0 ≤ d ≤ 0.5) is good to forecast the time series that persistence towards nonstationary. Refer Doornik and Ooms [38] for complete explanations on ARFIMA package that possible for MLE.
The ARFIMA model exposed as
 . Meanwhile, the autoregressive part determined as
. Meanwhile, the autoregressive part determined as
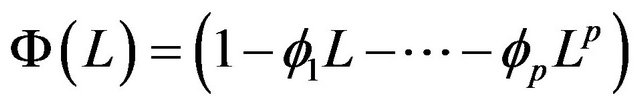 . The equation of
. The equation of
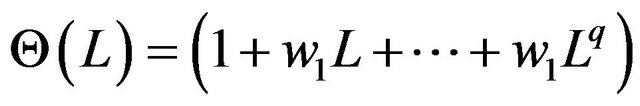 represents the elements of moving average. The main player in this model is the elements of fractionally difference
represents the elements of moving average. The main player in this model is the elements of fractionally difference 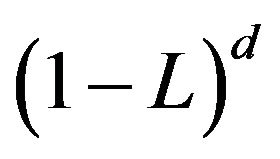 which define as
which define as
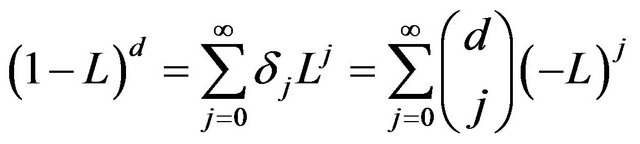 (12)
(12)
2.4. Analysis of the Result
In this study, we applied six of the statistical evaluation criterion for the sake of measuring the performance of the applied model. This statistical evaluation criterion are coefficient of determination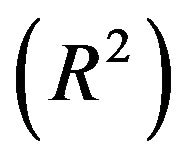 , mean square error (MSE), mean absolute deviation (MAD), mean absolute percentage error (MAPE), root mean square error (RMSE) and scatter index (SI). The statistical evaluation criterion are exposed as follow
, mean square error (MSE), mean absolute deviation (MAD), mean absolute percentage error (MAPE), root mean square error (RMSE) and scatter index (SI). The statistical evaluation criterion are exposed as follow
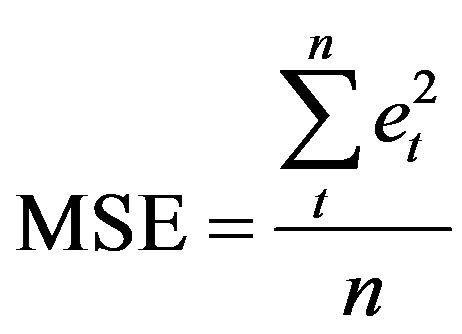 (13)
(13)
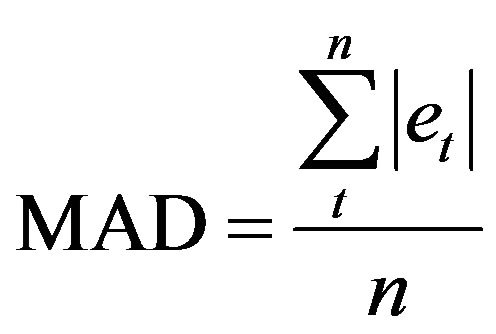 (14)
(14)
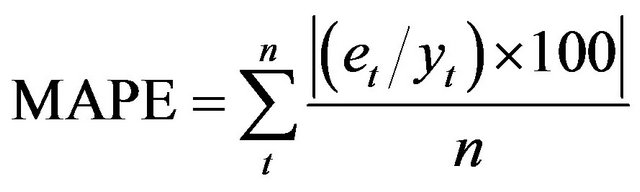 (15)
(15)
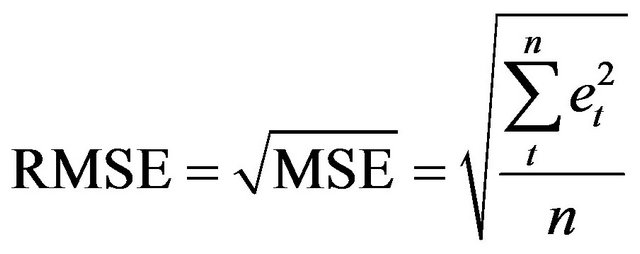 (16)
(16)
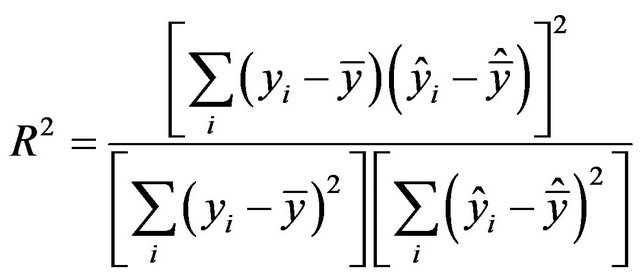 (17)
(17)
 (18)
(18)
3. Results and Discussion
In this study, the methodology is applied on the daily CPO prices in Malaysia. Table 1 displays the descriptive statistics of the CPO prices and the mean recorded at RM2284.55 per tonne. Based from the Jarque-Bera test result, the null of hypothesis of which the CPO prices are normal distribution was rejected.
3.1. Artificial Neural Network (ANN)
In this study, we randomly divide up the 100% of the target timesteps into 70% for training, 15% for validation and 15% for testing. As mention previously, we adopt the feed-forward neural network based for NAR model. Figure 5 display the NAR network architecture that utilized in projecting the CPO prices. The network architecture of the ANN model has been determined iteratively. The best fits of the number of hidden layer size and the feedback delays are 10 and 1:30 respectively. Meanwhile, the ANN network training was stopped up at the epoch point of 14 iterations.
Table 2 provides the result obtained from the analysis of the ANN model. The analysis of the result such as the value of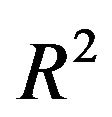 , MSE, MAD, MAPE and RMSE are also presented in Table 2. It is clearly seen that the reported RMSE performance is statically significant by considering the Diebold and Mariano [39] perspective stat ranging of −1.2 to +1.0.
, MSE, MAD, MAPE and RMSE are also presented in Table 2. It is clearly seen that the reported RMSE performance is statically significant by considering the Diebold and Mariano [39] perspective stat ranging of −1.2 to +1.0.
The plots of the training, validation and test errors of the ANN model are shown in Figure 6. This figure is quite revealing in several ways. In this case, there is no evidence of overfitting by considering the following circumstances. First, the plots of the test and validation er-
Table 1. Descriptive statistics of CPO prices.
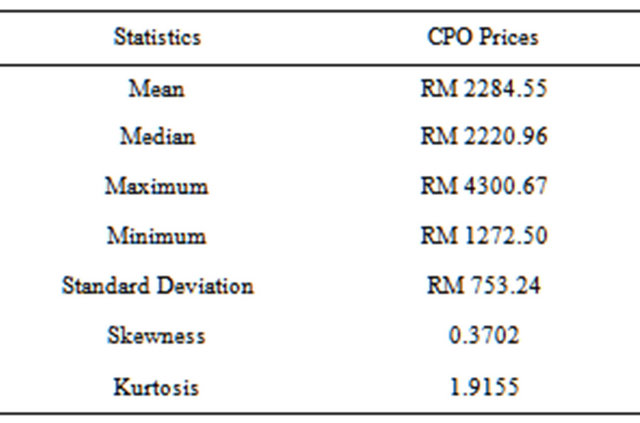
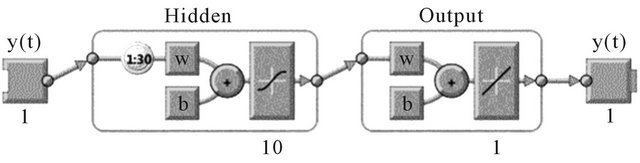
Figure 5. The NAR network architecture.
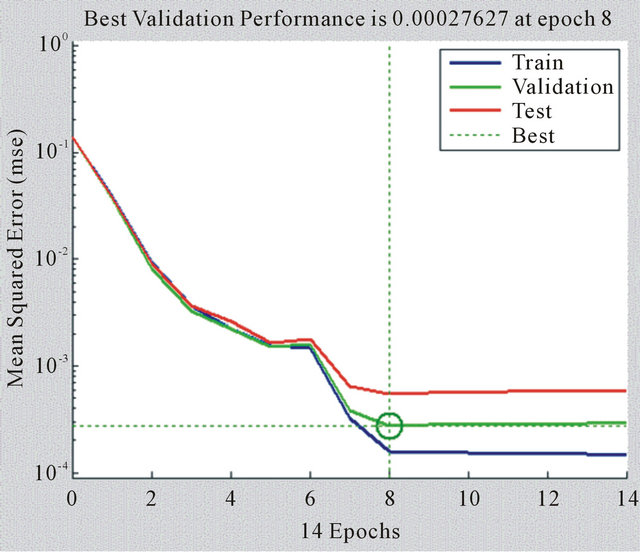
Figure 6. The training, validation and test errors of the ANN model.
rors are very similar. Since the plots of the test errors is not raise significantly earlier than the validation errors increase. Second, there is no significant of overfitting at the point of the best validation performance which occurred at 8 iterations. Third, the MSE are small in which present the evidence that the performance of the validation errors improve with the training errors. Figure 7 shows the depicted graph and scatter plots for the observed and predicted CPO prices.
3.2. Adaptive Neuro Fuzzy Inference System (ANFIS)
In this section, we applied the ANFIS model to forecast the CPO prices. We examined six types of membership functions (MFs) namely triangular, trapezoidal, gaussian, two gaussian, generalized bell and pi-shaped which clearly shows in Table 3. Among all types of the MFs, we provide two MFs on each of the four inputs, in which eight altogether. With this, the FIS structure consist 16 fuzzy rules with 104 parameters. So far, there is no readily available for the basic rule to verify the number of MFs of the ANFIS model. Therefore, we put an effort to avoid the large number of MFs since it would save time and calculation [1,40].
The result, shows in Table 3, indicate that triangular and trapezoidal shaped MFs better than other applied MFs. Observing two of the results, it can be seen that the trapezoidal shaped MFs outperformed than the triangular shaped MFs. In respond to the values of the applied statistical criterion, we applied the trapezoidal shaped MFs to present the ANFIS model in predicting the CPO prices. This prediction shows in the Figure 8. If we now turn to compare the scatter plots in Figure 8 with the scatter plots in Figure 7, the ANFIS prediction is more scattered.
Table 2. Forecasting performance of the ANN.

Table 3. The ANFIS prediction using different types of MFs.
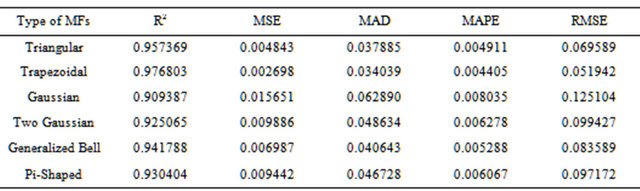
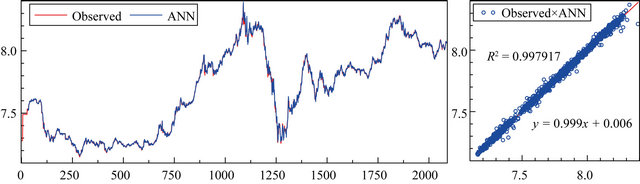
Figure 7. Depicted graph and scatter plots for the observed and ANN prediction.

Figure 8. Depicted graph and scatter plots for the observed and ANFIS prediction.
In this case, the ANN is superior compared to ANFIS predictions. However, there is not much difference between both of these models. All of the reported RMSE results are statically significant by considering Diebold and Mariano [39] perspectives and can be considered as an alternative model to predict the CPO prices in Malaysia. Figure 9 provides the graphical representation of the ANFIS structure.
3.3. Autoregressive Fractionally Integrated Moving Average (ARFIMA)
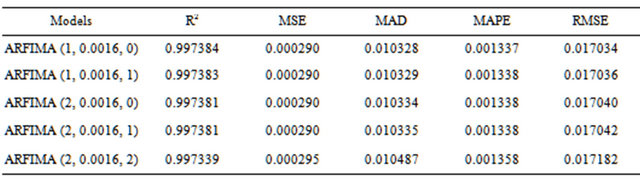
The forecasting performance of the ARFIMA model to forecast the CPO prices illustrates in Table 4. It is apparent from this table that all of the reported RMSE results are statically significant for by considering the Diebold and Mariano [39] perspectives. Additionally, it is obviously seen that the ARFIMA (1, 0.0016, 0) model provides an optimal result for CPO prices prediction. However, if we compared to its rival models, the ANN model is slightly better than the ARFIMA and ANFIS respectively. Figure 10 shows the depicted graph and scatter plots for observed and ARFIMA prediction.
4. Conclusions
Accurate prediction of CPO prices is significant toward investors when dealing with ever increasing risks and

Figure 9. Graphical representation of the ANFIS structure.
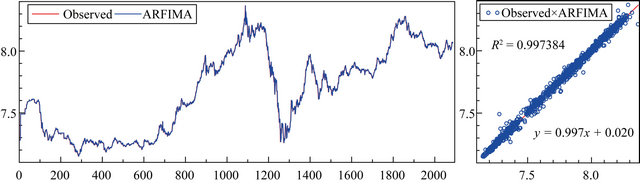
Figure 10. Depicted graph and scatter plots for the observed and ARFIMA prediction.
Table 4. Forecasting performance of the ARFIMA.
uncertainties in the future. Therefore, we proposed the ANN, ANFIS and ARFIMA models to forecast the CPO prices in Malaysia. Among all of the listed models, we seek out for the most appropriate model to forecast the CPO prices. For this reason, we found that the ANN provides the best fits result followed by ARFIMA and ANFIS respectively. Consistent with the previous findings done by Boyacioglu and Avci [32] and Malekmohamadi, Lari, Kerachian, Nikoo and Fallahnia [33], we found that all of the listed models provide almost similar and they display decent result to forecast the CPO prices. Besides, all of the reported RMSE are statically significant by considering the empirical evidence on Diebold and Mariano [39] perspectives.
The most striking result to emerge from the forecasting performance is that the ARFIMA model has same standard level of forecasting ability among the listed artificial intelligence approaches. More to the point, we found that the applied ARFIMA model outperformed compared the ANFIS model in predicting the CPO prices. Relying to the fact that the CPO prices are strongly autocorrelated as well as consisting linearity which significantly degrades the performance of the ANFIS model.
Through this study, the results show that the accuracy of prediction has reached a high level. However, this study only covers the in-sample forecasting analysis. Therefore, it is far more convincing with the extension of out-of-sample forecasting analysis.
5. Acknowledgements
An earlier version of this paper was presented at the International Trade & Academic Research Conference (ITARC), 7 to 8 November, 2012, London, United Kingdom. The authors are very indebted to the conference organizer, anonymous referee and the conference participants for their constructive comments.
REFERENCES
- O. Kisi, J. Shiri and B. Nikoofar, “Forecasting Daily Lake Levels Using Artificial Intelligence Approaches,” Computers & Geosciences, Vol. 41, 2012, pp. 169-180. doi:10.1016/j.cageo.2011.08.027
- M. Firat and M. Gungor, “Hydrological Time-Series Modelling Using An Adaptive Neuro-Fuzzy Inference System,” Hydrological Processes, Vol. 22, No. 13, 2008, pp. 2122-2132. doi:10.1002/hyp.6812
- B. Samanta, “Prediction of Chaotic Time Series Using Computational Intelligence,” Expert System with Applications, Vol. 38, No. 9, 2011, pp. 11406-11411. doi:10.1016/j.eswa.2011.03.013
- J. J. Flores, M. Graff and H. Rodriguez, “Evolutive Design of ARMA and ANN Models for Time Series Forecasting,” Renewable Energy, Vol. 44, 2012, pp. 225-230. doi:10.1016/j.renene.2012.01.084
- W. C. Wang, K. W. Chau, C. T. Cheng and L. Qiu, “A Comparison of Performance of Several Artificial Intelligence Methods for Forecasting Monthly Discharge Time Series,” Journal of Hydrology, Vol. 374, No. 3-4, 2009, pp. 294-306. doi:10.1016/j.jhydrol.2009.06.019
- A.A. Karia and I. Bujang, “Progress Accuracy of CPO Price Prediction: Evidence from ARMA Family and Artificial Neural Network Approach,” International Research Journal of Finance and Economics, No. 64, 2011, pp. 66-79.
- S. BuHamra, N. Smaoui and M. Gabr, “The Box-Jenkins Analysis and Neural Networks: Prediction and Time Series Modelling,” Applied Mathematical and Modelling, Vol. 27, No. 10, 2003, pp. 805-815. doi:10.1016/S0307-904X(03)00079-9
- S.-H. Chen, Y.-H. Lin, L.-C. Chang and F.-J. Chang, “The Strategy of Building a Flood Forecast Model by Neuro-Fuzzy Network,” Hydrological Processes, Vol. 20, No. 7, 2006, pp. 1525-1540. doi:10.1002/hyp.5942
- C. P. Kurian, V. I. George, J. Bhat and R. S. Aithal, “ANFIS Model for the Time Series Prediction of Interior Daylight Illuminance,” AIML Journal, Vol. 6, No. 3, 2006, pp. 35-40.
- A. Talei, L. H. C. Chua and T. S. W. Wong, “Evaluation of Rainfall and Discharge Inputs Used by Adaptive Network-Based Fuzzy Inference System (ANFIS) in Rainfall-Runoff Modelling,” Journal of Hydrology, Vol. 391, No. 3-4, 2010, pp. 248-262. doi:10.1016/j.jhydrol.2010.07.023
- Z. M. Yunos, S. M. Shamsuddin and R. Sallehuddin, “Data Modeling for Kuala Lumpur Composite Index with ANFIS,” 2nd Asia International Conference on Modelling & Simulation, 2008, pp. 609-614.
- L. Naderloo, R. Alimardani, M. Omid, F. Sarmadian, P. Javadikia, M. Y. Torabi and F. Alimardani, “Application of ANFIS to Predict Crop Yield Based on Different Energy Inputs,” Measurement, Vol. 45, No. 6, 2012, pp. 1406-1413. doi:10.1016/j.measurement.2012.03.025
- R. Hossain, A. M. T. Oo and A. B. M. S. Alia, “Historical Weather Data Supported Hybrid Renewable Energy Forecasting Using Artificial Neural Network (ANN),” Energy Procedia, Vol. 14, 2012, pp. 1035-1040. doi:10.1016/j.egypro.2011.12.1051
- M. Mohandes, S. Rehman and S. M. Rahman, “Estimation of Wind Speed Profile using Adaptive Neuro-Fuzzy Inference System (ANFIS),” Applied Energy, Vol. 88, No. 11, 2011, pp. 4024-4032. doi:10.1016/j.apenergy.2011.04.015
- A. Abraham and B. Nath, “A Neuro-Fuzzy Approach for Modelling Electricity Demand in Victoria,” Applied Soft Computing, Vol. 1, No. 2, 2001, pp. 127-138. doi:10.1016/S1568-4946(01)00013-8
- M. Buragohain and C. Mahanta, “A Novel Approach for ANFIS Modelling Based on Full Factorial Design,” Applied Soft Computing, Vol. 8, No. 1, 2008, pp. 609-625. doi:10.1016/j.asoc.2007.03.010
- T. V. T. Duy, Y. Sato and Y. Inoguchi, “Improving Accuracy of Host Load Predictions on Computational Grids by Artificial Neural Networks,” IEEE International Symposium on Parallel & Distributed Processing (IPDPS 2009), Rome, 23-29 May 2009, pp. 23-29. doi:10.1109/IPDPS.2009.5160878
- C. Hamzacebi, “Improving Artificial Neural Networks’ Performance in Seasonal Time Series Forecasting,” Information Sciences, Vol. 178, No. 23, 2008, pp. 4550- 4559. doi:10.1016/j.ins.2008.07.024
- I. Rojas, O. Valenzuela, F. Rojas, A. Guillen, L. J. Herrera, H. Pomares, L. Marquez and M. Pasadas, “Soft-Computing Techniques and ARMA Model for Time Series Prediction,” Neurocomputing, Vol. 71, No. 4-6, 2008, pp. 519-537. doi:10.1016/j.neucom.2007.07.018
- R. Sallehuddin, S. M. Shamsuddin, S. Z. Hashim and A. Abraham, “Forecasting Time Series Data Using Hybrid Grey Relational Artificial Neural Network and Autoregressive Integrated Moving Average Model,” Neural Network World, Vol. 6, No. 7, 2009, pp. 573-605.
- A. L. S. Maia, F. A. T. Carvalho and T. B. Ludermir, “Forecasting Models for Interval-Valued Time Series,” Neurocomputing, Vol. 71, No. 16-18, 2008, pp. 3344- 3352. doi:10.1016/j.neucom.2008.02.022
- H. R. Maier and G. C. Dandy, “Neural Network Models for Forecasting Univariate Time Series,” Water Resource Research, Vol. 32, No. 4, 1996, pp. 1013-1022. doi:10.1029/96WR03529
- M. Khashei, M. Bijari and G. A. R. Ardali, “Improvement of Auto-Regressive Integrated Moving Average Models using Fuzzy Logic and Artificial Neural Networks (ANNs),” Neurocomputing, Vol. 72, No. 4-6, 2009, pp. 956-967. doi:10.1016/j.neucom.2008.04.017
- G. P. Zhang, B. E. Patuwo and M. Y. Hu, “A Simulation Study of Artificial Neural Networks for Nonlinear TimeSeries Forecasting,” Computer & Operations Research, Vol. 28, No. 4, 2001, pp. 381-396. doi:10.1016/S0305-0548(99)00123-9
- T. Y. Kim, K. J. Oh, C. Kim and J. D. Do, “Artificial Neural Networks for Non-Stationary Time Series,” Neurocomputing, Vol. 61, 2004, pp. 439-447. doi:10.1016/j.neucom.2004.04.002
- W. Y. Hsu, “EEG-Based Motor Imagery Classification using Neuro-Fuzzy Prediction and Wavelet Fractal Features,” Journal of Neuroscience Methods, Vol. 189, No. 2, 2010, pp. 295-302. doi:10.1016/j.jneumeth.2010.03.030
- C. Vairappan, H. Tamura, S. Gao and Z. Tang, “Batch Type Local Search-Based Adaptive Neuro-Fuzzy Inference System (ANFIS) with Self-Feedbacks for Time-Series Prediction,” Neurocomputing, Vol. 72, No. 7-9, 2009, pp. 1870-1877. doi:10.1016/j.neucom.2008.05.010
- F. J. Chang and Y. T. Chang, “Adaptive Neuro-Fuzzy Inference System for Prediction of Water Level in Reservoir,” Advances in Water Resources, Vol. 29, No. 1, 2006, pp. 1-10. doi:10.1016/j.advwatres.2005.04.015
- L. C. Chang and F. J. Chang, “Intelligent Control for Modelling of Real-Time Reservoir Operation,” Hydrological Processes, Vol. 15, No. 9, 2001, pp. 1621-1634. doi:10.1002/hyp.226
- J. R. Chang, L. Y. Wei and C. H. Cheng, “A Hybrid ANFIS Model Based on AR and Volatility for TAIEX Forecasting,” Applied Soft Computing, Vol. 11, No. 1, 2011, pp. 1388-1395. doi:10.1016/j.asoc.2010.04.010
- Y. L. Loukas, “Adaptive Neuro-Fuzzy Inference System: An Instant and Architecture-Free Predictor for Improved QSAR Studies,” Journal of Medicinal Chemistry, Vol. 44, No. 17, 2001, pp. 2772-2783. doi:10.1021/jm000226c
- M. A. Boyacioglu and D. Avci, “An Adaptive Network-Based Fuzzy Inference System (ANFIS) for the Prediction of Stock Market Return: The Case of the Istanbul Stock Exchange,” Expert System with Applications, Vol. 37, No. 12, 2010, pp. 7908-7912. doi:10.1016/j.eswa.2010.04.045
- I. Malekmohamadi, M. R. B. Lari, R. Kerachian, M. R. Nikoo and M. Fallahnia, “Evaluating the Efficacy of SVMs, BNs, ANNs, and ANFIS in Wave Height Prediction,” Ocean Engineering, Vol. 38, No. 2-3, 2011, pp. 487-497. doi:10.1016/j.oceaneng.2010.11.020
- M. Wei, B. Bai, A. H. Sung, Q. Liu, J. Wang and M. E. Cather, “Predicting Injection Profiles Using ANFIS,” Information Sciences, Vol. 177, No. 20, 2007, pp. 4445- 4461. doi:10.1016/j.ins.2007.03.021
- C. M. Bishop, “Neural Networks for Pattern Recognition,” Clarendon Press, Oxford, 1995.
- P. Werbos, “Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences,” Ph.D. Dissertation, Harvard University, Cambridge, 1974.
- J. S. R. Jang, “ANFIS: Adaptive-Network Based Fuzzy Inference System,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 23, No. 3, 1993, pp. 665-685. doi:10.1109/21.256541
- J. A. Doornik and M. Ooms, “Inference and Forecasting for ARFIMA Models with an Application to US and UK Inflation,” Studies in Nonlinear Dynamics & Econometrics, Vol. 8, No. 2, 2004, pp. 1-23. doi:10.2202/1558-3708.1218
- F. X. Diebold and R. S. Mariano, “Comparing Predictive Accuracy,” Journal of Business & Economics Statistics, Vol. 13, No. 3, 1995, pp. 3-25.
- M. E. Keskin, O. Terzi and D. Taylan, “Fuzzy Logic Model Approaches to Daily Pan Evaporation Estimation in Western Turkey,” Hydrological Sciences Journal, Vol. 49, No. 6, 2004, pp. 1001-1010. doi:10.1623/hysj.49.6.1001.55718

