American Journal of Operations Research
Vol. 2 No. 2 (2012) , Article ID: 19924 , 6 pages DOI:10.4236/ajor.2012.22017
The Theory of Membership Degree of Γ-Conclusion in Several n-Valued Logic Systems*
Department of Mathematics, Quanzhou Normal University, Quanzhou, China
Email: zjcqz@126.com
Received April 14, 2012; revised May 18, 2012; accepted May 30, 2012
Keywords: N-Valued Propositional Logic; Γ-Conclusion; Theory; Root; Membership Degree
ABSTRACT
Based on the analysis of the properties of Γ-conclusion by means of deduction theorems, completeness theorems and the theory of truth degree of formulas, the present papers introduces the concept of the membership degree of formulas A is a consequence of Γ (or Γ-conclusion) in Łukasiewicz n-valued propositional logic systems, 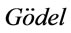 n-valued propositional logic system and the
n-valued propositional logic system and the 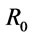 n-valued propositional logic systems. The condition and related calculations of formulas A being Γ-conclusion were discussed by extent method. At the same time, some properties of membership degree of formulas A is a Γ-conclusion were given. We provide its algorithm of the membership degree of formulas A is a Γ-conclusion by the constructions of theory root.
n-valued propositional logic systems. The condition and related calculations of formulas A being Γ-conclusion were discussed by extent method. At the same time, some properties of membership degree of formulas A is a Γ-conclusion were given. We provide its algorithm of the membership degree of formulas A is a Γ-conclusion by the constructions of theory root.
1. Introduction
Fuzzy logic is the theoretical foundation of fuzzy control. Spurred by the success in its applications, especially in fuzzy control, fuzzy logic has aroused the interest of many famous scholars, a series of important results have been created in documents [1-5]. For the sake of reasoning, we have to choose a subset  of well-formed formulas, which can reflect come essential properties, as the axioms of the logical system and we then deduce the so-called
of well-formed formulas, which can reflect come essential properties, as the axioms of the logical system and we then deduce the so-called  -conclusion through some reasonable inference rules [6-9]. So, a natural question then arises: how to judge whether or not a general formula
-conclusion through some reasonable inference rules [6-9]. So, a natural question then arises: how to judge whether or not a general formula 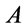 is a conclusion of a given theory
is a conclusion of a given theory , or to what extend the formula
, or to what extend the formula 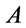 is a conclusion of
is a conclusion of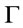 ? It is basic problem to judge one thing belong to one kind in artificial intelligence. As is well known, human reasoning is approximate rather than precise in nature. we basic starting point is to establish graded version of basic logical notions. In order to establish a solid foundation for fuzzy reasoning, professor G. J. Wang proposed the concept of root of theory [3], J. C. Zhang proposed the concept of generalized root of theory [10,11], in propositional logic systems. The graded description and properties of formulas
? It is basic problem to judge one thing belong to one kind in artificial intelligence. As is well known, human reasoning is approximate rather than precise in nature. we basic starting point is to establish graded version of basic logical notions. In order to establish a solid foundation for fuzzy reasoning, professor G. J. Wang proposed the concept of root of theory [3], J. C. Zhang proposed the concept of generalized root of theory [10,11], in propositional logic systems. The graded description and properties of formulas 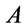 being
being 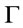 -conclusion were discussed. And provide its algorithm of membership degree of formulas A is a
-conclusion were discussed. And provide its algorithm of membership degree of formulas A is a 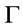 -conclusion, by the constructions of theory root in the above-mentioned logic systems.
-conclusion, by the constructions of theory root in the above-mentioned logic systems.
2. Preliminaries
It is well known that different implication operators and valuation lattices 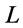 (i.e., the set of truth degrees for logic) determine different logic systems (see [12]). Here valuation lattices is
(i.e., the set of truth degrees for logic) determine different logic systems (see [12]). Here valuation lattices is 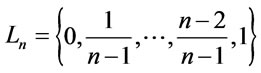 and three popularly used implication operators and the correspond ing t-norms defined as follows:
and three popularly used implication operators and the correspond ing t-norms defined as follows:

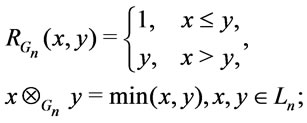
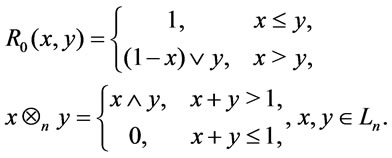
These three implication operators  and
and  are called Łukasiewicz implication operator
are called Łukasiewicz implication operator , Gödel implication operator
, Gödel implication operator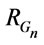 , and the
, and the 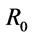 -implication operator
-implication operator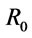 , respectively. The t-norm, which corresponds to
, respectively. The t-norm, which corresponds to 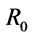 -implication operator
-implication operator , is called also Nilpotent Minimumtnorm [6]. If we fix a t-norm
, is called also Nilpotent Minimumtnorm [6]. If we fix a t-norm  above we then fix a propositional calculus (whose set of truth values is
above we then fix a propositional calculus (whose set of truth values is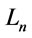 ):
):  is taken for the truth function of the strong conjunction &, the residuum
is taken for the truth function of the strong conjunction &, the residuum 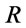 of
of  becomes the truth function of the implication operator and R(.,0) is the truth function of the negation. In more details, we have the following definitions.
becomes the truth function of the implication operator and R(.,0) is the truth function of the negation. In more details, we have the following definitions.
Definition 1 [7,8]. The propositional calculus 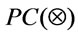 given by a t-norm
given by a t-norm  has the set
has the set 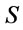 of propositional variables
of propositional variables 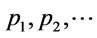 and connectives
and connectives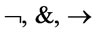 . The set
. The set 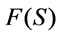 of well-formed formulas in
of well-formed formulas in  is defined inductively as follows: each propositional variable is a formula; if
is defined inductively as follows: each propositional variable is a formula; if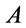 ,
, 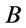 are formulas, then
are formulas, then ,
, 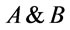 and
and 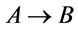 are all formulas.
are all formulas.
Definition 2 [8,9,13]. The formal deductive systems of 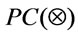 given by
given by  corresponding to
corresponding to 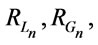 and
and , are called Łukasiewicz n-valued logic systems
, are called Łukasiewicz n-valued logic systems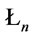 ,
, 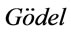 n-valued logic systems
n-valued logic systems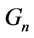 , and the
, and the 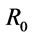 nvalued logic systems
nvalued logic systems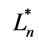 , respectively.
, respectively.
Define in the above-mentioned logic systems
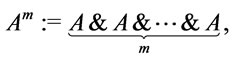 (1)
(1)
and in the corresponding algebras 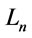
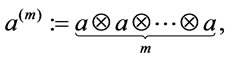 (2)
(2)
where  is the t-norm defined on
is the t-norm defined on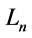 .
.
Remark 1. It is easy to verify that the following assertions are true:
(1) in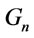 ,
, 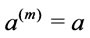 for every
for every 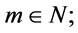 .
.
(2) in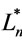 ,
,  for every
for every 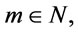 and
and 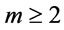 .
.
(3) in 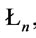
 , for every
, for every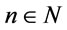 .
.
Definition 3 [7,8]. (1) A homomorphism 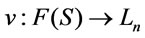 of type
of type  from
from 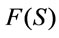 into the valuation lattice
into the valuation lattice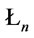 , i.e.
, i.e. 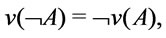
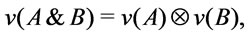
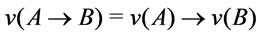 , is called an R-valuation of
, is called an R-valuation of . The set of all R-valuations will be denoted by
. The set of all R-valuations will be denoted by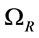 .
.
(2) A formula 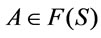 is called a tautology w.r.t.
is called a tautology w.r.t. 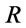 if
if 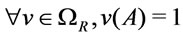 holds.
holds.
Remark 2 [8,13]. It is not difficult to verify in the above-mentioned three logic systems that  , and
, and 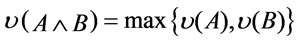 for every valuation
for every valuation 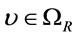 . Moreover, one can check in
. Moreover, one can check in  and
and 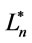 that
that  and
and 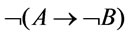 are logically equivalent.
are logically equivalent.
Definition 4 [8]. Assume that 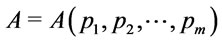 is a formula generated by propositional variables
is a formula generated by propositional variables 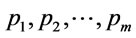 through connectives
through connectives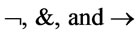 . Substitute
. Substitute  for
for 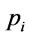 in
in 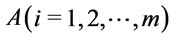 and keep the logic connectives in
and keep the logic connectives in 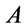 unchanged but explain them as the corresponding operators defined on the valuation lattice
unchanged but explain them as the corresponding operators defined on the valuation lattice . The we get a function
. The we get a function 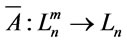 and call
and call 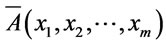 the truth degree function of
the truth degree function of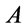 .
.
Definition 5 [7,8]. (1) A subset of 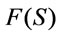 is called a theory.
is called a theory.
(2) Let 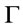 be a theory,
be a theory,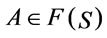 . A deduction of
. A deduction of 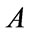 from
from , in symbols,
, in symbols, 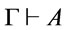 , is a finite sequence of formulas
, is a finite sequence of formulas 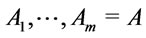 such that for each
such that for each 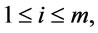
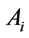 is an axiom of
is an axiom of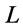 , or
, or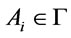 , or there are
, or there are 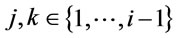 such that
such that 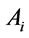 follows from
follows from  and
and  by MP. Equivalently, we say that
by MP. Equivalently, we say that 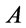 is a conclusion of
is a conclusion of  (or
(or  -conclusion). The set of all conclusions of
-conclusion). The set of all conclusions of  is denoted by
is denoted by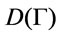 . By a proof of
. By a proof of 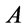 we shall henceforth mean a deduction of
we shall henceforth mean a deduction of 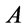 from the empty set. We shall also write
from the empty set. We shall also write  in place of
in place of 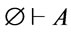 and call
and call  a theorem.
a theorem.
It is easy for the reader to check the following Proposition 1.
Proposition 1. Let 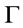 be a theory and
be a theory and 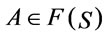 If
If  then there exist a finite subset of
then there exist a finite subset of 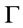 say,
say, 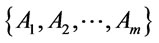 such that
such that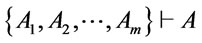 .
.
Theorem 1 (Generalized deduction theorems) [7, 8,12]. Suppose that 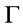 is a theory,
is a theory, 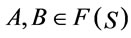 , then
, then
(1) in 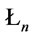 ,
,
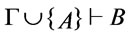 iff
iff 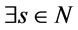 s. t.
s. t.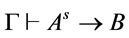 .
.
(2) in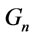 ,
,
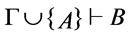 iff
iff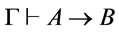 .
.
(3) in ,
,
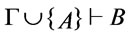 iff
iff .
.
Definition 6 [8,13]. Suppose that 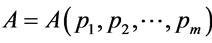 is a formula of
is a formula of 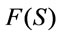 containing m atomic formulas
containing m atomic formulas , and
, and 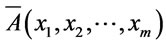 be the truth degree function of
be the truth degree function of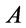 . Then
. Then
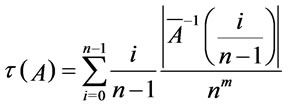
is called the truth degree of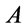 , where
, where 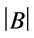 is the cardinal of set
is the cardinal of set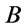 .
.
Theorem 2. Suppose that 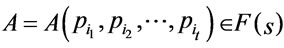 and
and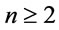 , then in
, then in  and
and 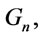
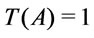 iff
iff 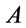 is a tautology i.e.,
is a tautology i.e.,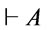 .
.
Proof. Assume that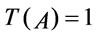 . Since
. Since
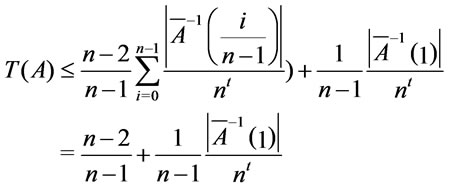 then
then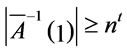 . By definite,
. By definite, 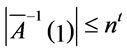 , thus
, thus 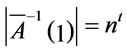 i.e.,
i.e., 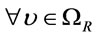 ,
, 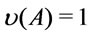 , then
, then 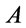 is a tautology. Conversely, assume that A is a tautology i.e.,
is a tautology. Conversely, assume that A is a tautology i.e.,
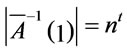 , then
, then 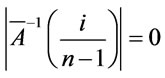
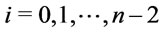 , so
, so
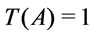 . This completes the proof.
. This completes the proof.
Theorem 3 [8]. Suppose that , then in
, then in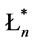 ,
, 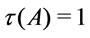 iff
iff 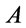 is a tautology, i.e.,
is a tautology, i.e.,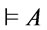 .
.
Theorem 4. Suppose that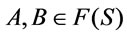 . If for every
. If for every , then
, then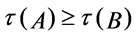 .
.
Proof. Suppose that 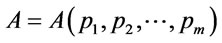 and
and  are all a formulas of
are all a formulas of  containing
containing 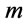 atomic formulas
atomic formulas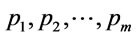 , it follows from
, it follows from 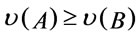 that
that
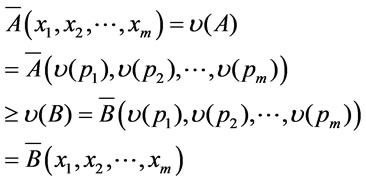
and

hence
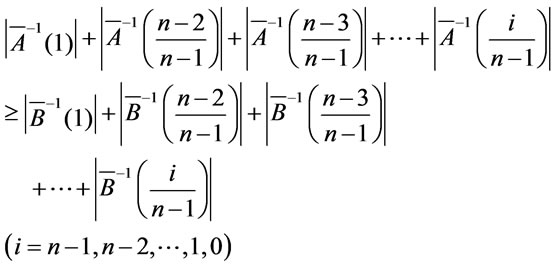 .
.
It is easy to verify that
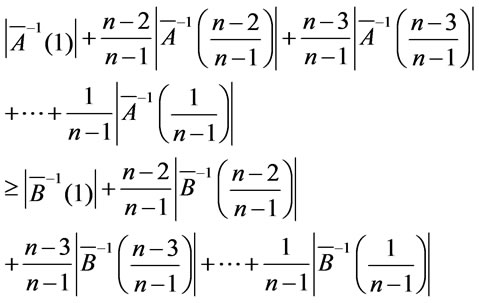
then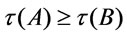 .
.
3. Properties of the Roots of Theories
Definition 7 [3]. Suppose that 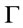 is a theory,
is a theory, . If for every
. If for every  we have
we have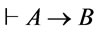 , then
, then 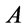 is called the root of
is called the root of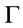 .
.
Theorem 5. Suppose that 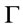 is a finite theory, say
is a finite theory, say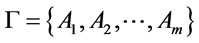 , then
, then
(1) in 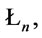
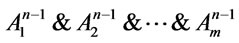 is a root of
is a root of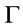 ;
;
(2) in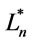 ,
,
 is a root of
is a root of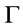 ;
;
(3) in ,
, 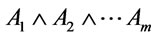 is a root of
is a root of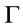 .
.
Proof. (1) It following form references [4] that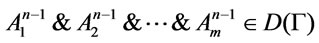 , for every
, for every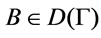 , there exist
, there exist 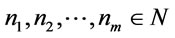 such that
such that
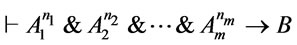 by Theorem 1. It is easy to check that
by Theorem 1. It is easy to check that 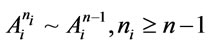 by Remark 1, it following from
by Remark 1, it following from 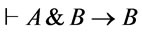 that
that 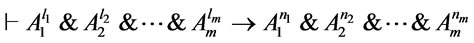 where
where 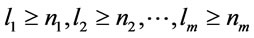 , thus
, thus 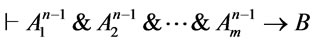 by Hypothetical, this shows that
by Hypothetical, this shows that 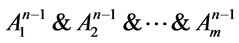 is a root of
is a root of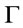 .
.
(2) It following form references [4] that 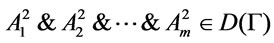 , for every
, for every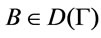 , it following from Theorem 1 that
, it following from Theorem 1 that 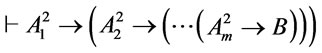 , since
, since 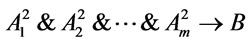 and
and 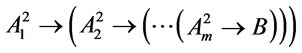 are provably equivalent, and so is
are provably equivalent, and so is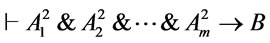 . This shows
. This shows 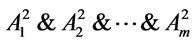 is a root of
is a root of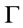 .
.
(3) It following from references [4] that 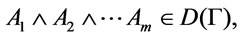 for every
for every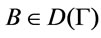 , we get
, we get 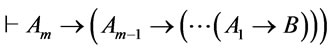 by Theorem 1, it is easy to verify that
by Theorem 1, it is easy to verify that 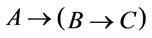 and
and  are provably equivalent, hence
are provably equivalent, hence 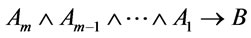 and
and 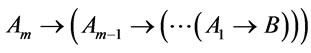 are provably equivalent, and so is
are provably equivalent, and so is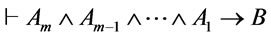 . This shows that
. This shows that  is a root of
is a root of .
.
4. Membership Degree of Formulas A Is Γ-Conclusion
In following, let us first take an analysis on the conditions of formulas A is a 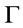 -conclusion in
-conclusion in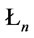 . Suppose that
. Suppose that 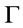 is a theory and A is a
is a theory and A is a  -conclusion , it follows from Proposition 1 and Theorem 1 that there exit a finite string of formulas
-conclusion , it follows from Proposition 1 and Theorem 1 that there exit a finite string of formulas 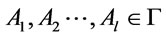 and
and 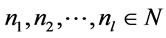 such that
such that 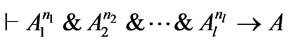 holds, i.e., the formula
holds, i.e., the formula 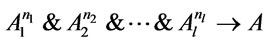 is a theorem of
is a theorem of , let
, let , hence
, hence 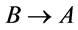 is a tautology, it follows from Theorem 2 that
is a tautology, it follows from Theorem 2 that . Conversely, if there exist a
. Conversely, if there exist a 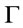 -conclusion
-conclusion 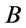 such that
such that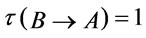 , then following from Theorem 2 that
, then following from Theorem 2 that 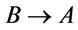 is a tautology, thus
is a tautology, thus 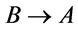 is a theorem of
is a theorem of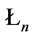 , i.e.,
, i.e., 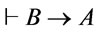 holds and
holds and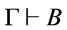 , we have that
, we have that 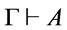 by MP, i.e.,
by MP, i.e., 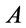 is a
is a  -conclusion. Moreover, the larger the membership degree of such formulas are, the more closer A is to be
-conclusion. Moreover, the larger the membership degree of such formulas are, the more closer A is to be 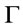 -conclusion. Hence it is natural and reasonable for us using the supremum of truth degree of all formulas with the form
-conclusion. Hence it is natural and reasonable for us using the supremum of truth degree of all formulas with the form 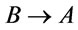 where
where  to measure A is a
to measure A is a 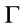 -conclusion.
-conclusion.
Definition 8. Suppose that  is a theory,
is a theory,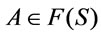 . Define
. Define

then 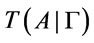 is called the membership degree of formulas A is a
is called the membership degree of formulas A is a 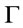 -conclusion.
-conclusion.
It is easy to verify that 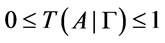 and following Proposition 2 by Definition 8.
and following Proposition 2 by Definition 8.
Proposition 2. In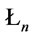 ,
, 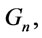 and
and If A is a
If A is a 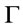 -conclusion, then
-conclusion, then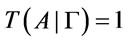 .
.
Theorem 6. In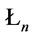 ,
, 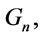 and
and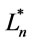 , if
, if  is a finite theory, say
is a finite theory, say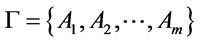 , then A is a
, then A is a  -conclusion iff
-conclusion iff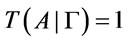 .
.
Proof. The necessity part by proposition 2, it is only necessary to prove the sufficiency. Let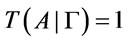 . For every number
. For every number 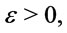 there exist a formulas
there exist a formulas  such that
such that 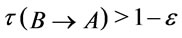 by Definition 8.
by Definition 8.
(1) In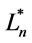 , it follows from Theorem 5 that
, it follows from Theorem 5 that 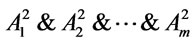 is a root of
is a root of 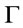 and
and 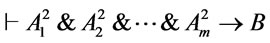 hold. Hence for every
hold. Hence for every  we have
we have 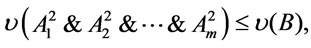 it follows from properties of implication operators that
it follows from properties of implication operators that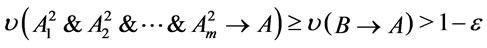 , since
, since 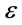 is arbitrary, we have
is arbitrary, we have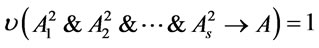 , thus
, thus 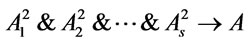 is a tautology, and
is a tautology, and  is a theorem , together with the result
is a theorem , together with the result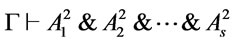 , then
, then 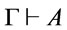 by MP, i.e.,
by MP, i.e., 
(2) In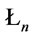 , notice that
, notice that 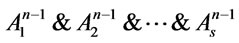 is a root of
is a root of 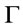 by Theorem 5, hence the proof of (2) is similar to that the proof of (1) and so is omitted.
by Theorem 5, hence the proof of (2) is similar to that the proof of (1) and so is omitted.
(3) In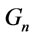 , notice that
, notice that 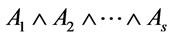 is a root of
is a root of  by Theorem 5, hence the proof of (2) is similar to that the proof of (1). In fact
by Theorem 5, hence the proof of (2) is similar to that the proof of (1). In fact 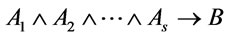 is a theorem by Definition 7, hence
is a theorem by Definition 7, hence 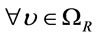 we have
we have 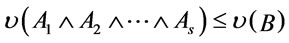 and
and  , thus
, thus 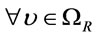 ,
, 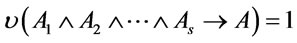 holds, then
holds, then 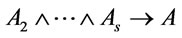 is a theorem , together with the result
is a theorem , together with the result 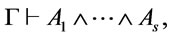 we have
we have 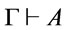 by MP. The proof is completed.
by MP. The proof is completed.
Theorem 7. Suppose that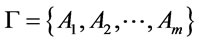 , then
, then
(1) in ,
,
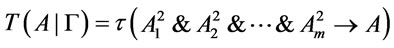 ;
;
(2) in ,
,
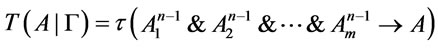 ;
;
(3) in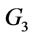 ,
,
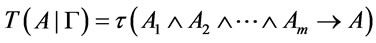 .
.
Proof. (1) Since 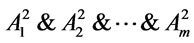 is a root of
is a root of 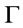 by Theorem 5, hence for every
by Theorem 5, hence for every 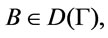 we have
we have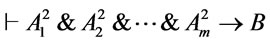 . Thus for every
. Thus for every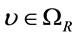 ,
, 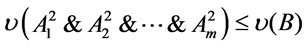 , and
, and 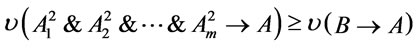 holds, then
holds, then 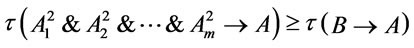 by Theorem 4. It follows from
by Theorem 4. It follows from 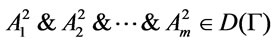 that
that  i.e.,
i.e.,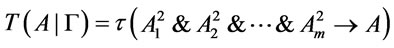 .
.
(2) Notice that in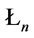 ,
, 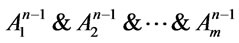 is a root of
is a root of 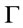 by Theorem 5, the proof of (2) is similar to that the proof of (1) and so is omitted.
by Theorem 5, the proof of (2) is similar to that the proof of (1) and so is omitted.
(3) Notice that in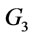 ,
, 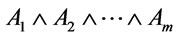 is a root of
is a root of 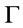 by Theorem 5, the proof of (2) is similar to that the proof of (1) and so is omitted.
by Theorem 5, the proof of (2) is similar to that the proof of (1) and so is omitted.
Theorem 8. Suppose that 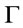 is a infinite theory. Then
is a infinite theory. Then
(1) in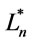 ,
,
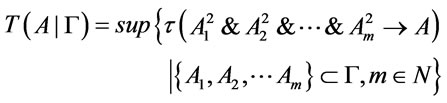 ;
;
(2) 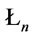 ,
,
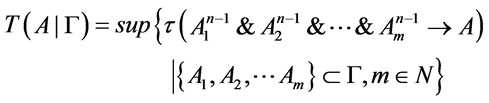 ;
;
(3) in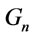 ,
,
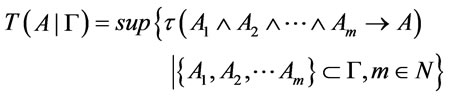 .
.
Proof. (1) For every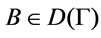 , it following from Proposition 1 that there exist a finite string of formulas
, it following from Proposition 1 that there exist a finite string of formulas 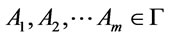 such that
such that  It follows from Theorem 1 that
It follows from Theorem 1 that 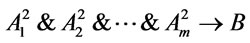 is a theorem, hence
is a theorem, hence 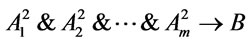 is a tautology by completeness theorem, and for every
is a tautology by completeness theorem, and for every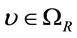 ,
, 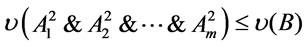 , we have
, we have
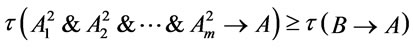 by Theorem 4.
by Theorem 4.
It following form references [14] that 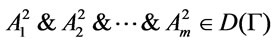 , then
, then
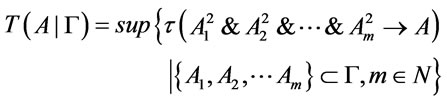 .
.
(2) Notice that in ,
, 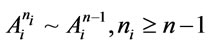 by Remark 1, the Proof of (2) is similar to that the Proof of (1) and so is omitted.
by Remark 1, the Proof of (2) is similar to that the Proof of (1) and so is omitted.
(3) Notice that in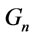 ,
,  and
and 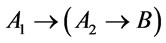 is Provably equivalent, the Proof of (3) is similar to that the Proof of (1) and so is omitted.
is Provably equivalent, the Proof of (3) is similar to that the Proof of (1) and so is omitted.
Theorem 9. Suppose that 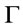 is a theory,
is a theory, 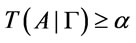 and
and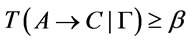 , then
, then 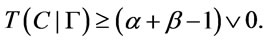
Proof. (1) If 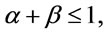 we get
we get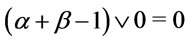 , then
, then 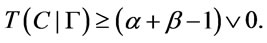
(2) If 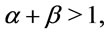 we get
we get 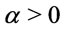 and
and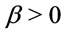 , for any given positive number
, for any given positive number 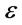 such that
such that  and
and 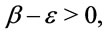 there exists formulas
there exists formulas 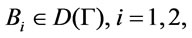 such that
such that 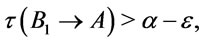 and
and 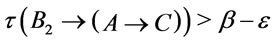 . It follows from properties of Regular implication operators that
. It follows from properties of Regular implication operators that 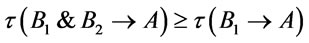 and
and 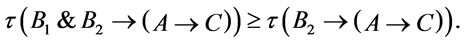 It is easy to verify that
It is easy to verify that 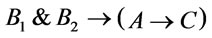 and
and  are provably equivalent (i.e., logically equivalent), hence
are provably equivalent (i.e., logically equivalent), hence 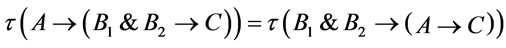 . It follows from the theory of truth degrees of formulas and
. It follows from the theory of truth degrees of formulas and 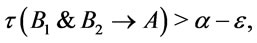
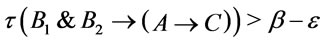 that
that 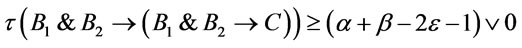 .
.
Bucas 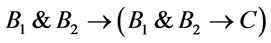 and
and 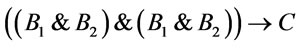 are provably equivalent (i.e., logically equivalent), hence
are provably equivalent (i.e., logically equivalent), hence  , it is easy to verify that
, it is easy to verify that 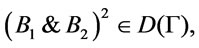 then
then 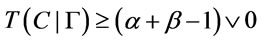 by the definition of the membership degree of formulas.
by the definition of the membership degree of formulas.
Example 1. Suppose that  In
In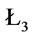 ,
, 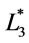 and
and , compute
, compute  respectively.
respectively.
Solution. (1) In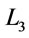 , assume that
, assume that 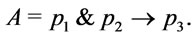 Since
Since  and
and
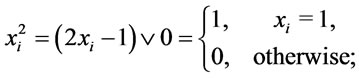
thus
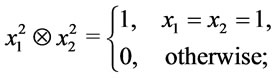
and

We have 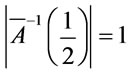 and
and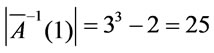 hence
hence
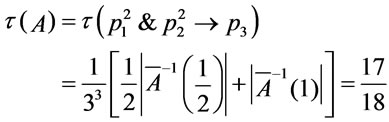 then
then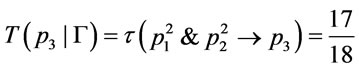 .
.
(2) In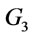 , assume that
, assume that 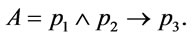 Since
Since 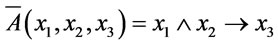 , and
, and
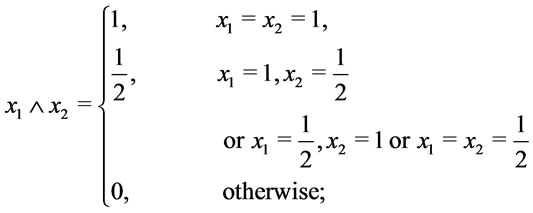
thus
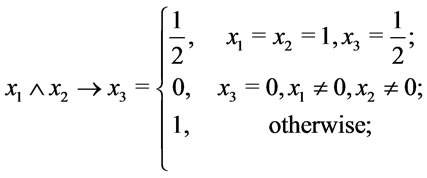
then

then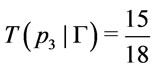 .
.
(3) In , assume that
, assume that  Since
Since 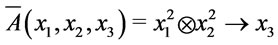 , and
, and
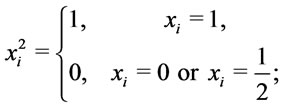
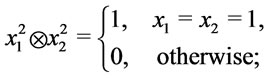
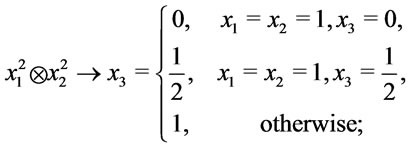
thus
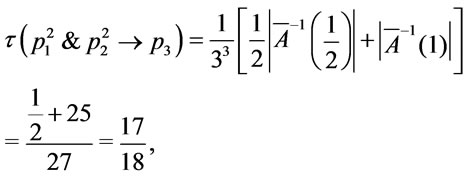
then 
Example 2. Suppose that 
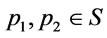 , in
, in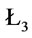 , compute
, compute 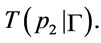
Solution. (1) Assume that  Since
Since
 , and
, and

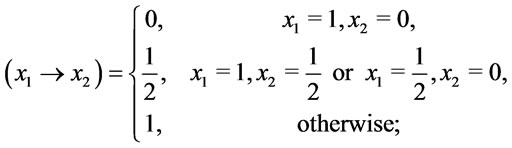
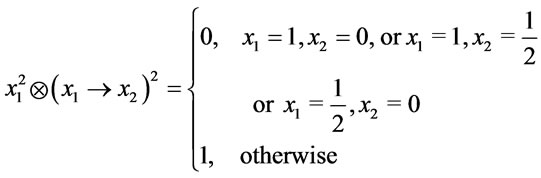
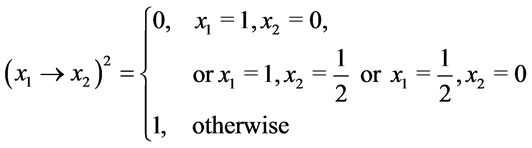
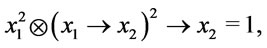

thus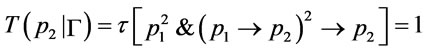 , then p2
, then p2
is a  -conclusion.
-conclusion.
REFERENCES
- H. W. Liu and G. J. Wang, “Unified Forms of Fully Implicational Restriction Methods for Fuzzy Reasoning,” Information Sciences, Vol. 177, No. 3, 2007, pp. 956-966. doi:10.1016/j.ins.2006.08.012
- J. Pavelka, “On Fuzzy Logic II-Enriched Residuated Lattices and Semantics of Propositional Calculi,” Zeitschrift für mathematische Logik und Grundlagen der Mathematik, Vol. 25, 2011, pp. 119-134.
- G. J. Wang and H. Wang, “Non-Fuzzy Versions of Fuzzy Reasoning in Classical Logic,” Information Sciences, Vol. 138, No. 1-4, 2011, pp. 211-236. doi:10.1016/S0020-0255(01)00131-1
- G. J. Wang, “On the Logic Foundation of Fuzzy Reasoning,” Information Sciences, Vol. 117, No. 1-2, 1999, pp. 47-88. doi:10.1016/S0020-0255(98)10103-2
- M. S. Ying, “Compactness, the Löwenheim-Skolem Property and the Direct Product of Lattices of Truth Values,” Zeitschrift für mathematische Logik und Grundlagen der Mathematik, Vol. 38, 1992, pp. 521-524.
- F. Esteva and L. Godo, “Monoidal t-Norm Based Logic: Towards a Logic for Left-Continuous t-Norms,” Fuzzy Set and Systems, Vol. 124, No. 3, 2001, pp. 271-288. doi:10.1016/S0165-0114(01)00098-7
- P. Hájek, “Metamathematics of Fuzzy Logic,” Kluwer Academic Publishers, Dordrecht, 1998.
- G. J. Wang and H. J. Zhou, “Introduction to Mathematical Logic and Resolution Principle,” 2nd Edition, Science in China Press, Beijing, 2006 (in Chinese).
- G. J. Wang, “A Formal Deductive System for Fuzzy Propositional Calculus,” Chinese Science Bulletin, Vol. 42, No. 14, 1997, pp. 1521-1525.
- J. C. Zhang, “Some Properties of the Roots of Theories in Propositional Logic Systems,” Computers and Mathematics with Applications, Vol. 55, No. 9, 2008, pp. 2086- 2093. doi:10.1016/j.camwa.2007.08.035
- J. C. Zhang and X. Y. Yang, “Some Properties of Fuzzy Reasoning in Propositional Fuzzy Logic Systems,” Information Sciences, Vol. 180, No. 23, 2010, pp. 4661- 4671. doi:10.1016/j.ins.2010.07.035
- S. Gottwald, “A Treatise on Many-Valued Logics, Studies in Logic and Computation,” Research Studies Press, Baldock, 2001.
- G. J. Wang, “Theory of Non-Classical Mathematical Logic and Approximate Reasoning,” Science in China Press, Beijing, 2000.
- D. Dubois, J. Lang and H. Prade, “Fuzzy Set in Approximate Reasoning,” Fuzzy Sets and Systems, Vol. 40, No. 1, 1991, pp. 143-244. doi:10.1016/0165-0114(91)90050-Z
NOTES
*The work was supported by the Science and Technology Item of the Education Department of Fujian Province of China (No. 2010JA10235).

