American Journal of Operations Research
Vol.3 No.3(2013), Article ID:31661,8 pages DOI:10.4236/ajor.2013.33029
An Existence Theorem of Solutions for the System of Generalized Vector Quasi-Variational-Like Inequalities
1Department of Applied Mathematics, Faculty of Engineering & Technology, Aligarh Muslim University, Aligarh, India
2Department of Applied Mathematics & Humanities, Sardar Vallabhbhai National Institute of Technology, Surat, India
Email: s_husain68@yahoo.com, *guptasanmp@gmail.com, vishnunarayanmishra@gmail.com
Copyright © 2013 Shamshad Husain et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 14, 2012; revised June 20, 2012; accepted July 8, 2012
Keywords: The System of Generalized Vector Quasi-Variational-Like Inequalities; Fixed Point Theorem; Open Lower Section; Upper Semicontinuous; C-Diagonal Quasiconvexity
ABSTRACT
In this paper, we introduce and study the system of generalized vector quasi-variational-like inequalities in Hausdorff topological vector spaces, which include the system of vector quasi-variational-like inequalities, the system of vector variational-like inequalities, the system of vector quasi-variational inequalities, and several other systems as special cases. Moreover, a number of C-diagonal quasiconvexity properties are proposed for set-valued maps, which are natural generalizations of the g-diagonal quasiconvexity for real functions. Together with an application of continuous selection and fixed-point theorems, these conditions enable us to prove unified existence results of solutions for the system of generalized vector quasi-variational-like inequalities. The results of this paper can be seen as extensions and generalizations of several known results in the literature.
1. Introduction and Formulation
In recent years, the system of generalized vector quasivariational-like inequality, which is a unified model for the system of vector quasi-variational-like inequalities, the system of vector variational-like inequalities, the system of vector variational inequalities, the system of vector equilibrium problems and the system of variational inequalities etc., has been studied (see [1-18] and references therein).
In this paper, we consider the systems of four kinds of generalized vector quasi-variational-like inequalities with set-valued mappings and discuss the existence of its solutions in locally convex topological vector space (l.c.s. in short), motivated and inspired by the recent works of Peng [1] and Ansari et al. [2].
Throughout this paper, unless otherwise specified, assume that  be an index set. For each
be an index set. For each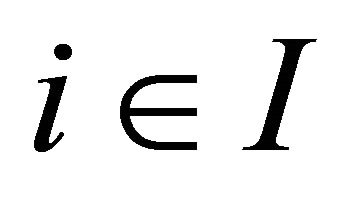 , let
, let 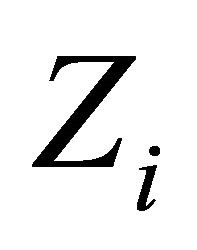 be a locally convex topological vector space (l.c.s., in short) and
be a locally convex topological vector space (l.c.s., in short) and 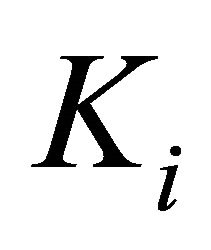 be a nonempty convex subset of Hausdorff topological vector space (t.v.s., in short)
be a nonempty convex subset of Hausdorff topological vector space (t.v.s., in short)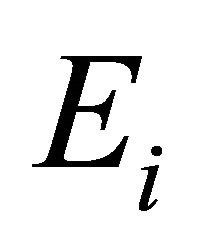 . Let
. Let 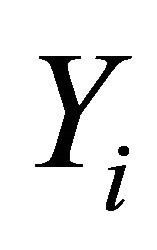 be a subset of continuous function space
be a subset of continuous function space  from
from 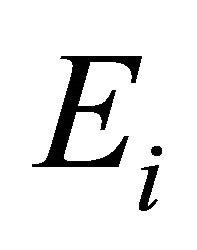 into
into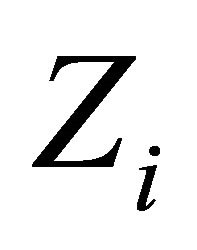 , where
, where 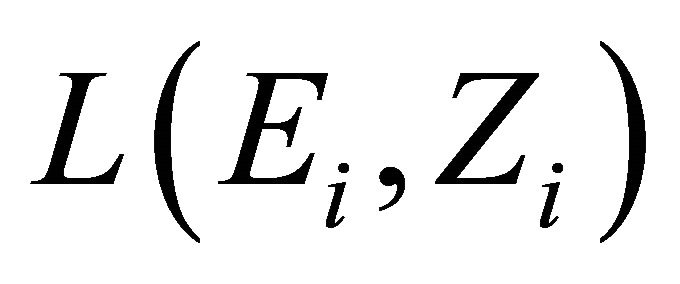 is equipped with a
is equipped with a  - topology. Let
- topology. Let 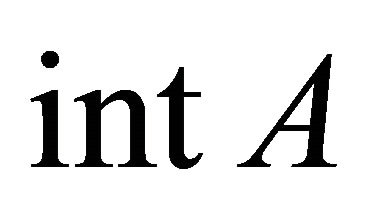 and
and  denote the interior and convex hull of a set
denote the interior and convex hull of a set  respectively. Let
respectively. Let 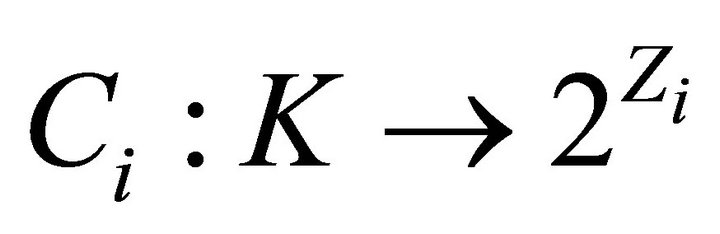 be a set-valued mapping such that
be a set-valued mapping such that  for each
for each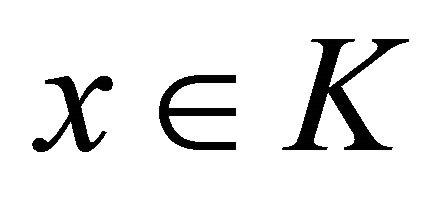 . Denote that
. Denote that  and
and  .
.
For each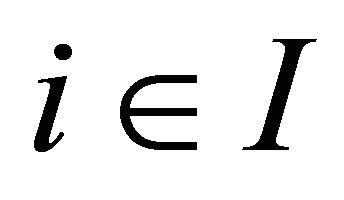 , let
, let 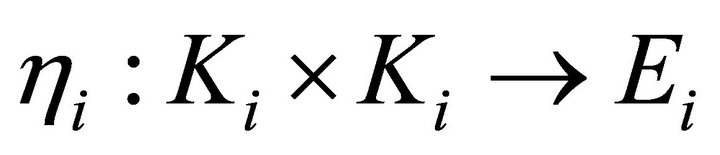 be a vectorvalued mapping,
be a vectorvalued mapping,  ,
,
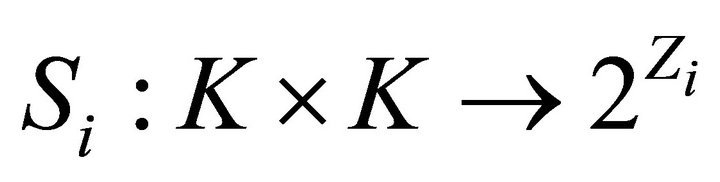 ,
, 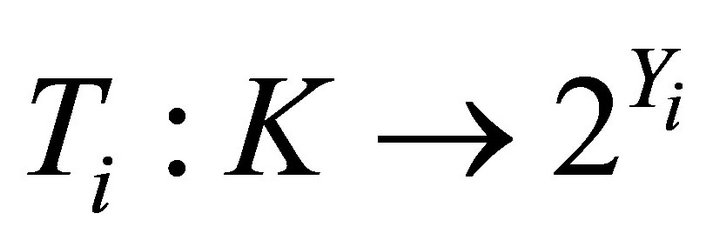 and
and  be four set-valued mappings. Then1) Strong type I system of generalized vector quasivariational-like inequalities which is to find
be four set-valued mappings. Then1) Strong type I system of generalized vector quasivariational-like inequalities which is to find  such that
such that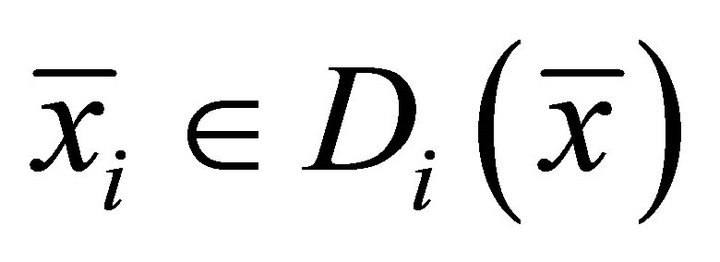 ,
, 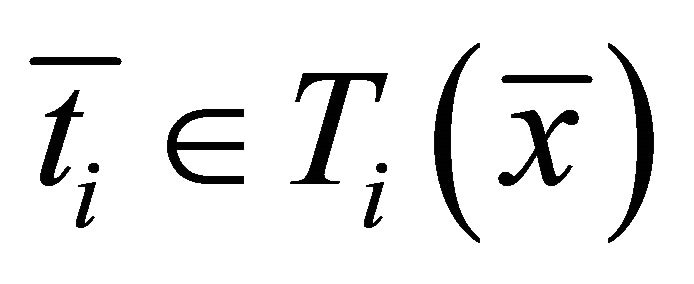 and
and
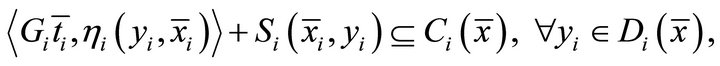 (1.1)
(1.1)
2) Strong type II system of generalized vector quasivariational-like inequalities which is to find 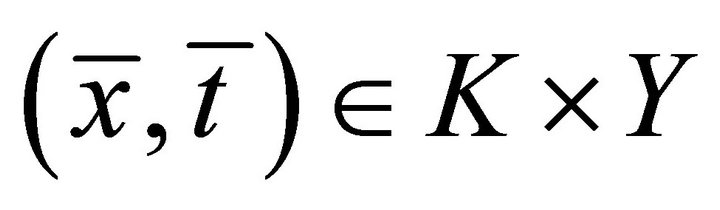 such that
such that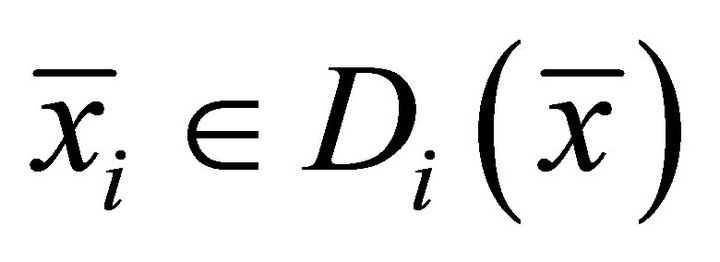 ,
, 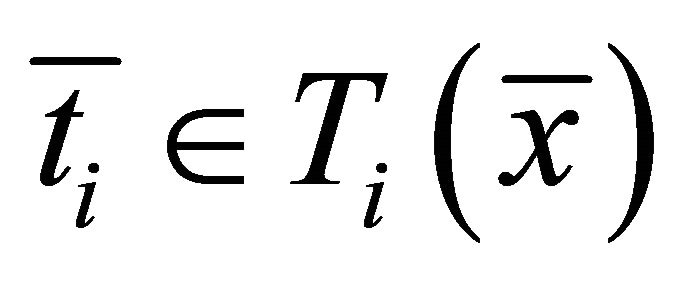 and
and
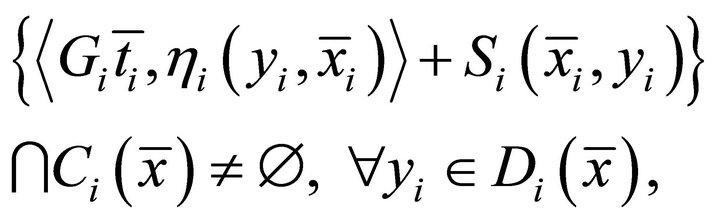 (1.2)
(1.2)
3) Weak type I system of generalized vector quasivariational-like inequalities which is to find 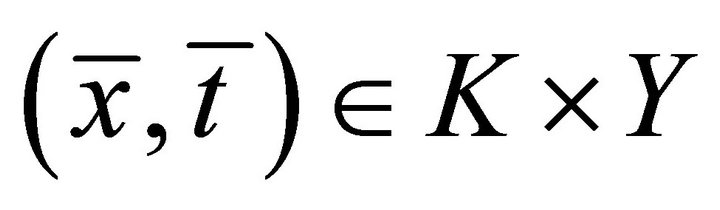 such that
such that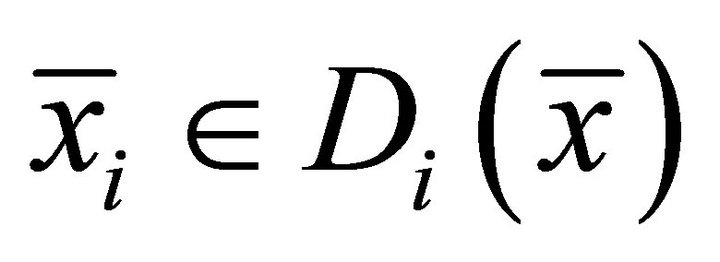 ,
, 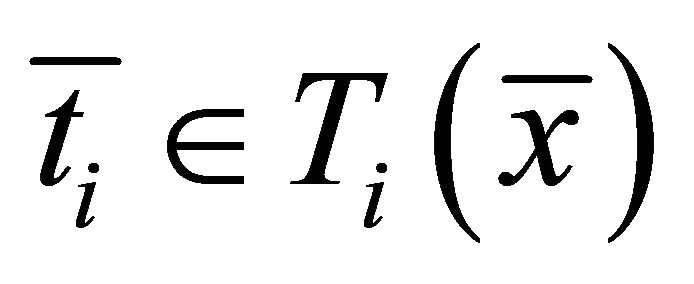 and
and
 (1.3)
(1.3)
4) Weak type II system of generalized vector quasivariational-like inequalities which is to find  such that
such that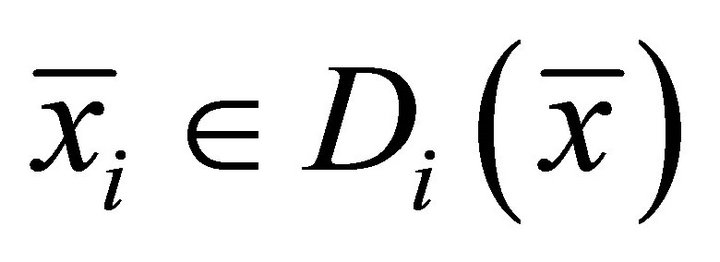 ,
, 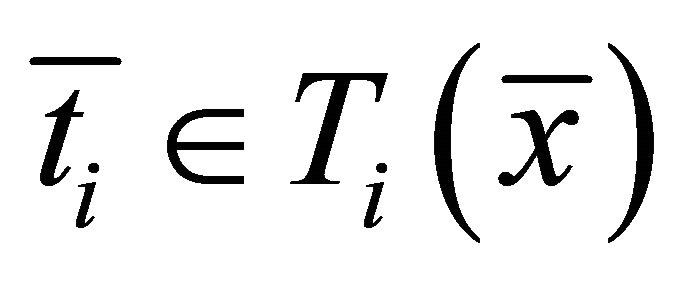 and
and
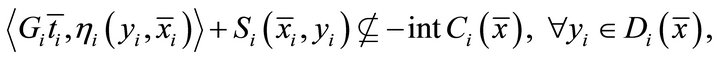 (1.4)
(1.4)
where 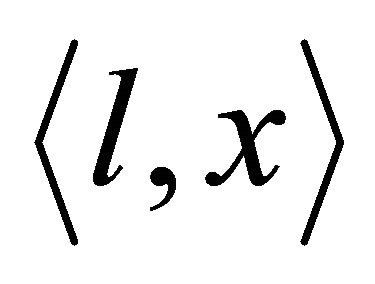 denotes the evaluation of
denotes the evaluation of  at
at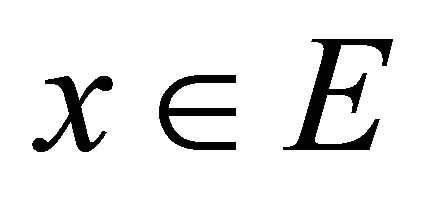 . By the corollary of the Schaefer [3],
. By the corollary of the Schaefer [3], 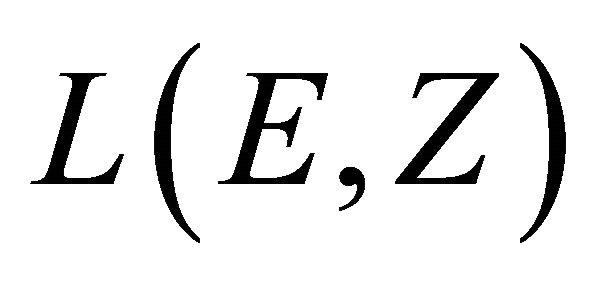 becomes a l.c.s.. By Ding and Tarafdar [4], the bilinear map
becomes a l.c.s.. By Ding and Tarafdar [4], the bilinear map 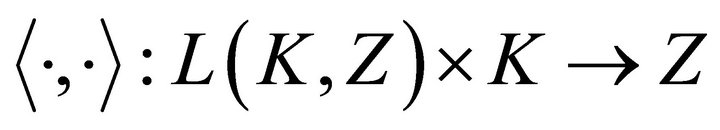 is continuous.
is continuous.
The following problems are the special cases of above four kinds of systems of generalized vector quasi-variational-like inequalities.
The above system of generalized vector quasi-variational-like inequalities encompass many models of system of variational inequalities. The following problems are the special cases of problem (1.4).
1) If for each 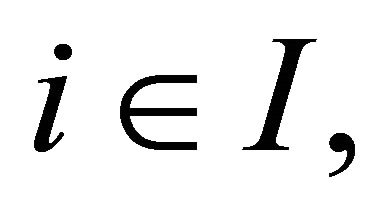 let
let 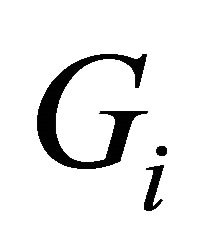 be an identity mapping,
be an identity mapping,  , problem (1.4) reduces to the system of generalized quasi-variational-like inequalities of finding
, problem (1.4) reduces to the system of generalized quasi-variational-like inequalities of finding 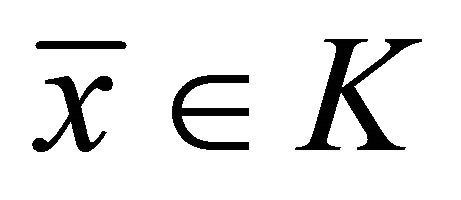 such that for each
such that for each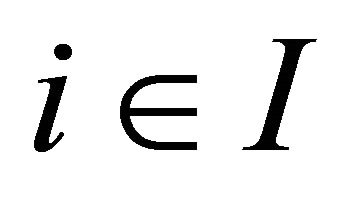 ,
, 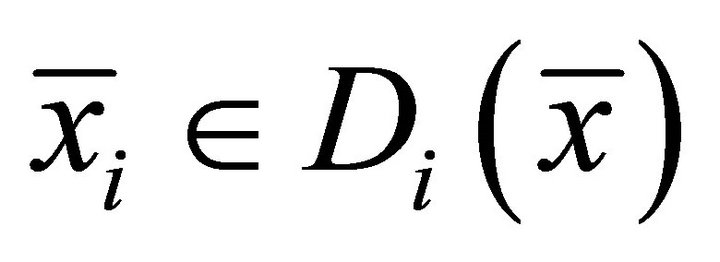 and
and
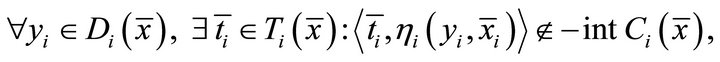 (1.5)
(1.5)
which was introduced and studied by Peng [1].
2) If for each  let
let  be an identity mapping,
be an identity mapping,  and
and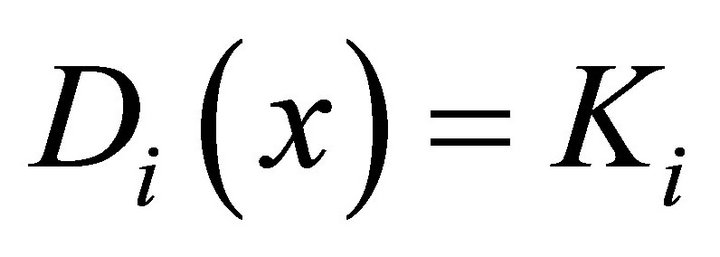 , problem (1.5) reduces to the system of generalized variational-like inequalities of finding
, problem (1.5) reduces to the system of generalized variational-like inequalities of finding 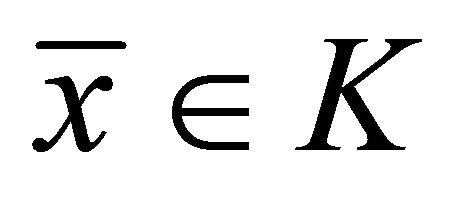 such that for each
such that for each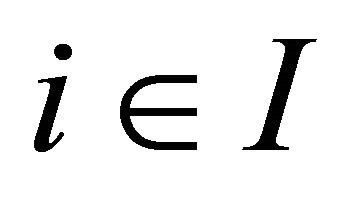 ,
,  and
and
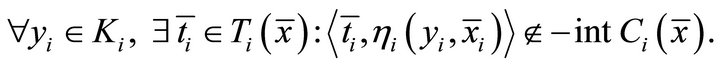 (1.6)
(1.6)
In addition, let 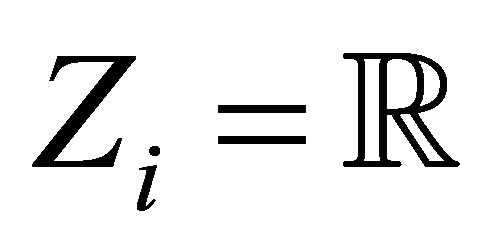 and let
and let  for all
for all , then problem (1.5) reduces to the system of generalized vector quasi-variational inequalities studied by Ansari and Yao [5].
, then problem (1.5) reduces to the system of generalized vector quasi-variational inequalities studied by Ansari and Yao [5].
3) If for each 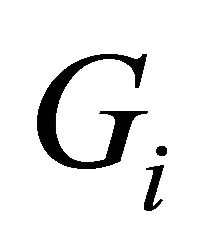
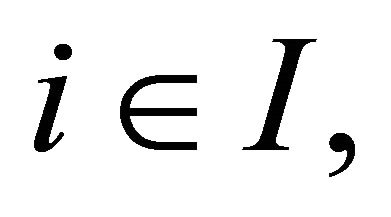 be an identity mapping,
be an identity mapping, 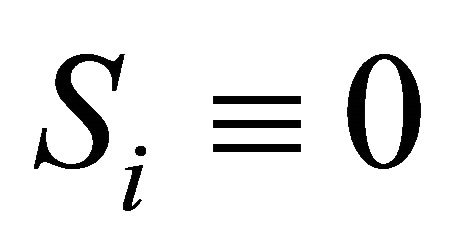 ,
, 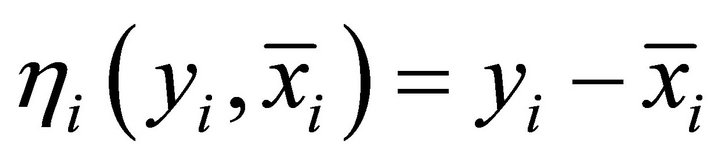 and
and 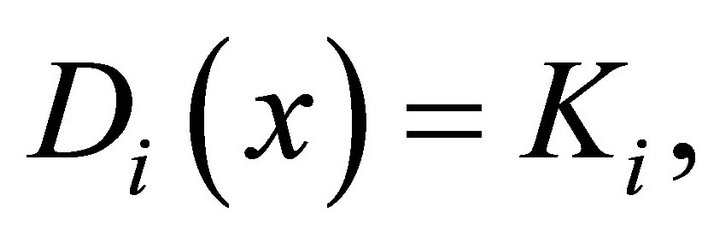 then problem (1.5) reduces to the system of generalized vector variational inequalities of finding
then problem (1.5) reduces to the system of generalized vector variational inequalities of finding  such that for each
such that for each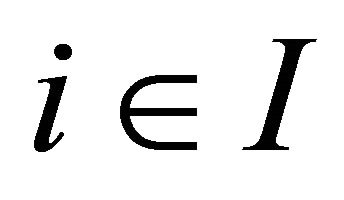 ,
, 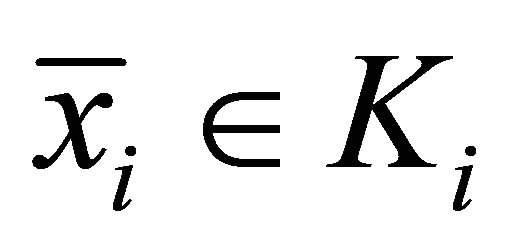 and
and
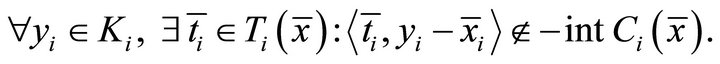 (1.7)
(1.7)
4) If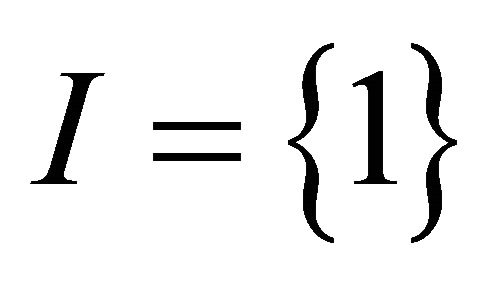 , problem (1.4) reduces to generalized vector quasi-variational-like inequalities of finding
, problem (1.4) reduces to generalized vector quasi-variational-like inequalities of finding 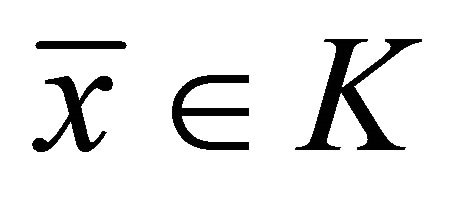 such that
such that 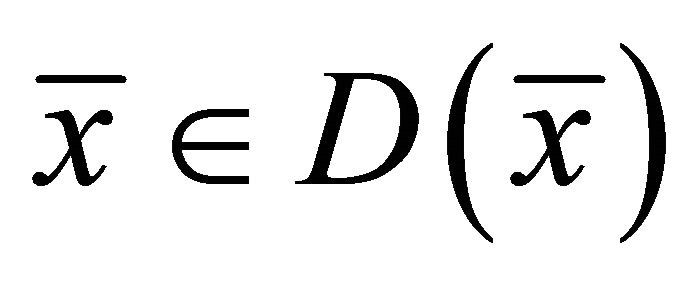 and
and
 (1.8)
(1.8)
such type of problem studied in [6-10].
5) If 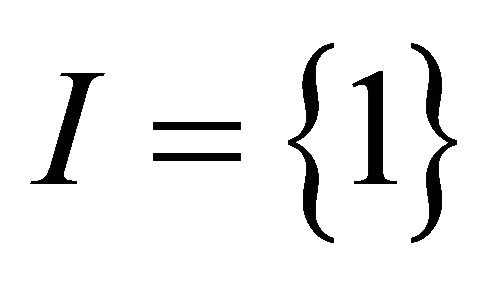 and
and 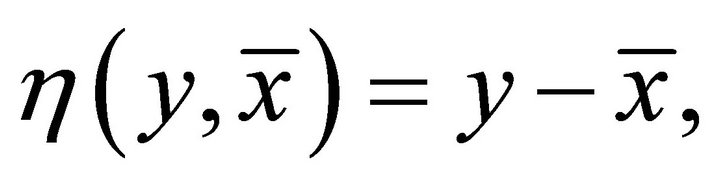
 is single valued mapping,
is single valued mapping,  be an identity mapping,
be an identity mapping, 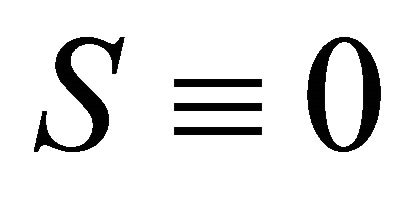 , and
, and  for all
for all 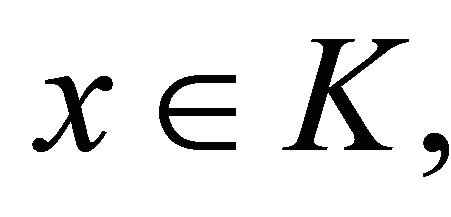 then problem (1.4) reduces to classical variational inequality problem of finding
then problem (1.4) reduces to classical variational inequality problem of finding 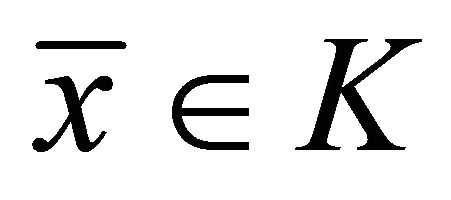 such that
such that 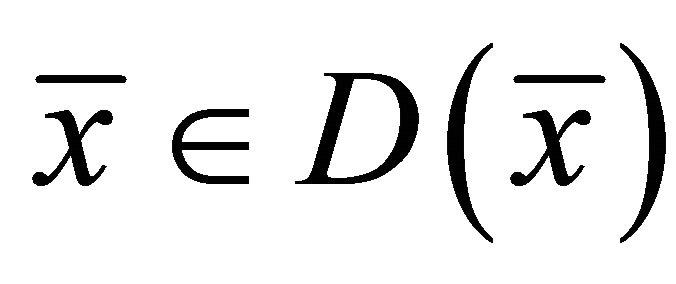 and
and
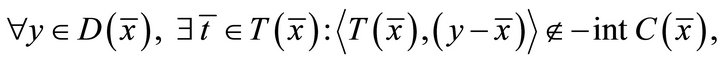 (1.9)
(1.9)
which was introduced and studied by Hartman and Stampacchia [11].
2. Preliminaries
Definition 2.1. [12] Let  and
and  be two t.v.s. and
be two t.v.s. and 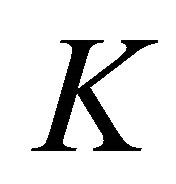 be a convex subset of t.v.s.
be a convex subset of t.v.s. . Let
. Let 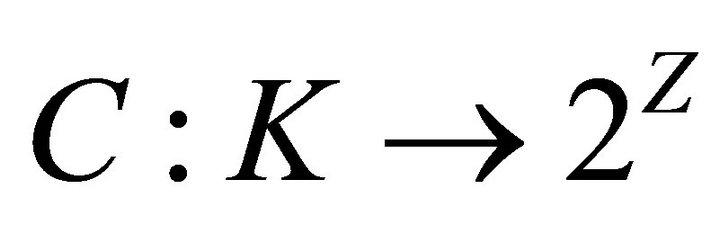 and
and
 be two set-valued mappings. Assume given any finite subset
be two set-valued mappings. Assume given any finite subset  in
in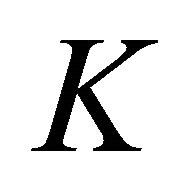 , any
, any
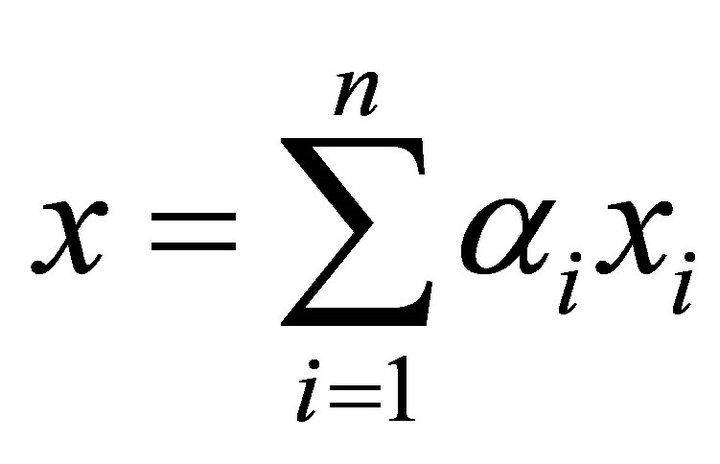 , with
, with 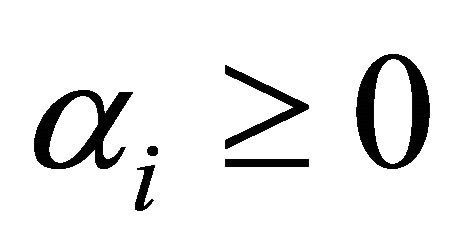 for
for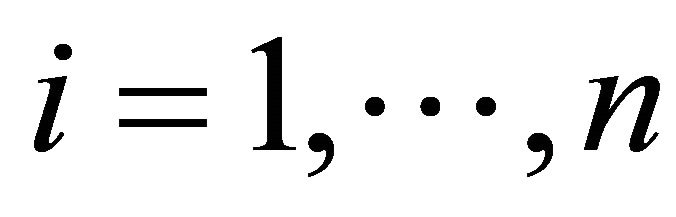 , and
, and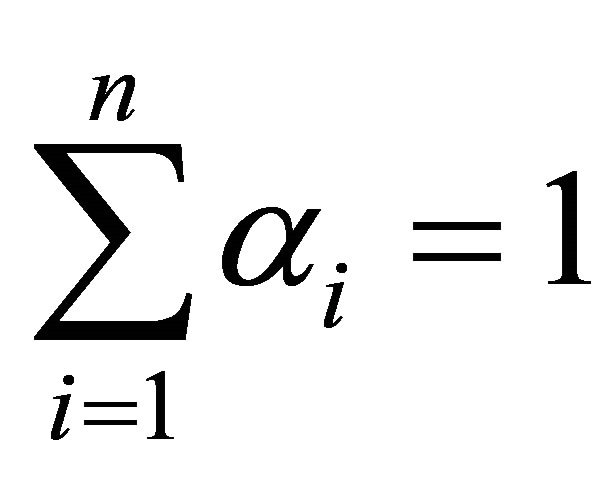 .
.
Then, 1)  is said to be strong Type I C-diagonally quasiconvex (SIC-DQC, in short) in the second argument if for some
is said to be strong Type I C-diagonally quasiconvex (SIC-DQC, in short) in the second argument if for some ,
,
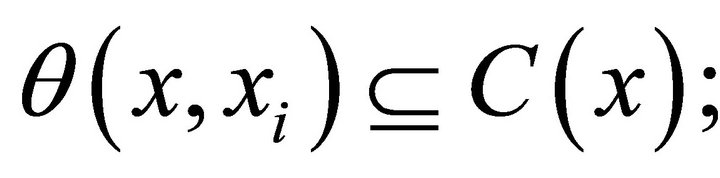
2)  is said to be strong Type II C-diagonally quasiconvex (SIIC-DQC, in short) in the second argument if for some
is said to be strong Type II C-diagonally quasiconvex (SIIC-DQC, in short) in the second argument if for some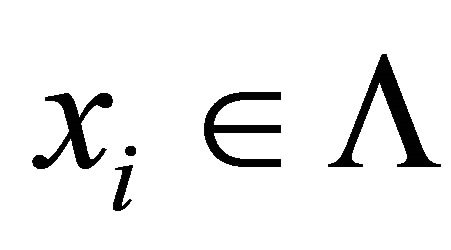 ,
,
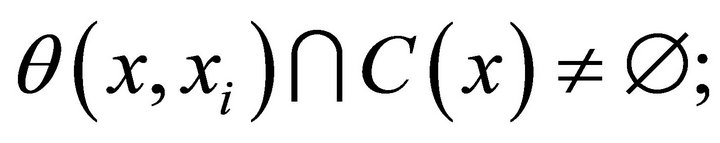
3)  is said to be weak Type I C-diagonally quasiconvex (WIC-DQC, in short) in the second argument if for some
is said to be weak Type I C-diagonally quasiconvex (WIC-DQC, in short) in the second argument if for some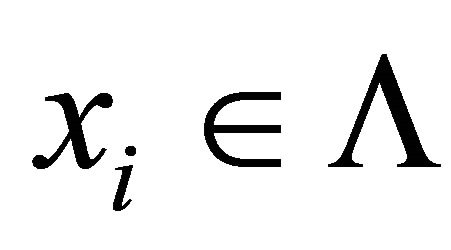 ,
,

4)  is said to be weak Type II C-diagonally quasiconvex (WIIC-DQC, in short) in the second argument if for some
is said to be weak Type II C-diagonally quasiconvex (WIIC-DQC, in short) in the second argument if for some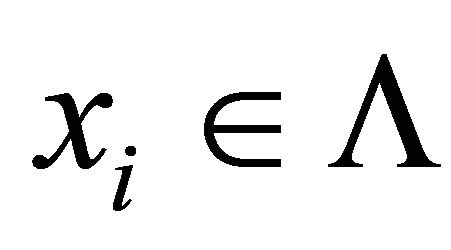 ,
,
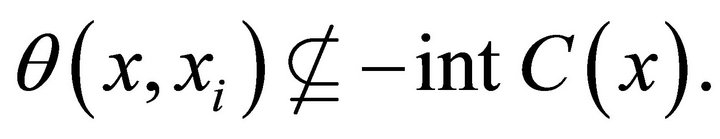
It is easy to verify that the following proposition, 1) SIC-DQC implies SIIC-DQC; 2) SIIC-DQC implies WIC-DQC; 3) WIC-DQC implies WIIC-DQC. The converse is not true. Following example shows that the con0 verse is not true.
Example 2.1. Let 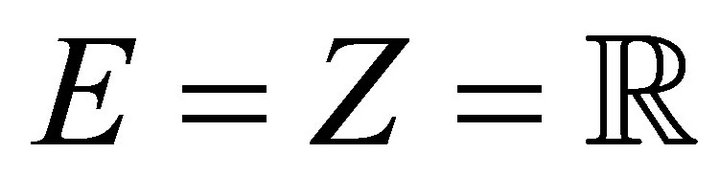 and
and  .
.
1) If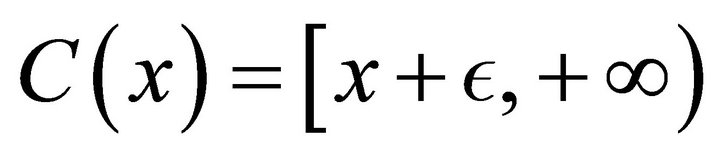 . Then
. Then  is SIIC-DQC, but it is not SIC-DQC.
is SIIC-DQC, but it is not SIC-DQC.
2) If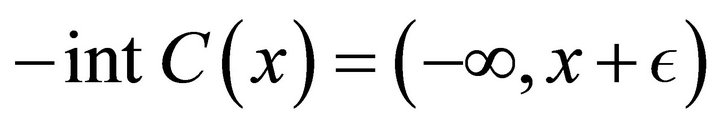 . Then
. Then  is WIICDQC, but it is not WIC-DQC.
is WIICDQC, but it is not WIC-DQC.
Definition 2.2. [13] Let 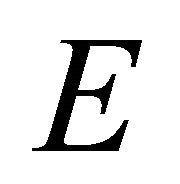 and
and  be two t.v.s. and
be two t.v.s. and 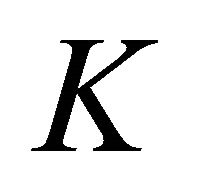 be a convex subset of t.v.s.
be a convex subset of t.v.s.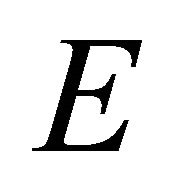 . A mapping
. A mapping 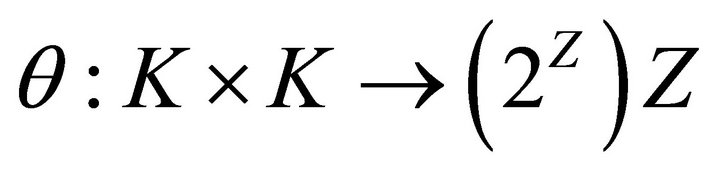 is called (generalized) vector 0- diagonally convex if for any finite subset
is called (generalized) vector 0- diagonally convex if for any finite subset
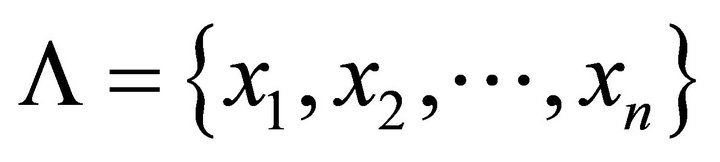 of
of 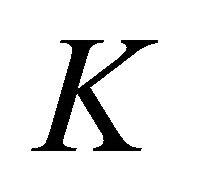 and any
and any 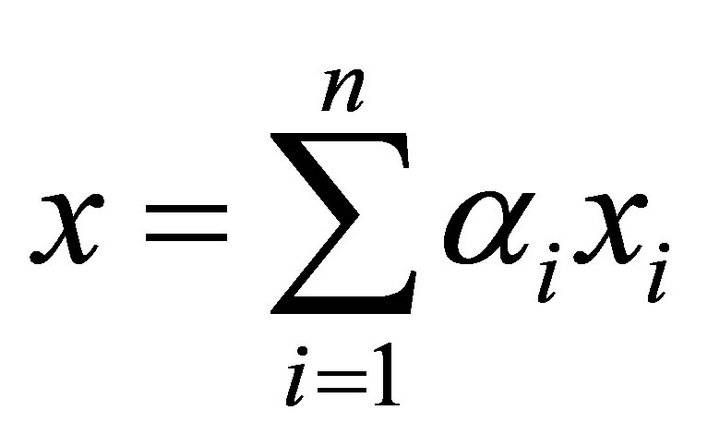 with
with 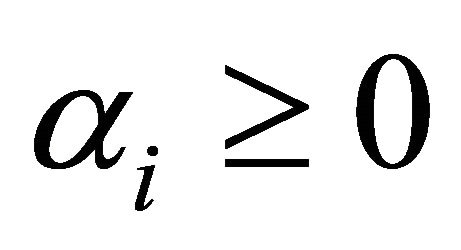 for
for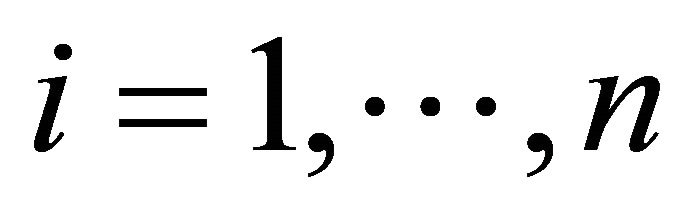 , and
, and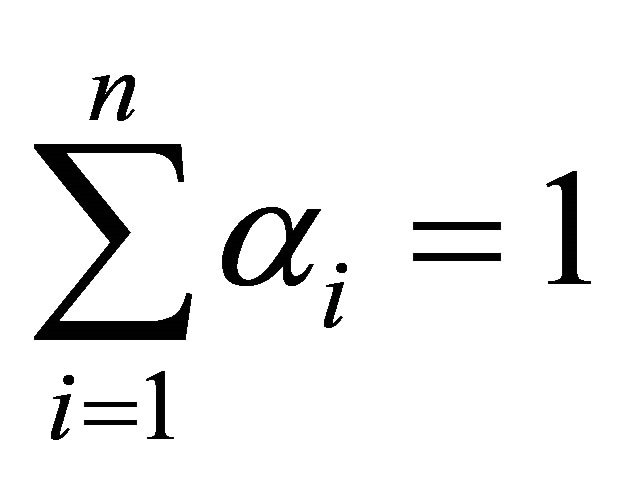 ,
,
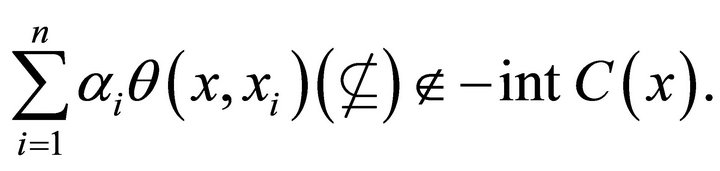
Definition 2.3. [14] Let 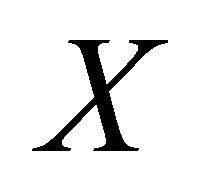 and
and  be two topological spaces and
be two topological spaces and  be a set-valued mapping. Then1)
be a set-valued mapping. Then1) 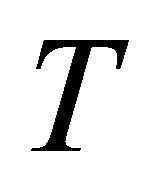 is said to have open lower sections if the set
is said to have open lower sections if the set  is open in
is open in 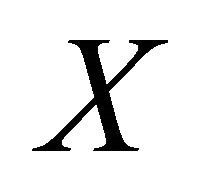 for every
for every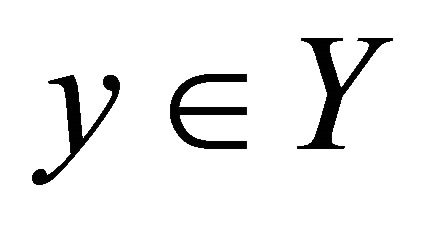 ;
;
2) 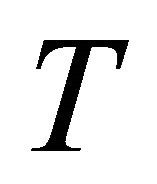 is said to be upper semicontinuous (u.s.c., in short) if for each
is said to be upper semicontinuous (u.s.c., in short) if for each 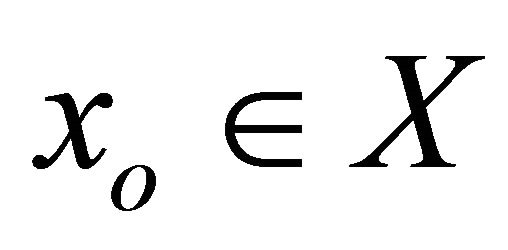 and each open set
and each open set 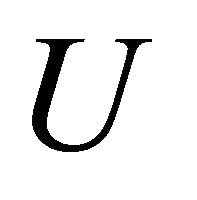 in
in 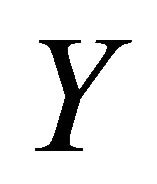 with
with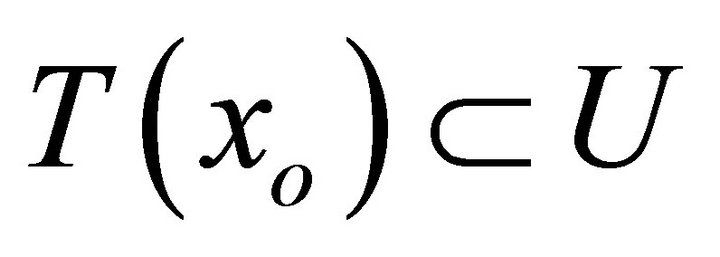 , there exists an open neighborhood
, there exists an open neighborhood 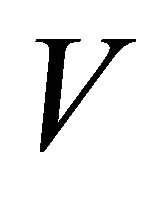 of
of 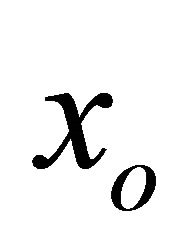 in
in 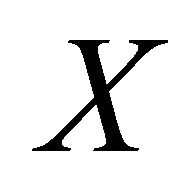 such that
such that 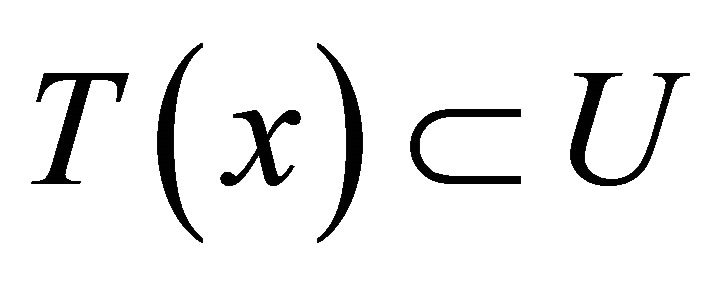 for each
for each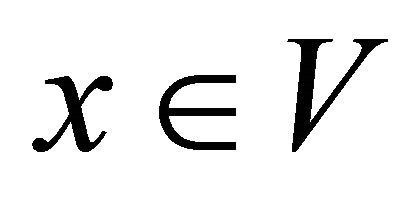 ;
;
3)  is said to be lower semicontinuous (l.s.c., in short) if for each
is said to be lower semicontinuous (l.s.c., in short) if for each  and each open set
and each open set 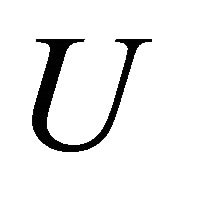 in
in 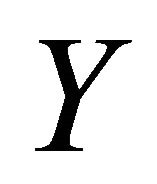 with
with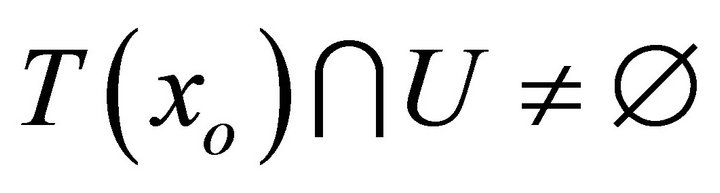 , there exists an open neighborhood
, there exists an open neighborhood 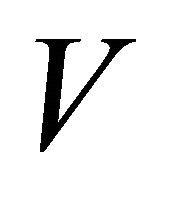 of
of 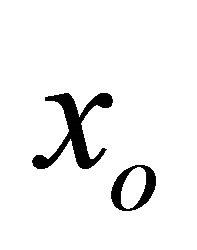 in
in 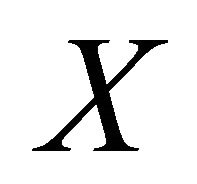 such that
such that 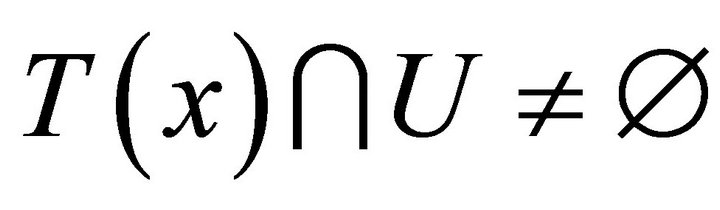 for each
for each ;
;
4) 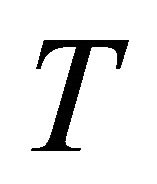 is said to be continuous if it is both upper and lower semicontinuous;
is said to be continuous if it is both upper and lower semicontinuous;
5) 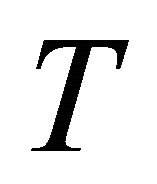 is said to be closed if for any net
is said to be closed if for any net 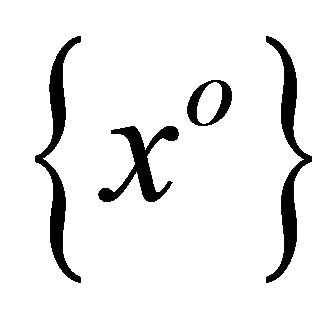 in
in 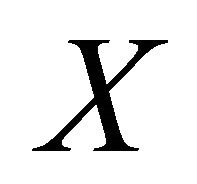 such that
such that  and any net
and any net  in
in  such that
such that  and
and  for any
for any , we have
, we have 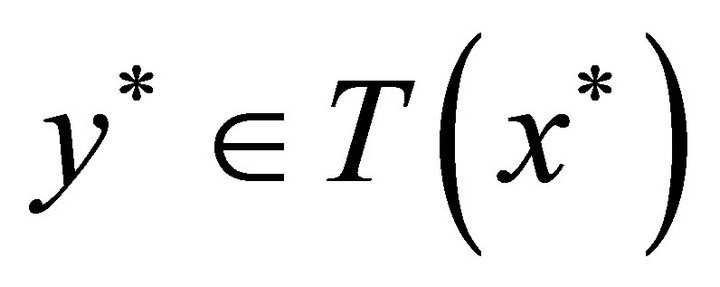 .
.
Lemma 2.1. [15] Let 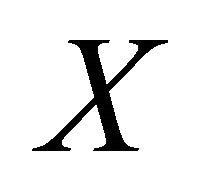 and
and 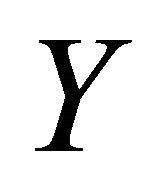 be two topological spaces. If
be two topological spaces. If  is u.s.c. set-valued mapping with closed values, then
is u.s.c. set-valued mapping with closed values, then 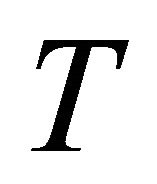 is closed.
is closed.
Lemma 2.2. [16] Let  and
and 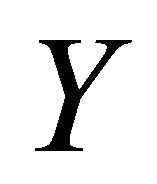 be two topological spaces and
be two topological spaces and 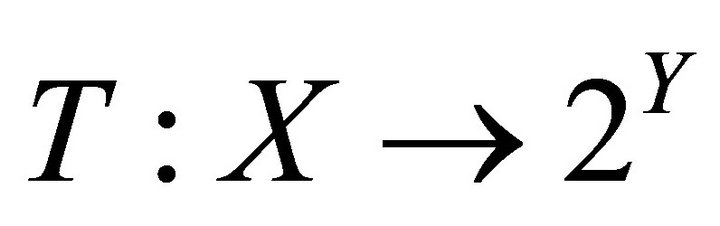 is u.s.c. mapping with compact values. Suppose
is u.s.c. mapping with compact values. Suppose 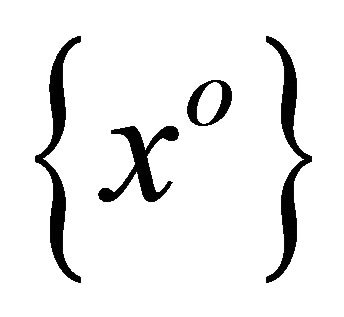 is a net in
is a net in 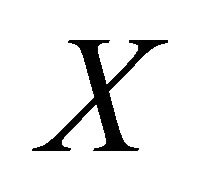 such that
such that
 . If
. If  for each
for each , then there are a
, then there are a 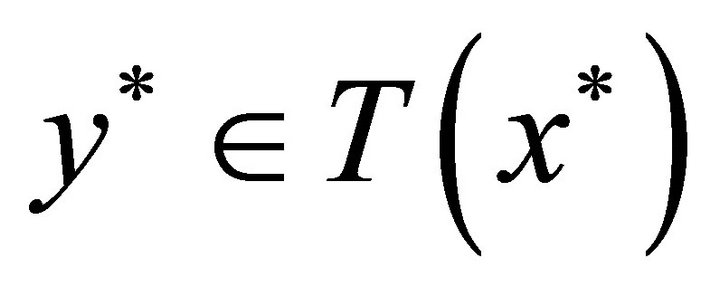 and a subnet
and a subnet 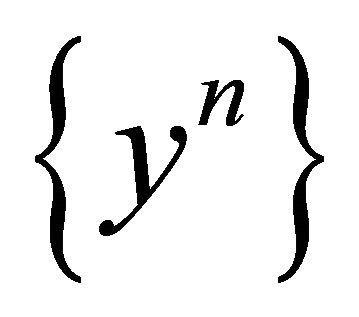 of
of 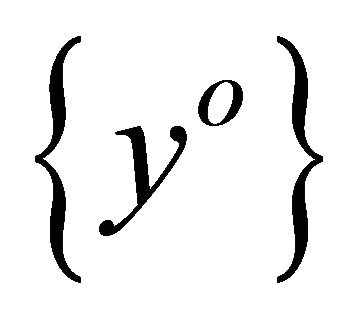 such that
such that
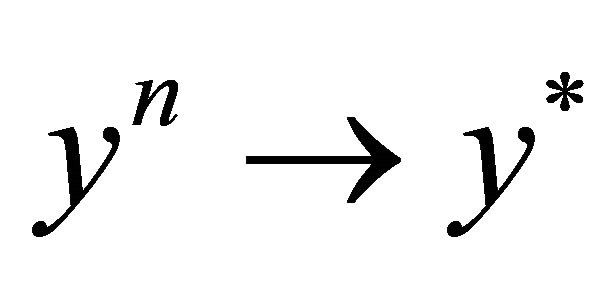 .
.
Lemma 2.3. [17] Let 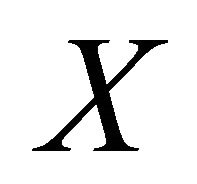 and
and  be two topological spaces. Suppose that
be two topological spaces. Suppose that 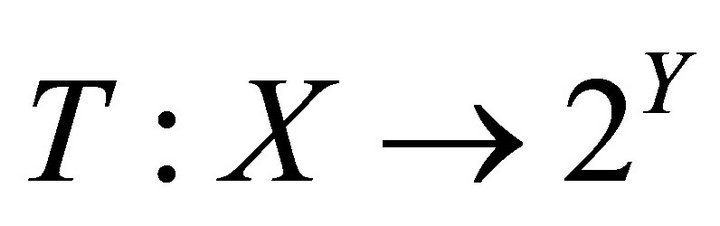 and
and 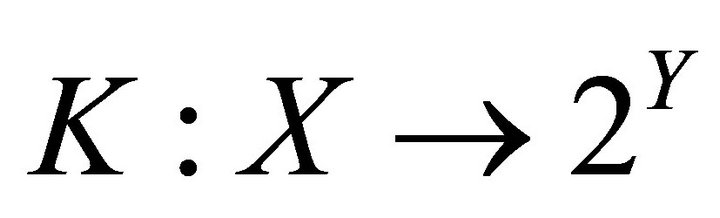 are set-valued mappings having open lower sections, then 1) A set-valued mapping
are set-valued mappings having open lower sections, then 1) A set-valued mapping  defined by, for each
defined by, for each ,
, 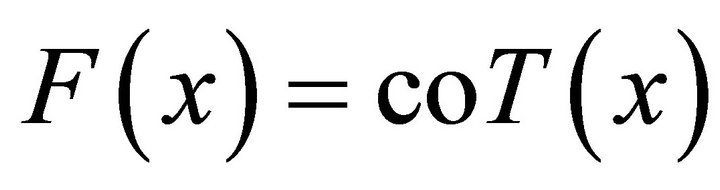 has open lower sections;
has open lower sections;
2) A set-valued mapping  defined by, for each
defined by, for each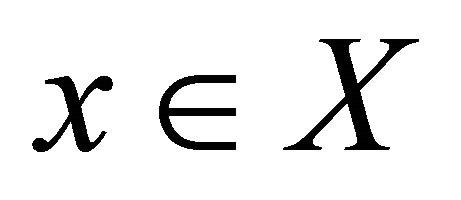 ,
, 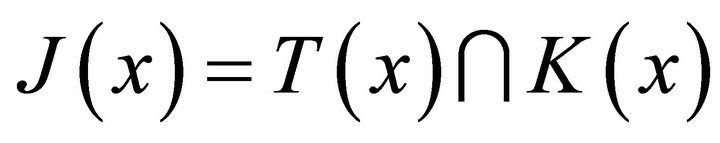 has open lower sections.
has open lower sections.
For each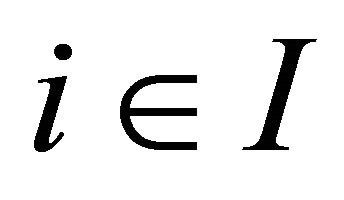 ,
, 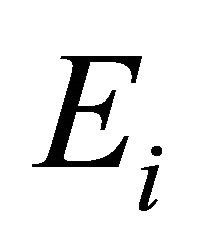 a Hausdorff t.v.s. Let
a Hausdorff t.v.s. Let  be a family of nonempty compact convex subsets with each
be a family of nonempty compact convex subsets with each  in
in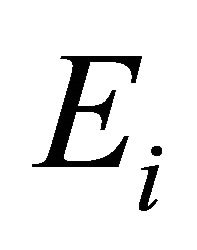 . Let
. Let 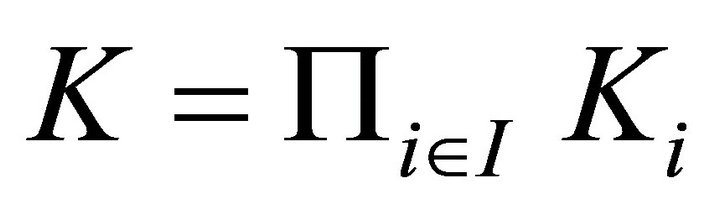 and
and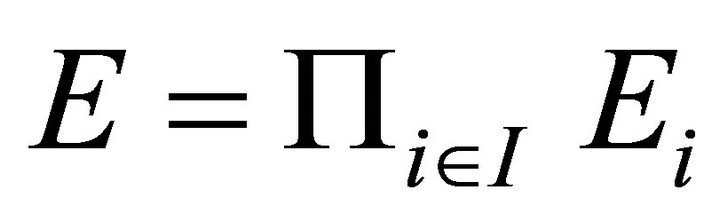 . The following system of fixed-point theorem is needed in this paper.
. The following system of fixed-point theorem is needed in this paper.
Lemma 2.4. [18] For each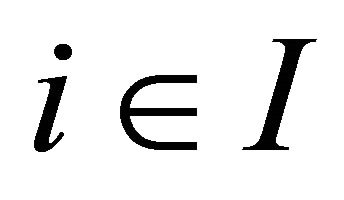 , let
, let 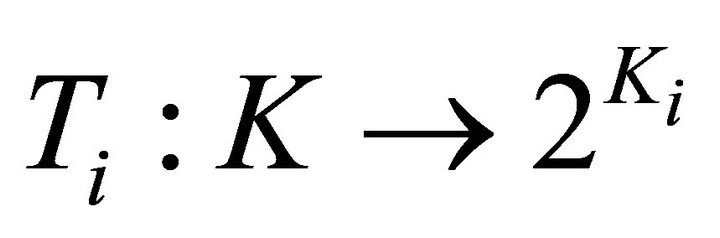 be a set-valued mapping. Assume that the following conditions hold.
be a set-valued mapping. Assume that the following conditions hold.
1) For each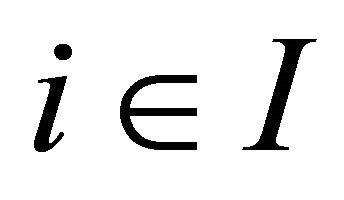 ,
, 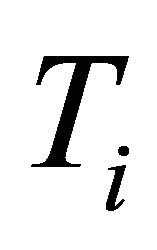 is convex set-valued mapping;
is convex set-valued mapping;
2) 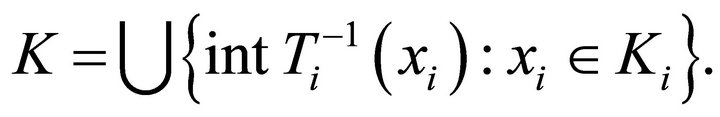
Then there exist  such that
such that
 , that is,
, that is, 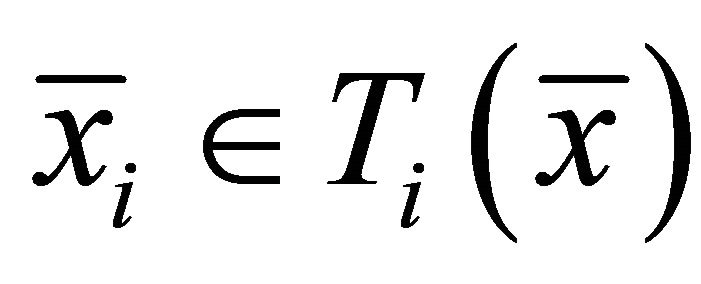 for each
for each
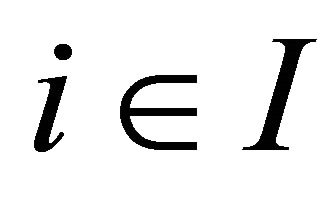 , where
, where 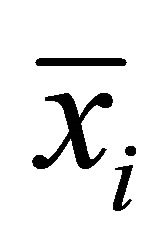 is the projection of
is the projection of 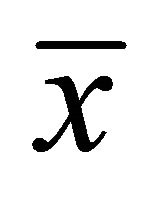 onto
onto 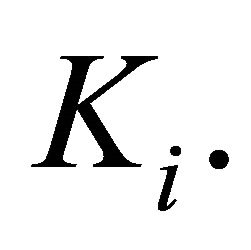
3. Main Results
Theorem 3.1. For each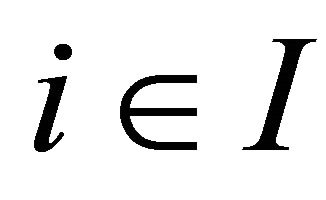 , let
, let 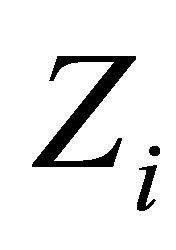 be a l.c.s.,
be a l.c.s., 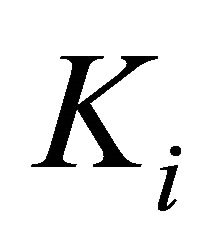 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.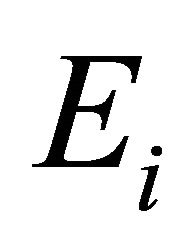 ,
, 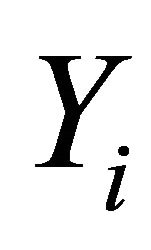 a nonempty compact convex subset of
a nonempty compact convex subset of , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each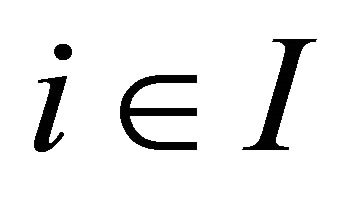 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 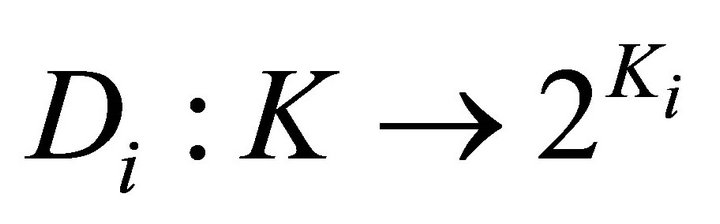 and
and 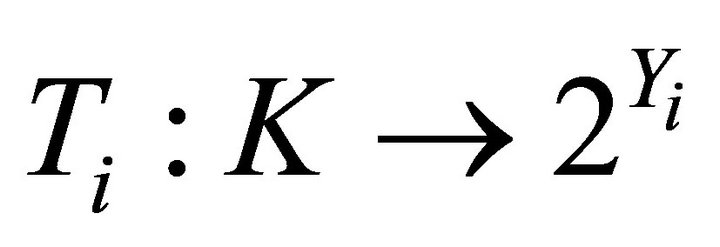 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 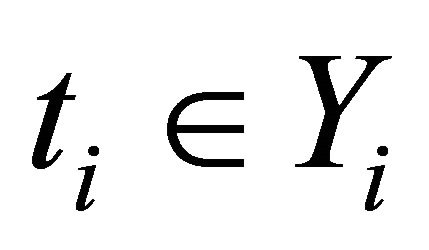 and
and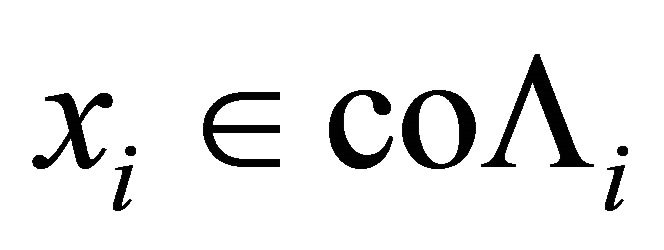 , the mapping
, the mapping
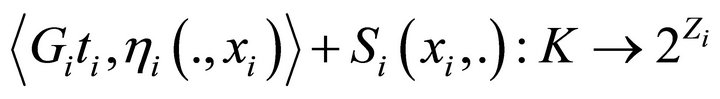 is WIIC-DQC;
is WIIC-DQC;
3) For each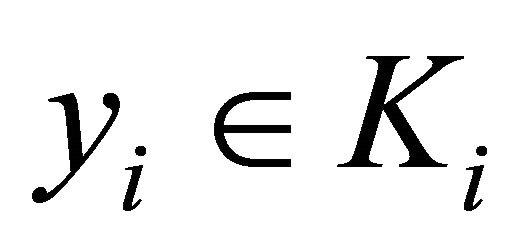 , the set
, the set
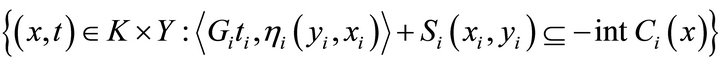
is open.
Then there exist  and
and 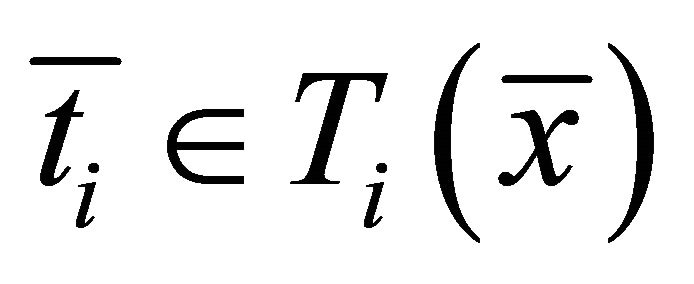 such that
such that
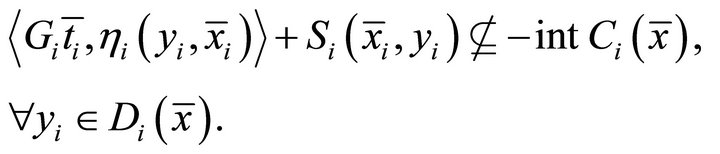
Proof. Define a set-valued mapping 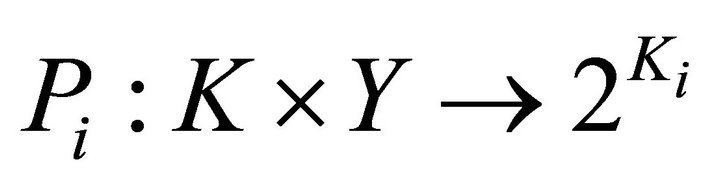 by
by
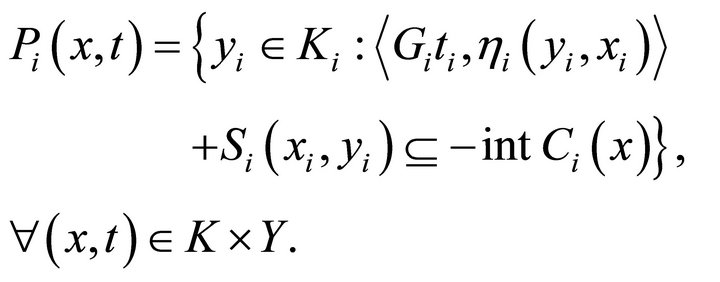
We first prove that 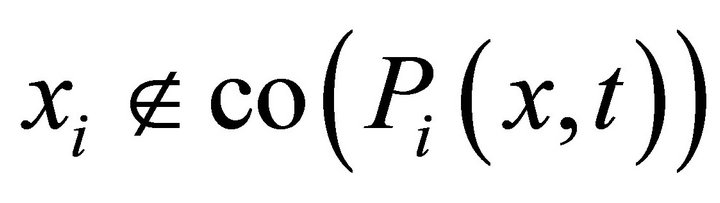 for all
for all
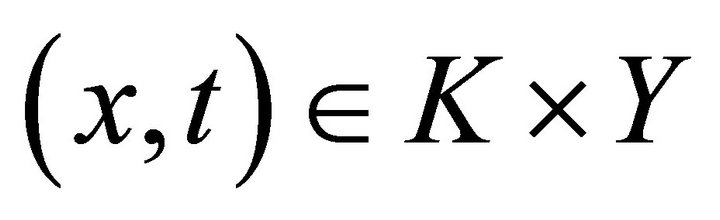 . To see this, suppose, by way of contradiction, that there exist some
. To see this, suppose, by way of contradiction, that there exist some  and some point
and some point 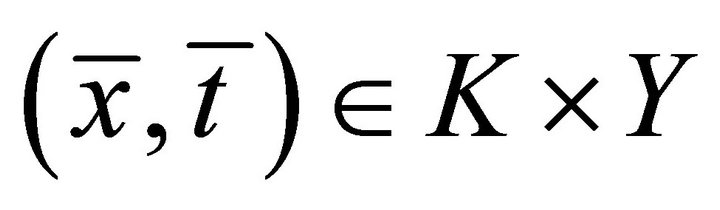 such that
such that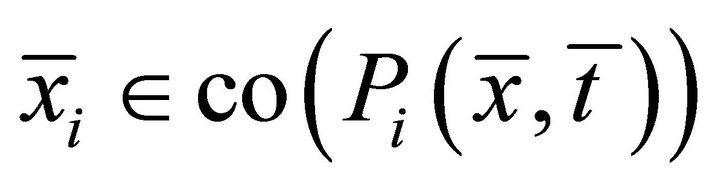 . Then, there exist finite points
. Then, there exist finite points 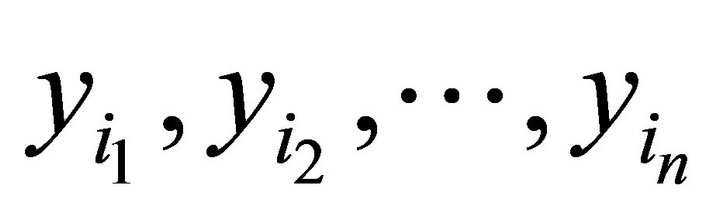 in
in 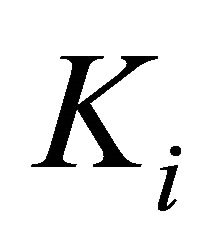 and
and 
with 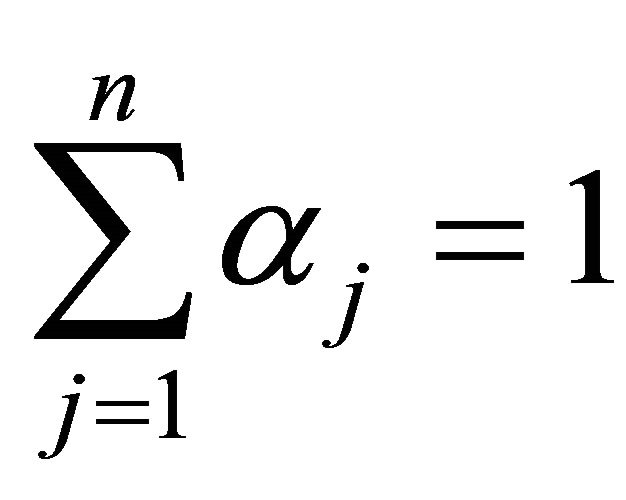 such that
such that 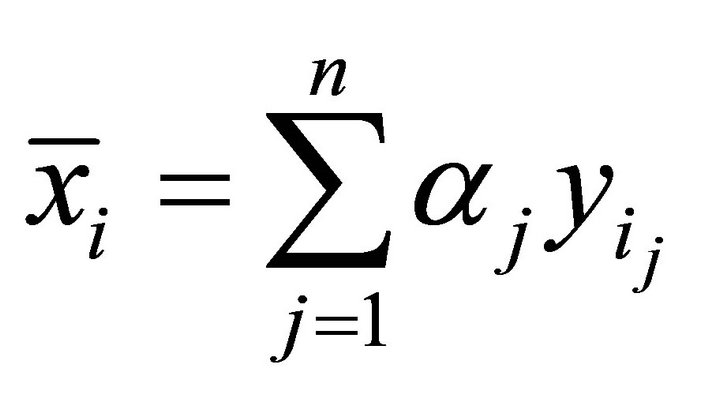 and
and
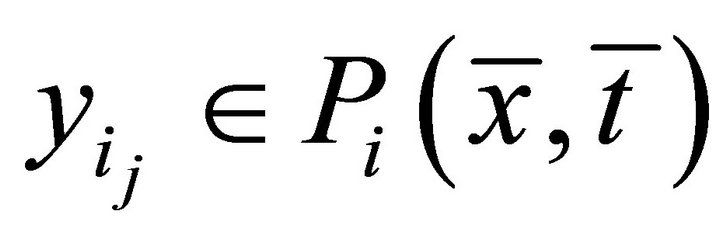 for all
for all  such that
such that
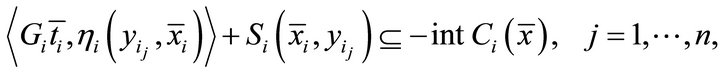
which contradicts the hypothesis 2). Hence, 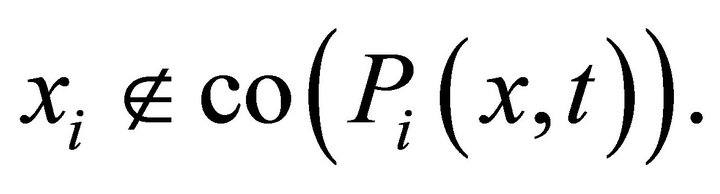
By hypothesis 3), for each 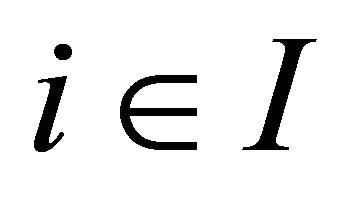 and each
and each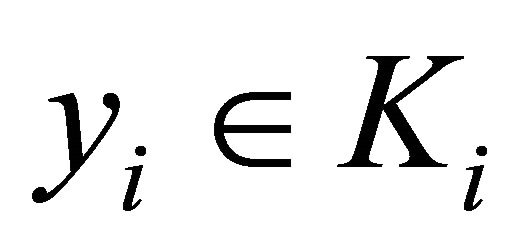 , we known that
, we known that
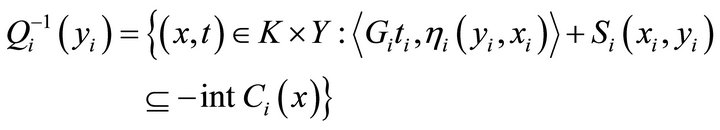
is open and so 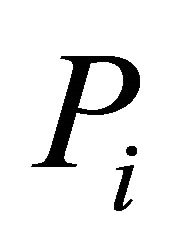 has open lower sections.
has open lower sections.
For each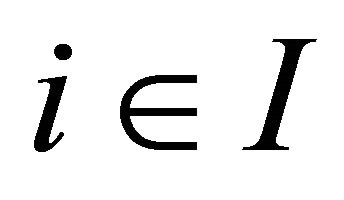 , consider a set-valued mapping
, consider a set-valued mapping 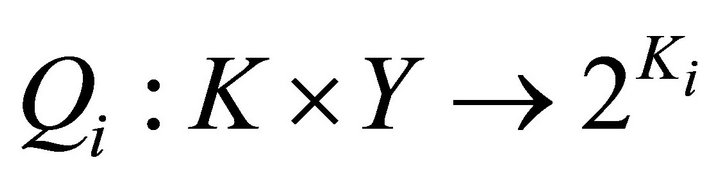 defind by
defind by

Since 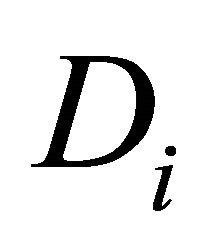 has open lower sections by hypothesis 1), we may apply Lemma 2.3 to assert that the set-valued mapping
has open lower sections by hypothesis 1), we may apply Lemma 2.3 to assert that the set-valued mapping 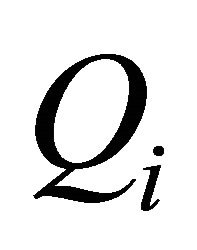 has also open lower sections. Let
has also open lower sections. Let

There are two cases to consider. In the case , we have
, we have
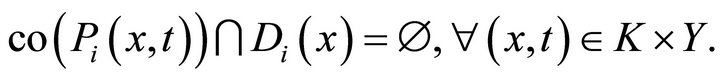
This implies that,  ,
,

On the other hand, by condition 1), and the fact 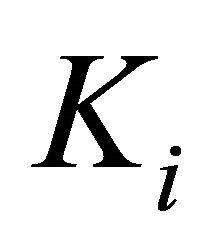 is a compact convex subset of
is a compact convex subset of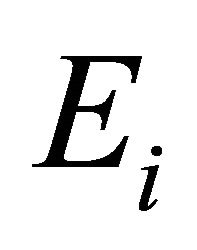 , we can apply Lemma 2.4 to assert the existence of a fixed point
, we can apply Lemma 2.4 to assert the existence of a fixed point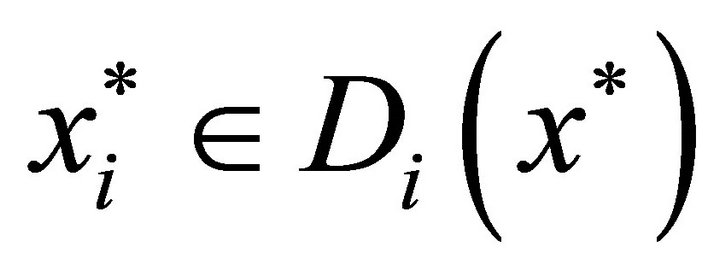 . Since
. Since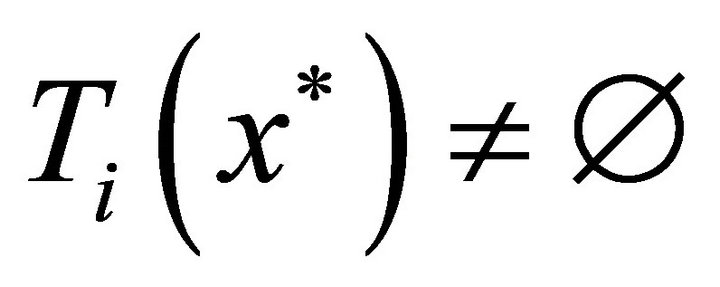 , picking
, picking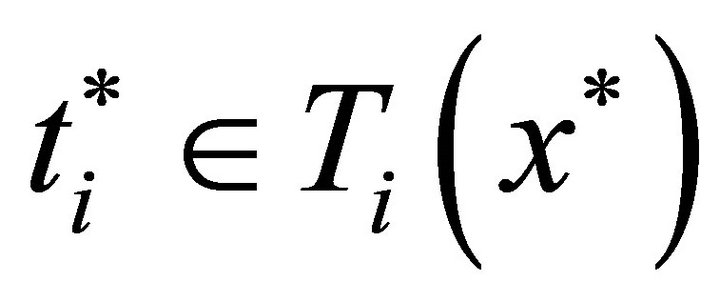 , we have
, we have
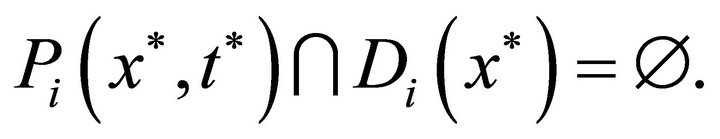
This implies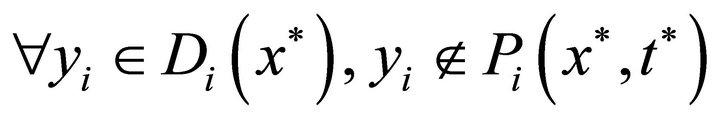 . Hence, in this particular case, the assertion of the theorem holds.
. Hence, in this particular case, the assertion of the theorem holds.
We now consider the case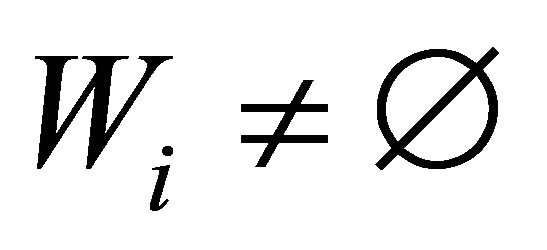 . Define a setvalued mapping
. Define a setvalued mapping 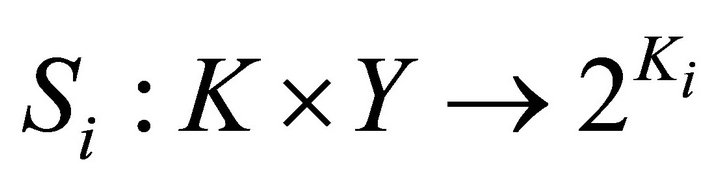 by
by
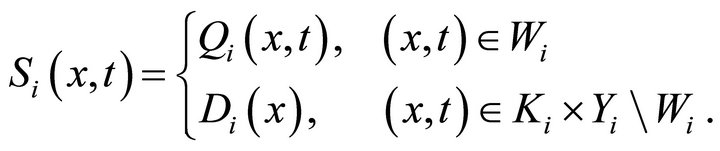
Then, 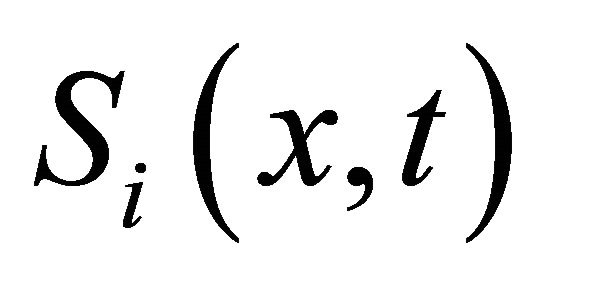 is a convex set-valued mapping and for each
is a convex set-valued mapping and for each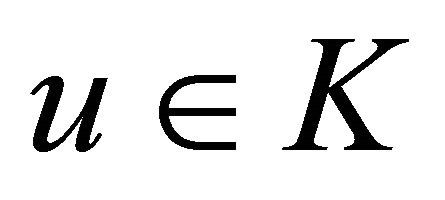 ,
, 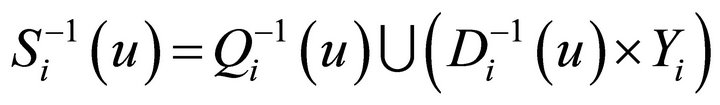 is open. For each
is open. For each , consider the set-valued mapping
, consider the set-valued mapping 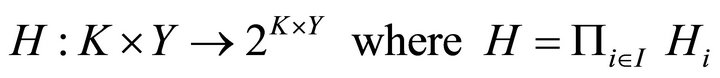 defined by
defined by
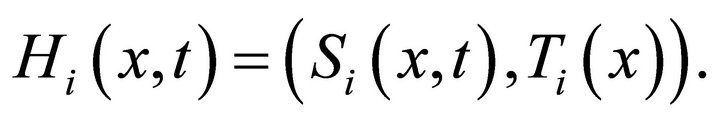
By condition 1) and the properties of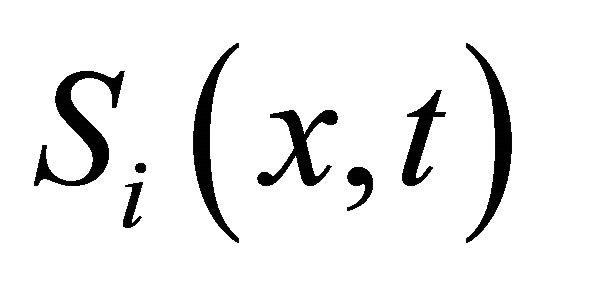 ,
, 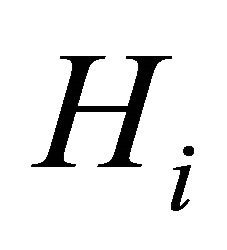 satisfies all the conditions of Lemma 2.4. Thereforethere exists
satisfies all the conditions of Lemma 2.4. Thereforethere exists  such that
such that
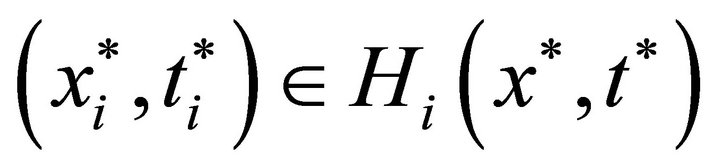 . Suppose that
. Suppose that , then
, then
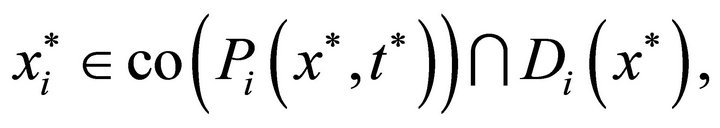
so that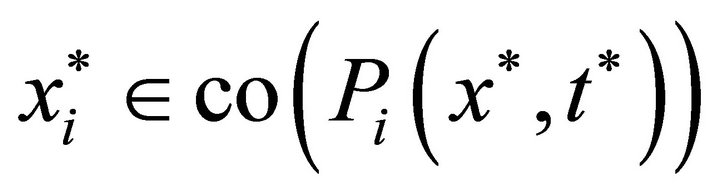 . This is a contradiction.
. This is a contradiction.
Hence, . Therefore,
. Therefore,
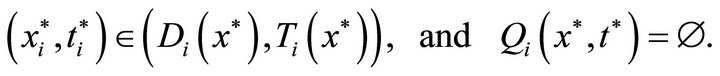
Thus
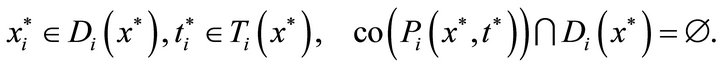
This implies
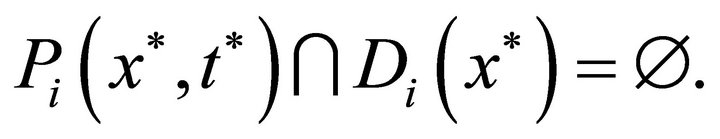
Consequently, the assertion of the theorem holds in this case.
Corollary 3.2. For each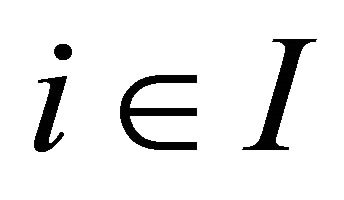 , let
, let 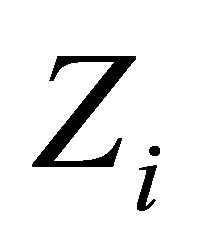 be a l.c.s.,
be a l.c.s., 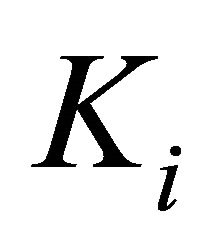 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.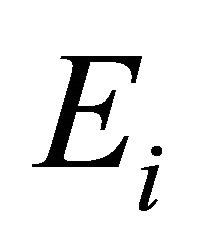 ,
, 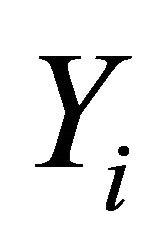 a nonempty compact convex subset of
a nonempty compact convex subset of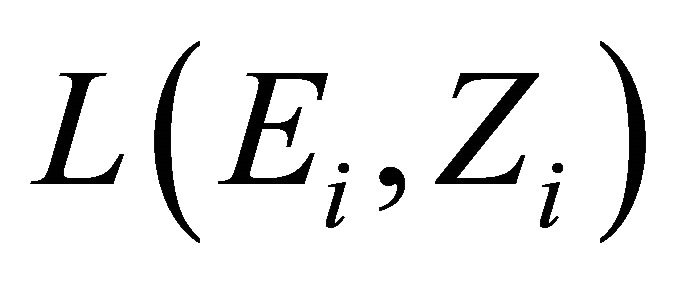 , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each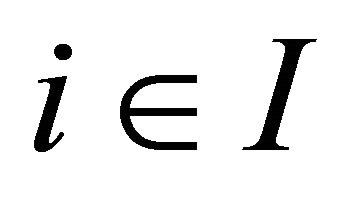 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 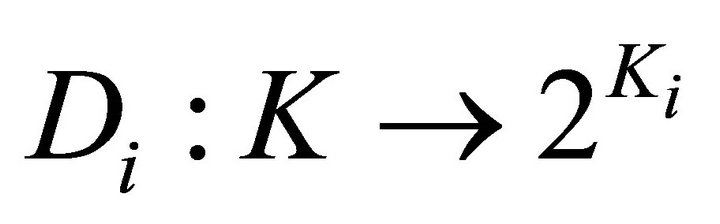 and
and  are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For all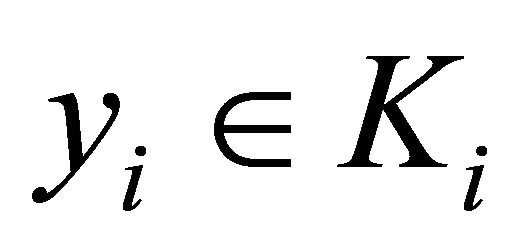 , the mapping
, the mapping
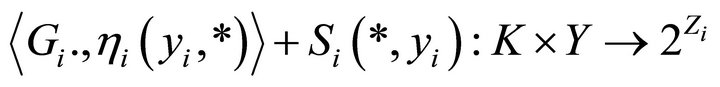 is an u.s.c. setvalued mapping;
is an u.s.c. setvalued mapping;
3) 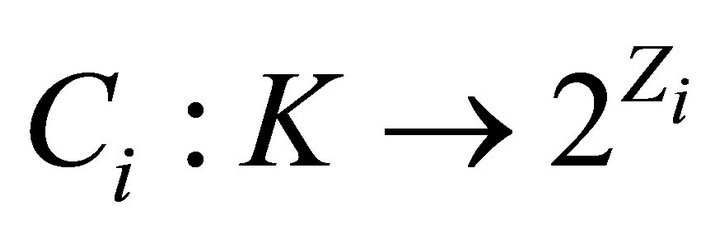 is a convex set-valued mapping with
is a convex set-valued mapping with 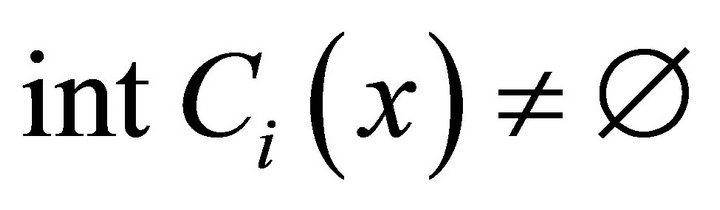 for all
for all ;
;
4) 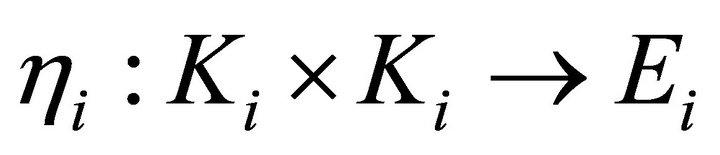 is affine in the first argument and for all
is affine in the first argument and for all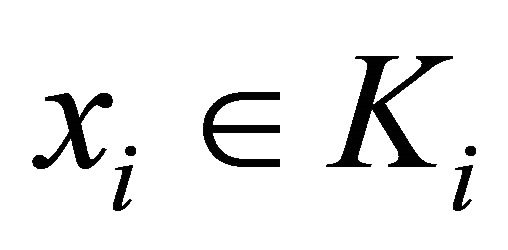 ,
, ;
;
5) 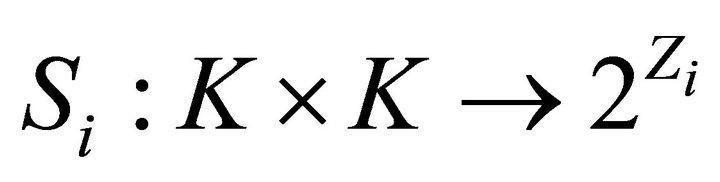 is a generalized vector 0-diagonally convex set-valued mapping;
is a generalized vector 0-diagonally convex set-valued mapping;
6) For a given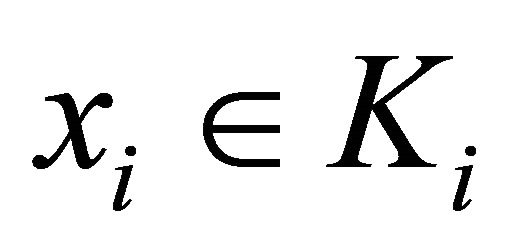 , and a neighborhood
, and a neighborhood 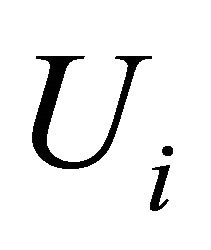 of
of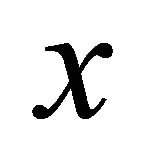 , for all
, for all 

Then there exists 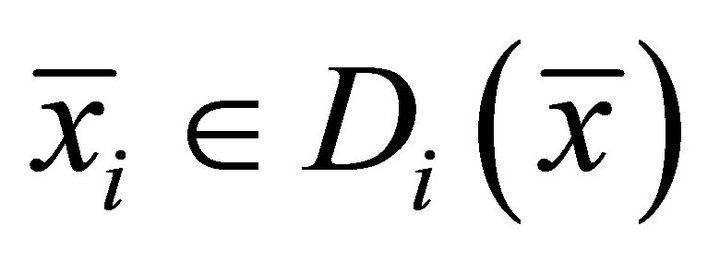 and
and 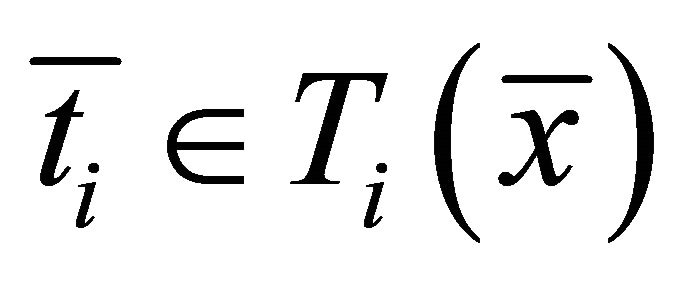 such that
such that

Proof. Define a set-valued mapping 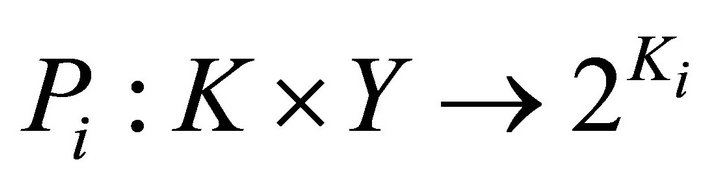 by
by
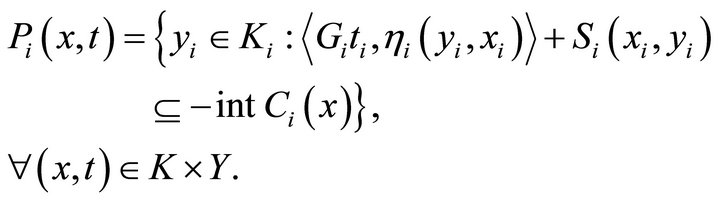
We first prove that 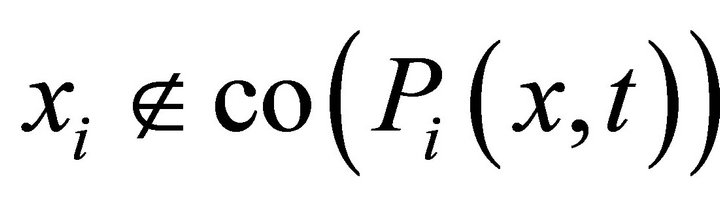 for all
for all 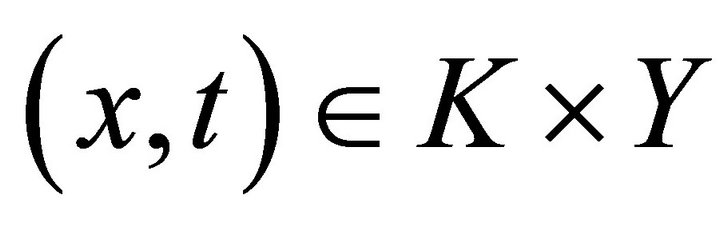 . By contradiction, for each
. By contradiction, for each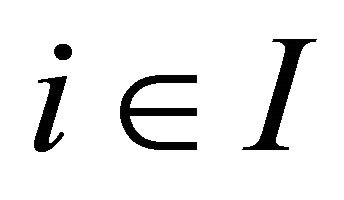 , suppose there exists some point
, suppose there exists some point 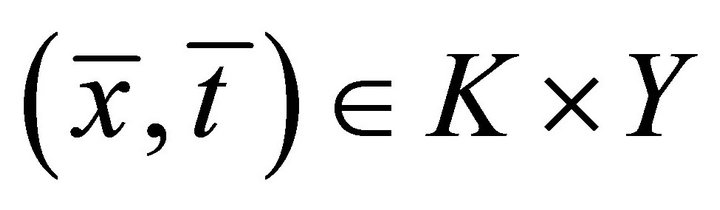 such that
such that 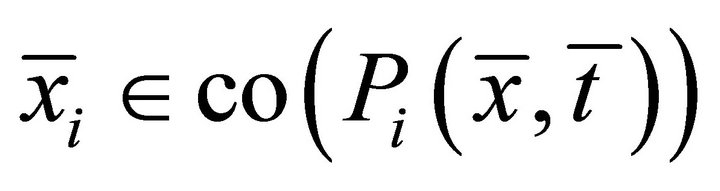 . Then, there exist finite points
. Then, there exist finite points 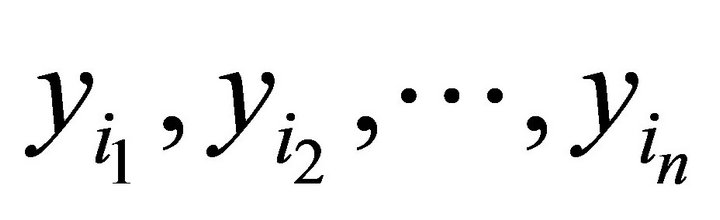 in
in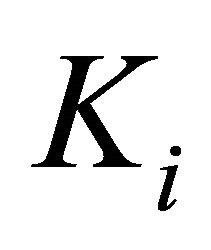 , such that
, such that
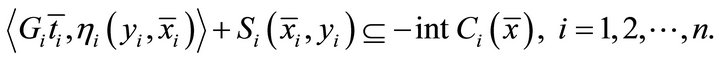
Since 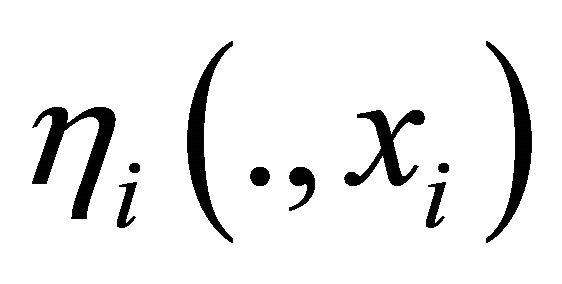 is affine and
is affine and 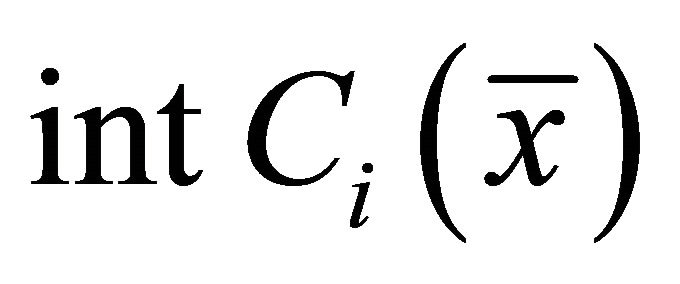 is convexfor
is convexfor 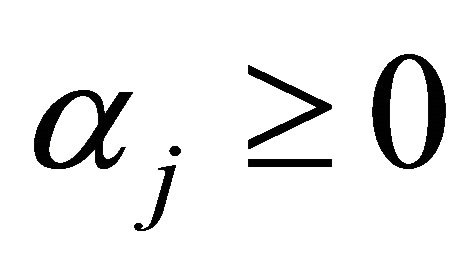 with
with 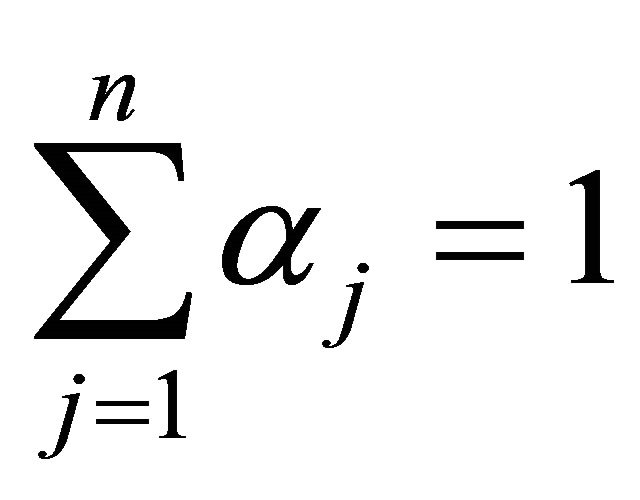 such that
such that 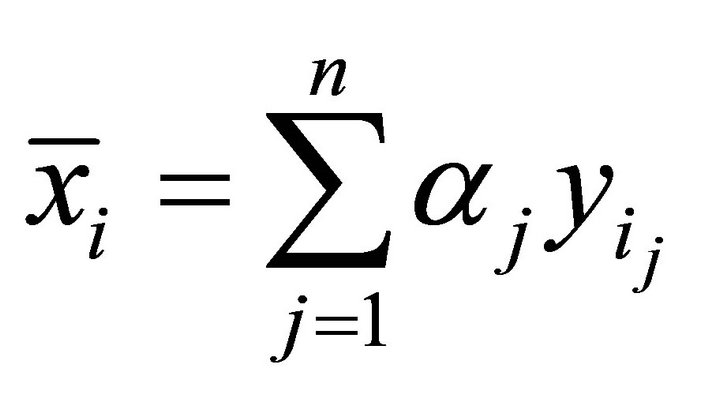
and  for all
for all 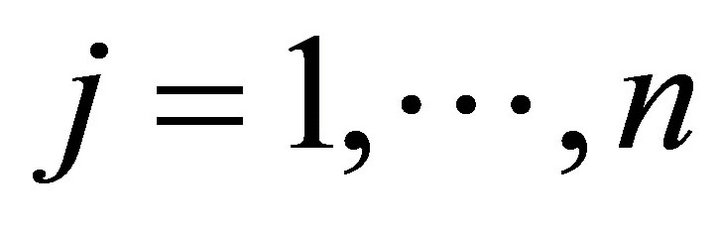 such that
such that
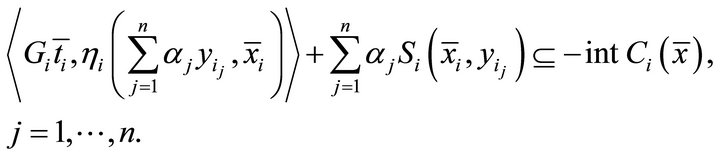
Since 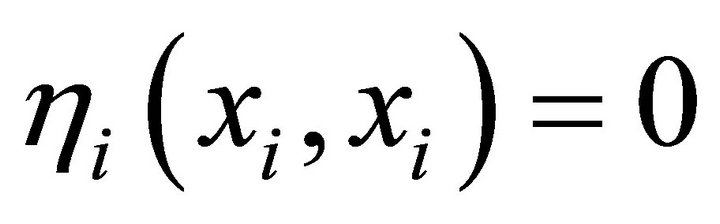 for all
for all 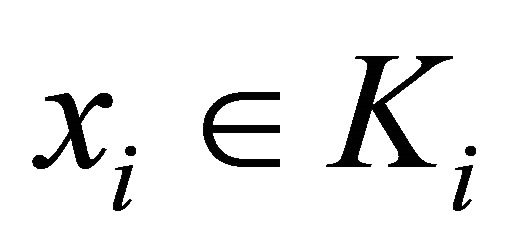
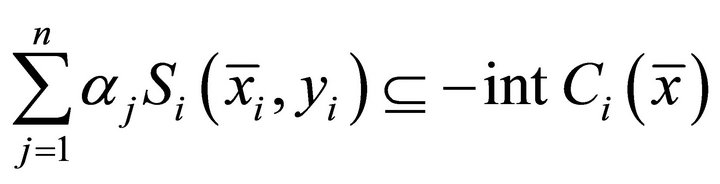
which contradicts the hypothesis 5). Therefore 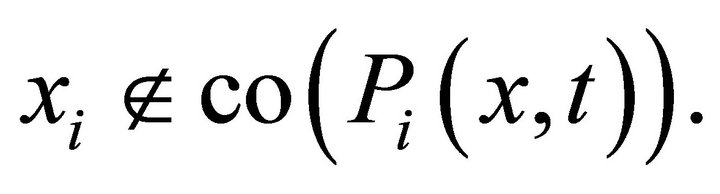
We now prove that for each
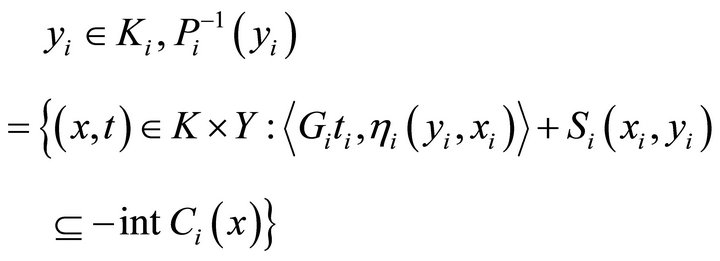
is open. Indeed, let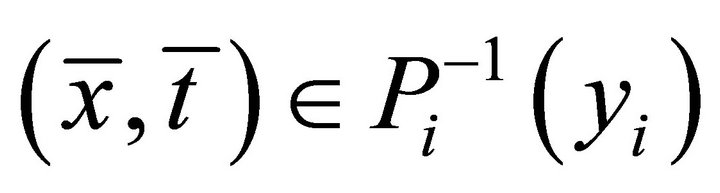 , that is
, that is
 . Since
. Since
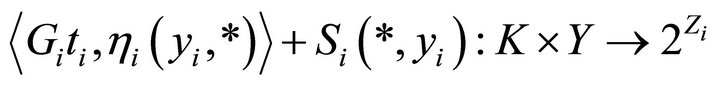 is an u.s.c. setvalued mapping, there exists a neighborhood
is an u.s.c. setvalued mapping, there exists a neighborhood  of
of 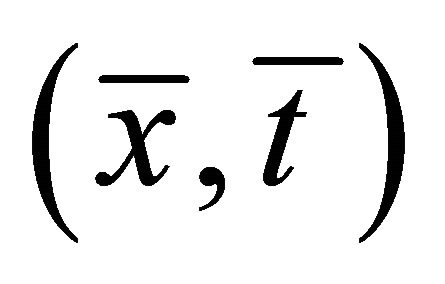 such that
such that
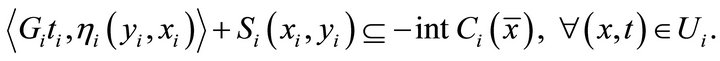
By 6),
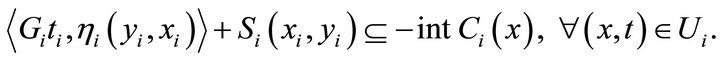
Hence, 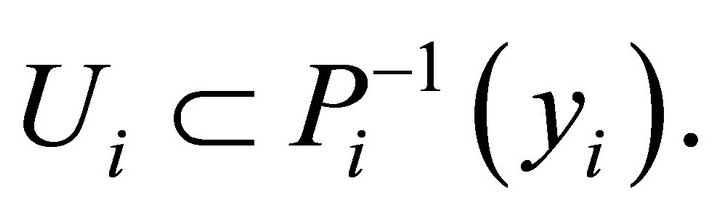 This implies,
This implies, 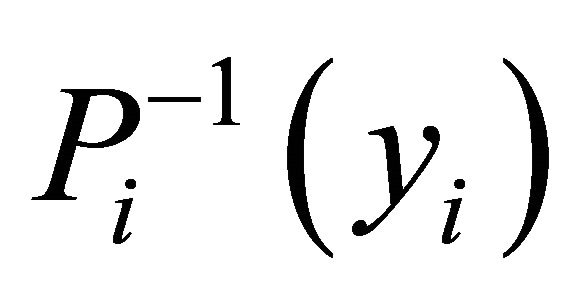 is open for each
is open for each 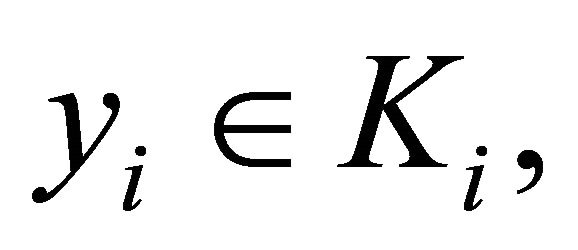 and so
and so 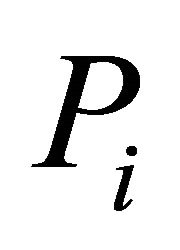 have open lower sections. For the remainder of the proof, we can just follow that of Theorem 3.1. This completes the proof.
have open lower sections. For the remainder of the proof, we can just follow that of Theorem 3.1. This completes the proof.
Corollary 3.3. For each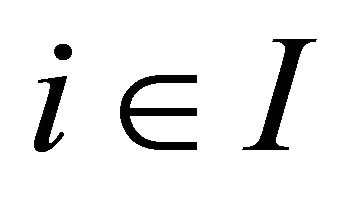 , let
, let  be a l.c.s.,
be a l.c.s.,  a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s. ,
,  a nonempty compact convex subset of
a nonempty compact convex subset of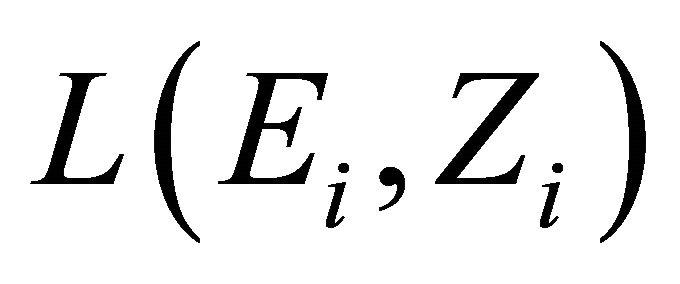 , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each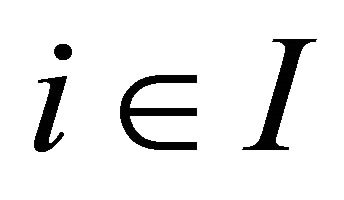 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 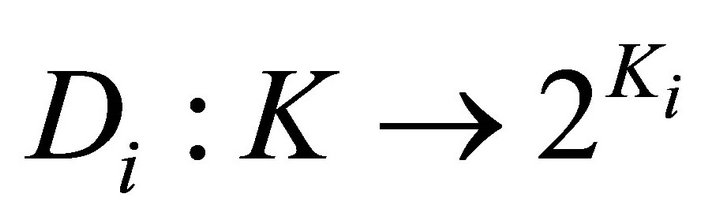 and
and 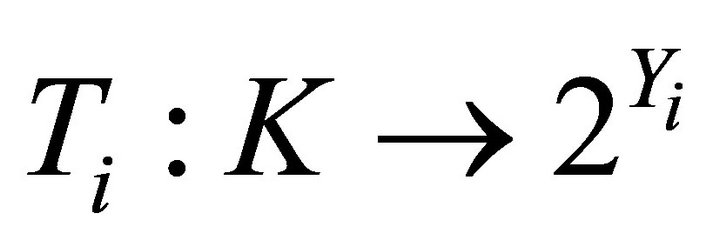 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For all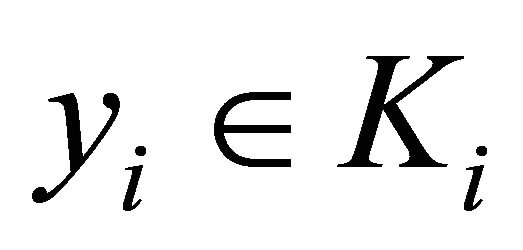 , the mapping
, the mapping 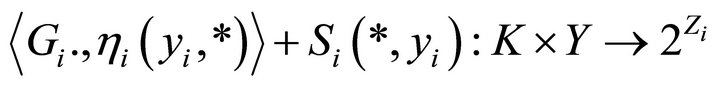 is an u.s.c. setvalued mapping;
is an u.s.c. setvalued mapping;
3) 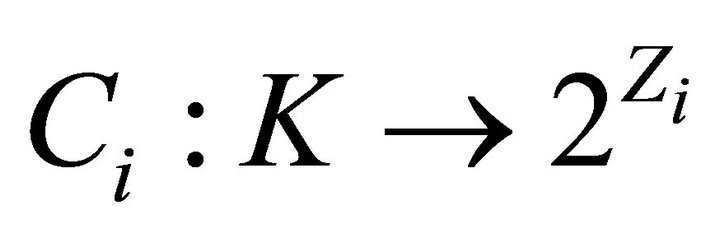 is a convex set-valued mapping such that for each
is a convex set-valued mapping such that for each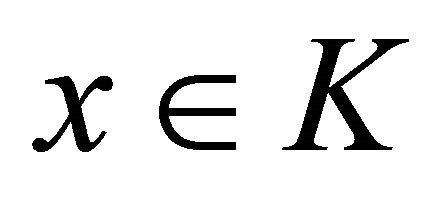 ,
, 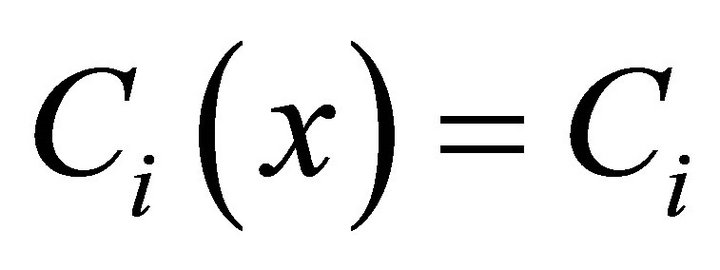 is a convex cone with
is a convex cone with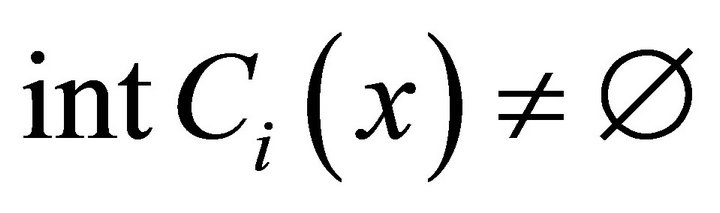 ;
;
4)  is affine in the first argument and for all
is affine in the first argument and for all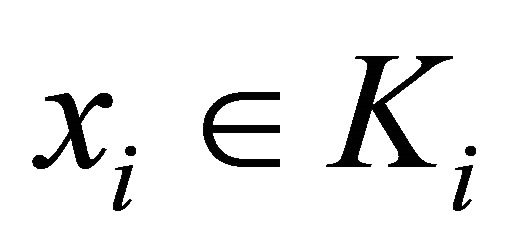 ,
, ;
;
5) 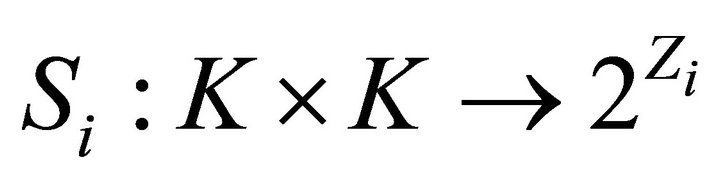 is a generalized vector 0-diagonally convex set-valued mapping;
is a generalized vector 0-diagonally convex set-valued mapping;
6) For a given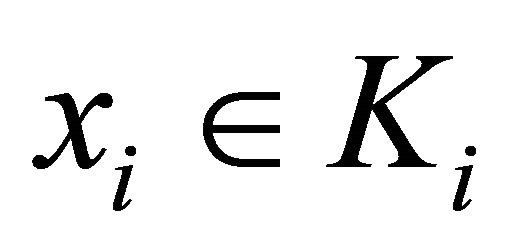 , and a neighborhood
, and a neighborhood 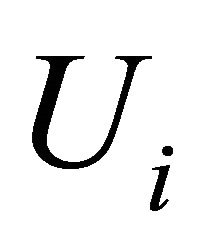 of
of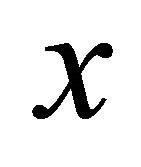 , for all
, for all 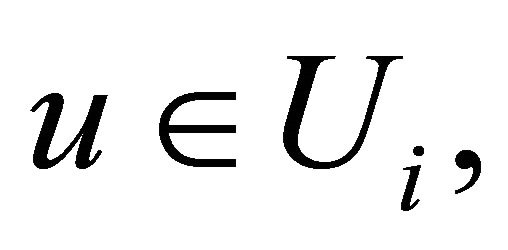
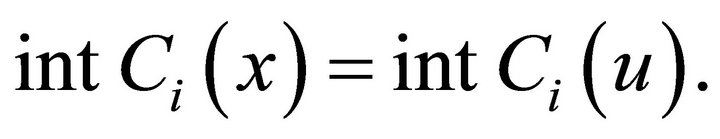
Then there exist 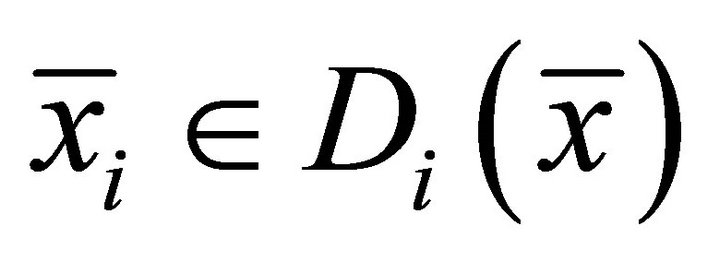 and
and 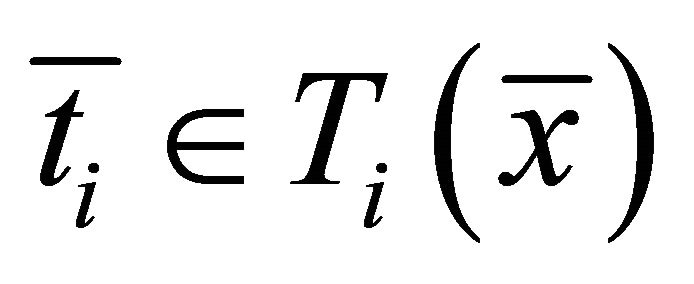 such that
such that
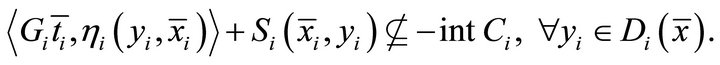
Proof. By hypothesis 3), the condition 4) in Corollary 3.2 is satisfied. Hence, all the conditions are satisfied as in Corollary 3.2.
Corollary 3.4. For each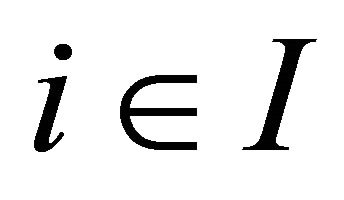 , let
, let  be a l.c.s.,
be a l.c.s., 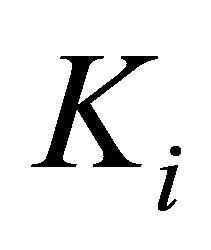 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s. ,
, 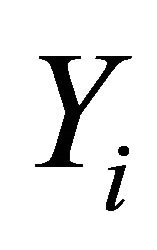 a nonempty compact convex subset of
a nonempty compact convex subset of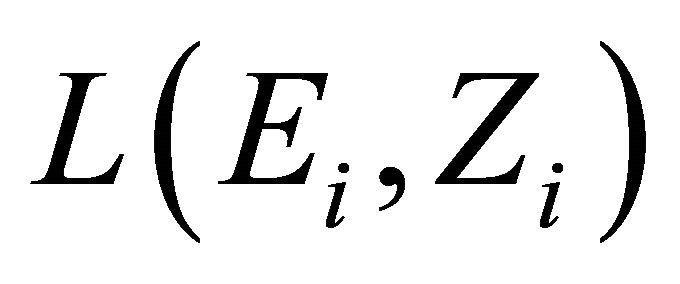 , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each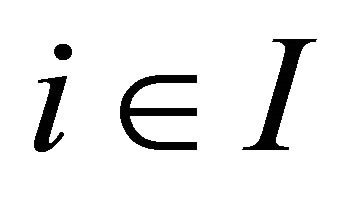 , assume that
, assume that 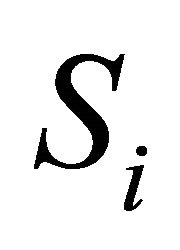 and
and  are single valued mappings and the following conditions are satisfied.
are single valued mappings and the following conditions are satisfied.
1) 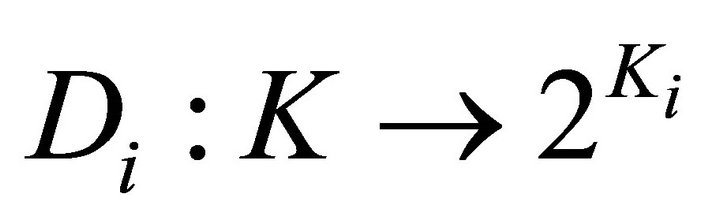 and
and  are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For all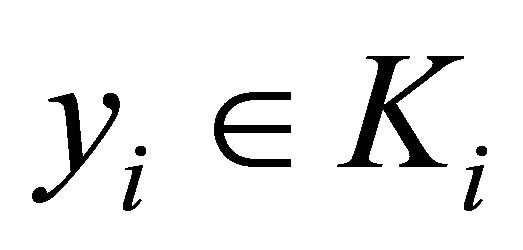 , the mapping
, the mapping
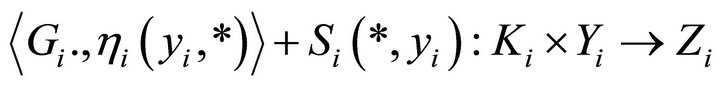 is continuous;
is continuous;
3) 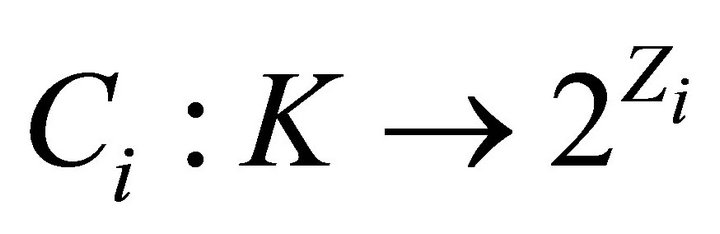 is a convex set-valued mapping with
is a convex set-valued mapping with 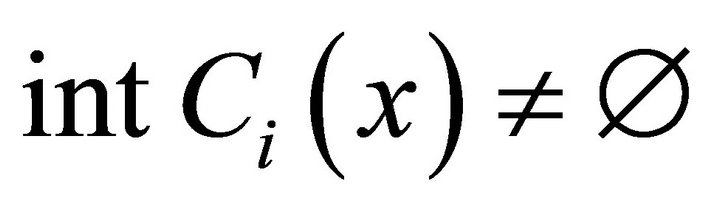 for all
for all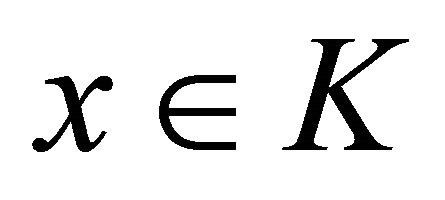 ;
;
4) 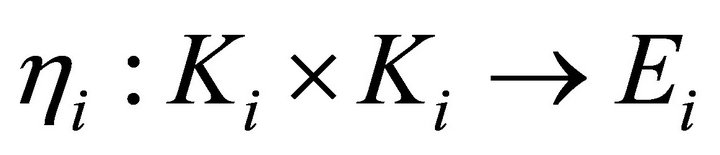 is affine in the first argument and for all
is affine in the first argument and for all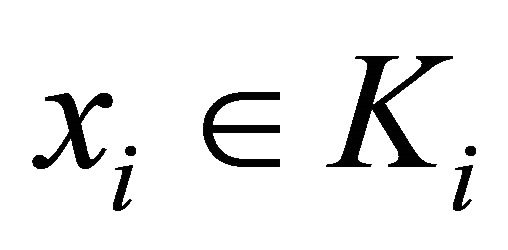 ,
,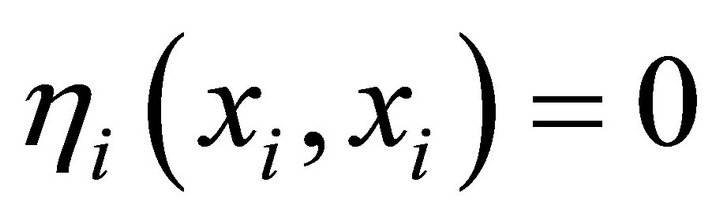 ;
;
5) 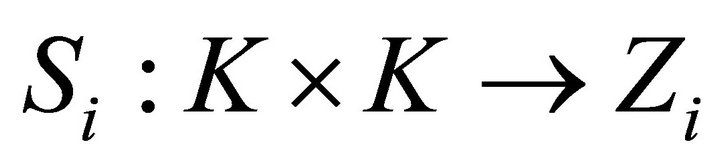 is a vector 0-diagonally convex mapping;
is a vector 0-diagonally convex mapping;
6) 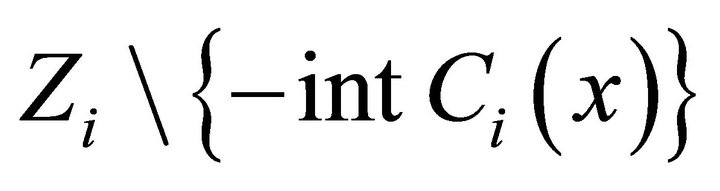 is an u.s.c. set-valued mapping.
is an u.s.c. set-valued mapping.
Then there exist 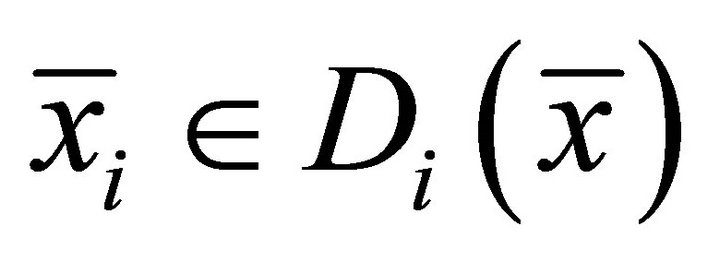 and
and 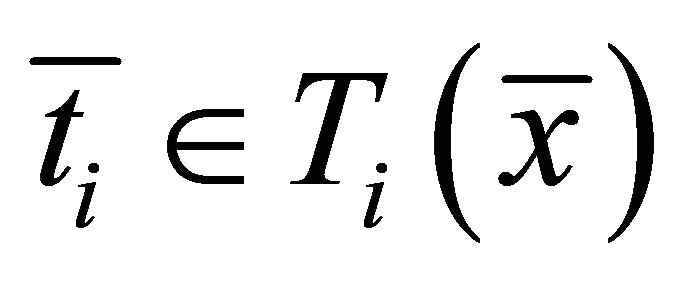 such that
such that
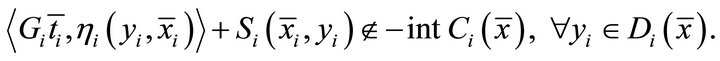
Proof. Define a set-valued mapping  by
by
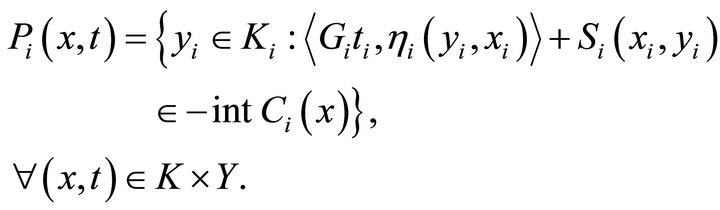
We now prove that for each
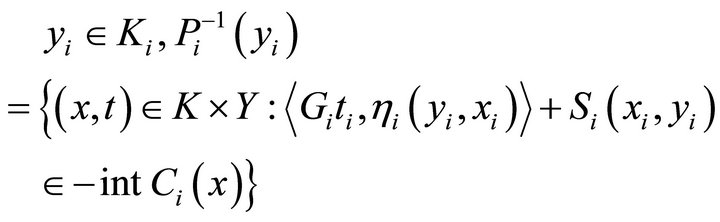
is open, that is, the set

is closed. Indeed, let 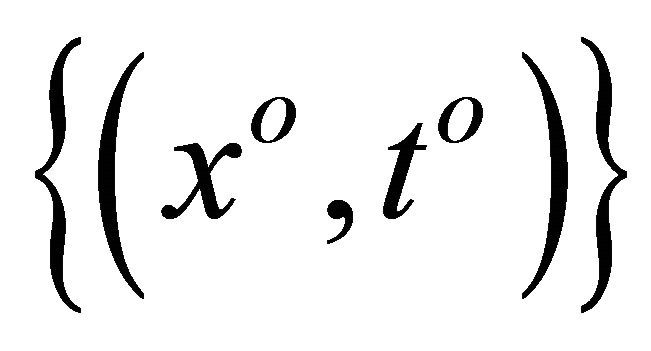 be a net in
be a net in 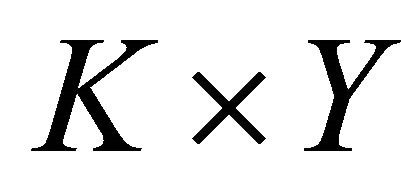 such that
such that 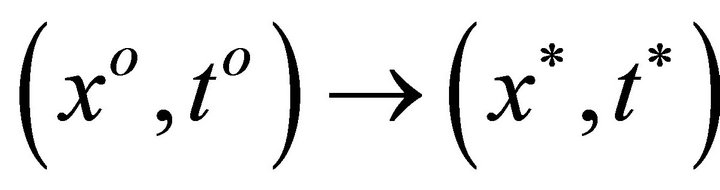 and
and
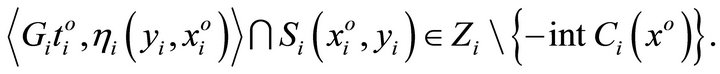
Since 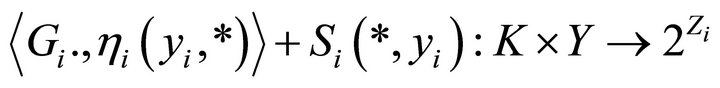 is continuous, hence
is continuous, hence
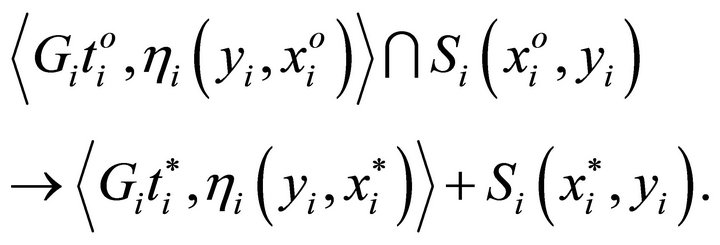
Since 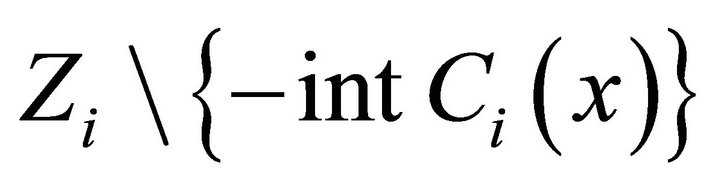 is an u.s.c. set-valued mapping with closed values, by Lemma 2.1, we have
is an u.s.c. set-valued mapping with closed values, by Lemma 2.1, we have
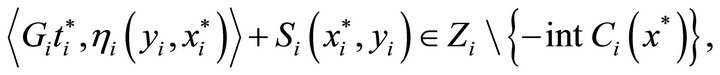
and hence 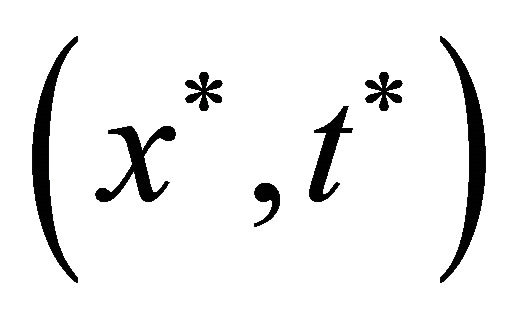 in the set
in the set
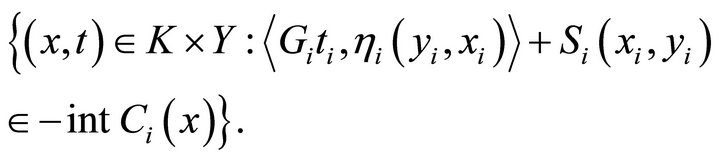
This implies 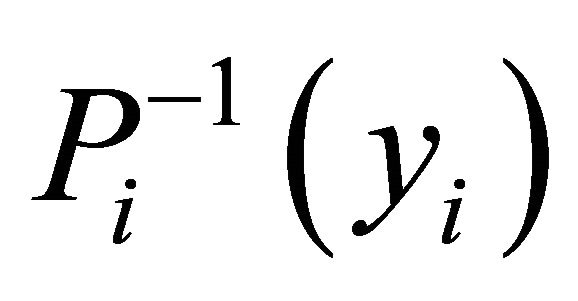 is open for each
is open for each 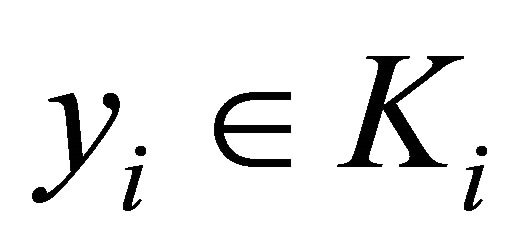 and so
and so 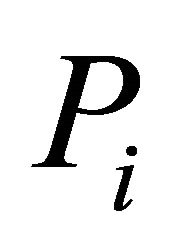 has open lower sections. For the remainder of the proof, we can just follow that of Theorem 3.1 and Corollary 3.2. This completes the proof.
has open lower sections. For the remainder of the proof, we can just follow that of Theorem 3.1 and Corollary 3.2. This completes the proof.
Theorem 3.5. For each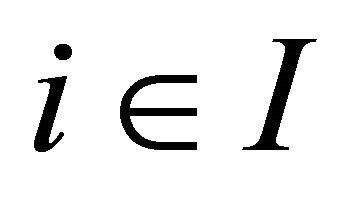 , let
, let 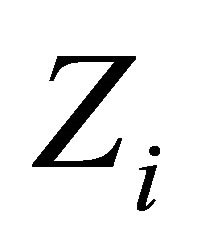 be a l.c.s.,
be a l.c.s., 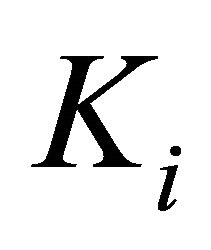 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.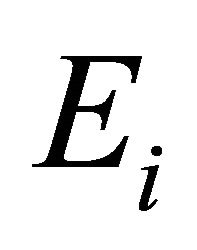 ,
, 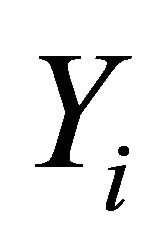 a nonempty compact convex subset of
a nonempty compact convex subset of , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each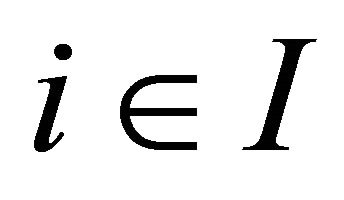 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 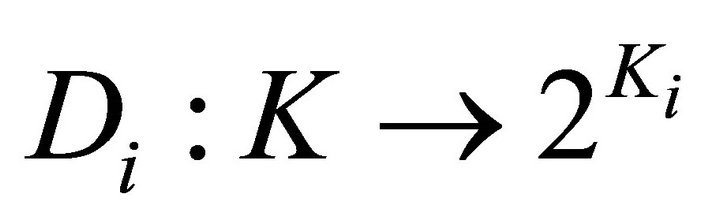 and
and 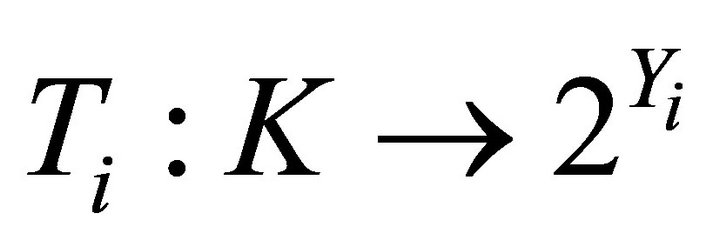 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 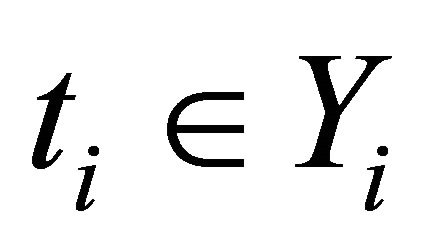 and
and , the mapping
, the mapping  is WIC-DQC;
is WIC-DQC;
3) for each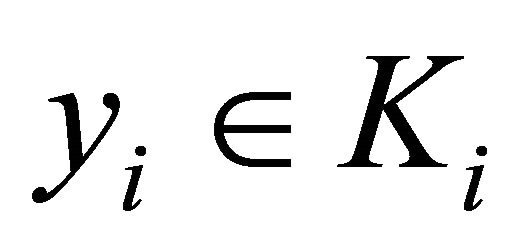 , the set
, the set
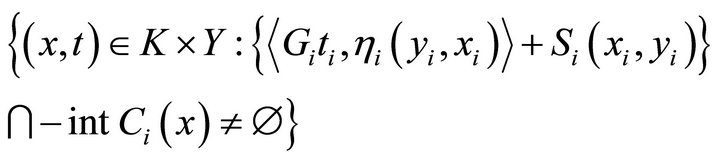
is open.
Then there exist 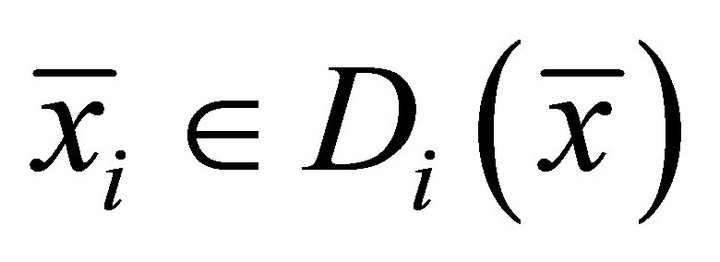 and
and 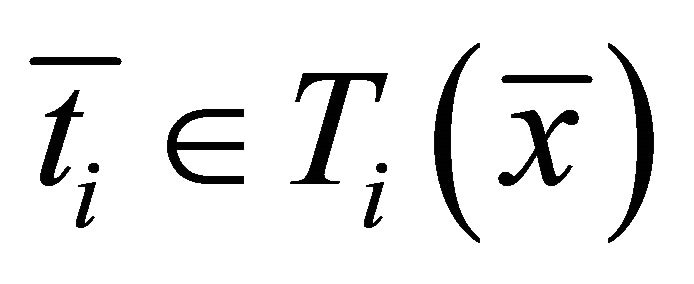 such that
such that
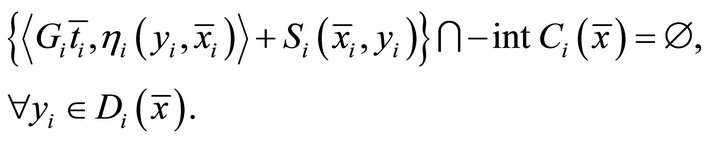
Proof. Define a set-valued mapping  by
by
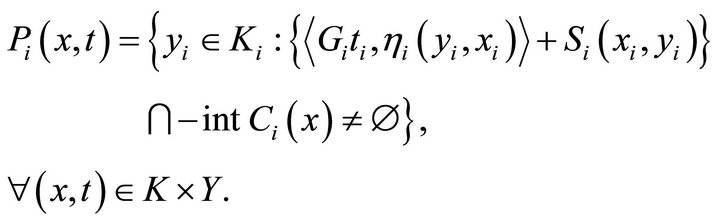
For the remainder proof, we just follow that of Theorem 3.1.
Corollary 3.6. For each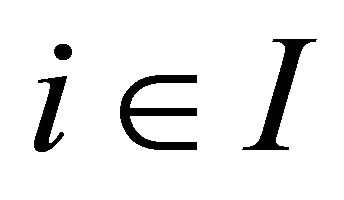 , let
, let 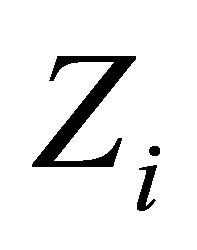 be a l.c.s.,
be a l.c.s., 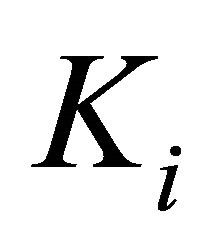 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.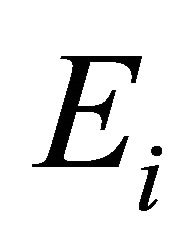 ,
,  a nonempty compact convex subset of
a nonempty compact convex subset of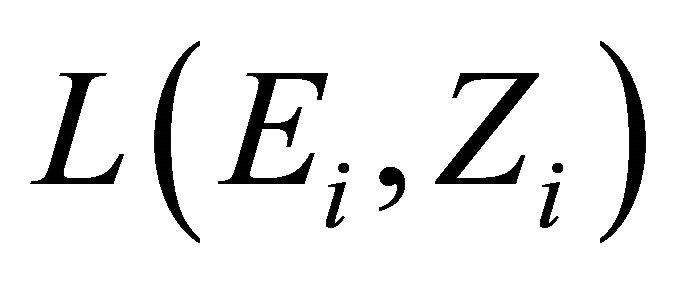 , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each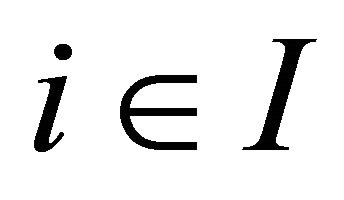 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 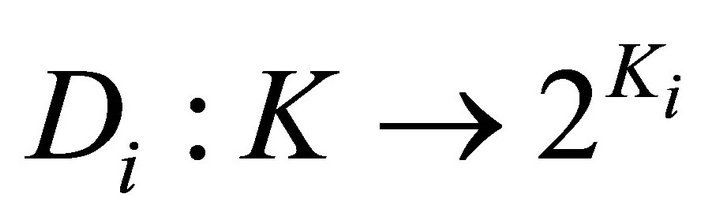 and
and 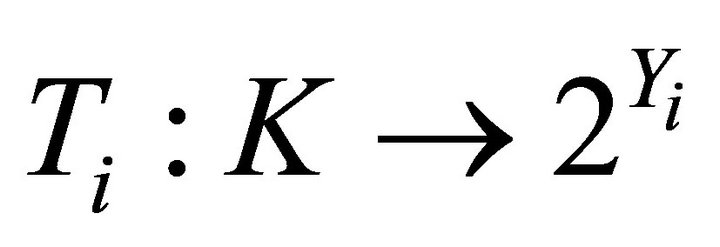 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 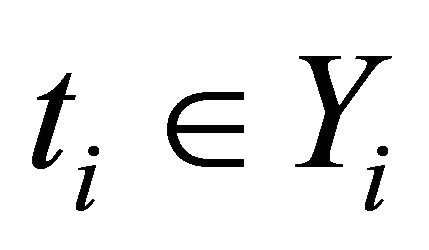 and
and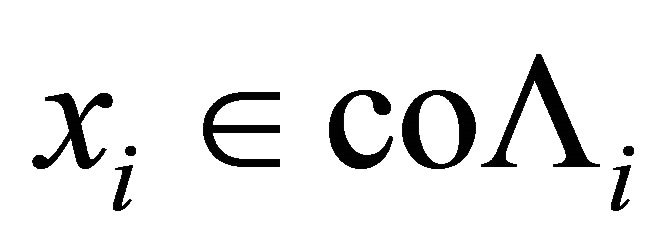 , the mapping
, the mapping
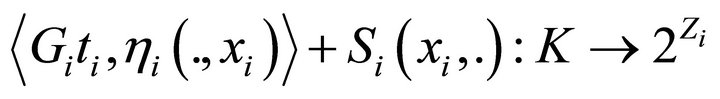 is WIC-DQC;
is WIC-DQC;
3) 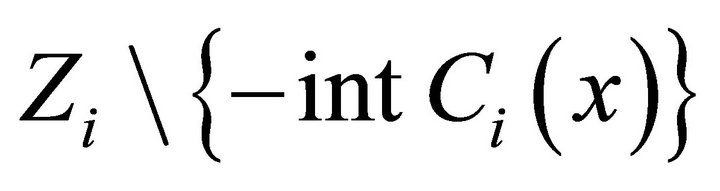 is an u.s.c. set-valued mapping.
is an u.s.c. set-valued mapping.
Then there exist 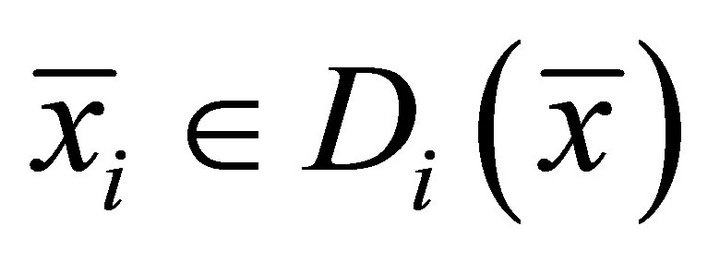 and
and 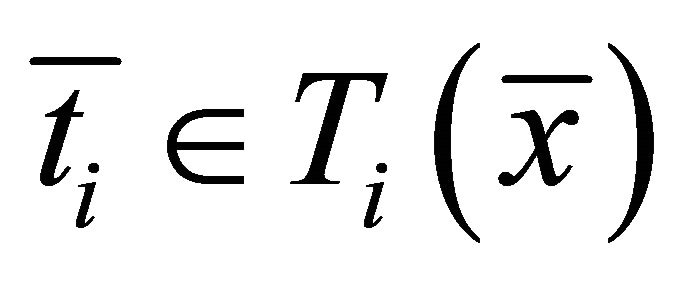 such that
such that
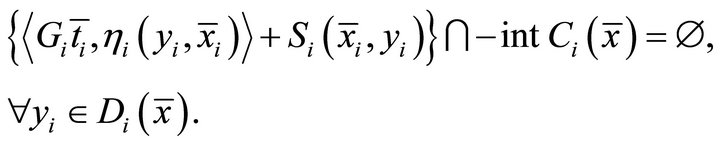
Proof. Let 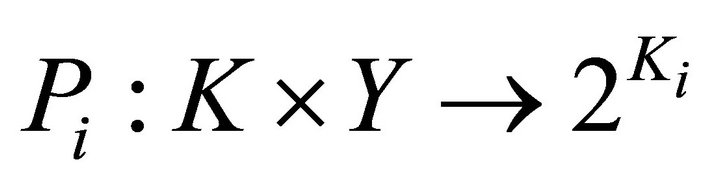 be a set-valued mapping define in Theorem 3.5. We just prove that for each
be a set-valued mapping define in Theorem 3.5. We just prove that for each
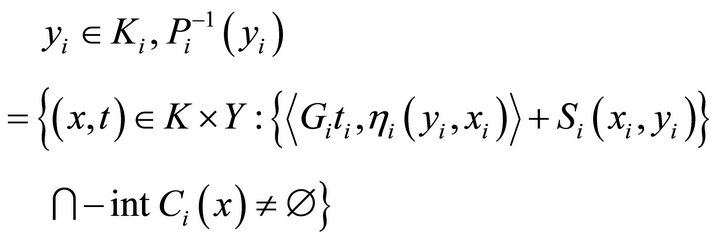
is open, that is, the set
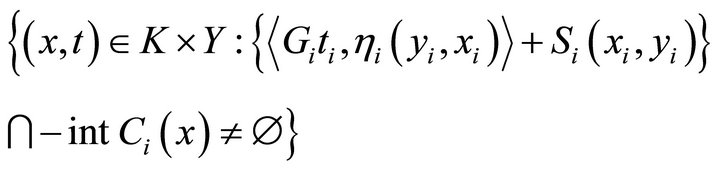
is closed. Indeed, let 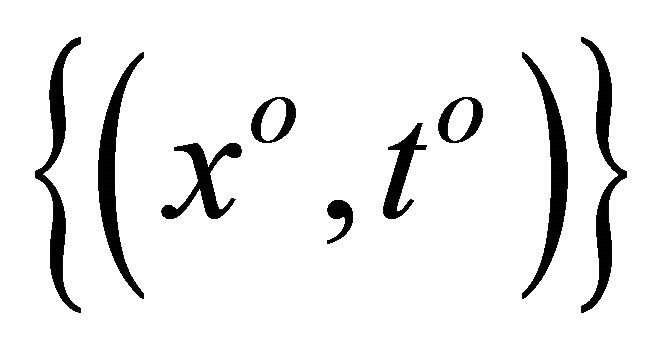 be a net in
be a net in 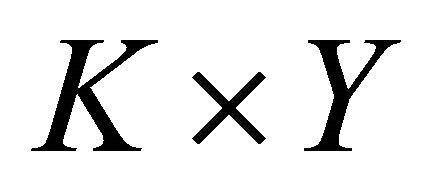 such that
such that 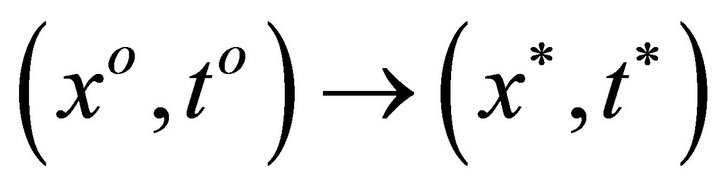 and
and
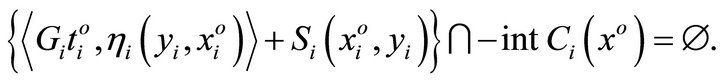
This implies

We now prove that
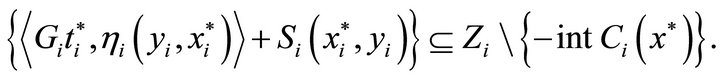
If it is not true, then there exists a
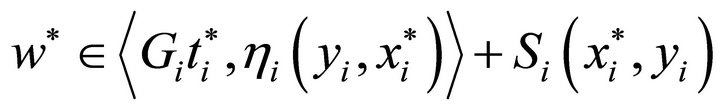 such that
such that
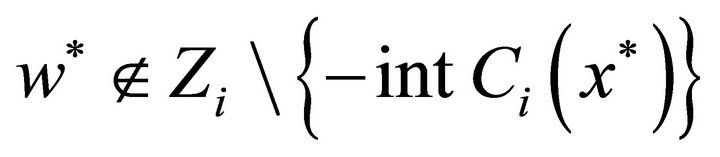 . Since
. Since 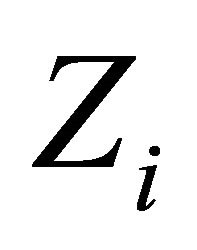 is Hausdorff t.v.s.
is Hausdorff t.v.s.
(l.c.s. is Hausdorff space) and 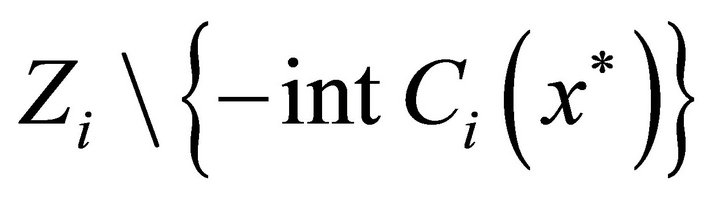 is closed, there exists two open sets
is closed, there exists two open sets 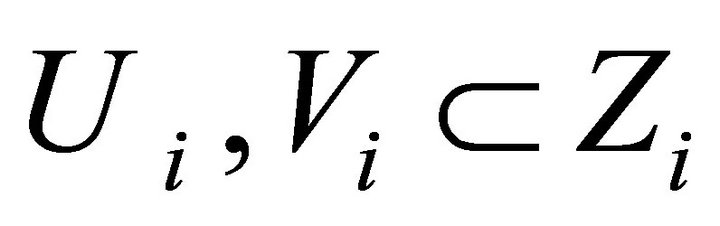 such that
such that
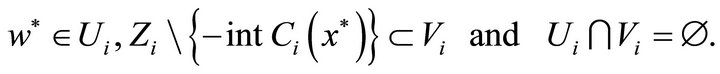
Since 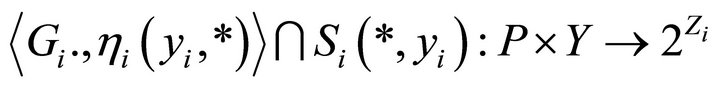 is an l.s.c.
is an l.s.c.
set-valued mapping and 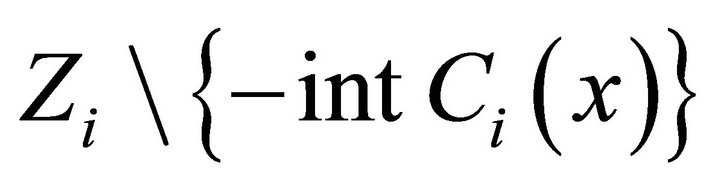 is an u.s.c. set-valued mapping, there exists a neighborhood
is an u.s.c. set-valued mapping, there exists a neighborhood
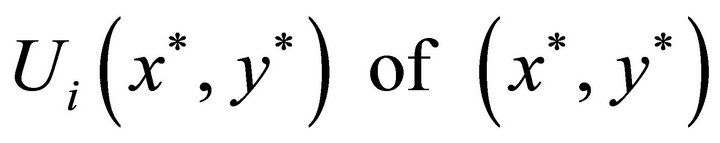 such that
such that

and a neighborhood 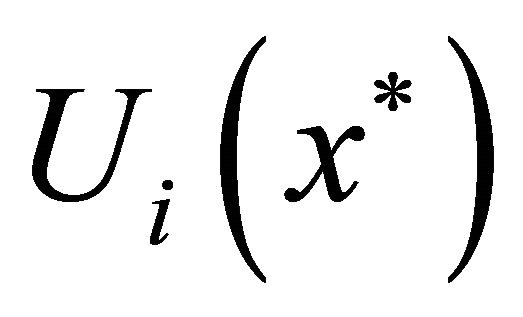 of
of  such that
such that
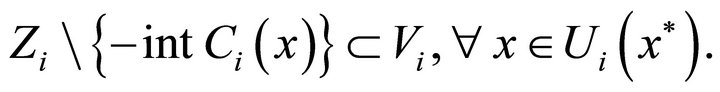
Hence, for all  there exists
there exists 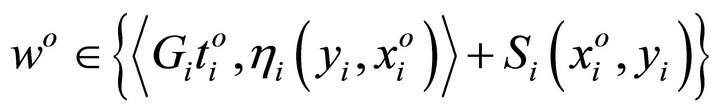 such that
such that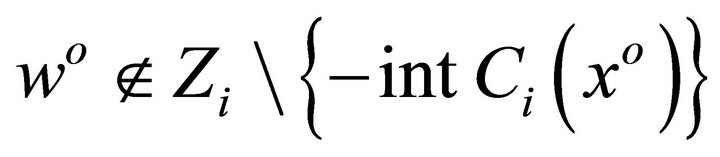 , which is contradiction.
, which is contradiction.
Therefore, the set
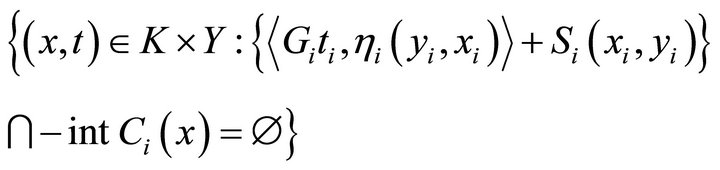
is closed. Hence, all the conditions of Theorem 3.5 satisfied. Consequently, the assertion of the theorem holds.
Theorem 3.7. For each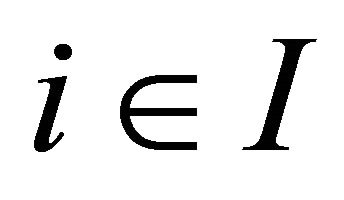 , let
, let 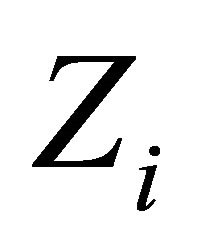 be a l.c.s.,
be a l.c.s., 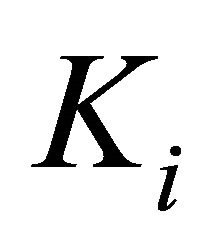 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.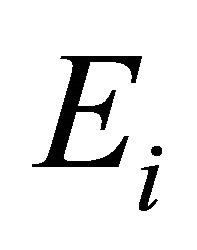 ,
, 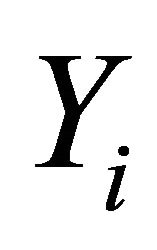 a nonempty compact convex subset of
a nonempty compact convex subset of , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each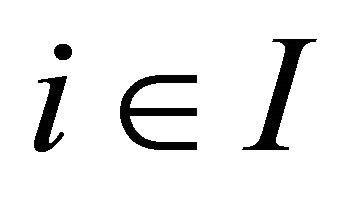 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1)  and
and  are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 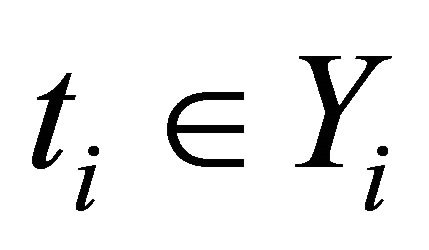 and
and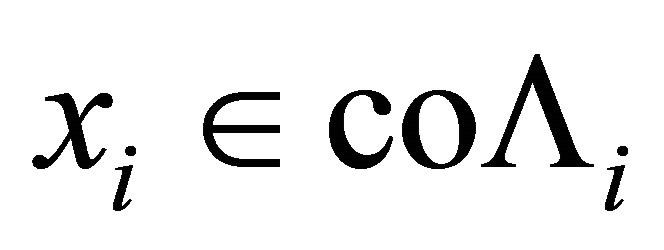 , the mapping
, the mapping 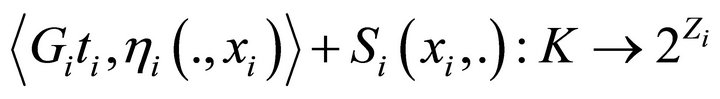 is SIIC-DQC;
is SIIC-DQC;
3) for each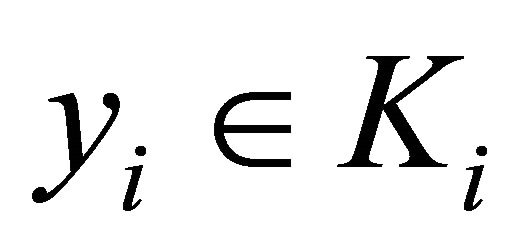 , the set
, the set
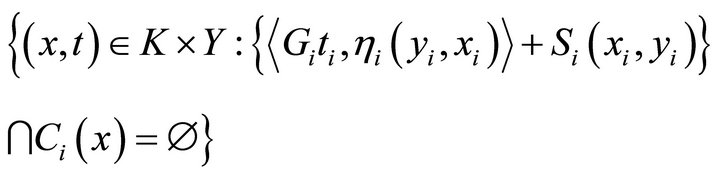
is open.
Then there exist 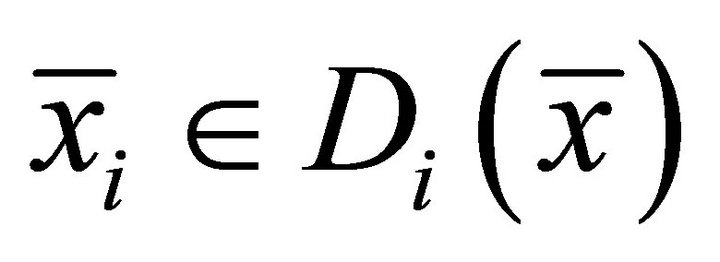 and
and 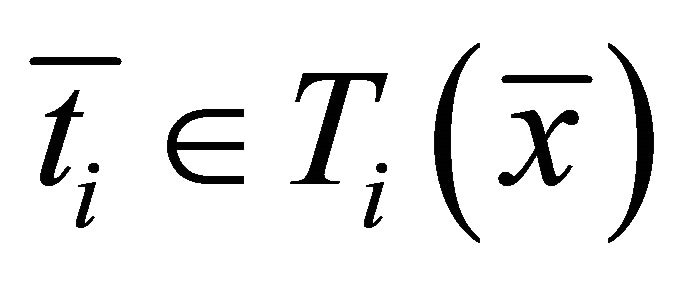 such that
such that
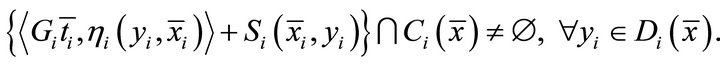
Proof. Define a set-valued mapping  by
by
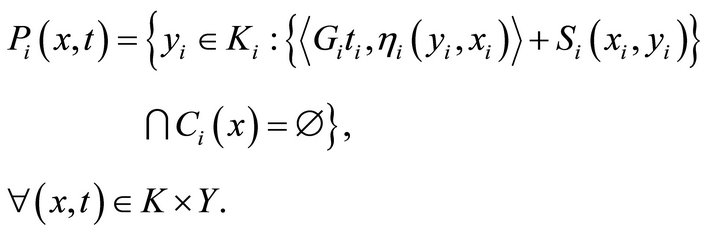
For the remainder proof, we just follow that of Theorem 3.1.
Corollary 3.8. For each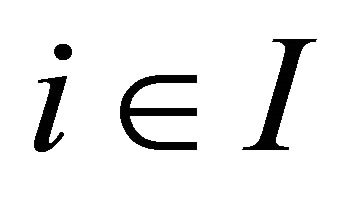 , let
, let 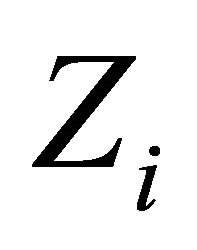 be a l.c.s.,
be a l.c.s., 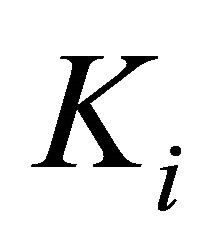 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.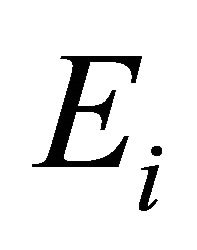 ,
, 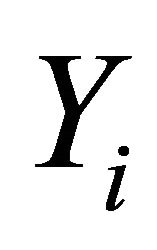 a nonempty compact convex subset of
a nonempty compact convex subset of , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each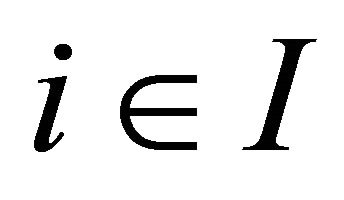 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 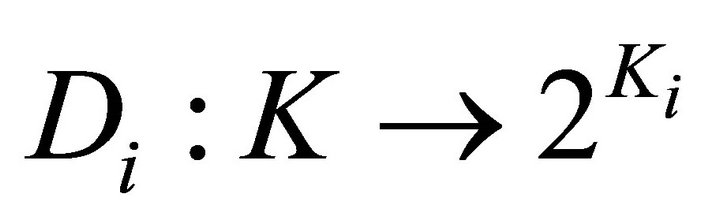 and
and 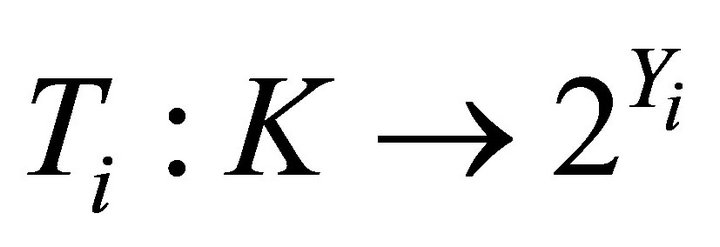 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 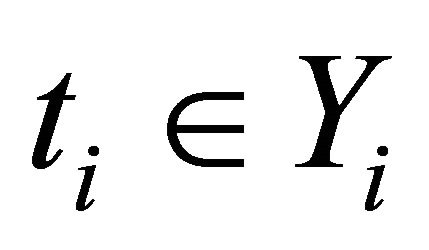 and
and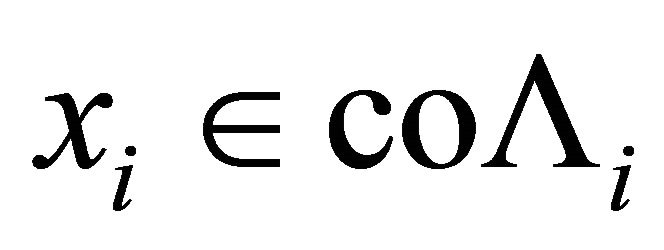 , the mapping
, the mapping 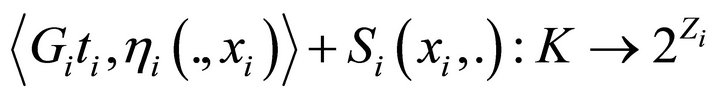 is SIIC-DQC;
is SIIC-DQC;
3) For all 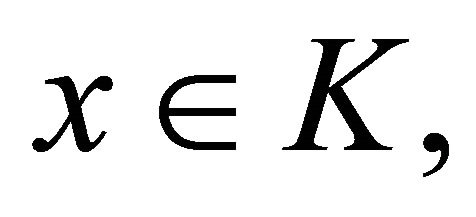
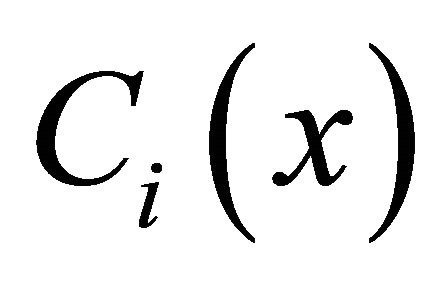 is closed convex cone
is closed convex cone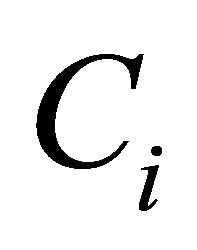 .
.
Then there exist 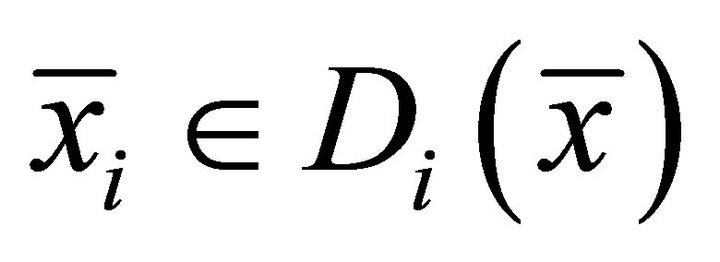 and
and 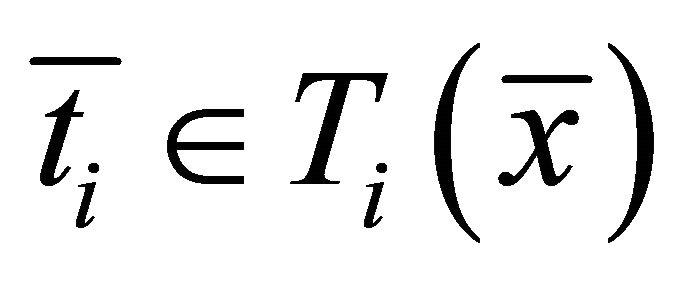 such that
such that

Proof. Let 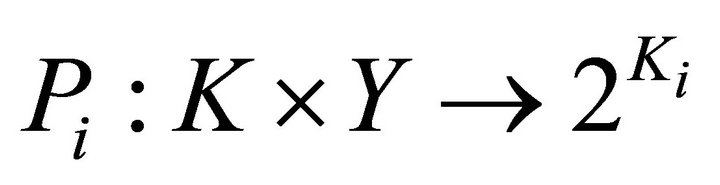 be a set-valued mapping defined in Theorem 3.7. We prove that for each
be a set-valued mapping defined in Theorem 3.7. We prove that for each
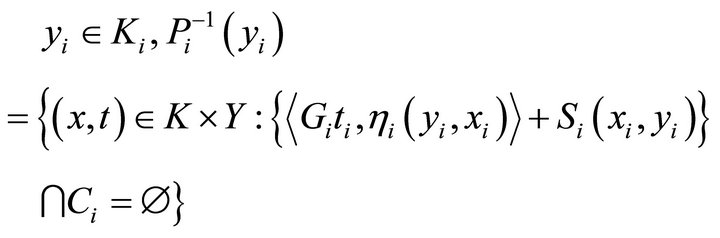
is open, that is, the set

is open. If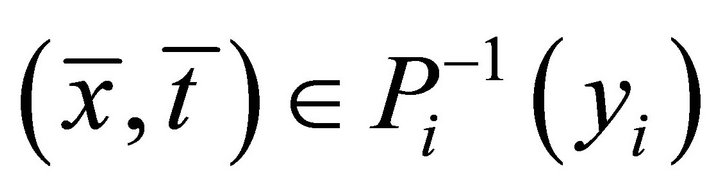 , since
, since 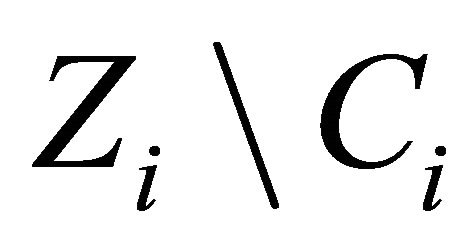 is open set and for all
is open set and for all
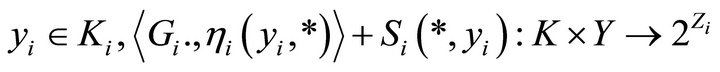 , an u.s.c. set-valued mapping, there exists a neighborhood
, an u.s.c. set-valued mapping, there exists a neighborhood 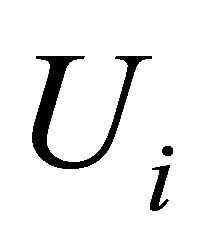 of
of , for all
, for all 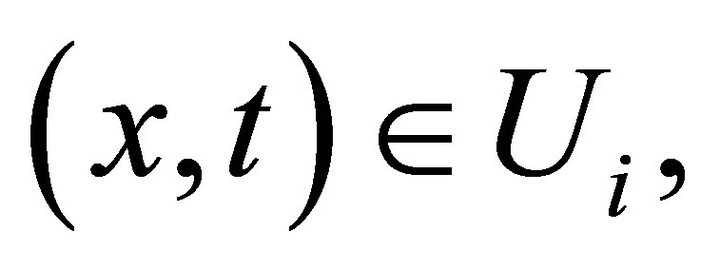

This implies 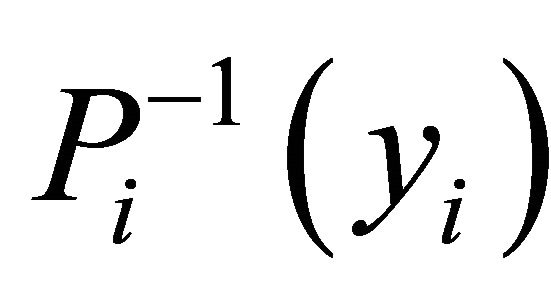 is open for each
is open for each 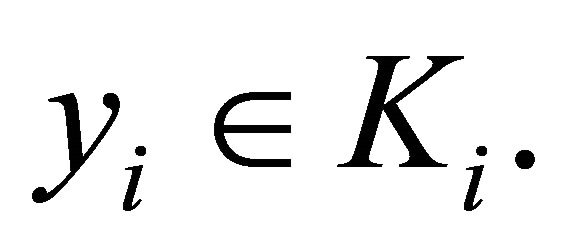 Therefore, all the conditions of Theorem 3.7 are satisfied. Consequently the assertion of the theorem holds.
Therefore, all the conditions of Theorem 3.7 are satisfied. Consequently the assertion of the theorem holds.
Theorem 3.9. For each , let
, let 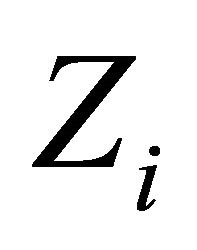 be a l.c.s.,
be a l.c.s., 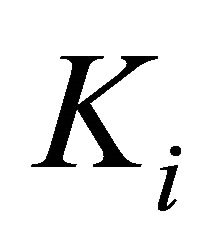 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.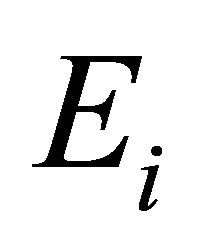 ,
, 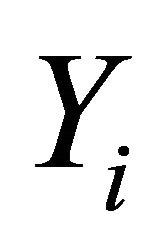 a nonempty compact convex subset of
a nonempty compact convex subset of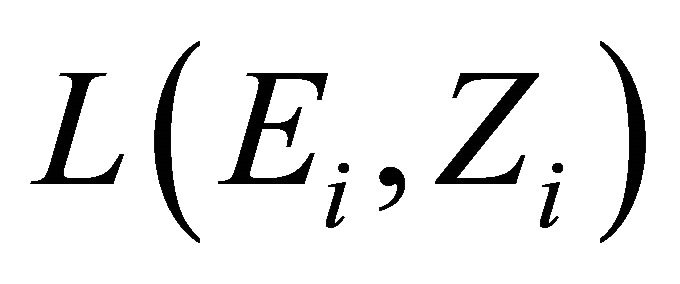 , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each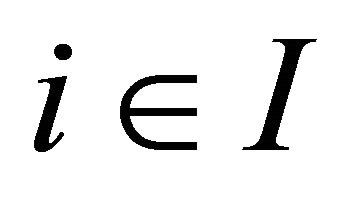 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1) 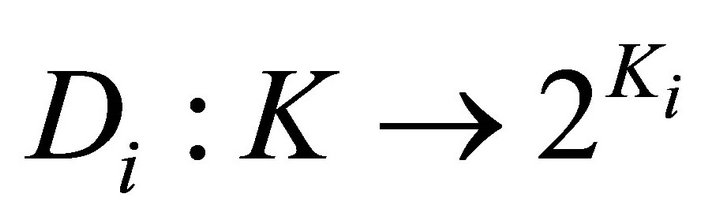 and
and 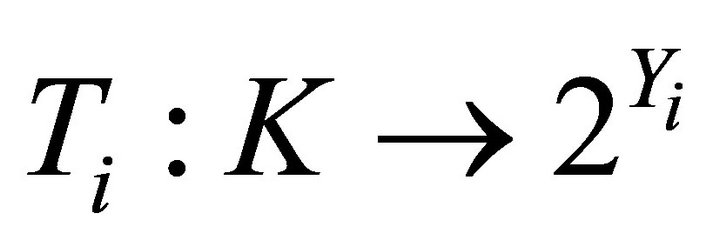 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each 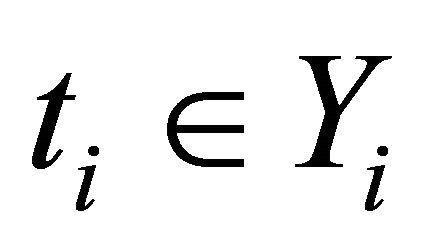 and
and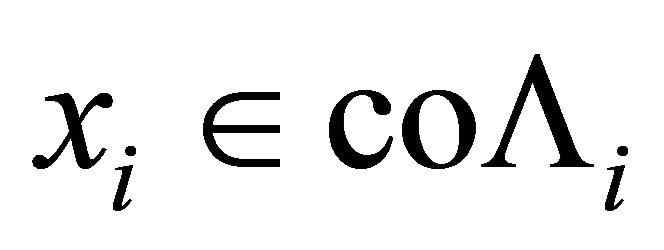 , the mapping
, the mapping 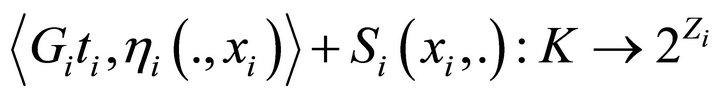 is SIC-DQC;
is SIC-DQC;
3) for each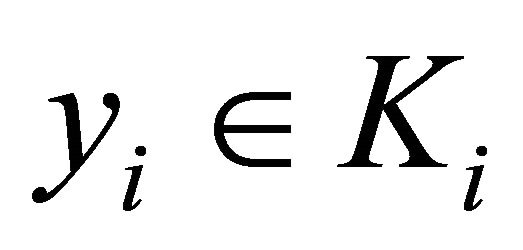 , the set
, the set
 is open.
is open.
Then there exist  and
and 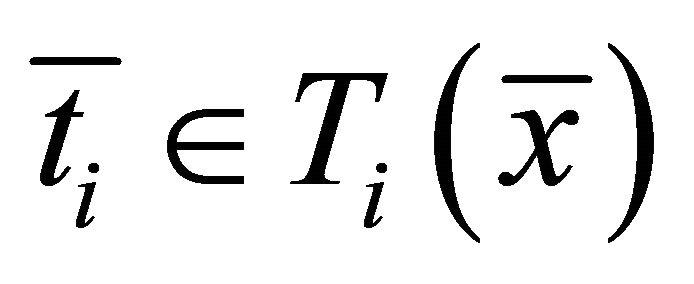 such that
such that
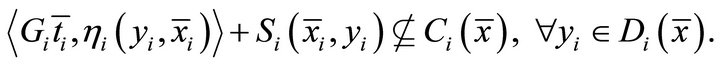
Proof. Define a set-valued mapping 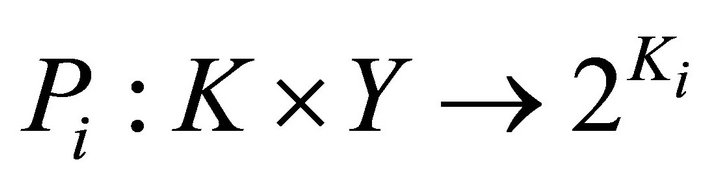 by
by
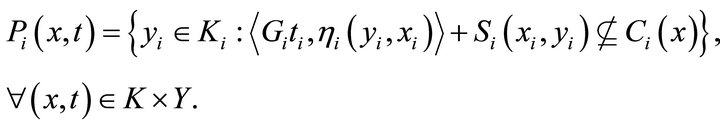
The rest of the proof is similar to that of Theorem 3.1.
Corollary 3.10. For each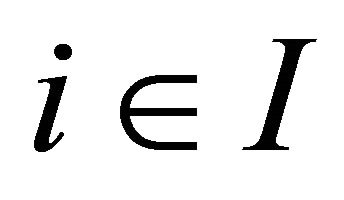 , let
, let 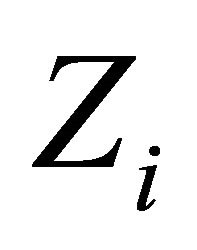 be a l.c.s.,
be a l.c.s., 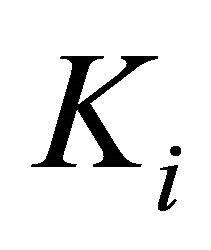 a nonempty compact convex subset of Hausdorff t.v.s.
a nonempty compact convex subset of Hausdorff t.v.s.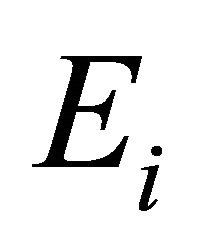 ,
, 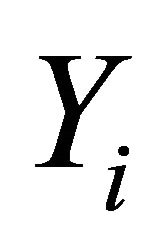 a nonempty compact convex subset of
a nonempty compact convex subset of , which is equipped with a
, which is equipped with a  -topology. For each
-topology. For each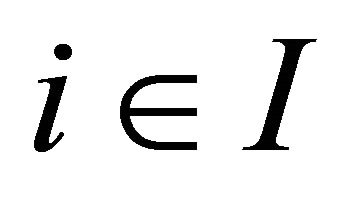 , assume that the following conditions are satisfied.
, assume that the following conditions are satisfied.
1)  and
and 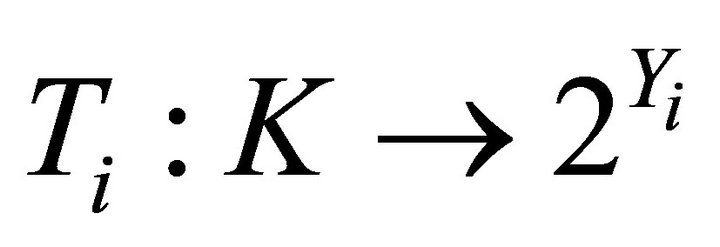 are two nonempty convex set-valued mappings and have open lower sections;
are two nonempty convex set-valued mappings and have open lower sections;
2) For each  and
and , the mapping
, the mapping  is SIC-DQC;
is SIC-DQC;
3) 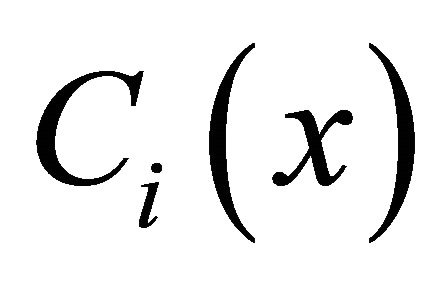 is an u.s.c. mapping with closed values.
is an u.s.c. mapping with closed values.
Then there exist 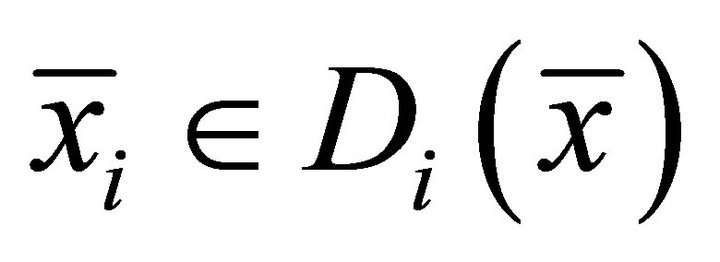 and
and 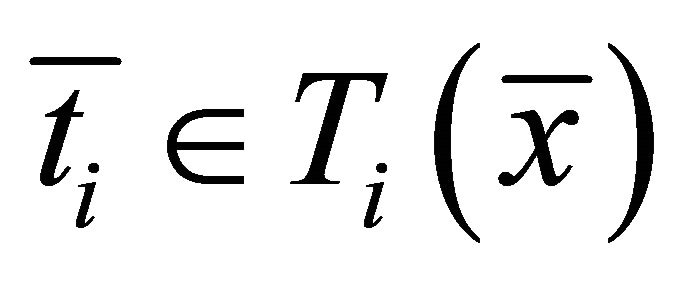 such that
such that
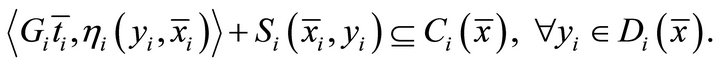
Proof. Let  a set-valued mapping defined in Theorem 3.9. We prove that for each
a set-valued mapping defined in Theorem 3.9. We prove that for each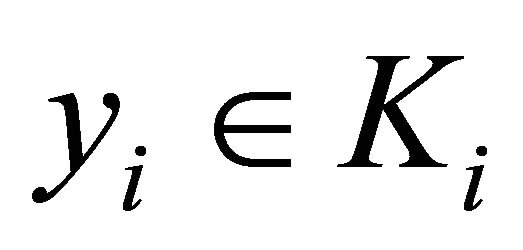 , the set
, the set
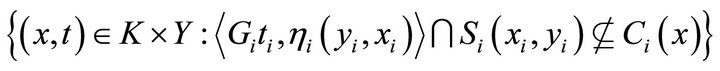 is open, that is, the set
is open, that is, the set
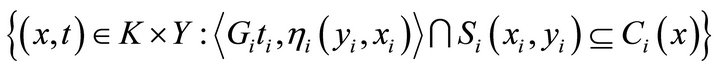 is closed. Indeed, let
is closed. Indeed, let 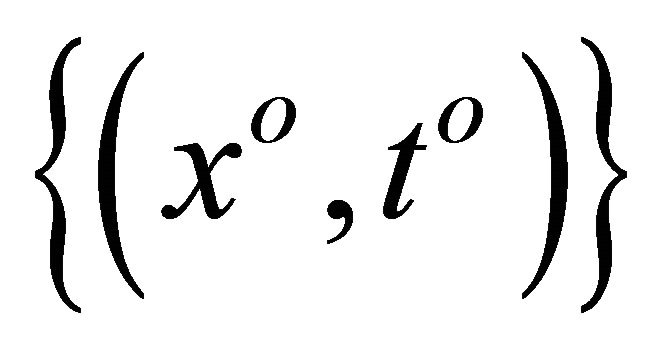 be a net in
be a net in  such that
such that  and
and
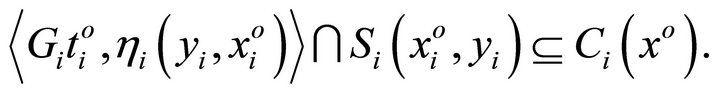
We claim that
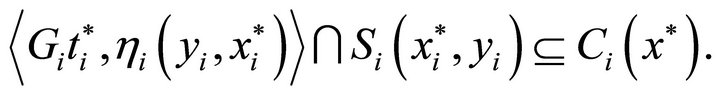
To prove this assertion, we can just follow that of Corollary 3.6. Hence, the set
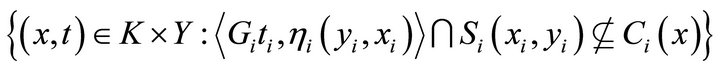 is open. Therefore, all the conditions of Theorem 3.9 are satisfied. Consequently, the assertion of the corollary hold.
is open. Therefore, all the conditions of Theorem 3.9 are satisfied. Consequently, the assertion of the corollary hold.
REFERENCES
- J.-W. Peng, “System of Generalized Set-Valued QuasiVariational-Like Inequalities,” Bulletin of the Australian Mathematical Society, Vol. 68, No. 3, 2003, pp. 501-515. doi:10.1017/S0004972700037904
- Q. H. Ansari, S. Schaible and J. C. Yao, “The System of Generalized Vector Equilibrium Problems with Applications,” Journal of Global Optimization, Vol. 22, No. 1, 2002, pp. 3-16. doi:10.1023/A:1013857924393
- H. H. Schaefer, “Topological Vector Space,” 2nd Edition, Graduate Texts in Mathematics, Springer, Berlin, 1999.
- X. P. Ding and E. Tarafdar, “Generalized VariationalLike Inequalities with Pseudomonotone Set-Valued Mappings,” Archive der Mathematik, Vol. 74, No. 4, 2000, pp. 302-313. doi:10.1007/s000130050447
- Q. H. Ansari and J. C. Yao, “System of Generalized Varitional Ineqalities and Their Applications,” Applicable Analysis, Vol. 76, No. 3-4, 2000, pp. 203-217. doi:10.1080/00036810008840877
- G. Xiao and S. Liu, “Existence of Solutions for Generalized Vector Quasi-Variational-Like Inequalities without Monotonicity,” Computers and Mathematics with Applications, Vol. 58, No. 8, 2009, pp. 1550-1557. doi:10.1016/j.camwa.2009.05.021
- G. Xiao, Z. Fan and X. Qi, “Existence Results for Generalized Nonlinear Vector Variational-Like Inequalities with Set-Valued Mapping,” Applied Mathematics Letter, Vol. 23, No. 1, 2010, pp. 44-47. doi:10.1016/j.aml.2009.07.023
- J.-W. Peng and X.-M. Yang, “Generalized Vector QuasiVariational-Like Inequalities,” Journal of Inequalities and Applications, Vol. 2006, No. 1, 2006, pp. 1-11.
- S. Husain and S. Gupta, “Existence of Solutions for Generalized Nonlinear Vector Quasi-Variational-Like Inequalities with Set-Valued Mappings,” Filomat, Vol. 26, No. 5, 2012, pp. 909-916. doi:10.2298/FIL1205909H
- S. Husain and S. Gupta, “Generalized Nonlinear Vector Quasi-Variational-Like Inequality,” International Journal of Pure and Applied Mathematics, Vol. 66, No. 2, 2011, pp. 157-169.
- P. Hartman and G. Stampacchia, “On Some Nonlinear Elliptic Differential Function Equations,” Acta Mathematica, Vol. 115, No. 1, 1966, pp. 271-310. doi:10.1007/BF02392210
- S. H. Hou, H. Yu and G. Y. Chen, “On Vector QuasiEquilibrium Problems with Set-Valued Maps,” Journal of Optimization Theory and Applications, Vol. 119, No. 3, 2003, pp. 485-498. doi:10.1023/B:JOTA.0000006686.19635.ad
- Q. M. Liu, L. Y. Fan and G. H. Wang, “Generalized Vector Quasi-Equilibrium Problems with Set-Valued Mappings,” Applied Mathematics Letters, Vol. 21, No. 9, 2008, pp. 946-950. doi:10.1016/j.aml.2007.10.007
- G. Q. Tian and J. Zhou, “Quasi-Variational Inequalities without the Concavity Assumption,” Journal of Mathematical Analysis and Applications, Vol. 172, No. 1, 1993, pp. 289-299. doi:10.1006/jmaa.1993.1025
- J. P. Aubin and I. Ekeland, “Applied Nonlinear Analysis,” Wiley-Interscience, New York, 1984.
- C. H. Su and V. M. Sehgal, “Some Fixed Point Theorems for Condensing Multifunctions in Locally Convex Spaces,” Proceedings of the American Mathematical Society, Vol. 50, No. 1, 1975, pp. 150-154. doi:10.1090/S0002-9939-1975-0380530-7
- X. Q. Yang, “Generalized Convex Functions and Vector Variational Inequalities,” Journal of Optimization Theory and Applications, Vol. 79, No. 3, 1993, pp. 563-580. doi:10.1007/BF00940559
- Q. H. Ansari and J. C. Yao, “A Fixed Point Theorem and Its Applications to the System of varItional Ineqalities,” Bulletin of the Australian Mathematical Society, Vol. 59, No. 3, 1999, pp. 433-442. doi:10.1017/S0004972700033116
NOTES
*Corresponding author.

