International Journal of Organic Chemistry
Vol.3 No.3(2013), Article ID:36285,7 pages DOI:10.4236/ijoc.2013.33021
Computational Study of the Cyclization of 5-Hexenyl, 3-Oxa-5-Hexenyl and 4-Oxa-5-Hexenyl Radicals
Department of Chemistry and Biochemistry, Oberlin College, Oberlin, USA
Email: *amatlin@oberlin.edu
Copyright © 2013 Albert R. Matlin, Matthew C. Leyden. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 2, 2013; revised June 5, 2013; accepted June 19, 2013
Keywords: Radical Cyclizations; Activation Energies; UB3LYP; UCCSD (T)
ABSTRACT
The intramolecular cyclization of 5-hexenyl radicals continues to be an important synthetic method for the construction of five-membered rings. The synthetic utility arises from the high degree of regioselectivity to give predominantly cyclopentyl products in high yield under mild conditions. Recently we reported product cyclization studies on 4-oxa perturbed 5-hexenyl radical. In this paper, we report our results from a computational study (UB3LYP and UCCSD (T)) of the cyclization of a series of 5-hexenyl and 3- and 4-oxa-5-hexenyl radicals. Three highly conserved cyclization transitions states (exo-chair, exo-boat and endo-chair) were located for 10 acyclic radicals. Activation energies were calculated for the three modes of cyclization for each radical. Calculated values for the exo/endo cyclization ratios had a high level of agreement with experiment and predictions were offered for two cases that have not been experimentally tested. The increased percentage of exo-cyclization with 3- and 4-oxa substitution is the result of an increase in the energy difference between the exoand endo-chair transition states compared to the hydrocarbon systems. The decreased rate of cyclization of the 4-oxa compounds is primarily due to the stabilization of the initial acyclic radical by the vinyl ether linkage. The increase in the rate of cyclization with 3-methyl substitution is due to the increased conformational energy of the starting acyclic radical.
1. Introduction
Radical cyclizations continue to be extremely useful reactions for the construction of ring systems via single [1-5] and tandem cyclizations [6-9]. The utility of these reactions stems from the relatively mild reaction conditions (low to moderate temperature and neutral pH), which makes the system compatible with multiple functionalities and the predictable regioselectivity of the cyclization. The cyclization of 5-hexenyl radical based systems has been the most widely employed and studied radical ring-closure reaction. Beckwith established rules to predict the regiochemical outcome for radical cyclizations [10]. In general, these systems cyclize under kinetic control to give exo cyclopentyl products. This is in contrast to the intermolecular addition of radicals to alkenes, which in general add endo [11,12].
In the mid-1980’s, Beckwith and Schiesser [13,14] and Spellmeyer and Houk [15] presented force-field molecular mechanics based models to analyze the intramolecular cyclization of radicals. These studies were quite successful in explaining the regiochemistry of the cyclizations and, in some cases, offered explanations for relative rates of the reactions. Both of these studies concluded that these exothermic cyclizations were characterized by an early transition state and that exo versus endo selectivity could be attributed to conformational and steric factors in the transition state. More recently, several groups have successfully employed DFT and/or ab initio methods to analyze a variety of radical cyclizations [16-19]. A few years ago, we reported a kinetic and product study on the cyclization of a series of 4-oxa-5-hexenyl radicals [20]. We found that 4-oxa substitution increased the preference for exo cyclization and decreased the rate of cyclization 3.7-fold compared to the related hydrocarbon 5-hexenyl radicals. In order to better understand these effects we initiated a computational study of the 4-oxa-5-hexenyl intramolecular radical cyclizations. The study was expanded to 5-hexenyl radicals and 3-oxa-5-hexenyl radicals in order to make comparisons using the same computational models. Here we present UB3LYP and UCCSD (T) calculations on ten 5-hexenyl-based radical cyclizations (Figure 1).
2. Computational Methods
Global energy minima conformations of the acyclic 5-hexenyl radicals (1, 4, 7) and the cyclization products (2, 3, 5, 6, 8, 9) were determined using the Spartan 08 program at UHF-3-21G level of theory [21]. These geometries were further optimized using UB3LYP/6-311+ G (d,p) in the Gaussian 03 program [22]. Transition states (TS) were identified at the UB3LYP/6-31G (d) level of theory and then further optimized at UB3LYP/6-311+ G (d,p). All stationary points were analyzed by calculation of their vibrational frequencies. G˚ values were calculated at 298 K and 1 atm. All transition states had one imaginary frequency that corresponded to the reaction coordinate for cyclization. Single-point energies were determined at the UCCSD (T)/6-31G (d) level of theory using geometries from the UB3LYP/6-31G (d) calculations: (UCCSD (T)/6-31G (d)// UB3LYP/6-31G (d)). All reported UCCSD (T) total electronic energies were not corrected for zero-point energy (ZPE).
The geometries determined at UB3LYP/6-31G (d) and the UB3LYP/6-311+G (d,p) levels of theory were very similar and, in general, differed by no more than 0.025 A in bond lengths, 0.2˚ in bond angles and 0.6˚ in dihedral angles. We found that the energy consequences of the

Figure 1. Cyclization of 5-hexenyl radicals.
geometries determined using the 6-31G (d) basis set vs. 6-311+G (d,p) to be insignificant when evaluated at a single level of theory: e.g. energies for UCCSD (T)/ 6-31G (d)//B3LYP/6-31G (d) were within 0.15 kcal/mol of the energies calculated using UCCSD (T)/6-31 G(d) //B3LYP/6-311+G (d,p). These small differences canceled out when we determined the activation energies (Ea = E(acyclic radical) − E(transition state)).
3. Results and Discussion
3.1. Transition States
We located three transition states for cyclization of the 5-hexenyl radicals that were similar to the structures previously reported by Spellmeyer and Houk (UHF-MP2/ STO-3G) [15] for the parent system: exo-chair, exo-boat and endo-chair (Figure 2). In general, we found that transition state bond lengths and bond angles for a particular transition state (e.g. exo-chair) were remarkably similar across the three systems that we examined: 5-hexenyl radical 1a, 3-oxa-5-hexenyl radical 7a and 4-oxa-5-hexenyl radical 4a. With the exception of the intrinsic difference of C-O vs. C-C bond lengths, the bond with the largest variation for a particular type of transition state is the partially formed new σ-bond which varies from system to system by a maximum of ~0.1 Å. Corresponding transition state bond angles are all within 3˚ of each other. The largest variations were seen in the dihedral angles (4˚ - 11.5˚) of the three 5-hexenyl transition states (1a-TS) compared with the respective 4-oxa-5-hexenyl transition states (4a-TS). The dihedral angles for the 5-hexenyl transition states were much closer to the values found for the 3-oxa-5-hexenyl system (7a-TS) varying only 4˚ - 7˚.
The transition state geometries for each pathway (exo-chair, exo-boat and endo-chair) across the 10 radicals examined are consistent with the previously identified early nature of the transition states (Table 1). At the transition state, the forming σ-bond (C1-C5 or C1-C6) is long at 2.25 - 2.35 Å while the breaking double bond (C5-C6) is only slightly elongated at 1.36 - 1.38 Å (compared to 1.33 Å in the acyclic radicals). Even strongly polarizing the double bond by 4-oxa substitution has only a small effect on the position of the transition states for all cyclization modes. The endo transition states have shorter C5-C6 bond lengths (~1.358 Å) than the exo transition states (~1.368 Å) and the forming bond (C1-C6 endo; C1-C5 exo) is ~0.07 Å longer for endo transition states (Table 1). These results indicate that the endocyclization mode has a slightly earlier transition state than the exo mode, which is consistent with the higher exothermicity of the endo pathway. There are also small differences in the C1-C5 bond distances in the kinetically dominant exo-chair transition states: 4a (2.255 Å) < 1a

Figure 2. Transition states for the cyclization of acyclic radical 4a.
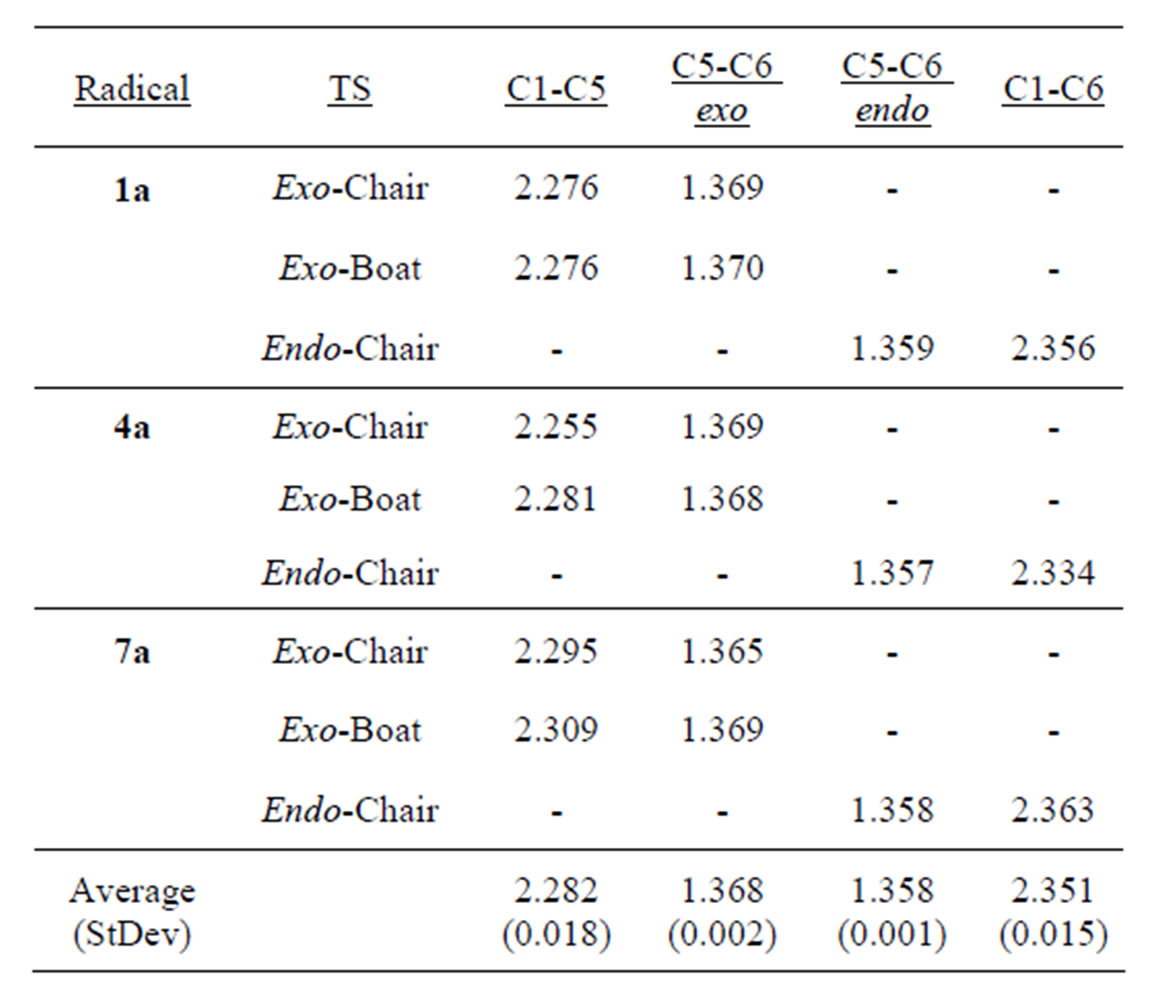
Table 1. Comparison of select transition state bond distances. (Å, UB3LYP/6-31G geometries).
(2.276 Å) < 7a (2.295 Å). These data suggest that exochair transition state for 7a is earlier than the exo-chair transition state for 1a, which in turn is earlier than the exo-chair transition state for 4a.
This trend also follows the calculated DGrxn (UB3LYP/ 6-311+G (d,p)//UB3LYP/6-31G (d)) for the exo mode of cyclization: 4a (−8.6 kcal/mol) ≤ 1a (−8.7 kcal/mol) < 7a (−14.4 kcal/mol).
The 3-methyl substituted systems give rise to a doubling of possible transition states as the methyl group can reside in either a pseudo-equatorial or pseudo-axial position. The transition states with the 3-methyl group in the pseudo-equatorial position were found to be lower in energy than the corresponding axial isomers.
3.2. Activation Energies and Exo/Endo Product Ratios
Table 2 lists the computed activation energies (Ea) calculated as the difference in the energy of the acyclic alkenyl radical in its lowest energy conformation and the energy of the specific transition state. While the trends for the DG‡ data derived from the DFT calculations mirrored the Ea’s derived from the UCCSD (T) calculations, we found that the UCCSD (T) values more closely reproduced the experimental data for the endo/exo ratios of the cyclizations (vide infra). With this in mind, most of the discussion below will focus on the UCCSD (T) total electronic energies.
In general, we found that the exo-chair TS had the lowest Ea for a given cyclization with the notable exception of the 5-methyl substituted hydrocarbon radicals 1b and 1d where the endo-chair was the lowest energy pathway. In all cases 5-methyl substitution increased the Ea for the exo-chair TS’s (1.2 - 2.9 kcal/mol) and exo-boat TS’s (0.9 - 2.6 kcal/mol) while having a smaller effect on the endo-chair TS’s (± 0.5 kcal/mol). The increase in Ea’s of the exo-chair TS’s are due (in part) to unfavorable 1,3-diaxial interactions with the pseudoaxial methyl group and axial ring hydrogens at C1 and C3 (for 1b and 4b). The 5-methyl endo-TS’s have the pseudo axial methyl group slightly canted away from the forming cyclohexyl ring. This increases the distance of the 1,3-diaxial interactions leading to smaller changes in the endo chair Ea’s with 5-methyl substitution. Interestingly the difference in Ea for the exo-chair and endo-chair in the hydrocarbons 1a (1.9 kcal/mol) and 1c (2.2 kcal/mol) is significantly smaller than the values for 3-oxa and 4-oxa compounds 4a (5.0 kcal/mol), 4c (5.3 kcal/mol) and 7a (4.0 kcal/mol). In the hydrocarbon radicals, the increase in the energy of the exo-chair Ea pathway with 5-methyl substitution is enough to raise the exo pathway above the endo pathway. In contrast 5- methyl substitution raises the Ea of the exo-chair pathway to a greater extent in the 3- and 4-oxa compounds than in the hydrocarbon radicals, but this increase is not enough to overcome the large initial energy difference favoring the exo-cyclization pathway for 3- and 4-oxa radicals. The result is that all 3- and 4-oxa radicals are predicted to cyclize to give almost exclusively exo products (cyclopentanes), while 5-methyl substituted hexenyl radicals 1b, and 1d should cyclize to give endo (cyclohexane) dominated product mixtures. Previously Houk’s force-field based calculations led him to explain the preference for exo closure for the 5-methyl-3-oxa radical 7b on
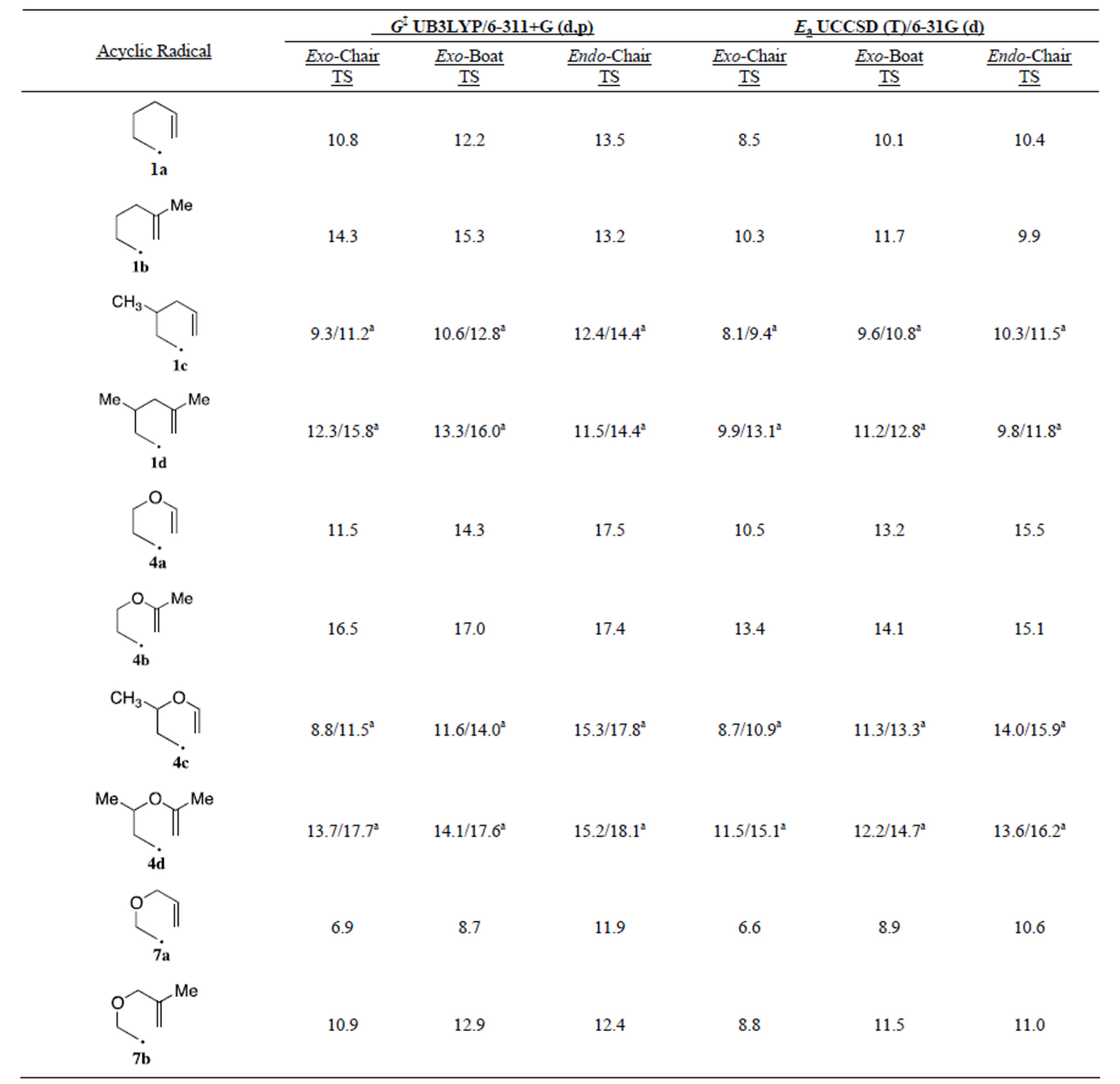
Table 2. Calculated activation energies (kcal/mol): Ea = E(acyclic radical) − E(transition state).
a. The first value is with the 3-methyl in the pseudo-equatorial position and the second value is with the 3-methyl in the pseudo-axial position.
decreased steric interactions for the exo-boat transition state with oxa versus methylene substitution at the 3-position. In contrast to our results, Houk found the exo-boat was the lowest energy transition state for both 7a and 7b.
Table 3 shows our calculated exo/endo product ratios (based on the relative Ea values) and compares these results with the available experimental data. While both the UB3LYP/6-311+G (d,p) and the UCCSD (T)/6-31G (d) calculations give excellent agreement with the experimental data, the UCCSD (T) calculations appear superior. Our calculations show that all 3-oxa and 4-oxa radicals should cyclize to give ≥95% exo products. The ratio for radical 4b stands out as the only entry that does not agree with the experimental data. In this case our calculations predict ~95% exo product and the reported value was 62%. Given the excellent agreement in the seven other cases for which we have both calculated and experimental endo/exo data suggests that there may be an error in the experimental determined value for 4b. In addition, we predict that the experimentally unobserved radical 1d will cyclize to produce an almost equal mixture of endo and exo products whereas the 4-oxa radical 4d should

Table 3. Exo/Endo product ratios.
cyclize with a strong preference for the exo pathway. The increased preference for exo cyclization with the 3- and 4-oxa substituted radicals make these systems well suited for the synthesis of tetrahydrofurans.
The exo cyclization of 3-methyl substituted radicals 1c and 4c can give either cis or trans substituted 1,3-dimethylcyclopentane 2c and 2,5-dimethyltetrahydrofuran 5c. The equatorial methyl exo-chair and the axial methyl exo boat transition states both lead to formation of the cis products, whereas the axial methyl exo-chair and equatorial methyl exo boat transition states lead to trans products. We calculated the cis/trans ratio by using a Boltzman distribution of DEa’s over the four exo transitions states. Our results give good-excellent agreement with the experimental data showing the strong preference for cis products (Table 4). The preference for cis products is driven by the dominance of the low energy equatorial methyl exo-chair pathway.
3.3. Activation Energies and Reaction Rates
The magnitude of the first order rate constant for cyclization is related to the lowest energy Ea. We have previously reported that 4-oxa radical 4a cyclizes 3.7 times slower than the hydrocarbon radical 1a [20]. We initially attributed this result to the less favorable nature of the nucleophilic radical adding to the electron rich vinyl ether double. Examination of the data from our calculations shows that the increase in the Ea’s for the three cyclization pathways for 4a compared to 1a is chiefly due to the lower energy of the conjugated vinyl ether linkage on the reactant acyclic radical. Table 5 compares the relative energies of isomeric radicals and their transition states. These data show that the vinyl ether linkage lowers the energy of the acyclic 4-oxa radicals 4a and 4b by ~6 kcal/mol compared to their isomeric 3-oxa radicals 7a and 7b. Radical 7a has been reported to cyclize ~40

Table 4. Cis/Trans product ratio for Exo-cyclizations.
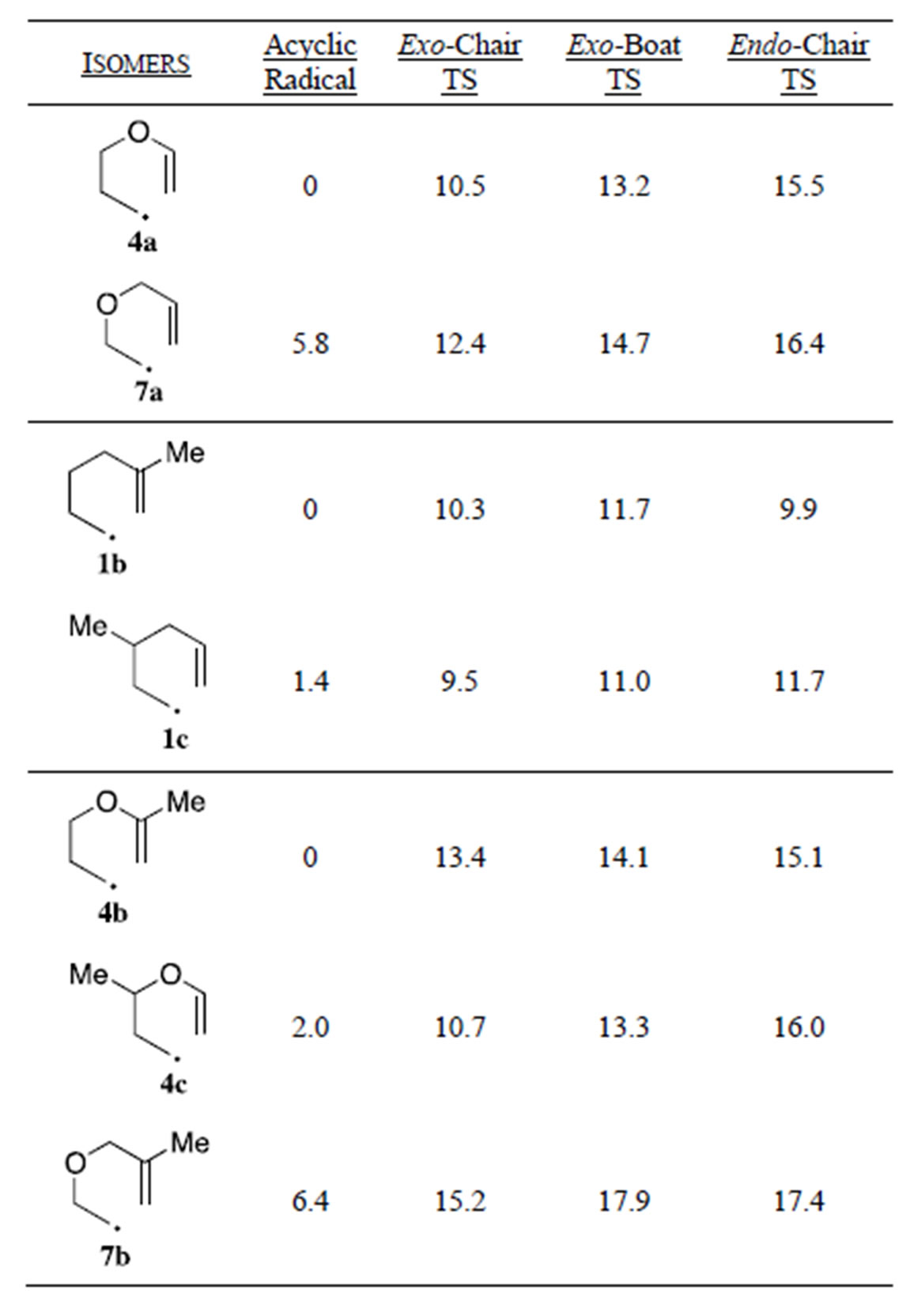
Table 5. Relative energies of hexenyl radical cyclization within isomeric compounds. (UCCSD (T)/6-31G(d), kcal/mol).
times faster than radical 1a [25], which is consistent with our finding that 7a has the lowest Ea value for all the cyclizations we have examined. It is interesting to note that all of the transition states for the cyclization of 7a are higher in energy than the respective transition states for 4a, but the large difference in the energy of the acyclic radicals give rise to smaller Ea’s and a faster rate of cyclization for 7a. The comparative rates of cyclization (7a > 1a > 4a) also correlate with the calculated DGrxn’s (the more exergonic cyclizations proceed faster).
An interesting feature of the 3-methyl substituted compounds (1c, 1d, 4c and 4d) is that they all have lower Ea’s for all three equatorial methyl transition states (exo-chair, exo-boat and endo-chair) when compared to the corresponding unmethylated compounds (e.g. 1a vs. 1c and 1d vs. 1b, etc). The equatorial 3-methyl group has little effect on the conformational energy and the geometry of the transition states. Therefore the lower Ea’s are principally the result of the increased conformational energy imposed by the methyl group on the acyclic starting radicals. This is analogous to the “gem dialkyl effect” [27], but here we see a substantial effect with only one substituent. The kinetic data is consistent with these findings: 4c cyclizes six times faster than 4a [20]; 1c cyclizes 3.2 times faster than 1a [24].
4. Conclusion
Our calculations show that the UB3LYP calculated transition state geometries are highly conserved across the three 5-hexenyl radical systems. We studied and the UCCSD (T) calculated Ea’s give excellent predictions for the exo/endo cyclization ratios. The increase in the preference for exo cyclization in the 3-oxa and 4-oxa radicals is due to the increased difference between the Ea’s for the exo-chair and endo-chair pathways. The high regioselectivity of these reactions make them well suited for the synthesis of tetrahydrofurans. The observed changes in the rates of cyclization for the 4-oxa and 3-methyl substituted radicals are primarily the result of differences in the relative energies of the starting acyclic radicals. These results highlight the importance of considering the effects of structural changes on both the starting material and the transition state when evaluating changes in activation energies.
5. Acknowledgements
We thank the National Science Foundation (Grant No. 0420717, for Beowulf Computer Cluster) and Oberlin College for financial support. We also thank Matthew Elrod for helpful discussions.
REFERENCES
- Z. Pianowski, L. Rupnicki, P. Cmoch and K. Stalinski, “Radical Cyclizations Leading to the Bicyclo[2.2.1]heptane Framework: A New Radical Approach to (+-(Z)- β-Santalol,” Synthetic Letters, Vol. 2005, No. 6, 2005, pp. 900-904.
- C. Zhou, O. Plashkevych and J. Chattopadhyaya, “Unusual Radical 6-Endo Cyclization to Carbocyclic-ENA and Elucidation of its Solution Conformation by 600 MHz NMR and Ab Initio Calculations,” Organic & Biomolecular Chemistry, Vol. 6, No. 24, 2008, pp. 4627- 4633. doi:10.1039/b813870b
- J. Hartung, R. Kneuer, C. Rummey and G. Bringmann, “On the 6-Endo Selectivity in 4-Penten-1-oxyl Radical Cyclizations,” Journal of the American Chemical Society, Vol. 126, No. 38, 2004, pp. 12121-12129. doi:10.1021/ja049010g
- J. C. Tripp, C. H. Schiesser and D. S. Curran, “Stereochemistry of Hexenyl Radical Cyclizations with tert-Butyl and Related Large Groups: Substituent and Temperature Effects,” Journal of the American Chemical Society, Vol. 127, No. 15, 2005, pp. 5518-5527.
- O. Moriya, Y. Urata, Y. Ikeda, Y. Ueno and T. Endo, “Synthesis of Tetrahydrofurans from Active Methylene Compounds via Radical Cyclization.” Journal of Organic Chemistry, Vol. 51, No. 24, 1986, pp. 4708-4709. doi:10.1021/jo00374a038
- S. J. Gharpure and S. K. Porwal, “Tandem Radical Cyclization-based Strategy for the Synthesis of Oxaand Aza-Cages: A Case of Fragmentation Versus Cyclization,” Tetrahedron Letters, Vol. 51, No. 25, 2010, pp. 3324-3329. doi:10.1016/j.tetlet.2010.04.081
- W. Du and D. P. Curran, “Synthesis of Carbocyclic and Heterocyclic Fused Quinolones by Cascade Radical Annulations of Unsaturated N-arylthiocarbamates, Thioamides and Thioureas,” Organic Letters, Vol. 5, No. 10, 2003, pp. 1765-1768. doi:10.1021/ol0344319
- B. M. Trost, H. C. Shen and J. P. Surivet, “Biomimetic Enantioselective Total Synthesis of (-)-Siccanin via the Pd-catalyzed Asymmetric Allylic Alkylation (AAA) and Sequential Radical Cyclization,” Journal of the American Chemical Society, Vol. 126, No. 39 2004, pp. 12565- 12579. doi:10.1021/ja048084p
- G. A. Kraus and J. Kim, “Synthesis of the Teracyclic Ring System of Cumbiasin A (II) via Tandem Radical Cyclizations,” Tetrahedron Letters, Vol. 47, No. 44, 2006, pp. 7797-7799. doi:10.1016/j.tetlet.2006.08.081
- A. L. J. Beckwith, C. J. Easton and A. K. Serellis. “Some Guidelines for Radical Reactions.” Journal of the Chemical Society, Chemical Communications, No. 11, 1980, pp. 482-483. doi:10.1039/c39800000482
- B. Giese, “Formation of CC Bonds by Addition of Free Radicals to Alkenes,” Angewandte Chemie International Edition English, Vol. 22, No. 10, 1983, pp. 753-764. doi:10.1002/anie.198307531
- J. M. Tedder and J. C. Walton, “The Importance of Polarity and Steric Effects in Determining the Rate and Orientation of Free Radical Addition to Olefins,” Tetrahedron, Vol. 36, No. 6, 1980, pp. 701-707. doi:10.1016/S0040-4020(01)93680-4
- A. L. J. Beckwith and C. H. Schiesser, “Regioand Stereo-Selectivity of Alkenyl Radical Ring Closure: A Theoretical Study,” Tetrahedron, Vol. 41, No. 19, 1985, pp. 3925-3941. doi:10.1016/S0040-4020(01)97174-1
- A. L. J. Beckwith and C. H. Schiesser. “A Force-Field Study of Alkenyl Radical Ring Closure,” Tetrahedron Letters, Vol. 26, No. 3, 1985, pp. 373-376. doi:10.1016/S0040-4039(01)80821-2
- D.C. Spellmeyer and K. N. Houk, “A Force-Field Model for Intramolecular Radical Additions,” Journal of Organic Chemistry, Vol. 52, No. 6, 1987, pp. 959-977. doi:10.1021/jo00382a001
- A. G. Leach, R. Wang, G. E. Wohlhieter, S. I. Khan, M. E. Jung and K. N. Houk, “Theoretical Elucidation of Kinetic and Thermodynamic Control of Radical Addition Regioselectivity,” Journal of the American Chemical Society, Vol. 125, No. 14, 2003, pp. 4271-4278. doi:10.1021/ja029342q
- D. Shanks, S. Berlin, M. Besev, H. Ottosson and L. Engman, “On the Origin of cis Selectivity in the Cyclization of N-protected 2-Substituted 3-Aza-5-Hexenyl Radicals: A Density Functional Study,” Journal of Organic Chemistry, Vol. 69, No. 5, 2004, pp. 1487-1491. doi:10.1021/jo030294h
- P. d’Antuno, A. Fritsch, L. Ducasse, F. Castet, P. James and Y. Landias, “Theoretical Study of Free-Radical-Mediated 5-Exo-Trig Cyclizations of Chiral 3-Substituted Hepta-1,6-dienes,” Journal of Physical Chemistry A, Vol. 110, No. 10, 2006, pp. 3714-3722. doi:10.1021/jp0549531
- C. W. Wu and J. J. Ho, “Calculated Effect of Subsitutions on the Regioselectivity of Cyclization of α-Sulfenyl-, α-Sulfinyl-, and α-Sulfonyl-(5R)-5-Hexenyl Radicals,” Journal of Organic Chemistry, Vol. 71, No. 26, 2006, pp. 9595-9601. doi:10.1021/jo061614a
- A. R. Matlin, K. F. Brinton and B. T. Nivaggioli, “Rule of Five Cyclizations in 5-Hexenyl Radicals and Photocycloadditions of 1,5-Hexadienes: Effect of 4-Oxa Substitution,” Journal of Physical Organic Chemistry, Vol. 20, No. 2, 2007, pp. 83-87. doi:10.1002/poc.1120
- Spartan08, Wavefunction Inc., Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O’Neill, R. A. DiStasio Jr., R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Z. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, “Advances in Methods and Algorithms in a Modern Quantum Chemistry Program Package,” Physical Chemistry Chemical Physics, Vol. 8, No. 27, 2006, pp. 3172-3191.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. AlLaham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, “Gaussian 03 Revision E.01,” Gaussian 03, Revision E.01, Gaussian, Inc., Wallingford, 2004.
- C. Walling and A. Cioffari, “Cyclizations of 5-Hexenyl Radicals,” Journal of the American Chemical Society, Vol. 94, No. 17, 1972, pp. 6059-6064. doi:10.1021/ja00772a020
- A. L. J. Beckwith, T. Lawrence and A. K. Serelis, “Stereoselectivity of Ring Closure of Substituted Hex-5-enyl Radicals,” Journal of the Chemical Society, Chemical Communications, Vol. 1980, No. 11, 1980, pp. 484-485. doi:10.1039/c39800000484
- A. L. J. Beckwith and S. A. Glover, “Determination of the Rates for Ring Closure of Oxygen Containing analogues of Hex-5-enyl Radicals by Kinetic E.S.R. Spectroscopy,” Australian Journal of Chemistry, Vol. 4, No. 1, 1987, pp. 157-173. doi:10.1071/CH9870157
- T. W. Smith and G. H. Butler, “Effect of Substituents on Ring Size in Radical Cyclizations. 1. Methyl vs. Phenyl,” Journal of Organic Chemistry.” Vol. 43, No. 1, 1978, pp. 6-13. doi:10.1021/jo00395a002
- E. L. Eliel, N. L. Allinger, S. J. Angyal and G. A., Morrison, “Conformational Analysis,” Wiley, New York, 1965, p. 191.
NOTES
*Corresponding author.

