Journal of Crystallization Process and Technology
Vol.04 No.04(2014), Article ID:50285,7 pages
10.4236/jcpt.2014.44022
Specific Surface Free Energy of As-Grown and Polished Faces of Synthetic Quartz
Takaomi Suzuki1*, Keiko Takahashi1, Masayuki Kawasaki2, Toshihiko Kagami2
1Faculty of Engineering, Shinshu University, Nagano, Japan
2Nihon Dempa Kogyo Co., Ltd. (NDK), Sayama, Japan
Email: *takaomi@shinshu-u.ac.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 July 2014; revised 23 August 2014; accepted 15 September 2014
ABSTRACT
Contact angles of water droplet on as-grown Z, +X, –X, and m faces of synthetic quartz crystals with growth term of 20 and 48 days, and polished Z, +X, –X, Y, and 45˚ cut faces of synthetic quartz crystal were observed. The average of the contact angles on as-grown Z, +X, and –X faces increased with the growth term, and they were larger than that on polished Z, +X, and –X faces. On the other hand, the average of the contact angles of water on m face decreased with the growth term, and they were smaller than that on polished Y cut face. Growth rate of the faces of synthetic crystals was measured and the order of growth rate was, m < –X < +X < Z. Specific surface free energy (SSFE) was calculated using Neumann’s equation. The SSFE of polished face was in the order of, m < –X < +X < Z, which corresponds to the order of the growth rate. The SSFE was larger for the face with larger growth rate.
Keywords:
Surface Free Energy, Quartz Crystals

1. Introduction
Specific surface free energy (SSFE) is significant value to discuss crystal growth thermodynamically, and SSFE is well discussed theoretically. However, experimental determination of SSFE of crystal is very few. One of the experimental trials to determine the surface energy of quartz crystal was performed by Brace and Walsh [1] . Brace and Walsh observed surface energy of quartz by introducing a single flat crack into a quartz crystal (Ob- reimoff-Gilman method). On the other hand, experimental study for SSFE of polymer surface using contact angle of liquid is well known and widely accepted [2] - [5] . We adopted the technique to determine the SSFE using the contact angle of liquids and determined the SSFE of as-grown face of synthetic ruby [6] and chlorapatite [7]
crystals, and reported that the crystals satisfy Wulff’s relationship, that is, SSFE is proportional to the grown length of the crystals. We also determined the SSFE of as-grown face of synthetic quartz crystal [8] and natural quartz crystals [9] . The surface of as-grown quartz crystal has hillocks, and hillocks have some different faces. This time we also determine the SSFE of polished cut plates in order to investigate the SSFE of flat face of quartz crystal.
2. Experimental Procedure
2.1. Sample Crystal
A single crystal of synthetic quartz was grown at NDK Co., Ltd., by the industrial hydrothermal method using NaOH solution [10] [11] . The crystals were grown from Z cut plate because quartz crystal has large growth rate in the direction of Z ax. Two crystals of which growth term are 20 days and 48 days were used. In order to estimate growth rate of the crystal face, the crystal was cut and the cross section of the crystal was polished. The boundary between the seed crystal and grown crystal became visible. The lengths of perpendicular lines from seed surface to each grown crystal face were measured. X, Y, Z, and 45˚ cut plates were also supplied by NDK Co., Ltd. These cut plates were polished as commercial optical device. The faces of X, Y, and Z cut plates are normal to X, Y, and Z axes. The face of 45˚ cut plate is intermediate between Z and Y axes as shown in Figure 1.
2.2. Measurement of Contact Angle
Water droplet was dropped on the face of crystal using a micropipet. The droplets sized −0.5 mm3 were observed using a digital camera (Canon ET-67B). The details of the measurement are described elsewhere [6] . We took more than 100 photographs for each crystal face and used the photographs in which the boundary between the liquid and solid was clearly recognized. The contact angles of the droplets were measured manually using a protractor and printed photographs.
3. Results and Discussion
3.1. Calculation of SSFE
The relationship between the surface tension and the contact angle is indicated by Young’s equation as the following:
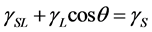 , (1)
, (1)
where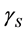 ,
, 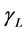 ,
, 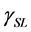 , and
, and 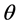 are the SSFE of solid, surface tension of liquid, interface tension between the solid and liquid, and contact angle, respectively. In order to determine the SSFE, Fowkes approximation is often used, and two kinds of liquid are used. For example, we determined the SSFE of synthetic quartz using water and formamide [8] . However this time we used water only, because contact angle of formamide was zero degree on some polished sample. Therefore, this time we adopted Neumann’s approximation to determine the SSFE using one kind of liquid [5] [7] . The SSFE could be calculated as following:
are the SSFE of solid, surface tension of liquid, interface tension between the solid and liquid, and contact angle, respectively. In order to determine the SSFE, Fowkes approximation is often used, and two kinds of liquid are used. For example, we determined the SSFE of synthetic quartz using water and formamide [8] . However this time we used water only, because contact angle of formamide was zero degree on some polished sample. Therefore, this time we adopted Neumann’s approximation to determine the SSFE using one kind of liquid [5] [7] . The SSFE could be calculated as following:
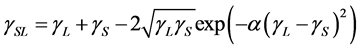 , (2)
, (2)
where 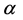 is a constant. This constant for quartz was calibrated as 0.0000278 (m2/mJ)2. Combining Equation (2) with Equation (1) yields
is a constant. This constant for quartz was calibrated as 0.0000278 (m2/mJ)2. Combining Equation (2) with Equation (1) yields
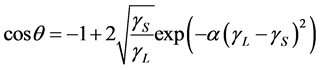 . (3)
. (3)
In this equation, only  is unknown, and it is a function of the contact angle,
is unknown, and it is a function of the contact angle,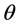 .
.
3.2. Z Face
The contact angles of the water droplets had a wide distribution on each face of the crystal. The measured contact angles of water droplets on the as-grown Z and polished Z cut face are shown in Figure 2. Averages and standard deviations of contact angles of water droplet on Z cut face and as-grown Z face of synthetic crystals
Figure 1. Schematic picture of synthetic quartz crystal and the cut plates.
Figure 2. Number of observation of contact angles of water droplet on (a) polished Z cut face, as-grown Z face of the crystal with growth term of (b) 20 days, and (c) 48 days.
with growth term of 20 and 48 days were 22 ± 2, 39 ± 6, and 47 ± 7 degree, respectively. Average of contact angle of as-grown Z face of 20 and 48 days grown is larger than that of polished Z cut face. The distribution of the contact angles is wider for the as-grown Z face than that of the polished Z cut face. The observed contact angle and the calculated SSFE summarized in Table 1.
Calculated SSFEs for Z cut, 20 and 48 days grown Z faces are 68 ± 1, 58 ± 4, and 53 ± 5 mN/m, respectively. Because the sample crystals were grown from Z cut plate, the SSFE of polished Z cut face is considered to be the SSFE of the seed crystal. The relationship between the average of SSFE and growth time is shown in Figure 3. The as-grown Z face has cobble texture and each cobble corresponding to a growth hillock with three-fold symmetry [10] [11] . The SSFE of flat Z face is considered to be the largest and the other faces has smaller SSFE than Z face. Therefore, SSFE of the as-grown Z face is smaller than polished Z cut face, and has wide distribution because of the wide variation of other faces.
Table 1. Average and standard deviation of contact angles of water on as-grown and polished faces of synthesized quartz crystal. SSFE’s calculated using the contact angles are also shown.
Figure 3. Relationship between the average contact angle of water and the growth term of the crystal face.
3.3. +X and –X Faces
The distributions of the contact angles of water droplets on +X face are shown in Figure 4. Averages and standard deviations of contact angles of water droplet on +X cut face and as-grown +X face of 20 and 48 days grown crystal were 26 ± 3, 48 ± 7, and 54 ± 6 degree, respectively. Average of contact angle for as-grown +X face of grown 20 and 48 days is larger than that of polished +X cut face. The distribution of the contact angles is wider for the as-grown +X face than that of the polished +X cut face. The distributions of the contact angles of water droplets on –X faces are shown in Figure 5. Average and standard deviation of the contact angle of water on the polished –X cut face and as-grown –X face of 20 and 48 days grown crystals were 34 ± 3, 39 ± 6, and 55 ± 4 degree, respectively. Average of the contact angles on as-grown +X and –X faces were larger than that on polished face and that was increased with the growth term.
Calculated SSFEs for polished +X cut, 20 and 48 days grown +X faces are 65 ± 1, 52 ± 5, and 48 ± 5 mN/m, respectively, and for polished –X cut, 20 and 48 days grown –X faces are 61 ± 2, 58 ± 4, and 47 ± 3 mN/m, respectively. The crystal was grown from Z cut plate, and Z cut plate has very narrow X and Y faces and it was
Figure 4. Number of observation of contact angles of water droplet on (a) polished +X cut face, as-grown +X face of the crystal with growth term of (b) 20 days, and (c) 48 days.
Figure 5. Number of observation of contact angles of water droplet on (a) polished –X cut face, as-grown –X face of the crystal with growth term of (b) 20 days, and (c) 48 days.
difficult to observe the contact angle of water on X or Y face of Z cut plate. Here, we postulated that the SSFE of polished X and Y cut face is regarded to the SSFE of X and Y face of the seed crystal. The relationship between the average of SSFE of ±X faces and growth term of each face is shown in Figure 3.
3.4. Y Face
The distributions of contact angles of water on the as-grown m and polished Y cut face are shown in Figure 6. Averages and standard deviations of contact angles of water droplet on Y cut face and as-grown m face of 20 and 48 days grown crystal were 82 ± 5, 53 ± 10, and 42 ± 6 degree, respectively. Average of the contact angles on Y cut face is much larger than that of other polished cut faces, as Z, +X, and –X faces. Average of the contact angles on as-grown m faces were larger than that on polished Y cut face, and that was increased with the growth term: average of the contact angles on m face of 20 days grown was 53 degree and that for 48 days grown was 42 degree. The distribution is wider for as-grown m face than that of polished Y cut face.
Calculated SSFE of polished Y cut face and m face of 20 and 48 days grown were 27 ± 4, 48 ± 7, and 56 ± 4 mN/m, respectively. The m face has growth hillocks with six vicinal faces. Each vicinal face shows the different step roughness. Because the flat m face, that is, polished Y cut face has the smallest SSFE, the SSFE of other faces of hillocks is larger than that of Y cut face. The SSFE of polished Y cut face can be regarded as that of seed crystal. The relationship between the SSFE and growth term is shown in Figure 3.
3.5. 45˚ Cut Face
The distribution of contact angles of water on the 45˚ cut face is shown in Figure 7. Averages and standard deviations of contact angles of water droplet was 33 ± 4 degree. SSFE of 45˚ cut face is calculated as 62 ± 2 mN/m. 45˚ cut face is geometrically intermediate between Y and Z face, and the SSFE of 45˚ cut face is also intermediate between the SSFE of Y and Z face. The average values and standard deviations of contact angles of water on each face are summarized in Table 1.
Figure 6. Number of observation of contact angles of water droplet on (a) polished Y cut face, as-grown m face of the crystal with growth term of (b) 20 days, and (c) 48 days.
Figure 7. Number of observation of water droplet on polished 45˚ cut face.
Table 2. Growth rate of each face of synthetic crystal with grown time of 20 days and 48 days (mm/day).
3.6. SSFE and Growth Rate
The growth rates of each face of 20 and 48 days grown crystal are summarized in Table 2. The value of growth rate was close to the reported value [12] . The order of growth rate was m < –X < +X < Z. As shown in Table 1, SSFE of polished face were 27 ± 4, 61 ± 2, 65 ± 1, and 68 ± 1 mN/m for Y, –X, +X, and Z faces. The order of SSFE is also m < –X < +X < Z. In our previous research, we determined the SSFE of as-grown face of synthetic quartz and compared with the growth rate [8] . The relationship between SSFE and growth rate was almost linear, and the surface with larger SSFE had larger growth rate. Because the growth rate of m face is the smallest and that of Z face is the largest, m cut face has the smallest and Z cut face has the largest SSFE.
4. Conclusion
Although the polished faces are flat enough by optical observation, there should be roughness in atomic scale. If the surface is ideally flat and uniform, the SSFE should be unique, and no distribution could be observed. However, the average value of SSFE of each polished face has obvious difference and reflects the difference of growth rate of each face.
References
- Brace, W.F. and Walsh, J.B. (1962) Some Direct Measurements of the Surface Energy of Quartz and Orthoclase. American Mineralogist, 47, 1111.
- Shimizu, R.N. and Demarquette, N.R. (2000) Evaluation of Surface Energy of Solid Polymers Using Different Models. Journal of Applied Polymer Science, 76, 1831-1845. http://dx.doi.org/10.1002/(SICI)1097-4628(20000620)76:12<1831::AID-APP14>3.0.CO;2-Q
- Li D., Moy E. and Neumann, A.W. (1990) The Equation of State Approach for Interfacial Tensions: Comments to Johnson and Dettre. Langmuir, 6, 885-888. http://dx.doi.org/10.1021/la00094a032
- Schultz, J., Tsutsumi, K. and Donnet, J.B. (1977) Surface Properties of High-Energy Solids: I. Determination of the Dispersive Component of the Surface Free Energy of Mica and Its Energy of Adhesion to Water and n-Alkanes. Journal of Colloid and Interface Science, 59, 272-276. http://dx.doi.org/10.1016/0021-9797(77)90008-X
- Kessaissia, Z., Papirer, E. and Donnet, J.B. (1981) The Surface Energy of Silicas, Grafted with Alkyl Chains of Increasing Lengths, as Measured by Contact Angle Techniques. Journal of Colloid and Interface Science, 82, 526-533. http://dx.doi.org/10.1016/0021-9797(81)90394-5
- Suzuki, T., Iguchi, E., Teshima, K. and Oishi, S. (2007) Wulff’s Relationship of Ruby Single Crystals Grown from Molybdenum Trioxide Flux Studied by Contact Angles of Liquid Droplets. Chemical Physics Letters, 438, 127-131. http://dx.doi.org/10.1016/j.cplett.2007.02.060
- Suzuki, T., Shimuta, M. and Oishi, S. (2006) Surface Free Energy and Morphology of Chlorapatite Crystals Grown from Sodium Chloride Flux. Bulletin of the Chemical Society of Japan, 79, 427-431. http://dx.doi.org/10.1246/bcsj.79.427
- Suzuki, T., Sugihara, N., Iguchi, E., Teshima, K., Oishi, S. and Kawasaki, M. (2007) Measurement of Specific Surface Free Energy of Ruby and Quartz Single Crystals Using Contact Angle of Liquids. Crystal Research and Technology, 42, 1217-1221. http://dx.doi.org/10.1002/crat.200711008
- Suzuki, T. and Kasahara, H. (2010) Determination of the Specific Surface Free Energy of Natural Quartz Crystals Using Measurement of Contact Angle of Liquid Droplets. Crystal Research and Technology, 45, 1305-1308. http://dx.doi.org/10.1002/crat.201000308
- Kawasaki, M., Onuma, K. and Sunagawa, I. (2003) Morphological Instabilities during Growth of a Rough Interface: AFM Observations of Cobbles on the (0 0 0 1) Face of Synthetic Quartz Crystals. Journal of Crystal Growth, 258, 188-196. http://dx.doi.org/10.1016/S0022-0248(03)01509-4
- Kawasaki, M. (2003) Growth-Induced Inhomogeneities in Synthetic Quartz Crystals Revealed by the Cathodoluminescence Method. Journal of Crystal Growth, 247, 185-191. http://dx.doi.org/10.1016/S0022-0248(02)01937-1
- Iwasaki, F., Iwasaki, H. and Okabe, Y. (1997) Growth Rate Anisotropy of Synthetic Quartz Grown in Na2CO3 Solution. Journal of Crystal Growth, 178, 648-652. http://dx.doi.org/10.1016/S0022-0248(97)00132-2
NOTES
*Corresponding author.










