ABSTRACT

The study of the calibration of a series of compounds of environmental concern (six perfluoroalkyl compounds (perfluorooctane sulfonic acid and five perfluoroalkyl carboxylic acids), three preservatives (methyl-, ethyl- and propylparabens) and the brominated flame retardant hexabromocyclododecane) by LC-MS/MS has been carries out, with a view to their simultaneous determination in samples of environmental interest. In some cases nonlinear calibration curves are obtained, but restricting the concentration range a linear model may be used to fit the data. Residual analysis has been performed in order to verify which models fit the data better, opting for a compromise decision given the apparent complexity of residuals plots. As Box states there are no perfect models (but models that work better than others).

Keywords:

Calibration, Non Linear Calibration, Residual Analysis, Liquid Chromatography-Tandem Mass Spectrometry, Emerging Pollutants

1. Introduction

Method validation is an important requirement in the practice of chemical analysis. General requirements in method validation for performance characteristics include, but are not limited to, linearity, accuracy, precision, sensibility and robustness [1] [2] [3] . Method validation is, therefore, an essential component of the measures that a laboratory should implement to allow it to produce reliable analytical data. This paper deals on the first ones: Linearity (calibration).

Calibration is an essentials part of every quantitative analytical method [3] - [10] and correct performance of the so important step is a critical part of method development and validation.

Calibration is a procedure to standardize the instrument by determining the deviation between a measurement system and a reference system represented by reference materials and their accepted values. Considering that the majority of analytical methods show linear relationships in one way of another, the recommended statistical methods to be used for the assessment of linearity are ordinary least squares regression or weighted least squares regression [3] .

Linearity is described as the ability of the method to elicit test results that are directly proportional to analyte concentration in a given range [5] [6] [7] . In practice, the range is the interval between the upper and lower levels of analyte for the intended analytical method, and for which acceptable precision and accuracy are obtained [3] .

However, for some analytical techniques, the relationship between the measured signals and the analyte concentrations is nonlinear and nonlinear or polynomial models are better fitted instead, i.e., a commonly observed phenomenon in atomic absorption spectrophotometry [8] is the ending of the calibration graph towards the concentration axis at elevated concentrations. In most real problems, the response becomes non-linear when the range of the calibration data becomes sufficiently large. In the field of liquid chromatography coupled to tandem mass spectrometry (LC-MS/MS) for instance matrix-related non-linearity can be observed [4] [11] [12] in several methods.

It is well known that when a wrong equation is fitted to data, the shape and the pattern of the residual plot contain valuable information that can be used to determine the way [13] - [20] in which the equation should be modified to achieve a better description of the data. So, residuals provide a convenient means of checking whether the calibration data is actually linear [21] [22] [23] [24] . The residuals are the vertical distances indicated in the y-direction between the points and the regression line (which gives a minimum sum of their squares) [21] . No rigorous mathematical treatment is required. If there is a true linear relationship between the variables with the error symmetrically distributed, residuals will be scattered randomly above and below zero, an equal number of plus and minus. Systematic deviations may indicate either a systematic error in the experiment or an incorrect or inadequate model. A curvilinear pattern in the residuals plot means that a non-linear curve, containing higher order terms, will be better fitted. A linear trend (descending or ascending) may indicate that an additional term in the model is needed. The “fan-shaped” residual pattern shows that experimental error increases with mean response (heteroscedasticity) so the constant variance assumption is inappropriate [21] . This last should be approach by weighted least squares method or by transforming the response.

Among the various statistical ways of numerically measuring some of the observed discrepancies, to date the most widely used method is still the visual examination of the residual plots because it gives more information in a direct way [21] . The simplest model or the model with the minimum number of parameters that adequately fit the data in question is usually the best choice [25] : “Non sunt multiplicanda entia praetor necessitaten” (Occam’s razor). However, things as we will have opportunity to see, are not always so simple and so easy.

The use of LC and MS have proved to be a powerful tool for the identification and quantification of these emerging pollutants in complex mixtures and/or for confirming their presence [26] [27] [28] . In this work, a LC-MS/MS preliminary study on compounds of environmental significance, i.e. perfluoroalkyl compounds, preservatives and brominated flame retardants, is carried out taken in mind their simultaneous determination in environmental samples because of their widespread use, potential toxicity, persistence or bioaccumulation [27] - [39] . Calibration curve were obtained and residual analysis [13] [14] has been applied in an attempt to check for model adequacy.

2. Simultaneous Determination of Three Parabens, Six Perfluoroalkyl Compounds and a Flame Retardant Made by LC-MS/MS

Calibration curves are prepared for the simultaneous determination of three parabens (methylparaben (MeP), ethylparaben (EtP), propylparaben (PrP)), six perfluoroalkyl compounds (perfluorooctane sulfonic acid (PFOS), perfluorooctanoic acid (PFOA), perfluoroheptanoic acid (PFHpA), perfluorohexanoic acid (PFHxA), perfluoropentanoic acid (PFPeA), perfluorobutanoic acid (PFBuA)) and a brominated flame retardant hexabromocyclododecane (HBCDD) by LC- MS/MS detection.

2.1. Brominated Flame Retardants

Brominated flame retardants are used in a wide variety of commercial products (furniture, plastics, fabrics, paints, electronic devices) to reduce their flammability [29] [30] . There are currently about 20 - 25 classes of brominated flame retardants, three of which are the main ones: tetrabromobisphenol A and its derivatives, polybrominated diphenyl ethers and hexabromocyclododecane (including three isomers). The concern for these compounds lies basically in their great ubiquity, since they have been detected in a wide range of human, animal and environmental samples [30] [31] . Indications of possible adverse effects [30] [31] [32] such as neurotoxicity, endocrine disruption and cancer have triggered the alarm and the consequent adoption of legislative measures for its control in water at European level [33] .

2.2. Perfluoroalkyl Compounds

Perfluorinated detergents are compounds for industrial use in a wide range of sectors. They are nowadays recognized as very dangerous pollutants and they are widely dispersed in the environment [34] . At the heart of the controversy are PFOS and PFOA. PFOS has been used as coolant, detergent, water and oil repellents, flame retardants, lubricants, adhesives, cosmetics, insecticides, etc. PFOA, on the other hand, is used in the manufacture of fluoropolymers (PTFE) and fluoroelastomers (PVDF) and also found used as fabrics, carpets, food containers, automobiles manufacture, etc. Both PFOA and PFOS compounds, according to recent studies, are toxic and persistent [31] [35] [36] , PFOA is also carcinogenic, and PFOS has a strong tendency to bioaccumulate.

2.3. Personal Care Products or Preservatives

Parabens (methyl, ethyl, propyl, benzyl, butyl parabens) are among the most commonly used synthetic preservatives in personal care cosmetics and pharmaceuticals, given their supposed low toxicity, broad spectrum of activity, inertia, widespread acceptance in international regulations, biodegradability and low cost [37] . But currently there is a tendency to avoid the use of these compounds due to increasing evidence of its effects of altering the endocrine system [38] [39] .

2.4. Materials and Methods

Reagents. The compounds studied (the parabens MeP, EtP and PrP, the perfluoroalkyl compounds PFOS, PFOA, PFHpA, PFHxA, PFPeA and PFBuA and the brominated flame retardant HBCDD) were supplied by Dr. Ehrenstorfer GmbH (between 97% - 99.5% purity). The stock solution of each compound (1000 mg/L) was prepared in methanol and stored in a refrigerator at 4˚C. Working solutions were prepared by diluting the stock standard solutions in methanol. Acetonitrile, water and methanol all of HPLC quality purity were supplied by Romil Ltd. (Barcelona, Spain). Ammonium acetate (reagent grade analysis) was supplied by Panreac (Barcelona, Spain).

Liquid chromatography and detector. High-resolution liquid chromatography (Agilent Series 1200, Agilent Technologies, Santa Clara, CA) equipped with a vacuum degasser, a binary pump, an autosampler and a thermostated column compartment (Figure 1). Zorbax Eclipse XDB C-18 Rapid Resolution column (50 × 4.6 mm i.d., 1.8 μm). Precolumn XDB C-18 (4 × 4 mm, 5 μm). Mass spectrometry detector (Agilent 6410 Series, Agilent Technologies, Santa Clara, CA) triple quadrupole (QqQ-MS) equipped with electrospray ionization source (ESI).

2.5. Chromatographic Analysis

Analytes were separated using an HPLC system equipped with XDB-C 18 column reverse column of 4.6 mm × 50 mm and 1.8 μm particle size (Agilent Technologies, Santa Clara, CA).

Our aim was to obtain high sensitivity and selectivity in a short time. First, the pH of mobile phase was studied and deionised water with different additives was studied as aqueous solvent. Acetic acid (from 0% to 0.2%, v/v), ammonia (from 0% to 0.050%, w/v) and mixtures of them (ammonium acetate) were assayed. Higher responses and better peak shapes were obtained using 10 mM ammonium acetate as aqueous solution and methanol as organicsolvent. Second, we analyzed the effect of substituting methanol for acetonitrile but no improvements were observed in peak shapes or resolution, so we selected the mobile phase previously mentioned. A linear gradient, as described in Table 1, was used. The flow rate was 0.6 mL/min.

Lastly, we increased the injection volume in order to enhance the analytical signal and consequently the limits of detection of the method. A range from 5 to 20 μL was analyzed and 20 μL was chosen as injection volume since a marked increase in sensitivity without loss of resolution was obtained. The increase of temperature from 30˚C to 50˚C did not improve significantly the characteristics of chromatographic method, therefore 30˚C was chosen as optimum.

The HPLC system is coupled to a triple quadrupole mass spectrometer with ESI working in negative mode. The parameters selected for the spectrometer are: capillary voltage, 3000 V; nebulizer pressure, 40 psig; drying-gas flow rate, 9.0 L/min and drying-gas temperature, 355˚C. The mode of operation of the spectrometer is MRM (Multiple Reaction Monitoring). Instrument control and data acquisition were carried out with Mass Hunter software (Agilent, USA). A previous optimization of the conditions of fragmentation was made using the Optimizer software. The MS/MS detection method was set up by continuous infusion of standard solutions of each individual compound (1 mg∙L⁻¹) to optimize the response of the precursor ion. The mass spectrometric conditions were optimized for each compound. ESI interface in positive and negative modes were evaluated. Negative mode was selected because it showed higher sensitivity for all compounds of interest. The two transitions, one for quantification and the other for confirmation, corresponding to the most abundant ion products were selected after the rupture of the precursor ion, in accordance with Decision 2002/657/EC [40] . The most abundant transition ion was selected to obtain maximum sensitivity for quantification. The parameters optimized for product ions were fragmentation voltage and collision energy. The parameters selected to obtain optimum responses are presented in Table 2. Figure 2 and Figure 3 show the mass spectrum corresponding to MeP and a chromatogram of a standard solution of the compounds under study, at a concentration of 100 ng/mL,

obtained after the fragmentation performed under the selected optimum conditions.

2.6. Standards for the Calibration Procedure

Prepare the calibration standards containing concentrations of the compounds in the concentration ranges 1 to 1500 ng/mL. Use methanol as solvent.

2.7. Calibration Curves

They are obtained from the peak areas of MRM (Multiple Reaction Monitoring) chromatograms. The results obtained are shown in Table 3, and are shown in Figures 4-6.

3. Results and Discussion

A glance at Figures 4-6 reveals that the pattern of the residuals obtained by simple linear regression is clearly curvilinear in all cases except for MeP, EtP and HBCDD, which is not surprising given the wide concentrations range used in the calibration process. This is, moreover, typical in instrumental analysis [8] [9] [11] [12] , as has been indicated previously. It may also stressed that the dispersion of the measurements in terms of absolute standard deviation increases with increasing concentration, a circumstance also typical in instrumental analysis, and specifically in LC-MS-MS. Figure 7 and Figure 8 plot the standard deviation (SD) and the coefficient of variation (CV = SD/MEAN), for the sake of comparison, determined from quatriplicate standard measurements (see Table 3) during the same day and at the concentration ranges from 1 to 1500 ng/mL. This leads us, once found the appropriate model, to the need to apply the weighted least squares method in the calibration process, once the Cochran test shows that the variances are not homogeneous. The coefficient of variation (relative standard deviation) can be considered constant in all the cases, except at low concentrations, in which an increase of the same takes place (Figure 7 and Figure 8). This circumstance is also typical of the instrumental analysis [21]

[22] [23] , provided that the concentrations are sufficiently high. The PFOA shows an abnormal behaviour in this sense, since its CV first decreases and then increases.

It has been tried to establish a linear range of work in a smaller range of concentrations, eliminating for that in the calibration curve the points placed to the concentration 1000 and 1500 ppb (Figures 9-11). Although the R² values thus

obtained are greater than 0.99 in most cases, the residuals show in this case an upward or downward trend. In cases where the curvature is apparent, a quadratic equation model (second degree polynomial) to the data (Figure 12), obtaining a considerable improvement in the values of R², being these of the order of 0.999, being the residuals above and below the zero, but not in a typical random pattern. This situation is not corrected with higher polynomial models, or with rational models [24] [41] of the type

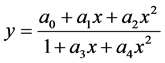(1)

As stated by Box: “There are no perfect models, but models that fit better than others” [42] [43] [44] . Linear or quadratic models, simpler, allow the calculation of concentrations with the required accuracy at the level of ppb, in which we are involved. The search of possible causes due to this phenomenon, as well as weighting factors to apply in the calibration and an analysis of the data in depth will be object of further search.

4. Final Comments

Calibration is an essentials part of every quantitative analytical method and correct performance of the so important step is a critical part of method development and validation. Analytical chemists are often interested in the fitting of mathematical equations to experimental data [6] [8] [17] [18] [21] [22] [23] .

The least squares method is widely used to find or estimate the numerical values of the parameters to fit a function to a set of data and to characterize the statistical properties of estimates. In spite of this, common situations when working with LC-MS/MS or absorption spectrophotometry that may be described by functional relationships include calibration curves relating measured values of response to a property, which may be nonlinear [4] [8] [11] [12] [24] [41] .

In most of situations, a statistical test for linearity between the variables is rarely undertaken in analytical studies despite the frequent assumption that such linearity prevails. Taylor and Schutsyer [45] quoted in 1986: “Although the theory concerning regression has since long been described, many errors can still be

encountered when it is applied to solve problems in analytical chemistry.”

Residual analysis is a very useful tool that helps select the model that fit more adequately the data. In considering residuals, a qualitative approach is often the most revealing and informative.

In many chemical, pharmaceutical and biological applications the use of LC and MS have proved to be a powerful tool for the identification and quantification of multiresidue compounds in complex mixtures and numerous new methods are developed and validated daily. So that, a preliminary study on the simultaneous determination of compounds of environmental significance (sixperfluoroalkyl compounds, three preservatives and a brominated flame retardant) by LC-MS/MS has been carried out in this work. For calibration purposes, nine concentration levels were prepared and calibration curve was built. Most of the studied compounds show curvilinear calibration curves, which is not surprising given the wide concentrations range used. By restricting the concentration range a linear region may be sometimes choice to determine some of the compounds of environmental concern subject to study in this paper. By using parabolic regression, the dynamic range of some of the standard curves may be broader.

Note that the best choice from a practical point of view is the simplest model, which fit properly the data, in agreement with the parsimony principle (Occam’s razor) [25] . However, things are no easy. As stated by Box [42] [43] [44] “all models are wrong”. There are no perfect models, but model that are more adequate than others.

Cite this paper

Martin, J., Gracia, A.R. and Asuero, A.G. (2017) Fitting Nonlinear Calibration Curves: No Models Perfect. Journal of Analytical Sciences, Me- thods and Instrumentation, 7, 1-17. https://doi.org/10.4236/jasmi.2017.71001

References