Received 22 October 2015; accepted 11 December 2015; published 14 December 2015

ABSTRACT

The correct approach, based on the rules of conservation and detailed physicochemical/thermo- dynamic knowledge on the system considered is opposed to conventional approach to solubility and dissolution, based on stoichiometry of a reaction notation and on the solubility product (K_sp) of a precipitate. The correct approach is realized according to Generalized Approach to Electroly- tic Systems (GATES) principles, with use of iterative programs applied for computational purposes. All the qualitative and quantitative knowledge is involved in the balances and independent ex- pressions for the equilibrium constants. Three two-phase electrolytic systems with diversified chemical properties were selected carefully, from the viewpoint of their diversity. The results of calculations are presented graphically and discussed. The advantages of the GATES in resolution of two-phase (static) non-redox systems and one complex (dynamic) redox system are proved.

Keywords:

Solubility, Dissolution, GATES

1. Introduction

The problem of solubility of chemical compounds occupies a prominent place in the scientific literature. This stems from the fact that among various properties determining the use of these compounds, the solubility is one of paramount importance. The distinguishing feature of a sparingly soluble (hydr) oxide [1] or a salt, is the solubility product K_sp value of this precipitate. However, it is not the only parameter defining the real solubility s [mol/L] of the precipitate in two-phase system. Such “simplifications” made e.g. in [2] , are unacceptable and give incorrect results, as proved in [3] -[6] . These objections, formulated in the light of the GATES [7] , are presented also in the current paper, related to two static non-redox systems, and one dynamic redox system.

The systems with three precipitates considered in details herein, namely: nickel dimethylglyoximate (NiL₂), struvite (MgNH₄PO₄) and copper (I) iodide (CuI), considered, illustrate different behavior of the solid phases in the related media. All soluble species formed by ions constituting a precipitate are involved in expression for solubility of the precipitates. NiL₂ is considered in context with gravimetric analysis of Ni²⁺ ions when treated with an excess of precipitating agent. The contact of struvite with pure water or CO₂ solution imitates the washing stage; it is stated that the struvite is not an equilibrium solid phase in the related systems. The solubility of CuI present in the system in two consecutive stages of four-stage titrimetric procedure is affected also by the components formed on earlier stages of this procedure.

2. Solubility and Dissolution

2.1. Preliminary Remarks Related to the Solubility Concept

One can consider two consecutive steps justifying calculation of the solubility of precipitates. This calculation is important from the viewpoint of gravimetry, where quantitative transformation of an analyte into sparingly soluble precipitate occurs. These steps are involved with 1) an excess of the precipitating agent added; 2) removing of this excess and of some other soluble species after washing the precipitate. Realization of the second step is practically equivalent to the addition of an excess of the precipitate into pure water.

The precipitates will be denoted below in bold letters.

The precipitation and further analytical operations made in gravimetric analyses (filtration, washing) are usually carried out at temperatures ca. 60˚C - 80˚C, i.e., far greater than the room temperature, at which the equilibrium constants values, known from the literature data, were determined, and then applied in calculations. On both steps, the solubility s [mol/L] of the precipitate should be considered as the sum of concentrations of all soluble species formed by the analyte in the liquid phase (solution). However, the results thus obtained may be helpful in the choice of optimal a priori conditions of the analysis, ensuring minimal solubility of the precipitate.

In literature, e.g. [2] [8] [9] , and in numerous educational links offered in Internet networks [10] devoted to equilibria with a solid phase involved, one can prevalently find the approach to the calculation of solubility (s^*, mol/L) of pure precipitate when introduced in excess into pure water; this approach is based on the stoichiometric reaction notation, involved with dissociation of the precipitate. Thus for A_aB_b = aA + bB, we have

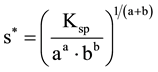(1)

and for A_aB_bC_c = aA + bB + cC, we have

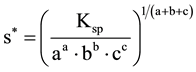(2)

That approach was widely criticized in [11] .

As a rule, Equations (1) and (2) are invalid for different reasons. This invalidity results, among others, from inclusion of minor species in Equations (1) and (2); other soluble species formed by A and B are thus omitted. In other words, not only the species entering the expression for the related solubility product are present in the solution considered.

As indicated e.g. in [12] , different solid phases may be formed in the system in question, depending on pH of the solution. This raises further, serious problems involved with calculating of the solubility s^* value. Namely, in Equation (1) or (2) it is assumed, that a solution formed after introducing a precipitate into pure water is saturated with respect to this precipitate; this fundamental requirement is not often fulfilled. For example, pure struvite MgNH₄PO₄ when introduced into pure water is not the equilibrium solid phase [13] . This effect, confirmed by evolution of ammonia on the step of washing this precipitate with water [14] , can be explained by the reaction [1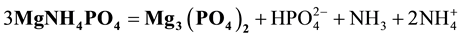3] .

(3)

Therefore, the formula s^* = (K_sp)^1/3, obtained from Equation (2) at a = b = c = 1 and related to

(4)

is inapplicable for calculation of solubility of struvite, for the reasons specified above. Nonetheless, it is still quoted in different papers, e.g. [15] [16] , and Internet [17] .

2.2. Solubility of Nickel Dimethyglyoximate (NiL₂)

In an immediate experimental option, nickel dimethylglyoximate NiL₂ (=C₈H₁₄N₄O₄Ni, named commonly as nickel dimethylglyoxime, see e.g. [18] [19] ) is precipitated after addition of an excess of dimethylglyoxime (HL = CH₃C(NOH)C(NOH)CH₃) [20] into Ni²⁺ solution with ammonia buffer. Protons liberated in reaction Ni²⁺ + 2HL = NiL₂ + 2H⁺ are bound in reaction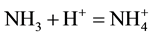; the buffer pair 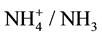added in excess gives pH ca. 9 - 9.5, as a rule. In analytical practice, another manner of NiL₂ precipitation is applied [21] .

A remark. The term: nickel dimethylglyoxime is incorrect. Dimethylglyoxime is the name of the precipitating reagent and NiL₂ is the salt. The names of the salts are formed by addition of ending -ate to the cores of oxyacids, e.g. copper oxyquinolinate [22] , or more properly as copper 8-quinolate [23] . The name copper 8-hy- droxyquinoline [24] is not correct, too; Cu²⁺ replaces here two protons from ?OH groups of two molecules of 8-hydroxyquinoline. Copper 8-hydroxyquinoline is not a synonym for properly written terms: bis(8-oxyquino- line)copper, copper oxinate [24] ; oxine is the shortest name of 8-hydroxyquinoline [25] . Compare with sulfate, nitrate.

The logs vs. pH relationships presented in Figure 1, refer to the systems with C_Ni mol/L NiSO₄ and other components indicated in the legend. The plots refer to the equilibrium data taken from [26] , related to room temperature. The soluble Ni-species enter the formula

(5)

for the solubility s of NiL₂ and ascribed to the curve c in Figure 1, where H₄Ci-citric acid. At equilibrium we have: [NiL₂] = K₂∙[Ni²⁺][L⁻]² = K₂∙K_sp, where K₂ = 10^17.24, K_sp = [Ni²⁺][L⁻]² = 10^−23.66 [5] [6] , and then [NiL₂] = 10^−6.42 (i.e., log[NiL₂] = −6.42). The [NiL₂] value is the limiting component in expression for the solubility s of NiL₂ (Equation (5)), i.e. min s @ [NiL₂]. In context of Equation (5) with Figure 1, we see that the soluble complex NiL₂ is the predominant species for pH > 5.5 (curves a and b), and pH > 8 (curve c); i.e., the effect of NiH_iCit⁺ⁱ⁻² species on the s-value is negligible in ammonia buffer media.

Calculations of solubility s were made here at C_Ni = 0.001 mol/L and C_L = 0.003 mol/L HL, i.e., at the excessive HL concentration equal C_L − 2C_Ni = 0.001 mol/L. Solubility of HL in water, equal 0.063 g HL/100 mL H₂O (25˚C) [27] , corresponds to concentration 0.63/116.12 = 0.0054 mol/L of the saturated HL solution, 0.003 <

0.0054. Applying higher C_L values, needs the HL solution in ethanol, where HL is fairly soluble. However, the aqueous-ethanolic medium is thus formed, where equilibrium constants are unknown. To avoid it, lower C_Ni and C_L values were applied in calculations.

2.3. Dissolution of Struvite

After introducing pr1 = MgNH₄PO₄ into water, at initial concentration of pr1 equal C₀ = [pr1]_t=0 = 10⁻³ mol/L (pC₀ = (ppr1)_t=0 = 3; ppr1 = −log[pr1]), the precipitation of pr2 = Mg₃(PO₄)₂ starts (Equation (3)) at ppr1 = 3.088; solubility products for other solids as pre-assumed precipitates are not crossed [13] . The expression for solubili-

ty s, in absence of carbonate species (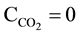, i.e.,),

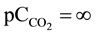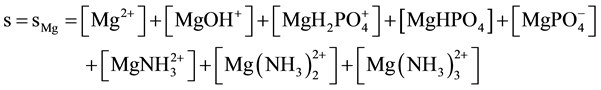(6)

involving all soluble magnesium species, is identical in its form, irrespectively on the equilibrium solid phase(s) present in this system. Moreover, it is stated that pH of the solution equals ca. 9 - 9.5 (Figure 5 in [13] ); this

pH can be affected by the presence of CO₂ from air, i.e., at. Under such conditions, NH₄⁺ and NH₃ are at comparable concentrations, 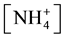≈ [NH₃], but 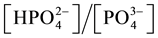= 10^12.36−pH ≈ 10³. This way, the scheme MgNH₄PO₄ = Mg²⁺ + NH₃ + 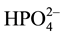would be more advantageous than one given by Equation (4), with, provided that struvite is the equilibrium solid phase; but it is not the case, see above;,.

The reaction 3 occurs also in presence of CO₂ in water, where struvite was introduced; . Struvite is the equilibrium solid phase only at a due excess of at least one of the precipitating reagents [13] [28] [29] . It was noticed that the system obtained after mixing magnesium, ammonium and phosphate salts at the molar ratio 1:1:1 contains an excess of ammonium species in the solution and the precipitate that “was not struvite, but was probably composed of magnesium phosphates” [14] was obtained; it confirms the data obtained from [13] . Such inferences were formulated on the basis of X-ray diffraction (XRD) [30] - [32] of the crystallographic structure of the solid phase thus obtained. This remark is important in context with gravimetric analysis of magnesium as pyrophosphate [13] .

The behavior of the system can be formulated on the basis of formulas similar to those presented in [13] and referring to the system where pure pr1 is introduced into aqueous solution with dissolved CO₂ (mol/L) + KOH (C_b mol/l); initial (t = 0) concentration of MgNH₄PO₄ in the system equals C₀ mol/L. We apply here the notations [13] :

, , ,

, , .

At (pC₀, , pC_b) = (2, 2, ¥); after the solubility product for pr3 attained (line ab at ppr1 = 2.376), pr3 is

the equilibrium solid phase up to ppr1 = 2.393 (line cd), where the solubility product for pr2 is attained, see Figure 2 and Figure 3. For ppr1 Î <2.393, 2.506>, two equilibrium solid phases (pr2 and pr3) exist in the system. Then, at ppr1 = 2.506 (line ef), pr3 is totally depleted, and then pr1 is totally transformed into pr2. At ppr1 > 2.506, only pr2 is the equilibrium solid phase. On particular steps, the following, predominating reactions occur:

(7)

(8)

(9)

(10)

The pH vs. ppr1 relationship is presented in Figure 4.

At (pC₀, , pC_b) = (2, 4, 2), the dissolution process consists on three stages (Figure 5 and Figure 6). On the stage 1, pr4 precipitates first

(11)

nearly from the very start of pr1 dissolution, up to ppr1 = 2.151, where K_sp2 for pr2 is attained. Within the stage 2, the solution is saturated toward pr2 and pr4. On this stage, the reaction, expressed by the notation

(12)

occurs up to total depletion of pr4 (at ppr1 = 2.896), see Figure 6. On the stage 3, the reaction

(13)

occurs up to total depletion of pr1, i.e., solubility product (K_sp1) for pr1 is not crossed. The pH changes, occurring during this process, are presented in Figure 7.

On the stage 1, pr4 precipitates first, , nearly from the very start of pr1 dissolution, up to ppr1 = 2.151, where K_sp2 is attained. Within the stage 2, the solution is saturated toward pr2 and pr4. On this step, the reaction expressed by the notation 2pr1 + pr4 = pr2 + 2NH₃ + 2H₂O occurs up to total depletion of pr4 (at ppr1 = 2.896). On the stage 3, the reaction occurs up to total depletion of pr1, i.e., the solubility product K_sp1 for pr1 is not crossed.

The curve s’ (Figure 6) is related to the function

(14)

where s is expressed by Equation (6).

2.4. Solubility of CuI in a Dynamic Redox System

General Remarks

The system considered in this section is related to iodometric, indirect analysis of an acidified (H₂SO₄) solution of CuSO₄ [33] . On the preparatory step, an excess of H₂SO₄ is neutralized with NH₃ until a blue colour appears, which is derived from complexes. Then CH₃COOH is added, to attain a pH ca. 3.6. After subsequent introduction of an excess of KI solution, the mixture with CuI precipitate and dissolved iodine formed in the reactions:

(15)

(16)

is titrated with Na₂S₂O₃ solution, until the reduction of iodine:

(17)

(18)

is completed. The reactions (17) and (18) proceed quantitatively in neutral or mildly acidic solutions, where the thiosulphate species are in a metastable state. In strongly acidic media, thiosulphuric acid disproportionates according to the scheme H₂S₂O₃ = H₂SO₃ + S [34] .

The analytical procedure involved with this system consists of the following stages (all concentrations specified below are expressed in mol/L):

Ÿ stage 1: addition of V mL of NH₃ (C₁) into V₀ mL CuSO₄ (C₀) + H₂SO₄ (C₀₁);

Ÿ stage 2: addition of V mL of CH₃COOH (C₂) into V₀ + V_N mL of the resulting solution;

Ÿ stage 3: addition of V mL of mol/L KI (C₃) into V₀ + V_N + V_Ac mL of the resulting solution;

Ÿ stage 4: addition of V mL of mol/L Na₂S₂O₃ (C) into V₀ + V_N + V_Ac + V_K mL of the resulting solution.

In this system, CuSO₄ (C₀) + H₂SO₄ (C₀₁) is considered as the sample tested; V_N is the total volume of NH₃ (C₁) added in stage 1; V_Ac is the total volume of HAc = CH₃COOH (C₂) added in stage 2; V_K is the total volume of KI (C₃) added in stage 3. The non-redox stages (1 and 2) are then followed by the redox stages (3 and 4). In the calculations, the concentrations [mol/L]: C₀ = 0.01, C₀₁ = 0.01, C₁ = 0.25, C₂ = 0.75, C₃ = 2.0, C₄ = C = 0.1, and volumes [mL]: V₀ = 100, V_N = 20, V_Ac = 40, V_K = 20 were assumed. For further details-see [33] .

To keep track of the gradual changes affected by addition of reagents in this system, it was assumed that the solutions of these reagents (NH₃, CH₃COOH, KI, Na₂S₂O₃) are added according to titrimetric mode.

The solution on the i + 1-th step contains new Cu-species in comparison with the i-th stage (i = 1, 2, 3). Maximal volumes on the abscissas for the stages 1, 2 and 3, are equal to V_N, V_Ac and V_K respectively, assumed in the analysis; then e.g., log[CuCH₃COO⁺] at V = V_Ac in stage 2 is equal to log[CuCH₃COO⁺] at V = 0 in stage 3.

At each stage, the variable V is considered as a volume [mL] of the solution added, consecutively: NH₃, CH₃COOH, KI and Na₂S₂O₃, although the true/factual titrant in this method is the Na₂S₂O₃ solution, added on the stage 4.

The results of calculations are presented graphically in Figures 8-10.

It is a very interesting system, both from analytical and physicochemical viewpoints. Because the standard potential E₀ = 0.621 V for (I₂, I⁻) exceeds E₀ = 0.153 V for (Cu²⁺, Cu⁺), one could expect, at a first sight, the oxidation of Cu⁺ by I₂. However, such a reaction does not occur, due to the formation of sparingly soluble CuI precipitate (pK_sp = 11.96).

The solubility s [mol/L] of CuI in this system is put in context with the speciation diagrams presented in Figure 8. This precipitate appears in the initial part of titration with KI (C₃) solution (Figure 9(a)) and further it accompanies the titration, also in the stage 4 (Figure 9(b)). Within the stage 3, at V ³ 0.795 mL, we have

(19)

and on the stage 4

(20)

Small concentration of Cu⁺ (Figure 8, stage 3) at a relatively high total concentration of Cu²⁺ determines the potential ca. 0.53 - 0.58 V, [Cu²⁺]/[Cu⁺] = 10^{A(E − 0.153)}, see Figure 9(a). Therefore, the concentration of Cu(+2) species determine relatively high solubility s in the initial part of stage 3. The decrease in s value in further parts of the stage 3 is continued in the stage 4, at V < V_eq = C₀V₀/C = 0.01 × 100/0.1 = 10 mL. Next, a growth in the solubility s₄ at V > V_eq is involved with formation of thiosulfate complexes, mainly. The species and I₂ are consumed during the titration on the stage 4 (Figure 8(d)). A sharp drop of E value at V_eq = 10 mL (Equation (8)) corresponds to the fraction titrated F_eq = 1.

The course of the E vs. V relationship within the stage 3 is worth a remark (Figure 10(a)). The corresponding curve initially decreases and reaches a “sharp” minimum at the point corresponding to crossing the solubility product for CuI. Precipitation of CuI (Equations (9) and (10)) starts after addition of 0.795 mL of 2.0 mol/L KI (Figure 10(c)). Subsequently, the curve increases, reaches a maximum and then decreases. At a due excess of the KI (C₃) added on the stage 3 (V_K = 20 mL), solid iodine (I₂, of solubility 0.00133 mol/L at 25˚C) is not precipitated.

The solubility curves are related to an excess of KI as the precipitating agent; such a case occurs at V ≥ C₀V₀/C₃ = 0.5 mL. Because 0.5 < 0.795, it means that the stoichiometric excess includes herein the entire V-range where CuI is the equilibrium solid phase, i.e. V ≥ 0.795.

3. Final Comments

The paper criticizes the description of two-phase electrolytic systems, of different degree of complexity, based on stoichiometric reaction notation (Equation (1) or (2)). Even in relatively simple cases, this scheme leads to an incorrect assessment of the real solubility, s.

Instead of that (schematic) approach to the issue, the calculations of s, based on the matter and charge conservation, with all attainable physicochemical knowledge involved in complete set of equilibrium constants related to the system in question, is suggested. The solubility s is expressed as total concentration of all species formed by a given element in the solution in equilibrium with a sparingly soluble precipitate, not only the species specified in the related reaction notation, as were practiced hitherto. Diversity of K_sp value that depends on the dissociation reaction notation, disqualifies the calculation of s^* on the basis of K_sp value. Generalizing, nearly all approximate formulae applied for calculation of solubility on the basis of stoichiometric dissociation reactions are worthless.

In relatively simple systems [5] -[7] , the procedure based on calculation of pH = pH₀ value zeroing charge balance equation can be applied for calculation of concentrations for all the species involved in expression for solubility s value. More complex two-phase systems require a calculation procedure based on iterative computer programs, offered e.g. by MATLAB [7] , applied to algorithms based on principles of the Generalized Approach to Electrolytic Systems (GATES). The MATLAB was applied, among others, to monitor processes in non-equi- librium systems; such systems are exemplified by the system obtained after introduction of struvite into water, or to a solution with pre-assumed composition. On the basis of calculations and graphical presentation of the results thus obtained, one can track phase transitions in the system, assuming quasistatic course of the relevant processes, realized under isothermal conditions.

Cite this paper

Anna MariaMichałowska-Kaczmarczyk,TadeuszMichałowski,MarcinToporek,AndrzejPietrzyk, (2015) Solubility and Dissolution in Terms of Generalized Approach to Electrolytic Systems Principles. Journal of Analytical Sciences, Methods and Instrumentation,05,47-58. doi: 10.4236/jasmi.2015.54006

References

NOTES

^*Corresponding author.