Journal of Analytical Sciences, Methods and Instrumentation
Vol.4 No.2(2014), Article
ID:46335,7
pages
DOI:10.4236/jasmi.2014.42006
Compact Formulation of Redox Systems According to GATES/GEB Principles
Anna Maria Michałowska-Kaczmarczyk1, Tadeusz Michałowski2
1Department of Oncology, The University Hospital in Cracow, Cracow, Poland
2Faculty of Engineering and Chemical Technology, Cracow University of Technology, Cracow, Poland
Email: michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 March 2014; revised 19 April 2014; accepted 25 April 2014
ABSTRACT
The Generalized Electron Balance (GEB), together with charge balance and concentration balances, completes the set of equations needed for resolution of electrolytic redox systems. The general formulae for GEB were obtained according to Approach II to GEB, i.e., on the basis of the equation 2∙f(O) − f(H) obtained from elemental balances: f(H) for H, and f(O) for O. Equivalency of the Approach II and the Approach I to GEB was proved for an aqueous solution and a binary-solvent system. On this basis, a compact form of GEB was derived.
Keywords:Electrolytic Redox Systems, Generalized Electron Balance

1. Introduction
The mathematical description of electrolytic redox systems in aqueous media is realizable with use of the set of equations composed of Generalized Electron Balance (GEB), charge balance, and elemental balances, related to elements E(i) different from H and O [1] -[4] . Ultimately, all the balances are expressed in terms of molar concentrations. The GEB concept can be extended on non-aqueous and mixed-solvent media (binary-solvent systems, in particular), where amphiprotic solvents/co-solvents are involved [5] . The charge balance is based on the principle of electroneutrality of the solution, whereas elemental balances express the preservation of particular elements in the closed system, separated from its environment by diathermal walls; it enables any process in the system to proceed under isothermal conditions. It will also be assumed that none nuclear transformations occur for all elements of the system.
Concentrations of the species in the appropriate equations are also involved in dependencies resulting from the expressions for the equilibrium constants. Because the equilibrium constants are dependent (among others) on the temperature, the assumption concerning the possibility of carrying out the process under isothermal conditions is advisable.
In the papers issued previously (and ones cited mainly in [1] [3] ), two approaches to GEB, named as Approach I and Approach II, were introduced. The Approach I (named as “short” version of GEB) is based on the principle of common pool of electrons, and applicable in the cases where oxidation numbers for all elements in the redox system considered are known beforehand. Combination 2f(O)-f(H) of elemental balances: f(H) for H and f(O) for O is the quintessence of the Approach II to GEB. The fundamental advantage of the Approach II (in context with the Approach I) to GEB is that none prior knowledge on oxidation degrees of elements in complex species of definite elemental composition and charge is needed. Also the terms: “oxidizer” and “reductant” are not applicable as starting terms in considerations on redox systems. These facts are of capital importance, when redox equilibria in the systems with complex organic species, involving radicals and ion-radicals, are considered. Both approaches were realized in numerous examples, where results of calculations obtained according to iterative computer programs [4] [6] were illustrated graphically. In the algorithms applied in calculations, all attainable physicochemical knowledge was involved. This knowledge is of qualitative (particular species) and quantitative (equilibrium constants) nature. For example, in the system where the acidified (H2SO4) solution of FeSO4 + H2C2O4 is titrated with KMnO4, we have 41 species and 29 equilibrium constants, whereas in the system CuSO4 + H2SO4 + NH3 + CH3COOH + KI titrated with Na2S2O3, we have 47 species interrelated in 35 equilibrium constants [6] . In the system KIO3 + HCl + H2SeO3 + HgCl2 titrated with ascorbic acid C6H8O6 we have 49 species and 39 equilibrium constants [4] [7] [8] . These numbers give an idea of the complexity of relevant systems. On the other hand, the number of these species makes notation of the appropriate balances lengthy, i.e., they take up many space in the text. The present paper is an attempt of generalizing the notation. This allows the synthesis of certain problems associated with the description of the system using a mathematical formalism.
2. Notations
Let an electrolytic system, of volume V [mL], be formed by mixing J different components, 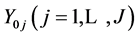 and N0j be the number of entities (uncharged molecules) of
and N0j be the number of entities (uncharged molecules) of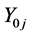 . In this mixture we have I different kinds of species
. In this mixture we have I different kinds of species ![]() and Ni be the number of
and Ni be the number of 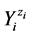 entities, where zi is the external charge (qi = zi·e, zi = 0±1, ±2, ···) of
entities, where zi is the external charge (qi = zi·e, zi = 0±1, ±2, ···) of , expressed in elementary charge units, e = F/NA; F—Faraday’s constant, NA—Avogadro’s number. Let K be the number of different elements E(k)
, expressed in elementary charge units, e = F/NA; F—Faraday’s constant, NA—Avogadro’s number. Let K be the number of different elements E(k)  composing the system, and mjk be the number of atoms of the k-th element in Y0j , and nik be the number of atoms of the k-th element in the species
composing the system, and mjk be the number of atoms of the k-th element in Y0j , and nik be the number of atoms of the k-th element in the species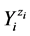 .
.
All the species  in the system are considered in their natural form, i.e. as solvates. So, in aqueous solutions the species exist as hydrates, in principle, i.e.
in the system are considered in their natural form, i.e. as solvates. So, in aqueous solutions the species exist as hydrates, in principle, i.e.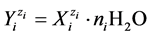 , where ni ≥ 0 is the mean number of water molecules attached to
, where ni ≥ 0 is the mean number of water molecules attached to![]() . For Ni entities
. For Ni entities  we apply the notation
we apply the notation![]() , e.g. for
, e.g. for 
we have H+1(N2, n2); N2 ions 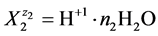 involve: N2(1 + 2n2) atoms of H, and N2n2 atoms of O. For
involve: N2(1 + 2n2) atoms of H, and N2n2 atoms of O. For
![]() in binary-solvent medium, composed of A = CH3CN and B = C2H5OH as co-solvents, we apply the notation
in binary-solvent medium, composed of A = CH3CN and B = C2H5OH as co-solvents, we apply the notation
![]() , where niA ≥ 0 and niB ≥ 0 are the mean numbers of A and B attached to
, where niA ≥ 0 and niB ≥ 0 are the mean numbers of A and B attached to ![]() (not solvated species are included in this notation); e.g. for
(not solvated species are included in this notation); e.g. for 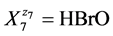 we have HBrO (N7, n7A, n7B);
we have HBrO (N7, n7A, n7B);
N7 entities of HBrO·n7ACH3CN·n7BC2H5OH involve: N7(1 + 3n7A + 6n7B) atoms of H, N7(1 + n7B) atoms of O, N7(2n7A + 2n7B) atoms of C, and N7n7A atoms of N.
The notation can be extended on other co-solvents A, B or more complex systems, with co-solvents A, B, C, ··· included. In all instances, the (external) charge of  is introduced by
is introduced by![]() ; the solvating molecules (e.g., H2O, CH3CN, C2H5OH) are neutral.
; the solvating molecules (e.g., H2O, CH3CN, C2H5OH) are neutral.
Referring again to ni or nAi and nBi values, one should also take into account the fact that the solvents are not always the dominant components of an electrolytic system. In some instances, e.g. concentrated H2SO4 , HNO3 or HCl solutions, the roles of solvent and solute may be interchanged. The hydration number of individual species varies with the concentration of a suitable, aqueous solution. It should be noted that these values are factually unknown and vary with concentration of solutes. It suffice to say that even the hydration number of H+1 ion in aqueous solutions is not clearly specified, see e.g. [9] .
3. Examples
3.1. The (Br2, H2O) System
N01 molecules of Br2 is mixed with N02 molecules of H2O, and V mL of the solution is thus obtained. There are the following species: H2O (N1), H+1 (N2, n2), OH–1 (N3, n3), HBrO3 (N4, n4), 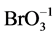 (N5, n5), HBrO (N6, n6)BrO–1 (N7, n7), Br2 (N8, n8),
(N5, n5), HBrO (N6, n6)BrO–1 (N7, n7), Br2 (N8, n8), 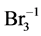 (N9, n9), Br–1 (N10, n10), involved in the elemental balances:
(N9, n9), Br–1 (N10, n10), involved in the elemental balances:
f(H):
 (1)
(1)
f(O):
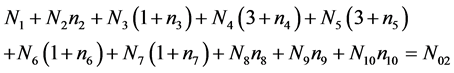 (2)
(2)
f(Br):
 (3)
(3)
Then we get 2∙f(O) - f(H)
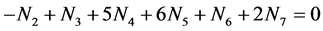 (4)
(4)
Addition of (4) to charge balance
 (5)
(5)
gives the equation
 (6)
(6)
Subtraction of (6) from ZBr∙ f(Br), where ZBr = 35 is the atomic number for Br, gives
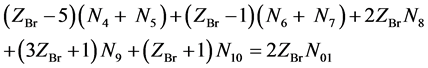 (7)
(7)
Applying the relations:
 (8)
(8)
 (9)
(9)
 (10)
(10)
obtained according to Approach I for C mol/L Br2. It is assumed that Br2 does not react with H2O, i.e., none products of this (virtual, not real) reaction are formed, i.e., application of (8) and (9) to (3) – (6) gives the balances, expressed in terms of molar concentrations:
 (3a)
(3a)
 (4a)
(4a)
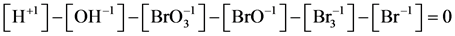 (5a)
(5a)
 (6a)
(6a)
The Br is the only one electron-active element in the system (Br2, H2O). In the terminology relating to card games [11] , applied in the Approach I, the redox systems have electron-active elements called as “players” and electron-non-active elements, named as “fans”. In this context, the electrons are seen as “money”. The “player” in HBrO∙n7H2O is Br, whereas the elements: H, O are considered as “fans”. The species H+1·n2H2O involves only “fans”. Equation (4a), obtained from 2·f(O) – f(H), involves concentrations of the species, composed only from “fans”: H and O.
3.2. The (Br2, CH3CN, C2H5OH) System
V mL of the solution is obtained by introducing N01 molecules of Br2 into the mixture of N02 molecules of CH3CN (=A) and N03 molecules of C2H5OH (=B). According to notation applied above, in the mixture thus formed we have the following species:
CH3CN (N1), C2H5OH (N2), 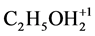 (N3, n3A, n3B)C2H5O–1 (N4, n4A, n4B), HBrO3 (N5, n5A, n5B),
(N3, n3A, n3B)C2H5O–1 (N4, n4A, n4B), HBrO3 (N5, n5A, n5B),
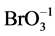 (N6, n6A, n6B), HBrO (N7, n7A, n7B), BrO–1 (N8, n8A, n8B)Br2 (N9, n9A, n9B),
(N6, n6A, n6B), HBrO (N7, n7A, n7B), BrO–1 (N8, n8A, n8B)Br2 (N9, n9A, n9B), 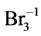 (N10, n10A, n10B)Br–1 (N11, n11A, n11B) (11)
(N10, n10A, n10B)Br–1 (N11, n11A, n11B) (11)
The N1 and N2 in (11) refer to the numbers of molecules of the co-solvents A and B not involved in the related solvates. On this basis, we formulate the elemental balances:
f(H) :
 (12)
(12)
f(O) :
 (13)
(13)
f(C) :
 (14)
(14)
f(N) :
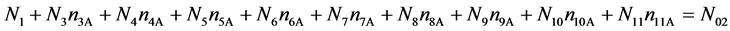 (15)
(15)
f(Br) :
 (16)
(16)
From (12) and (13) we get

 (17)
(17)
Addition of (15) to (17) gives
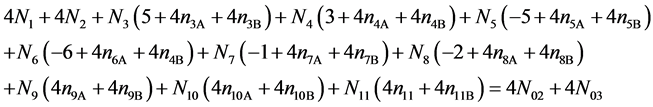 (18)
(18)
Addition of (18) to 2·f(C) (19)
 (19)
(19)
gives
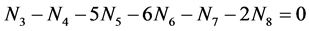 (20)
(20)
Subtraction of (19) from the charge balance (21)
 (21)
(21)
gives the equation  equivalent to Equation (6); then we get Equations (6a) and (10).
equivalent to Equation (6); then we get Equations (6a) and (10).
Note that the procedure involved with multiplication, e.g. 2·f(O), 2·f(C), f(N) = 1·f(N), and then addition/ subtraction of the corresponding equations is a realization of linear combination [4]. Generally, a linear combination of equations 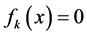 has the form
has the form
 (22)
(22)
where bk—the pre-assumed numbers.
3.3. Comparison of (Br2, H2O) and (Br2, CH3CN, C2H5OH) Systems
From linear combination of the charge balance and elemental balances related to “fans”: H, O, N and C, we obtain the simplest/shortest form of GEB, expressed by Equation (6a); the bk values (Equation (22)) are properly chosen for this purpose. Equation (10) is the more extended, but equivalent to (6a), form of GEB, obtained for C mol/L according to Approach I. We see that the form of GEB does not depend on the solvent composition—assuming that the solvent does not form other (new) species with a solute.
It should be noted that the balance 2·f(O) – f(H) obtained for the system (Br2, H2O) does not contain, as components, the numbers: N02, N1 and the ni (i = 2, ···, 10) associated with the (undefined - except N02) numbers of water molecules. The balance –(2·f(O) – f(H)) (and then the balance 2·f(O) – f(H)) formulated for the system (Br2, CH3CN, C2H5OH) contain the numbers involved with water molecules; the water molecules are cancelled completely after due combination of elemental balances for all “fans”. The difference
 plays the role of [H+1] – [OH–1] in aqueous media.
plays the role of [H+1] – [OH–1] in aqueous media.
4. Some Generalizing Remarks
Let us assume that the aqueous system involves K elements E(k),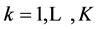 ; P elements are considered as “players” and then F = K – P elements are treated as “fans”; the elemental balance related to the element E(k) will be denoted by f(E(k)).
; P elements are considered as “players” and then F = K – P elements are treated as “fans”; the elemental balance related to the element E(k) will be denoted by f(E(k)).
A special role among the elements related to aqueous systems play H and O; the related balances are: f(E(1)) = f(H), and f(E(2)) = f(O). The balances for successive “fans” are denoted as f(E(3)), ···, f(E(K–P)), whereas f(E(K–P+1)), ···, f(E(K)) are formulated for “players”. Applying the notations specified above, we have:
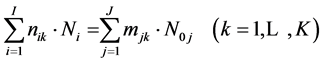 (23)
(23)
On this basis we formulate the balance 2·f(O) - f(H)
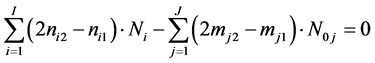 (24)
(24)
The elemental balances f(E(3)), ···, f(E(K–P)) are multiplied by the corresponding numbers:  and the linear combination
and the linear combination
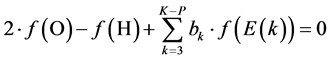 (25)
(25)
i.e.
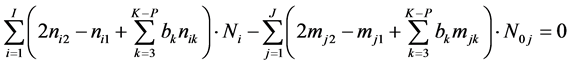 (26)
(26)
Denoting
 (27)
(27)
from Equations. (26), (8), (27), after addition of charge balance (28) [12] [13]
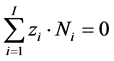 (28)
(28)
we have
 (29)
(29)
After a proper choice of bk 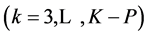 and cancellations, Equation (29) does not involve “fans”; it is the simplest form of GEB. The nik and mjk values should involve particular elements in the corresponding solvates, considered as the species, see Sections 3.1 and 3.2.
and cancellations, Equation (29) does not involve “fans”; it is the simplest form of GEB. The nik and mjk values should involve particular elements in the corresponding solvates, considered as the species, see Sections 3.1 and 3.2.
5. Final Comments
In the article it is proved that the Generalized Electron Balance (GEB), referred to a redox electrolytic system (aqueous media), is derivable from the equation 2·f(O) – f(H) resulting from comparison of elemental balances: f(H) for H and f(O) for O. This approach, named as the Approach II, is equivalent to the Approach I, based on a common pool of electrons brought by elements forming the system, of any degree of complexity.
The GEB is ultimately expressed in terms of molar concentrations, as charge and concentrations balances, and the expressions for equilibrium constants. Contrary to a redox system, the equation 2·f(O) – f(H) related to a non-redox system of any degree of complexity, is linearly independent on charge and elemental balances, related to elements ≠ H, O. This property, valid for the systems of any degree of complexity, distinguishes between redox and non-redox systems. The GEB is perceived as a rule of a matter conservation, related to electrolytic redox systems.
The terms: Generalized Electron Balance (GEB) and Generalized Approach to Electrolytic Systems (GATES) are still unknown to a wider community. This article aims to fill this gap. Therefore, this article present a concise description of redox systems, in the context of linear transformations of algebraic equations.
References
- Michalowski, T., Toporek, M., Michalowska-Kaczmarczyk, A.M. and Asuero, A.G. (2013) New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta, 109, 519-531. http://dx.doi.org/10.1016/j.electacta.2013.07.125
- Michalowski, T., Michalowska-Kaczmarczyk, A.M. and Toporek, M. (2013) Formulation of General Criterion Distinguishing between Non-Redox and Redox Systems, Electrochimica Acta, 112, 199-211. http://dx.doi.org/10.1016/j.electacta.2013.08.153
- Michalowska-Kaczmarczyk, A.M. and Michalowski, T. (2013) Comparative Balancing of Non-Redox and Redox Electrolytic Systems and Its Consequences. American Journal of Analytical Chemistry, 4, 46-53. http://dx.doi.org/10.4236/ajac.2013.410A1006
- Michalowski, T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems, Chapter 1, 1-34. In: Michalowski, T., Ed., Applications of MATLAB in Science and Engineering, InTech. http://www.intechopen.com/books/show/title/applications-of-matlab-in-science-and-engineering.
- Michalowski, T., Pilarski, B., Asuero, A.G. and Michalowska-Kaczmarczyk, A.M. (2014) Modeling of Acid-Base Properties in Binary-Solvent Systems, Chapter 9.4. In: Wypych, G., Ed., Handbook of Solvents (2nd Edition), in print.
- Michalowski, T. (2001) Calculations in Analytical Chemistry with Elements of Computer Programming (in Polish) PK, Cracow. http://suw.biblos.pk.edu.pl/resourceDetails&rId=3974
- Michalowski, T. and Lesiak, A. (1994) Formulation of Generalized Equations for Redox Titration Curves. Chemia Analityczna (Warsaw), 13, 623-637.
- Michalowski, T., Rymanowski, M. and Pietrzyk, A. (2005) Non-Typical Bronsted’s Acids and Bases. Journal of Chemical Education, 82, 470-472. http://dx.doi.org/10.1021/ed082p470
- Mancinelli, R., Sodo, A., Bruni, F., Ricci, M.A. and Soper, A.K. (2009) Influence of Concentration and Anion Size on Hydration of H+ Ions and Water Structure. Journal of Physical Chemistry B, 113, 4075-4080. http://dx.doi.org/10.1021/jp805220j
- Michalowski, T. (1994) Calculation of pH and Potential E for Bromine Aqueous Solutions. Journal of Chemical Education, 71, 560-562. http://dx.doi.org/10.1021/ed071p560 .
- http://www.allposters.pl/-sp/Commuter-Card-Game-Saturday-Evening-Post-Cover-March-15-1947-plakaty_i8290036_.htm
- Asuero, A.G. and Michalowski, T. (2011) Comprehensive Formulation of Titration Curves Referred to Complex Acid-Base Systems and Its Analytical Implications. Critical Reviews in Analytical Chemistry, 41, 151-187. http://dx.doi.org/10.1080/10408347.2011.559440
- Michalowski, T. and Asuero, A.G. (2012) New Approaches in Modelling the Carbonate Alkalinity and Total Alkalinity. Critical Reviews in Analytical Chemistry, 42, 220-244. http://dx.doi.org/10.1080/10408347.2012.660067

