Journal of Analytical Sciences, Methods and Instrumentation
Vol. 3 No. 2 (2013) , Article ID: 32344 , 8 pages DOI:10.4236/jasmi.2013.32008
Quantitative Registration of the Degree of the Voluntariness and Involuntariness (of the Chaos) in Biomedical Systems
![]()
Surgut State University, Surgut, Russia.
Email: valery.eskov@gmail.com
Copyright © 2013 Valery M. Eskov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 1st, 2013; revised April 2nd, 2013; accepted April 29th, 2013
Keywords: Chaos; Attractor; Phase Space; Tremor
ABSTRACT
What does it mean: certainty and uncertainty, chaos and order? The understanding of such definition and real interpretation of chaotic behavior the third type of systems in nature was presented. The practical realization of different medical problems was presented too.
1. Introduction
At present we know of at least a dozen hypotheses about the mechanisms of the brain activity related to the notion of dynamic chaos. However, there are no quantitative methods in all these hypotheses, which could describe the characteristics of these chaotic regimes, i.e. parameter of chaos. The problem of the chaos control stays still more uncertain. Thus, the problem of complex registration of chaos parameters (and not the fact of its emergence) and the problem of dynamic chaos control in the framework of traditional science, that is, if it is based on a deterministic approach or stochastic approach (all these we now define as deterministic-stochastic paradigm-DSP) currently remain open. Problem of such measurements in real biomedical research is still uncertain.
However, now in Russia, a new third approach is being developed (differs from DSP) [1,2], which attempts to combine the notions of chaos and order in a unit in the new theory of chaos-selforganization (TCS)). The necessity to create TCS arose from attempts to resolve the contradictions between H. Haken’s synergetics and I. R. Prigogine’s complexity. In fact, we had to create original compartment-cluster theory of neural brain networks, and then all of biosystems-(CCTB) for the mathematical interpretation of the first H. Haken’s postulate [3]. Established in 70 - 80 years CCTB led to a new understanding of the basic principles of the mammalian brain and then the new principles of artificial neural networks and neuroemulators-neurocomputers. At the same time the impossibility of using neurocomputers was proved when a single iteration for the purpose of identification of the order parameter (OP) in the various purposes of medical diagnosis (neurocomputer is not applicable in the diagnosis of the main diagnostic features in medicine at a single iteration). Since each iteration (for example, the binary classification problem) determines its own special set of OP [4,5].
The result of all these efforts is the formation of the five basic principles of the functioning of any complex biological systems (including the neural brain networks) and 13 differences of special systems of the third type (STT), which are in constant and continuous chaos [1,2, 6-11]. This chaos is emerged in continuous, chaotic motion, the system state vector (SSV) in the phase states space (PSS). Number of outstanding scientists paid attention to it but quantitative identification methods [3,4,11] of these special properties and a special dynamic behavior of STT had not been established. The current report is aimed to the practical application of these methods in neurosciences. In this case, we show the new restrictions neurocomputers and new opportunities of TCS, its identification methods and chaos control in TTS [1,2,11,13, 14].
2. The New Methods of Measuring of Neuro-Muscles System’s Chaotic Dynamics
According to the theory of chaos-selforganization we have uninterrupted movements of SSV x = x(t) = (x1, x2, ···, xm)T in phase space of state (PSS). Let us introduce a series of postulates (assumptions) according to TCS which are presented the formal description of TTS:
1) Any biological dynamical system as the third type of systems can be described by a state vector x = (x1, x2, ···, xm)T in an m-dimensional phase space of states. The components of this vector can be any variables (parameters) of the cardiorespiratory system, biochemical parameters of the blood, parameters of various physiological and psychophysiological human functions, etc. In this case, the main point is that methods and devices exist for their objective measurement. This has already been discussed in earlier papers [1,6], when for example the parameters were constructed and measured for models of respiratory neural networks (or other neural networks) within the compartmental/cluster approach, where as xi we took the bioelectric activity of the efferent nerves or muscles.
2) When the maximum set xi exists, we can always minimize the dimensionality of the phase space of states, i.e., we can go from m to k where k < m (or k  m). These procedures allow us to minimize the dimensionality of the phase space and to obtain some compact model of the system under study. For these purposes, we use three approaches: 1) minimization of the dimensionality of the phase space of states within the compartmental/cluster theory of biological dynamical systems; 2) according to neural net technologies we construct the algorithm of older parameters identification, and the method for analysis of the parameters of quasi-attractors for the motion of the human state vector in the phase space of states. The latter is based on the third postulate of TCS, but gives a realistic assessment of the meaning of xi [1,2,11].
m). These procedures allow us to minimize the dimensionality of the phase space and to obtain some compact model of the system under study. For these purposes, we use three approaches: 1) minimization of the dimensionality of the phase space of states within the compartmental/cluster theory of biological dynamical systems; 2) according to neural net technologies we construct the algorithm of older parameters identification, and the method for analysis of the parameters of quasi-attractors for the motion of the human state vector in the phase space of states. The latter is based on the third postulate of TCS, but gives a realistic assessment of the meaning of xi [1,2,11].
3) The variability (the degree of spread in the biosystem state vector in the phase space of states, as a certain analog to fluctuations in physics) of the parameters of the biological dynamical system (the values of xi) is the information for evaluating the state of biosystems and predicting their transition to other states (other regions of phase space, change in the order parameters, transition to other phase spaces of states). It is important that the level of variability in the biological dynamical system be a measurable quantity and that it can be monitored longterm, and compared for different groups of biosystems or for the same biosystem found in different functional states [2,11,13,14].
Based on these three assumptions (postulates), we can measure the parameters of the quasi-attractors (QA) for regions of phase spaces within which motion of the biosystem state vector occurs. Here we do not deny the existence of real attractors for the motion of the human state vector, but in principle they are not accessible in measurements. A certain analog to the Bernoulli theorem (the law of large numbers) is postulated in measuring the parameters of these real attractors, i.e., if the number of experiments (repetitions of the measurements) is made infinite, then the parameters of the quasi-attractors will approximate the parameters of an ideal attractor (as in statistics, P*(A) ® P(A) as the number of measurements n ® ∞). But the five properties of biological dynamical systems indicated early [1,2] impose fundamental limits on the inaccessibility of measurements of the parameters of an ideal attractor, since a biological dynamical system cannot be kept in approximately the same state for as long as desired (evolution of the biological dynamical system occurs, its death is prescribed teleologically, it is constantly changing dramatically—a human gets sick, ages, changes lifestyle, etc.). Since the number of repetitions n is finite and small, we have to make do with the parameters of quasi-attractors. The algorithm for calculating them contains several operations which are executed each time during processing of the data obtained in measurements of xi from a group of biological objects found in approximately the same functional state (arbitrarily identical disease, identical environmental conditions, identical physiotherapeutic treatments, etc.).
The algorithm for calculating the parameters of quasiattractors for the human state vector based on chaotic analysis of SSV of patients (in medicine). The data obtained from one or a group of test subjects by repetitions of the measurements in the form of a set m of data blocks (compartments) where m is the number of measured biological indices, are transferred in the form of points to an m-dimensional phase space of states, in which, fixing the extreme left-hand and right-hand values of the parameters for the human state vector along each coordinate xi, they generate a quasi-attractor in the form of an m-dimensional parallelepiped, for which we determine the volume Vg, the center, and the asymmetry value.
Using these three quantities (absolute or relative), we decide if the recovery is effective by comparing these parameters before and after treatment. Essentially, each group of test subjects forms a certain “cloud” in the phase space of states, which has its own limits ∆xi along each of the coordinates xi (i = 1, 2, ···, m). These limits ∆xi are the faces of the m-dimensional parallelepiped in the m-dimensional phase space, and each face represents the level of variability of the ith parameter (diagnostic index), a component of the vector x in the phase space of states. The total volume of this parallelepiped is the volume Vg of some quasi-attractor, which for different groups of test subjects has its own parameters before and after treatment. These parameters include: the volume of the quasi-attractor Vg, the coordinates of its center C in the phase space of states, the asymmetry r. We determine either the absolute values (∆Vg = Vg2 − Vg1, where Vg2 are the values of Vg after treatment, and Vg1 are the values before treatment) or the relative values in percent ((∆Vg/Vg1) × 100) of these parameters. If the relative changes in the parameters of the quasi-attractor exceed the uncertainty in the measurement of the diagnostic indices, then they are already considered significant (in many cases, they are 5% or 10% or more). The larger the changes in these three overall (integrated) indices, the more effective is recovery.
One simple example of the algorithm realization includes the investigation of the role of voluntary or involuntary control (by the human brain) of postural tremor. It is evident according to classic physiological theories that postural tremor isn’t voluntary movement because we have not any possibility for achievement of stationary mode (dx/dt ≠ 0 and xi ≠ const) for every time t [15,16]. But the brain (its control) can provides the regulation of postural tremor quasi-attractor volume. Such volumes changing present the proofs of the role of voluntary control from the brain in postural tremor organization. But the control has chaotic form (see below, chapter 2).
According to tremorgrams (I1) we obtain amplitudefrequency diagram (AFD), see the Figure 1 at (II1). The main point of the experiment is static keeping of the forefinger under the plate securing the hand position for two coordinates-micro-movement of fingers (x1, m) and the speed of micro-movement (x2 = dx1/dt, m/s). Each subject takes part in the experiment being in different organism state three times: before sighting, during sighting and after sighting. It means every subject has a task to keep goal. It is obvious that on the second stage of the experiment mind activity process has been involved, that is important to keep a hand in one position (statically), control its fixity consciously. We must remark that for anytime t we never have the condition: dx/dt = 0, where x = (x1, x2)T is a state vector of biomechanical system (tremor). And for every little period of time—we cannot obtain two equivalent phase trajectory or full equivalent simple dynamic xi(t). So we have nonrepeatable processes (for AFD (II2) it is evident) and full uncertainty for future prognoses of xi(t), value. It is chaotic process for ever t and AFD we can’t use for investigation of tremor. It is the first reason of our article presentation.
In addition to the amplitude-frequency diagram, we have considered a two-dimensional or six-dimensional phase space, which describes the dynamics of the human organism state vector (HOSV) at two coordinates x1 and x2 or six coordinates (x, y, z, ··· respectively). We have determined the area of the obtained quasi-attractors—QA. Having identified the characteristics that correspond to a chaotic dynamics (quasi-attractors in the parameters and the values of entropy for comparison with DSP).
Experimental findings have been treated in the phase coordinates x1 (the absolute movement of the finger) and x2 = dx1/dt. According to two-dimensional vector space x = (x1, x2)T it is easy to represent the tremor in the phase plane. In general, we have made the monitoring of the human body motion in three-dimensional space (three coordinates x, y, z of space) and then the dimension of the phase space of states is equal to six (m = 6), where three are real physical coordinates (x, y, z) and three others are their speed, i.e. х = (x1, ···, x6)T.
Such an approach is made in the framework of the classical interpretation of biophysics as science (see Hill “Why biophysics” [17]), using methods of physics if we study biological systems. In one of our articles [2,3,5-10] coordinates xi of SSV will have no physical meaning, but it will be also the coordinates of SSV in the phase space of states (PSS), they also characterize the dynamics of movement of SSV in PSS, and this dynamic has a pronounced chaotic character like our the first exampletremor.
Now we present a typical example for the subject of the experiment No. 1—D. D. (Figure 2) and general number of all subjects is 120 people (information is similar, but the numerical results are individual). For all such systems (third type with chaotic dynamics of SSV in PSS) we can calculate the volume VG of PSS (this volume we define as quasi-attractor), and the parameters of the quasiattractor have a significant informational value as opposed to a specific AFD and others value of SSV behavior in PSS, which has no any information about chaos.
As we take two instrument readings-speed (х2 = dx1/dt, m/s) and motion of fingers of the subject (x1, m), the latter is measured in conventional amplitude values-in volts, then to construct the phase portrait (Figures 1 and 2) representing the dependence of the rate on volt movement are converted to meters. So, we consider the results of QA calculations and some special changing of its volume VG for such three type of complexity system (effector system —the second cluster of two cluster’s hierarchical system). The Figures 1 and 2 presents the result of quasi-attractor calculation to the two stages of mister D. D. It is easy to see that voluntary brain control changes the volume of quasi-attractor and we transform the quasi-attractor III1 (see Figure 1) into quasi-attractor III2 (see Figure 2). The changes of quasi-attractor volume VG (under such transformation) present the role of voluntarism in involuntary process-postural tremor (see Table 1). So we can use the volume of quasi-attractor VG for registration of human
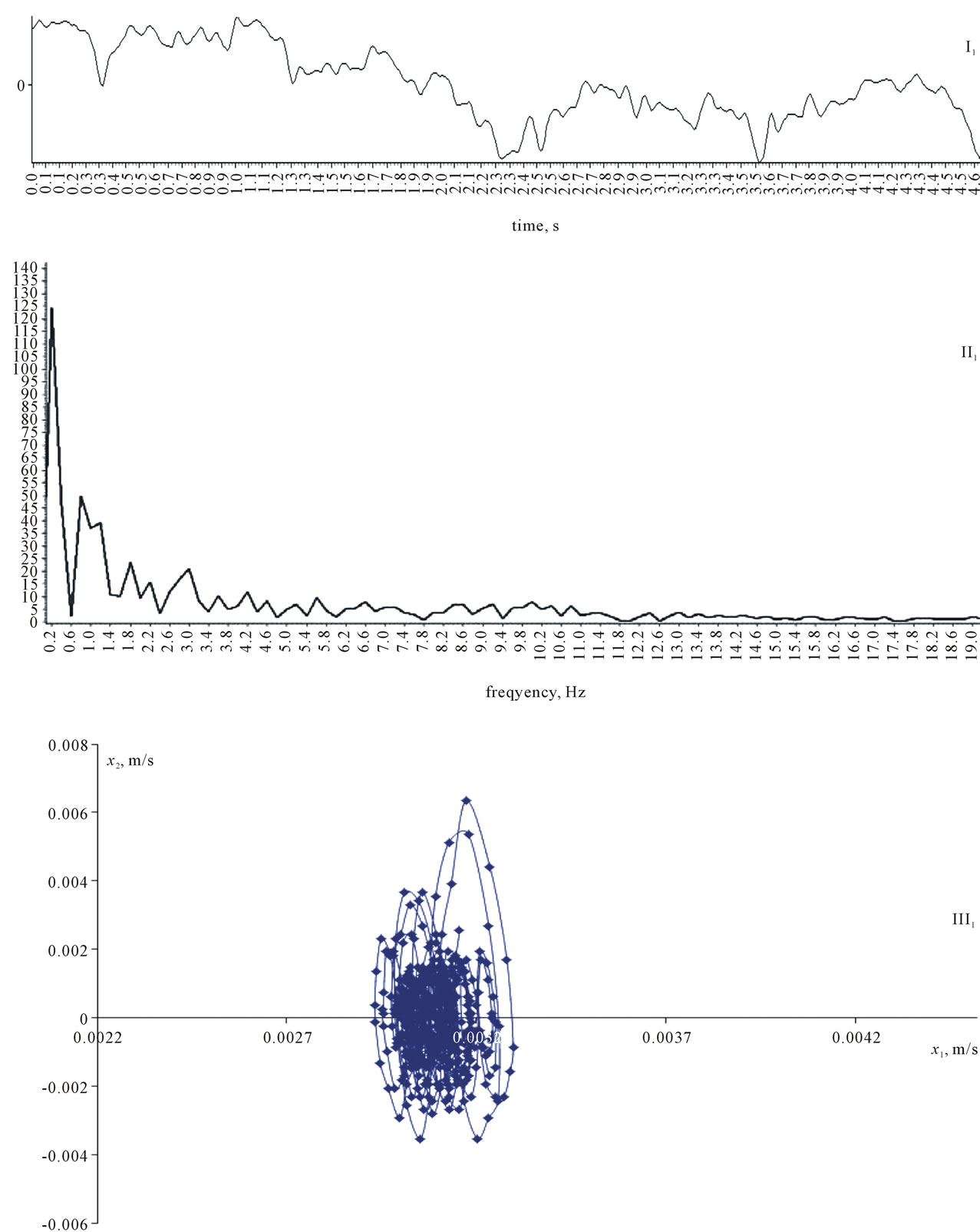
Figure 1. Real tremorgrams (I1), their amplitude-frequency diagram-AFD (II1) and phase portraits (III1), taken from the fingers of the subject D.D. at the pre-sighting stage. The tremorograms and AFD changes every second and only volume of quasi-attractor is constant for constant physiological state of human organism.

Figure 2. Real tremorgrams (I2), their amplitude-frequency diagram (II2) and phase portraits (III2), taken from the fingers of the subject DD at the while-sighting stage.
organism stage (normal, pathological …) under different changing (different treatment in medicine, ecological factors in ecology, different training in sport …).
So it is easy to see that Figure 2 presents the role of voluntary (purposeful)-control (from brain) but chaos is uninterrupted process (see Figure 3 below). We have global chaos but the volume of quasi-attractors presents the value of voluntarism (the role of brain control). The volumes of represented quasi-attractors are shown in Table 1, where it is easy to see that the smallest QA size we have at while-sighting stage (Figure 2), by order of magnitude different from the state before and after sighting (Figure 1). Such result we use for selection of sportsmen. If sportsmen almost rate the great changing of VG (before and after sighting stage) he has a good future of his sport career. The VG present now for us the result of therapy in medicine, in psychology, etc.
So we use such approach for identification of effectiveness of different medical or other treatment. The volume VG before treatment and after it presents the effectiveness of our voluntary treatment for man with pathological state and its transformation into normal state. It is new method in medicine, sport physiology, ecology, etc. We have a great number of results of such VG calculations (50 books in Russsia).
3. How Does the Brain Realize the Control of Effector Systems?
Some general approach is presented in this message in evaluation of the work of brain neuronets and artificial neuronets from positions of the new and actively developing theory of chaos-self-organization (as a new consciousness and new understanding of nature (life system)). The principles of biological objects work as special third type systems (TTS) are shown in a continuous chaotic movement. As a whole, the work of a brain can be considered as one chaotic quasi-attractor influencing the work of various regulatory systems by means of which it keeps in a mode of a homeostasis and keeps all functional systems of an organism (FSO) of the person in a homeostasis. But all of this FSO are chaotic biosystems

Table 1. Quasi-attractor volume of the subject Mr. D. D. under special voluntary control and like quasi-voluntary control from the brain.
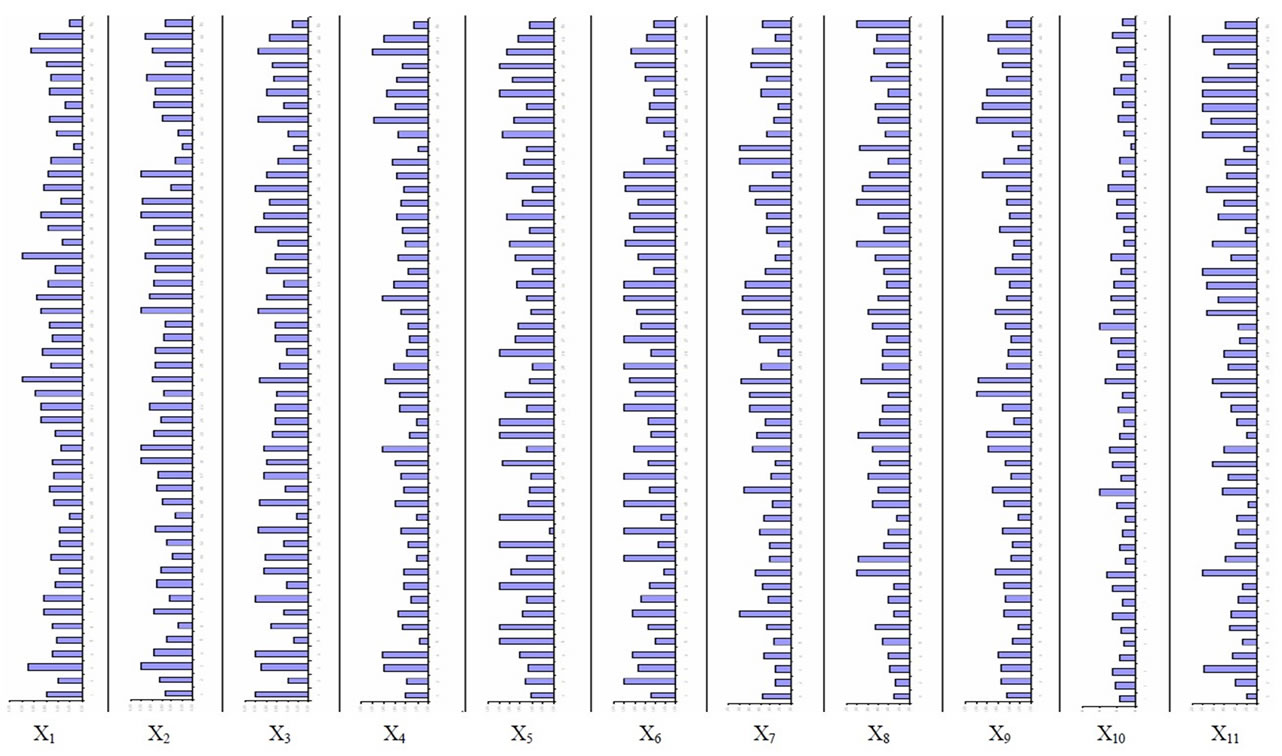
Figure 3. Diagram of distribution of weights for each parameter (xi) for each of the j-th repetition of equal artificial neural network training (gradient descent method, j = 1, ···, 50).
for which the stationary regime take the other interpretation (opposite to traditional science) [1,2,5-14].
So if we use the artificial neuron network in medicine we must answer to the question: why can’t we use the neuroemulator in medicine for diagnostic procedure? The answer to the question is connected with the second question: why the brain (as the first cluster) has chaotic behavior? Very often in medicine we have the task of binary classification. The objectives of detection of distinctions between two (or more) groups of objects having some general signs quite often arise in medicine and biology. These can be two groups of patients having an identical disease, but being, for example, in various conditions (ecological, physiological, mental) or exposed, for example, to treatment by two different methods. In these cases the problem of detection of the importance of influence on the state of an organism of these external influencing factors or conditions (medicines, methods of treatment, action of adverse ecological factors, etc.) is solved at the same time. For these two groups of people (two selections) diagnostic signs of xi which form the m-dimensional phase space of states (PSS), that is the vector of a state x = (x1, x2, ···, xm)T is set. It is obvious that thus in PSS these two groups occupy some areas and the neuroemulator can reveal if these areas differ significantly or insignificantly.
Meanwhile the neuroemulator (NE) is set an objective: to reveal whether these two selections (groups) significantly differ or don’t differ. It is obvious, that similar tasks are also in the field of recognition of images (for example, do two similar photos represent different people or one and the same person?). Let’s admit that such a task can be solved and the neurocomputer reaches the goal—it distinguishes these two groups, i.e. the problem of diagnostics has its solution. At once we note that irrespective of the methods of neuronet control the task is either solved or not, i.e. the objective is either reached or not. However, if we still solve the problem and ask the neuronet how it solved it, for example, we will request the weight of communications between neurons or we will demand to present the weight figures of used diagnostic signs, it will appear that the more we force a neuronet to solve the same problem (at the same initial selections) the more variants of weight figures for xi we will receive. Million times we will repeat an identical task of binary classification and one million times we will receive different weight figures. The internal architecture of a neuronet, character and the weight of communications, the importance of the diagnostic signs forming m-dimensional phase space in which these two groups of patients are set will be various each time [1,2,11,13,14]. So the one cycle of NE presents the value of xi (the order parameter-OP) and this OP isn’t valid. The NE is not usefulness in medicine in such regime.
As it was stated in our early publications [1,2,11] the distinctive feature in the work of special third type of systems is the “glimmering property”, i.e. their continuous, chaotic movement of its system state vector (SSV) of such TTS in phase space of states. This movement of SSV in PSS shouldn’t be perceived as real (mechanic) movement since for neuronets it can be shown in continuous change of a network architecture (any neurons can join, be switched off, can change the weight of synoptic communications, etc.). Thus the general architecture (morphology) won’t undergo any changes.
Externally the neuronet (and the neuroemulator) will show a steady result. For example, the problem of binary classification will repeat (the exit will be identical) and the number of elements, their arrangement in a network won’t change. In rough consideration all this seems permanent. However, the internal state of a network (neuroemulator) will be thus in continuous chaotic change. Thus any of such instant internal states won’t repeat. For example, muscles can’t identically repeat this or that movement (it repeats within quasi-attractors), we can’t execute two identical respiration, two identical kneebends. Moreover, hand suspension (or a finger) in space doesn’t lead to a stationary mode, i.e. dx/dt ≠ 0 and we observe the postural tremor. This tremor is caused by chaos in the main controller—the brain, its neural networks and in the work of an effector—a group of muscles which are carrying out any movement (finger suspension in space), but it’s done involuntarily, i.e. chaotically, within a quasi-attractor. On the Figure 1 we are presented diagram of distribution of weights for each parameter (xi) for each of the j-th artifical neural network training (method of linked gradients, j = 1, ···, 50).
The 11-th dimensions of phase space of state consists some special biological parameters for characterization of state of cardio-vascular system (CVS) of group of patients. Here xi are parameters of CVS: x1—NN, mc; x2— SpO2, %; x3—SIM, x4—PAR, x5—SDNN, x6—HRV, x7—IB, x8—VLF, x9—LF, x10—HF, x11—LF/HF (the biological means of xi we presented early [1,2,10]).
All underlying structures also start working chaotically (though they themselves also undergo continuous chaos within their own quasi-attractors). However, the change of the QA parameters of the hierarch (the brain) can lead to an essential change of the QA parameters of the underlying clusters. For example, changing a brain state (within QA at the change of the basic purpose i.e. any movement) can lead to the change of the QA parameters in the organization and effector system in the form of a tremor, chaotic work of heart, biochemical parameters of blood, and many other effector systems connected with the brainwork. We will present this fact and in other messages and now we will show an example of internal chaotic dynamics in the work of quasi-attractors as the real models of work of living neuronets (i.e. brainwork) [1,2,10]. It is evident: if we have the brain (or artificial neuron network) chaotic behavior we can’t obtain the order parameter in medicine and the behavior or effector systems of human organism will be chaotic too. But we can use the parameters of quasi-attractor as a diagnostic method in medicine and biology. Now we calculate the matrix of quasi-attractor distances for analyses of effectiveness of therapy [1,2,10,13,14].
4. Conclusions
1) Every complex biological dynamic systems as the third type of systems—TTS (which is describing by system’s state vector (SSV) x = x(t) = (x1, x2, ···, xm)T in phase space of state—PSS) has uninterrupted movements of SSV in PSS and dx/dt ≠ 0 at all.
2) The traditional science (DSP) hasn’t possibility for the TTS description and we present the TCS and its quasi-attractors for such description.
3) The quasi-attractor presents the real chaotic behavior of brain, neuroemulator and many other TTS with chaotic dynamics. In medicine we must do the monitoring of quasi-attractors parameters. For such chaotic systems we can’t use the neuro emulator for identification of order parameters (main diagnostic parameters) in medicine. Now we create the special procedure with neuroemulator for such purposes (see the next our presentation).
REFERENCES
- V. M. Eskov, V. V. Eskov and O. E. Filatova, “Characteristic Features of Measurements and Modeling for Biosystems in Phase Spaces of States,” Measurement Techniques (Medical and Biological Measurements), Vol. 53, No. 12, 2011 pp. 1404-1410.
- V. M. Eskov, V. V. Eskov, O. E. Filatova and M. A. Filatov, “Two Types of Systems and Three Types of Paradigms in Systems Philosophy and System Science,” Journal of Biomedical Science and Engineering, Vol. 5. N. 10. 2012. pp. 602-607. doi:10.4236/jbise.2012.510075
- H. Haken, “Principles of Brain Functioning: A Synergetic Approach to Brain Activity, Behavior and Cognition (Springer Series in Synergetics),” Springer, Berlin, 1995.
- M. M. Churchland, J. P. Cunningham, M. T. Kaufman, J. D. Foster, P. Nuyujukian, S. I. Ryu and K. V. Shenoy, “Neural Population Dynamics during Reaching,” Nature, Vol. 487, No. 7405, 2012, pp. 51-58.
- V. M. Eskov and O. E. Filatova, “Respiratory Rhythm Generation in Rats: The Importance of Inhibition,” Neurophysiology, Vol. 25, No. 6, 1993, pp. 420-426.
- V. M. Eskov, “Direct Control by Dissipation Factor in Respiratory Neuron Networks,” Neural Network World, Vol. 6, 1994, pp.663-670.
- V. M. Eskov, “Models of Hierarchical Respiratory Neuron Networks,” Neurocomputing, Vol. 11. 1996, pp. 203- 226. doi:10.1016/0925-2312(95)00048-8
- V. M. Eskov and K S. V. ulaev, “Role of Connectedness Configuration at Neuron Network Behaviour. The Compartmental Approach,” Advances in Modeling. Automatic Control (Theory and Applications), Vol. 59. No. 1, 2004, pp. 9-24.
- V. M. Eskov, “Hierarchical Respiratory Neuron Networks,” Modelling, Measurement & Control, Vol. 48, No. 2, 1995, pp. 47-63.
- V. M. Eskov, “The Dependence of Activity of Cyclic Respiratory Neuron Network with Subcycles on Damping Coefficient,” Neural Network World, Vol. 1, 1996, pp. 57-67.
- V. M. Eskov, “Third Paradigm. Samara. (Russia),” Ofort, Samara, 2011.
- V. M. Eskov, “Indirect Control by Chemoreceptor Drive in Respiratory Neuron Networks,” Modelling, Measurement & Control, Vol. 48, No. 3, 1995, pp. 1-12.
- M. A. Filatov, D. Y. Filatova, O. I. Himikova, J. V. Romanova, “Matrixes of Quasiattractor Distances at Identification of Human Psychophysiology Function,” Complexity Mind Postnonclassic, Vol. 1, 2012, pp. 19-24.
- T. V. Gavrilenko, A. A. Baltikova, D. A. Degtyarev and A. S. Pashnin, “The Comparison of the Efficiency of Classic Stochastic Theory and Theory of Chaos-Selforganization (TCS),” Complexity Mind Postnonclassic, Vol. 1. 2012, pp. 81-91
- W. Weaver, “Science and Complexity. Rockefeller Foundation,” American Scientist, New York, 1948.
- I. Prigogine, “The Die Is Not Cast. Futures,” Bulletin of the Word Futures Studies Federation, Vol. 25. No. 4 2000, pp. 17-19.
- A. V. Hill, “Why Biophysics?” Science, Vol. 124. No. 3234, 1956, pp. 1233-1237.

