Int'l J. of Communications, Network and System Sciences
Vol.6 No.2(2013), Article ID:28149,5 pages DOI:10.4236/ijcns.2013.62009
Faster Method for Secure Transmission of Information with Sender Identification
Computer Science Department, New Jersey Institute of Technology, Newark, USA
Email: verb73@gmail.com
Received December 3, 2012; revised January 8, 2013; accepted January 24, 2013
Keywords: Digital Signature; RSA Algorithm; Diffie-Hellman Key Exchange; ElGamal Cryptosystem; Encryptor; Discrete Logarithm; Sender Identification; Multiplicative Inverse
ABSTRACT
This paper describes an algorithm for secure transmission of information via open communication channels based on the discrete logarithm problem. The proposed algorithm also provides sender identification (digital signature). It is twice as fast as the RSA algorithm and requires fifty percent fewer exponentiations than the ElGamal cryptosystems. In addition, the algorithm requires twice less bandwidth than the ElGamal algorithm. Numerical examples illustrate all steps of the proposed algorithm: system design (selection of private and public keys), encryption, transmission of information, decryption and information recovery.
1. Introduction
This paper describes a protocol for secure transmission of information that resembles the RSA algorithm [1]. However, the crypto-immunity of the proposed protocol is not based on computational complexity of integer factorization. Hardness of its cryptanalysis is based on the computational complexity of a discrete logarithm problem (DLP) [2,3] if the base g is a generator in modular arithmetic with prime modulus p. Definition1.1: A prime integer p is called a safe prime if
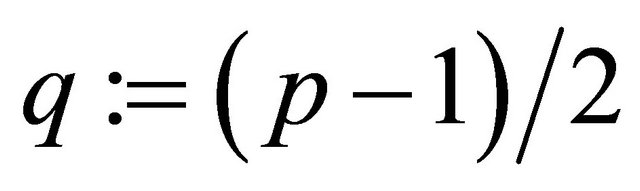 (1.1)
(1.1)
is also a prime; and for every 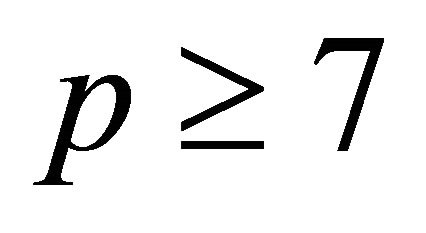 q is odd.
q is odd.
Here are examples of safe primes: 44618543, 64542503, 171534179, 1111127819, 2176078679, 2382062063.
As it is demonstrated in [4], if p is a safe prime, then the computation of a generator g is a computationally fast procedure.
2. Private and Public Keys
The proposed protocol is based on parallel establishment of a secret encryptor [5] by a sender and receiver.
Proposition2.1: If p is a safe prime greater than or equal 7, then
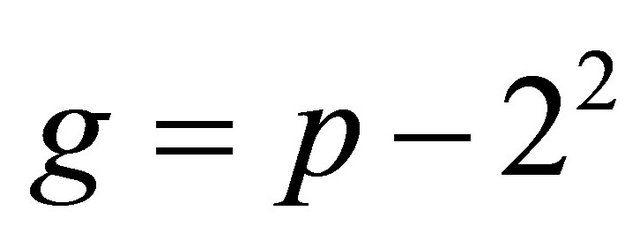 (2.1)
(2.1)
is a generator for every p.
Indeed, the Fermat Little Theorem [2] and (1.1) imply that
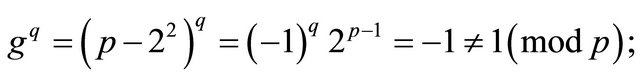 (2.2)
(2.2)
and
 , (2.3)
, (2.3)
if 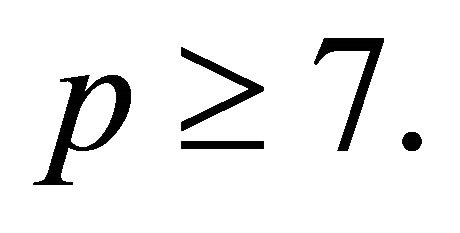
Remark2.1: Observe that for every integer n
 . (2.4)
. (2.4)
Integer parameters p and g are used by all participating users.
Alice selects her private key a and computes her public key
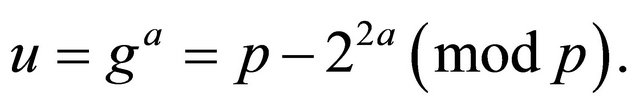 (2.5)
(2.5)
Analogously and independently, Bob selects his private key b and computes his public key
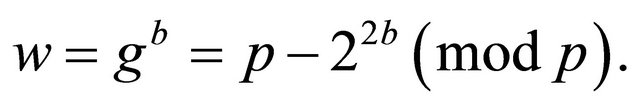 (2.6)
(2.6)
Remark2.2: both private keys must satisfy the inequality
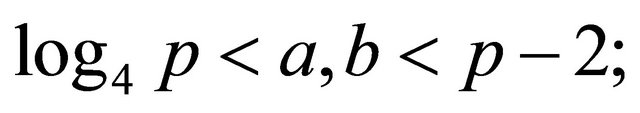 (2.7)
(2.7)
otherwise the intruder will be able to deduce a from (2.5) and/or b from (2.6) without confronting the complexity of the DLP; in addition, the private keys a and b must be distinct from q.
Suppose that Bob sends a plaintext m {represented in a numeric form}, where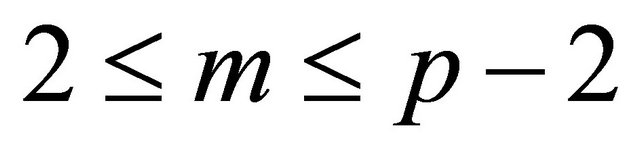 .
.
3. Encryption via Exponentiation
System design:
a) Each user computes his/her common secret encryptor
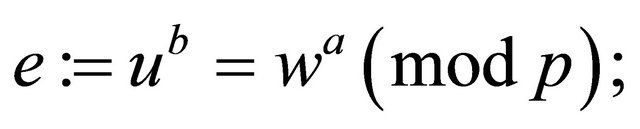 (3.1)
(3.1)
b) If e is distinct from 2, q and 2q, i.e., if
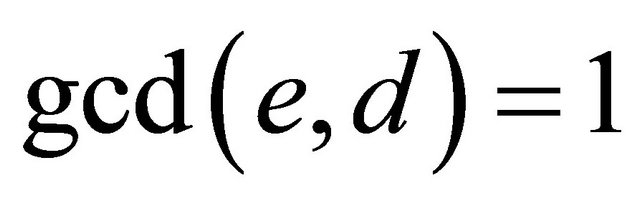 ; (3.2)
; (3.2)
then the users compute an integer d that satisfies the equation
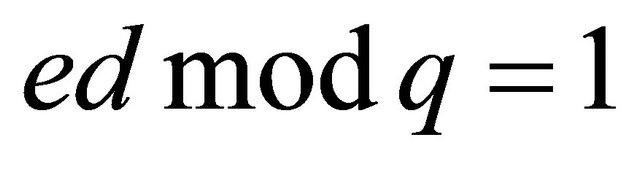 ; (3.3)
; (3.3)
Remark3.1: Although the users can find d (decryptor) from (3.4)
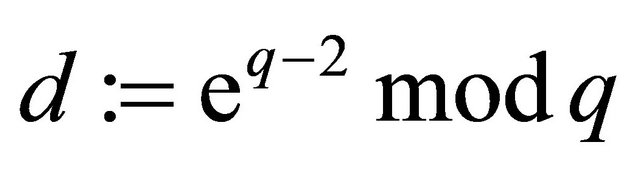 ; (3.4)
; (3.4)
there is a more efficient algorithm for modular multiplicative inverse (MMI) proposed by the author of this paper in [6] and analyzed in [7]; see Example 2 and Table 1 below.
Encryption:
c) The sender of message m computes the ciphertext
 (3.5)
(3.5)
d) The ciphertext c is sent to a receiver via an open communication channel;
Decryption:
e) The receiver computes
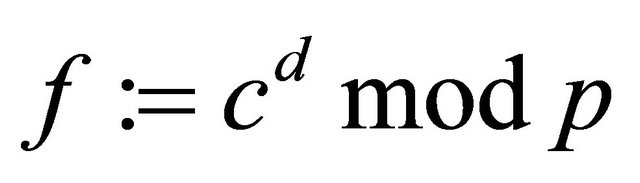 . (3.6)
. (3.6)
Remark3.2: Although (3.5) and (3.6) resemble the RSA protocol [1], there are two distinct features: the encryptor e is a secret (not public!) key and modulo reduction is done by the prime q which is a public key rather than by a product 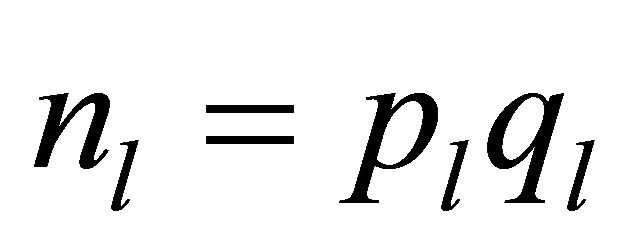 of two large primes that are the private keys of the l-th user.
of two large primes that are the private keys of the l-th user.
Proposition3.1: If m is a quadratic residue modulo p, then 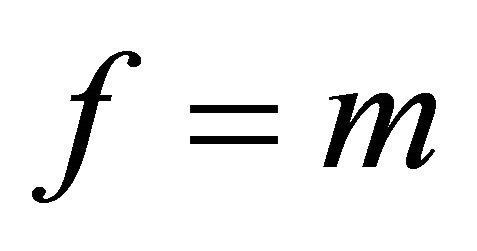 otherwise
otherwise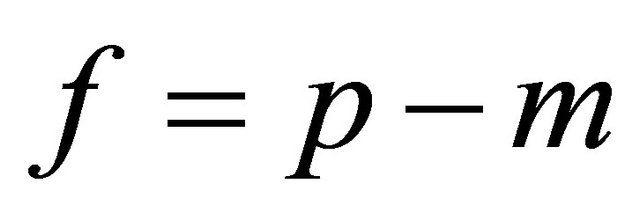 .
.
Proof: Let us consider two outcomes:
• both e and d are odd;
• either e or d or both are even.
Outcome1: (3.3) and the FLT imply that there exists an even integer k such that
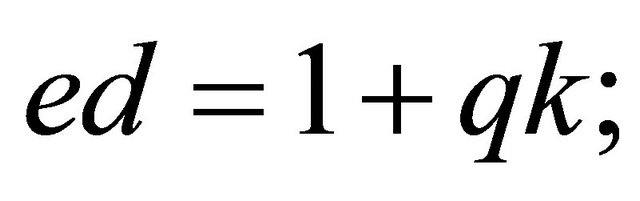 (3.7)
(3.7)
then
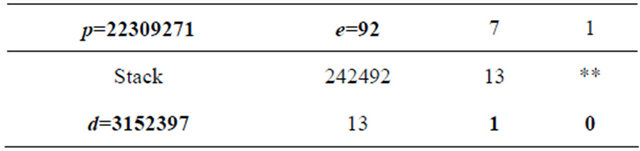
Table 1. MMI of e=92 mod p=22309271.
 . (3.8)
. (3.8)
Outcome2: in this case (3.3), the FLT and Euler criterion of quadratic residuosity imply that there exists an odd integer k such that 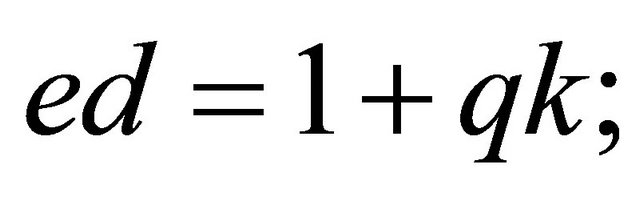 then
then
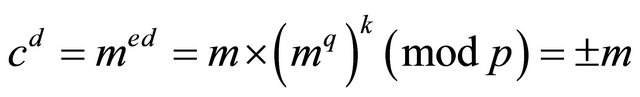 . (3.9)
. (3.9)
Remark3.3: If m is a quadratic residue modulo p, then 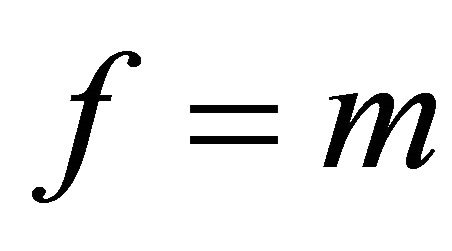 for each outcome, otherwise in (3.9)
for each outcome, otherwise in (3.9) 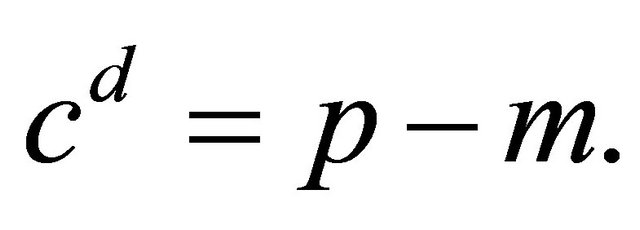
However, the verification of quadratic residuosity of every plaintext block m is a time-consuming process. There are two options to overcome this hurdle:
Option1: together with the ciphertext c the sender transmits a binary indicator R, i.e., 0 or 1: if m is even, then he/she sends 0 else the sender transmits 1.
The receiver action: If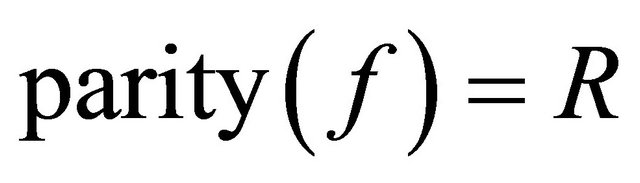 , then
, then 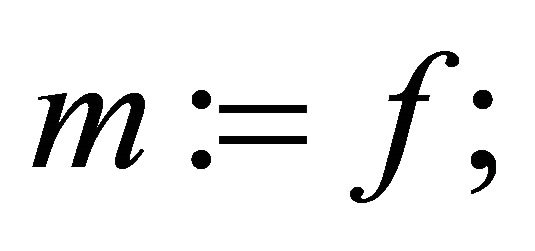 else
else
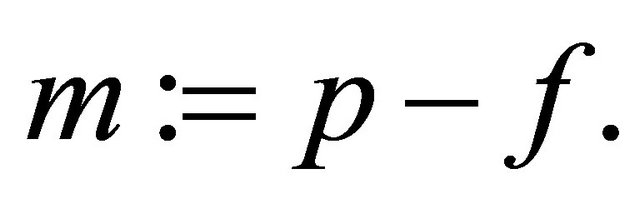 (3.10)
(3.10)
All cases of Option1 are summarized in Table 2:
Option2: The sender pre-conditions m and assigns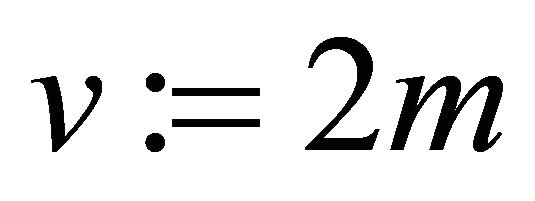 ; and computes
; and computes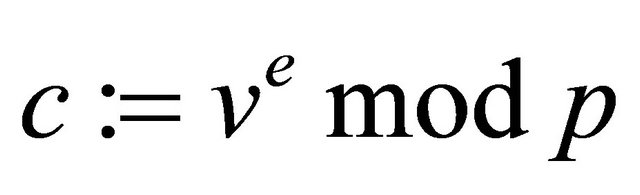 .
.
If 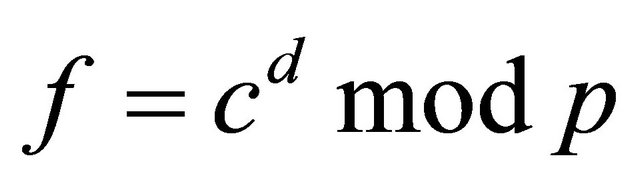 is even, then
is even, then 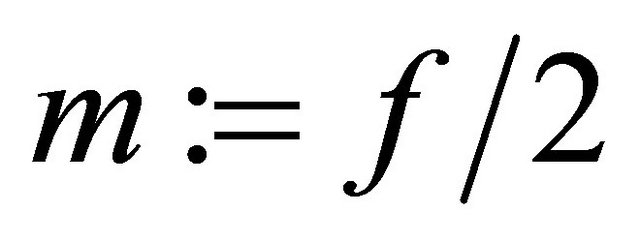 else
else
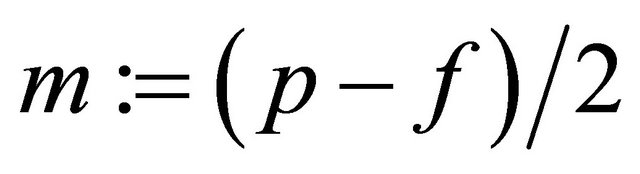 . (3.11)
. (3.11)
4. Numeric Illustrations
Example1: Let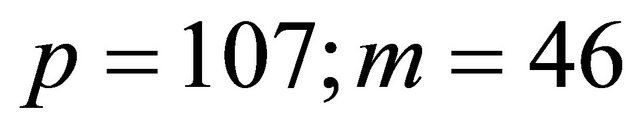 ; and suppose that the private keys a and b are selected in such a way that
; and suppose that the private keys a and b are selected in such a way that 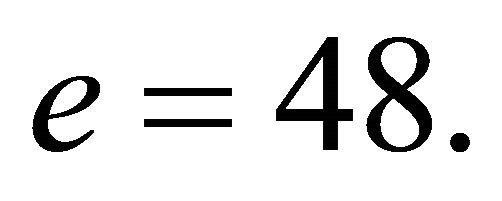
Let us find the decryptor d using the MMI algorithm:
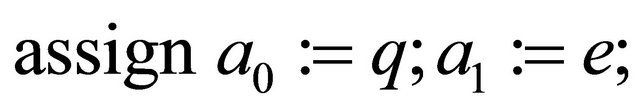
repeat
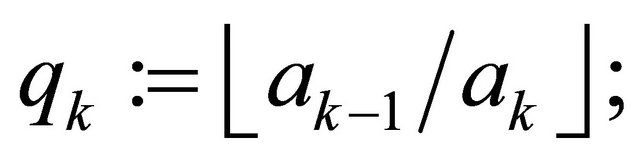
{store all quotients 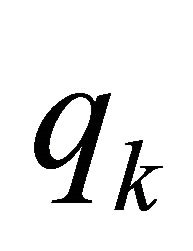 in a stack};
in a stack};
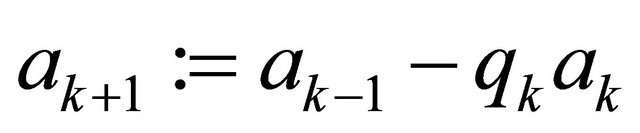 ;
;
until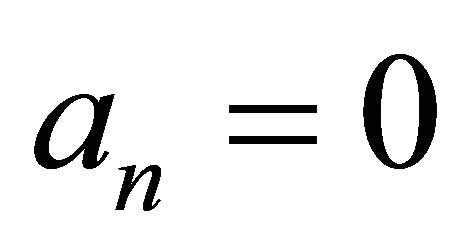 ; or
; or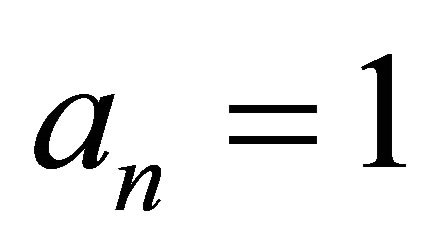 ;
;
if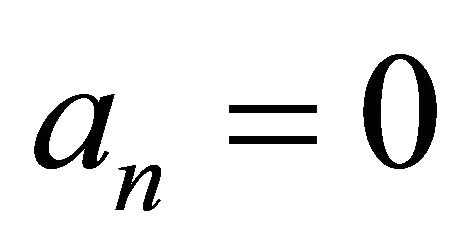 , then the MMI does not exist; stop;
, then the MMI does not exist; stop;
if  then assign
then assign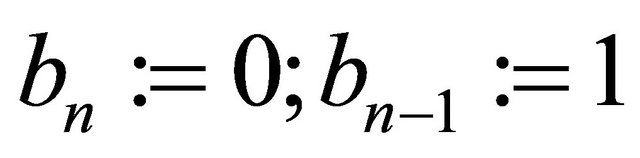 ;
;
for k from n−1 down to 1 iterate 
if n is odd, then 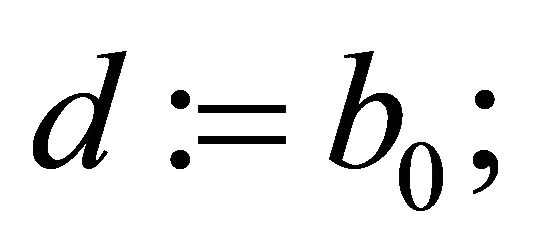 else
else  [8].
[8].
Therefore, from the MMI algorithm d=21.
Table 2. Cases for information recovery.

Indeed: 
Encryption/decryption via Option1:
Encryption1:
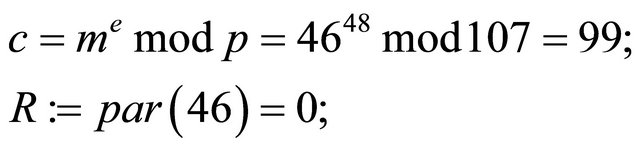
the sender transmits 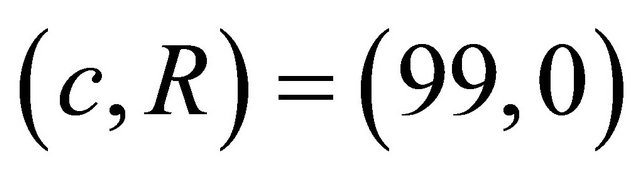 to the receiver Decryption1:
to the receiver Decryption1:
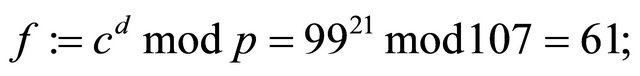
Since 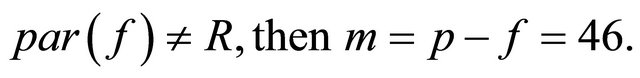
Encryption/decryption via Option2:
Encryption2: 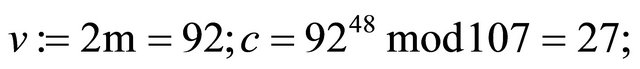
Decryption2: ;
;
Since f is even, then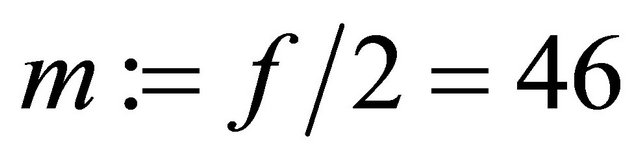 .
.
Example2: p=44618543; then q=22309271.
If a plaintext is divided into blocks of five characters each, and the size of an alphabet is 26, then
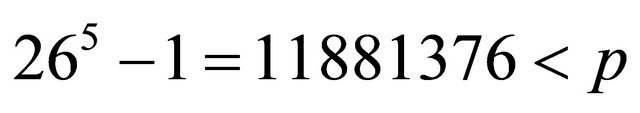 .
.
Suppose that the private keys a and b are selected in such a way that e=92. Therefore, from the MMI algorithm d=3152397 (see Table 1). Indeed:
 .
.
Example3: Let 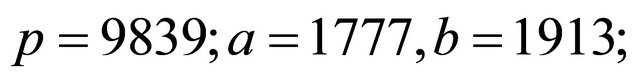 (private keys); therefore, the public keys are
(private keys); therefore, the public keys are
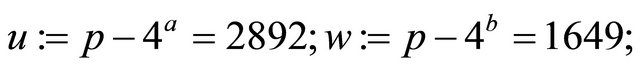
and the mutual secret encryptor for Alice and Bob:
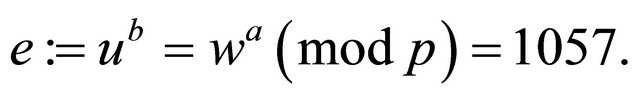
Then both Alice and Bob solve independently 1057dmod4919=1 (3.3).
Table 3 demonstrates step-by-step how the MMI algorithm operates.
Since the number of columns in Table 1 is even, then d=1680.
Indeed, 
Table 4 provides an array of seven plaintext blocks, shows their encryption and information recovery by the receiver. In this case, the sender transmits with each ciphertext a corresponding binary indicator R=0 if m is even; and R=1 if m is odd.
5. Complexity Analysis of EvESE
Cryptosystem
On the system design level, each user performs two exponentiations to compute their public key (2.5) and (2.6), and the secret encryptor (3.1).
For the encryption, it is necessary to perform only one exponentiation (3.5). Analogously, for decryption, every receiver performs only one exponentiation (3.6). Although
Table 3. MMI of e=1057 modulo q=4919.
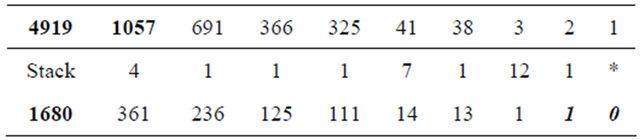
Table 4. Encryption and information recovery: p=9839; e=1057; d=1680.
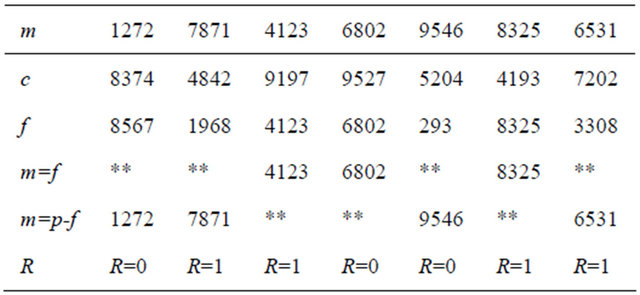
for the purpose of maintaining the high security level we need to periodically select new private keys and recompute the encryptor and decryptor, we do not need to send the hints with every block of the transmitted message as it is done in the ElGamal algorithm [9] (see Table 5).
Since the proposed algorithms (3.1)-(3.6) are based on computational complexity of the DLP, it has certain advantages over the RSA algorithm based on factorization. It is also more efficient than the ElGamal algorithm. Indeed, it needs twice fewer exponentiations for the secure transmission of each block than in the RSA algorithm with digital signature, and 1.5 fewer exponentiations for the secure transmission of each block than in ElGamal. In addition, the ElGamal algorithm requires twice as much bandwidth since together with the ciphertext it is necessary to send an ephemeral public key {the hint}
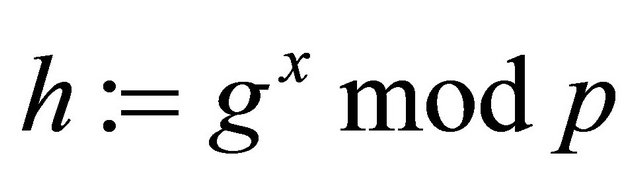 ;
;
with every encrypted block m.
An idea of “binary” shift is proposed in [8] if e is an even integer: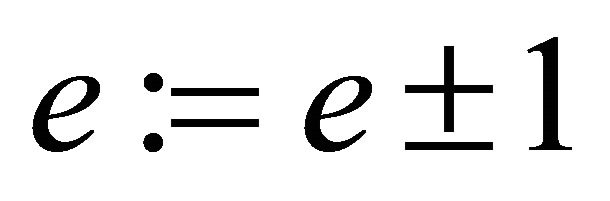 . However, even if the encryptor e is an odd integer, there is an additional advantage to find the decryptor d from the Equation (3.3).
. However, even if the encryptor e is an odd integer, there is an additional advantage to find the decryptor d from the Equation (3.3).
Proposition5.1: Suppose that
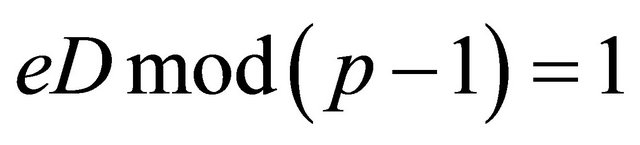 ; (5.1)
; (5.1)
and e is odd; then
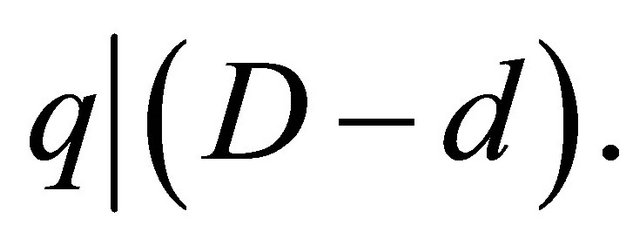 (5.2)
(5.2)
Proof: Let
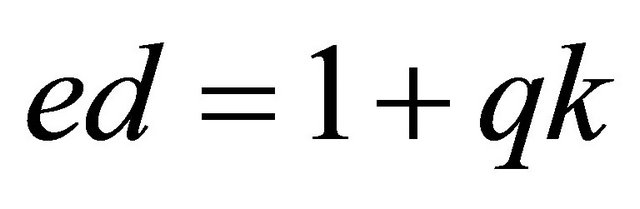 ; and
; and ; (5.3)
; (5.3)
then (5.3) implies that
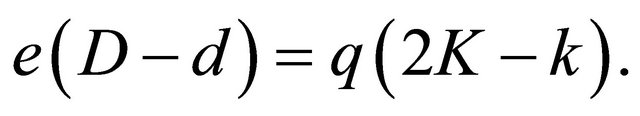 (5.4)
(5.4)
Since e and q are relatively prime, then (5.4) implies that q divides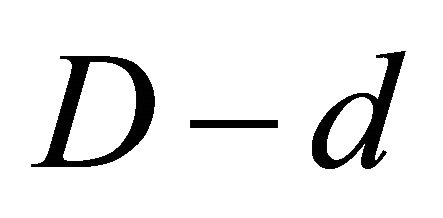 .
.
Thereforeeither d=D or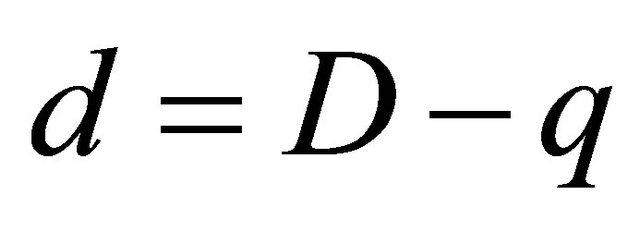 . (5.5)
. (5.5)
Now, suppose that , where z is either 0 or 1; {
, where z is either 0 or 1; {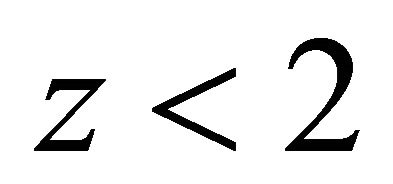 since from (5.1)
since from (5.1) 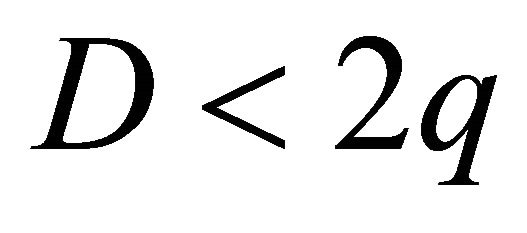 }.
}.
Hence, if 
then  implies that
implies that
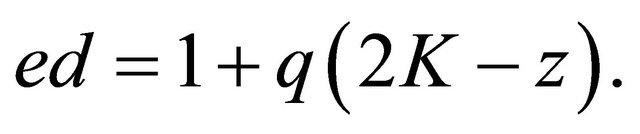 (5.6)
(5.6)
Finally, from analysis of parities in (5.6) we deduce that if d is odd, then z=0; and, if d is even, then z=1.
Table 5 provides several examples of corresponding decryptors D and d. Since in many cases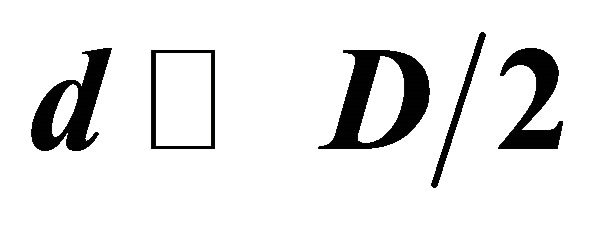 , therefore recovery of information with decryptor d is faster rather than with D.
, therefore recovery of information with decryptor d is faster rather than with D.
Therefore, for 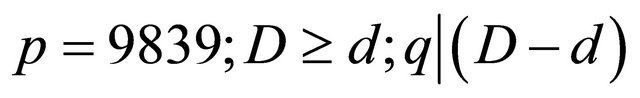 and on average
and on average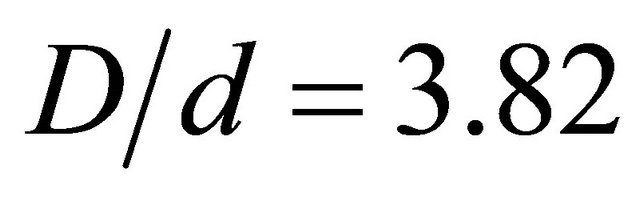 .
.
In addition, the encryptor and decryptor provide a digital signature (sender identification) since they are computed for communication between the specific pair of users (Alice and Bob).
6. Novelty Elements and Conclusion
Notice that the ElGamal algorithm is just one of several constructive ways to dynamically apply the DiffieHellman key establishment scheme for hiding information in secret communication. Indeed, both parties are dynamically establishing a common secret key (encryptor e(m)) and then its inverse value d(m) (decryptor). In the ElGamal algorithm the sender conceals message m by multiplying it on the encryptor e(m).
Other options: instead of multiplying, the sender adds the encryptor e(m) to m or he/she uses exponentiation 
Although it seems that addition of e or even multiplication by e is computationally simpler than the exponentiation, the analysis shows the opposite (see Table 6 below).
In the proposed EvESE cryptographic algorithm we use the following novelties:
a) a safe prime p is considered as the modulus (1.1);
b) a computationally simple and deterministic method is proposed to select the generator (primitive element) g for all users (2.1);
c) the encryptor e for secure communication between the sender and receiver is private (3.1);
d) the plaintext block m is concealed via the exponentiation (3.5) rather than by multiplication or any other binary operation;
e) a deterministic procedure based on the equation  (3.3) finds a mutual decryptor d for the communicating parties [6];
(3.3) finds a mutual decryptor d for the communicating parties [6];
f) one of two options is applied for the information recovery: we either transmit a binary indicator R (3.1) or every plaintext block m is pre-conditioned (3.11) prior to its encryption;
g) even if encryptor e is an odd integer, the decryption with d (3.3) in many cases is faster than with D (see Table 5 and (5.1)-(5.5)).
I express my deep appreciation to Dr. Roberto Rubino
Table 5. Corresponding D and d; p=9839.

Table 6. Comparison of ElGamal, RSA and EvESE {Alice sends signed m to Bob}.

Legends: In (#)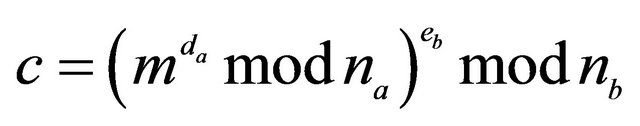 ; in ($)
; in ($)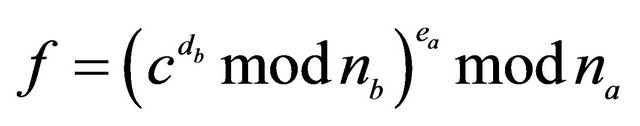 . The RSA algorithm with digital signature works for every m only if
. The RSA algorithm with digital signature works for every m only if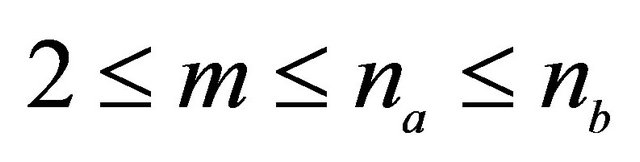 ; [10,11].
; [10,11].
for his comments that improved the style of this paper.
REFERENCES
- R. L. Rivest, A. Shamir and L. M. Adleman, “Cryptographic Communications System and Method”, US Patent #4405829, 1983.
- C. F. Gauss, “Disquisitiones Arithmeticae”, 2nd Edition, Springer, New York, 1986.
- P. Garrett, “Making, Braking Codes: An Introduction to Cryptology”, Prentice Hall, Upper Saddle River, 2001.
- B. Verkhovsky, “Deterministic Algorithm Computing All Generators: Application in Cryptographic Systems Design”, International Journal of Communications, Network and System Sciences, Vol. 5, No. 11, 2012, pp. 715-719. doi:10.4236/ijcns.2012.511074
- W. Diffie and M. E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, Vol. 22, No. 6, 1976, pp. 644-654. doi:10.1109/TIT.1976.1055638
- B. Verkhovsky, “Multiplicative Inverse Algorithm and Its Space Complexity”, Annals of European Academy of Sciences, 2004, pp. 110-124.
- B. Verkhovsky, “Space Complexity of Algorithm for Modular Multiplicative Inverse”, International Journal of Communications, Network and System Sciences, Vol. 4, No. 6, 2011, pp. 357-363. doi:10.4236/ijcns.2011.46041
- B. Verkhovsky, “Public-Key Cryptosystems with Secret Encryptor and Digital Identification”, International Journal of Communications, Network and System Sciences, Vol. 6, No. 1, 2013, pp. 1-6.
- T. ElGamal, “A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms”, Proceedings of CRYPTO 84 on Advances in Cryptology, SpringerVerlag New York, Inc., New York, 1985, pp. 10-18.
- A. J. Menezes, P. C. van Oorschot and S. A. Vanstone, “Handbook of Applied Cryptography”, CRC Press, Boca Raton, 1997.
- G. I. Davida, “Chosen Signature Cryptanalysis of the RSA (MIT) Public Key Cryptosystem”, Technical Report TR-CS-82-2, University of Wisconsin, Milwaukee, 1982.

