Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 11 (2012) , Article ID: 24683 , 5 pages DOI:10.4236/ijcns.2012.511074
Deterministic Algorithm Computing All Generators: Application in Cryptographic Systems Design
Computer Science Department, New Jersey Institute of Technology, University Heights, Newark, USA
Email: verb73@gmail.com
Received September 27, 2012; revised November 4, 2012; accepted November 8, 2012
Keywords: Diffie-Hellman Key Exchange; ElGamal Cryptosystem; Generator; Generator of Pseudo-Random Numbers; Information Hiding; Primitive Element; Safe Prime
ABSTRACT
Primitive elements play important roles in the Diffie-Hellman protocol for establishment of secret communication keys, in the design of the ElGamal cryptographic system and as generators of pseudo-random numbers. In general, a deterministic algorithm that searches for primitive elements is currently unknown. In information-hiding schemes, where a primitive element is the key factor, there is the freedom in selection of a modulus. This paper provides a fast deterministic algorithm, which computes every primitive element in modular arithmetic with special moduli. The algorithm requires at most 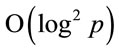 digital operations for computation of a generator. In addition, the accelerated-descend algorithm that computes small generators is described in this paper. Several numeric examples and tables illustrate the algorithms and their properties.
digital operations for computation of a generator. In addition, the accelerated-descend algorithm that computes small generators is described in this paper. Several numeric examples and tables illustrate the algorithms and their properties.
1. Introduction and Basic Definitions
To ensure a high level of crypto-immunity of some cryptographic systems, it is necessary to select a system parameter g (called a primitive element) that satisfies certain conditions.
The primitive elements are used in the Diffie-Hellman secret key establishment (DHKE) protocol [1] and in the ElGamal algorithm [2] for secure exchange of information via open channels. They are also used in the design of generators of pseudo-random numbers [3].
In modular arithmetic, a primitive element g modulo p is an integer having the property that every integer h coprime with p can be expressed as a power of g modulo p.
Therefore, powers of g generate all non-zero elements of the Hmultiplicative group of integers modulo pH.
Definition 1.1: If an integer g has a property that for every integer 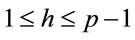 there exists a corresponding integer x such that
there exists a corresponding integer x such that
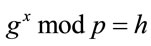 , (1.1)
, (1.1)
then g is called a primitive element (generator, in short) and x is called the discrete logarithm of h to the base g modulo p.
For every prime p there exist several generators. For instance, if p = 31, then g = 3, 11, 12, 13, 17, 21, 22 and 24 are generators.
Leonhard Euler discovered the primitive elements, and Carl F. Gauss described their properties in [4]. A mathematically-oriented reader can find further results in [5,6].
The elliptic curve cryptography (ECC), initially described in [7,8], is an analogue of the ElGamal protocol. As a result, the ECC also requires selection of a point G on the elliptic curve, which is an analogue of the generators in cyclic groups based on real integers. However, an efficient algorithm that computes G is an open problem.
2. Verification Procedure
In order to verify whether g is a generator for prime p, consider all factors of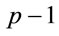 .
.
Proposition 2.1: Suppose
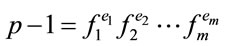 ; (2.1)
; (2.1)
where every integer 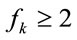 and every integer
and every integer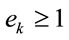 ; if
; if
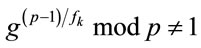 ; (2.2)
; (2.2)
holds for every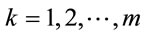 , then g is a generator [9].
, then g is a generator [9].
Example 2.1: Suppose p = 71; let us find a generator. Since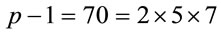 , then g is a generator if and only if
, then g is a generator if and only if 
 and
and  (2.3)
(2.3)
Table 1 shows values of 
Since g = 7 satisfies every condition in (2.3), therefore, after fifteen exponentiations we find that it is the generator for p = 71.
Although the conditions (2.2) are straight-forward to verify, if m is large, then (2.2) requires factorization of 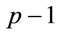 [10] and m exponentiations for each potential candidate. Also, if at least one of these conditions does not hold, it is necessary to consider the next candidate. In general, non-deterministic algorithms are typical for various problems in modular arithmetic.
[10] and m exponentiations for each potential candidate. Also, if at least one of these conditions does not hold, it is necessary to consider the next candidate. In general, non-deterministic algorithms are typical for various problems in modular arithmetic.
3. Two Deterministic Algorithms
In information-hiding schemes, where a primitive element is necessary, there are alternatives for selecting a prime modulus.
Definition 3.1: If both p and 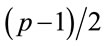 are primes, then p is called a safe prime [9].
are primes, then p is called a safe prime [9].
Example 3.1: Integers 5, 7, 11, 23, 47, 59, 83, 107, 167, 179, 227, 263, 347, 863, 9839, 6935459, 8331923 and 9522167 are examples of safe primes. Although the search for safe primes is not the goal of this paper, the following properties of safe primes eliminate numerous false candidates: p mod 20 = 3 or 7 or 19, otherwise 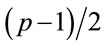 is not a prime.
is not a prime.
A non-deterministic algorithm for the selection of safe primes is provided in [9] {see 4.86 Algorithm}.
Proposition 3.1: If 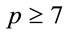 is a safe prime, then
is a safe prime, then
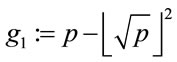 ; (3.1)
; (3.1)
is a generator.
Remark 3.1: Although (3.1) does not always compute the smallest generator, its value is small in comparison
with p: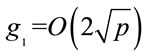 .
.
Indeed,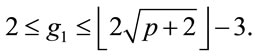 (3.2)
(3.2)
Moreover, if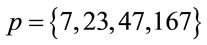 , then
, then
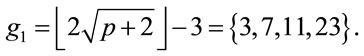
If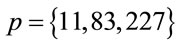 , then for every p
, then for every p

Proposition 3.2: If 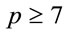 is a safe prime, then
is a safe prime, then
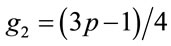 ; is a generator. (3.3)
; is a generator. (3.3)
Proofs of both propositions are provided in the next section.
Table 2 provides fifteen examples of safe primes and three corresponding generators for each of them. For every safe prime, the procedures (3.1), (3.3) as well as (6.4), described in the sixth section, are deterministic and require at most one integer multiplication. As a result, in the ElGamal algorithm, the generator can be periodically renewed for enhancement of communication security. Notice that in Table 2 for p = 11, 23, 47, 59, 167, 179 and 347 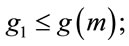 and for the rest of these primes it is otherwise, i.e.,
and for the rest of these primes it is otherwise, i.e., 
4. Algorithm Computing All Generators
Both Propositions 3.1 and 3.2 are special cases of more general proposition.
Proposition 4.1: Let 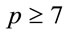 be a safe prime; then for every integer z that satisfies the inequalities
be a safe prime; then for every integer z that satisfies the inequalities
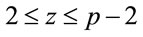 ; (4.1)
; (4.1)
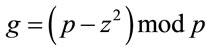 ; (4.2)
; (4.2)
is a generator.
Proof: Definition 3.1 implies that for a safe prime
 ; (4.3)
; (4.3)
where q is an odd prime. Therefore, g is a generator because by Fermat’s Little Theorem [3,4]
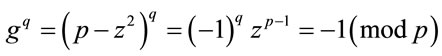 (4.4)
(4.4)
and 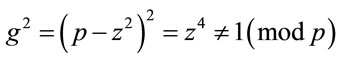 . (4.5)
. (4.5)
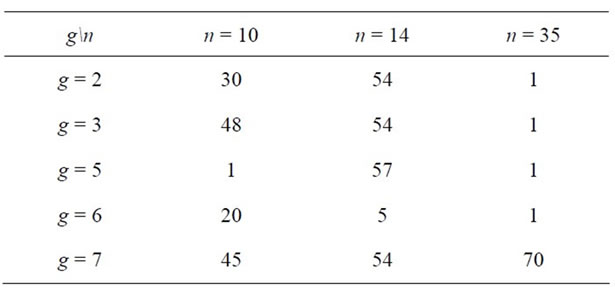
Table 1. Choice of generator for p = 71.

Table 2. Safe primes and corresponding generators.
Suppose that (4.5) does not hold, i.e., there exists at
least one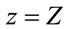 , for which
, for which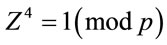 .
.
Therefore, it implies that
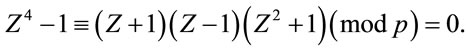 (4.6)
(4.6)
However, none of three factors in (4.6) are congruent with zero modulo p: the first two are excluded by the constraints in (4.1); and the case
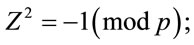 (4.7)
(4.7)
is also infeasible, since by Euler’s criterion of quadratic residuosity [4,9]
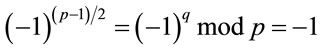 ; (4.8)
; (4.8)
which implies that 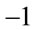 does not have a square root modulo p. In other words, z in (4.7) has no real integer solution. Q.E.D.
does not have a square root modulo p. In other words, z in (4.7) has no real integer solution. Q.E.D.
Proof of Proposition 3.2: It is easy to verify that (3.3) is a special case of (4.2) for z = q. Indeed, consider
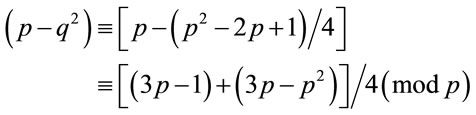 (4.9)
(4.9)
Since for every safe prime p mod 4 = 3 holds, then
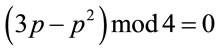 (4.10)
(4.10)
In addition,
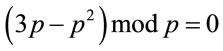 . (4.11)
. (4.11)
Because the last term in (4.9) is an integer, therefore, (4.9)-(4.11) imply (3.3). Q.E.D.
Table 3 lists all generators for p = 47 as functions of parameter z {see (4.2)}.
Since every safe prime p has
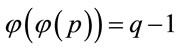 ;(4.12)
;(4.12)
distinct generators, {here 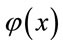 is Euler’stotient function [4]}, the function g(z) generates each of them if z is changing on the interval [2, q]; {see (4.1) and Table 3}. In addition, (4.2) implies that
is Euler’stotient function [4]}, the function g(z) generates each of them if z is changing on the interval [2, q]; {see (4.1) and Table 3}. In addition, (4.2) implies that
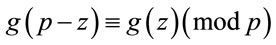 .(4.13)
.(4.13)
For an illustration of (4.13), compare 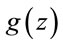 in Table 3 for z = 23 and 24; or for z = 22 and 25.
in Table 3 for z = 23 and 24; or for z = 22 and 25.
Proposition 4.2: If 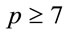 is a safe prime, then for every
is a safe prime, then for every 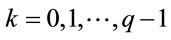
 (4.14)
(4.14)
is a generator.
5. Algorithm for a “Small” Generator
This algorith m computes a small generator for every safe prime .
.
Step 5.1: Compute
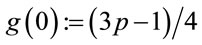 ;(5.1)
;(5.1)
Step 5.2: Compute
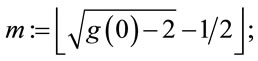 (5.2)
(5.2)
Step 5.3: Compute the generator
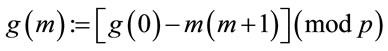 (5.3)
(5.3)
6. Validation of Algorithm (5.1)-(5.3)
Let us consider a sequence of acceleratingly decreasing generators.
Let 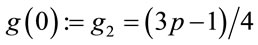 (3.3);
(3.3);
Consider 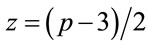 ; (6.1)
; (6.1)
and let
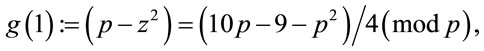 (6.2)
(6.2)
where every term in (6.2) is an integer. Hence (4.10), (4.11) and (6.2) imply that

Proposition 6.1: For every safe prime p there exists a subset S of generators  such that for
such that for 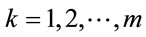 holds
holds
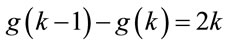 .(6.3)
.(6.3)

Table 3. p = 47 and corresponding generators g(z).
For instance, if p = 83, then g(0) = 62; g(1) = 60; g(2) = 56; g(3) = 50; g(4) = 42; g(5) = 32; g(6) = 20; g(7) = 6.
Therefore, (6.3) implies that for 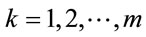
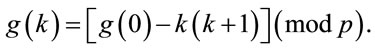 (6.4)
(6.4)
As a result, we derive a monotone decreasing sequence of generators
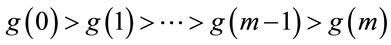 ; (6.5)
; (6.5)
where an optimal m minimizes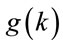 , {see (6.4)}, under the constraints
, {see (6.4)}, under the constraints
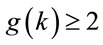 and
and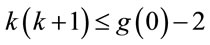 . (6.6)
. (6.6)
Remark 6.1: In the worst case
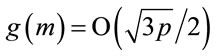 .(6.7)
.(6.7)
Example 6.1: Let p = 47; then g(0) = 35 and from (6.6) m = 5. Hence g(m) = 5, which is the smallest generator. Yet, 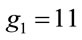 (3.1).
(3.1).
Example 6.2: Let p = 83; then g(0) = 62 and m = 7. Therefore, g(7) = 6, which is the third smallest one after the generators 2 and 5.
Yet, 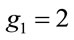 (3.1), is the smallest generator.
(3.1), is the smallest generator.
Example 6.3: Let now p = 9522167; then g(0) = 7141625; and from (5.2) m = 2671. Therefore, g(2671) = 4713. Yet, g1 = 4942.
The procedure described above finds small generators. In some cases, it even provides the smallest generators; {as in Example 6.1}. However, it does not find the smallest generator for every safe prime p. In that case select
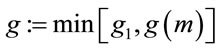 .(6.8)
.(6.8)
7. Results of Computer Experiments
Several hundred computer experiments with the safe prime p randomly-selected on interval (107, 1010) confirm that for every p there exists a monotone-decreasing subset S of generators g(0), g(1), g(2), ···, g(m) that satisfy the inequalities (6.3).
For instance, if p = 9622580663, then the number m of generators in the subset S is equal 84952. The experiments also indicate that  with frequency
with frequency 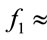 0.382 and
0.382 and 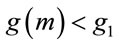 with frequency
with frequency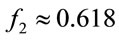 . It implies that, if only one algorithm is used to compute a “small” generator, then
. It implies that, if only one algorithm is used to compute a “small” generator, then  should be computed, because
should be computed, because 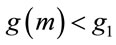 with probability close to 62%.
with probability close to 62%.
Remark 6.2: Notice that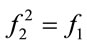 , i.e., these frequencies satisfy the golden ratio equality.
, i.e., these frequencies satisfy the golden ratio equality.
8. Acknowledgements
I express my appreciation to W. Gruver and R. Rubino for their helpful suggestions for improvement of the manuscript. I am also grateful to E. Gerda and Y. Polyakov for their assistance in computer experiments.
REFERENCES
- W. Diffie and M. E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, Vol. 22, No. 6, 1976, pp. 644-654. doi:10.1109/TIT.1976.1055638
- T. ElGamal, “A Public Key Crypto-System and a Signature Scheme Based on Discrete Logarithms”, IEEE Transactions on Information Theory, Vol. 31, No. 4, 1985, pp. 469-472. doi:10.1109/TIT.1985.1057074
- D. Knuth, “The Art of Computer Programming, Vol. 2: Seminumerical Algorithms”, 3rd Edition, Addison-Wesley, Reading, 1998, pp. 18-21.
- C. F. Gauss, “Disquisitiones Arithmeticae”, 2nd Edition, Springer, New York, 1986.
- P. Ribenboim, “The New Book of Prime Number Records”, Springer, New York, 1996. doi:10.1007/978-1-4612-0759-7
- E. Bach and J. Shallit, “Algorithmic Number Theory: Vol. 1: Efficient Algorithms”, MIT Press, Cambridge, 1996.
- V. S. Miller, “Use of Elliptic Curves in Cryptography”, Advances in Cryptography-CRYPTO (LNCS 218), 1986, pp. 417-426.
- N. Koblitz, “Elliptic Curve Crypto-Systems”, Mathematics of Computation, Vol. 48, No. 20, 1987, pp. 203-209. doi:10.1090/S0025-5718-1987-0866109-5
- A. Menezes, P. van Oorschot and S. Vanstone, “Handbook of Applied Cryptography”, CRC Press, Boca Raton, 1997, pp. 162-164.
- B. Verkhovsky, “Integer Factorization of Semi-Primes Based on Analysis of a Sequence of Modular Elliptic Equations”, Int. J. of Communications, Network and System Sciences, Vol. 4, No. 10, 2011, pp. 609-615.
Appendix
Alternative Search for Small Generators
Consider a safe prime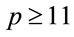 ;
;
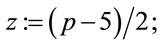
and let
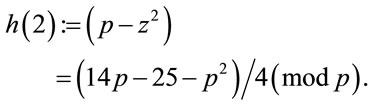 (A.1)
(A.1)
Since every term in (A.1) is an integer, therefore now,
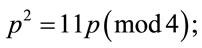 (A.2)
(A.2)
and
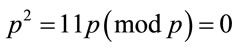 .(A.3)
.(A.3)
Hence 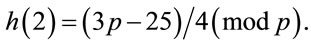
In general, for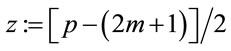 ; (A.4)
; (A.4)
 (A.5)
(A.5)
Thus,
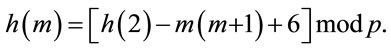 (A.6)
(A.6)
Since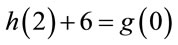 , therefore (A.6) and (6.4) provide the same results.
, therefore (A.6) and (6.4) provide the same results.

