Natural Science
Vol.06 No.12(2014), Article ID:49349,38 pages
10.4236/ns.2014.612096
Blast Waves in Multi-Component Medium with Thermal Relaxation
Vyacheslav O. Vakhnenko
Institute of Geophysics, National Academy of Sciences of Ukraine, Kyïv, Ukraine
Email: vakhnenko@ukr.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 June 2014; revised 30 July 2014; accepted 12 August 2014
ABSTRACT
The mathematical models of relaxing media with a structure for describing nonlinear long-wave processes are explored. The wave processes in non-equilibrium heterogeneous media are studied in terms of the suggested asymptotic averaged model. On the microstructure level of the medium, the dynamical behavior is governed only by the laws of thermodynamics, while, on the macrolevel, the motion of the medium can be described by the wave-dynamical laws. It is proved rigorously that on the acoustic level, the propagation of long waves can be properly described only in terms of dispersive dissipative properties of the medium, and in this case, the dynamical behavior of the medium can be modeled by a homogeneous relaxing medium. At the same time, the dynamical behavior of the medium cannot be modeled by a homogeneous medium even for long waves, if they are nonlinear. For a finite-amplitude wave, the structure of medium produces nonlinear effects even if the individual components of the medium are described by a linear law. The heterogeneity of the structure of medium always introduces additional nonlinearity. It is shown that the solution of many problems for multi-component media with incompressible phases can be obtained through the known solution of a similar problem for a homogeneous compressible medium by means of the suggested transformation. It is not necessary to solve directly the problem for the medium with incompressible component, and it is sufficient just to transform the known solution of the similar problem for a homogeneous medium. The scope for the suggested transformation is demonstrated by the reference to the strong explosion state in a two-phase medium. The special attention is focused on the research of blast waves in multi-component media with thermal relaxation. The dependence of the shock damping parameters on the thermal relaxation time is analyzed in order to provide a deeper understanding of the damping of shock waves in such media and to determine their effectiveness as localizing media. This problem attracts the interest also in view of the practical possibility to estimate the efficiency of medium for damping the shock wave action. To find the nature of the relaxation interaction between the components of medium and to estimate the attenuation of shock waves generated by solid explosives, we have studied experimentally both the velocity field of shock waves and the pressure at front in an air foam. The comparison of experimental and theoretical investigations of the relaxation phenomena which accompany the propagation of shock waves in foam indicates that within the scope of relaxation hydrodynamics it is possible to explain the observed phenomena and estimate the efficiency of medium as localizer of the shock wave action.
Keywords:
Structured Medium, Asymptotic Model, Relaxation, Nonlinear Wave, Explosion

1. Introduction
Natural media are not structureless. The experiments have shown that the intrinsic structure of a medium influences the wave motions [1] - [7] . Existing inhomogeneities complicate the problem and, at the same time, are fully manifested under the propagation of nonlinear waves.
The wave processes in heterogeneous media are usually described in terms of more or less complicated mod- els. Under the conditions of local equilibrium, the media are traditionally modeled irrespective of their structure. In the framework of continuum mechanics, the known idealization of a real medium as a homogeneous one has been fairly successive in the description of wave processes (see, for instance, [8] - [10] ). The continuum models are commonly applied to the mixtures whose dispersive dissipative properties are treated with regard for the in- teractions between the components [11] - [15] . On this level the media are modeled in the framework of a homo- geneous elastic, viscous elastic, and elastic plastic medium [12] [16] . In this case the features of the structure in medium are taken into account indirectly through the kinetic parameters (relaxation time, viscous coefficients etc.) [3] [4] [9] [11] - [16] .
The model of multivelocity interpenetratable continua was developed in terms of classical continuum mechanics [17] and statistical physics [18] in order to describe the dynamical behavior of multi-component media. A fundamental assumption in the theory of mixtures [15] reproduces the assumption in the model of multivelocity interpenetratable continua [17] ; namely that each micro-volume  is occupied by a particle of each constituent. The equations of motion for each component involve the terms describing the mass, force and energy interactions between the components. The problem is complicated by the necessity to employ, in the general case, the experimental data for establishing theoretical relations between the macroparameters at the component interaction level. Moreover, if the component interaction is determined, these models would be indispensable in the theory of multi-component media.
is occupied by a particle of each constituent. The equations of motion for each component involve the terms describing the mass, force and energy interactions between the components. The problem is complicated by the necessity to employ, in the general case, the experimental data for establishing theoretical relations between the macroparameters at the component interaction level. Moreover, if the component interaction is determined, these models would be indispensable in the theory of multi-component media.
In all the models mentioned, the formalism of continuum mechanics is based on the principle of local action as well as on the generalization of the mechanics laws relating the point mass to the continuum [10] .
When going from the integral equations to differential balance equations, the existence of a differentially small microvolume 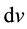 is assumed. On the one hand, this volume is so small that the mechanics laws of the point can be extended to the whole microvolume. On the other hand, the volume contains so many structural elements of the medium that, in this sense, it can be regarded as macroscopic one in spite of its smallness as compared to the entire volume occupied by the medium. So, the passage to the differential balance equations is based on the assumption that microstructural scales
is assumed. On the one hand, this volume is so small that the mechanics laws of the point can be extended to the whole microvolume. On the other hand, the volume contains so many structural elements of the medium that, in this sense, it can be regarded as macroscopic one in spite of its smallness as compared to the entire volume occupied by the medium. So, the passage to the differential balance equations is based on the assumption that microstructural scales 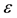 are small as compared to the characteristic macroscopic scale of the
are small as compared to the characteristic macroscopic scale of the , and the passage should be made to the limiting case
, and the passage should be made to the limiting case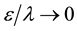 . Contraction of the volume
. Contraction of the volume 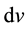 to the point in the general case is correct for continuous functions [10] [15] . This means that all points within the differentially small volume are equivalent. Hence, for the case of a mixture, the equivalence of the points implies that field characteristics should be averaged over
to the point in the general case is correct for continuous functions [10] [15] . This means that all points within the differentially small volume are equivalent. Hence, for the case of a mixture, the equivalence of the points implies that field characteristics should be averaged over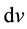 . Hence, it is assumed that the equations of motion can be written in terms of average density, mass velocity, and pressure of each individual component. We note that these models do not contain explicit sizes of components.
. Hence, it is assumed that the equations of motion can be written in terms of average density, mass velocity, and pressure of each individual component. We note that these models do not contain explicit sizes of components.
The application of the models of a homogeneous medium to the description of the dynamical wave processes in a structured natural medium is associated with certain fundamental difficulties [2] [3] [6] [7] [16] . In what follows we treat the structure of medium at the macrolevel. We abandon the assumption that the differentially small volume  contains all the components of the medium, nevertheless we consider the longwave approach with the wavelength
contains all the components of the medium, nevertheless we consider the longwave approach with the wavelength 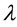 much greater than the characteristic length of the structure in medium
much greater than the characteristic length of the structure in medium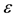 . We consider a structured medium (Figure 1) in which separated components are considered as a homogeneous medium (the differentially small volume
. We consider a structured medium (Figure 1) in which separated components are considered as a homogeneous medium (the differentially small volume 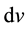 is much smaller than the characteristic size of a particular component
is much smaller than the characteristic size of a particular component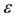 ).
).
Figure 1. Model of the layered medium with two homogeneous components in period.
We describe the wave processes in non-equilibrium heterogeneous media in terms of an asymptotic averaged model [19] - [23] . In this case the obtained integral differential system of equations cannot be reduced to the average terms (pressure, mass velocity, specific volume) and contains the terms with characteristic sizes of individual components.
On the microstructure level of the medium, the dynamical behavior is governed only by the laws of thermo- dynamics. On the macrolevel, the motion of the medium can be described by the wave-dynamical laws for the averaged variables with the integrodifferential equation of state containing the characteristics of the medium microstructure. A rigorous mathematical proof is given to show that on the acoustic level, the propagation of long waves can be properly described only in terms of dispersive dissipative properties of the medium, and in this case, the dynamical behavior of the medium can be modeled by a homogeneous relaxing medium. However, finite-amplitude long waves respond to the structure of the medium in such a way that the homogeneous me- dium model is insufficient for the description of the behavior of the structured medium. An important result that follows from this model is that, for a finite-amplitude wave, the structure of medium (in particular, existence of microcracks) produces nonlinear effects even if the individual components of the medium are described by a li- near law.
We have considered averaged systems of hydrodynamical equations in both Lagrangian and Eulerian coordi- nates. These systems are not expressed in the average hydrodynamical terms; hence the dynamical behavior of the medium cannot be modeled by a homogeneous medium even for long waves, if they are nonlinear. The structure of the medium influences the nonlinear wave propagation. The heterogeneity of the structure of me- dium always introduces additional nonlinearity that does not arise in a homogeneous medium.
We suggest a transformation that enables one to reduce, with certain accuracy (the transformation is exact for planar symmetry as well as for stationary flows), the known solutions of gas-dynamic problems to the two-phase media with arbitrary volume portion of incompressible components.
This transformation enables one to obtain the solution of many problems for multi-component media with incompressible phases from the similar problem for perfect gas. In this case it is not necessary to solve directly the problem for the medium with incompressible component, and it is sufficient just to transform the known solution of the similar problem for a homogeneous medium. Thus, the solutions of many hydrodynamical problems for multi-component media with incompressible phases can be obtained without solving the initial system of equations. The scope for the suggested transformation is demonstrated by the reference to the strong explosion state in a two-phase medium.
The features of the dynamical behavior of two-component media with interphase interaction will be considered by solving a problem associated with the strong explosion stage. This problem attracts the interest also in view of the practical possibility to estimate the efficiency of medium as the localizer of shock wave action. The attenuation of shock waves in a gas-liquid foam generated by condensed explosive charges will be described in terms of a relaxed transfer of heat from the gas phase to the condensed phase. The problem is how to describe/find the dependence of the flow behind the shock front on the thermophysical properties of the medium and the completeness of relaxation processes. We will analyze the dependence of the shock damping parameters on the thermal relaxation time in order to provide a deeper understanding of the damping of shock waves in such media and to determine their effectiveness as localizing media. Besides, it is of interest to define the dependence of shock wave attenuation on the shock loading, especially on the explosion energy.
2. Asymptotic Averaged Model for Structured Medium
The current status of experimental researches demands to develop the models of dynamical behavior of media with account of their inner structure. The real media are not structureless. For example, the geophysical medium has a complicated hierarchical structure. It turns out that the ratio of typical sizes between the neighboring hierarchical levels is a constant value [5] [6] . The inner structure of a medium affects the propagation of waves. Fast high-gradient processes, such as earthquakes, explosions, etc., lead to irreversible processes [6] [7] .
Within continuum mechanics [24] the known idealization of a real medium as homogeneous has a wide application to model their dynamic behavior. Traditionally, it was considered that in heterogeneous media with wavelength appreciably exceeding the size of the structural heterogeneities, the perturbations propagate in the same way as in homogeneous media [8] [9] [15] . However, this statement should be proved, and we shall show that this approximation is not universally true.
The properties of a medium deviate from the equilibrium state under the propagation of intensive waves. Moreover, an unperturbed medium can be in one of unstable stationary states. So, a geophysical medium, within a current physical concept, is an open thermodynamic system, which essentially influences on the exchanges of energy and mass. Thus, a description of open systems should take into account the peculiarities of their inner structure, dynamical processes occurring on the level of structural elements. What is more, the state of media under the action of high-frequency wave perturbations departs from equilibrium, and, thus, the behavior of media can not be described in the framework of equilibrium thermodynamics. Consequently, there is necessity to develop the new mathematical models in order to take into account the nonlinear wave perturbations and irreversible inner exchange processes.
2.1. Background and Initial Equations
The simplest heterogeneous media for which the effect of the structure can be analyzed are media with a regular structure. Features of the propagation of long wave perturbations will be investigated by using as an example, a periodic medium under conditions of an equality of stresses and mass velocities on the boundaries of neighboring components. It is supposed that the microstructure elements of medium 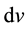 (see Figure 1) are large enough that it is possible to submit to the laws of classical continuum mechanics for each individual component. At the same time the inner processes in each component will be considered within a relaxation approach. The notions based on the relaxation nature of a phenomenon are regarded to be promising and fruitful. We consider that the properties of the medium, such as density, sound velocity and relaxation time vary in a periodic manner (although this assumption is unessential in the final result).
(see Figure 1) are large enough that it is possible to submit to the laws of classical continuum mechanics for each individual component. At the same time the inner processes in each component will be considered within a relaxation approach. The notions based on the relaxation nature of a phenomenon are regarded to be promising and fruitful. We consider that the properties of the medium, such as density, sound velocity and relaxation time vary in a periodic manner (although this assumption is unessential in the final result).
2.1.1. Motion Equations for Individual Component
The analysis of wave motions is based on the hydrodynamic approach. This restriction can be imposed for the modeling of nonlinear waves in watersaturated soils, bubble media, aerosols, etc. [12] [13] . The set of acceptable media could be extended to solid media where the powerful loads are studied in the condition that the strength and plasticity of the material can be neglected [25] . In the hydrodynamic approach we have considered the media without tangential stresses while there are equalities of the stresses as well as of mass velocities on boundaries of neighboring components. Also, we assume that the medium is barothropic. The individual compo- nents of the medium are considered to be described by the classical equations of hydrodynamics. In the Lagrangian coordinate system  the equations of one-dimensional motion for each individual component have the form
the equations of one-dimensional motion for each individual component have the form
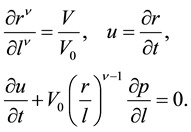 (2.1.1)
(2.1.1)
The equation of continuity can also be used in the alternative form

Here 




Conditions for matching are the equality of mass velocities and pressures on the boundaries of the components

2.1.2. Dynamic State Eqution
Considering the models of a relaxing medium as more general than the equilibrium models for describing the evolution of high-gradient waves, we will take into account the relaxing processes for each component. Thermodynamic equilibrium is disturbed owing to the propagation of fast perturbations in a medium. There are processes of the interaction that tend to return the equilibrium. The parameters characterizing this interaction are referred to as the inner variables unlike the macroparameters such as the pressure p, mass velocity

An equilibrium state equation of a barothropic medium is an one-parameter equation. As a result of relaxation, an additional variable 

There are two limiting cases:
(i) the lack of the relaxation (inner interaction processes are frozen)

(ii) the relaxation complete (there is the local thermodynamic equilibrium)

The state Equations (2.1.5) and (2.1.6) are considered to be known. These relationships enable us to introduce the sound velocities for fast processes

and for slow processes

The slow and fast processes are compared by means of the relaxation time

The equilibrium equations of state are considered to be known

Clearly, for the fast processes 

The substantiation of Equation (2.1.9) within the framework of the thermodynamics of irreversible processes has been given in [24] [26] - [28] . As far as we know the first work in this field was the article by Mandelshtam and Leontovich [29] (see also Section 81 in [24] ). We note that the mechanisms of the exchange processes are not defined concretely when deriving Equation (2.1.9), and the thermodynamic and kinetic parameters appear only in this equation. These characteristics can be found experimentally.
The phenomenological approach for describing the relaxation processes in hydrodynamics has been developed in many publications [12] [13] [24] [27] . The dynamic equation of state was used (a) for describing the propagation of sound waves in a relaxing medium [24] , (b) for taking into account the exchange processes within media (gas-solid particles) [27] , (c) for studying wave fields in gas-liquid media [12] and in soil [13] . In most works, the equation of state has been derived from the concept of concrete mechanism for the inner process. Within the context of mixture theory, Biot [11] attempted to account for the non-equilibrium in velocities between components directly in the equations of motion in the form of dissipative terms.
We assume that the relaxation time and sound velocities do not depend on time, but they are functions of pressure and the individual properties of the components. This means that in the process of a relaxation interaction we can take into account the exchange of moment and heat but not that of mass. Peculiarities of the intrastructure interaction are determined by the dynamic equation of state for each component.
The equations of motion (2.1.1) have been written in the Lagrangian coordinate system. The necessity of such a description stems from the fact that the dynamic equation of state (2.1.9) has been written to the mass element of a medium. Besides, the use of the Lagrangian coordinates is important for the application of the method of asymptotic averaging, since in these coordinates the structure is independent of a wave process.
2.2. Asymptotic Averaged System of Equations
A regularity of structure and a nonlinearity of long-wave processes investigated here specify the choice of mathematical methods. One way of studying this heterogeneous medium is based on a method of asymptotic averaging of equations with high-oscillating coefficients [30] - [33] . The essence of this method consists in the application of a multiscale method in combination with space averaging. In accordance with this method, the mass space coordinate 



The slow coordinate 



where




We now will prove that



pendent of the fast variable
According to the general theory of the asymptotic method, the terms of equal powers of 
independently of each other. Thus, 







Thus, we can average the equations during the period















with the averaged equation of state

Unlike the values






The averaged system of Equations (2.2.4), (2.2.5) is an integro-differential one and, in the general case, is not
reduced to the averaged variables p, 

rigorous periodic medium. However, it may be shown that Equations (2.2.4), (2.2.5) are also relevant to media with a quasi-periodic structure. Indeed, the pressure 





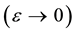
In the case of nonlinear wave propagation, the individual components suffer different compressions. The structure of medium is changed, with the result that the averaged specific volume 



2.3. System of Equations in Eulerian Coordinates
In certain cases of theoretical analysis it is more convenient to use the Eulerian coordinate system. The immediate employment of the averaging asymptotic method in Eulerian variables is impossible because of the variability of the microstructure sizes. However, from the zero approximation in the equations of motion (2.2.1), which are presented by the averaged values





There is an important presumption that the velocity of the particle in the zero approximation is constant over a period of the structure and, consequently, we can describe an averaged trajectory for the particle

From the physical point of view, it is clear that the position of the particle is unambiguously defined by its coordinate and time

From the mathematical point of view this means that in the transformation (2.3.3) the value 
This condition is satisfied if

It is reasonable to define the slow Lagrangian coordinate (non-mass one) as

Equations (2.2.4) in the Eulerian system of coordinates then take the form

It is convenient to determine the fast Eulerian coordinate 

It should be noted that the average density 

proves that 



it is expressed as the ratio of the volume to the mass inside this volume. This value can be determined experimentally. At the same time the averaged values 


We have proved in Ref. [19] that the known Lyakhov model for the natural multi-component media [13] is an actual case of the asymptotic averaged model, i.e., it is inherently asymptotic.
2.4. Analysis of the Averaged System of Equations
Now we will study some general properties of the averaged system of equations, and will obtain a rigorous mathematical proof that for the acoustic level the long wave dynamic behavior of the medium with a microstructure can be modeled within the framework of a homogeneous relaxing medium. At the same time the description of nonlinear waves can not be reduced to the average characteristics of wave field.
2.4.1. Acoustic Waves
Let us consider an acoustic wave
Now we shall show it for a two-layer periodic medium with one process of relaxation in each structure element. The averaged equation of state (2.2.5)
for small perturbations in this medium can be represented as

where index 1 relates to the first component, and index 2―to the second component. Here 


For comparison we take the homogeneous medium with two independent relaxation processes. The state equation of this medium for small perturbations has a form [24]

It should be noted that the alphanumeric indices for the homogeneous medium and for the periodic one have a reverse succession. Here, index 1 relates to the first relaxation process, and index 2―to the second process.
Now we can write six relationships

These equations show that for any two-component medium with the two relaxation components 
(see Equation (2.4.2)). In such media the perturbations





The similarity of the propagation of small perturbation in periodic and homogeneous media has been verified numerically. As it was expected, we obtained the traditional result. An inner structure of the medium manifests itself only by means of the dispersive dissipative properties. For the acoustic level the long wave dynamic behavior of the medium with a microstructure can be modeled within the homogeneous relaxing medium. In the past such a statement was accepted a priori. In our case we have obtained a rigorous mathematical proof of this statement on the basis of a account, in details, of the structure of medium.
2.4.2. Nonlinear Waves
We will analyze the propagation of nonlinear waves in a structured medium. To make the results more clear, we will restrict our consideration to a nonrelaxation media

and we can introduce an effective sound velocity by the formula

We obtain a traditional representation of the system of Equations (2.2.4), (2.2.5) and (2.4.4).
The system of the equations is concerned in the hyperbolic type of a system. Now we restrict ourselves to the plane symmetry

The combination of this equation with the last Equation (1) 

From this relationship it is seen that the averaged system of the equations pertains to the hyperbolic system. The equations for the characteristic in Lagrangian coordinates (mass space coordinate) have the forms

In characteristic the relations are the following

Analogously to the homogeneous medium we call these relations as the Riemann invariants. The value (2.4.8) has the physical meaning, namely, it is the averaged velocity of the wave propagation in the Lagrangian coordinates. This velocity depends on a pressure and integrally on a structure. Note the special case. It is known that in vacuum the wave does not propagate. This result also follows formally from Equation (2.4.8). The hyperbolism of a system points up that this system can describe the shock wave. The equations for the characteristic (2.4.8) and the Riemann invariants (2.4.9) are the integro-differential equations, since they retain
the variable
Normalization on the averaged specific volume 

It should be noted that 



The system of Equation (2.2.4) is hyperbolic ones, and this specifies the breaking solutions which are shock waves. For the analysis of such solutions, it is necessary to present Equation (2.2.4) in the form of integral conservation laws

Now we can easily formulate the conditions on the shock front, when there is conservation of the fluxes of mass and of impulse through the shock front

where indexes 0 and 1 relate to the parameters of the flow before and after the front, respectively. Hence, the formula for the averaged velocity of the shock front in terms of the Lagrangian variable 



2.4.3. The Increase of Nonlinearity in Medium with Structure
We shall prove the statement that the structure of medium always exalts the nonlinear effects under the propagation of long waves. Let us derive the evolution equations with a weak nonlinearity in homogeneous medium and heterogeneous one and compare the coefficients of nonlinearity in these media. First of all, we have to note that the mass velocity 


A functional dependence of an average specific value on the pressure increment 

In this case the system of Equation (2.3.6) for planar symmetry 
The relationship 

used for derivation of the first equation. The evolution equation for one variable assumes the form

Now let us consider the waves propagating in one direction, then with the indicated accuracy we can write (hereinafter index 0 is omitted)
(see, for example, Section 93 in Ref. [24] ). Thus, after factorization of Equation (2.4.14) we get

The coefficient of nonlinearity 

For all cases we take


In certain media the value 
does not depend on





like the homogeneous media under the action of the nonlinear wave perturbations.
For media when the sound velocity is independent of the pressure 



Using the conditions (2.4.5) we can obtain

This inequality is the well-known Cauchy-Schwarz inequality (see Formula (15.2-3) in Ref. [34] ). Since


It only remains to find the condition for equality sign in (2.4.16). For this purpose we apply the Cauchy- Schwarz inequality in vector form (see Formula (15.2-5) in Ref. [34] )
Whereas the equality sign is realized if and only if the vectors 




if and only if
(see Sections 14.2-6 in Ref. [34] ), i.e. when the value 

media for which the value 


3. Waves in Relaxing Two-Component Medium
In this section we will simulate the wave fluids in media consisted of the uniform distributed gaseous and condensed components (solid particles, liquid, etc.). The gas-suspensions, foams, bubble media are the mixtures with regular structure.
Of special interest is the decrease of a shock wave action under propagation of shock waves in two-phase me- dia [35] - [42] . The analysis of this phenomenon shows that effectiveness of a medium as a means for shock wave location depends on capacity to retain heat in a condensed phase. The intensity of the heat transfer is determined by the complex physical chemical processes involved in the interaction between components.
Unfortunately, nowadays the experimental results on various interactions between components are insuffi- cient in order to formulate the mechanisms of interaction and, consequently, to formalize them in mathematical models. There can be no doubt that the inner processes (although their mechanism is not known in details) ma- nifest themselves in the behavior of a medium. We will study the action of inner processes on a change of ma- croparameters within the relaxation notations. As a result of inner interaction is the effect of the relaxation of macroparameters. Additionally the medium can be subject to the external actions, for example, wave perturba- tion, shock wave, dynamic loading, etc. The medium as a dynamic system is specified both the relaxation time and the time of propagation of the shock wave perturbation. We consider the wave processes when the relaxa- tion time and time of an external action are the values of the same order. An irreversible energy loss in a gaseous component (a pressure of gas predetermins the pressure medium as a whole) through the heat transfer by radia- tion and/or by means of contact considerably influences on shock wave parameters. These processes, associated with the transfer of energy from one form that specifies a pressure in medium to another form that does not pos- sess partial pressure, are definitely important for describing the attenuation of shock waves. We will consider these various processes from general point of view as the thermal relaxation. The processes of thermal relaxation will be described by dynamic state equation suggested in the next Subsection 3.1.
3.1. Asymptotic Averaged Model for Mixture with Thermal Relaxation
For mathematical modeling of dynamic behavior of a medium with thermal relaxation, we will consider the constitutive properties, basing upon following assumptions. The partial pressure of the condensed phase is negligibly small, while the medium pressure is specified by the gaseous component only. The gaseous component is generally the relaxing gas. The condensed components show the evidence of relaxation too.
Let us refine the asymptotic averaged model in order to remove the restriction connected with a barothropic medium (as it is studied in Section 2). The constitutive hydrodynamic equations for describing one-dimensional motions (2.1.1), (2.1.2)
are added by the energy equation for each individual component

We analyze the longwave perturbations and assume that the velocities of gas and condensed phase are equal. Similarly to Section 2 let us apply the method of asymptotic averaging, whereas the variable 

where



The procedure similar to that in Subsection (2.2) enables us to obtain additionally the averaged energy equation (index (0) is omitted). Then the system of the equations in the Lagrangian coordinates 

Note that the averaged variables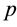





Now we can rewrite out the equations of motion in the Eulerian coordinates 

Finally the averaged equations of motion in the slow Eulerian coordinate have the form (index 


Consequently, the equations of motion are reduced to the terms of the average values







It is worthwhile that at this point we can avoid the restriction in which the structure of medium should be strong periodic. The wavelength is long and covers many periods (see Figure 1). In suggested approximation, the pressure 

3.2. Dynamic State Equation for Mixture with Thermal Relaxation
The practical interest in the gas-liquid-solid mixtures is connected with a capacity of such media to damp the shock waves. We focus our attention upon the study of such inner processes that revel the transfer of a energy defining the medium pressure to the other energy that does not contribute in partial pressure. As a result of the existence of inner processes, we have that the functional dependence between energy


It is convenient to write a state equation for each individual component in the form of dependence of specific energy 




which can successfully be applied both for gaseous component and for condensed component. Generally, both gas and condensed phase are relaxing components. Now we will derive the dynamic state equation for mixture with thermal relaxation [38] [40] - [42] . For one-velocity model, there are two limiting cases: (i) full equilibrium between phases; (ii) lack of transfer of heat between phases. Let us introduce the notations for fast and slow processes for the two components.
1) For gaseous component

2) For condensed component

According to the formalism [27] , we can write a dynamic state equation for each individual component

It is clear that at 


Hence the dynamic state Equation (3.2.5) is not reduced to the variables



However, in particular case it is possible to simplify the dynamic state Equation (3.2.5). The appropriate conditions are realized in the two-components medium with gaseous component and incompressible component.
Indeed, for this medium 


Hence, the specific heat of gaseous component is not constant, i.e. gas is the relaxing component. It is clear that the mentioned reservoir is the condensed phase, whereas, on the one hand, this phase is incompressible, on the other hand, the partial pressure of this phase is negligibly small. It is convenient hereafter to introduce the new notations


is close to 1, while the inequality 




Now the averaged dynamic state Equation (3.2.5) can be reduced to the form

where 

The Equation (3.2.7) describes the nonequilibrium transition of a mixture from one state

to other state

Rudinger [43] - [45] was the first who established the equilibrium state equation for mixture with incom- pressible component (3.2.10).
Thus, the Equation (3.2.7) together with Equation (3.1.4) constitutes the closed system of equations. For this system of the differential equations the initial and boundary conditions depending on problem being studied should be given.
The suggested asymptotic averaged model allows one to analyze the influence of relaxation under the wave propagation in gas-liquid-solid media.
3.3. Similarity in Motions of Gas and Two-Phase Medium with Incompressible Component
We compare the motion of a perfect gas and that of a two-phase medium with any volume occupied by the incompressible condensed component. It is known [43] - [45] that in one-velocity approach at low volume portion of the condensed phase



We focus our attention on transformation between the equations for a perfect gas and the equations describing, in one-velocity approach, the two-phase medium with any volume occupied by the incompressible phase [36] [39] [41] [48] [49] . It shall be proved that the motion of a two-phase medium in the transformed coordinate system is similar with certain accuracy to that of a perfect gas. It means that the solutions obtained for perfect gas can be used to solve the wave problems for media with incompressible component. There is no necessity directly to solve the problem for medium with incompressible component, and it is only sufficient to transform the known solution of the similar problem for a homogeneous medium. Thus, the solutions of many hydrodynamic problems for multi-component media with incompressible phase can be obtained without solving the original system of equations. The scope for the suggested transformation is demonstrated by reference to the strong explosion in a two-phase medium.
3.3.1. System of Equations in the Lagrangian Coordinates
In some sense the progress in finding the transformation was achieved owing to the stimulating support of colleagues. One of a concept consists in analyzing the considered problem in the Lagrangian coordinates


For convenience of the description, we here introduce new notations for independent variables



The parameter 


Since the state Equation (3.3.2) contains value of the volume portion as additional value, then

Equation (3.3.2) does not coincide with the state equation for a perfect gas with certain effective adiabatic parameter


Thus, the closed system of the equations consists of first three equations of system (3.3.1) and Equations (3.3.3), (3.3.4).
Since the Eulerian space coordinate 

We now show that (i) for planar motions


The following physical background provides a basis for eliminating the volume portion 

3.3.2. Similarity of Stationary Flows
We need to reduce the system of Equations (3.3.1)-(3.3.4) to the system of equations describing the motion of a perfect gas (hereafter the notations for gas primed)

For the latter system (3.3.6) the relation between the Eulerian space coordinate and the Lagrangian coordi- nates is as follows:

One of the key requirement is as follows: the time should be equivalently running in all systems of coordinates
The perturbations in incompressible component propagate with infinite velocity. Hence, the volume occupied by incompressible phase can be eliminated, then the connection between the Equation (3.3.4) and the last Equation (3.3.6) is presented in the form


The relationship (3.3.8) indicates that the volume occupied by incompressible component is eliminated, and all masses of the medium are distributed over the residual volume of the compressible component.
Comparing the mass equations with each other, i.e. first equations from system (3.3.1) and system (3.3.4), the condition

should be satisfied.
We need also to make consistent the momentum equations (i.e. third equation in (3.3.1) and third equation in (3.3.6)). The required condition after several reductions can be written as


For deriving (3.3.11) we use the relation
which follows from
Let us take advantage of key relationship between the independent variables in the Eulerian coordinates

appearing in the transformation for planar motion 
terms with 


symmetry 

The suggestion (3.3.13) enables us to assume that the connection between variables 


Thus we satisfy the important condition: the value 

The connection between the mass velocities follows immediately from (3.3.14)

Substitution of the relation (3.3.15) directly into the condition (3.3.10) reduces this condition to the transfor- mation

Trying to transform Equation (3.3.11) into (3.3.12) we can obtain new equation in which in addition to all terms of the Equation (3.3.12) we get unfortunately the additional term

The additional term (3.3.18) vanishes for stationary flows as well as for any flows with planar symmetry, and possibly for self-similar motions.
Consequently, the transformation (3.3.8), (3.3.9), (3.3.15)-(3.3.17) between the systems of equations (3.3.1)- (3.3.4) and (3.3.6) is valid (i) at least for stationary flows, i.e. one can state that for cylindrical 

In the next point 3.3.3 we analyze the transformation (3.3.8), (3.3.9), (3.3.15)-(3.3.17) between equation systems (3.3.1), (3.3.4) for self-similar motions in order to estimate the error included in the term (3.3.18).
3.3.3. Self-Similar Motions with Shock Waves
The above-mentioned transformation allows one to use its advantage for describing the self-similar problems. Let us apply the method for solving the problem related to the strong explosion stage in a two-phase medium.
Let a finite amount of energy 


where 


Let us define new dimensionless variables for the equation systems describing the two-phase flow (3.3.1), (3.3.3), (3.3.4)

and gas (3.3.6)

According to (3.3.15) we write

At strong explosion in a two-phase medium the self-similar motion is realized, whereas, the derivatives with respect to 


with boundary conditions at shock wave front [46] [47]
and for the homogeneous medium (perfect gas) in the form

with boundary conditions
We prove the last equation in (3.3.23) only. Let us consider the sequence of relations taking into account (3.3.4) and (3.3.20),
The transformation (3.3.8), (3.3.9), (3.3.15)-(3.3.17) is easy reduced to the dimensionless form

It turns out that for self-similar motion with shock wave (in contrast to the stationary flow) the transformation between systems (3.3.22) and (3.3.23) is not succeeded in finding. Anyway for 
Using the point explosion as an example, we estimate the error introduced by the additional term. The results of the calculations for strong explosion are demonstrated in Figures 2-5. We calculate the dimensionless specific volume

























Figure 2. The profiles of dimensionless velocity
Figure 3. The profiles of dimensionless density
Figure 4. The profiles of dimensionless pressure
Figure 5. The distributions of volume portion of incompressible component 
important that complete agreement is observed for





Thus, since for a problem of strong explosion in gas the self-similar solution is known in forms of analytical dependencies [50] [51] and tabulated data [52] , one can obtain with certain accuracy the solution for strong explosion in two-phase medium with incompressible component. Moreover, the solution obtained in this manner has the analytical dependencies on value of volume portion of incompressible phase

We present below the example of successful applying the analytical transformation to estimate the velocity of shock wave propagation in two-phase medium [36] [39] [41] .
3.3.4. Shock Front Parameters
It is fairly simple to establish analytically the effects of the volume portion of condensed phase on the motion of the shock wave and the shock front parameters without finding the distributions



where 

The dimensional method [51] allows us to obtain the equation for the shock wave

For 








We use (3.3.28), (3.3.29) and (3.3.20) to get a relation between the shock front pressure and the distance from the explosion center:

These equations indicate that the increase in the shock wave parameters when the medium contains an incompressible phase is due to the increase in the shock wave velocity by a factor 


It follows from (3.3.30) that the minimum pressure occurs at a given distance from the explosion center in a medium having the maximal shock compressibility for the gas phase (by definition






Consequently, we have suggested the transformation that allows one to obtain the wave fields in two- component media with arbitrary volume portion of the incompressible component from the similar problem for perfect gas. The solutions of many hydrodynamic problems for mixtures with incompressible component can be obtained without solving the original system of equations. The scope for the suggested transformation is shown through the analysis of the strong explosion in a two-phase medium.
4. Blast Waves in Medium with Thermal Relaxation
The features of dynamic behavior of two-component media, the influence of interphase interaction under the wave propagation can be elucidated by means of solution of a problem related to the strong explosion in a two- phase medium. This problem attracts interest also in practical possibility to estimate the efficiency of a medium for localizing the sock wave action. The expanded range of pulsed materials processing requires the develop- ment of means for damping of the action of shock wave in the surrounding medium generated by high-power energy sources. In addition to the special chambers, recently the multiphase media (bubble screens in liquids [54] [55] , gas-liquid foams [56] [37] , foam plastics [57] , etc.) have been used for damping of the shock waves. The studies have shown that the energy of explosions is most efficiently absorbed by the water foams [57] .
A qualitative theoretical analysis of strong shock waves in two-phase media with a small volume fraction of condensed material shows that the potential capacity of foam to damp the shock waves is greater. It turns out that the estimated parameters of shock waves at a fixed distance can be below the parameters found in experi- ments [53] [37] . It is noticed that the failure to reach the calculated parameters can apparently be explained by means of the fact that the characteristic time of interphase relaxations, which describes the conversion of thermal energy from the gaseous component (which determines the pressure of a medium) to the internal energy of the condensed phase (which does not contribute to the pressure), are substantially greater than the time required to peak the pressure at the shock front. We will clarify that the properties of own medium determine the attenuation of shock waves. We will analyze the dependence of the shock wave attenuation on the thermal relaxation in order to explain the damping of shock waves by such media and find out their effectiveness as localizing media as well. Besides, it is of interest to define the dependence of the shock wave attenuation on a shock loading, in par- ticular, on an explosion energy.
4.1. System of Equations for Describing the Strong Explosion
The molecular relaxation following an explosion in a gaseous or liquid medium proceeds so fast that the perturbation front can be regarded as a discontinuity surface (a shock wave). In that case the self-similar theory of point explosion can be applied for describing the evolution of a shock wave during the high-intensity stage of the explosion process also at distances where the shape of the energy source does not play a significant role [50] - [52] . Hence, in this classical case when there are no relaxation processes in flow behind the front of a shock wave, the unsteady motion of a medium induced by the instantaneous release of energy at a point is described by a self-similar solution [50] - [52] . Then the pressure and velocities of the wave flows are uniquely determined by the energy of explosion and the thermophysical properties of the gas/liquid surrounding the energy source.
However, there are media in which the relaxation processes occur in flow behind the shock front. If the medium possesses the relaxation processes with characteristic time compared with a time of wave propagation, the parameters behind the front depend significantly on the completeness of relaxation processes in a medium. One glowing example of these media is the gas-liquid foam. After explosion in a two-phase medium only the gaseous component reaches the equilibrium immediately. There is the wide relaxation zone behind the shock front, since the equalization time between the parameters of the phases is well long than the relaxation time in a gas [37] [56] . Consequently, formation of a shock wave after explosion in two-phase medium cannot any more be regarded as occurring within an infinitesimally short time, and the relaxation processes in wave should be taken into account [37] to define the shock wave.
This section is concerned with the effect of thermal relaxation behind the shock front on the evolution of a shock wave. For example, the attenuation of shock waves in gas-liquid foam generated by the condensed explosive charge shall be described in terms of heat transfer from the gas phase into the condensed phase [36] - [38] [40] [42] . Let an explosion occur in this medium and, as a result, an energy 
On the basis of these assumptions, the fundamental system of equations for describing the shock-wave flows at point explosion in mixture (spherical symmetry




The dynamic state Equation (4.1.4) relates to the certain mass of medium, thereby the full derivative with
respect to time 


function of an averaged specific volume 
Since there is an additional variable 

equations is supplemented by the balance equation of the total energy: the energy of the medium bounded by the shock wave is equal to the initial energy of the medium 

The state Equation (4.1.4) can be formally rewritten down in a form

The physical sense of the operator 




For wave propagation it is succeeded to reduce the form 


The parameter 







In general, 




with 


We shall restrict ourselves the consideration of the strong shock wave where the initial internal energy of the
gas can be neglected 
front and center symmetry take the following form [46]

In the case of a point source of energy 
Since the dependence on the volume fraction of a condensed phase

Consequently, we have obtained a closed system of Equations (4.1.1)-(4.1.3), (4.1.5)-(4.1.8) with boundary conditions (4.1.9) for the motion of a two-phase medium including the thermal nonequilibrium behind the shock front. This system consists of seven equations which have seven unknown variables:






The system of Equations (4.1.1)-(4.1.3), (4.1.5)-(4.1.8) is reduced to the dimensionless form by means of transformation of the dependent variables

and independent variables

as follows:

We have seven equations for seven unknown variables






The boundary conditions for this system take the form

In the limiting case without relaxation processes 








sidered to determine the initial conditions.
The system of Equation (4.1.12) differs from the self-similar system of equation by the dependence of 


It is clearly that at time instant 





4.2. Calculation of Shock Waves
The occurrence of thermal relaxation is shown to make the description of the shock waves more complicated. The relaxation affects on rate of shock wave attenuation, on ratio between kinetic and internal energies, on impulse of the pressure in transient shock wave. In general case the shock wave parameters depend on properties of a medium




The basic features of the evolution of strong shock waves in a relaxing medium are shown in Figures 6-9. The effect of the relaxation process on the change of the pressure profile is shown in Figure 6. In the central region a decrease in 

The parameter 


The effect of heat exchange on the attenuation of pressure in the shock wave is conveniently characterized by the parameter 



Figure 6. The pressure profile of shock wave at different time propagation. For all curves




Figure 7. The pressure on the wave front 


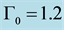



Figure 8. The dependence of the energy redistribution from the explosion between the internal 







Figure 9. The dependence of the dimensionless impulse of the pressure 






It should be noted that for strong shocks, in which the relaxation processes occur within the shock front, the variable 


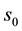
The presence of the relaxation process leads to a qualitative change in the nature of the attenuation of the shock wave. Unlike the case of a nonrelaxing medium, where the pressure and propagation velocity of the shock wave vary according to the power laws (





In Table 1 we show the dimensionless time 









Figure 7 where the dependence of the pressure on the wave front 


curves approach the asymptotic value at the same distance from the energy source. We note that the increase of the exponent 

An important characteristic related to the attenuation of the shock wave in the medium with relaxation is the variation of the ratio of the internal energy to the kinetic one during the relaxation process. The dependence of the energy redistribution from the explosion between the internal and kinetic energies of the medium on the dimensionless time is shown in Figure 8. We see that the energy redistribution in time also reaches a limiting value corresponding to thermodynamic equilibrium in the medium, and this process occurs more rapidly for larger value of the parameter



The attenuation of shock waves in a relaxing medium is intimately connected with the need to decrease their intensity in order to avoid the breakup of the structures and objects. In practice, a breakup is determined in the most cases either by the impulse of the shock wave or by a quantity involving the impulse and the pressure on the shock front [61] . Since the relaxing multiphase media are so widely used in the damping of shock waves, the knowledge how the impulse of the shock wave changes throughout relaxation processes is of current interest. This is shown in Figure 9 as the dependence of the dimensionless impulse of the pressure

on the distance



Table 1. The time 



the value for a less dense nonrelaxation medium (see Figure 9), in spite of the decrease of the peak pressure 
4.3. Blast Waves in Foam
Nature of the relaxation interaction between gas and liquid must be understood in order to predict the parameters of shock waves generated by the ignition of explosive in foam. At the explosion in foam the degree of completion of relaxation processes depends both upon the thermophysical properties of phases and the energy of the explosion determining the period of wave disturbance.
Considering the attenuation of shock waves generated by nonpoint energy sources, such as chamical explosives, it should be noted that the increase of the density of the condensed phase in medium for purposes to reduce the shock wave parameters simultaneously causes a decrease of the shock formation region and, hence, an increase of the shock parameters at the interface between the two-phase medium and the explosion products. It is natural to assume that in some region of shock wave formation the pressure amplitude at the shock front in the two-phase medium will also be greater than in a gas.
4.3.1. Experimental Study
To find the nature of the relaxation interaction between the phases and to obtain quantitative estimates of shock attenuation in the formation region for the shock waves generated by solid explosives, we have studied experimentally both the velocity field of shock waves (see Figure 10) and the pressure at front (see Figure 11) in an air foam with a mass concentration of liquid of 10 - 15 kg/m3. The experimental results for air from Refs. [6] [62] - [66] are also represented in Figure 10 and Figure 11.
The experiments were conducted with spherical explosive charges having a bulk mass of 0.5 - 2.8 kg



be seen that at closer distances from the charge, there is a sharp reduction in the differences between the shock velocities in the foam and gas.
For 


Figure 10. The velocity of the wave front 


Figure 11. The pressure on the wave front 


Here 

the zone nearest to the explosion charge the pressure ratio at the wave front is close to the ratio for kinematic equilibrium between the phases. Thus, we may assume with this accuracy that the kinematic interphase equilibrium exists in the shock front. The curve 1 of Figure 11 represents the pressure field of a point explosion
in foam taking the thermal relaxation into account. As can be seen in Figure 11, when 
pressure in a foam becomes comparable to the pressure at a shock front in air and sharply increases as the charge is approached, whereas at the boundary of charge, judging from the shock velocity, the pressure must be



It is important that there are the abrupt reductions of the wave parameters both for pressure

and for propagation velocity

in foam with distance. Note that for nonrelaxation medium these exponents can not exceed the values 
The experimental dependencies of the reduced impulse of the pressure 

Figure 12. The reduced impulse of the pressure 

different dependencies of impulse of the pressure in these media. The dependence observed in air [62] [63] relates to the shock wave formation. Simultaneously, the monotone dependence of the impulse in foam points up the more near formation of the shock wave to the explosive charge. The experimental results confirm that the gas-liquid foam is one of media in which the relaxation phenomena are more pronounce usually.
The abrupt attenuation of the wave observed in foam in comparison with attenuation in gas is associated with the processes of heat exchange between liquid and gas. In this case the increase of attenuation of the shock wave parameters, depending on a distance, enables us to make the conclusion that the thermal relaxation occurs more slowly than the kinematic equilibrium is established between phases.
4.3.2. Comparison of Calculation with Experiment
The correlation between the experimental results for the wave velocity 

thermal equilibrium. Indeed, 


the completeness of thermal relaxation, while this value 
The results of Ref. [67] confirm the suggested approach. It is noted [67] that in dusty gas at initial time instant the particles lag from the gas. However, henceforth the gas flow involves the particles and the velocity of particles increases. Furthermore, the geometrical divergence of gas flow provides the decrease of its velocity and as a results the particles velocity can exceed the gas velocity. The particles involved by flow move to the shock front, whereas their velocity becomes sufficient to sustain the shock wave.
The process of formation and propagation of a shock wave generated by chemical explosion can be imagined as follows. At explosion of a charge the explosive products with high pressure transmit gradually the energy to the surrounding medium. Since the shock wave velocity is lower in two-component medium (the foam) than in gas, the transfer of energy from explosive products to a foam occurs more fast than to a gas possessing lesser density. Thus, the shock wave in foam should be formed nearer to a charge than the shock wave in gas. Here, we point out once again that the formation of the shock wave in near zone to a charge in foam confirms by the experiments on the pressure impulse in foam and air (see Figure 12). On the basis of the experimental results, we can claim that in zone, where the direct measurements of pressure and impulse have been performed, the shock wave had already been formed.
After the formation of shock wave, the mechanism which energetically supports the wave perturbation is likely to be caused by both the pressure of a gas phase and the kinetic energy of a condensed phase. This last process is considered to lead to the equalization of velocities between phases in flow behind the shock front.
The more near formation of the shock wave to the explosive charge enables us to use the assumption on the kinematic equilibrium, and, thus, to estimate the pressure through the Mach number in zone, where the direct measurements of pressure have not been performed (dashed line 1 in Figure 11). The estimations point that here pressure in foam exceeds the pressure in air.
In flow behind front, where the kinematic equilibrium is considered to take place, the relaxation effects concern with other interphase interactions such as heat exchange, radiation, partial mass exchange between phases, etc. Such internal processes evidently lead to the loss of energy determining the pressure of medium. The process of thermal relaxation is slow in a comparison with the time to attain a maximal pressure at wave front. The effect from the energy transfer caused by above-mentioned processes in flow behind shock front is not immediately manifested in front parameters of wave. The hydrodynamic laws constitute the transmission of information on the loss of heat in gas phase from the deepness of flow to the shock front. Consequently, in order to describe the propagation of shock wave, it is necessary to solve the time-dependent hydrodynamic equations. The simulation of propagation of the shock waves generated by point explosive charge has been carried out in Subsecetions 4.1, 4.2.
Now we compare computer calculation with experimental results on the propagation of shock waves in the foam possessing the relaxation effects. The assumption on the ideal energy source (i.e., the point charge and the instantaneous energy release) does not allow us to compare directly numerical data with experimental results where waves have been generated by the real chemical explosion. For example, the comparison of the pressure in air from point charge and real one shows that at distances where the dependence 















Apart from the comparison of absolute values, we have compared the relative values related to the appropriate values in air. It is interesting to compare the change in pressure for a transient wave in relaxing medium (foam) and in nonrelaxation one (for example, in air). Such a value can be the pressure attenuation coefficient. As usually, by definition the pressure attenuation coefficient is the ratio of the pressure in nonrelaxation medium to the pressure in relaxing medium at a fixed distance.
Since the pressure attenuation coefficient under conditions of the kinematic equilibrium between phases depends only on the heat transfer between phases, then it becomes possible to deduce the trend of thermal relaxation in a two-phase medium, without distortion, from experimental data on attenuation of shock waves. In order to establish the model kinetics here, it is appropriate to compare the experimental curves of shock wave attenuation in foam and in medium describable in terms of the state equation for gas without relaxation properties. Since such a medium can, specifically, serve gas, then the available data on explosion in air [62] [63] can be used for this purpose.
From these experimental data one calculates the pressure attenuation coefficient as the ratio of pressure in air to pressure in foam at the fixed dimensionless distance. It must be taken into consideration that in the zone where the energy source cannot be regarded as a point source, the pressure attenuation coefficient 
To predict the shock wave attenuation in foam on the basis of the suggested model, one needs to have an experimental point as reference, inasmuch as the parameter 

attenuation coefficient calculated from the experimental results (see Figure 11) and estimated theoretically is observed for 
Figure 13 depicts the dependence of the pressure attenuation coefficient on the reduced distance


Figure 13. Pressure attenuation coefficient for a blast wave in foam. The estimated values are represented by curve 1; the experimental values―by curve 2.
The represented analysis showed that thermal relaxation significantly changes the flow parameters and increases the attenuation of strong shock waves in two-phase media. The dependence of the shock attenuation coefficient on the inner heat-exchange processes in medium has been demonstrated. It has been found that the parameters of shock waves in foam are enhanced in comparison with the parameters in gas near a nonpoint energy source because of the conditions under which energy is transferred from the source to the medium.
Since the thermal relaxation times obtained by two independent methods correlate, it appears that an adequate description of the relaxation processes in foam is possible within the framework of the suggested theory. The results of experimental and theoretical investigations of the relaxation phenomena which accompany the propagation of shock waves in foam indicate that within the scope of relaxation hydrodynamics it is possible to explain the observed phenomena and estimate the efficiency of medium as localizer of the sock wave action.
5. Conclusions
The asymptotic averaged model has been developed for describing nonlinear long-wave processes in relaxing media with a structure. The derived integral differential system of equations cannot be reduced to the average terms (pressure, mass velocity, specific volume) and contains the terms with characteristic sizes of individual components. On the microstructure level of the medium, the dynamical behavior is governed only by the laws of thermodynamics. On the macrolevel, the motion of the medium can be described by the wave-dynamical laws for the averaged variables with the integrodifferential equation of state containing the characteristics of the medium microstructure. On the acoustic level, the propagation of long waves can be properly described only in terms of dispersive dissipative properties of the medium, i.e. the dynamical behavior of the medium can be modeled by a homogeneous relaxing medium. However, finite-amplitude long waves respond to the structure of the medium in such a way that the dynamical behavior of the medium cannot be modeled by a homogeneous medium even for long waves, if they are nonlinear. The structure of the medium influences the nonlinear wave propagation. The heterogeneity of the structure of medium always introduces additional nonlinearity that does not arise in a homogeneous medium.
It was shown that the solution of many problems for multi-component media with incompressible phases can be obtained through the known solution of a similar problem for a homogeneous compressible medium by means of the suggested transformation. Thus, it is not necessary to solve directly the problem for the medium with incompressible component, and it is sufficient just to transform the known solution of the similar problem for a homogeneous medium. The scope for the suggested transformation has been demonstrated by the reference to the strong explosion state in a two-phase medium.
The special attention was focused on the research of blast waves in multi-component media with thermal relaxation. The dependence of the shock damping parameters on the thermal relaxation time has been analyzed in order to provide a deeper understanding of the damping of shock waves in such media and to determine their effectiveness as localizing media. This problem attracts the interest also in view of the practical possibility to estimate the efficiency of medium for damping the shock wave action. The attenuation of shock waves in a gas-liquid foam generated by condensed explosive charges is described in terms of a relaxed transfer of heat from the gas phase to the condensed phase. We have solved the problem on finding of the dependence of the flow behind the shock front on the thermophysical properties of the medium and the completeness of relaxation processes. To find the nature of the relaxation interaction between the components of medium and to estimate the attenuation of shock waves generated by solid explosives, we have studied experimentally both the velocity field of shock waves and the pressure at front in an air foam. The comparison of experimental and theoretical investigations of the relaxation phenomena which accompany the propagation of shock waves in foam indicates that within the scope of relaxation hydrodynamics we can explain the observed phenomena and estimate the efficiency of medium as localizer of the sock wave action. The dependence of shock wave attenuation on the shock loading, especially on the explosion energy has been defined.
Acknowledgements
It is my pleasure to thank and acknowledge colleagues B.I. Palamarchuk, S.G. Lebed, A.V. Cherkashin, and A.T. Malakhov for creative work, exchange by ideas and discussion of the results. Special thanks go to V.M. Kudinov, V.A. Danylenko for current interest, stimulating criticism.
Cite this paper
Vyacheslav O.Vakhnenko, (2014) Blast Waves in Multi-Component Medium with Thermal Relaxation. Natural Science,06,1055-1092. doi: 10.4236/ns.2014.612096
References
- 1. Bonner, B.P. and Wanamaker, B.J. (1991) Acoustic Nonlinearities Produced by a Single Macroscopic Fracture in Granite. In: Thompson, D.O. and Chimenti, D.E., Eds., Review of Progress in Quantitative Nondestructive Evaluation, Springer, New York, 1861-1867.
http://dx.doi.org/10.1007/978-1-4615-3742-7_94 - 2. Guyer, R.A. and Johnson, P.A. (2009) Nonlinear Mesoscopic Elasticity: The Complex Behaviour of Rocks, Soil, Concrete. WILEY-VCH Verlag GmbH and Co. KgaA, Weinheim.
http://dx.doi.org/10.1002/9783527628261 - 3. Johnson, P.A. and McCall, K.R. (1994) Observation and Implications of Nonlinear Elastic Wave Response in Rock. Geophysical Research Letters, 21, 165-168.
http://dx.doi.org/10.1029/93GL03162 - 4. Johnson, P.A., Shankland, T.J., O’Connell, R.J. and Albright, J.N. (1987) Nonlinear Generation of Elastic Waves in Crystalline Rock. Journal of Geophysical Research, 92, 3597-3602.
http://dx.doi.org/10.1029/JB092iB05p03597 - 5. Rodionov, V.N., Sizov, I.A. and Tsvetkov, V.M. (1986) Fundamentals of Geomechanics. Nedra Press, Moscow. (in Russian)
- 6. Sadovsky, M.A. and Pisarenko, G.F. (1991) Seismic Process in Block Medium. Nauka, Moscow. (in Russian)
- 7. Sadovsky, M.A., Ed. (1989) Discrete Properties of Geophysics Medium. Nauka, Moscow. (in Russian)
- 8. Achenbach, J.D. (1973) Wave Propagation in Plastic Solids. North-Holland, Amsterdam.
- 9. Aki, K. and Richards, P.G. (1980) Quantitative Seismology. Theory and Methods, Vol. I and II. W.H. Freeman, San Francisco.
- 10. Truesdell, C. (1984) Rational Thermodynamics. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-1-4612-5206-1 - 11. Biot, M.A. (1956) Theory of Propagation of Elastic Waves in a Fluid-Saturated Solid. I. Low-Frequency Range. Journal of the Acoustical Society of America, 28, 168-178.
http://dx.doi.org/10.1121/1.1908239 - 12. Kutateladze, S.S. and Nakoryakov, V.E. (1984) Heat Exchange and Waves in Gas-Liquid Systems. Nauka, Novosibisk. (in Russian)
- 13. Lyakhov, G.M. (1982) Waves in Soils and Porous Multicomponent Media. Nauka, Moscow. (in Russian)
- 14. Raats, P.A.C. (1984) Applications of the Theory of Mixtures in Soil Physics. In: Truesdell, C., Ed., Rational Thermodynamics, Springer, New York, 326-343.
http://dx.doi.org/10.1007/978-1-4612-5206-1_16 - 15. Rajagopal, K.R. and Tao, L. (1995) Machanics of Mixtures. World Scientific Publishing, Singapore.
- 16. Nikolaevskii, V.N. (1985) Viscoelasticity with Internal Oscillators as a Possible Model of Seismoactive Medium. Doklady Akademii Nauk SSSR, 283, 1321-1324. (in Russian)
- 17. Nigmatulin, R.I. (1987) Dynamics of Multiphase Media, Vol. I and II. Nauka, Moscow. (in Russian)
- 18. Struminskii, V.V. (1980) Mechanics and Technical Progress. Nauka, Moscow. (in Russian)
- 19. Vakhnenko, V.O., Danylenko, V.A. and Michtchenko, A.V. (1999) An Asymptotic Averaged Model of Nonlinear Long Waves Propagation in Media with a Regular Structure. International Journal of Non-Linear Mechanics, 34, 643-654.
http://dx.doi.org/10.1016/S0020-7462(98)00014-6 - 20. Vakhnenko, V.O., Danylenko, V.A. and Michtchenko, A.V. (2000) Diagnostics of the Medium Structure by Long Wave of Finite Amplitude. International Journal of Non-Linear Mechanics, 35, 1105-1113.
http://dx.doi.org/10.1016/S0020-7462(99)00082-7 - 21. Vakhnenko, V.A., Danylenko, V.A. and Kulich, V.V. (1993) Averaged Description of Wave Processes in Geophysical Medium. Geophysics Journal (Ukraine), 15, 66-71.
- 22. Vakhnenko, V.A., Danylenko, V.A. and Kulich, V.V. (1994) Averaged Description of Shock-Wave Processes in Periodic Media. Soviet Journal of Chemical Physics, 12, 534-546.
- 23. Vakhnenko, V.A. and Kulich, V.V. (1992) Long-Wave Processes in Periodic Media. Journal of Applied Mechanics and Technical Physics, 32, 814-820.
- 24. Landau, L.D. and Lifshitz, E.M. (1988) Fluids Mechanics. Pergamon, New York.
- 25. Lavrentiev, M. and Chabat, B. (1980) Effets Hyrdodynamiques et Modéles Mathématiques. Traduction franc. éditions, Mir, Moscow.
- 26. Clarke, J.E. (1984) Lectures on Plane Waves in Reacting Gases. Annals of Physics, 9, 211-306.
http://dx.doi.org/10.1051/anphys:0198400902021100 - 27. Yasnikov, G.P. and Belousov, V.S. (1978) Effective Thermodynamic Functions of a Gas with Solid Particles. Journal of Engineering Physics, 34, 734-737.
http://dx.doi.org/10.1007/BF00860421 - 28. Danylenko, V.A., Sorokina, V.V. and Vladimirov, V.A. (1993) On the Governing Equations in Relaxing Models and Self-Similar Quasiperiodic Solutions. Journal of Physics A, 26, 7125-7135.
http://dx.doi.org/10.1088/0305-4470/26/23/047 - 29. Mandel’shtam, L.I. and Leonovich, M.A. (1937) To the Theory of a Sound Attenuation in Liquids. Journal of Experimental and Theoretical Physics, 3, 438-449. (in Russian)
- 30. Bakhvalov, N.S. and Panasenko, G.P. (1984) Averaging of Processes in Periodic Media. Nauka, Moscow. (in Russian)
- 31. Bakhvalov, N.S. and Eglit, M.E. (1983) Processes in Periodic Media Not Described in Terms of Averaged Characteristics. Doklady Akademii Nauk SSSR, 268, 836-840.
- 32. Berdichevsky, V.L. (2010) Variational Principles of Continuum Mechanics. Springer-Verlag, Berlin-Heidelberg.
- 33. Sanchez-Palencia, E. (1980) Non-Homogeneous Media and Vibration Theory. Springer, New York.
- 34. Korn, G. and Korn, T. (1961) Mathematical Handbook for Scientists and Engineers. McGraw-Hill, New York-Toronto- London.
- 35. Kudinov, V.M. and Palamarchuk, B.I. (1976) Parameters of Shock Waves under Explosion of Explosive Charge in Foam. Soviet Physics Doklady, 228, 555-557.
- 36. Kudinov, V.M., Palamarchuk, B.I. and Vakhnenko, V.A. (1983) Attenuation of a Strong Shock Wave in a Two-Phase Medium. Soviet Physics Doklady, 272, 1080-1083.
- 37. Kudinov, V.M., Palamarchuk, B.I., Vakhnenko, V.A., et al. (1983) Relaxation Phenomena in a Foamy Structure. In: Bowen, J.R., Manson, N., Oppenheim, A.K. and Soloukhin, R.I., Eds., Shook Waves, Explosions, and Detonations, American Institute of Aeronautics and Astronautics, New York, 96-118.
- 38. Vakhnenko, V.A., Kudinov, V.M. and Palmarchuk, B.I. (1982) Effect of Thermal Relaxation of Attenuation of Shock Waves in Two-Phase Medium. Soviet Applied Mechanics, 18, 1126-1133.
http://dx.doi.org/10.1007/BF00882225 - 39. Vakhnenko, V.A., Kudinov, V.M. and Palmarchuk, B.I. (1983) Analogy of Motion of the Two-Phase Media Containing Incompressible and Gaseous Phases with Gas Motion. Doklady Akademii Nauk Ukrainskoj SSR Serija A, 6, 22-24. (in Russian)
- 40. Vakhnenko, V.A., Kudinov, V.M. and Palmarchuk, B.I. (1984) Damping of Strong Shocks in Relaxing Media. Combustion, Explosion and Shock Waves, 20, 97-103.
http://dx.doi.org/10.1007/BF00749928 - 41. Vakhnenko, V.A. and Palmarchuk, B.I. (1984) Description of Shock-Wave Processes in a Two-Phase Medium Containing an Incompressible Phase. Journal of Applied Mechanics and Technical Physics, 25, 101-107.
http://dx.doi.org/10.1007/BF00916876 - 42. Vakhnenko, V.A. and Palmarchuk, B.I. (1986) Evolution of Strong Shock Waves in a Medium with Thermal Relaxation. Soviet Applied Mechanics, 22, 267-272.
http://dx.doi.org/10.1007/BF00887250 - 43. Rudinger, G. (1965) Some Effects of Finite Particle Volume on the Dynamics of Gas-Particle Mixtures. AIAA Journal, 3, 1217-1222.
http://dx.doi.org/10.2514/3.3112 - 44. Rudinger, G. (1964) Some Properties of Shook Relaxation in Gas Plows Garring Small Particles. Physics of Fluids, 7, 658-663. http://dx.doi.org/10.1063/1.1711265
- 45. Rudinger, G. and Chang, A. (1964) Analysis of Nonsteady Two-Phase Flow. Physics of Fluids, 7, 1747-1754.
http://dx.doi.org/10.1063/1.2746772 - 46. Pai, I., Menon, S. and Fan, Z.Q. (1980) Similarity Solution of a Strong Shock Wave Propagating in a Mixture of Gas and Dusty Particles. International Journal of Engineering Science, 18, 1365-1378.
http://dx.doi.org/10.1016/0020-7225(80)90093-2 - 47. Suzuki, T., Ohyagi, S., Higashino, F., et al. (1976) The Propagation of Reacting Blast Waves through Inert Particle Clouds. Acta Astronautica, 3, 517-529.
http://dx.doi.org/10.1016/0094-5765(76)90158-2 - 48. Vakhnenko, V.O. (2010) An Analogy of the Self-Similar Flows of a Gas and a Two-Phase Medium with Noncompressive Component. Reports of the National Academy of Sciences of Ukraine, 12, 97-104. (in Ukrainian)
- 49. Vakhnenko, V.O. (2011) Similarity in Stationary Motions of Gas and Two-Phase Medium with Incompressible Component. International Journal of Non-Linear Mechanics, 46, 1356-1360.
http://dx.doi.org/10.1016/j.ijnonlinmec.2011.07.009 - 50. Korobeinikov, V.P. (1991) Problems of Point-Blast Theory. American Institute of Physics Press, New York.
- 51. Sedov, L.I. (1993) Similarity and Dimensional Methods in Mechanics. CRC Press, Boca Raton.
- 52. Kestenboim, Kh.S., Roslyakov, G.S. and Chudov, L.A. (1974) Point Explosion. Methods of Calculation. Tables. Nauka Press, Moscow.
- 53. Gel’fand, B.E., Gubanov, A.V. and Timofeev, E.I. (1981) Features of Shock-Wave Propagation in Foams. Fizika Goreniya i Vzryva, 17, 129-136.
- 54. Gel’fand, B.E., Gubanov, A.V. and Gubin, S.A. (1977) Attenuation of Shock Waves in a Two-Phase Liquid-Gas-Bubble Medium. Izvestiya Akademii Nauk SSSR, Mekhanika Zhidkosti i Gaza, 1, 173-176.
- 55. Tseitlin, Ya.I., Gil’manov, R.A. and Nilov, V.G. (1980) On Localization of Action of the Blast Hydro-Shock Wave by Bubble Screen. In: Korenistov, A.V., Ed., Vzryvnoe delo (Explosives), 82/39, Nedra Press, Moscow, 264-272.
- 56. Kudinov, V.M., Palamarchuk, B.I., Gel’fand, B.E. and Gubin, S.A. (1976) The Use of Foam for Damping Shock- Waves at Welding and Cutting by Explosion. Avtomaticheskaya Svarka (Automatic Welding), 69, 12-16.
- 57. Kherrmann, V. (1976) Governing Equations for Compressible Porous Materials. In: Mechanics (New Results in Foreign Science). Problems in the Theory of Plasticity, 7, Mir, Moscow, 178-216. (in Russian)
- 58. Nakoryakov, V.E., Pokusaev, B.G. and Shreieber, I.R. (1993) Wave Propogation in Gas-Liquid Media. Begell House, New York.
- 59. Noordrij, L. and Van Wijngaarden, L. (1979) Relaxation Effects Caused by Relative Motion on Shook Waves in Gas-Bubble-Liguid Mixtures. Journal of Fluid Mechanics, 66, 1-9.
- 60. Parkin, B.R., Gilmore, F.R. and Broud, G.L. (1974) Shock Waves in Water with Bubbles of Air. In: Underwater and Underground Explosions (Russian Translation), Mir, Moscow, 152-258.
- 61. Held, M. (1983) Blast Waves in Free Air. Propellants, Explosives, Pyrotechnics, 8, 1-7.
http://dx.doi.org/10.1002/prep.19830080102 - 62. Adushkin, V.V. (1963) On Shock Wave Forming and Explosion Products Flying Away. Journal of Applied Mechanics and Technical Physics, 5, 107-120. (in Russian)
- 63. Adushkin, V.V. and Korotkov, A.I. (1961) Shock Wave Parameters near Chemical Explosion in Air. Journal of Applied Mechanics and Technical Physics, 5, 119-123. (in Russian)
- 64. Baker, W.E., Cox, P.A., Westine, P.S., et al. (1983) Explosion Hazards and Evaluation. Elsevier Scientific Publishing Company, Amsterdam-Oxford-New York.
- 65. Brode, H.I. (1955) Numerical Solutions of Spherical Blast Waves. Journal of Applied Physics, 26, 766-775.
http://dx.doi.org/10.1063/1.1722085 - 66. Brode, H.I. (1976) Point Explosion in Air. In: Ishlinsky, A.Yu. and Chornyy, G.G., Eds., Mechanics, Numerical Solutions of Explosions, Mir, Moscow, 4, 7-70.
- 67. Gekber, N. and Bartos, J.M. (1974) Strong Spherical Blast Waves in a Dust-Laden Gas. AIAA Journal, 12, 120-122.
http://dx.doi.org/10.2514/3.49176
















































