Received 10 March 2016; accepted 26 April 2016; published 29 April 2016

ABSTRACT

The pattern of isentropes in the vicinity of a first-order phase transition is proposed as a key for a sub-classification. While the confinement-deconfinement transition, conjectured to set in beyond a critical end point in the QCD phase diagram, is often related to an entropic transition and the apparently settled gas-liquid transition in nuclear matter is an enthalphic transition, the conceivable local isentropes w.r.t. “incoming” or “outgoing” serve as another useful guide for discussing possible implications, both in the presumed hydrodynamical expansion stage of heavy-ion collisions and the core-collapse of supernova explosions. Examples, such as the quark-meson model and two-phase models, are shown to distinguish concisely the different transitions.

Keywords:

Entropic and Enthalpic Phase Transitions, Chiral Phase Transition, Isentropes, Quark-Meson Model, Linear Sigma Model with Linearized Fluctuations

1. Introduction

The beam energy scan at RHIC [1] - [7] is aimed at searching for a critical end point (CEP) in the phase diagram of strongly interacting matter, which is related to confinement-deconfinement effects. At a CEP [8] - [11] , a line of first-order phase transitions (FOPT) is conjectured to set in. Still, the hypothetical CEP could not (yet) be localized by ab initio QCD calculations. Therefore, details of the FOPT curve and details of the equation of state in its vicinity are unsettled to a large extent.

The utmost importance of the search for a CEP is also manifested by the fact that further ongoing relativistic heavy-ion collision experiments, such as NA61/SHINE [12] - [15] , have it on the their priority list, and planned experiments at FAIR, e.g. CBM [16] , at NICA, e.g. by the MPD group [17] , and at J-PARC, e.g. by the J-PARC heavy-ion collaboration [18] , are primarily motivated by it. The proceedings of the CPOD conferences [19] [20] document well the theoretical expectations and experimental achievements in this field.

The CEP itself (which may occur also as a tricritical point [21] ) is interesting, as it is expected to show up in specific fluctuation observables [22] - [27] , related to critical exponents, however, also the emerging FOPT curve can give rise to interesting physics phenomena. If the hypothetical FOPT curve continues to small or even zero temperatures, astrophysical consequences for neutron stars [28] - [41] proto-neutron star formation and core-collapse supernova explosions [33] [36] [42] - [44] are directly related to the physics of heavy-ion collisions, supposed the FOPT curve is accessible in such experiments (cf. [45] for searches for two-phase mixture effects related to the deconfinement FOPT).

From the theory side, the famous Columbia plot (cf. [21] for an update) unravels the following qualitative features: (i) At zero chemical potential, three-flavor QCD in the chiral limit displays a first-order confinement-

deconfinement transition which extends to non-zero strange-quark masses 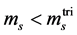and light-quark masses; the delineation curve to the region 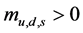is related to a 2nd order transition with 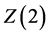symmetry, beyond which the transition turns into a cross over; for and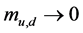, the 2nd order transition line is related to 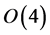symmetry. The physical point 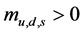is in the cross over region. (ii) For 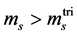and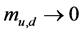, the phase structure in the temperature-chemical potential plane is determined by a 2nd order transition curve of presumably negative slope (with the above mentioned universal 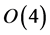scaling

properties) which ends in a tri-critical point, where the 1st order transition sets in, expected to continue to zero temperature. (iii) Upon enlarging 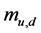toward the physical values and keeping the conjectured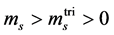, the 2nd oder transition curve turns into the pseudo-critical (cross over) curve which ends at non-zero chemical potential in a CEP. The latter one can be thought to arise from the previous tri-critical point along a 2nd order 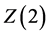curve when enlarging. Therefore, the expectation for 2 + 1 flavor QCD with physical quark masses

is the existence of a CEP at a temperature below the pseudo-critical temperature of and non-

zero chemical potential and an emerging 1st oder transition curve going to zero temperature [21] . Present day lattice QCD evaluations attempt to quantify these features, cf. [46] , for example.

In a recent series of papers [47] - [49] , the authors promote a useful sub-classification of FOPTs by attributing the confinement-deconfinement transition to an entropic one, while the established gas-liquid transition in nuclear matter [8] - [11] is classified as enthalpic one. The key is the Clausius-Clapeyron equation

(1)

which relates the slope of the critical pressure, , along the FOPT w.r.t. temperature, T, to entropy densities and baryon densities. Denoting by the label “1” the dilute (confined/hadron) phase and by “2” the dense (deconfined/quark-gluon) phase, the slope of the critical pressure curve is positive, , for larger entropy per baryon in phase “1”, meaning an enthalpic FOPT. In contrast, for larger entropy per baryon in phase “2” the critical curve has a negative slope, meaning an entropic FOPT.

Some guidance for the trajectories of fluid elements is given by the isentropic curves, determined by, when having in mind the adiabatic expansion of matter created in the course of a heavy-ion collision as long as the respective fluid element is in a pure phase, “2” or “1”. The details of the transit through the two-phase coexistence region depend on the latent heat and other details of the equation of state. With respect to investigations of the heavy-ion dynamics (cf. [50] ) seeking for imprints of the conjectured QCD FOPT and CEP signatures, it seems tempting to clarify in a clear-cut picture the different patterns of isentropes being related to a FOPT.

Our note is organized as follows. In Section 2 we discuss obvious types of isentropic patterns which may accompany a FOPT in strongly interacting matter. The pattern classification is put in relation to the entropic and enthalpic sub-classes. We see enthalpic transitions either with incoming-only or incoming + outgoing isentropes, thus qualifying also the latter one for modeling the QCD deconfinement-confinement transition. Examples based on transparent models are presented in Section 3 and Appendix. In Section 4, we summarize.

2. Isentropic Patterns

We restrict our discussion to the grand canonical description of matter by an equation of state with one conserved charge, e.g. baryon number, related to the chemical potential. Entropy density and baryon density are given by and and the Gibbs-Duhem relation holds (e is the energy density). Considering the region and, the isobars have negative slopes in the T-m diagram upon. We assume locally a FOPT which is signaled by a kinky behavior of over the T-m plane, both in T and directions. refers here to stable states; if multi-valued regions emerge, the branch with maximum pressure is the stable one. We further assume, for the sake of definiteness, the FOPT curve has a negative slope,. In fact, on the FOPT curve delivers, where we suppose and.

We also recall from the equilibrium conditions, and on the FOPT curve the relation

(2)

which is another form of the Clausius-Clapeyron Equation (1).

From selected examples we can infer three different patterns of isentropes in the T-m plane:

Type IA: Isentropes come in from the phase “2”, enter the critical curve and leave it toward the phase “1” at lower temperature, see Figure 1, left top panel. According to Clausius-Clapeyron (1) one has, i.e. a gas-liquid or enthalpic transition in the nomenclature of [49] .

Type IB: Isentropes come in from the phase “2”, enter the critical curve and evolve toward phase “1” at higher temperature, see Figure 1 middle top panel. Clausius-Clapeyron tells us for that case, i.e. a QCD type or entropic FOPT in the nomenclature of [49] .

Type II: Isentropes come in from both sides, i.e. phases “1” and “2”, enter the critical curve and run down on it, see Figure 1, right top panel. According to our experience with a number of models, in a point on the critical curve, i.e. also a gas-liquid type or enthalpic FOPT with.

The direction of isentropes is such to describe expansion, i.e. both temperature and density drop in pure phases. Type I is related to in-out (or going-through) isentropes, while type II has incoming-only. A prominent example for type II is the van der Waals equation of state, cf. [51] and Figure 1 in [52] . We emphasize the local character of our consideration, that is the restriction to the vicinity of a T-m point on the presumed phase boundary. These patterns translate directly into the T-n plane, see bottom row of Figure 1, where one verifies that dropping temperatures along isentropes in pure phases imply in fact dropping densities, too, i.e. proper

expansion. Types IA and IB are delineated by, resulting in. Types IA and II share as common feature flatter isobars than the critical curve; for type IB, the critical curve is flatter than the isobars. For the moment being we do not see the need to study further fine details, e.g. slopes and relative slopes of isentropes near the critical curve.

We would like to emphasize that also models of type IA could serve as an illustration of the possible structure of the phase diagram, despite they belong to the gas-liquid transition type: Suppose, where is the nuclear saturation density and denotes the density of phase “1” at the critical curve, then nothing

seems to speak against the scenario with an expanding and cooling fluid element initially in phase “2”, which traverses the confinement transition region (two-phase coexistence) and arrives in the hadronic world of phase “1”. That means, if “2” is a deconfined state, then both IA and IB allow for a graceful exit into the pure (hadronic) phase “1”, while II ends locally in a two-phase mixture of “1 + 2” for adiabatic expansion dynamics, i.e. some part of matter remains in the deconfined state “2”, e.g. as quark nuggets, contrary to our present expectations and in agreement with the failure of previous searches for them [53] - [57] , (see however [58] [59] for considering them as candidates of dark matter). Whether realistic models can be designed to do so (cf. [60] for a recent attempt), in agreement with serving for two-solar mass neutron stars, is a question beyond the schematic phenomenological approaches. Anyhow, type IA supplements the considerations favored in [48] [49] .

3. Examples

We are going to present a few examples for the above discussed transition types. For that, we select the quark-meson model¹ (cf. [63] for a description of the setting used here²) with linearized meson field fluctuations³ and show that only shifting the nucleon/quark vacuum mass parameter relative to the critical chemical potential at zero temperature is sufficient to switch from IA to II. The latter one is to a large extent determined by the product of the sigma mass parameter and the (classical) vacuum expectation

value of the sigma field. We are fully aware of the shortcomings of such a model w.r.t. proper account of

nuclear matter properties at low temperatures and QCD thermodynamics at high temperatures, as discussed in [48] . But in view of the pertinent complexity of the QCD degrees of freedom in the strong coupling regime such a model with chiral symmetry breaking and restoration may give some glimpses of what is conceivable, in principle.

Also our model for the type IB (cf. Appendix) has, at best, illustrative character: It is a two-phase construction with states in “2” modeled by the extrapolation of weakly interacting quarks and gluons, supplemented by an effective bag constant to account for some non-perturbative aspects, and states in “1” referring to thermal light-meson (pion) excitations and nucleons in some mean field approximation including a realistic incompressibility modulus.

Figure 2 exhibits the isobars over the T-m plane for two parameter sets (see figure caption for the values) of the quark-meson model in linearized fluctuations approximation [63] [65] - [67] . These patterns look fairly similar at a first glance. The isobars are flatter than the phase border line (fat white curve). The CEP

coordinates are for the parameter set depicted on the left panels and on the right ones. (Note that we use actually quark chemical potential

and net quark density.) One must not consider these values as predictions of the CEP location since the proper account of fluctuations can significantly change them. Furthermore, the inclusion of some gluon dynamics, e.g. via a coupling to the Polyakov loop, thermal gluon fluctuations as well as extending the invoked hadron species can also cause substantial changes of the CEP coordinates.

Despite of the apparently marginal differences of the isobar patterns, the isentropes are drastically different. In the left bottom panel of Figure 2, type IA isentropes are seen which mean incoming from phase “2” and outgoing into phase “1” whenever they meet the critical curve. In contrast, the right bottom panel in Figure 2 displays a type II FOPT with incoming-only isentropes into the critical curve.

Figure 3 exhibits the isentropes in pure phases “2” and “1” over the T-n plane. This presentation verifies that both the temperature and the density drop along the isentropes in pure phases. One can infer directly from the bottom panels of Figure 2 the above claim w.r.t. outgoing isentropes from the low-density phase border curve

for type IA, see left panel of Figure 3, while for type II (right panel) only incoming isentropes appear (isentropes with enter the two-phase region at smaller densities which are not displayed).

Consistent to the Clausius-Clapeyron Equation (1), the critical pressure as a function of the temperature is increasing, see Figure 4. The inclined numbers at the top axis depict the (critical) chemical potential values

corresponding to the temperature given at the lower axis thus highlighting the shape of which is actually decreasing in agreement with (2).

We mention that the employed minimum set-up of the quark-meson model does not allow for type IB transitions since thermal gluon fluctuations are not included, i.e. the number of effective degrees of freedom accounting for thermal fluctuations is too small. One may, however, easily construct two-phase models with a high-temperature quark-gluon phase and a low-temperature hadron phase. Figure 5 in the Appendix presents such an example. Without fine tuning, such models do not display a CEP at, instead the constructed phase border curve continues form the T axis down to the axis. Reference [68] provides an example of enforcing a CEP at to obtain also a type IB transition.

The focus of the present note is on the isentropes relevant for the expansion dynamics in relativistic heavy-ion collisions. As emphasized, e.g. in [40] and references therein, analog considerations are useful for discussing the impact of peculiarities of the QCD phase diagram in core-collapse supernova explosions. There, one has to consider adiabatic paths along compression with proper leptonic contributions including also trapped neutrinos. For a first orientation, the pressure as a function of the energy density at suitable values of the entropy per baryon is to be analyzed to figure out whether the FOPT effects in iso-spin symmetric matter translate into modifications of neutron star configurations (with stability, no trapped neutrinos) such as the occurrence of a third stable island (cf. [28] ), nowadays often refered to as twin configurations [29] - [31] [37] [69] - [74] , or modify the core collapse dynamics (with trapped neutrinos) toward proto-neutron stars or even black holes such as discussed in [40] [42] and references therein. We leave according investigations to separate dedicated analyses.

4. Conclusions and Summary

In summary we discuss options for modeling a hypothetical first-order phase transition which is related to a critical end point in a strongly interacting medium. Guided by the expectation that the QCD cross-over (as remnant of the transition of massless 2 + 1 flavor QCD, cf. [21] ) at a temperature of about 150 MeV at small chemical potential turns, at the critical point at large chemical potential, into a first-order transition we consider scenarios where initially deconfined matter can evolve completely into confined (hadronic) matter. We emphasize that both enthalpic and entropic phase transitions are consistent with such an expectation provided a

graceful exit from the deconfined state into pure hadron matter is possible upon adiabatic expansion. At low temperature, the low density part of the two-phase coexistence region must be at larger densities than nuclear matter at saturation (for isospin symmetric nuclear matter). This implies that the pattern of isentropes must “go through” the phase border curve to be conform with the envisaged scenario. In contrast, the van der Waals type transition is of a different kind as it has locally incoming isentropes only. Obviously, more complicated phase border curves may allow for mixtures of the mentioned types. Our discussion also completely ignores flavor- locked color superconducting phases which are expected at larger densities.

Our discussion is based on equilibrium thermodynamics, and the medium is assumed to obey one conserved charge―the baryon density. Accounting for more conserved charges, e.g. related to isospin, strangeness, electric charge etc., complicates the picture. Transient states related to under saturated or over saturated gluons [75] or under saturated quark state occupation [76] give rise to many interesting phenomena beyond our discussion.

The lacking of ab intio information from first-principle calculations of QCD thermodynamics lets many options still be conceivable. This makes the concerted experimental hunt for signals of the critical end point and the related first-order transition so important.

Acknowledgements

We thank J. Randrup, V. Koch, F. Karsch, K. Redlich, M.I. Gorenstein, S. Schramm, H. Stöcker and B. Friman for enlightening discussions of phase transitions in nuclear matter. The work is supported by BMBF grant 05P12CRGH.

Cite this paper

F. Wunderlich,R. Yaresko,B. Kämpfer, (2016) Arguing on Entropic and Enthalpic First-Order Phase Transitions in Strongly Interacting Matter. Journal of Modern Physics,07,852-862. doi: 10.4236/jmp.2016.78077

References

Appendix

A two-phase model for type IB

The constructed FOPT is based on the extrapolation of a hadron equation of state with pressure

(3)

to be calculated from

(4)

with

(5)

The temperature follows self consistently from

(6)

and the baryo-chemical potential is then. We utilize the nucleon mass, the nucleon binding energy, nuclear incompressibility coefficient and

saturation density.⁴ The equation of state in the high temperature phase is defined by the extrapolation of a quark-gluon equation of state from leading-order weak-coupling (cf. [78] for advanced calculations) supplemented by a bag constant B

(7)

where we employ for the number of effective quark degrees of freedom and. These branches are matched by the above mentioned Gibbs criteria for equilibrium, , ,. The resulting isobars, the critical pressure as well as isentropes, both over the T-m and the T-n-planes are exhibited in Figure 5.

NOTES

¹We chose this since in the chiral limit it obeys the same symmetries (an [61] ) as QCD [62] putting both into the same universality class and thus rendering the model a good prototype for studying the properties of the QCD chiral transition.

²In a nutshell, the employed model, also coined linear sigma model, is based on a doublett of quark degrees of freedom, an iso-scalar sigma field and an iso-triplett pion field with standard coupling among these fields.

³According to our experience with numerical evaluations, the account of linearized meson field fluctuations modifies significantly the results of the mean field approximation. (For the inclusion of the complete fluctuations spectrum within the functional renormalization group approach, see [64] .) In particular, the fluctuating meson degrees of freedom deliver explicit contributions to the pressure.

⁴This is a model in the spirit of [77] for nuclear matter and pions.