Journal of Modern Physics
Vol.06 No.15(2015), Article ID:62345,5 pages
10.4236/jmp.2015.615227
A Computer Program for the Newman-Janis Algorithm
Carlos Gutiérrez-Chávez1, Francisco Frutos-Alfaro2, Iván Cordero-García3, Javier Bonatti-González4
1Technological Institute of Costa Rica, Cartago, Costa Rica
2Space Research Center and School of Physics, University of Costa Rica, San José, Costa Rica
3School of Physics, University of Costa Rica, San José, Costa Rica
4Nuclear Research Center and School of Physics, University of Costa Rica, San José, Costa Rica

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 June 2015; accepted 26 December 2015; published 29 December 2015
ABSTRACT
A REDUCE code for the Newman-Janis algorithm is described. This algorithm is intended to include rotation into nonrotating solutions of the Einstein field equations with spherically symmetry or perturbed spherically symmetry and has been successfully applied to many spacetimes. The applicability of the code is restricted to metrics containing potentials of the form 1/r.
Keywords:
General Relativity, Newman-Janis Formalism, Null Tetrads, Complex Transformations

1. Introduction
In 1965, Newman and Janis [1] found that it is possible, by means of a very peculiar complex coordinate transformation applied to Schwarzschild’s spacetime [2] [3] , to generate the spinning Kerr solution [2] [4] of the Einstein field equations. In the original paper they refer to the method as a curious derivation since the series of steps to obtain the desired Kerr metric do not have a simple or clear explanation on why they should generate a new solution (different from Schwarzschild) or even why those steps should provide a solution to vacuum field ecuations at all. However, they do mention that in a private communication, Kerr has shown this procedure work for the class of solutions 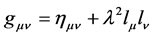 which contains Schwarzschild as a special case. In the same issue of the journal where this work was published, Newman et al. [5] used a similar argument and applied the exact same complex transformation to the Reissner-Nordström metric [2] [6] [7] to obtain what they claimed to be directly shown to be a solution of the Einstein-Maxwell equations. Nowadays it is well known as the Kerr-New- man spinning and charged black hole solution. A short time after that, Demia?ski and Newman [8] succeeded in pulling out another solution by applying the same method to Schwarzschild’s metric (Appendix) again, but this time using a more involved complex coordinate transformation. The result was the Kerr-Taub-NUT like Demia?ski-Newman spacetime [9] [10] . Talbot [11] , on an attempt to explain the effectiveness of the method, briefly elaborated an argument on why the complex coordinate trick had been successful on its applications so far. Also, he provided criteria on which metrics the procedure should work according to the form of a given component of the Weyl tensor, all of this within the context of an application of the Newman-Penrose formalism to find twisting degenerate solutions to field equations. Later, Demia?ski proposed to find the most general solution which could be obtained by this method, assuming a spherical symmetric seed line element and requiring the presence of a non-vanishing
which contains Schwarzschild as a special case. In the same issue of the journal where this work was published, Newman et al. [5] used a similar argument and applied the exact same complex transformation to the Reissner-Nordström metric [2] [6] [7] to obtain what they claimed to be directly shown to be a solution of the Einstein-Maxwell equations. Nowadays it is well known as the Kerr-New- man spinning and charged black hole solution. A short time after that, Demia?ski and Newman [8] succeeded in pulling out another solution by applying the same method to Schwarzschild’s metric (Appendix) again, but this time using a more involved complex coordinate transformation. The result was the Kerr-Taub-NUT like Demia?ski-Newman spacetime [9] [10] . Talbot [11] , on an attempt to explain the effectiveness of the method, briefly elaborated an argument on why the complex coordinate trick had been successful on its applications so far. Also, he provided criteria on which metrics the procedure should work according to the form of a given component of the Weyl tensor, all of this within the context of an application of the Newman-Penrose formalism to find twisting degenerate solutions to field equations. Later, Demia?ski proposed to find the most general solution which could be obtained by this method, assuming a spherical symmetric seed line element and requiring the presence of a non-vanishing 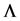 term. He thus demonstrated that he could obtain the generalization of Kerr- Taub-NUT including cosmological constant, but he was also surprised on the fact that he was not able to get a version of Kerr with non-vanishing
term. He thus demonstrated that he could obtain the generalization of Kerr- Taub-NUT including cosmological constant, but he was also surprised on the fact that he was not able to get a version of Kerr with non-vanishing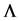 . Although he gave an expression for his solution, it was later corrected by Quevedo [12] who also pointed out the limitations of the Newman-Janis (NJ from now on) method on generating certain solutions, just like Demia?ski failed to obtain Kerr with a
. Although he gave an expression for his solution, it was later corrected by Quevedo [12] who also pointed out the limitations of the Newman-Janis (NJ from now on) method on generating certain solutions, just like Demia?ski failed to obtain Kerr with a 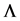 term.
term.
Despite still not being fully understood and the fact that a complete satisfactory explanation of why it works has not been given yet [13] , one can see that the Newman-Janis method has proved to be successful in generating new stationary solutions of the Einstein field equations [14] [15] . Because of this effectiveness, applications have also been studied outside the domain of general relativity and in various modified gravitation theories. For example, it was shown by Krori and Bhattacharjee [16] that the NJ technique could be applied within the context of Brans-Dicke theory of gravitation. Then, calculations were carried out to obtain not only a NUT-like metric in this theory but also a Kerr-like solution which turns out to be the rotating generalization of the Janis-Newman- Winicour solution [17] for a spherically symmetric space time coupled to a zero rest mass scalar field.
To perform the NJ transformation, a REDUCE program [18] was written. The interested reader can get our code, called Newman-Janis.red, and send us an email. The main goal of the code is to facilitate the application of the algorithm to metrics with spherically symmetry or perturbed spherically symmetry.
2. The Newman-Janis Algorithm
The method is easily described as a series of steps to be followed once one has the seed metric to which the algorithm is meant to be applied.
1) The seed metric in spherical coordinates needs to be transformed to the advanced null coordinates, also known as Eddington-Finkelstein coordinates [2] [19] [20] .
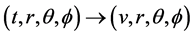
2) The next step is to find the null tetrad system that satisfies the contravariant metric.
3) Once the null tetrads are obtained, the Newman-Janis trick is used. The trick goes as follows, the radial coordinate of your metric is allowed to belong to a complex domain, this meaning merely that it can acquire complex values, but is required specifically that it must be always real, therefore terms of the form
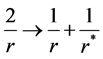
where 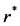 is the complex conjugate of r.
is the complex conjugate of r.
4) Then, perform the NJ complex transformation on the advanced and radial coordinates:
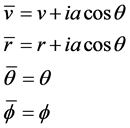 (1)
(1)
where a is the rotation parameter.
5) Finally, it is applied the Boyer-Lindquist coordinate transformation [21] on the obtained advanced contravariant metric.
In the following section, these different steps will be described as the code makes the calculation.
3. The Program
The code Newman-Janis.red is explained in detail as we go through the above exposed steps. The metric that the code needs to run, has the form:
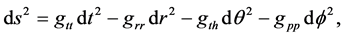 (2)
(2)
where one has to define explicitly the metric components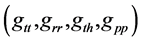 . A subroutine finds the generalized Eddington-Finkelstein transformation:
. A subroutine finds the generalized Eddington-Finkelstein transformation:
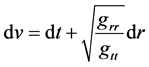 (3)
(3)
in terms of the seed metric.
Now, we have the metric in terms of the advanced null coordinates:
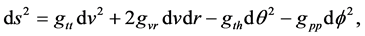 (4)
(4)
where
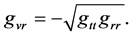
The code enlists the components of this new metric tensor, writes it in matrix notation to calculate the inverse matrix. Then, the null tetrads are computed in terms of the components of this metric. To avoid errors the program computes the contravariant metric and verifies that both the tetrads and the metric components fulfill the following relation
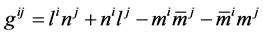 (5)
(5)
The step 3 of the Newman-Janis procedure can only be done by hand, this is because it is cumbersome to do it with REDUCE [18] , and it may be impossible to compute at all.
The next step is to apply the Newman-Janis transformation (1) to the latter obtained null tetrads, which is the key step in the whole process. For the sake of simplicity in notation the code displays the following quantity in all the tetrads expressions
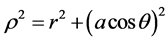 (6)
(6)
Then, the new contravariant metric components are obtained using Equation (5). The expression for it is of the form

The new covariant metric is determined from the contravariant one. The code computes again the new covariant metric in a more compacted way and confirms that both expressions are equivalent by performing the difference between them.
Next, the transformation to the generalized Boyer-Lindquist coordinates is performed by the program in order to display the final metric in the standard form. The code rewrites the expressions in a simpler and standard way:

and compares them to avoid mistakes. In (8) we have used
4. Test Results
We tested the program for the Schwarzschild [3] and Brans-Dicke metrics [16] . The first metric is given by
where

where
The second metric is given by
where

The resulting metric [16] is given by
where
5. Conclusion
This REDUCE program is very useful to include rotation to metrics with spherical symmetry. It should not be used for metrics with cosmological constant and with no spherical symmetry. The inputs to the program that the user has to provide, are the metric and the change in term like
Cite this paper
CarlosGutiérrez-Chávez,FranciscoFrutos-Alfaro,IvánCordero-García,JavierBonatti-González, (2015) A Computer Program for the Newman-Janis Algorithm. Journal of Modern Physics,06,2226-2230. doi: 10.4236/jmp.2015.615227
References
- 1. Newman, E.T. and Janis, A.I. (1965) Journal of Mathematical Physics, 6, 915-917.
http://dx.doi.org/10.1063/1.1704350 - 2. d’Inverno, R. (1992) Introducing Einstein’s Relativity. Oxford University Press, USA.
- 3. Schwarzschild, K. (1916) Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften, 7, 189-196.
- 4. Kerr, R.P. (1963) Physical Review Letters, 11, 237-238.
http://dx.doi.org/10.1103/PhysRevLett.11.237 - 5. Newman, E.T., Couch, E., Chinnapared, K., Exton, A., Prakash, A. and Torrence, R. (1965) Journal of Mathematical Physics, 6, 918-919. http://dx.doi.org/10.1063/1.1704351
- 6. Reissner, H. (1916) Annalen der Physik, 50, 106-120.
http://dx.doi.org/10.1002/andp.19163550905 - 7. Nordstrøm, G. (1918) Verhandelingen der Koninklijke Nederlandse Akademie van Wetenschappen, 20, 1238-1245.
- 8. Demiański, M. and Newman, E.T. (1966) Bulletin de l Académie Polonaise des Sciences, 14, 653-657.
- 9. Taub, A.H. (1951) Annals of Mathematics (Second Series), 53, 472-490.
http://dx.doi.org/10.2307/1969567 - 10. Newman, E., Tamburino, L. and Unti, T. (1963) Journal of Mathematical Physics, 4, 915-923.
http://dx.doi.org/10.1063/1.1704018 - 11. Talbot, C.J. (1969) Communications in Mathematical Physics, 13, 45-61.
http://dx.doi.org/10.1007/BF01645269 - 12. Quevedo, H. (1992) General Relativity and Gravitation, 24, 693-703.
http://dx.doi.org/10.1007/BF00760076 - 13. Flaherty, E.J. (1976) Hermitian and Kählerian Geometry in Relativity (Lecture Notes in Physics 46). Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/3-540-07540-2 - 14. Kim, H. (1999) Physical Review D, 59, Article ID: 064002.
- 15. Ibohal, N. (2005) General Relativity and Gravitation, 37, 19-51.
http://dx.doi.org/10.1007/s10714-005-0002-6 - 16. Krori, K.D. and Bhattacharjee, D.R. (1982) Journal of Mathematical Physics, 23, 637-638.
http://dx.doi.org/10.1063/1.525401 - 17. Janis, A.I., Newman, E.T. and Winicour, J. (1968) Physical Review, 20, 878-880.
- 18. Hearn, A.C. (1999) REDUCE (User’s and Contributed Packages Manual). Konrad-Zuse-Zentrum für Informationstechnik, Berlin.
- 19. Drake, S.P. and Szekeres, P. (2000) General Relativity and Gravitation, 32, 445-458.
http://dx.doi.org/10.1023/A:1001920232180 - 20. Glass, E.N. and Krisch, J.P. (2004) Classical and Quantum Gravity, 21, 5543.
http://dx.doi.org/10.1088/0264-9381/21/23/015 - 21. Boyer, R.H. and Lindquist, R.W. (1967) Journal of Mathematical Physics, 8, 265-281.
http://dx.doi.org/10.1063/1.1705193
Appendix
The output for main result in the case of the Schwarzschild metric is:







