Journal of Modern Physics
Vol.4 No.11(2013), Article ID:40051,8 pages DOI:10.4236/jmp.2013.411184
On the Metric of Space-Time
Department of Physics, University of the Pacific, Stockton, USA
Email: wulfmanc@wavecable.com
Copyright © 2013 Carl E. Wulfman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 26, 2013; revised October 27, 2013; accepted August 28, 2013
Keywords: Space-Time; Metric; Hubble; Dark Matter; Red Shift; Astrophysics; Electrodynamics
ABSTRACT
Maxwell’s equations are obeyed in a one-parameter group of isotropic gravity-free flat space-times whose metric depends upon the value of the group parameter. An experimental determination of this value has been proposed. If it is zero, the metric is Minkowski’s. If it is non-zero, the metric is not Poincare invariant and local frequencies of electromagnetic waves change as they propagate. If the group parameter is positive, velocity-independent red-shifts develop and the group parameter play a role similar to that of Hubble’s constant in determining the relation of these red-shifts to propagation distance. In the resulting space-times, the velocity-dependence of red shifts is a function of propagation distance. If 2c times the group parameter and Hubble’s constant have approximately the same value, observed frequency shifts in radiation received from stellar sources can imply source velocities quite different from those implied in Minkowski space. Electromagnetic waves received from bodies in galactic Kepler orbits undergo frequency shifts which are indistinguishable from shifts currently attributed to dark matter and dark energy in Minkowski space, or to a non-Newtonian physics.
1. Introduction
Because cosmology so heavily depends upon interpretations of the properties of electromagnetic radiation, any misunderstandings of these properties can have extensive consequences. Maxwell’s equations govern the propagation and modification of this radiation and permit relations between observations of cosmic events to be codified in global metrics which determine geometric relations in space-time.
These geometric relations provide the framework for the analyses in this paper, which is based on work of Harry Bateman, Ebenezer Cunningham, and E.L. Hill. We show that Minkowski’s metric cannot be assumed, a priori, to be the metric of physical gravitation-free spacetime. It is just one member of a one-parameter family of allowed metrics. As a consequence, current observations allow Hubble’s relations to have consequential new interpretations. Among these are interpretations that eliminate the current need for dark matter and dark energy.
In 1909, Bateman [1] and Cunningham [2] proved that Maxwell’s equations are invariant under an inversion, and the transformations of a fifteen-parameter Lie group. Thirty-six years later, just as WW II ended, E. L. Hill showed that the infinitesimal transformations of a oneparameter subgroup of the Bateman-Cunningham Lie group define a relation isomorphic to Hubble’s law [3].
Hill’s discovery was overlooked for 65 years. In the year 2000, unaware of it, Hoyle, Burbidge, and Narlikar used the Bateman-Cunningham Lie group in their development of a generalized relativistic cosmology [4], and in 2010, Tomilchik [5] argued that Hubble’s relations are a consequence of properties of transformations of the special conformal subgroup of the Bateman-Cunningham group. Hill’s paper is however listed in Kastrup’s recent review of papers dealing with conformal invariance [6], which led to the research reported here, and to the realization that the value of Hill’s group parameter can be determined by experiments proposed by Wulfman [7,8]. A more recent list of references to research on the physical role of conformal transformations is contained in an article on the quantum mechanics of accelerated relativistic particles written by Calixto, et al. [9].
Section 2 of the present paper describes the finite transformations that result from the infinitesimal transformations investigated by Hill. In determining these transformations and their effects on electromagnetic waves and Minkowski’s metric, we make use of properties of Lie transformation groups that can be found in recent texts by Cantwell [10], by Hydon [11], by Stephani [12], and by Wulfman [13].
In Section 3, it is shown that the transformations convert the usual plane-wave and spherical-wave solutions of Maxwell’s equations into one-parameter families of solutions with local wave-numbers that evolve as the waves propagate.
The action of the transformations on Minkowski’s metric is determined in Section 4. They convert Minkowski’s metric into a one parameter family of metrics which define a one parameter family of space-times. It is shown that for each value of the group parameter, the transformed waves propagate in a transformed space-time, whose metric is fixed by the value of the group parameter. The transformed Minkowski metrics are not Poincare invariant.
In Section 5, to develop physical consequences of the mathematical connection between the metric of the space-times and the behavior of electromagnetic radiation in them, local measurements are expressed in terms of coordinates of points in Minkowski space, and in terms of the transformed coordinates produced by the action of the group. Locally observed frequency shifts in the one-parameter family of space-times are thereby related to “Doppler shifts” in Minkowski space. The development of velocity-independent frequency shifts in the transformed space-times leads to fundamental revisions of current interpretations of Hubble’s relations.
Then, in Section 6, it is shown that the transformed space-times have a surprising property: in them, electromagnetic waves received from bodies in galactic Kepler orbits can undergo frequency shifts which are indistinguishable from the shifts currently attributed to the hypothesized presence of dark matter and dark energy in Minkowski space.
The final section of the present paper contains a brief discussion dealing with the relation between the metrics considered here, and those applicable in the presence of gravitational fields.
2. The Isotropic Transformations of the Special Conformal Group
Hill’s one-parameter group of isotropic special conformal transformations inter-converts the vectors X, X’, and r, r’ with
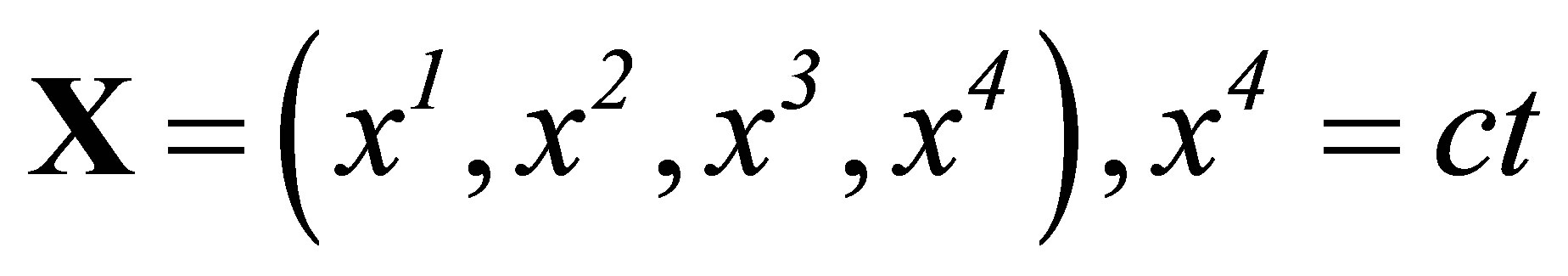 (1,2)
(1,2)
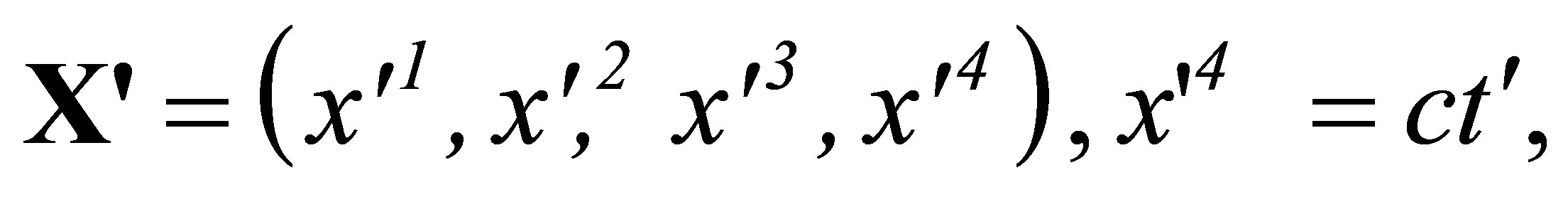 (3,4)
(3,4)
and
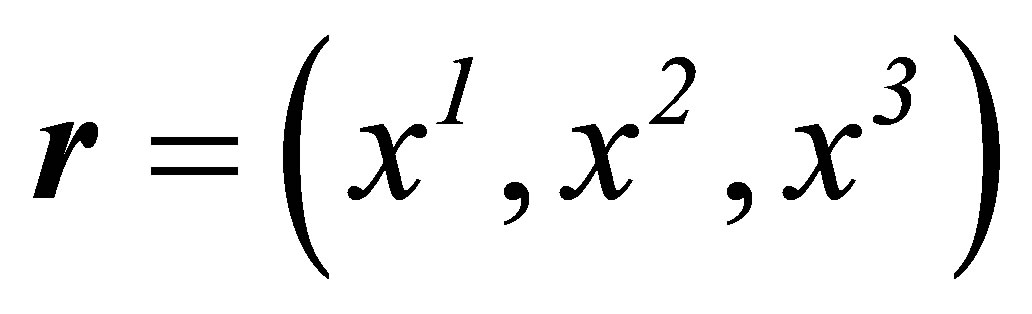 (5)
(5)
 (6)
(6)
The italic superscripts denote locally Cartesian components. Here, and in some of the following paragraphs, italics are also used to call attention to variables such as r and 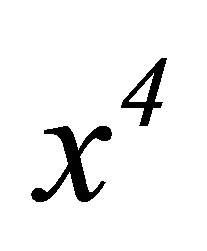 that may take on initial values, final values, and all values in between, as the group parameter varies from zero to its final value, except we will use “v” to refer to velocity and “n” to refer to frequency. The Lie generator of the group can be expressed as
that may take on initial values, final values, and all values in between, as the group parameter varies from zero to its final value, except we will use “v” to refer to velocity and “n” to refer to frequency. The Lie generator of the group can be expressed as
 (7)
(7)
The transformations can be carried out by the operator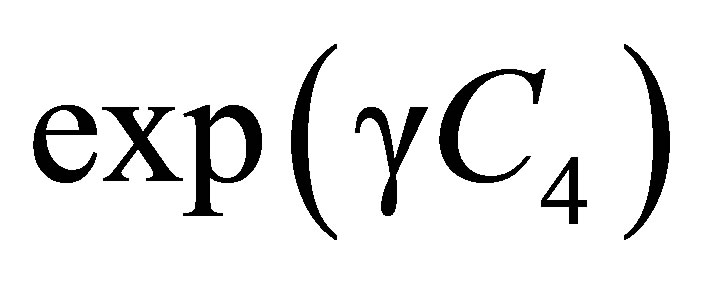 . It produces the projective transformations
. It produces the projective transformations
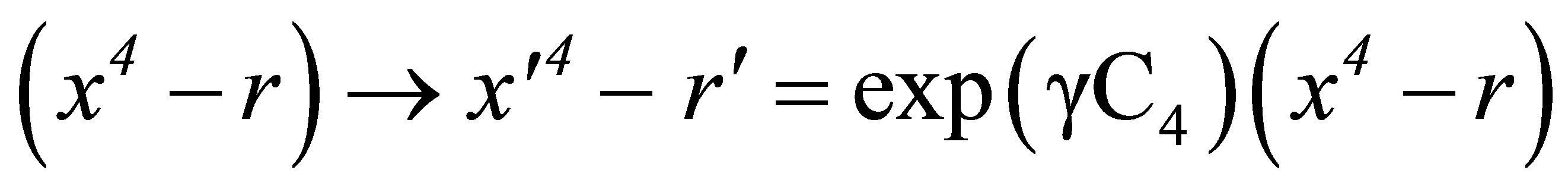 (8)
(8)
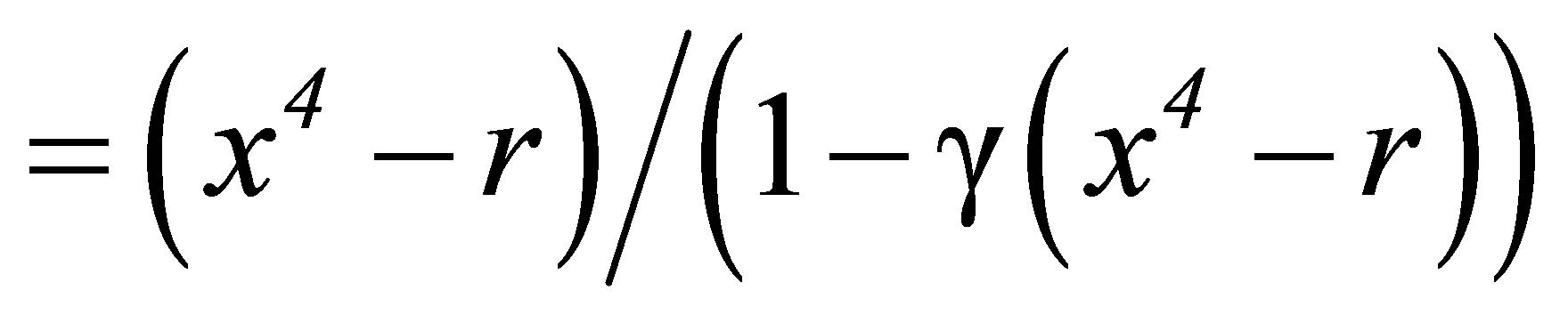 (9)
(9)
and
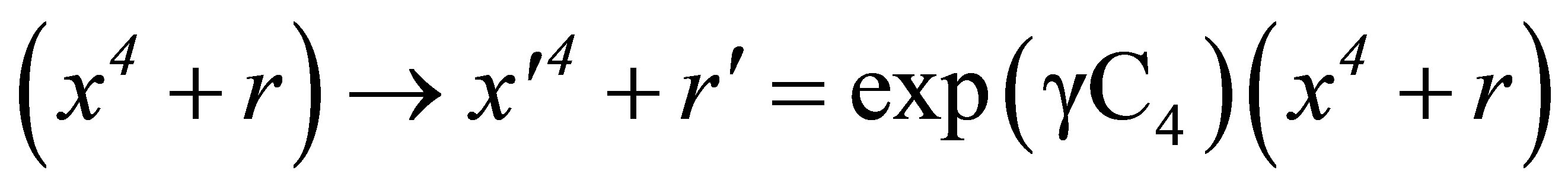 (10)
(10)
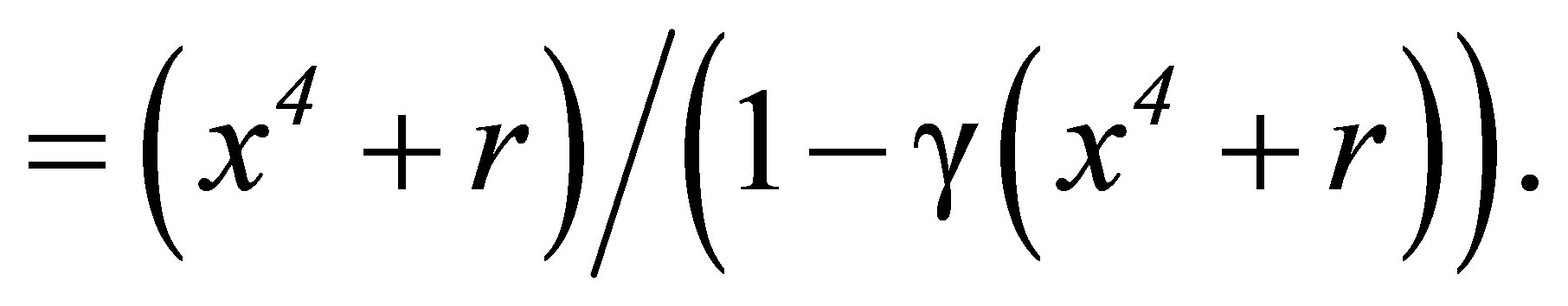 (11)
(11)
Acting on 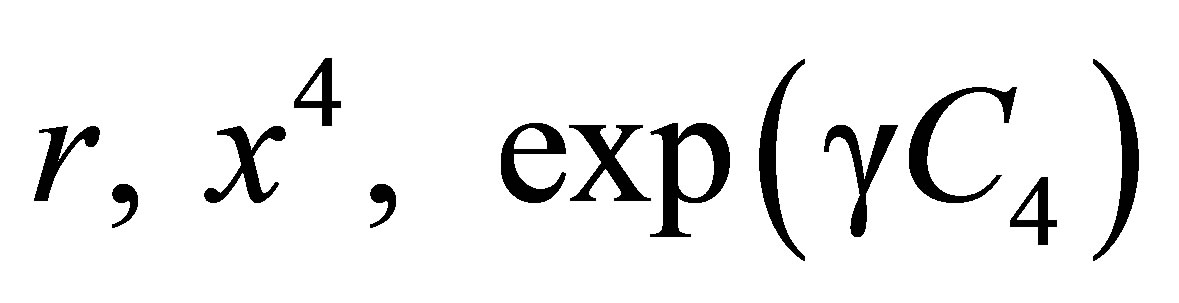 produces the transformations
produces the transformations
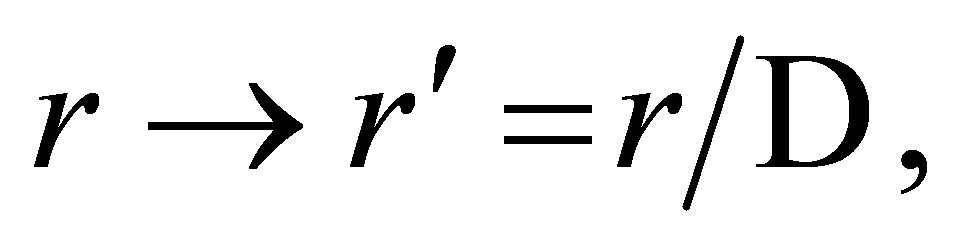 (12)
(12)
 (13)
(13)
with
 (14)
(14)
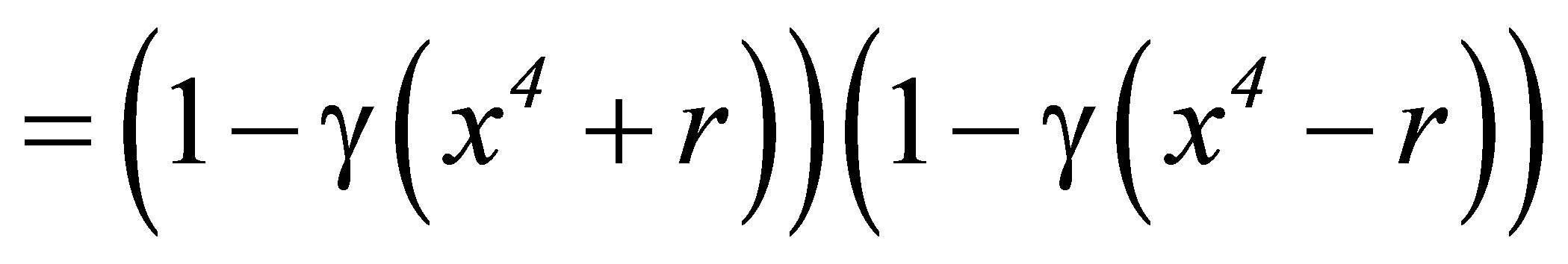 (15)
(15)
The inverse transformations are
 (16)
(16)
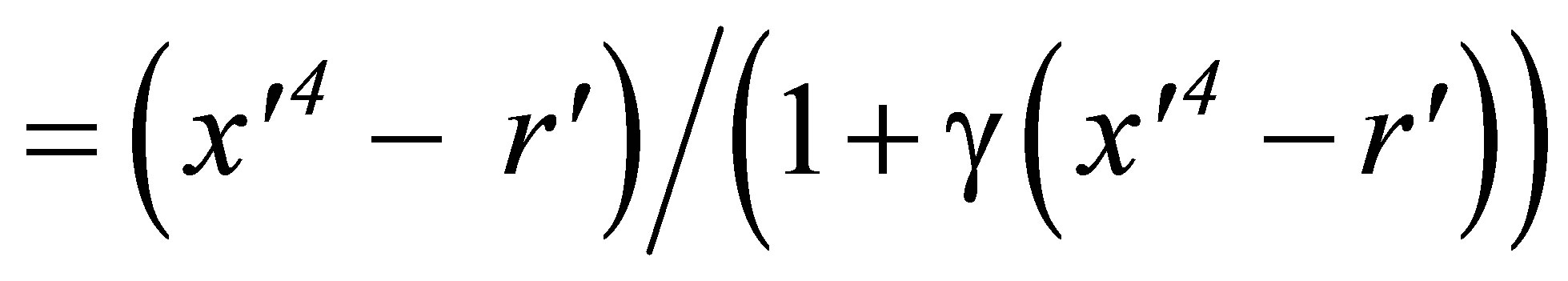 (17)
(17)
and
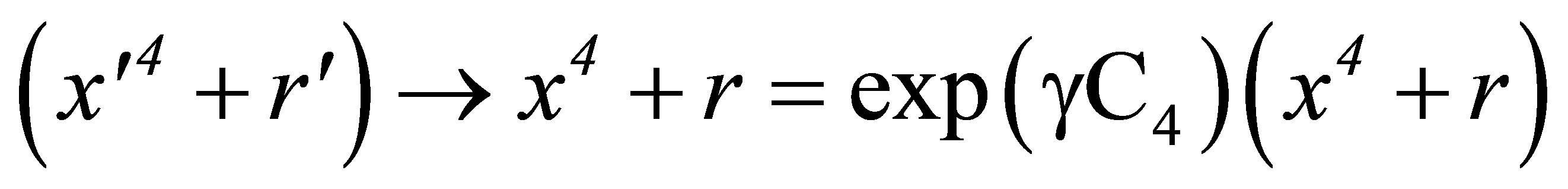 (18)
(18)
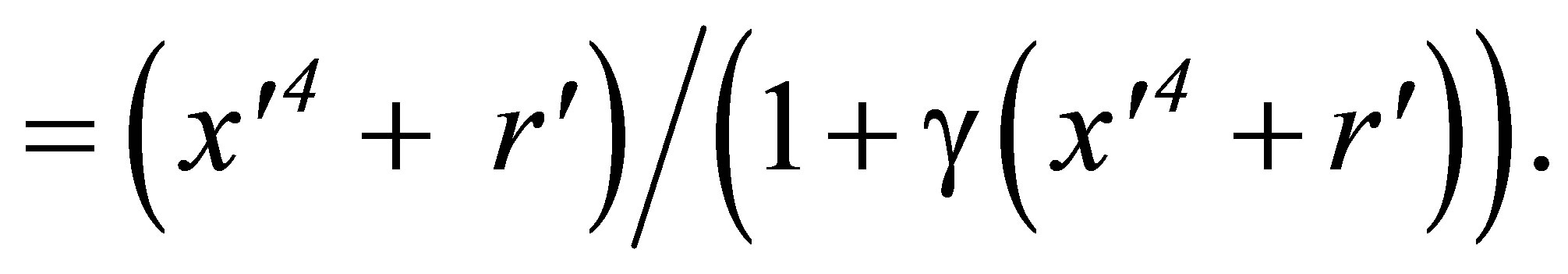 (19)
(19)
and
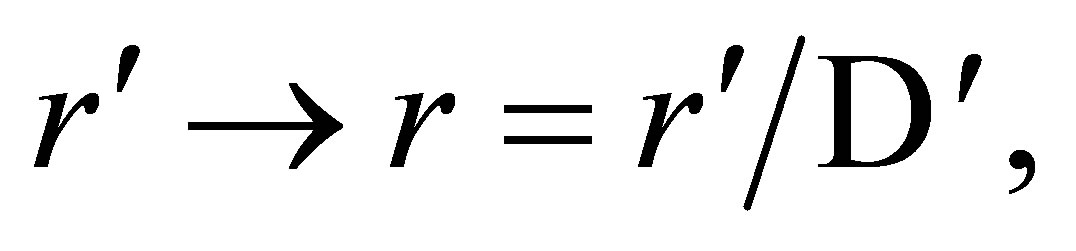 (20)
(20)
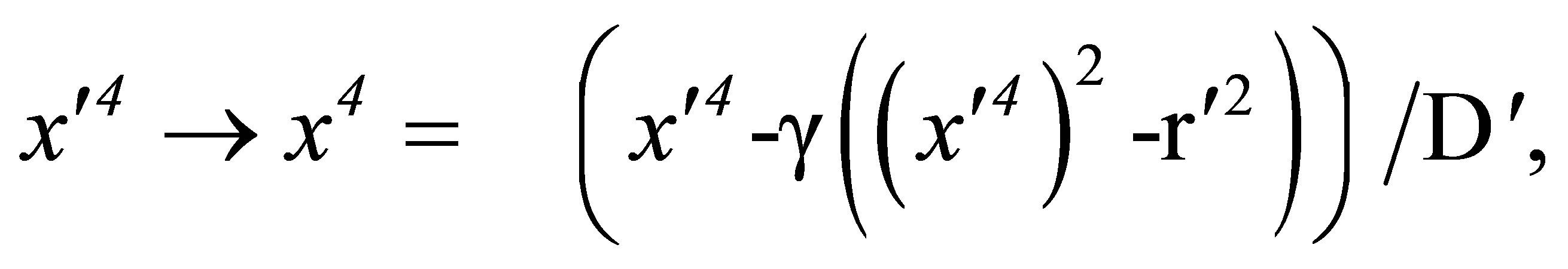 (21)
(21)
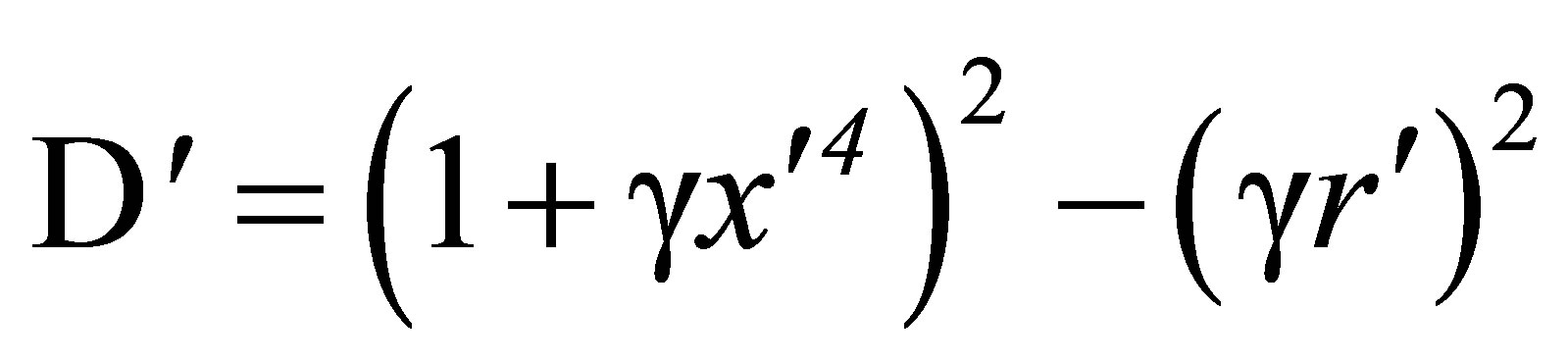 (22)
(22)
 (23)
(23)
Changing γ to −γ and also interchanging 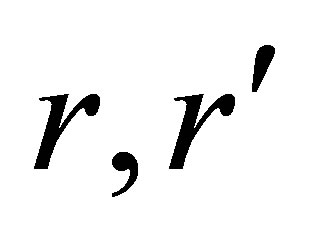 and
and 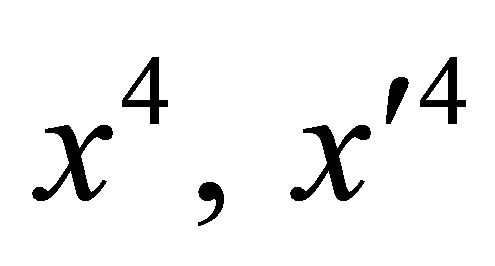 produces the inverse transformation.
produces the inverse transformation.
The transformations of the Bateman-Cunningham group are conformal in the sense that they do not alter angles between spatial vectors. The transformations generated by  also do not alter the origin of coordinates. They interconvert
also do not alter the origin of coordinates. They interconvert
 (24)
(24)
and
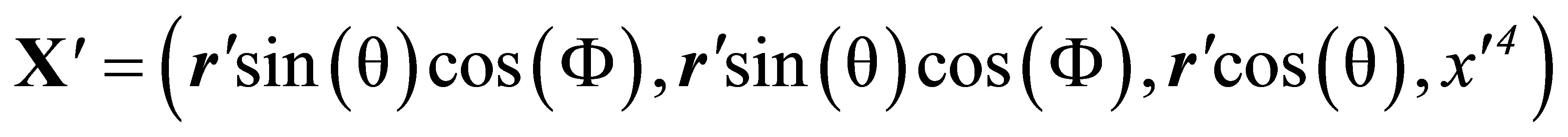 . (25)
. (25)
If X has its origin at the vertex of a light cone where a source is located, then Xʹ will originate at the same source. If the time coordinates have non-negative values, we will say the coordinates are those of points on “source cones” on which x4 = r and x’4 = r’ A continuously emitting source produces a continuum of light cones with a common time axis. The vertex of any one of these may be considered that of a source cone.
The first extension of C4 is
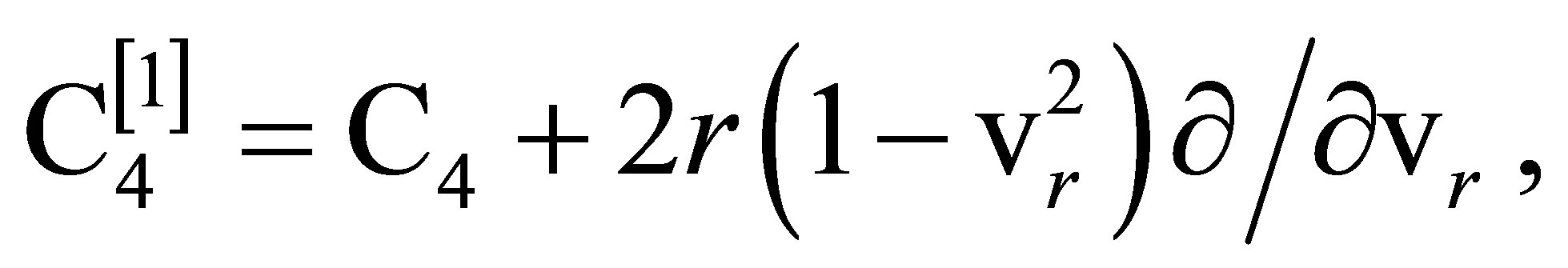 (26)
(26)
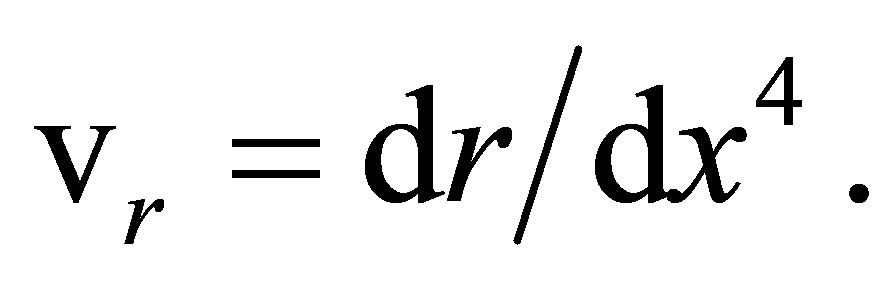 (27)
(27)
It generates transformations of radial velocities in which:
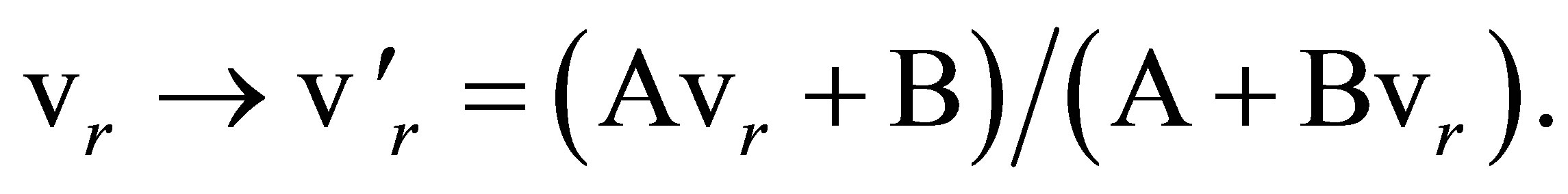 (28)
(28)
The inverse of this is
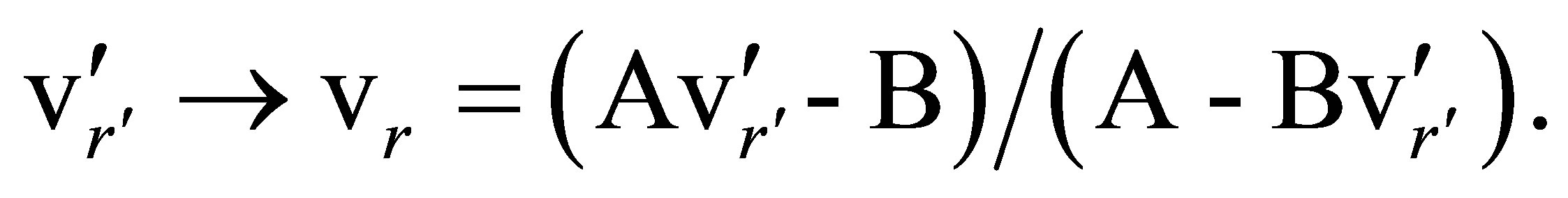 . (29)
. (29)
In these relations
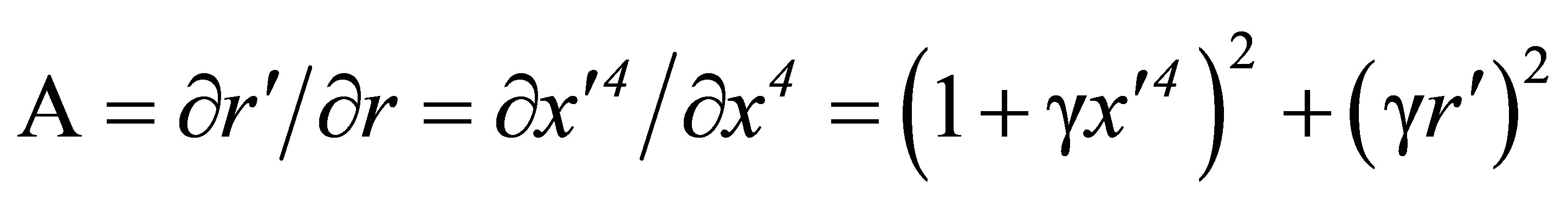 (30-32)
(30-32)
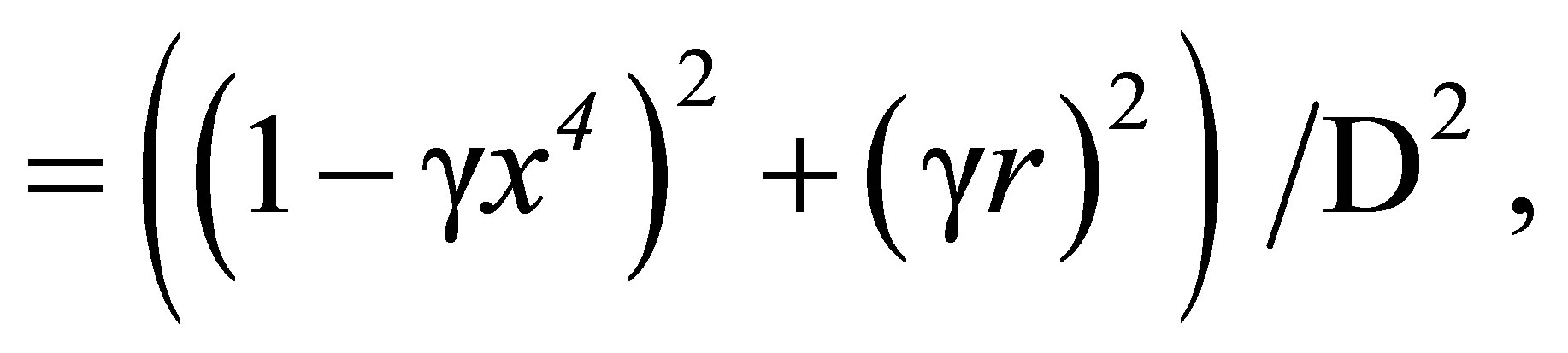 (33)
(33)
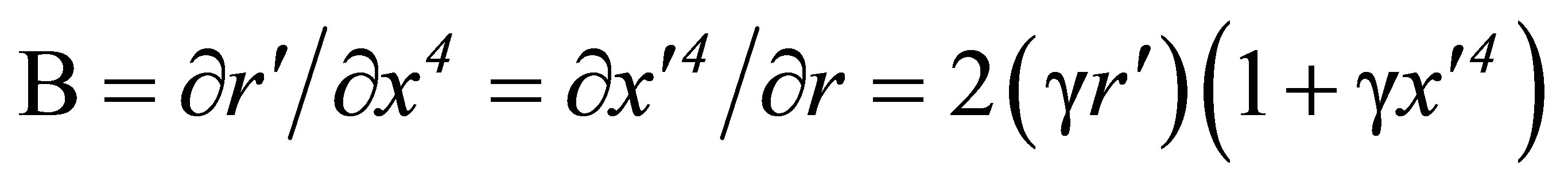 (34-36)
(34-36)
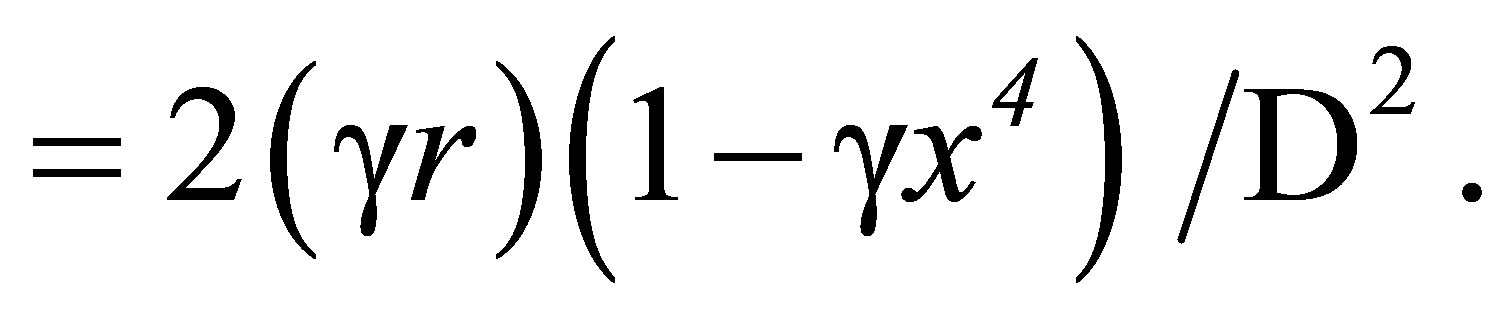 (37)
(37)
D is the function defined in (15). Because of the 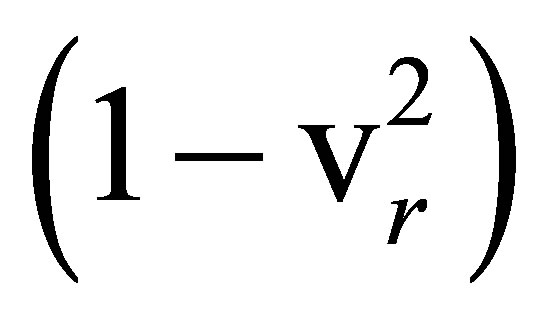 factor in
factor in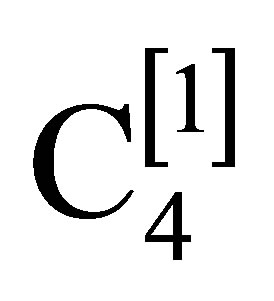 , the effects of these transformations weaken as
, the effects of these transformations weaken as 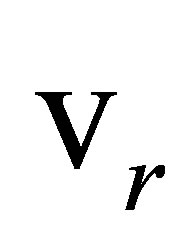 approaches the speed of light, 1, which they cannot alter. Because both C4 and
approaches the speed of light, 1, which they cannot alter. Because both C4 and 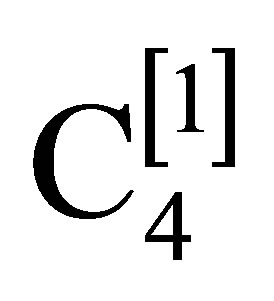 are quadratic functions of
are quadratic functions of 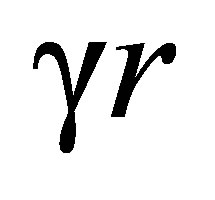 and
and , they generate transformations that are a weak function of both the coordinates and the group parameter near sources, terrestrial as well as celestial.
, they generate transformations that are a weak function of both the coordinates and the group parameter near sources, terrestrial as well as celestial.
As C4 annihilates,
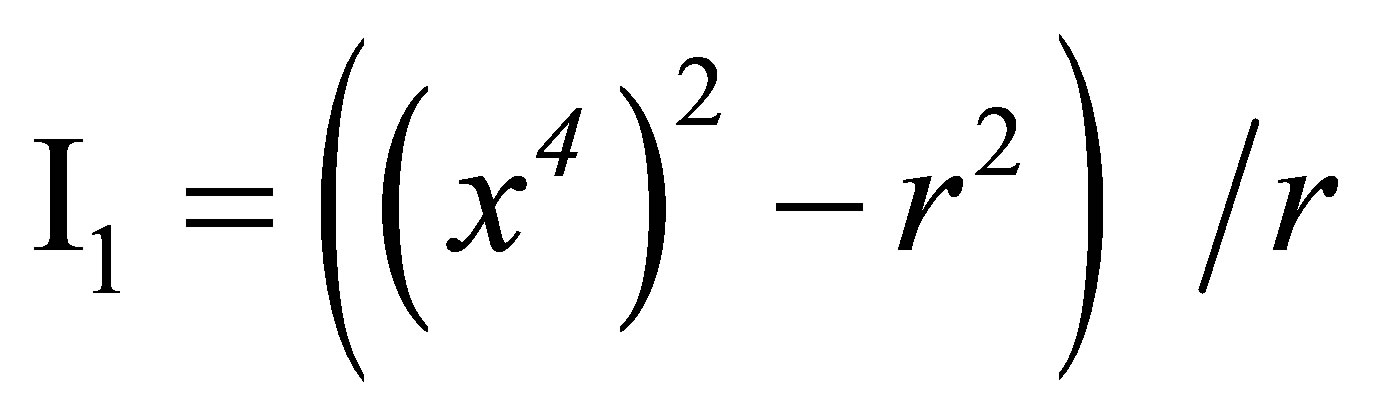 (38)
(38)
the transformations generated by it leave this function invariant. The transformations generated by 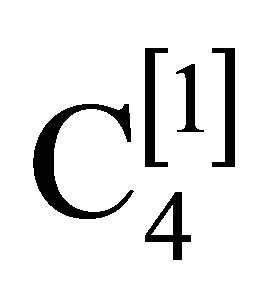 also leave invariant the velocity-dependent function
also leave invariant the velocity-dependent function
 (39)
(39)
This invariant has implications which will be used in Section 7.
Because C4 does not commute with any of the generators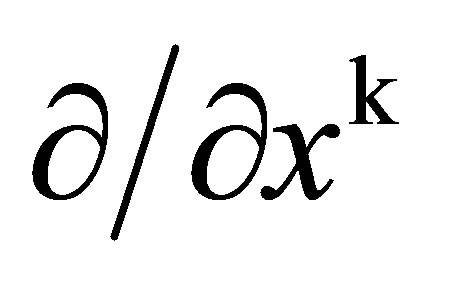 , the transformations generated by it and
, the transformations generated by it and 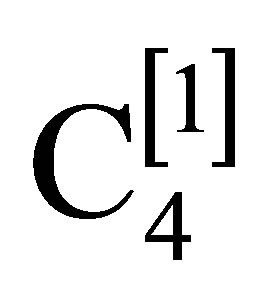 are not translation invariant. A translation that moves the origins of the vectors X from O to
are not translation invariant. A translation that moves the origins of the vectors X from O to
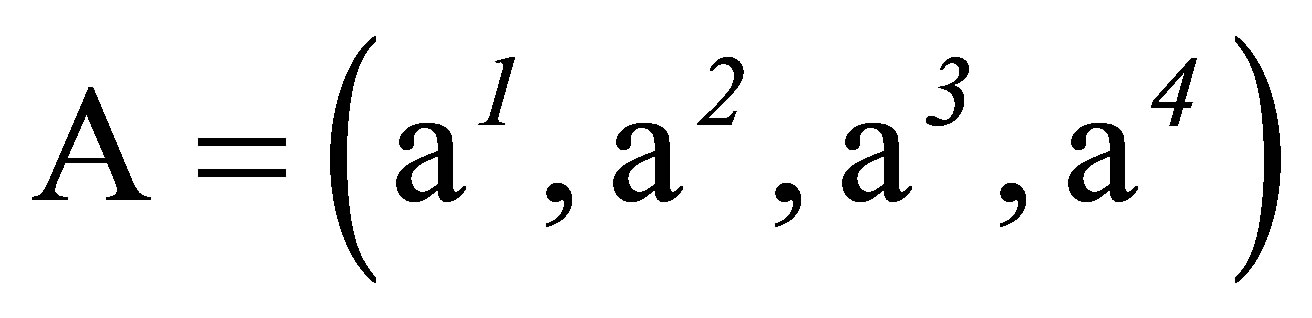 (40)
(40)
converts X to X + A. It moves the origin of the vectors Xʹ from O to
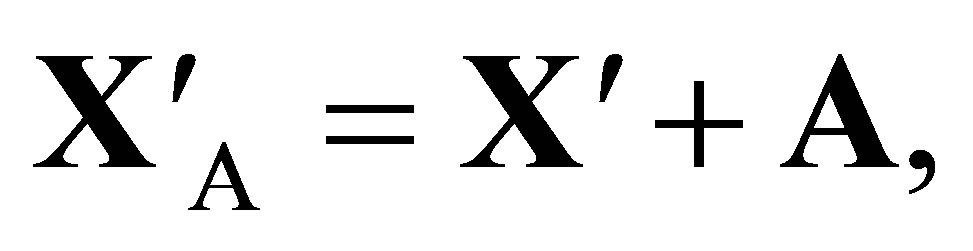 (41)
(41)
which is not the same as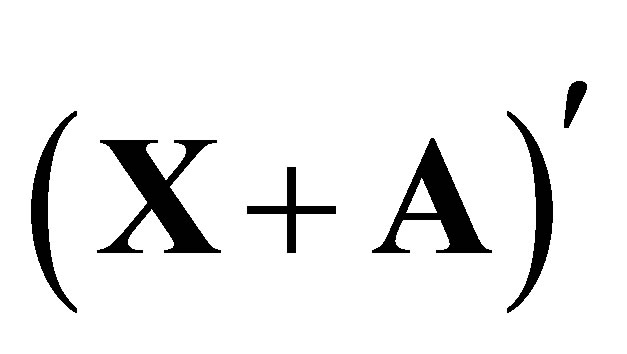 .
.
3. Electromagnetic Waves with Evolving Wave Numbers
In this section, we first deal with plane waves, the waves that are potentially observable at great cartesian distances from sources. An electromagnetic plane wave with wave number k propagating in the direction of 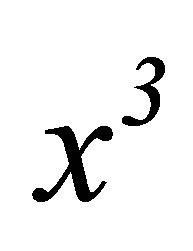 may be defined by the equation
may be defined by the equation
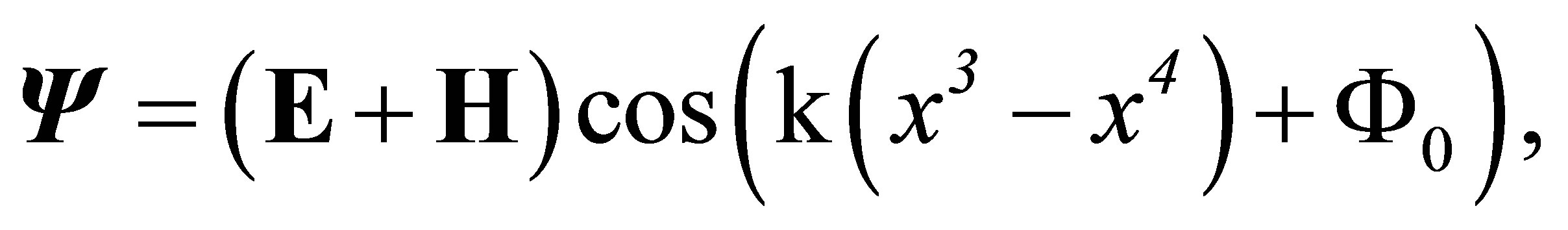 (42)
(42)
with
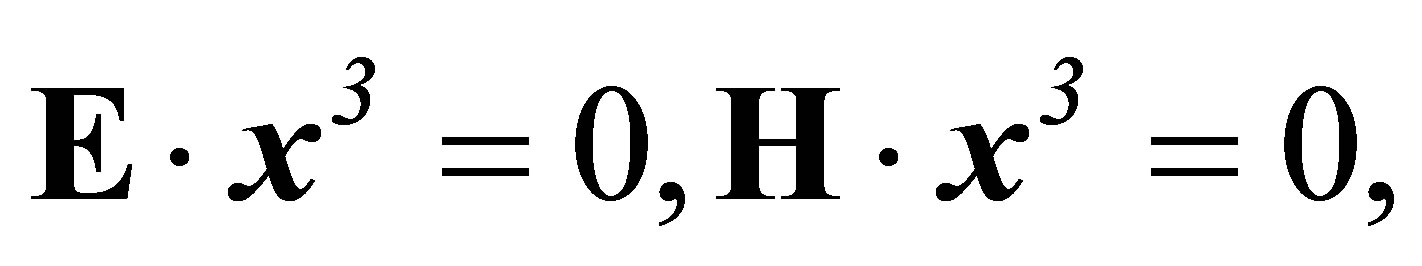 (43,44)
(43,44)
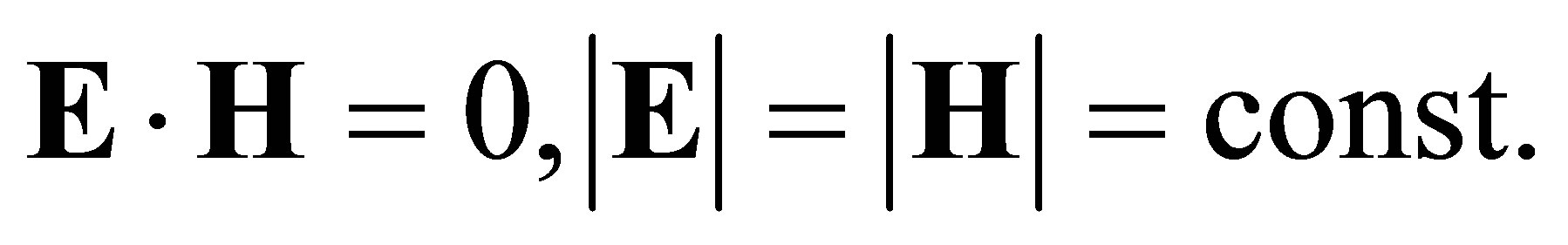 (45-47)
(45-47)
Both curl (E) and curl (H) vanish, and the function 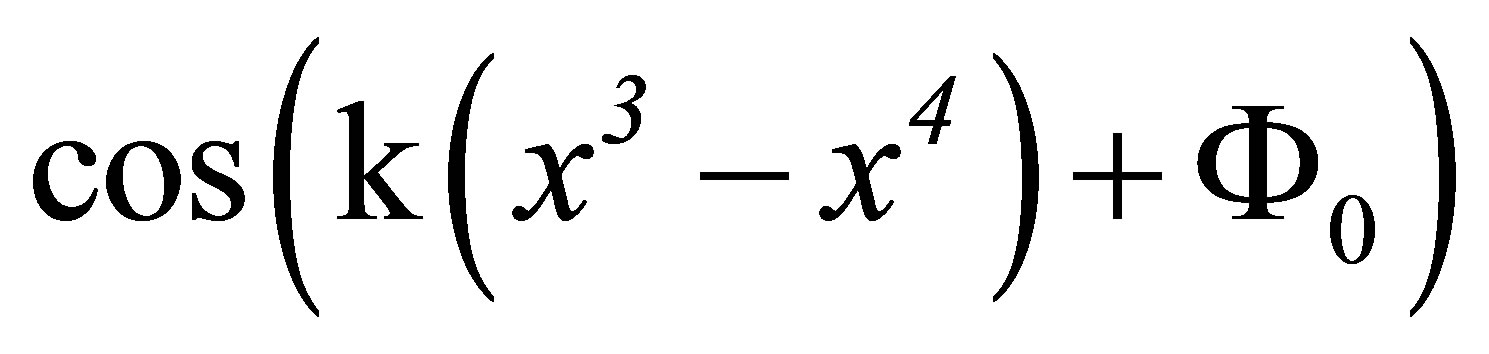 satisfies the wave equation, which reduces to the requirement that
satisfies the wave equation, which reduces to the requirement that
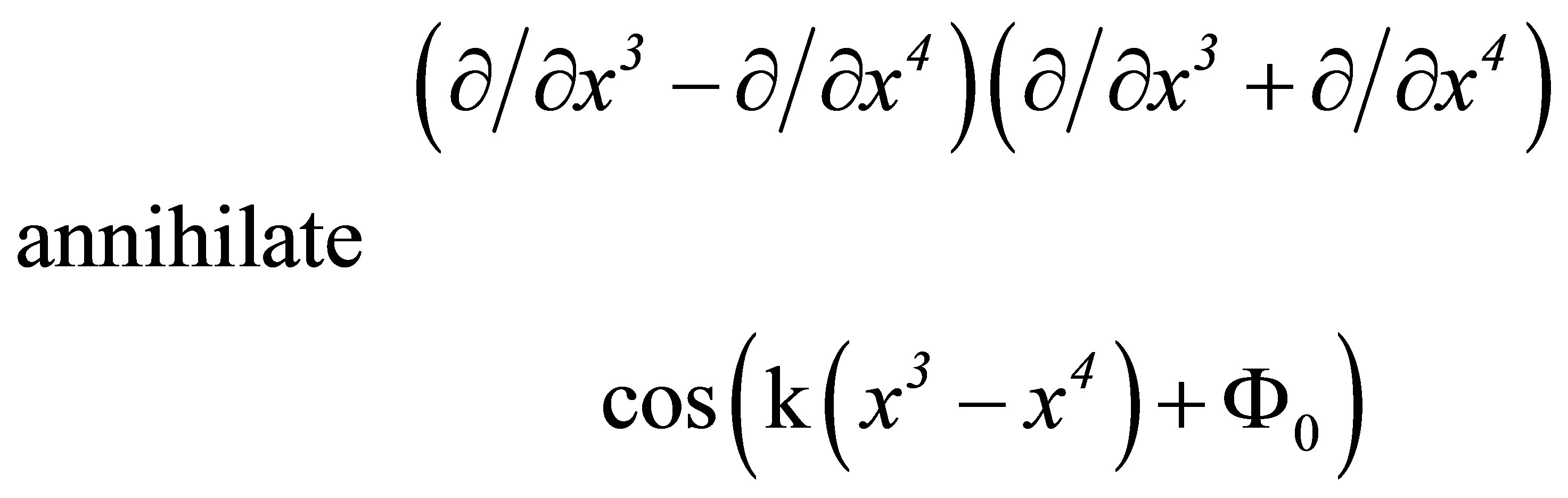 (48)
(48)
Spherical waves with the same wave number are obtained if the cosine function is replaced by 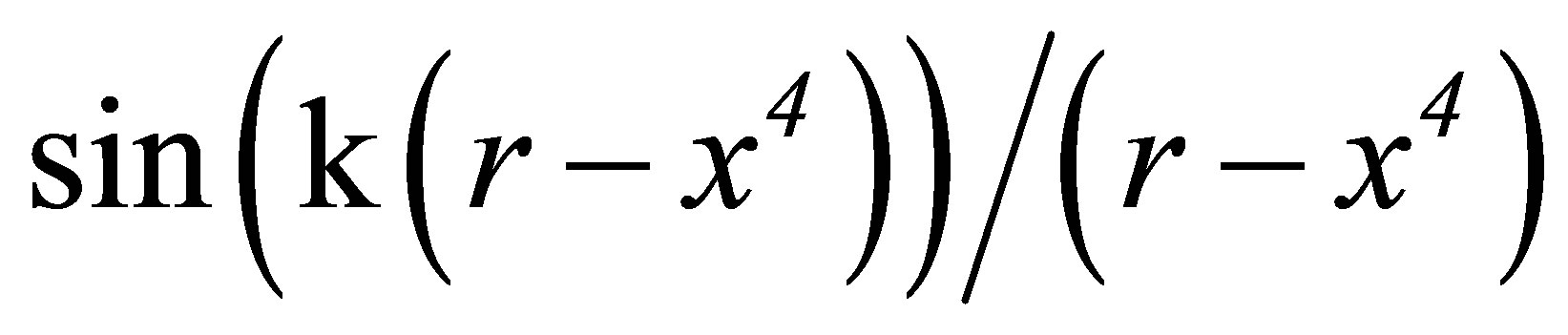 .
.
The inverse of (9) produces the relation
 (49)
(49)
Consequently, in the X’ system, the wave defined by (42) becomes defined by
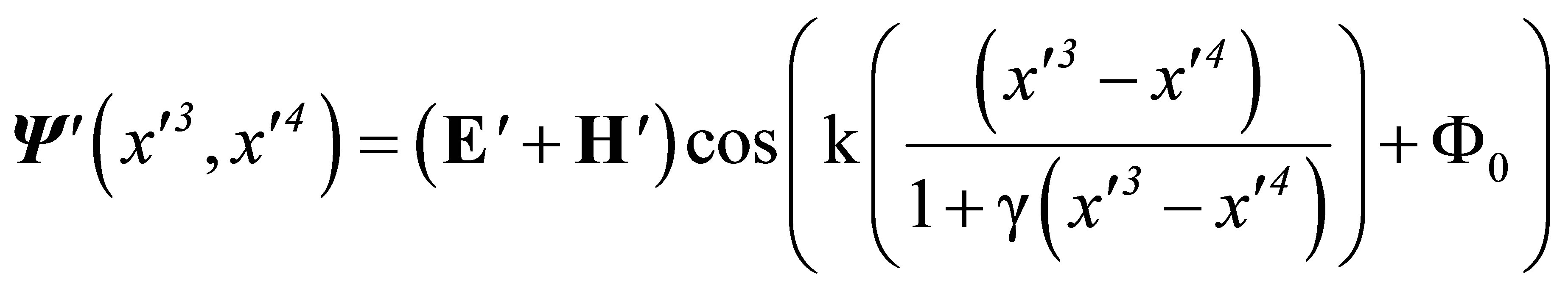
(50)
with
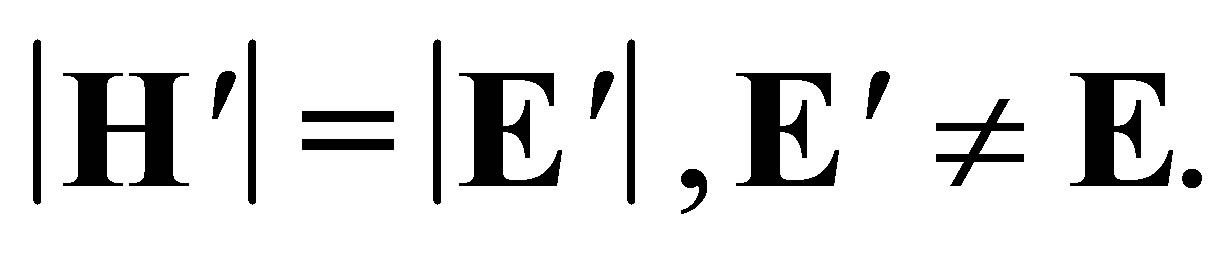 (51,52)
(51,52)
One thus need only require that  continues to satisfy the wave equation. Equation (48) ensures that it does so everywhere that the denominator does not vanish. Furthermore, because
continues to satisfy the wave equation. Equation (48) ensures that it does so everywhere that the denominator does not vanish. Furthermore, because 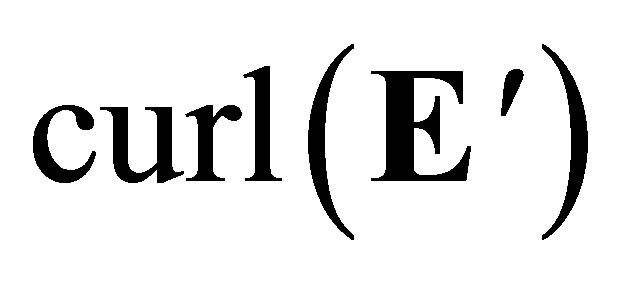 and
and 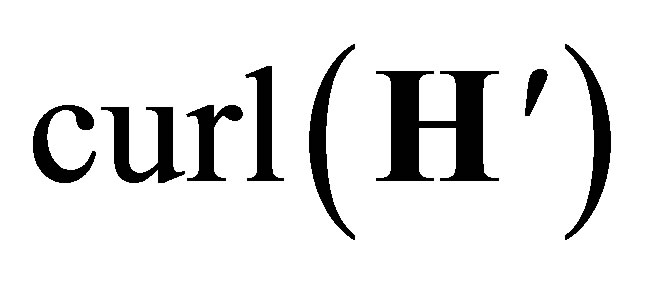 vanish, no external potentials or currents are required to produce the EM waves defined by (42) and those defined by (50).
vanish, no external potentials or currents are required to produce the EM waves defined by (42) and those defined by (50).
The wave that carries the fields can be considered to have wave number
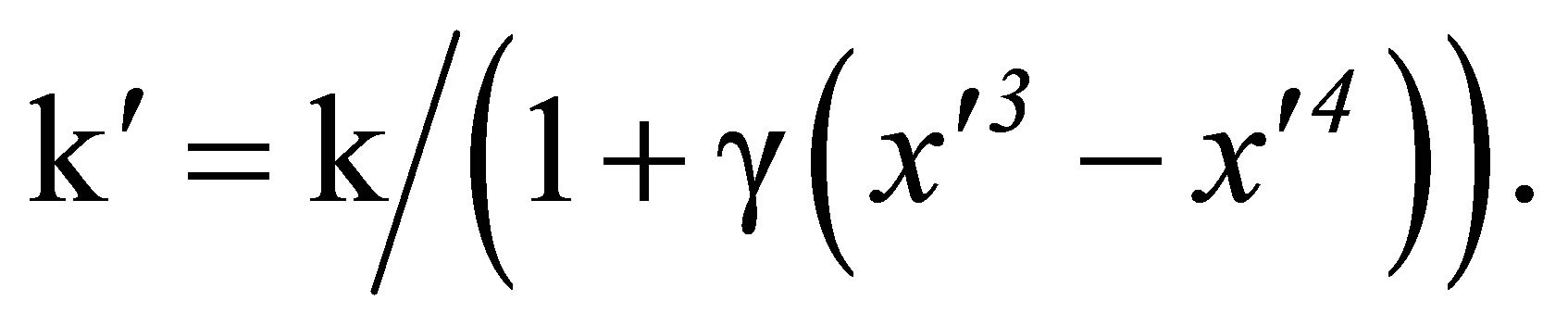 (53)
(53)
At a stationary point with coordinate 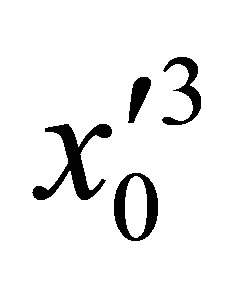 the waves oscillate with a frequency
the waves oscillate with a frequency
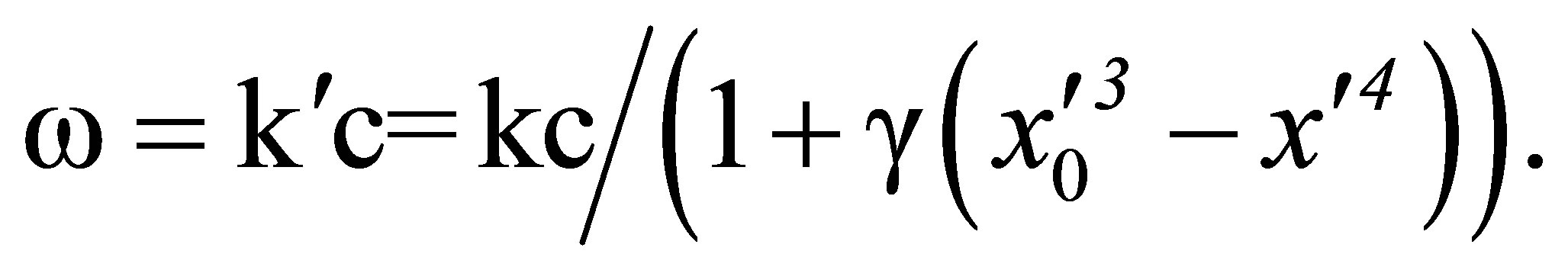 (54)
(54)
The corresponding spherical waves are defined by
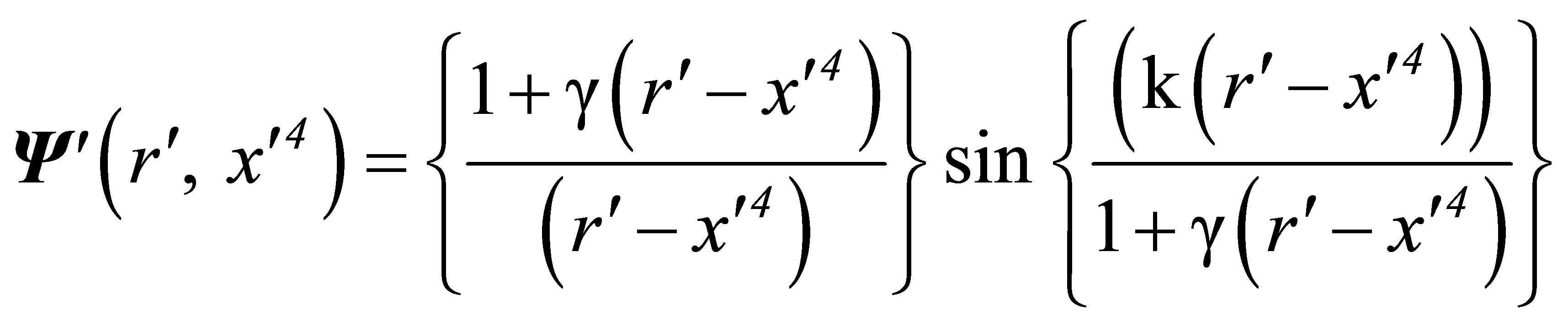 (55)
(55)
They carry electromagnetic fields in which E’ and H’ are everywhere orthogonal to the wave-front and to each other.
4. The One-Parameter Family of Metrics
Differentiation of the finite C4 transformation (29) produces the relations
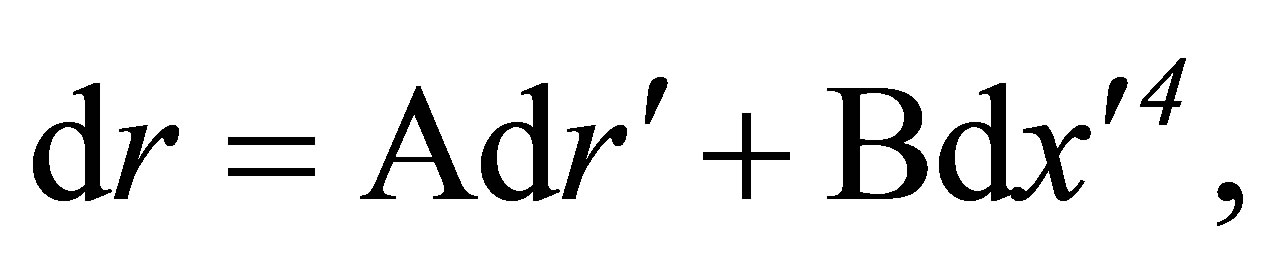 (56)
(56)
 (57)
(57)
These, together with (14-17) imply that the Minkowski line element
 (58)
(58)
becomes
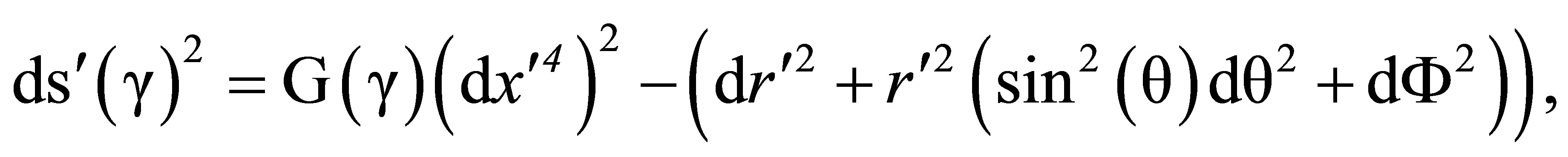
(59)
with
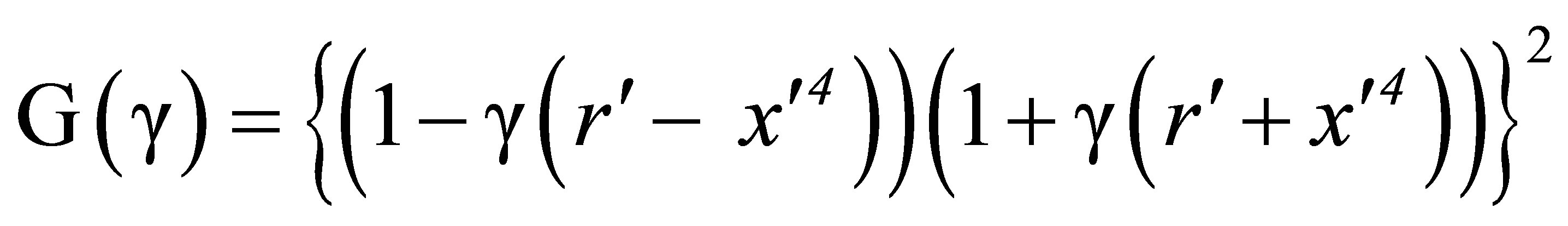 (60)
(60)
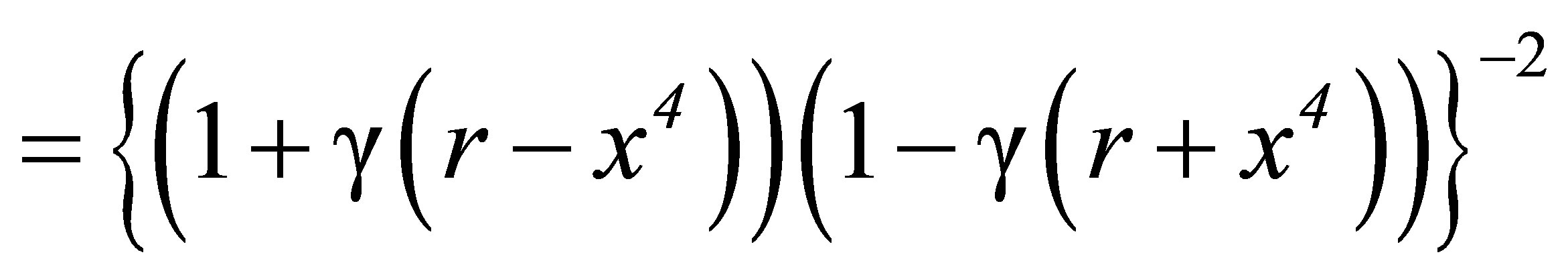 (61)
(61)
The metric tensor, 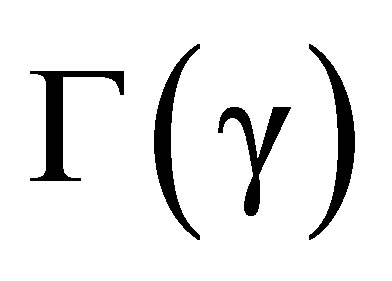 , is diagonal with elements
, is diagonal with elements
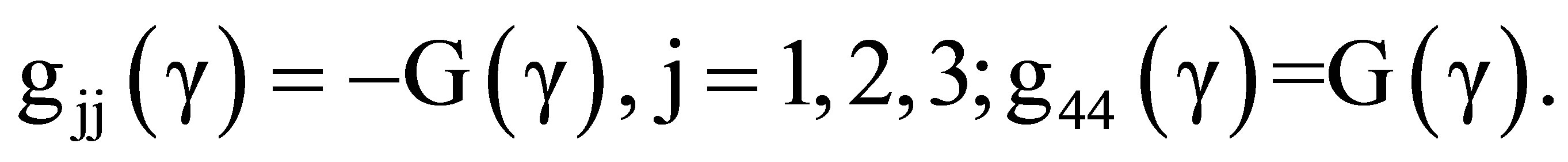 (62)
(62)
Minkowski’s metric tensor is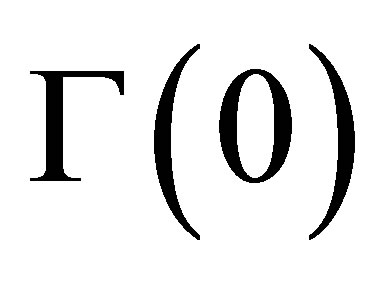 .
.
The 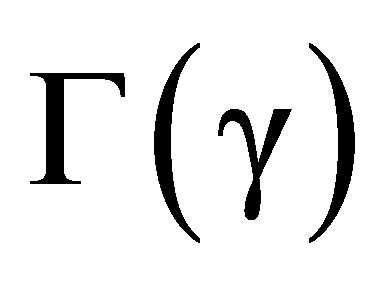 metric is invariant under the transformations of the rotation group SO(3). If
metric is invariant under the transformations of the rotation group SO(3). If  is not zero,
is not zero,  and
and 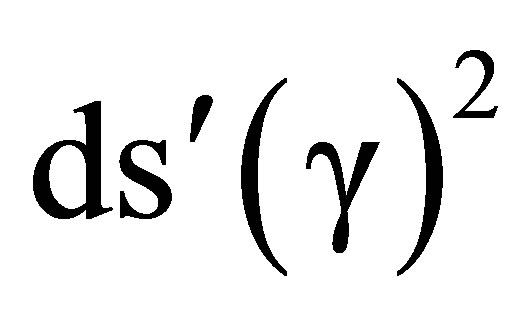 are not invariant under the translations and Lorentz transformations of the Poincare group. Thus the general
are not invariant under the translations and Lorentz transformations of the Poincare group. Thus the general 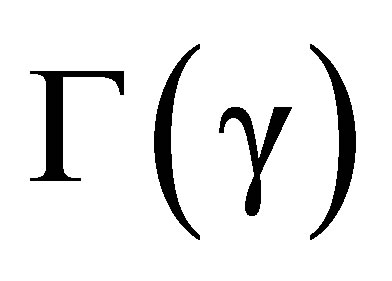 metric and line element express the properties of a space-time in which each source of an electromagnetic field reduces Poincare invariance to a rotational invariance about itself.
metric and line element express the properties of a space-time in which each source of an electromagnetic field reduces Poincare invariance to a rotational invariance about itself.
5. Interpretation of Observed Spectral Shifts
The 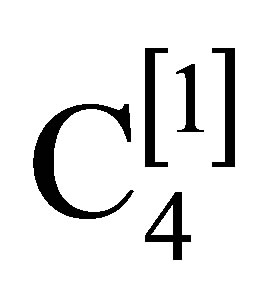 transformations relating primed and unprimed variables define mappings that relate two sets of coordinates,
transformations relating primed and unprimed variables define mappings that relate two sets of coordinates, 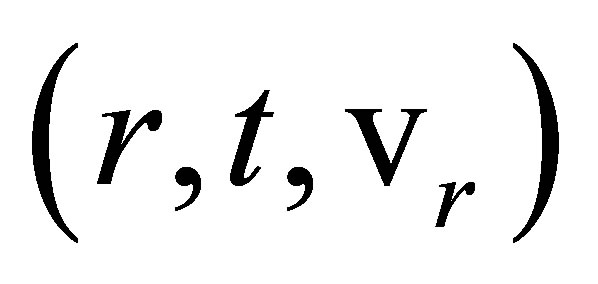 and
and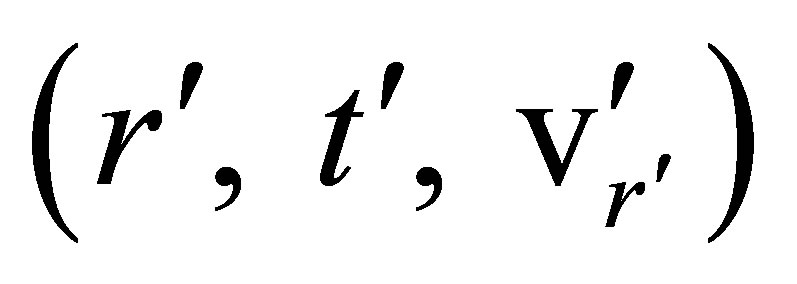 , of the same point. Motions of physical points in Minkowski space will be described by changes in the value of the
, of the same point. Motions of physical points in Minkowski space will be described by changes in the value of the  coordinates of the points, and motions in
coordinates of the points, and motions in 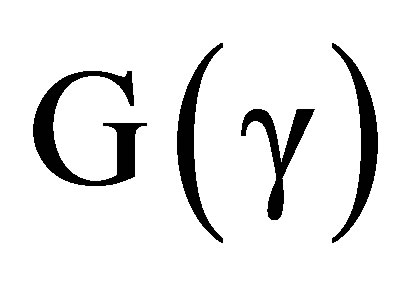 space-times will be described by changes in the value of the
space-times will be described by changes in the value of the 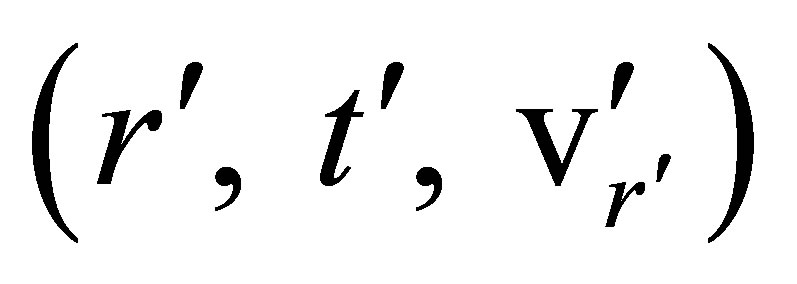 coordinates of the same physical points.
coordinates of the same physical points.
A point П fixed on an electro-magnetic wave can be assigned the pair of coordinates  and
and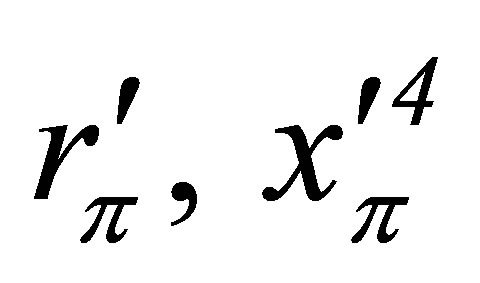 . Let П1 and П2 be two such points separated by one wavelength and centered at П0 on a locally monochromatic EM wave propagating in otherwise field-free space-time. Let an observing apparatus at a point P momentarily on the wave’s source cone have coordinates
. Let П1 and П2 be two such points separated by one wavelength and centered at П0 on a locally monochromatic EM wave propagating in otherwise field-free space-time. Let an observing apparatus at a point P momentarily on the wave’s source cone have coordinates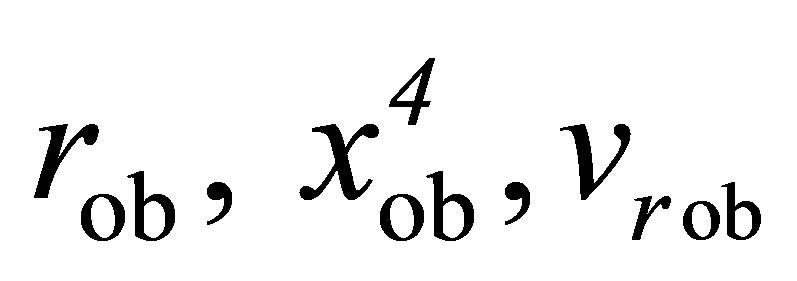 , and
, and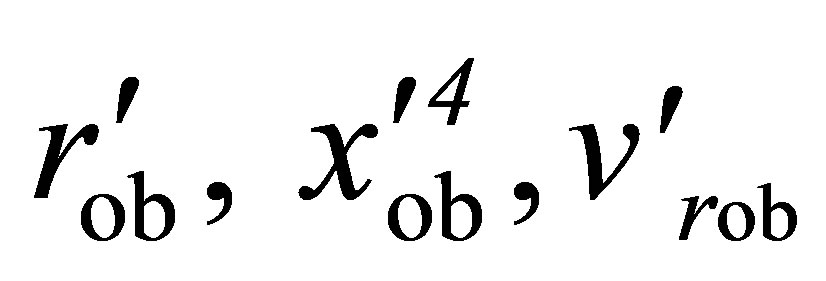 . Let v and v’ be frequencies, and λ and
. Let v and v’ be frequencies, and λ and 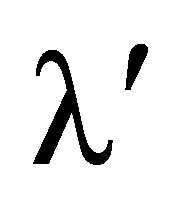 wavelengths measured at P in the two systems. Then measuring frequencies in the two sets of coordinates determines the times
wavelengths measured at P in the two systems. Then measuring frequencies in the two sets of coordinates determines the times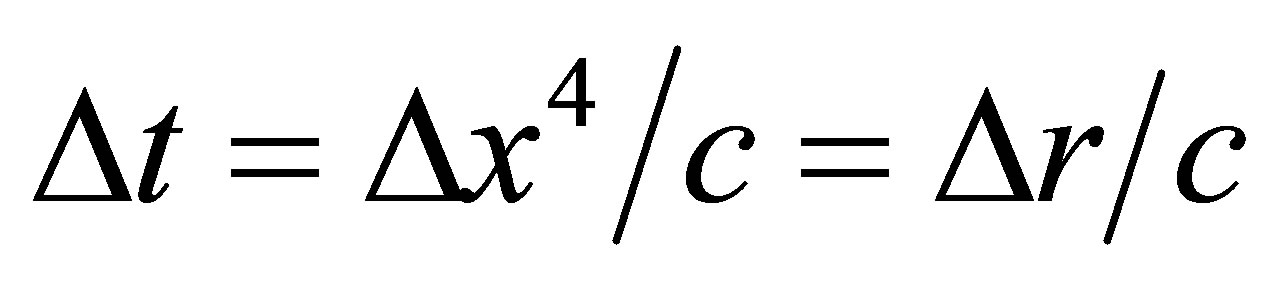 , and
, and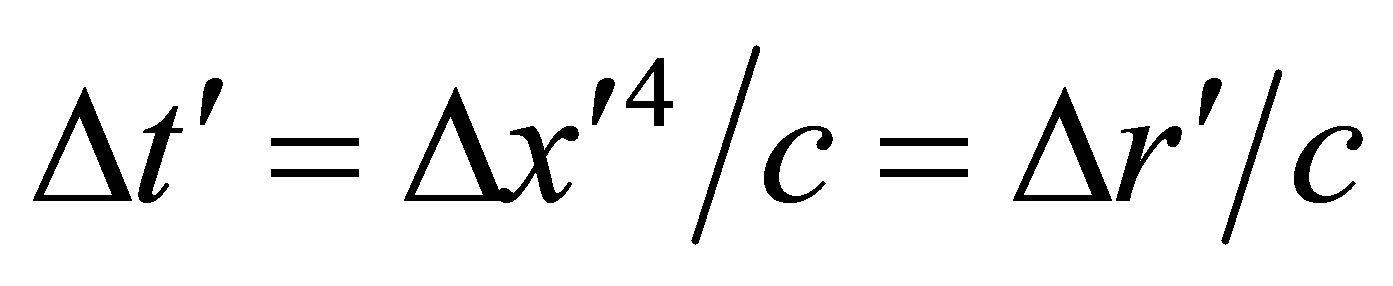 , that it takes one wavelength to pass the point P. The observations thereby relate time intervals at P in the two systems to frequency and wavelength measurements in the two systems via the equations
, that it takes one wavelength to pass the point P. The observations thereby relate time intervals at P in the two systems to frequency and wavelength measurements in the two systems via the equations
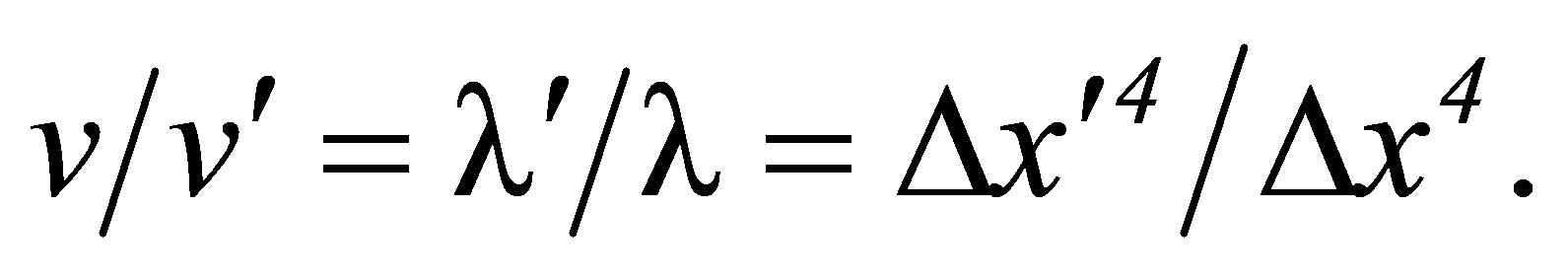 (63,64)
(63,64)
We shall assume that the group parameter γ is small enough to ensure that approximating the last ratio by 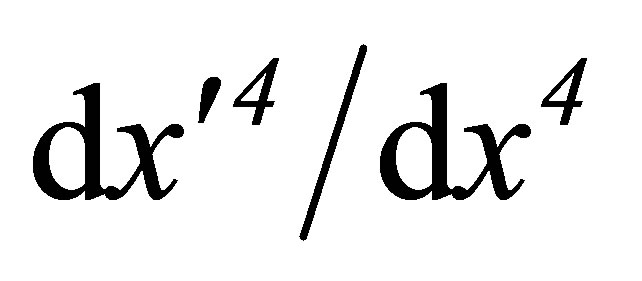 leads to no detectable error. In this approximation
leads to no detectable error. In this approximation
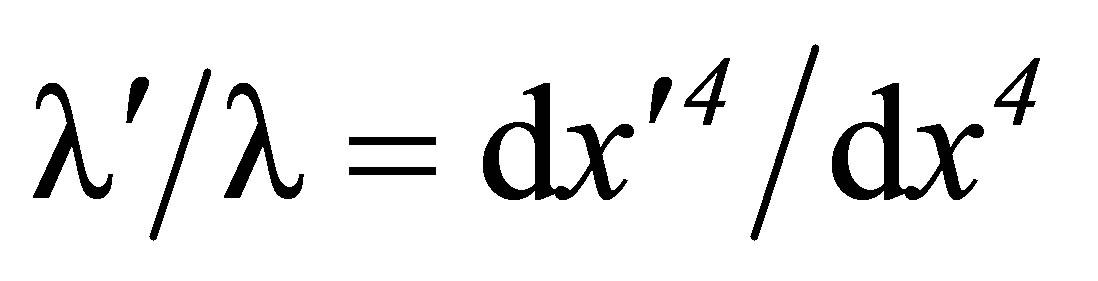 (65)
(65)
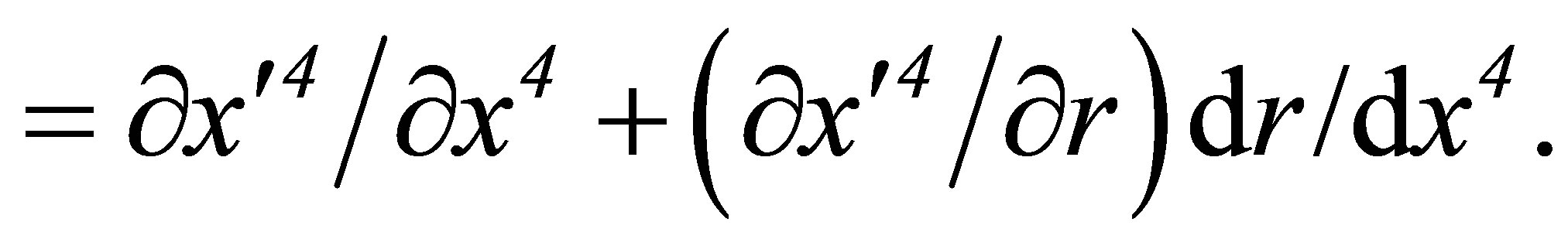 (66)
(66)
Here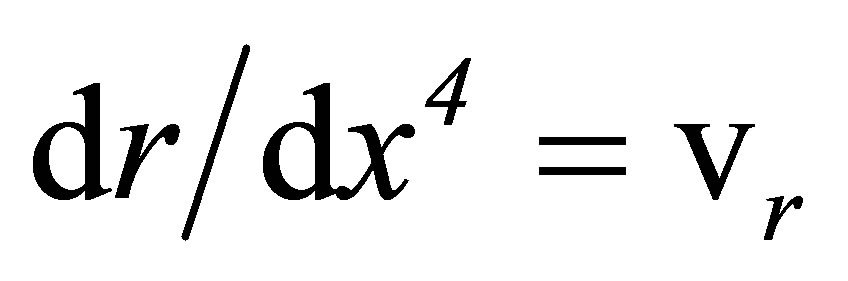 , represents the radial velocity of the observing apparatus at r, t, in Minkowski space. Equations (64-66), and (24-30) together imply that
, represents the radial velocity of the observing apparatus at r, t, in Minkowski space. Equations (64-66), and (24-30) together imply that
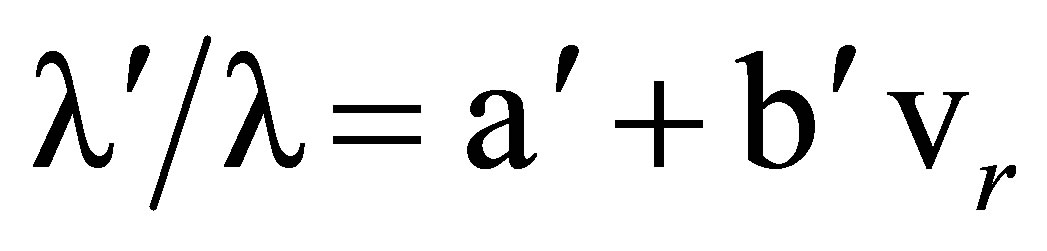 , (67)
, (67)
with
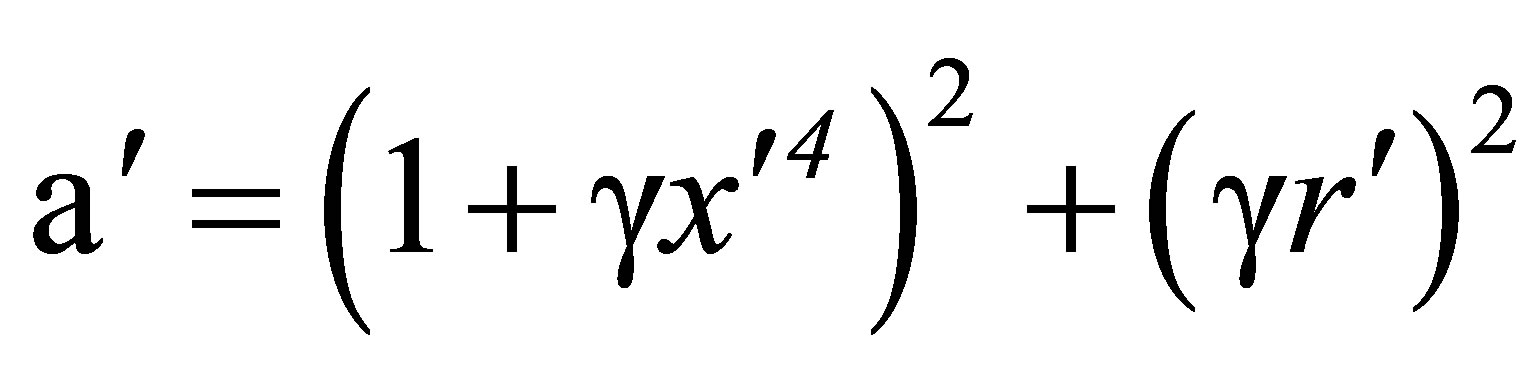 (68)
(68)
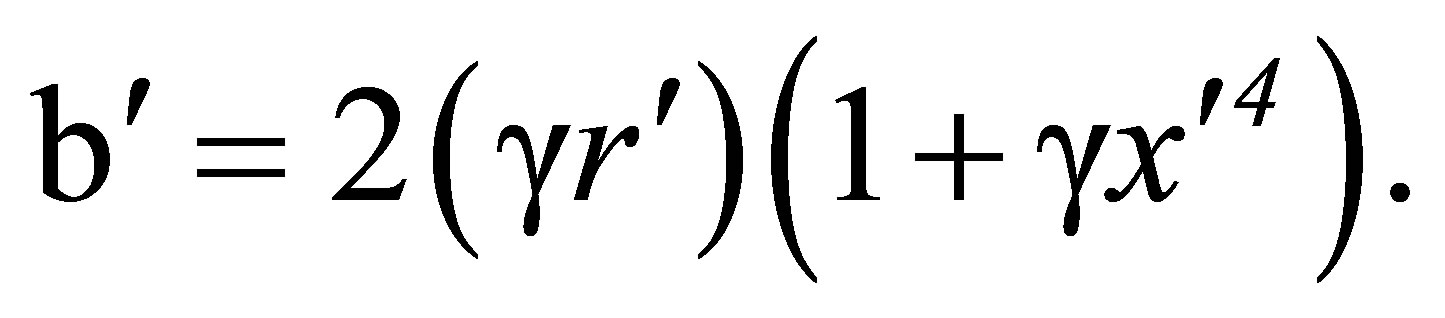 (69)
(69)
To simplify notation, define
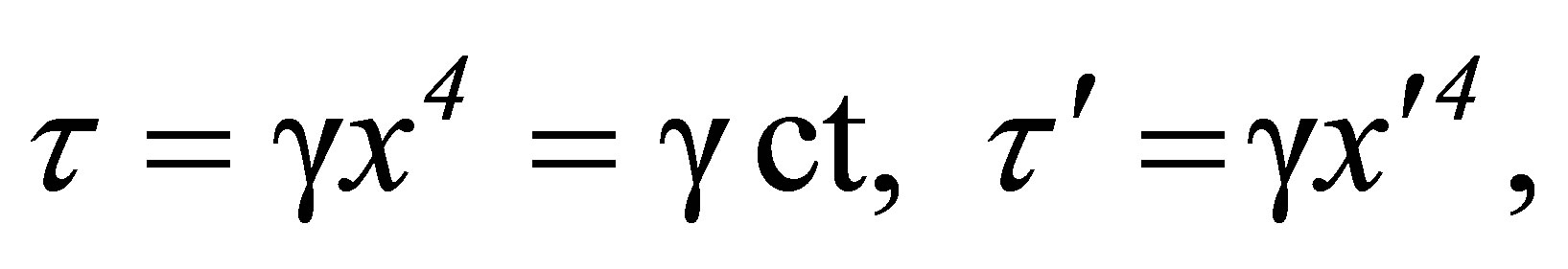 (70-72)
(70-72)
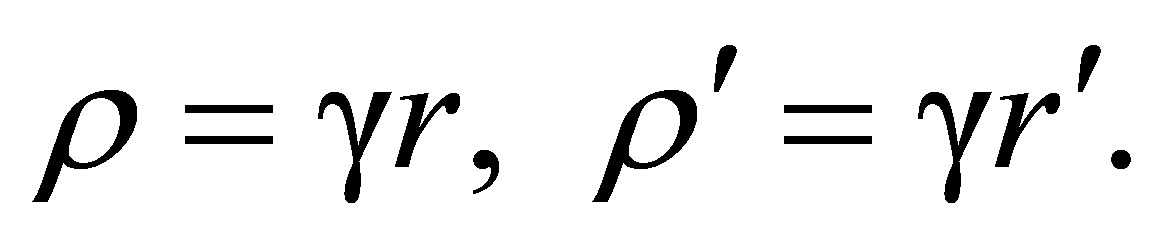 (73,74)
(73,74)
On source cones, 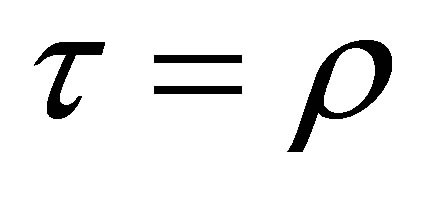 and
and .
.
When expressed in terms of the velocity and position coordinates of an observer’s apparatus in  spacetimes, (67) becomes
spacetimes, (67) becomes
 (75)
(75)
These equations state that  is a function of the time
is a function of the time 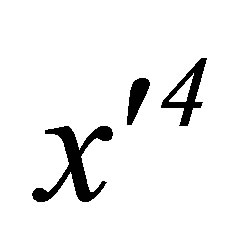 as well as
as well as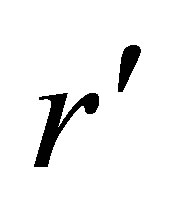 . However on a source cone
. However on a source cone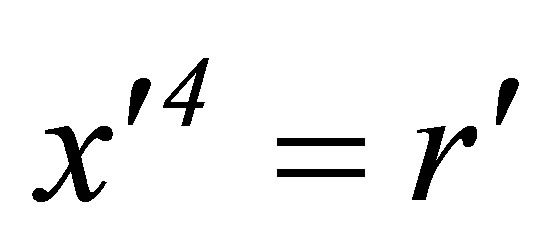 , so for observations of any particular source
, so for observations of any particular source
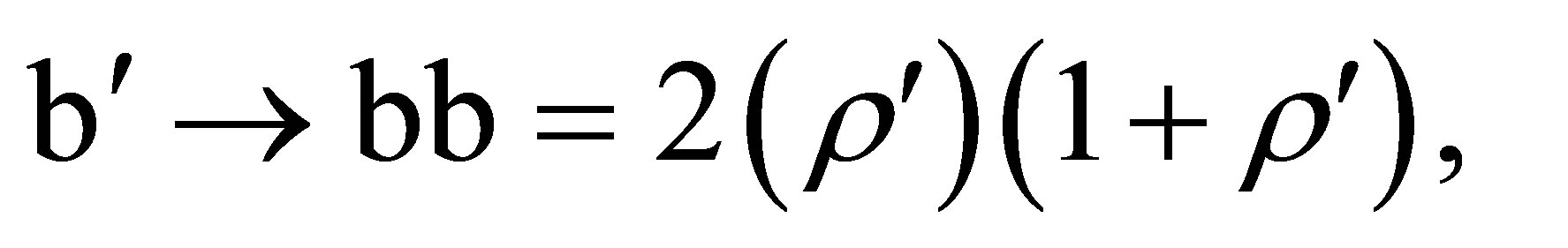 (76)
(76)
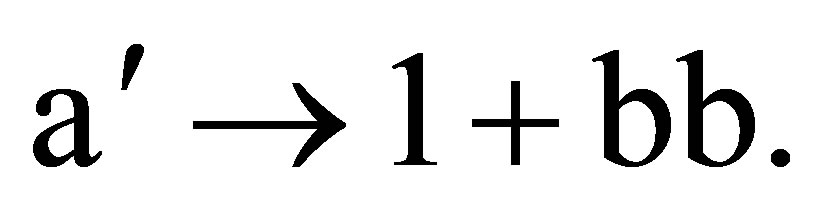 (77)
(77)
We suppose that 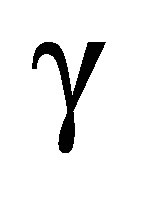 is so small that reference wavelengths,
is so small that reference wavelengths, 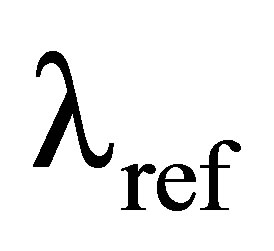 produced and observed by local sources, have the same observable value in Minkowski space as in the
produced and observed by local sources, have the same observable value in Minkowski space as in the 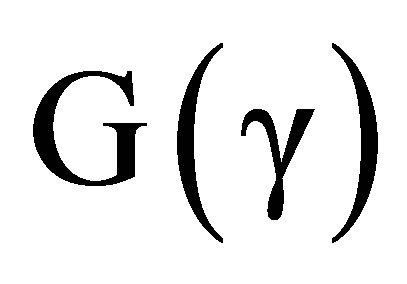 space-times. Equations (72-77) then relate observables in a
space-times. Equations (72-77) then relate observables in a 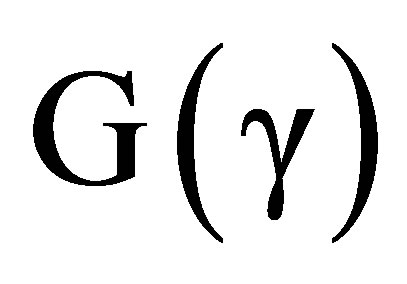 space-time. We now consider two cases:
space-time. We now consider two cases:
1) If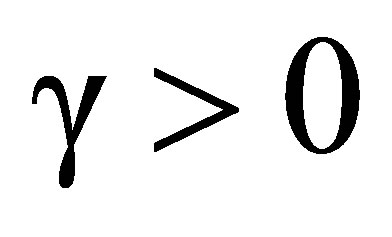 , and
, and , then (72-75) predict red shifts that depend solely on
, then (72-75) predict red shifts that depend solely on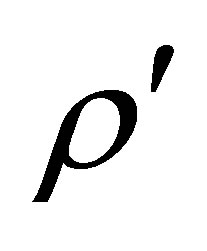 . These shifts are given by
. These shifts are given by
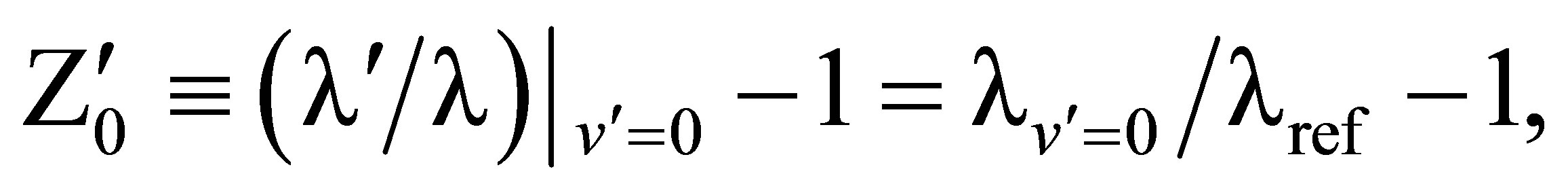 (78)
(78)
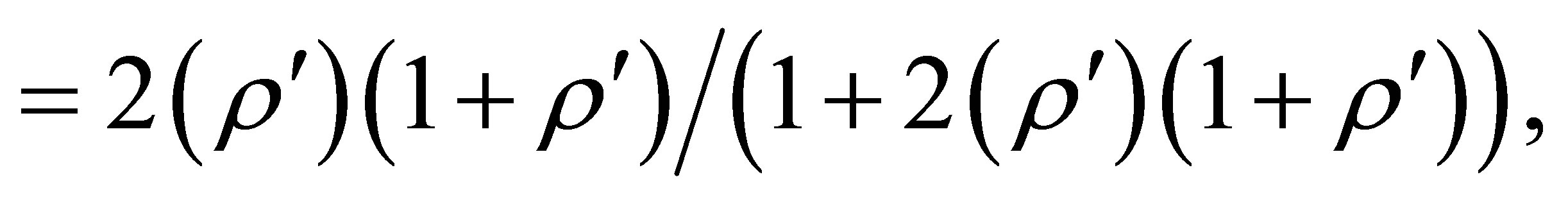 (79)
(79)
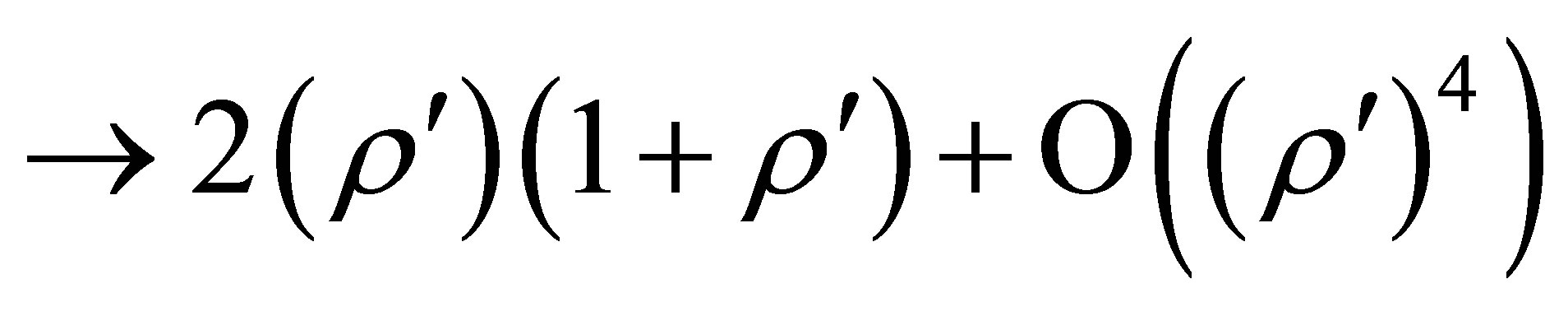 (80)
(80)
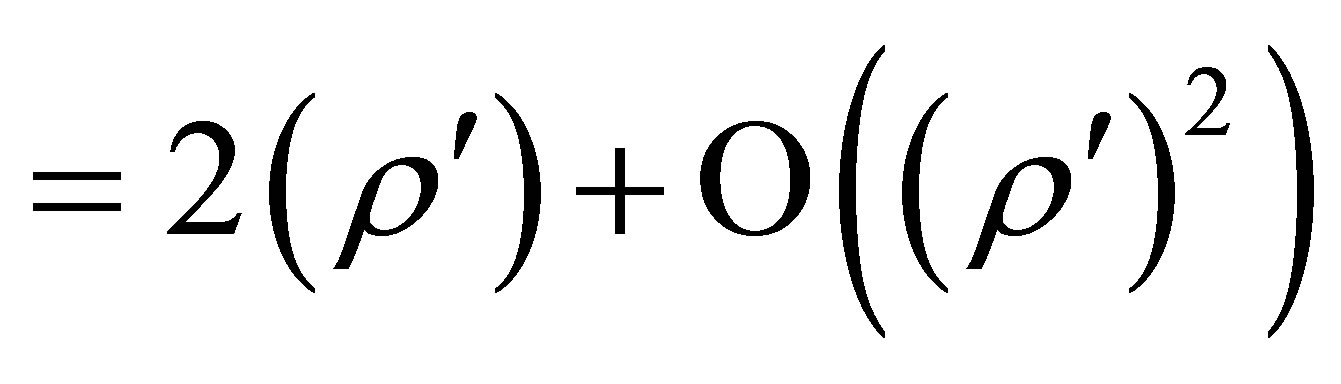 . (81)
. (81)
These relations may be compared with the Hubble relation
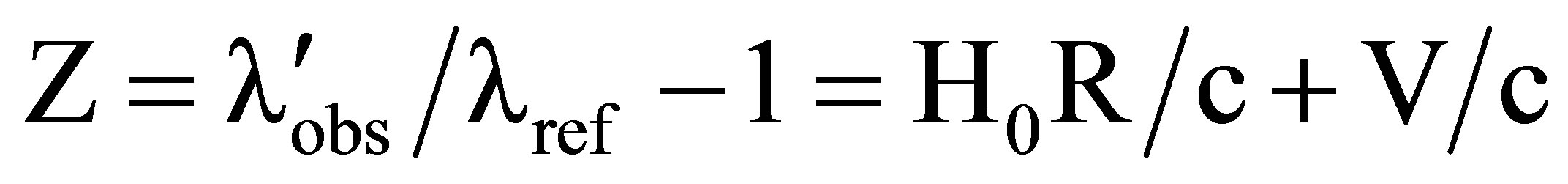 (82,83)
(82,83)
Here 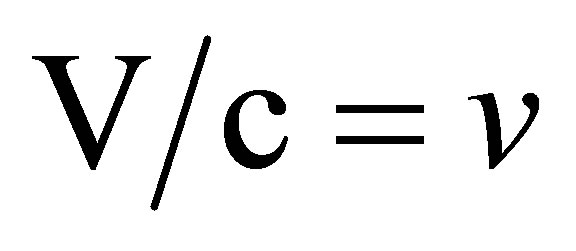 represents a “peculiar velocity”. If it is zero, setting
represents a “peculiar velocity”. If it is zero, setting  and γ equal to
and γ equal to 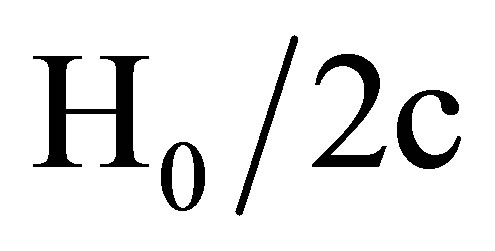 in (83) yields
in (83) yields
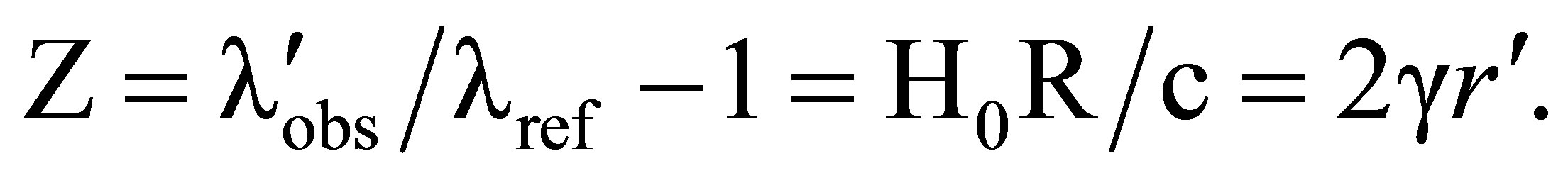 (84-86)
(84-86)
This puts (83) in 1:1 correspondence with the Hubble relation.
2) If 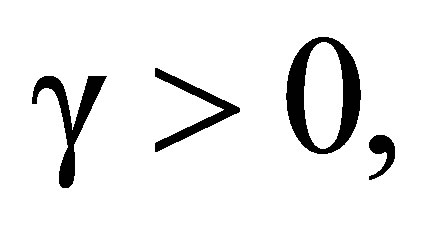 and
and  is nonzero, (76-77) define frequency shifts that are a function of the radial velocity
is nonzero, (76-77) define frequency shifts that are a function of the radial velocity  and the position
and the position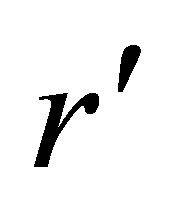 , of the observer relative to the source. These shifts are defined by the equations
, of the observer relative to the source. These shifts are defined by the equations
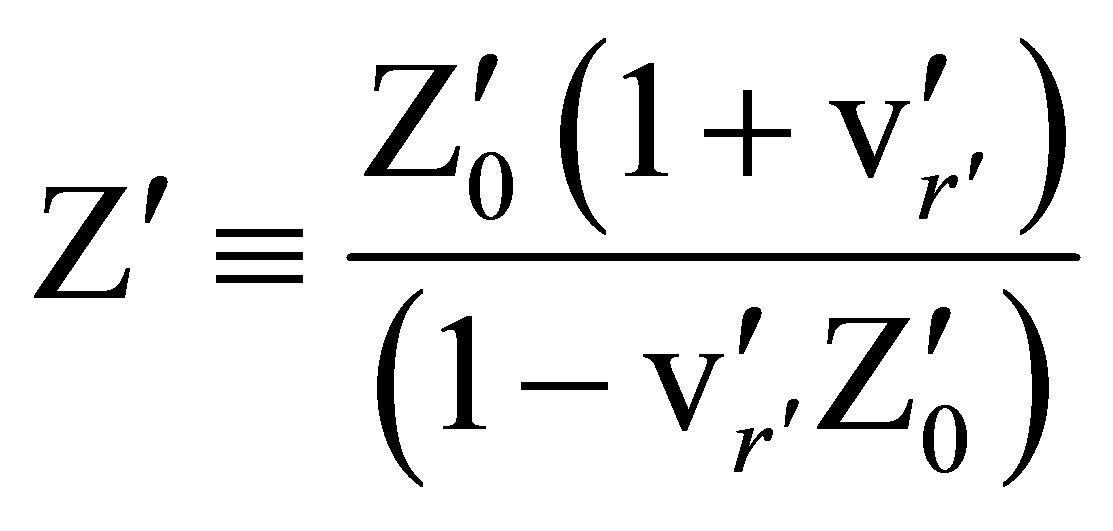 (87)
(87)
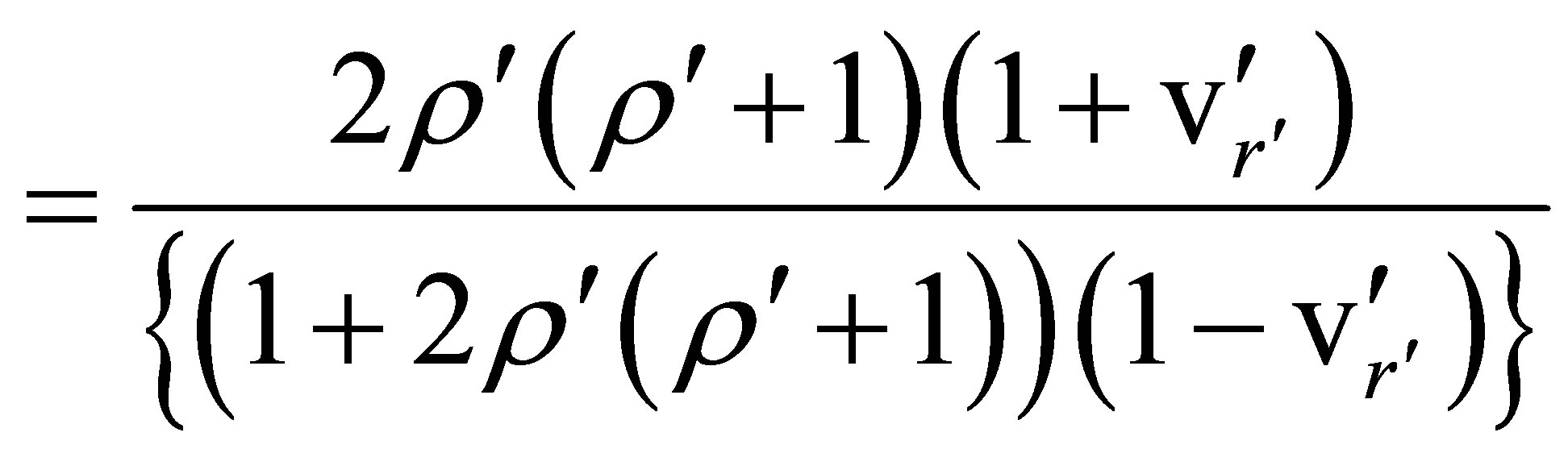 (88)
(88)
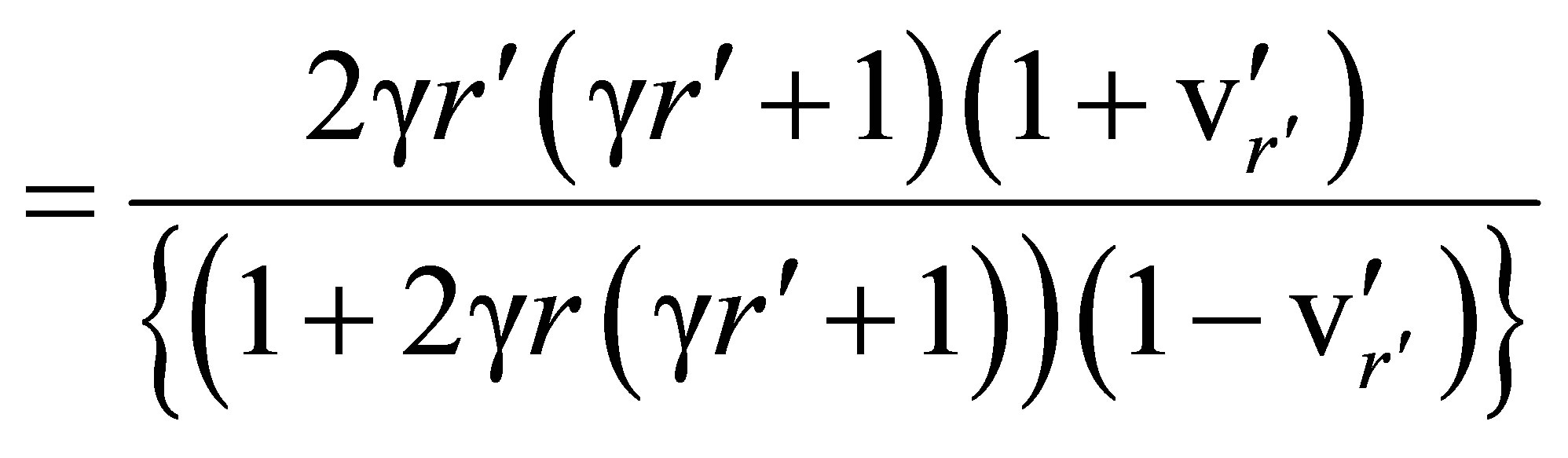 (89)
(89)
When  is <0.1, (89) implies that in the Xʹ system the position and velocity dependence is well approximated by
is <0.1, (89) implies that in the Xʹ system the position and velocity dependence is well approximated by
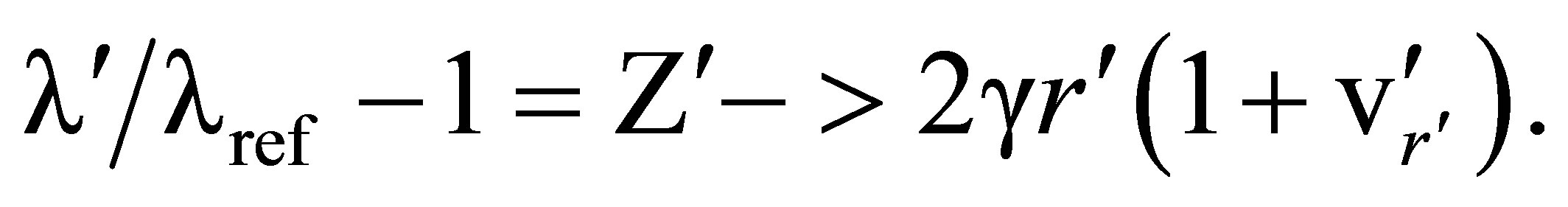 (90)
(90)
This is to be compared with the result of setting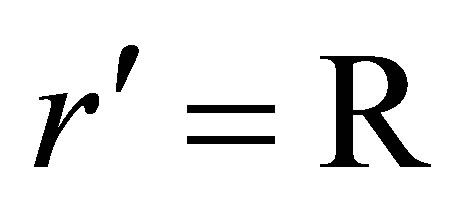 , 2γ equal to
, 2γ equal to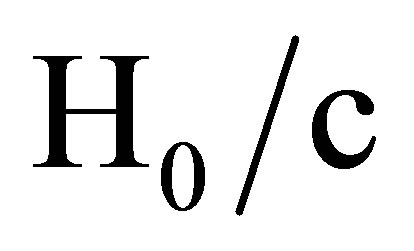 , and
, and  in (83) which yields
in (83) which yields
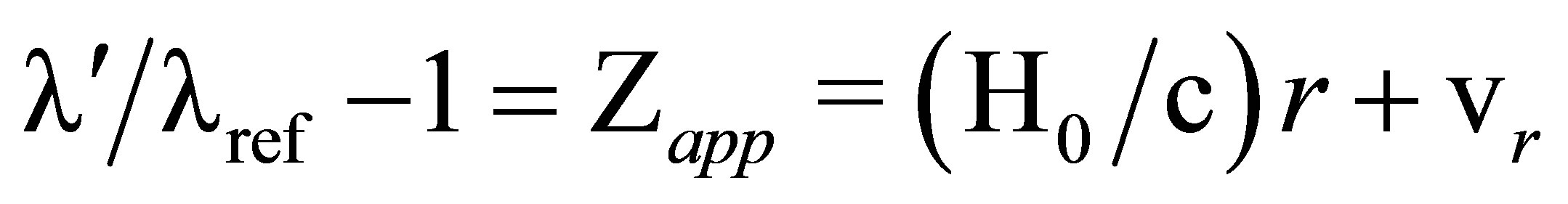 .(91-92)
.(91-92)
The functional form of this connection between radial velocities and frequency shifts is quite different than that of the connection in (90). In the next Section we investigate a relation of (90) and (91-92) to observations.
6. Observations of Distant Keplerian Motions
In 1914, V. Slipher discovered the existence of internal rotations in nebulae [14]. When F. Zwicky [15] pointed out in 1933 that motions in the Coma cluster of nebulae failed to obey the virial theorem, he suggested that the failure might be due to unobserved “dunkel Materie”, or to a failure of the known laws of physics. By 1980, Vera. C. Rubin and her coworkers W. Kent Ford, Jr. and N. Thonnard had established that the motions of stars associated with many spiral galaxies demonstrate the same effect [16].
The failure is now known to be very general, and it is commonly attributed to the presence of unobserved mass and energy, and less commonly, to a modification of Newtonian dynamics. The following paragraphs show that the apparent failure to obey the virial theorem can arise from interpreting observations in a  spacetime as observations in Minkowski space.
spacetime as observations in Minkowski space.
We follow Peebles [17] and exploit the fact that for circular orbits the mean values in the virial theorem become single values. For a body of mass m and orbital speed  orbiting a center with effective mass
orbiting a center with effective mass , the speed is related to r, the radius of the orbit by the well-known equation
, the speed is related to r, the radius of the orbit by the well-known equation
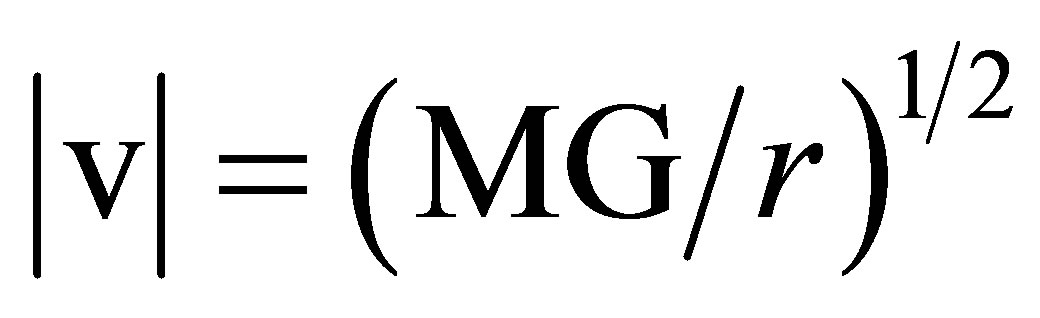 . (93)
. (93)
The failure of nebulae to obey (93) is known to appear when observations of luminosities and 21 cm microwave intensities establish that the luminous mass of a nebula lies within a sphere of radius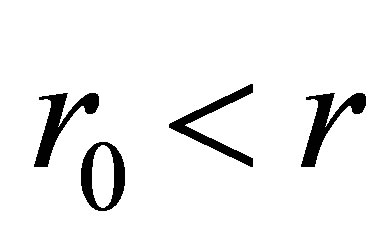 . An especially clear example of the phenomenon occurs when the rotational velocities are observed “edge-on”. In most cases, the Doppler shifts then observed are those of velocities indistinguishable from the tangential velocities of bodies moving on circular orbits about the center of mass of the nebulae. These tangential velocities of bodies in Kepler orbits then become radial velocities along the line of sight of the observer.
. An especially clear example of the phenomenon occurs when the rotational velocities are observed “edge-on”. In most cases, the Doppler shifts then observed are those of velocities indistinguishable from the tangential velocities of bodies moving on circular orbits about the center of mass of the nebulae. These tangential velocities of bodies in Kepler orbits then become radial velocities along the line of sight of the observer.
When the velocities of such motions of massive bodies, and hydrogen, orbiting spiral galaxies have been deduced from observed Doppler shifts, the masses are found to be moving on arcs with radii, r, less than the value expected from the mass of the nebulae deduced from luminosities. The velocities also undergo little change as r increases. The observed Doppler shifts are thus those that would be obtained if there is sufficient dunkel Materie within the region to keep MG/r nearly constant as r varies over a wide range.
Equations (90) and (91) suggest that when observations of the motion of bodies in galactic orbit are expressed in 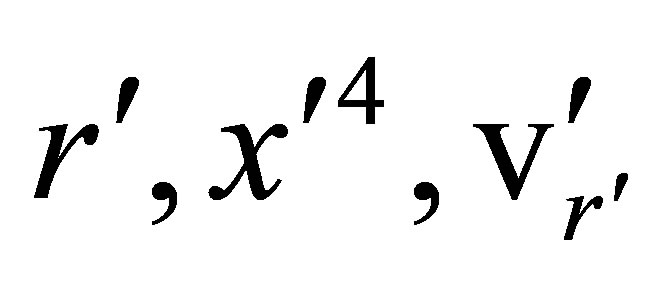 coordinate systems a very different physical interpretation of the observed motions is implicated. This may be shown by examining what would be observed in a G(g) space-time if a distant orbiting body of mass << than M is moving on a circular Kepler orbit centered on the position of the effective mass M, which is at rest with respect to the observer.
coordinate systems a very different physical interpretation of the observed motions is implicated. This may be shown by examining what would be observed in a G(g) space-time if a distant orbiting body of mass << than M is moving on a circular Kepler orbit centered on the position of the effective mass M, which is at rest with respect to the observer.
To investigate this question, we consider the orbiting bodies to be origins of source cones, on which the observed orbital tangential velocities become radial velocities of the observer relative to the source. If the observations are being made in an , system, and the observer is at a distance
, system, and the observer is at a distance 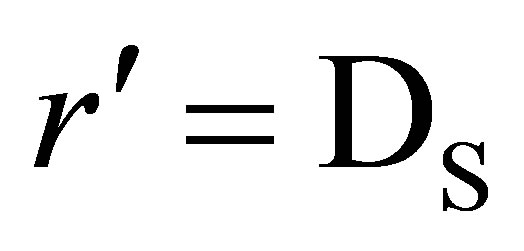 from the source, then the spectral shifts Zʹ arising from
from the source, then the spectral shifts Zʹ arising from 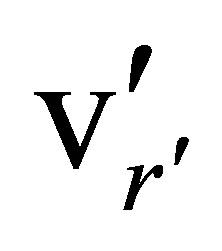 will satisfy the previously noted relation,
will satisfy the previously noted relation,
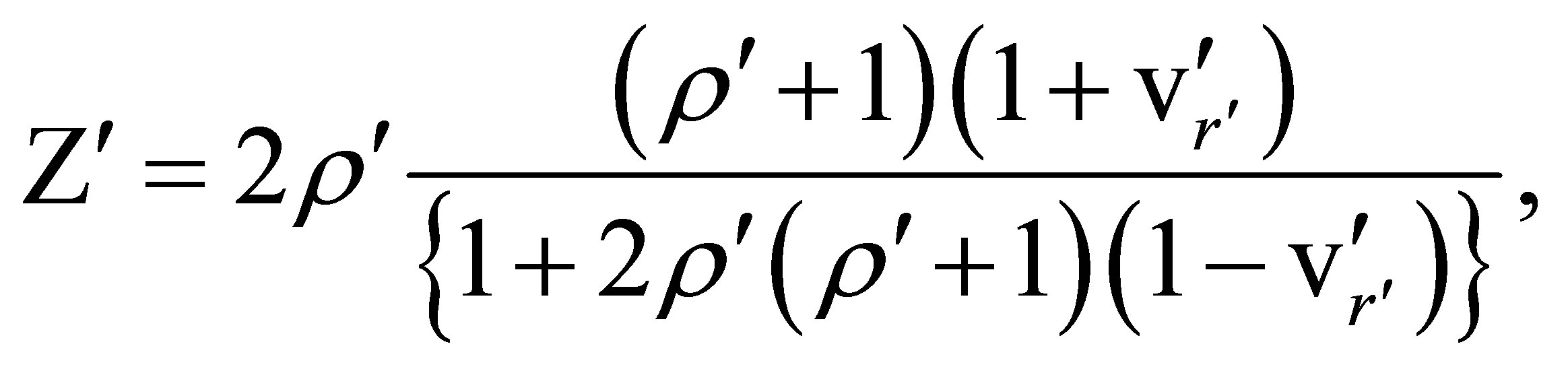 (94)
(94)
with , and r’ equal to the distance, DS, from the body of mass m to the observer in
, and r’ equal to the distance, DS, from the body of mass m to the observer in 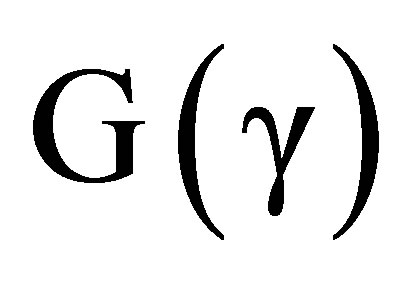 space-time. The velocity v’r’ is a radial velocity of the observer with respect to the body. Now let
space-time. The velocity v’r’ is a radial velocity of the observer with respect to the body. Now let  represent radial coordinates of the central mass in the source cone system, and let
represent radial coordinates of the central mass in the source cone system, and let  represent the value of its tangential velocity in the source cone system. Then,
represent the value of its tangential velocity in the source cone system. Then, 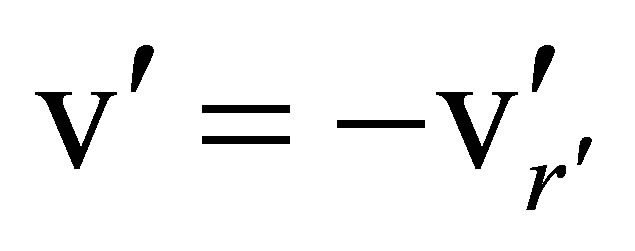 and we may replace (94) with the equation
and we may replace (94) with the equation
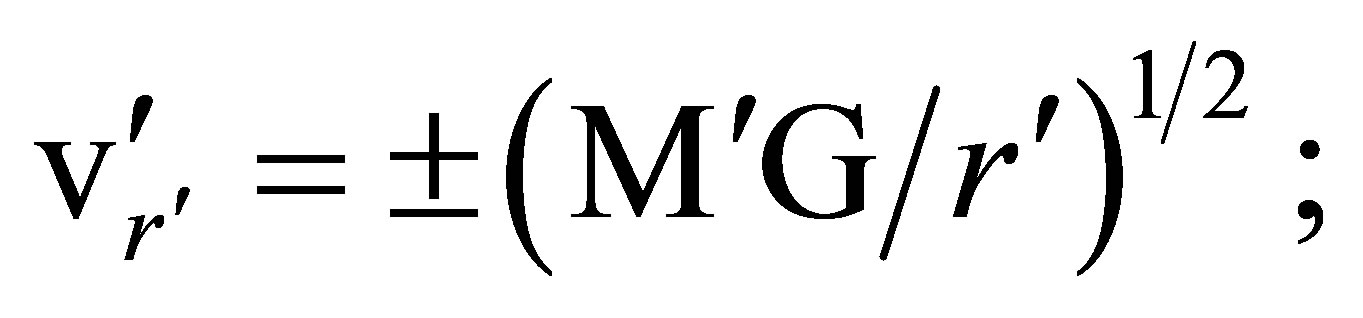 (95)
(95)
in which
 (96)
(96)
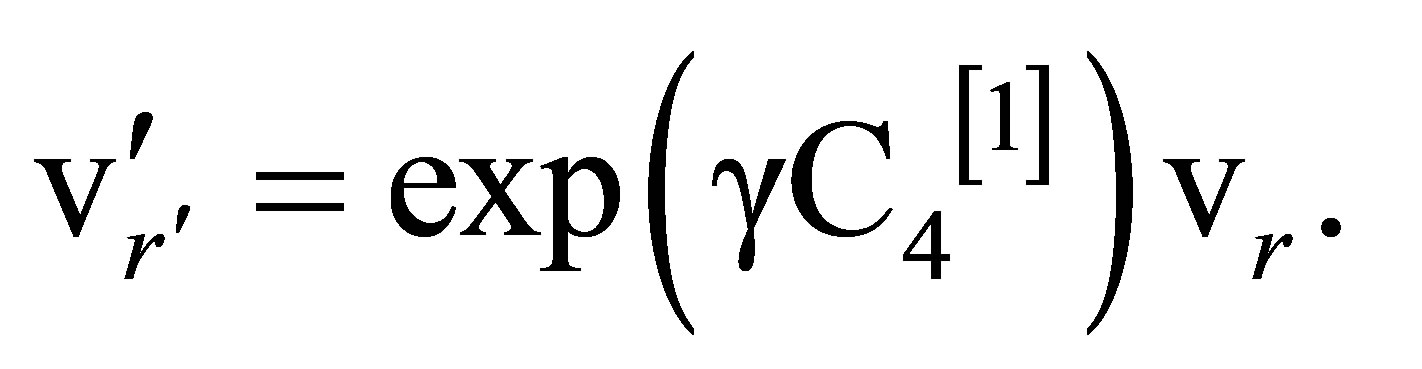 (97)
(97)
It is revealing to assign values to MG that are those of two of the galaxies investigated in the paper “Dark Matter in Spiral Galaxies” by van Albada and Sancisi [18]. The authors analyze orbital motions observed in five galaxies whose distance from earth ranges from 3.2 to 9.2 mpc. The observed trajectories of the bodies have radii ranging from a few, to 36 kpc, and deduced orbital velocities,  , less than 10−3. The orbital radii are such a small fraction of the distance DS, that the distance from the observers to the centers of the orbits, DG, is at most 1% greater than DS. As a consequence, the first factor, 2ρʹ, in (94), gives Zʹ a linear dependence upon the distance DG from earth to the galaxy, a dependence like that of the Hubble relation (87) if one supposes that 2cγ and H0 have the same order of magnitude.
, less than 10−3. The orbital radii are such a small fraction of the distance DS, that the distance from the observers to the centers of the orbits, DG, is at most 1% greater than DS. As a consequence, the first factor, 2ρʹ, in (94), gives Zʹ a linear dependence upon the distance DG from earth to the galaxy, a dependence like that of the Hubble relation (87) if one supposes that 2cγ and H0 have the same order of magnitude.
In the cases being considered, the peculiar velocities have the same magnitude as the velocities of the center of mass of the nebulae relative to the orbiting source. Consequently, for  values of the order of 10−4 to 10−3, the factors
values of the order of 10−4 to 10−3, the factors  in (92) differ from unity by less than 0.1%. Thus, for the reason noted at the end of Section 5, the relation of Zʹ to these peculiar velocities is entirely different than that expected from Hubble’s relations.
in (92) differ from unity by less than 0.1%. Thus, for the reason noted at the end of Section 5, the relation of Zʹ to these peculiar velocities is entirely different than that expected from Hubble’s relations.
The resulting effect on values of Zʹ is displayed in Table 1. It contains values of Zʹ that would result from measuring spectra of radiation emitted from bodies with velocities vʹ orbiting centers with masses equal to those of NGC 2403 and NGC 2841, the galaxies with the smallest, and the largest, mass of the galaxies considered by van Albada and Sancisi. The radii r’ of the orbits, and the orbital velocities, vʹ, of the orbiting bodies, are labeled rNewt, and vKep in the table. In it, the hundred-fold change in the radii rNewt changes the local orbital velocities vKep by a factor of 10. If the red and blue shifts in the G(g) space-time are interpreted as arising from peculiar velocities in Minkowski space, they produce the values denoted V“Mink”. For NGC 2403, over the whole range of rNewt, the value of Zʹ and V“Mink” vary by 0.02%. For NGC 2841 they change by 0.23%. These results are a direct consequence of the weak dependence of Zʹ upon velocity that was noted in Section 5. When Zʹ becomes as large as 0.2, increasing the velocity from 0% to 10% of the velocity of light makes a 10% change in Zʹ.
The results in Table 1, taken together with the analysis in the previous Section, make it evident that if earthbased observations are actually being made in a G(γ) space-time with 2cγ having a value roughly equal to H0, it is not necessary to modify Newtonian dynamics, or introduce dark matter, to explain the observations: they are a consequence of an unexpected weak dependence of Zʹ on vKep. This conclusion applies to observed frequency shifts in the radiation received from bodies orbiting a large category of distant galaxies.
The vKep → 0 entries in Table 1 illustrate another revealing property of such 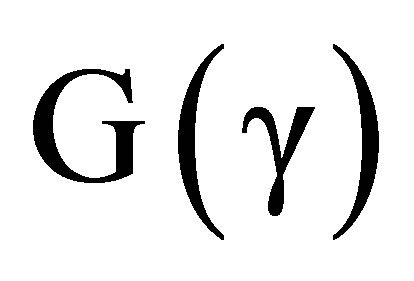 metrics: observations in their space-times do not require the presence of dark en-
metrics: observations in their space-times do not require the presence of dark en-
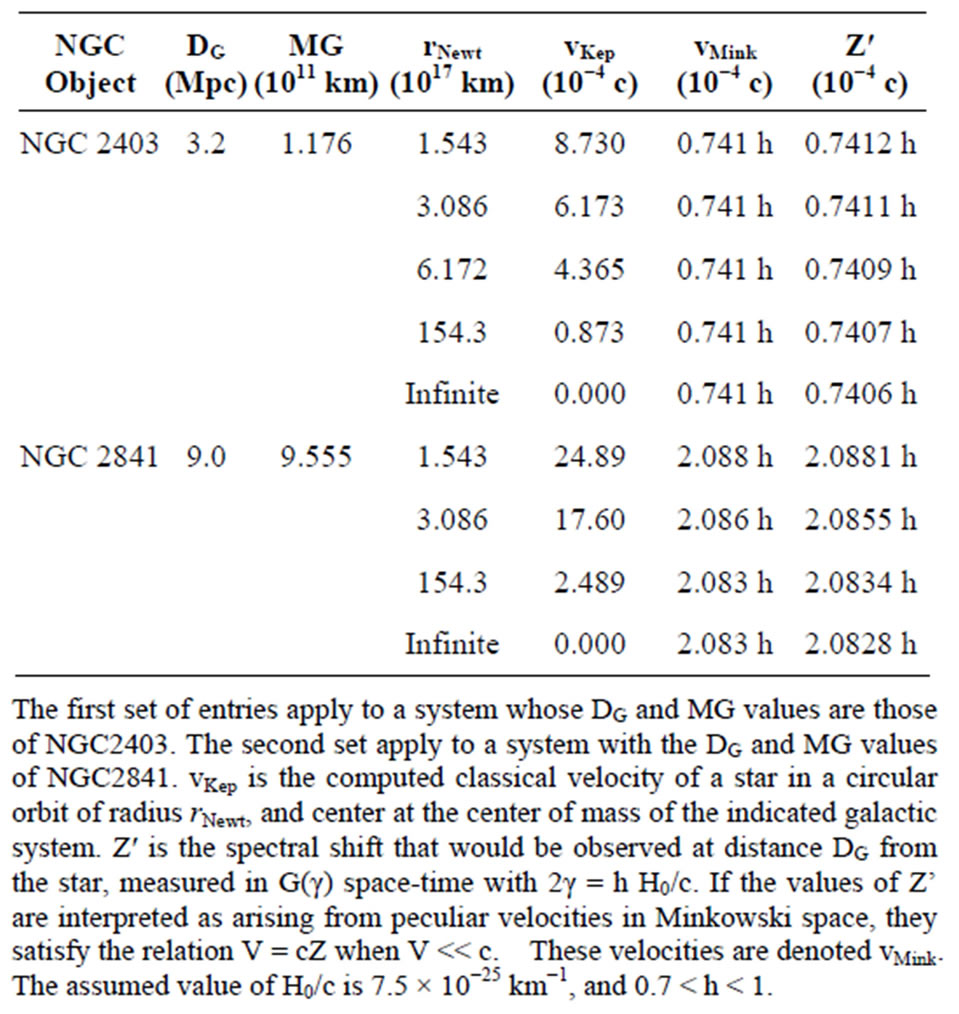
Table 1. Velocities of bodies orbiting the center of mass of spherically distributed masses of galactic magnitude.
ergy, or any other type of mass, to explain the spectra of radiation received from objects orbiting at very small velocities in regions arbitrarily distant from centers of gravitational attraction.
7. Conclusions
The mere fact that Maxwell’s equations allow a 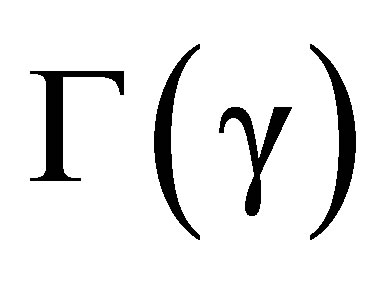 metric implies that Minkowski’s metric, G(0), cannot be assumed to be the metric of physical gravitation-free space-time.
metric implies that Minkowski’s metric, G(0), cannot be assumed to be the metric of physical gravitation-free space-time.
The analyses in the previous pages establish that observed shifts in the wavelengths of stellar radiations may well imply a relation of frequency shifts to recessionary velocities and peculiar velocities fundamentally different from those codified in Hubble’s relations as currently understood. The analyses also establish that the need to introduce dark matter and dark energy, or a modified Newtonian physics, could be eliminated if observed frequency shifts are related to velocities in a space-time in which the 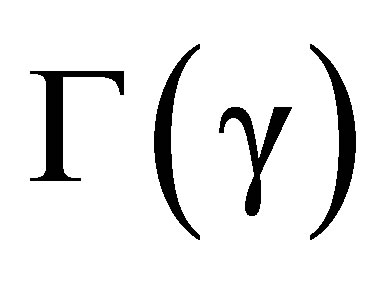 metric is one with 2cγ approximately equal to H0.
metric is one with 2cγ approximately equal to H0.
In the past, it has not seemed possible to determine whether Minkowki’s metric is valid over distances relevant to Hubble’s relation: it is not at all possible to transport clocks and meter sticks to astronomical distances and use them to test Einstein’s arguments that lead to Minkowski’s metric. However, the value of the group parameter γ could be determined by measuring successive return times, as well as frequency shifts within radar wave-pulses sent to receding spacecraft. The uncertainty in the resulting value of the group parameter can be expected to be less than the uncertainty in the value of Hubble’s constant [7,8].
If the value turns out to be indistinguishable from zero, the known range of validity of Minkowski’s metric will be greatly extended, and much existing astrophysics and cosmology will receive further validation. If the experiments confirm a non-zero value for γ, they will establish that sources of electromagnetic radiation, in fact, break Poincare and Lorentz invariance in a consequential manner that is both subtle and fundamental.
Such results would have another consequence. Tomilchik [5] and Wulfman [7,8] have both argued that the magnitudes of the “Pioneer Anomalies” roughly correspond to the value of the Hubble constant because the anomalies are primarily due to the assumption that the space-time is Minkowskian. However, Turyshev, et al. [19] argue that the anomalies can be explained by a recoil effect which had not been properly accounted for. The proposed experiments would determine the extent to which each explanation is correct.
More importantly, the proposed experiments would effectively establish the metric governing the transmission of electromagnetic waves over distances approaching 100AU.
If it turns out that the value of 2cγ and Hubble’s constant are of the same order of magnitude, it will be necessary to revise currently standard interpretations of the spectra of light that has propagated over astronomical distances. The analyses set forth in Sections 5 and 6 establish that the revisions could make it possible to reduce the number of hypotheses currently required to relate astrophysical observations.
Finally, it should be noted that the relations in (29-37) imply that two points moving with the same velocity in the Minkowski coordinate system X have relative accelerations in the Xʹ system if they are at different distances from the source. This property is reflected in the existence of non-zero forces with components ∂gk,k/∂xj. Hill’s approximation does not make it evident that these accelerations are not constant. The penetrating paper “Conformal Invariance in Physics” by Fulton, Rohrlich, and Witten investigates accelerations produced by conformal transformations [20]. It deals with the mathematics and the physical applications of both conformal function groups and conformal Lie groups. In its final section, the authors state their conclusion, “··· conformal transformations are a special way of describing certain phenomena which in general relativity are accounted for by a restricted class of coordinate transformations”. Thus the relation between the G(γ) metric and the metrics of general relativity can be expected to be different than the relation between Minkowski’s metric and the metrics of general relativity.
8. Acknowledgements
It is a pleasure to acknowledge many clarifying conversations with Andrew S. Wulfman and his assistance with the bibliographic research and preparation of the manuscript.
REFERENCES
- H. Bateman, Proceedings London Mathematical Society, Vol. 8, 1909, pp. 223-264.
- E. Cunningham, Proceedings London Mathematical Society, Vol. 8, 1909, pp. 77-98.
- E. L. Hill, Physical Review, Vol. 68, 1945, pp. 232-233. http://dx.doi.org/10.1103/PhysRev.68.232.2
- Hoyle, F., et al., “A Different Approach to Cosmology,” Cambridge University Press, Cambridge, 2000.
- L. M. Tomilchik, AIP Conference Proceedings, Vol. 1205, 2010, pp. 177-184. http://dx.doi.org/10.1063/1.3382326
- H. A. Kastrup, Annals of Physics, Vol. 17, 2008, pp. 631- 690. http://dx.doi.org/10.1002/andp.200810324
- C. E. Wulfman, “Dynamical Symmetry,” World Scientific Publishing Co., Singapore, 2011, pp. 426-429.
- C. E. Wulfman, AIP Conference Proceedings, Vol. 1323, 2010, pp 323-329. http://dx.doi.org/10.1063/1.3537862
- M. Calixto, et al., Journal of Physics A: Mathematical and Theoretical, Vol. 45, 2012, pp. 244010-244026. http://dx.doi.org/10.1088/1751-8113/45/24/244010
- B. J. Cantwell, “Introduction to Symmetry Analysis,” Cambridge University Press, Cambridge, 2002.
- P. Hydon, “Symmetry Methods for Differential Equation,” Cambridge University Press, Cambridge, 2000. http://dx.doi.org/10.1017/CBO9780511623967
- F. H. Stephani, “Differential Equations: Their Solution Using Symmetries,” Cambridge University Press, Cambridge, 1989.
- C. E. Wulfman, “Dynamical Symmetry,” loc cit.
- V. M. Slipher, Lowell Observatory Bulletin, Vol. 2, 1914, p. 66.
- F. Zwicky, Helvetica Physica Acta, Vol. 6, 1933, pp. 110- 125.
- V. C. Rubin, W. K. Ford Jr. and N. Thonnard, Astrophysical Journal, Vol. 238, 1980, pp. 471-487. http://dx.doi.org/10.1086/158003
- P. J. E. Peebles, “Principles of Physical Cosmology,” Princeton University Press, Princeton, 1993.
- T. S. van Albada and R. Sancisi, Philosophical Transactions of the Royal Society A, Vol. 320, 1986, pp. 447-464. http://dx.doi.org/10.1098/rsta.1986.0128
- S. G. Turyshev, et al., Physical Review Letters, Vol. 108, 2012, pp. 241101-241104. http://dx.doi.org/10.1103/PhysRevLett.108.241101
- T. Fulton, F. Rohrlich and L. Witten, Reviews of Modern Physics, Vol. 34, 1962, pp. 442-457. http://dx.doi.org/10.1103/RevModPhys.34.442

