Applied Mathematics
Vol.3 No.8(2012), Article ID:21481,6 pages DOI:10.4236/am.2012.38130
General Periodic Boundary Value Problem for Systems
1Department of Mathematics, Faulty of Educations, Khartoum University, Omdurman, Sudan
2Department of Mathematics, Northwest Normal University, Lanzhou, China
Email: mohdnajy@hotmail.com
Received May 20, 2012; revised July 2, 2012; accepted July 9, 2012
Keywords: Systems; Principle Eigenvalues; Positive Solutions; Green’s Function; Fixed Point Index Theorem in Cones
ABSTRACT
The paper deals with the existence of nonzero periodic solution of systems 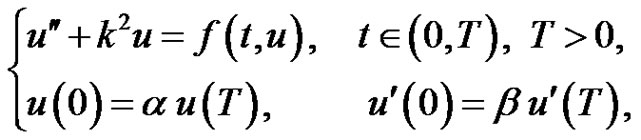 where
where ,
,  are
are  real nonsingular matrices,
real nonsingular matrices, 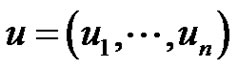 ,
,
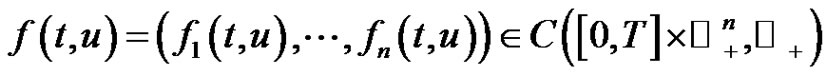 is periodic of period
is periodic of period 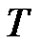 in the
in the 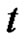 variable are continuous and nonnegative functions. We determine the Green’s function and prove that the existence of nonzero periodic positive solutions if one of
variable are continuous and nonnegative functions. We determine the Green’s function and prove that the existence of nonzero periodic positive solutions if one of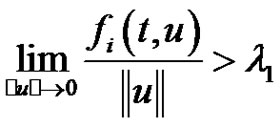 . In addition, if all
. In addition, if all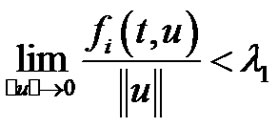 ,
,  where
where 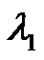 is the principle eigenvalues of the corresponding linear systems. The proof based on the fixed point index theorem in cones. Application of our result is given to such systems with specific nonlinearities.
is the principle eigenvalues of the corresponding linear systems. The proof based on the fixed point index theorem in cones. Application of our result is given to such systems with specific nonlinearities.
1. Introduction
In this paper, we study the existence of nonzero positive periodic solution of systems
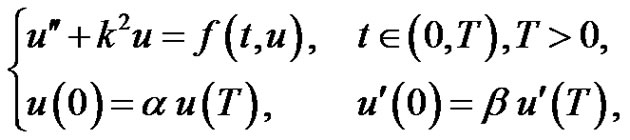 (1.1)
(1.1)
where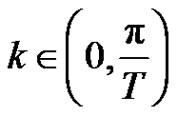 ,
, 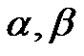 are
are 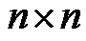 real nonsingular matrices,
real nonsingular matrices, 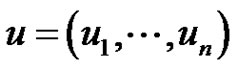 , and
, and
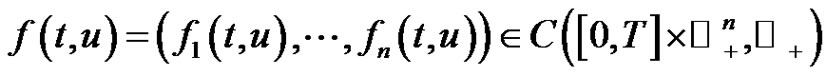
are periodic of period  in the
in the , are continuous and nonnegative functions and
, are continuous and nonnegative functions and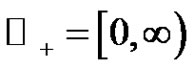 .
.
Beginning with the paper of Erbe and Palamides [1], obtained the sufficient conditions for existence solution of the systems of nonlinear boundary value problem
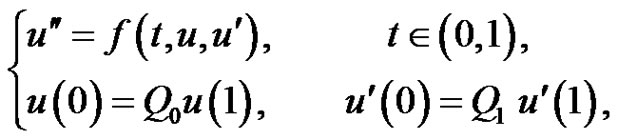 (1.2)
(1.2)
where 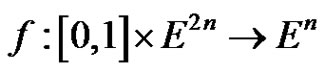 is continuous (
is continuous (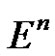 is n-dimensional real Euclidean space) and
is n-dimensional real Euclidean space) and 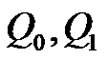 are nonsingular matrices, with
are nonsingular matrices, with 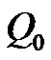 orthogonal matrix, Erbe and Palamides generalize earlier conditions of Bebernes and Schmitt [2] for periodic case. Erbe and Schmitt [3] extend the results in [1] established the sufficient conditions for existence solution of the systems (1.2). The results in [1,3] were obtained via a modifications of a degree-theoretic approach and Leray-Schuader degree and eliminates the modified function approach respectively. None of these earlier results use Green’s function and the first eigenvalues of the corresponding to the linear systems of (1.1).
orthogonal matrix, Erbe and Palamides generalize earlier conditions of Bebernes and Schmitt [2] for periodic case. Erbe and Schmitt [3] extend the results in [1] established the sufficient conditions for existence solution of the systems (1.2). The results in [1,3] were obtained via a modifications of a degree-theoretic approach and Leray-Schuader degree and eliminates the modified function approach respectively. None of these earlier results use Green’s function and the first eigenvalues of the corresponding to the linear systems of (1.1).
There has been progress in the study of the existence of positive solutions of system problem. If 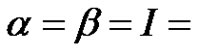 identity, then (1,1) reduces to the usual periodic boundary value problem for which the literature in both the scalar and systems versions is very extensive (We refer to [4-22] and references therein). For instance a recent paper, Wang [4] obtained the existence of periodic solution of a class of non-autonomous second-order systems
identity, then (1,1) reduces to the usual periodic boundary value problem for which the literature in both the scalar and systems versions is very extensive (We refer to [4-22] and references therein). For instance a recent paper, Wang [4] obtained the existence of periodic solution of a class of non-autonomous second-order systems
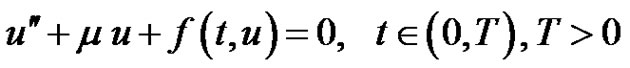
where
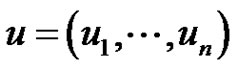 ,
,
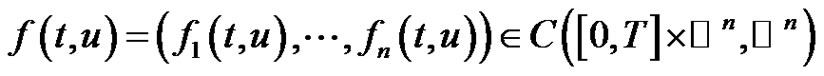
are periodic of period 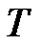 in the
in the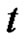 , and
, and 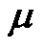 is a constantif
is a constantif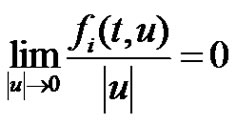 ,
, 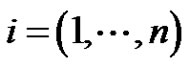 and
and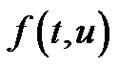 , is bounded below or above for appropriate ranges of
, is bounded below or above for appropriate ranges of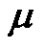 , via fixed point theorem in cones. Franco and Webb [5] established the existence of
, via fixed point theorem in cones. Franco and Webb [5] established the existence of  -periodic solutions for systems of (1.1) with
-periodic solutions for systems of (1.1) with 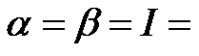 identity, in the boundary conditions, where
identity, in the boundary conditions, where  and
and  is a continuous vector valued function, periodic in
is a continuous vector valued function, periodic in 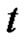 with period
with period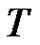 , and
, and  is allowed to have a singularity when
is allowed to have a singularity when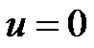 . Non-singular systems, which are included in the same framework that we study here (i.e., they can be reduced to a Hammerstein integral system with positive kernel), have been considered using some other approaches based on fixed point theorems in conical shells, but previously it has always been assumed that the nonlinearity
. Non-singular systems, which are included in the same framework that we study here (i.e., they can be reduced to a Hammerstein integral system with positive kernel), have been considered using some other approaches based on fixed point theorems in conical shells, but previously it has always been assumed that the nonlinearity 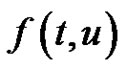 has a constant sign behaviour:
has a constant sign behaviour: 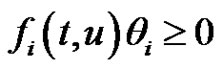 where
where 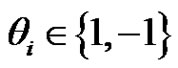 for
for 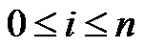 (see [6]) with
(see [6]) with  identity, in the boundary conditions. For systems problem see also [7-12] and references therein.
identity, in the boundary conditions. For systems problem see also [7-12] and references therein.
Even in the scalar case the existence of periodic solutions for problems with nonsingular and singular case has commanded much attention in recent years (see [13-22] and references therein. In particular, in [13-15] fixed point theorems in conical shells are used to obtain existence and multiplicity results, some of these are improved in this paper. In this notes, we prove result in the case where 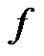 has no singularity. In scalar case problem see [16-22] and references therein.
has no singularity. In scalar case problem see [16-22] and references therein.
Motivated by these problems mentioned above, we study the existence of nonzero positive solution of (1.1) while we assume that if one components satisfy
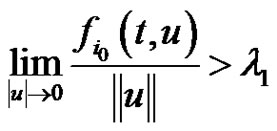 ,
, 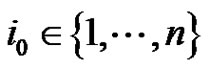 , and all components of nonlinearity are
, and all components of nonlinearity are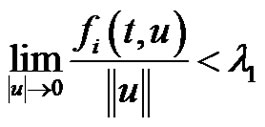 ,
, 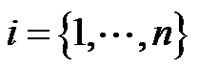 , where
, where
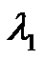 , is the largest characteristic value of the linear system corresponding to (1.1). The approach is to use the theory of fixed point index for compact maps defined on cones [23]. To apply this theory one needs to find the Green’s function. Our purpose here is prove that (1.1) has nontrivial nonnegative solution, assuming the following conditions:
, is the largest characteristic value of the linear system corresponding to (1.1). The approach is to use the theory of fixed point index for compact maps defined on cones [23]. To apply this theory one needs to find the Green’s function. Our purpose here is prove that (1.1) has nontrivial nonnegative solution, assuming the following conditions:
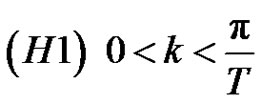 ,
,
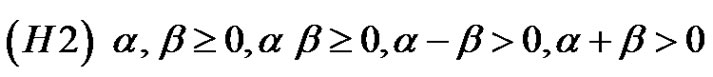
and
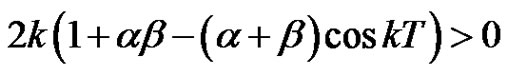 ,
,

are continuous and periodic of period 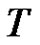 in the
in the 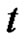 variable and
variable and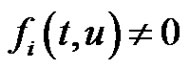 ,
,  on any subinterval of
on any subinterval of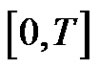 .
.
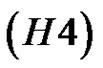 There exits
There exits 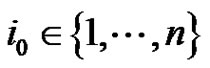 such that
such that
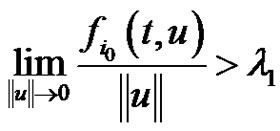 where
where 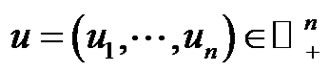 and
and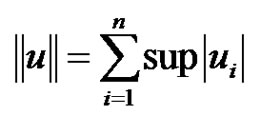 , and
, and
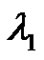 is the largest characteristic value of the linear system corresponding to (1.1),
is the largest characteristic value of the linear system corresponding to (1.1),
 For all
For all ,
,
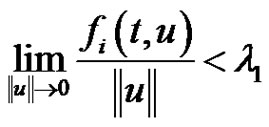 where
where 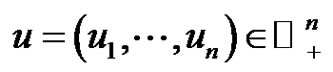 and
and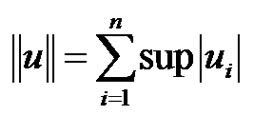 , and
, and
 is the largest characteristic value of the linear system corresponding to (1.1).
is the largest characteristic value of the linear system corresponding to (1.1).
Remark 1.1. The assumptions 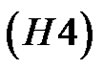 and
and 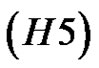 appeared in Lan [24].
appeared in Lan [24].
Remark 1.2. The nonzero positive solution has been studied by Lan [24] and Hai and Wang [25].
Throughout this paper, we will use the notation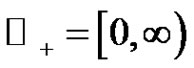 ,
,  , and denote by
, and denote by 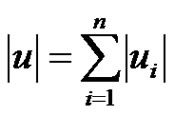
the usual norm of 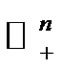 for
for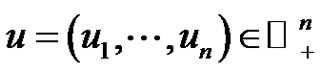 ,
, 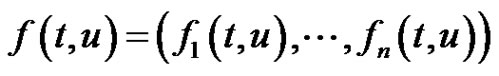 and
and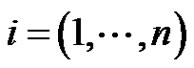 .
.
2. Preliminaries
In this section, we shall introduce some basic lemmas which are used throughout this paper.
Lemma 2.1. Let 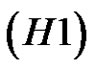 and
and 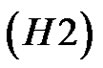 holds. Let
holds. Let 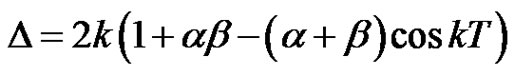 then for
then for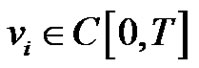 , the periodic boundary value problems problem
, the periodic boundary value problems problem
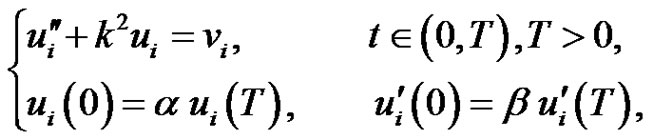 (2.1)
(2.1)
has a unique solution
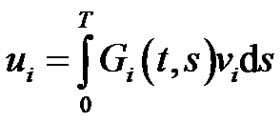 where
where
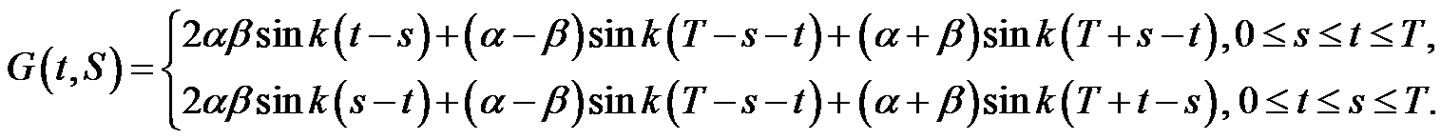
(2.1*)
where .
.
Proof. Consider the scalar periodic boundary value problems of (2.1) and let  and
and 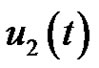 be linearly distinct solutions of the scalar equation of (2.1) and consider the function
be linearly distinct solutions of the scalar equation of (2.1) and consider the function
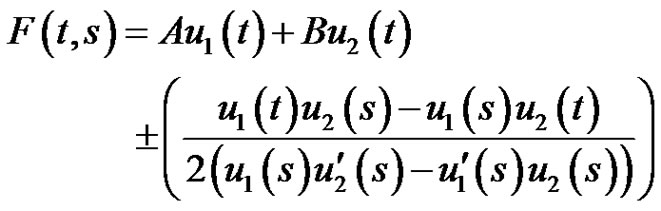
where the positive sign is taken when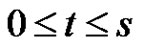 , and the negative sign when
, and the negative sign when 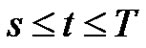 we can obtain this result by routine substitutions of scalar boundary conditions, we do not state it here.
we can obtain this result by routine substitutions of scalar boundary conditions, we do not state it here. 
Lemma 2.2. Let conditions 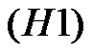 hold, then
hold, then ,
, 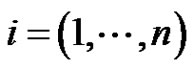 , is continuous and positive on
, is continuous and positive on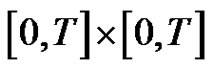 , and we can find it’s positive minimum value
, and we can find it’s positive minimum value 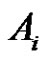 and maximum value
and maximum value 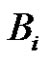 of
of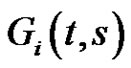 ,
, 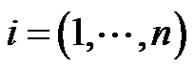 by
by
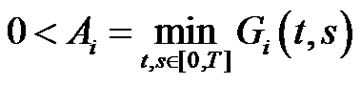 ,
,  and
and
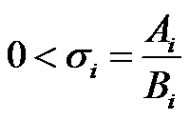 ,
,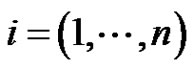 .
.
Proof. It is easy to check that , is continuous and positive on
, is continuous and positive on ,
, .
.
It is clear that the problem (1.1) has a solution 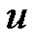 if and only if
if and only if 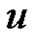 solves the operator equation
solves the operator equation
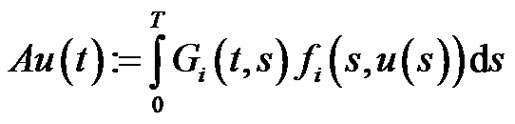 (I)
(I)
It is easy to verify that the operator 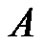 is completely continuous.
is completely continuous.
We define 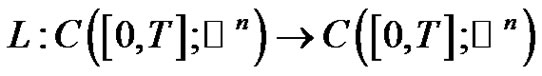 corresponding to linear equation of (1.1) by
corresponding to linear equation of (1.1) by
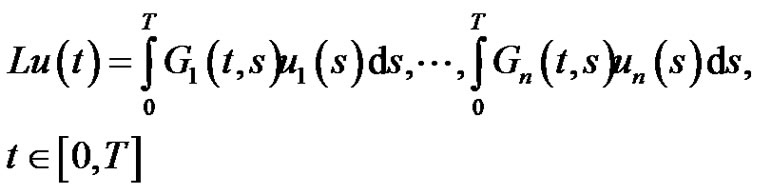 (2.2)
(2.2)
where 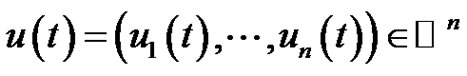 and
and  is Green’s function define in (2.1*), and define
is Green’s function define in (2.1*), and define
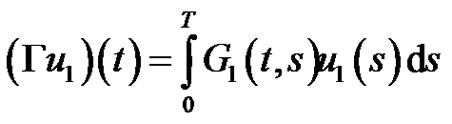
and
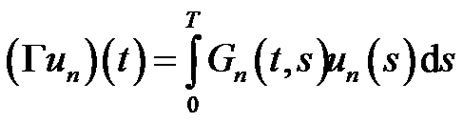 where
where 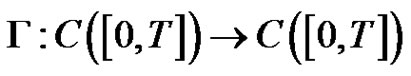 is completely continuous.
is completely continuous.
Remark 2.1. Equations (2.2) appeared in [26].
It is known that , is a bounded and surjective linear operator and has a unique extension, denoted by
, is a bounded and surjective linear operator and has a unique extension, denoted by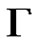 , to
, to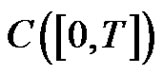 . We write
. We write
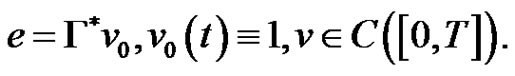 (2.3)
(2.3)
It is known that 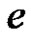 is an interior point of the positive cone
is an interior point of the positive cone 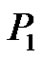 in
in , where
, where
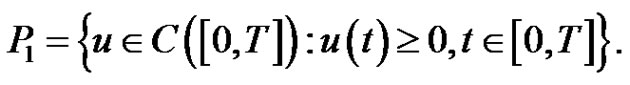 (2.4)
(2.4)
Lemma 2.3. [24] 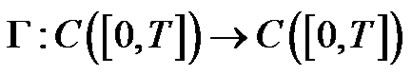 is a compact linear operator such that
is a compact linear operator such that 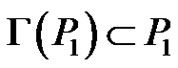 and for each
and for each 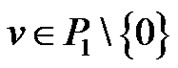 there exists
there exists 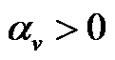 such that
such that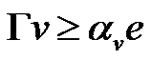 .
.
By Lemma 2.3 and the well-known Krein-Rutman theorem (see [23, Theorem 3.1] or [27], it is easy to see that 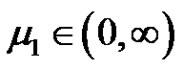 and there exists
and there exists 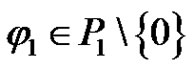 such that
such that
 (2.5)
(2.5)
where 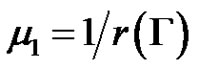 and
and 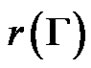 is the spectral radius of
is the spectral radius of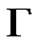 .
.
We use the following maximum norm in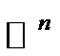 :
:
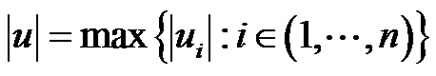 (2.6)
(2.6)
where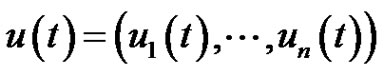 . We denote by
. We denote by
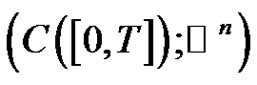 the Banach space of continuous functions from
the Banach space of continuous functions from 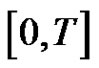 into
into 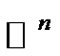 with norm
with norm
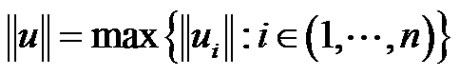 where
where 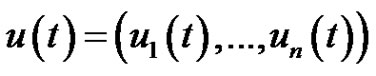 for
for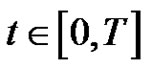 .
.
We use the standard positive cone in 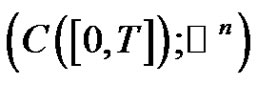 defined by
defined by
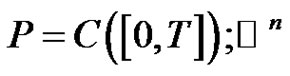 (2.7)
(2.7)
We can write 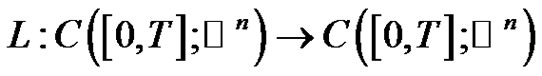 defined in (2.2) as operator equations
defined in (2.2) as operator equations
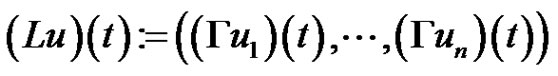 (2.8)
(2.8)
where 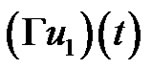 and
and 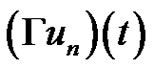 are define above and define a Nemytskii operator
are define above and define a Nemytskii operator
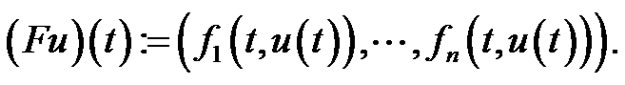 (2.9)
(2.9)
It is easy to verify that (1.1) is equivalent to the following fixed point equation:
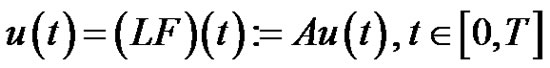 (2.10)
(2.10)
Note that (2.10) same as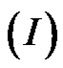 .
.
Recall that a solution  of (1.1) is said to be a nonzero positive solution if
of (1.1) is said to be a nonzero positive solution if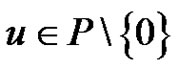 ; that is,
; that is, 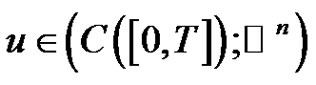 and
and 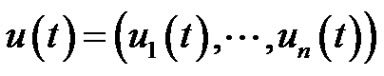 satisfies
satisfies 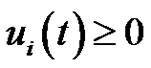 for
for 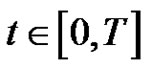 and
and 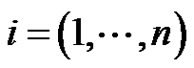 and there exists such that
and there exists such that 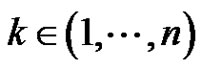
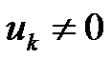 on
on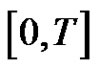 .
.
Let 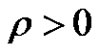 and let
and let
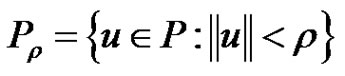 ,
, 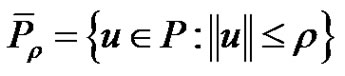
and
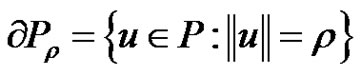 .
.
We need some results from the theory of the fixed point index for compact maps defined on cones in a Banach space  (see [23]).
(see [23]).
Lemma 2.4. Assume that 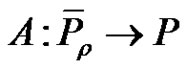 is a compact map. Then the following results hold:
is a compact map. Then the following results hold:
1) If there exists 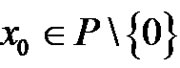 such that
such that 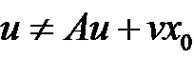 for
for 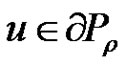 and
and , then
, then 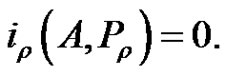
2) If 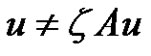 for
for  and
and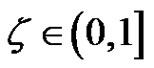 , then
, then 
3) If 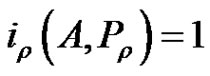 and
and  for some
for some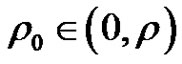 , then
, then 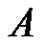 has a fixed point in
has a fixed point in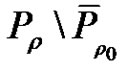 .
.
Now, we are in a position to give our main result and proof analogous results were established in [24].
Theorem 2.1. Assume that 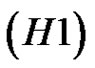 -
-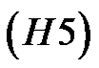 holds.
holds. 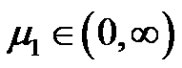 be the same as in (2.5). Assume that the following conditions hold:
be the same as in (2.5). Assume that the following conditions hold:
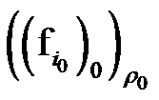 . There exist
. There exist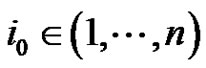 ,
, 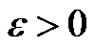 and
and 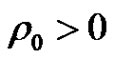 such that
such that 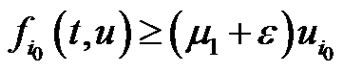 for
for 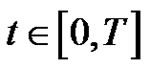 and all
and all 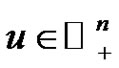 with
with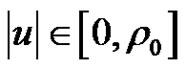 .
.
 . There exist
. There exist 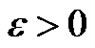 and
and 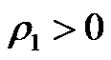 such that for
such that for ,
,  for
for 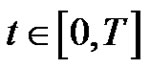 and all
and all 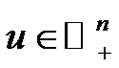 with
with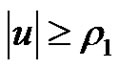 . Then (1.1) has a nonzero positive solution in
. Then (1.1) has a nonzero positive solution in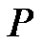 .
.
Proof. By Lemma 2.1, Lemma 2.2 and Lemma 2.3, 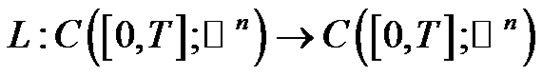 is compact and satisfies
is compact and satisfies .
.
This, together with the continuity of  in
in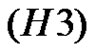 , implies that
, implies that 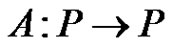 is compact. Without loss of generalization, we assume that
is compact. Without loss of generalization, we assume that 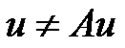 for
for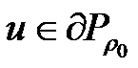 . Let
. Let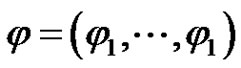 , where
, where 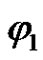 is the same as in (2.5). We prove that
is the same as in (2.5). We prove that
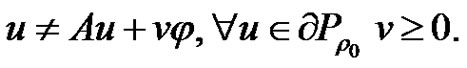 (2.11)
(2.11)
In fact, if not, there exist  and
and 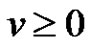 such that
such that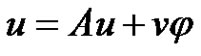 . Then
. Then
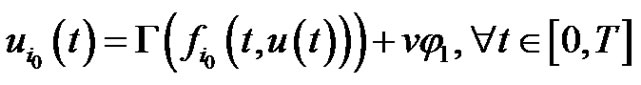 (2.12)
(2.12)
It follows that 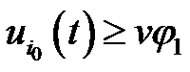 for
for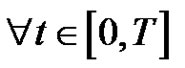 . Let
. Let
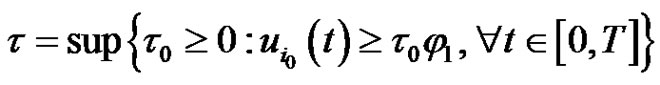 .
.
Then 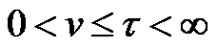 and
and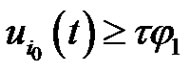 ,
,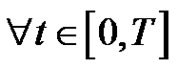 . This, together with (2.12),
. This, together with (2.12), 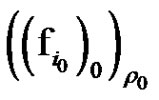 and (2.5), implies that for all
and (2.5), implies that for all 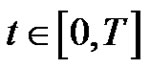
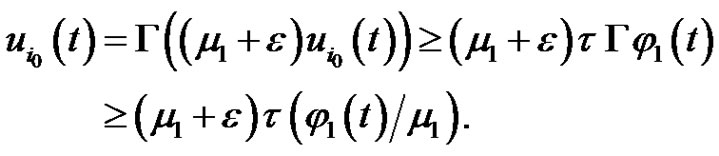
Hence, we have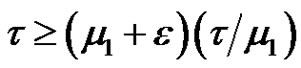 , a contradiction. It follows from (2.11) and Lemma 2.4 (1)
, a contradiction. It follows from (2.11) and Lemma 2.4 (1) 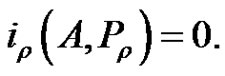
For each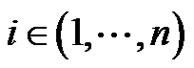 , by the continuity of
, by the continuity of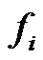 , there exists
, there exists 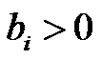 such that
such that 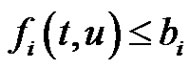 for
for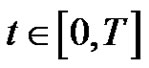 ,
, 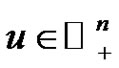 with
with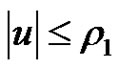 .
.
This, together with 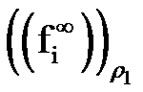 implies that, for each
implies that, for each 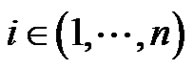
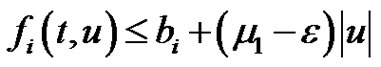 for
for 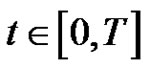 and all
and all
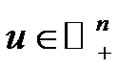 (2.13)
(2.13)
Since
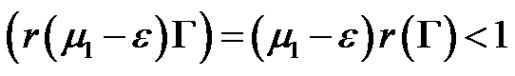 ,
,
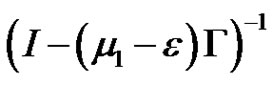 exists and is bounded and satisfies
exists and is bounded and satisfies
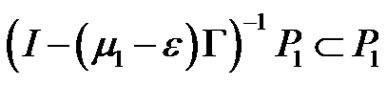 .
.
Let  for
for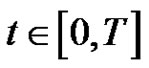 ,
,
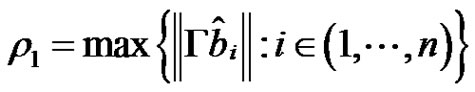
and
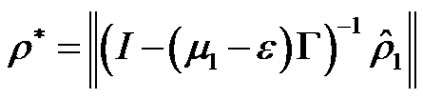 where
where 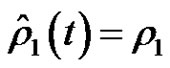 for
for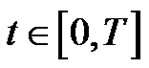 . Let
. Let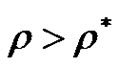 . We prove
. We prove
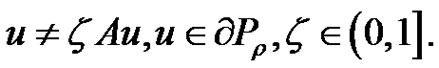
Indeed, if not, there exist 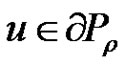 and
and 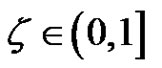 such that
such that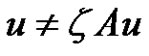 . By (2.13), we have for each
. By (2.13), we have for each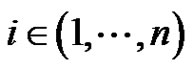 ,
,
 for
for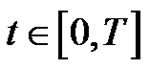 where
where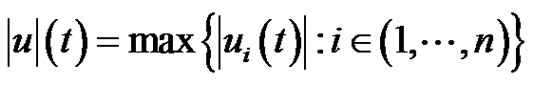 . Taking the maximum in the above inequality implies that
. Taking the maximum in the above inequality implies that
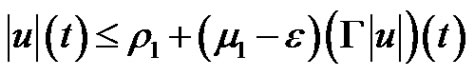
for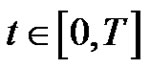 , and
, and
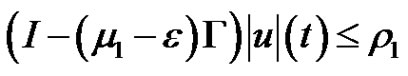
for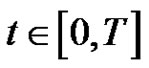 .
.
Since
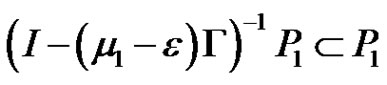 ,
,
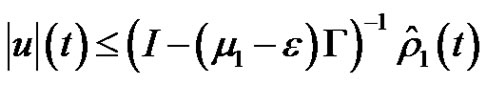
for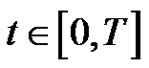 .
.
Hence, we have
 .
.
a contradiction. By (2.14) and Lemma 2.3 (2), 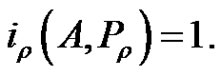 By Lemma 2.4 (3), (1.1) has a solution in
By Lemma 2.4 (3), (1.1) has a solution in .
.
3. Application
Let the systems
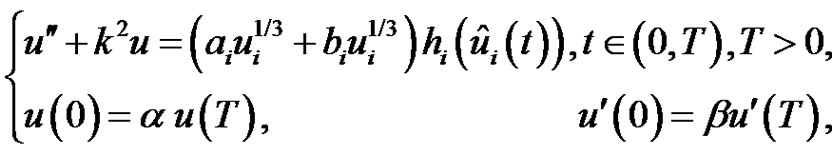 (3.1)
(3.1)
where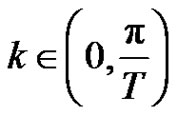 ,
, 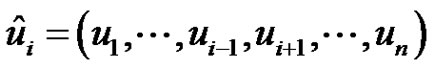 and
and
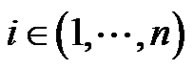 . Assume that the following conditions hold:
. Assume that the following conditions hold:
1) For each ,
, 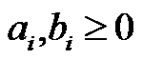 and
and 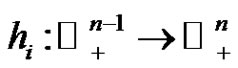 is continuous and let
is continuous and let
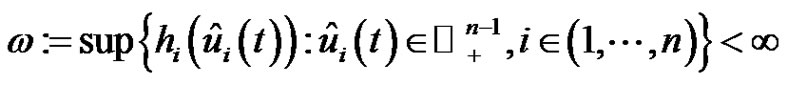 .
.
2) There exists 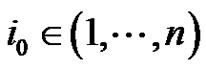 such that
such that 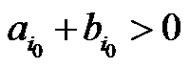 and
and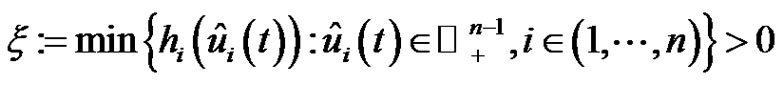 .
.
Then equation (3.1) have a nonzero positive solution in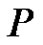 .
.
Proof. For each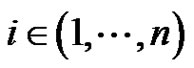 , we define a function
, we define a function 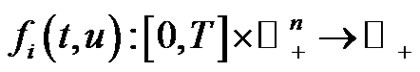 by
by
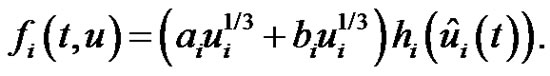
Let  and
and
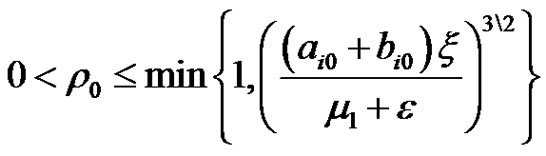 .
.
Then for  and
and  with
with 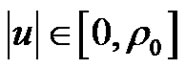 and
and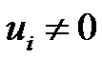 ,
,
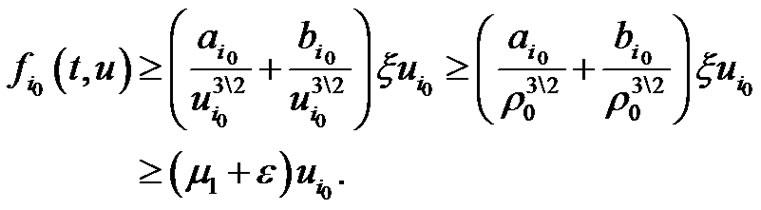
Hence, 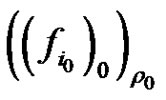 holds. Let
holds. Let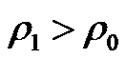 ,
,
 .
.
Then for 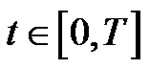 and
and 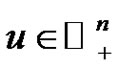 with
with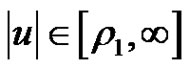 ,
,
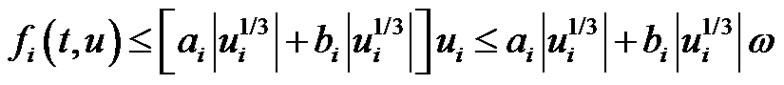
for 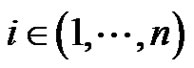 it follows that
it follows that  holds. The result follows from Theorem 2.1.
holds. The result follows from Theorem 2.1. 
REFERENCES
- L. H. Erbe and P. K. Palamides, “Boundary Value Problems for Second-Order Differential Systems,” Journal of Mathematical Analysis and Applications, Vol. 127, No. 1, 1987, pp. 80-92. doi:10.1016/0022-247X(87)90141-7
- J. W. Bebernes and K. Schmitt, “Periodic Boundary Value Problems for Systems of Second Order Differential Equations,” Journal of Differential Equations, Vol. 13, No. 1, 1973, pp. 32-47. doi:10.1016/0022-0396(73)90030-2
- L. H. Erbe and K. Schmitt, “Boundary Value Problems for Second-Order Differential Systems,” In: V. Lakshmikantham, Ed., Nonlinear Analysis and Applications, New York and Basel, 1987, pp. 179-183.
- H. Wang, “Periodic Solutions to Non-Autonomous Second-Order Systems,” Nonlinear Analysis, Vol. 71, No. 3-4, 2009, pp. 1271-1275. doi:10.1016/j.na.2008.11.079
- D. Franco and J. R. L. Webb, “Collisionless Orbits of Singular and Nonsingular Dynamical Systems,” Discrete and Continuous Dynamical Systems, Vol. 15, No. 3, 2006, pp. 747-757. doi:10.3934/dcds.2006.15.747
- R. P. Agarwal, D. O’Regan and P. J. Y. Wong, “Constant-Sign Solutions of a System of Fredholm Integral Equations,” Acta Applicandae Mathematicae, Vol. 80, No. 1, 2004, pp. 57-94. doi:10.1023/B:ACAP.0000013257.42126.ca
- D. ORegan and H. Wang, “Positive Periodic Solutions of Systems of Second Order Ordinary Differential Equations,” Positivity, Vol. 10, No. 2, 2006, pp. 285-298. doi:10.1007/s11117-005-0021-2
- X. Lin, D. Jiang, D. ORegan and R. Agarwal, “Twin Positive Periodic Solutions of Second Order Singular Differential Systems,” Topological Methods in Nonlinear Analysis, Vol. 25, 2005, pp. 263-273.
- L. H. Erbe and K. Schmitt, “On Solvability of Boundary Value Problems for Systems of Differential Equations,” Journal of Applied Mathematics and Physics, Vol. 38, 1987.
- H. Wang, “Positive Periodic Solutions of Singular Systems with a Parameter,” Journal of Differential Equations, Vol. 249, No. 12, 2010, pp. 2986-3002. doi:10.1016/j.jde.2010.08.027
- X. Li and Z. Zhang, “On the Existence of Positive Periodic Solutions of Systems of Second Order Differential Equations,” Mathematische Nachrichten, Vol. 284, No. 11-12, 2011, pp. 1472-1482. doi:10.1002/mana.200710145
- Z. Cao and D. Jiang, “Periodic Solutions of Second Order Singular Coupled Systems,” Nonlinear Analysis, Vol. 71, No. 9, 2009, pp. 3661-3667. doi:10.1016/j.na.2009.02.053
- J. R. Graef, L. Kong and H. Wang, “A Periodic Boundary Value Problem with Vanishing Greens Function,” Applied Mathematics Letters, Vol. 21, No. 2, 2008, pp. 176- 180. doi:10.1016/j.aml.2007.02.019
- I. Rachunkova, M. Tvrdy and I. Vrkoc, “Existence of Nonnegative and Nonpositive Solutions for Second Order Periodic Boundary Value Problems,” Journal of Differential Equations, Vol. 176, No. 2, 2001, pp. 445-469. doi:10.1006/jdeq.2000.3995
- P. Torres, “Existence of One-Signed Periodic Solutions of Some Second-Order Differential Equations via a Krasnoselskii’s Fixed Point Theorem,” Journal of Differential Equations, Vol. 190, No. 2, 2003, pp. 643-662. doi:10.1016/S0022-0396(02)00152-3
- F. Li and Z. Liang, “Existence of Positive Periodic Solutions to Nonlinear Second Order Differential Equations,” Applied Mathematics Letters, Vol. 18, No. 11, 2005, pp. 1256-1264. doi:10.1016/j.aml.2005.02.014
- D. Jiang, J. Chu, D. ORegan, R. Agarwal, “Multiple Positive Solutions to Superlinear Periodic Boundary Value Problem, with Repulsive Singular Forces,” Journal of Mathematical Analysis and Applications, Vol. 286, No. 2, 2003, pp. 563-576. doi:10.1016/S0022-247X(03)00493-1
- X. Li and Z. Zhang, “Periodic Solutions for Second-Order Differential Equations with a Singular Nonlinearity,” Nonlinear Analysis, Vol. 69, No. 11, 2008, pp. 3866-3876. doi:10.1016/j.na.2007.10.023
- D. Jiang, J. Chu and M. Zhang, “Multiplicity of Positive Periodic Solutions to Superlinear Repulsive Singular Equations,” Journal of Differential Equations, Vol. 211, No. 2, 2005, pp. 282-302. doi:10.1016/j.jde.2004.10.031
- P. J. Torres and M. Zhang, “A Monotone Iterative Scheme for a Nonlinear Second Order Equation Based on a Geeralized Anti-Maximum Principle,” Mathematische Nachrichten, Vol. 251, No. 1, 2003, pp. 101-107. doi:10.1002/mana.200310033
- R. Ma, “Nonlinear Periodic Boundary Value Problems with Sign-Changing Green’s Function,” Nonlinear Analysis, Vol. 74, No. 5, 2011, pp. 1714-1720. doi:10.1016/j.na.2010.10.043
- B. Liu, L. Liu and Y. Wu, “Existence of Nontrivial Periodic Solutions for a Nonlinear Second Order Periodic Boundary Value Problem,” Nonlinear Analysis, Vol. 72, No. 7-8, 2010, pp. 3337-3345. doi:10.1016/j.na.2009.12.014
- H. Amann, “Fixed Point Equations and Nonlinear Eigenvalue Problems in Ordered Banach Spaces,” SIAM Review, Vol. 18, No. 4, 1976, pp. 620-709.
- K. Q. Lan, “Nonzero Positive Solutions of Systems of Elliptic Boundary Value Problems,” AMS, Vol. 139, No. 12, 2011, pp. 4343-4349. doi:10.1090/S0002-9939-2011-10840-2
- D. D. Hai and H. Wang, “Nontrivial Solutions for p-Laplacian Systems,” Journal of Mathematical Analysis and Applications, Vol. 330, No. 1, 2007, pp. 186-194. doi:10.1016/j.jmaa.2006.07.072
- K. Q. Lan and W. Lin, “Multiple Positive Solutions of Systems of Hammerstein Integral Equations with Applications to Fractional Differential Equations,” Journal London Mathematical Society, Vol. 83 No. 2, 2011, pp. 449-469. doi:10.1112/jlms/jdq090
- R. D. Nussbaum, “Eigenvectors of Nonlinear Positive Operators and the Linear Krein-Rutman Theorem, in Fixed Point Theory,” In: E. Fadell and G. Fournier, Eds., Lecture Notes in Math, Vol. 886, Springer, 1981, pp. 309-330.

