Applied Mathematics
Vol.3 No.1(2012), Article ID:16753,4 pages DOI:10.4236/am.2012.31009
Mapping Properties of Generalized Robertson Functions under Certain Integral Operators
Department of Mathematics, Abdul Wali Khan University, Mardan, Pakistan
Email: {*marifmaths, ismail1350}@yahoo.com, wasim474@hotmail.com
Received July 24, 2011; revised November 24, 2011; accepted December 2, 2011
Keywords: p-valent analytic functions; Bounded boundary rotations; bounded radius rotations; Integral operators
ABSTRACT
In the present article, certain classes of generalized p-valent Robertson functions are considered. Mapping properties of these classes are investigated under certain p-valent integral operators introduced by Frasin recently.
1. Introduction
Let 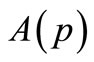 be the class of functions
be the class of functions 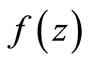 of the form
of the form
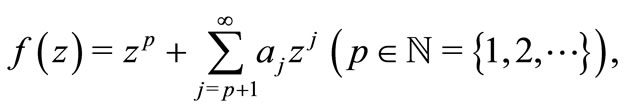
which are analytic in the open unit disc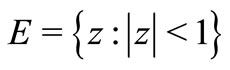 . We write
. We write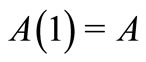 . A function
. A function 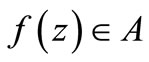 is said to be spiral-like if there exists a real number
is said to be spiral-like if there exists a real number 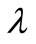
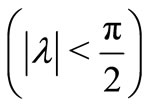
such that
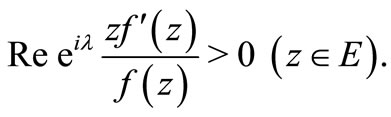
The class of all spiral-like functions was introduced by L. Spacek [1] in 1933 and we denote it by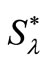 . Later in 1969, Robertson [2] considered the class
. Later in 1969, Robertson [2] considered the class 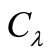 of analytic functions in
of analytic functions in 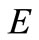 for which
for which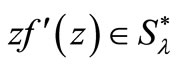 .
.
Let 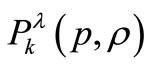 be the class of functions
be the class of functions 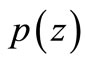 analytic in
analytic in  with
with 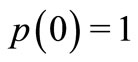 and
and
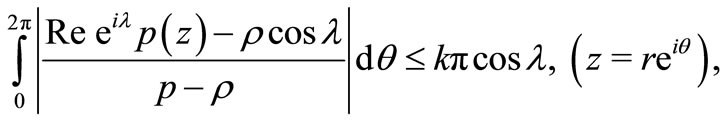
where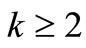 ,
, 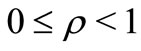 and
and 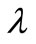 is real with
is real with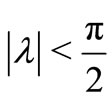 .
.
For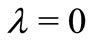 ,
, 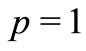 , this class was introduced in [3] and for
, this class was introduced in [3] and for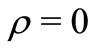 , see [4]. For
, see [4]. For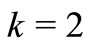 ,
, 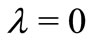 and
and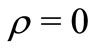 , the class
, the class 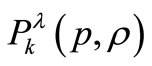 reduces to the class
reduces to the class 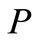 of functions
of functions 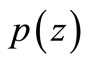 analytic in
analytic in 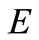 with
with 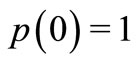 and whose real part is positive.
and whose real part is positive.
We define the following classes
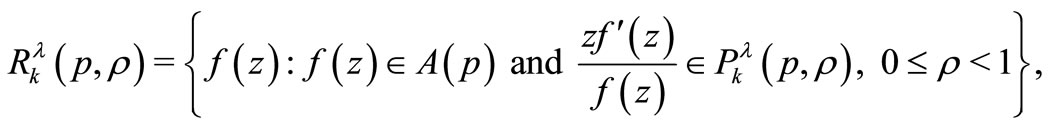
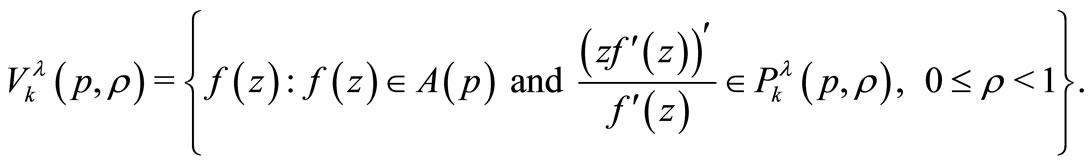
For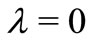 ,
, 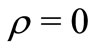 and
and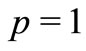 , we obtain the well known classes
, we obtain the well known classes 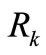 and
and 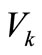 of analytic functions with bounded radius and bounded boundary rotations studied by Tammi [5] and Paatero [6] respectively. For details see [7-12]. Also it can easily be seen that
of analytic functions with bounded radius and bounded boundary rotations studied by Tammi [5] and Paatero [6] respectively. For details see [7-12]. Also it can easily be seen that 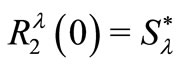 and
and 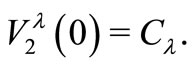
Let us consider the integral operators
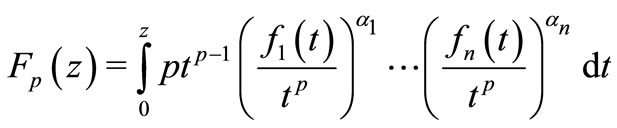 (1.1)
(1.1)
and
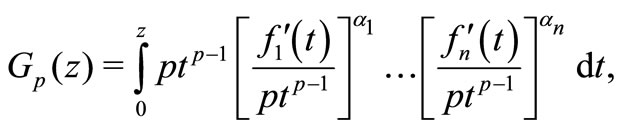 (1.2)
(1.2)
where 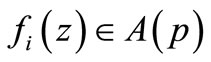 and
and 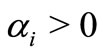 for all
for all 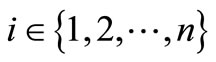 .
.
These operators, given by (1.1) and (1.2), are defined by Frasin [13]. If we take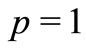 , we obtain the integral operators
, we obtain the integral operators 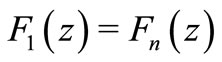 and
and 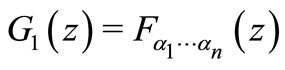 introduced and studied by Breaz and Breaz [14] and Breaz et al. [15], for details see also [16-20]. Also for
introduced and studied by Breaz and Breaz [14] and Breaz et al. [15], for details see also [16-20]. Also for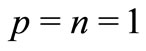 ,
, 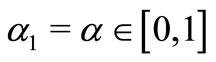 in (1.1), we obtain the integral operator studied in [21] given as
in (1.1), we obtain the integral operator studied in [21] given as
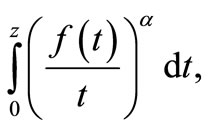
and for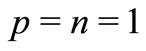 ,
, 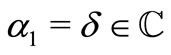 ,
, 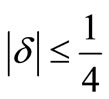 in (1.2), we obtain the integral operator
in (1.2), we obtain the integral operator
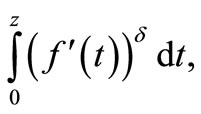
discussed in [22,23].
In this paper, we investigate some propeties of the above integral operators 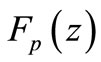 and
and 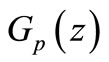 for the classes
for the classes 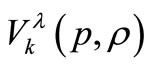 and
and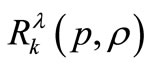 respectively.
respectively.
2. Main Result
Theorem 2.1. Let 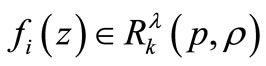 for
for 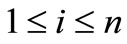 with
with
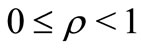 . Also let
. Also let 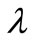 is real with
is real with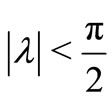 ,
, 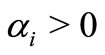 ,
,
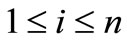 . If
. If
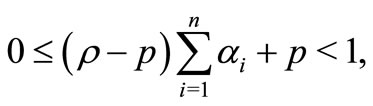
then 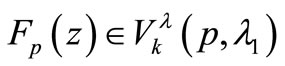 with
with
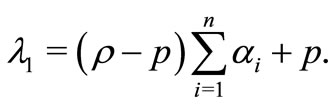 (2.1)
(2.1)
Proof. From (1.1), we have
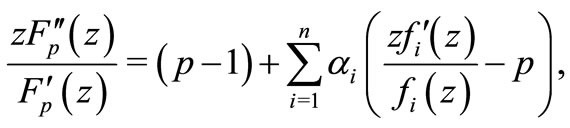 (2.2)
(2.2)
or, equivalently
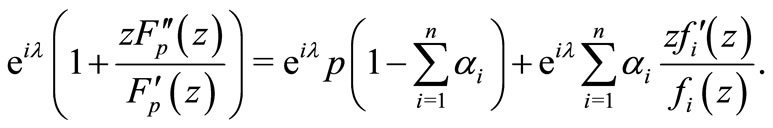 (2.3)
(2.3)
Subtracting and adding 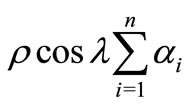 on the right hand side of (2.3), we have
on the right hand side of (2.3), we have
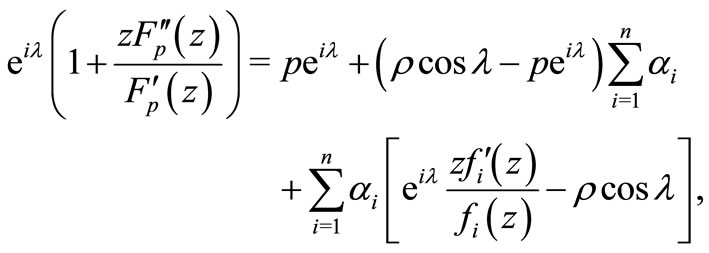 (2.4)
(2.4)
Taking real part of (2.4) and then simple computation gives
 (2.5)
(2.5)
where 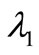 is given by (2.1). Since
is given by (2.1). Since 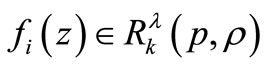 for
for , we have
, we have
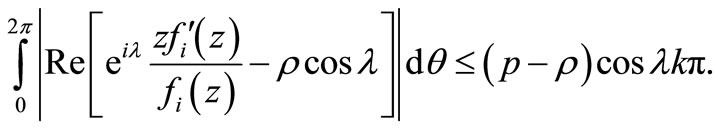 (2.6)
(2.6)
Using (2.6) and (2.1) in (2.5), we obtain
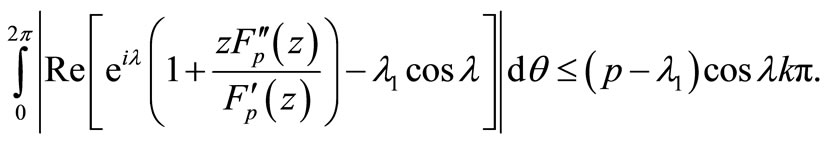
Hence 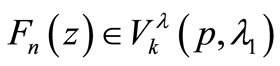 with
with 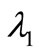 is given by (2.1).
is given by (2.1).
By setting 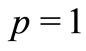 and
and 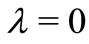 in Theorem 2.1, we obtain the following result proved in [9].
in Theorem 2.1, we obtain the following result proved in [9].
Corollory 2.2. Let 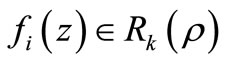 for
for 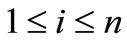 with
with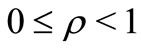 . Also let
. Also let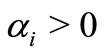 ,
,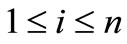 . If
. If
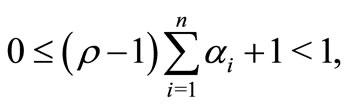
then 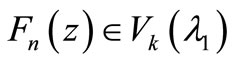 and
and 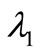 is given by (2.1).
is given by (2.1).
Now if we take 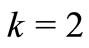 and
and 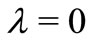 in Theorem 2.1, we obtain the following result.
in Theorem 2.1, we obtain the following result.
Corollory 2.3. Let 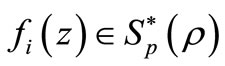 for
for 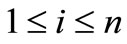 with
with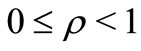 . Also let
. Also let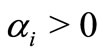 ,
,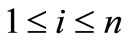 . If
. If
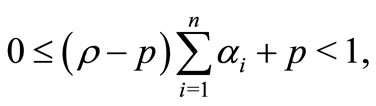
then 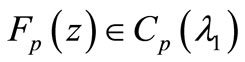 and
and 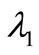 is given by (2.1).
is given by (2.1).
Letting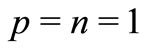 ,
, 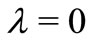 ,
, 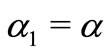 and
and 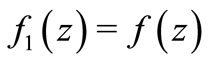 in Theorem 2.1, we have.
in Theorem 2.1, we have.
Corollory 2.4. Let 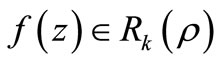 with
with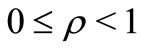 . Also let
. Also let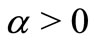 . If
. If
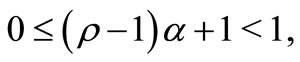
then
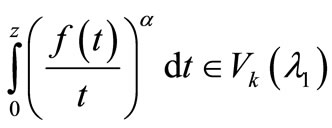
with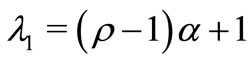 .
.
Theorem 2.5. Let 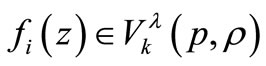 for
for 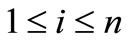
with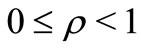 . Also let
. Also let 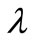 is real is real with
is real is real with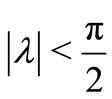 ,
,
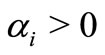 ,
,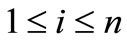 . If
. If
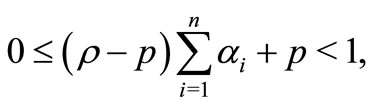
then 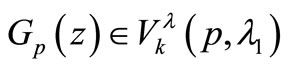 and
and 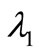 is given by (2.1).
is given by (2.1).
Proof. From (1.2), we have
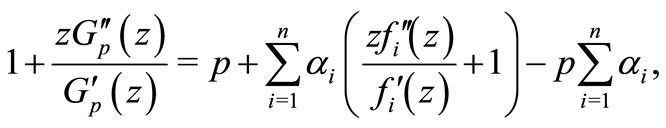
or, equivalently
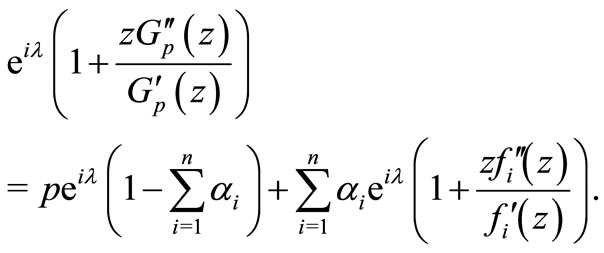
This relation is equivalent to
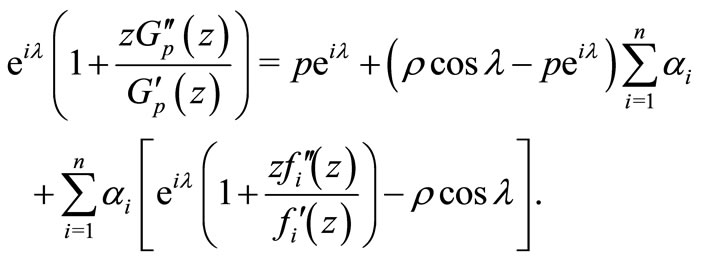 (2.7)
(2.7)
Taking real part of (2.7) and then simple computation gives us
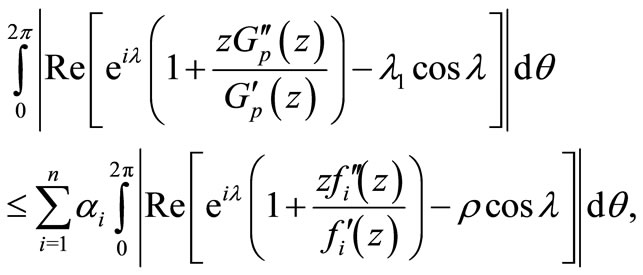 (2.8)
(2.8)
where 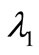 is given by (2.1). Since
is given by (2.1). Since 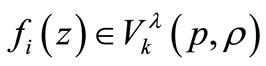 for
for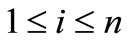 , we have
, we have
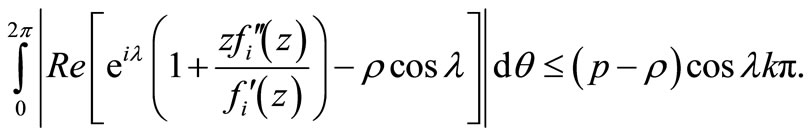 (2.9)
(2.9)
Using (2.9) in (2.8), we obtain
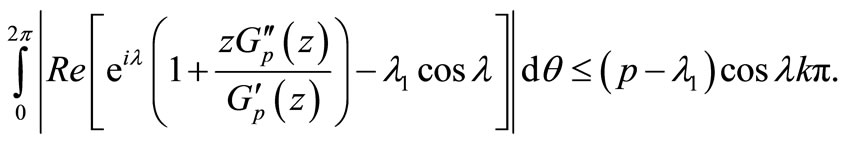
Hence 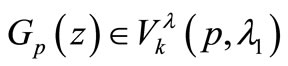 with
with 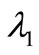 is given by (2.1).
is given by (2.1).
By setting 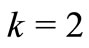 and
and 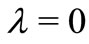 in Theorem 2.5, we obtain the following result.
in Theorem 2.5, we obtain the following result.
Corollory 2.6. Let 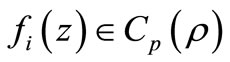 for
for 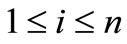 with
with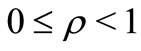 . Also let
. Also let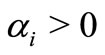 ,
,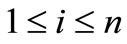 . If
. If
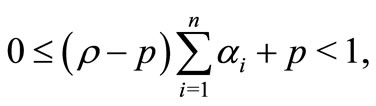
then 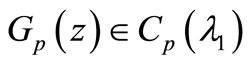 with
with 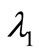 is given by (2.1).
is given by (2.1).
Letting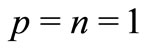 ,
, 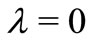 ,
, 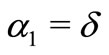 and
and 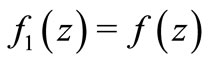 in Theorem 2.5, we have.
in Theorem 2.5, we have.
Corollory 2.7. Let 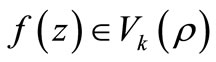 with
with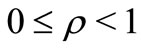 . Also let
. Also let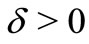 . If
. If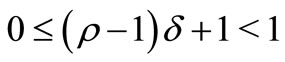 , then
, then
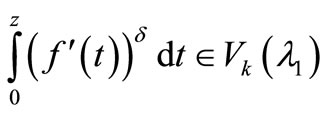
with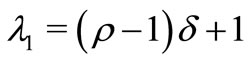 .
.
REFERENCES
- L. Spacek, “Prispěvek k teorii funkei prostych,” Časopis pro pěstováni matematiky a fysiky, Vol. 62, No. 2, 1933, pp. 12-19.
- M. S. Robertson, “Univalent functions f(z) for wich zf'(z) is spiral-like,” Michigan Mathematical Journal, Vol. 16, No. 2, 1969, pp. 97-101.
- K. S. Padmanabhan and R. Parvatham, “Properties of a class of functions with bounded boundary rotation,” Annales Polonici Mathematici, Vol. 31, No. 1, 1975, pp. 311-323.
- B. Pinchuk, “Functions with bounded boundary rotation,” Israel Journal of Mathematics, Vol. 10, No. 1, 1971, pp. 7-16. doi:10.1007/BF02771515
- O. Tammi, “On the maximization of the coefficients of Schlicht and related functions,” Annales Academiae Scientiarum Fennicae. Series A I. Mathematica, Vol. 114, No. 1, 1952, p. 51
- V. Paatero, “Uber Gebiete von beschrankter Randdrehung,” Annales Academiae Scientiarum Fennnicae, Vol. 37-39, No. 9, 1933.
- M. Arif, M. Ayaz and S. I. Ali Shah, “Radii problems for certain classes of analytic functions with fixed second coefficients,” World Applied Sciences Journal, Vol. 13, No. 10, 2011, pp. 2240-2243.
- K. I. Noor, “On some subclasses of fuctions with bounded boundary and bounded radius rotation,” Pan American Mathematical Journal, Vol. 6, No. 1, 1996, pp. 75-81.
- K. I. Noor, M. Arif and W. Haq, “Some properties of certain integral opertors,” Acta Universitatis Apulensis, Vol. 21, 2010, pp. 89-95.
- K. I. Noor, M. Arif and A. Muhammad, “Mapping properties of some classes of analytic functions under an integral operator,” Journal of Mathematical Inequalities, Vol. 4, No. 4, 2010, pp. 593-600.
- K. I. Noor, W. Haq, M. Arif and S. Mustafa, “On bounded boundary and bounded radius rotations,” Journal of Inequalities and Applications, 2009, Article ID: 813687.
- K. I. Noor, S. N. Malik, M. Arif and M. Raza, “On bounded boundary and bounded radius rotation related with Janowski function,” World Applied Sciences Journal, Vol. 12, No. 6, 2011, pp. 895-902.
- B. A. Frasin, “New general integral operators of p-valent functions,” Journal of Inequatilies Pure and Applied Mathematics, Vol. 10, No. 4, 2009
- D. Breaz and N. Breaz, “Two Integral Operators,” Studia Universitatis Babes-Bolyai, Mathematica, Clunj-Napoca, Vol. 47, No. 3, 2002, pp. 13-21.
- D. Breaz, S. Owa and N. Breaz, “A New Integral Univalent Operator,” Acta Universitatis Apulensis, Vol. 16, 2008, pp. 11-16.
- N. Breaz, V. Pescar and D. Breaz, “Univalence criteria for a new integral operator,” Mathematical and Computer Modelling, Vol. 52, No. 1-2, 2010, pp. 241-246. doi:10.1016/j.mcm.2010.02.013
- B. A. Frasin, “Convexity of integral operators of p-valent functions,” Mathematical and Computer Modelling, Vol. 51, No. 5-6, 2010, pp. 601-605.
- B. A. Frasin, “Some sufficient conditions for certain integral operators,” Journal of Mathematics and Inequalities, Vol. 2. No. 4, 2008, pp. 527-535.
- G. Saltik, E. Deniz and E. Kadioglu, “Two new general p-valent integral operators,” Mathematical and Computer Modelling, Vol. 52, No. 9-10, 2010, pp. 1605-1609. doi:10.1016/j.mcm.2010.06.025
- R. M. Ali and V. Ravichandran, “Integral operators on Ma-Minda type starlike and convex functions,” Mathematical and Computer Modelling, Vo. 53, No. 5-6, 2011, pp. 581-586. doi:10.1016/j.mcm.2010.09.007
- S. S. Miller, P. T. Mocanu and M. O. Reade, “Starlike integral operators,” Pacific Journal of Mathematics, Vol. 79, No. 1, 1978, pp.157-168.
- Y. J. Kim and E. P. Merkes, “On an integral of powers of a spirallike function,” Kyungpook Mathematical Journal, Vol. 12, No. 2, 1972, pp. 249-252.
- N. N. Pascu and V. Pescar, “On the integral operators of Kim-Merkes and Pfaltzgraff,” Mathematica, Universitatis Babes-Bolyai Cluj-Napoca, Vol. 32, No. 2, 1990, pp. 185- 192.
NOTES
*Corresponding author.

