Creative Education
Vol.5 No.4(2014), Article ID:43700,14 pages DOI:10.4236/ce.2014.54032
The Extent of Mathematical Creativity and Aesthetics in Solving Problems among Students Attending the Mathematically Talented Youth Program
Einav Aizikovitsh-Udi
School of Education, Beit-Berl College, Kfar Saba, Israel
Email: einav_aizikovitsh@mail.harvard.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 7 January 2014; revised 7 February 2014; accepted 14 February 2014
ABSTRACT
This study investigates the extent of mathematical creativity among 57 eight-grade talented students in the Mathematically Talented Youth Program. We examine the reasoning these students applied in solving a problem; the degree of mathematical creativity and aesthetic in their approach in solving a non-routine mathematical problem; and explore whether the students’ mathematical thinking is dependent solely upon previous mathematical knowledge and skills. We found that majority of the students relied on technical algorithm to solve the problem. Although talented students coped well with the thinking challenge, most of them operated at the basic level of creativity. One implication drawn from this study is the need to broaden and develop mathematical-logical thinking both as specific lessons and also as an integral part of other lessons in the program.
Keywords:Mathematically Talented Students; Mathematical Reasoning; Mathematical Creativity; Mathematical Aesthetics; Non-Routine Problem Solving

1. Introduction
Problem solving has increasingly become the focus of school mathematics. In the United States, the Principles and Standards of School Mathematics (NCTM, 2000) suggests that students need to be provided with challenging problems that can stimulate their development of creative mathematical thinking. Problem solving is closely associated with the development of mathematical creativity in school mathematics (Silver, 1997). Thus, it can be argued that problem solving plays an essential role in the development of mathematically talented students. Developing mathematical creativity and aesthetics in the context of problem solving is considered to be the central aim in education for the gifted and talented (Mann, 2006). Therefore, understanding the extent to which students’ mathematical reasoning, creativity, and aesthetics develop in problem solving situations is important for educators to support these students to fully cultivate their talents. The purpose of this study is to examine the degree of mathematical creativity and aesthetics among talented students in a problem-solving situation. Specifically, this study explores whether distinct levels of creativity is found among these students, and if so whether such level stems from the “mental flexibility” and high level of intelligence of the students, or rather from previous mathematical knowledge on various subjects and from acquiring various skills.
Past studies have looked at mathematical creativity as a single construct. This study adds another dimension to this line of research by examining mathematical aesthetic in students’ problem solving solutions. The aim of this study is to examine the extent of mathematical creativity and aesthetics in solving non-routine problems at a reasonable level, among students in the Mathematically Talented Youth Program. The study was conducted to answer following research questions:
1) What kinds of reasoning did the talented students use in solving a non-routine problem?
2) What was the degree of creativity and aesthetics in problem solving among students who attended the Mathematically Talented Youth Program?
3) According to the degree of creativity, can we conclude that mathematical thinking among the students of the Mathematically Talented Youth Program is dependent solely upon previous mathematical knowledge and skills?
2. Literature Review
2.1. Non-Routine Problem-Solving
A problem is defined as a relatively new and complex situation, in which the problem solver must invent the algorithm for the solution. Here, unlike in the repetitive exercises or algorithm-based problems, there is no given path for the solution (Lester, 1980). A non-routine problem presents the learner with a novel, unknown situation, and stimulates his or her imagination and senses, and offers a challenge—motivating the desire to succeed. Solving non-routine problems should be the heart of teaching and learning mathematics. Solutions to non-routine problems can be reached in various ways. According to Silver (1997) and Ervynck (1991), solving problems in various ways is a tool for both evaluating and developing mathematical creativity and aesthetics.
2.2. Mathematical Creativity
In general, creativity is defined as “the cognitive skill of proposing a solution to a problem or making something useful or novel from ordinary” (Hwang, Chen, Dung, & Yang, 2007: p. 193). Mathematical creativity in school mathematics is usually connected with problem solving or problem posing (e.g., Silver, 1997). Ervynck (1991) posits that mathematical creativity in problem solving is the ability to formulate mathematical objectives and find their innate relationships; it is the capacity to solve problems according to the appropriateness of integrating both the nature of logic-deduction in mathematics education and its evolved concepts into its core. According to Silver (1997) and Ervynck (1991), mathematical creativity has two characteristics, general and specific. General original or creative thinking enables the ability for problem-solving or problem-posing in various fields, creating innovative and original solutions of high quality. These ideas or solutions are usually elegant and surprising. Such thinking is characterized by mental flexibility, curiosity, a well-developed imagination, high interestor motivation in finding solutions, the creation of metaphors, and goal-oriented thinking.
Sriraman and Liljedahl (2006) define mathematical creativity in the context of school level as a process that results in original (insightful) solutions to a given problem and/or approaches to an old problem from a new perspective. This contextualization is important to distinguish mathematical creativity in general pertaining to mathematicians. Leikin (2009) refers to this distinction as relative and absolute creativity, in which school-level creativity falls under relative creativity, referring to discoveries by a specific person within a specific reference group. In relation to problem solving, Kwon, Park, and Park (2006) suggest mathematical creativity as the creation of new knowledge and flexible problem-solving abilities, establishing a relationship between mathematical creativity and problem solving. Chamberlain and Moon (2005) suggest that creatively gifted students have an unusual ability to generate novel and useful solutions to simulated or real applied problems, using mathematical modeling. Chiu (2009) further connected mathematical creativity with the students’ ability to solve routine and non-routine problems and even to approach ill-structured problems.
Creativity has been considered to be a critical component of advanced mathematical thinking (Ervynck, 1991). Ervynck (1991) suggested three necessary stages for the development of mathematical creativity: (1) a preliminary technical stage, (2) a stage of algorithmic activity, and (3) a stage of creative (conceptual, constructive) activity. The first stage refers to the practical application of mathematical rules and procedures without knowledge of the theoretical source. The second stage emphasizes the use of procedures in order to perform a mathematical operation with the knowledge of the theoretical source. Finally, the third stage involves activity that is unrelated to a known algorithm, where it entails a new understanding of definitions or wording a new theorem and its proof. Base on these stages, Ervynck (1991) identified three levels of mathematical creativity. The first level (Stage 1) is based on operating an algorithm. For example, an algorithmic solution is used when solving a word problem by constructing an equation or solving a system of equations by linear combination or by substitution. The second level (Stage 2) involves modeling a situation and may include solving a word problem with graph or linear diagram. It departs from the direct operation of the algorithm, and is based on an explanation from within a mathematical model, developing a method from a given situation. The third level (Stage 3) employs sophisticated methods usually based on assumptions embedded in the problem, and makes use of the problem’s internal structure. It leaves the model, and reaches conclusions from outside an existing theory and constructing a solution by analyzing what is stated in the problem.
Silver (1997) suggests developing creativity through problem solving by developing fluency, flexibility, and novelty. Generating multiple ideas, multiple answers to a problem (when such exist), exploring situations, and raising multiple ideas develop fluency. Generating new solutions when at least one has already been produced advances flexibility. Exploring many solutions to a problem and generating a new one advances novelty.
“Both the process and product of (problem solving) can be evaluated in order to determine the extent to which creativity is evident” (Silver, 1997: p. 76).
2.3. Mathematical Aesthetic
Sinclair (2004) identifies three roles of aesthetic in mathematical inquiry: evaluative role, generative role, and motivational role. Evaluative role concerns the “aesthetic nature of the mathematical entities and is involved in judgments about the beauty, elegance, and significance of entities such as proofs and theorems” (Sinclair, 2004: p. 264). Generative role “involves nonpropositional, modes of reasoning used in the process of inquiry, (which is) ... responsible in generating new ideas and insights that could not be derived by logical steps alone” (Sinclair, 2004: p. 264). Motivational role refers to “the aesthetic responses that attract mathematicians to certain problems and even to certain fields of mathematics” (Sinclair, 2004: p. 264). Sinclair (2004) contends that in the education settings, much of the emphasis of aesthetic has been exclusively on the evaluative role.
Sinclair (2004) argues that the emphasis that school mathematics places on propositional, logical reasoning might actually discourage students from recognizing and trusting the generative type of aesthetic responses that operate in inquiry. It is important to draw the inquirer back from the mechanics of the problem (the unknown, the data, and the conditions) to the qualitative relations perceivable by the inquirer.
Dreyfus and Eisenberg (1986) agree with the claim that aesthetics is the motivating force of mathematical creativity, and that the aesthetic criteria that characterize good mathematics are of great importance. Researchers characterize the aesthetic value of a problem by using the path taken from the data to the solution (citation?). Several interconnected attributes must exist along this path in order for a solution to be considered elegant. First, a minimum of preliminary knowledge should be relied upon. Clarity, simplicity, and brevity are all important.
2.4. Studies on Talented Youth in Mathematics and Science
According to Allan (1991), a basic assumption of a talented student is the realization of potential. The learner’s mathematical potential is a complex function of ability, motivation, and learning opportunities. The realization of students’ potential and the nurturing of excellence will allow for the training of a new generation of scientists and creative artists who will contribute to the development of society, sciences, and technology in the modern age. Equal opportunity is a basic condition here, not in the sense of identical learning materials, but rather in the sense of identical opportunities for students to realize their personal potential, discover interests, and find personal motivation. The researchers Shore and Kanevsky (1993) quote studies that state that talented or gifted students have distinctive thinking characteristics. Some of these differentiate the thinking of talented students from that of ordinary students: a wide memory and knowledge base, self-control mechanisms (meta-cognition), quick thinking, problem presentation, and mental flexibility.
2.5. Studies on Non-Routine Problem Solving among Talented and/or Gifted Youth
Various studies (Stepien, 1993; Boyce, 1997) report that problem-based learning is a new approach in the education of talented and gifted students that is becoming popular in the USA. Many studies have demonstrated that the thinking and learning characteristics of gifted students are different from those of other students (Hong & Aqui, 2004). Creative students in mathematics are more cognitively resourceful than their peers who achieved high grades in school mathematics (Hong & Aqui, 2004). In order to fully realize their potential, talented students need opportunities for more rapid and deep learning that focuses on topics connected to their fields of interest. The current trend in education—and not just in gifted education—is to take into account the changing needs of the developing world in which we live. The abilities that students needed in the past-reading, writing, calculating—are not sufficient today. There is a need to emphasize the provision of learning tools and skills that will allow the student to cope with vast quantities of accumulated data; a narrow base of knowledge is no longer sufficient. Here a different sort of learning is required—active learning that allows the student to experience the acquisition of new learning skills, and does not limit him or her to a specific body of knowledge or method. Teaching non-routine problems answers the need for this kind of experience. When people learn something, they give it a certain meaning that is not dictated by a teacher or any other source, but is, rather, personal and distinctive. Active learning allows these meanings to be broadened because it does not even try to force its own meaning on the student. It recognizes that forcing such a meaning would be futile and harmful, and thus leaves students a free operating space for thinking from the stage of preliminary interpretation of the knowledge or the process being learned. Teaching using problem-based learning is appropriate for all age groups, because problems can be composed for all ages, from kindergarten to high school. The literature describes numerous successful attempts made in all of the age groups that space does not permit me to describe here in detail.
3. Research Methods and Content
3.1. Subjects
Subjects of this study consisted of 57 eight-grade students attending the Mathematically Talented Youth Program. They were in the second year of the program. The Mathematically Talented Youth Program is open to students who excel in mathematics and have passed the Bar-Ilan University entrance examination. The curriculum was developed by the Israeli Center for the Advancement of Mathematical Sciences at Bar-Ilan University, with the support of the Ministry of Education. The program’s aim is to have the students take their matriculation examination in mathematics (5-point matriculation—the highest level) in the tenth grade, allowing them to study university level mathematics in the eleventh and twelfth grades. The goals of the program are:
• To provide enrichment math classes for excellent students across the country in order to encourage them to pursue advanced academic studies in all fields and to progress in these studies.
• To nurture talented youth from across the country in the period prior to their academic studies in mathematics while they are still in high school—motivating them to obtain college degrees in the sciences (including medicine, economics, life sciences, etc.)
The curriculum for the eighth, ninth and tenth grades includes mathematical enrichment topics and topics required for academic studies in mathematics and natural sciences, including subjects that are taught at later stages in the regular high school curriculum (the seven questionnaire new 5-point matriculation examination). Students who graduate from the program may finish their mathematics studies in high school and take the matriculation examination at the end of the tenth grade. They continue to study mathematics in the Department of Mathematics at Bar-Ilan University in the eleventh and twelfth grades. Finishing the first year of academic study in math grants the student a significant advantage in other scientific fields in science or fields that require a strong background in mathematics. The first year courses are: infinitesimal mathematics, linear algebra and introduction to set theory.
3.2. Instrument
A questionnaire with one mathematical task was used in this study (Figure 1). The single item tested depth of thinking based on the strategy in which the problem was solved. This question was taken from a set of enrichment examination published by the TechnionIsrael Institute of Technology (2005). There were several reasons for choosing the item. First, minimal preliminary mathematical knowledge was required in order to arrive at the solution. Second, a straightforward (unsophisticated) solution exists. Third, the problem was set in a familiar context involving a daily situation (sharing cake in a family). Finally, missing data (only small and large squares are given) and there were a number of methods to solve the problem.
3.3. Possible Answers/Solutions
3.3.1. Geometrical Method
In Figure 2, the four triangles marked with * (triangles AEK, AGK, DLF, and DLI) are congruent and thus have the same area. Rectangles EBCF and GHJI are congruent because they have the same width (the side of the small square KHJL) and the same length (the side of the big square ABCD). Since both rectangles share the same square KHJI, the remaining pieces of the rectangles should have the same area (i.e., rectangles EBHK and LJCF have the same area as rectangle GKLI). Therefore, the son’s piece (trapezoid AKLD) is the same as the sum of the father’s two pieces (trapezoids ABHK and DLJC).
3.3.2. Algebraic Method
We mark the length of the cake “a” and the side of the black square “b” (Figure 3). Using the area formula of a trapezoid (or a variation of the same formula) , the area of the son’s piece i
, the area of the son’s piece i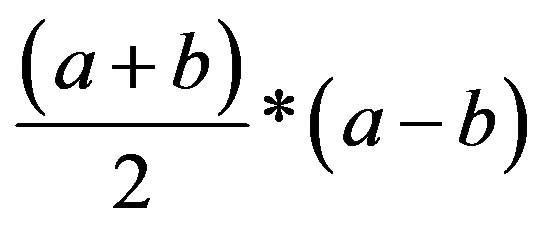 or
or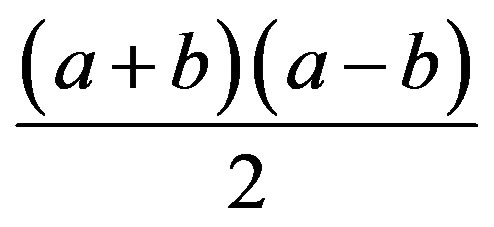 . The area of one of the father’s piece is
. The area of one of the father’s piece is 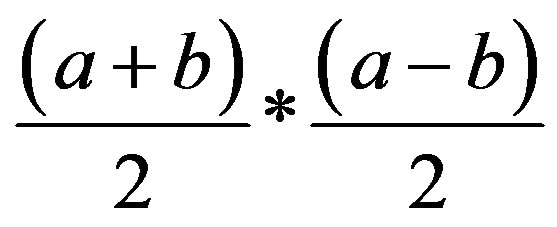 or
or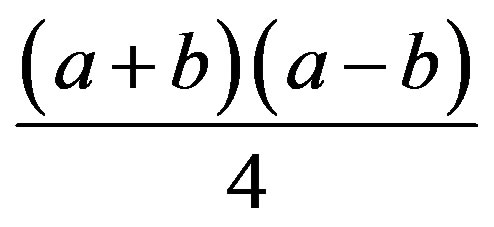 , so two pieces have the area of
, so two pieces have the area of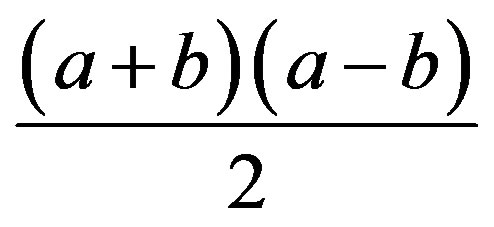 . Therefore, both the father and son’s pieces have the same area.
. Therefore, both the father and son’s pieces have the same area.
3.3.3. Visual Manipulation Method
When we move the small square along the right side of the cake (Figure 4), the area of the large trapezoid does
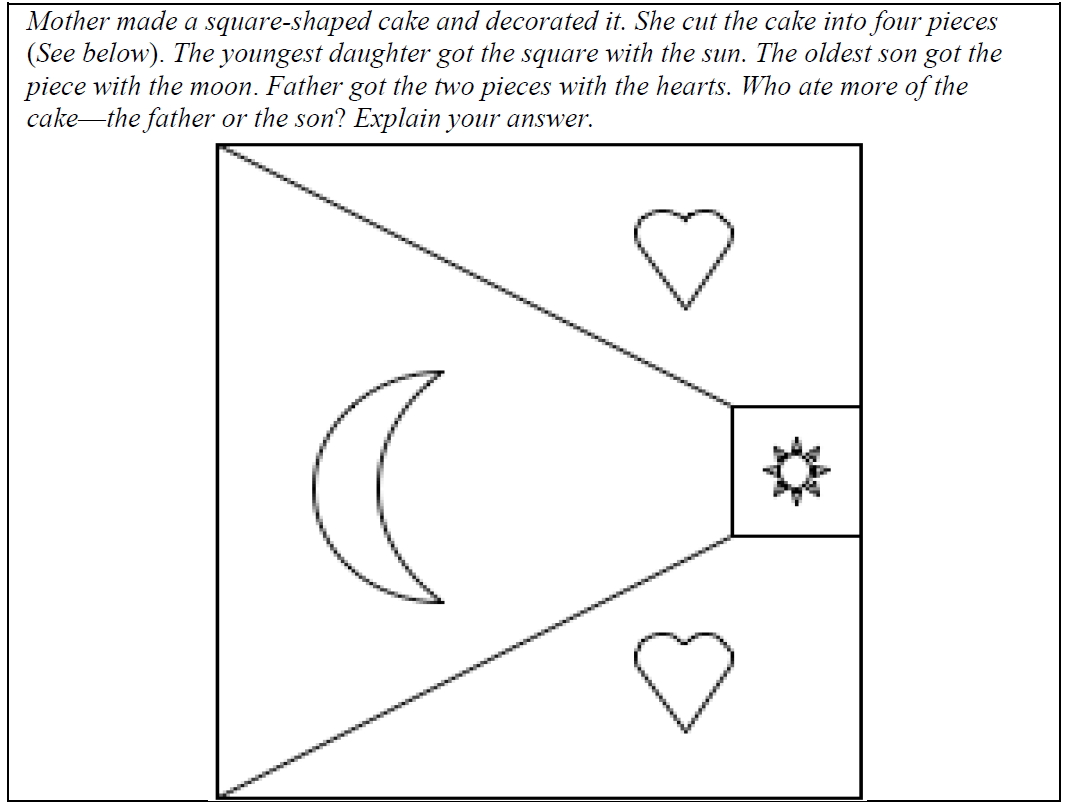
Figure 1. The mathematical task given to the students (The Technion Israel Institute of Technology, 2005).
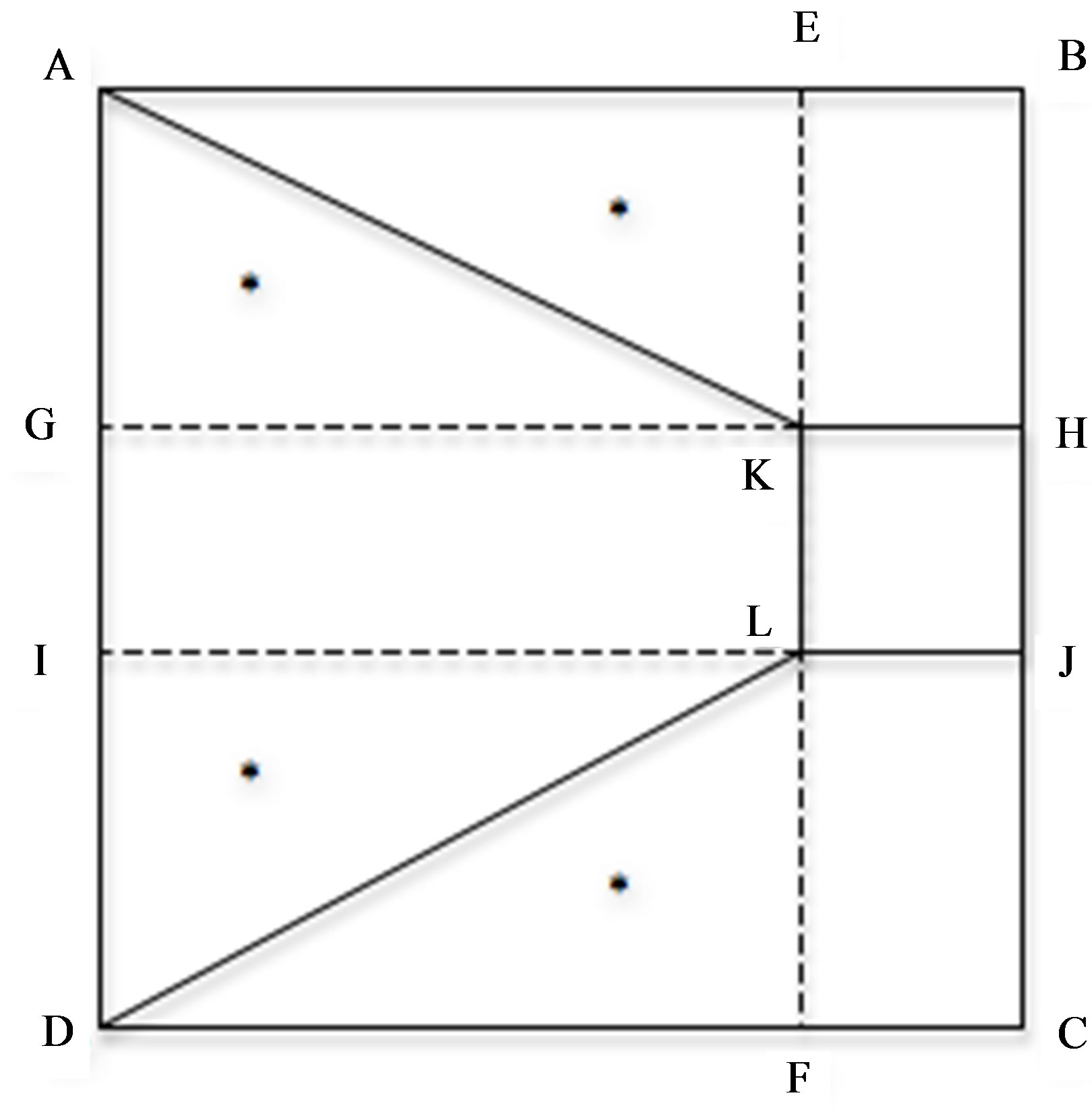
Figure 2. A geometrical solution.

Figure 3. An algebraic solution.

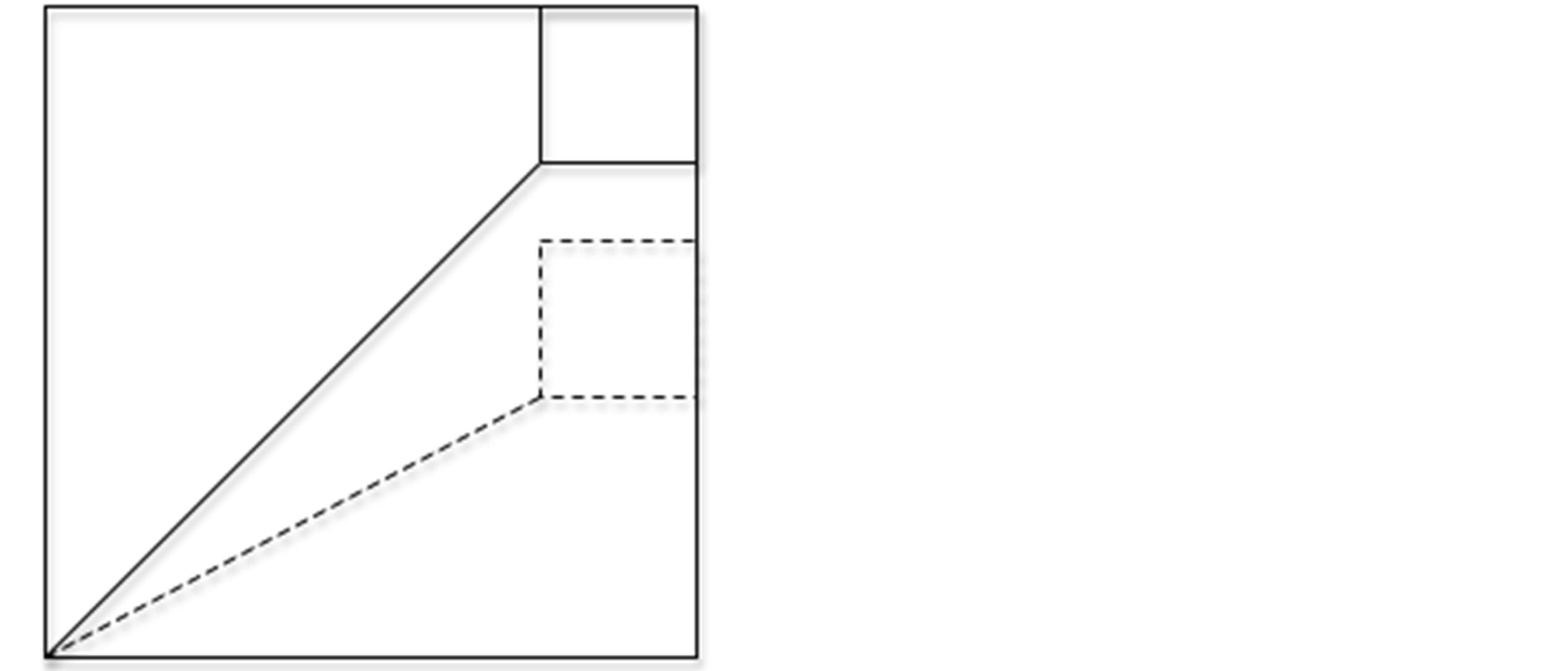
Figure 4. A visual manipulation solution.
not change because the bases and the height are maintained. The sum of the areas of the small trapezoids also does not change either, because the sum of their heights is constant. Thus, the solution does not depend upon the position of the small square. With the small square at the corner, the father’s portion and the son’s portion are congruent.
3.4. Procedure
The questionnaire was handed out to three classes of eight-grade students taught by three different instructors in the Mathematically Talented Youth Program in central Israel. These students were in their second year of the program. There was no time limit for the students to solve the problem. There was no explicit instruction to the students as how they should approach the problem, and they were allowed to use any tools they need, including calculators, to help them solve the problem. They were encouraged to write their explanations on how they came up with the solution and to provide justifications of their thinking. All their written responses were collected for analysis.
3.5. Data Analysis
Students’ written responses were first analyzed qualitatively to identify the types of reasoning used to solve the problem. The number of correct responses for each type of reasoning was calculated. The responses were also coded for the level of creativity based on Ervynck’s (1991) framework (Table 1): Level 1 (employing algorithms), Level 2 (developing a method from a situation), and Level 3 (constructing a solution by exploring what is stated in the problem). The percentage for each level was also calculated. Finally, only students’ solutions that scored high on the level of creativity (Level 3) were analyzed for the level of aesthetics using Dreyfus and Eisenberg’s (1986) framework (Table 2).
Table 1. Level of creativity with descriptions and indicators.
Table 2. Category for level of mathematical aesthetics and coding scheme.
The required information comes from local community residents of Tainan, Kaohsiung, and Taichung City. These members of the community live around the area where Southeast Asian migrant workers like to gather in the business districts. Designing a questionnaire of “urban business district’s migrant workers’ gathering in urban business districts and the its relations between the partitioning of urban space” (community residents section) as one set, and we’ll go to the commercial area for sampling, in order to study the relations between migrant workers’ gathering and the partitioning of urban space. The questionnaire’s content mainly included: 1) The attitude reflection on migrant workers’ weekend gathering and its impact of urban space partitioning, and 2) the basic information of the respondents. About data analysis, we use version 10.3 of SPSS as the statistical software to do the statistical analysis.
4. Results
As expected, majority of the students (about 96%) provided correct answer to the problem, and only about 3% answered incorrectly. In the first part of this section we present four types of reasoning that emerged from the students’ responses and their distributions. Representative examples were taken from the students’ responses. In the second part of the section, we present the levels of creativity of the students, the levels of aesthetics for the selected sample, and their distributions.
4.1. Types of Reasoning
After examining the students’ answers, the following four types of reasoning were found:
1) Explanation based on calculating the area using plane geometry: The students referred to axioms and definitions of plane geometry, writing the solution as a geometrical proof, with a theorem and an explanation. A correct link was made between the problem and plane geometry.
2) Explanation based on area calculation: The students related to the geometrical figures as given shapes, such as rectangles or trapezoids, as part of the problem’s data. They used known formulas to calculate the areas.
3) Explanation based on verbal area description: Students referred to the problem as a collection of areas of given geometrical figures. Areas were related to as equal and overlapping and were “cut out” and moved around.
4) Other: Explanations that do not fit any of the above categories.
Table 3 shows that majority of the students (about 40%) answered the thinking challenge using area calculations where the solutions are based on a completely technical algorithm. 28% of the subjects answered the thinking challenge with a verbal explanation containing explanations of the problem as a collection of given geometrical figures, overlapping areas, equal areas, “cutting out” areas and moving them around. Approximately 16% of the subjects answered the thinking challenge using a geometrical proof where they referred to definitions, axioms, and proofs in plane geometry and wrote the solution as a geometrical proof according to theorem and explanation. A similar percentage was categorized under “Other”.
4.2. Analysis According to “Level of Creativity”
Table 4 shows that the majority of the subjects, (40.4%), were found to be at the most basic level of creativity —using the algorithm-based solution (Calculating areas using simple formulas). 17.5% of the subjects who solved this thinking challenge were found to be at the basic level of creativity, developing a method from a given situation, relating to overlapping and equal areas, “cutting out” areas and moving them around. 15.8% of the subjects were found to be at the third level of creativity, the highest level. These students knew how to examine the problem in an educated manner, that is, they related to the given figures as not pre-defined, proving them, and using their proofs in their solutions. During the analysis some answers were categorized as “other” because they did not fit to any of the other categories. 26.3% of the subjects were included in this category.
4.3. Analysis of the Findings in Terms of Aesthetics
The degree of aesthetic in the students’ solutions was evaluated qualitatively using Dreyfus and Eisenberg’s (1986) characterization of aesthetic values of a problem solution: (a) reliance on minimum preliminary knowledge; (b) importance of clarity; (c) simplicity, brevity, and conciseness; and (d) cleverness of the solution and element of surprise. Only subjects who scored in the high level of mathematical creativity (N = 9) were included in this analysis.
Table 3. Distribution of reasoning (N = 57).
Table 4. Table describing the distribution of reasoning according to levels of creativity.
Reliance on minimum preliminary knowledge.
None of the subjects scored a 2, “Relies on minimum prerequisite knowledge”, in this category. The students relied heavily on broad mathematical knowledge such as definitions, theorems, and axioms. Because the context of the problem hinted examination of the areas for comparison (“… who ate more …”), the students relied on their knowledge of finding areas by partitioning into regular shapes they were familiar and in which they know the area formulas (square, rectangle, and trapezoid).
4.3.1. Clarity
A high degree of clarity was found in the subjects’ solutions to the thinking challenge. The arguments that students in this group provided tended to be simple and straightforward. The focus was on linking the problem to definitions, theorems, and axioms, and relating to known formulas of area of regular shapes.
4.3.2. Simplicity, Brevity, and Conciseness
A high degree of simplicity was found in all aspects of the solutions, with the exception of questionnaire 24A (See Figure 5) where the solution consisted of substantial number of steps and complex argument.
4.3.3. Cleverness of the Solution and the Element of Surprise
Despite the fact that in this study all the subjects were talented students, we did not find the element of surprise, with the exception of one response. This solution (Figure 6) was categorized as high in creativity because the student related the height of the trapezoid AEFD and the sum of the heights of the two trapezoids ABHE and DCGF because in both cases they are missing the length of the square. Although this transitive reasoning shows cleverness, it did not fully satisfy the demands of criteria for the element of surprise since there was still a reliance on the formula of trapezoids.

Figure 5. A sample of student work showing substantial steps and complex argument.
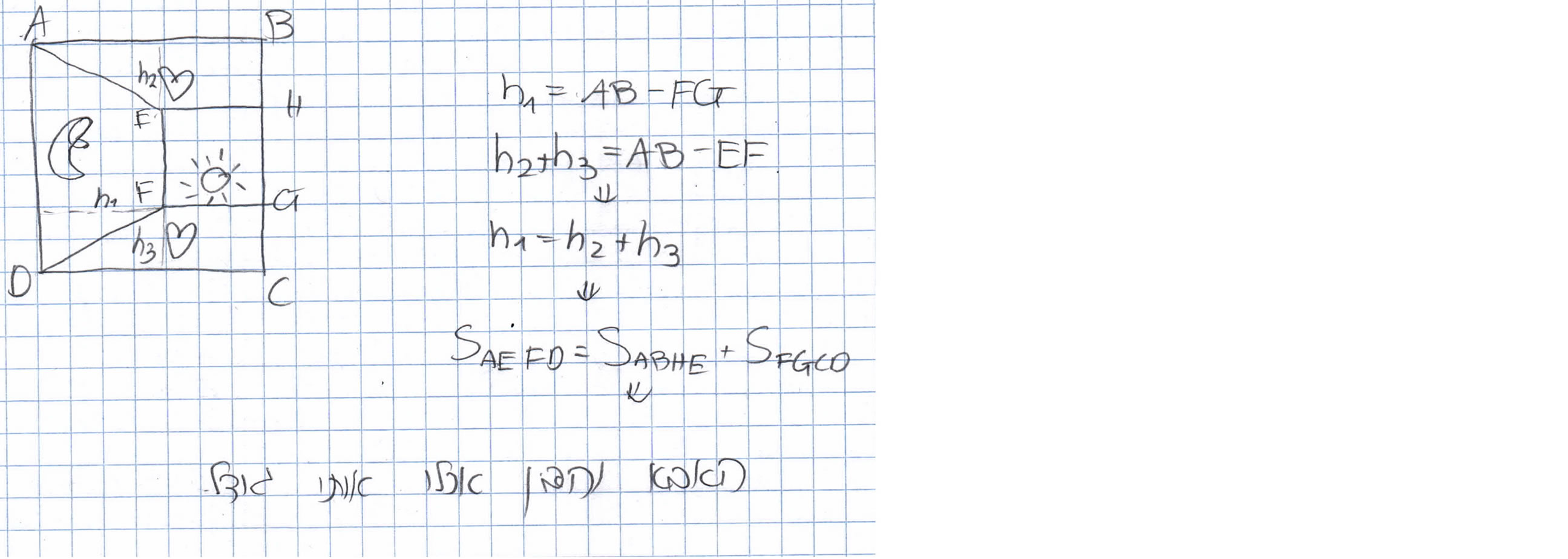
Figure 6. A student’s work showing clever manipulation of the assumptions of the mathematical structure.
5. Discussion and Conclusions
Problem solving is a significant means of developing mathematical understanding that includes interest and enjoyment. It is also a vehicle to express mathematical creativity and aesthetics that are often neglected, especially when working with talented students, and even with the general student population. The development of mathematical creativity requires solid foundation of mathematical knowledge (Meissner, 2000) and its transformation into new knowledge (Nakakoji, Yamamoto, & Ohira, 1999) because excellent knowledge in content helps individuals to make connections between different concepts and types of information (Sheffield, 2009). This strong foundation knowledge provides the basis for flexibility to move within concepts and between concepts. Thus, the extent of prior knowledge is prerequisite to how new information will be organized and determines the degree to which such information will be explored (Sheffield, 2009). Therefore, it comes to no surprise that creative thinking is more inherent among students who exhibit mathematical accuracy and fluency, especially in the context of working with non-routine and novel mathematical tasks, requiring them to pose original and meaningful solutions (Binder, 1996). However, other researchers proposed that creative potential contributes to the improvement of mathematical knowledge, suggesting that students who use mathematical content in creative ways lead to further mathematical learning (Starko, 1994). These two views lead to the old age the chicken or the egg causality dilemma. With no intention of resolving this philosophical conundrum, this paper assumes the double-helix nature of creativity and mathematical content knowledge, suggesting a synergistic interaction of the two.
5.1. Discussion
5.1.1. Types of Reasoning
Based on the students’ responses, three types of reasoning emerged when they solved the thinking challenge problem: (1) area calculation using geometrical proofs, (2) area calculation without using geometrical proofs, and (3) verbal explanations describing area calculations by moving, “cutting,” and overlapping areas. Sternberg and Ben-Zeev (1996) identified three types of reasoning within the mathematical domain: analytical reasoning, practical reasoning, and creative reasoning. First, analytical reasoning refers to the ability to think about formulas and applications of those to abstract mathematical problems that usually have single correct answers. Those who are able to complete problem solving tasks that are basically academic are considered having analytical reasoning ability. In this study, students who used area calculations based on plane geometry proof can be categorized as analytical thinkers because they emphasized on definitions, axioms, and proofs.
Second, practical reasoning refers to the ability to solve everyday problems or reason about applications in a practical way. Students in this study who solved the problem by manipulating the figure, either by moving the pieces around or cutting them, approached the problem from a practical stance. Using the context of the problem (sharing cake among family members), these students focused on the dimensions of the figure and devising a way to relate the area of the shapes.
Finally, creative reasoning refers to the invention of methods in thinking about problems. Those who draw on their current understanding of ideas in dealing with new situations are considered to have creative reasoning abilities.
5.1.2. Mathematical Creativity and Aesthetics
Using Ervynck (1991) and Silver’s (1997) criteria, the students were assigned a level of creativity based on their solution to the thinking challenge problem. Majority of the students fell under the basic level while only about 16% had a high level of creativity. Dreyfus and Eisenberg (1986) suggest that most students are not expected to come up with creative and/or elegant solutions when solving problems. They tend to adopt a practical stance, that is, just get to the solution. This attitude is prevalent among students, which is quite different from mathematicians. For instance, when Dreyfus and Eisenberg (1986) presented the elegant solution to a problem to university level mathematics students, they did not find the elegant version to be more attractive than the one they had come up with on their own. Because of the lack of emphasis on creativity and aesthetics when solving problems during instructions, students tend to focus on the product rather than the process of solving the problem. The structure of the setting for problem solving also inhibits attention to elegance. Typically, students have a set amount of time (classroom period) to solve a set of problems, which creates tension and encourages students to “get to the answer”.
5.1.3. Development of Mathematical Creativity
Students’ reasoning, level of creativity, and degree of aesthetics when solving the given thinking challenge in this study suggest that they rely heavily on known algorithms and formulas or use models to simplify the problem into manageable pieces. They failed, however, to leave the model and look beyond what was presented and manipulate the internal structure of the problem. Students followed the more mechanistic approach when solving the problem, and failed to come up with elegant solutions. The emphasis that school mathematics and instructions place on propositional, logical reasoning may have hindered students from recognizing and trusting generative type of aesthetic responses that operate in inquiry (Sinclair, 2004).
5.2. Conclusions
The level of difficulty of the thinking challenge presented to the students in this study was appropriate as shown by the majority of the students answering the question correctly. However, the type of reasoning, the level of creativity, and the degree of mathematical aesthetics varied greatly among the students. Three types of reasoning emerged among the talented students in the program: analytical reasoning, practical reasoning, and creative reasoning. Majority of the students in the program (about 40%) were at the most basic level (Level 1) of mathematical creativity. Although students can be categorized as talented, but the level of mathematical creativity may not necessarily. The students in this study did not seem to develop a high level of mathematical aesthetics when solving the problem. Students relied heavily on prerequisite knowledge and although presented their solutions with high clarity, they failed to express simplicity, structure, and cleverness in their solutions. Furthermore, there lacked elements of surprise in their solutions.
Although the research literature on talented students support the notion that talented students are more creative, no specific level of creativity was found in this segment of the population. There are several limitations to this study. First, the use of a single item to assess the students’ level of mathematical creativity and aesthetic was problematic. This study presented a glimpse of the students’ ability and the results were not meant to be conclusively. A more comprehensive set of questions is deemed necessary to provide a more coherent picture of their capability. In addition, cognitive interview with the students will be beneficial to gauge students’ thinking process and examine their decision for choices regarding specific strategies. The interview will inform us whether these students are solving the problems from a practical stance, which is evidence in their lack of attention to the aesthetic value of the solutions.
5.3. Teaching Recommendations and Directions for Further Studies
Understanding the development of mathematical creativity and aesthetics among gifted and talented students is crucial to initiate and support their growth. Future studies should examine instructional support and classroom practices that afford the development of mathematical creativity and aesthetics over a period of time during their program. Teachers need to emphasize not only creative ways to solve problems, but also the elegance of the solutions because that is what mathematicians do. This can be done by providing time and attention to the process and structure of mathematics.
6. Limitations of This Research
Educators around the world disagree on the best way of promoting thinking in general and creative hinking in particular. There are two central questions in dispute: (a) Are thinking skills general, or do they depend on specific content and system of concepts? (b) To what extent and under what circumstances can critical thinking be “transferred” from one discipline to another? I will attempt to provide an answer to the second question, since it has greater implications for teaching strategies. The characterization of the transfer procedure is highly controversial, since this procedure depends to a large extent on the specific context and creative. In this research the “transfer problem” has not been thoroughly examined. We know that transfer has taken place in this research, yet do not know to what extent or under what circumstances it took place.
References
- Aizikovitsh-Udi, E. (in Press). The Extent of Mathematical Creativity and Aesthetics in Solving Problems among Students Attending the Mathematically Talented Youth Program. Proceedings of the 2013 Conference for European Research in Mathematics Education (CERME-8). (To Be Published) http://cerme8.metu.edu.tr/wgpapers/WG7/WG7_Aizikovitsh_Udi.pdf
- Allan, S. D. (1991). Ability-Grouping Research Reviews: What Do You Say about Grouping and Gifted? Educational Leadership, 48, 60-65.
- Artzt, A. F., & Armour-Thomas, E. (1997). Mathematical Problem Solving in Small Groups: Exploring the Interplay of Students’ Metacognitive Behaviors, Perceptions, and Ability Levels. Journal of Mathematical Behavior, 16, 63-74. http://dx.doi.org/10.1016/S0732-3123(97)90008-0
- Artzt, A. F., & Yaloz-Femia, S. (1999). Mathematical Reasoning during Small-Group Problem Solving. In L. V. Stiff, & F. R. Curcio (Eds.), Developing Mathematical Reasoning K-12 Yearbook (pp. 115-126). Reston, VA: National Council of Teachers of Mathematics.
- Binder, C. (1996). Behavioral Fluency: Evolution of a New Paradigm. The Behavior Analyst, 19, 163-197. http://www.abainternational.org/TBA.asp
- Boyce, L. N., VanTassel-Baska, J., Burruss, J. D., Sher, B. T., & Johnson, D. T. (1997). A Problem-Based Curriculum: Parallel Learning Opportunities for Students and Teachers. Journal of the Education of the Gifted, 20, 363-379.
- Bloom, B. S., et al. (1956). Taxonomy of Educational Objects: The Classification of Educational Goals, Vol. 1. London: Longman.
- Chamberlin, S. A., & Moon, S. (2005). Model-Eliciting Activities: An Introduction to Gifted Education. Journal of Secondary Gifted Education, 17, 37-47.
- Chiu, M.-S. (2009). Approaches to the Teaching of Creative and Non-Creative Mathematical Problems. International Journal of Science and Mathematics Education, 7, 55-79. http://dx.doi.org/10.1007/s10763-007-9112-9
- Dreyfus, T., & Eisenberg, T. (1986). On the Aesthetics of Mathematical Thought. For the Learning of Mathematics, 6, 2-10.
- Ervynck, G. (1991). Mathematical Creativity. In: D. Tall (Ed.), Advanced Mathematical Thinking (pp. 42-53). Dordrecht: Kluwer Academic.
- Hong, E., & Aqui, Y. (2004). Cognitive and Motivational Characteristics of Adolescents Gifted in Mathematics: Comparisons among Students with Different Types of Giftedness. Gifted Child Quarterly, 48, 191-201. http://dx.doi.org/10.1177/001698620404800304
- Hwang, W. Y., Chen, N. S., Dung, J. J., & Yang, Y. L. (2007). Multiple Representation Skills and Creativity Effects on Mathematical Problem Solving Using a Multimedia Whiteboard System. Educational Technology & Society, 10, 191-212.
- Kwon, O.-N., Park, J.-S., & Park, J.-H. (2006). Cultivating Divergent Thinking in Mathematics through an Open-Ended Approach. Asia Pacific Education Review, 7, 51-61. http://dx.doi.org/10.1007/BF03036784
- Lester, K. (1980). Research on Problem Solving. In: R. J. Shumway (Ed.), Research in Mathematics Education. Reston, VA: National Council of Teachers of Mathematics.
- Leung, S. S., & Silver, E. (1997). The Role of Task Format, Mathematics Knowledge, and Creative Thinking on the Arithmetic Problem Posing of Prospective Elementary School Teachers. Mathematics Education Research Journal, 9, 5-24. http://dx.doi.org/10.1007/BF03217299
- Liljedahl, P., & Sriraman, B. (2006). Musings on Mathematical Creativity. For The Learning of Mathematics, 26, 20-23.
- Mann, E. L. (2006). Creativity: The Essence of Mathematics. Journal for the Education of the Gifted, 30, 236-262.
- Meissner, H. (2000). Creativity in Mathematics Education. The Meeting of the International Congress on Mathematics Education, Tokyo, Japan.
- National Council of Teachers of Mathematics (2000). Principles and Standards for School Mathematics. Reston, VA: Author.
- Nakakoji, K., Yamamoto, Y., & Ohira, M. (1999). A Framework That Supports Collective Creativity in Design Using Visual Images. In E. Edmonds, & L. Candy (Eds.), Proceedings of the 3rd Conference on Creativity & Cognition (pp. 166-173). New York: ACM Press. http://www.informatik.unitrier.de/~ley/db/conf/candc/candc1999.html
- Polya, G. (1957). How to Solve It: A New Aspect of Mathematical Method (2nd ed.) Princeton, NJ: Princeton University Press.
- Polya, G. (1968). Mathematical Discovery: On Understanding, Learning and Teaching Problem Solving. New York: Wiley.
- Silver, E. (1997). Fostering Creativity through Instruction Rich in Mathematical Problem Solving and Problem Posing. ZDM, 3, 75-80. http://dx.doi.org/10.1007/s11858-997-0003-x
- Sinclair, N. (2004).The Role of the Aesthetics in Mathematical Inquiry. Mathematical Thinking and Learning, 6, 261-284. http://dx.doi.org/10.1207/s15327833mtl0603_1
- Sheffield, L. (2009). Developing Mathematical Creativity-Questions May Be the Answer. In R. Leikin, A. Berman, & B. Koichu (Eds.), Creativity in Mathematics and the Education of Gifted Students (pp. 87-100). Rotterdam: Sense Publishers.
- Shore, B. M., & Kanevsky, L. (1993). Thinking Processes: Being and Becoming Gifted. In K. A. Heller, F.J. Monks, & A. H. Passow (Eds.), International Handbook for Research and Development on Giftedness and Talent (pp. 133-148). London: Pergamon.
- Starko, J. A. (1994). Creativity in the Classroom. New York: Longman.
- Stepien, W. J., & Pike, S. L. (1997). Designing Problem-Based Learning Units. Journal for the Education of the Gifted, 20, 380-400.
- Sternberg, R. J., & Ben-Zeev, T. (1996). The Nature of Mathematical Thinking (335p). New York: Lawrence Erlbaum Assoc.
- The Technion Israel Institute of Technology (2005). Number 3 Unified Examination for Ninth Grade Students Studying Toward a 5-Point Matriculation Examination in the Program for Realizing Mathematical Excellence: 19 FILL IN Year Part 3 Enrichment. Haifa: The Technion Israel Institute of Technology.


