ABSTRACT

The aim of the present paper is to establish some new integral inequalities of Gronwall type involving functions of two independent variables which provide explicit bounds on unknown functions. The inequalities given here can be used as tools in the qualitative theory of certain partial differential and integral equations.

Keywords:Integral Inequalities, Two Independent Variables, Partial Differential Equations, Nondecreasing, Nonincreasing

1. Introduction

The Gronwall type integral inequalities provide a necessary tool for the study of the theory of differential equations, integral equations and inequalities of the various types (please, see Gronwall [1] and Guiliano [2] ). Some applications of this result to the study of stability of the solution of linear and nonlinear differential equations may be found in Bellman [3] . Numerous applications to the existence and uniqueness theory of differential equations may be found in Nemyckii-Stepanov [4] , Bihari [5] , and Langenhop [6] . During the past few years several authors (see references below and some of the references cited therein) have established several Gronwall type integral inequalities in one or two independent real variables [1] -[14] . Of course, such results have application in the theory of partial differential equations and Volterra integral equations.

In [14] , Pachpatte investigated the following inequality:

Lemma: Let be nonnegative continuous functions defined on 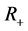and be nonnegative constant. Let 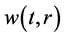be a nonnegative continuous function defined for, and monotonic nondecreasing with respect to 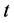for ant fixed. If

For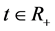, then

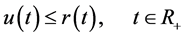
where 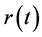is the maximal solution of

For.

2. Main Results

Theorem 2.1: Let 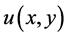and be nonnegative continuous functions defined on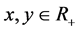. Let be a positive continuous and nondecreasing functions in both variables and defined for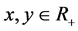. If

(2.1)

Then

where and

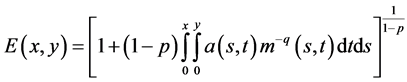, (2.2)

and 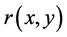is the maximal solution of

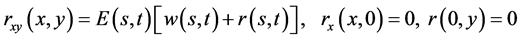(2.3)

Proof: Define a function by the right-hand side of (2.1).Then

(2.4)

By using (2.4) in (2.1), we get

(2.5)

Since is a positive continuous and nondecreasing function, then

(2.6)

Let

(2.7)

From (2.6) and (2.7), we observe that

(2.8)

And

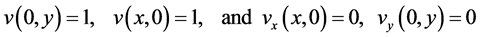(2.9)

Differentiating both sides of (2.8) with respect to and, we get

(2.10)

By keeping first 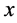fixed in (2.10) and set and integrate from 0 to then again keeping fixed, set and integrate from 0 to respectively and using (2.9), we get

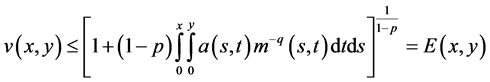(2.11)

From (2.7) and (2.11), it is clear that

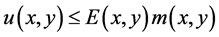
From (2.4), it can be restated as

where 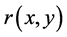is the maximal solution of

This completes the proof.

Theorem 2.2: Let 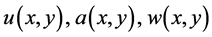be defined as in Theorem 2.1. If

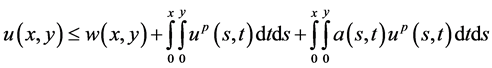(2.12)

Then

where and

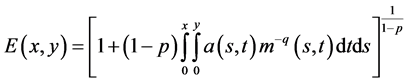, (2.13)

where 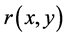is the maximal solution of

Proof: Define a function by the right-hand side of (2.12).Then

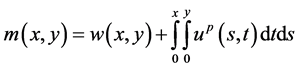(2.14)

By using (2.14) in (2.12), we get

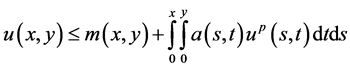(2.15)

By following the same steps of Theorem 2.1 from (2.5)-(2.11), we get

(2.16)

From (2.7), (2.14) and (2.16), we observe that

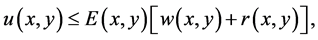
where is the maximal solution of

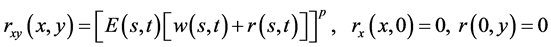
This completes the proof.

Theorem 2.3: Let 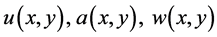be defined as in Theorem 2.1. If

(2.17)

Then

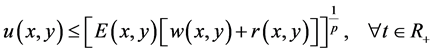
where and

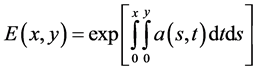, (2.18)

where 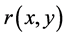is the maximal solution of

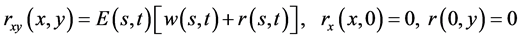
Proof: Define a function by the right-hand side of (2.17).Then

(2.19)

where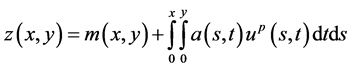

By using (2.19) in the above equation, we get

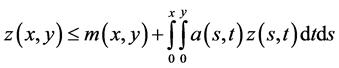(2.20)

and

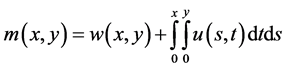(2.21)

Since 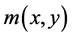is a positive continuous and nondecreasing function, then from (2.20),

(2.22)

Let

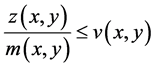(2.23)

where

(2.24)

And

(2.25)

Differentiating both sides of (2.24) with respect to and, and from (2.23), we get

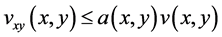
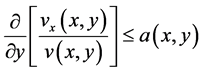(2.26)

By keeping first x fixed in (2.26) and set and integrate from 0 to y then again keeping y fixed, set and integrate from 0 to x respectively and using (2.25), we get

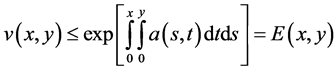(2.27)

From (2.19), (2.23) and (2.27), it is clear that

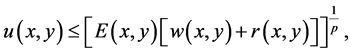
where 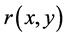is the maximal solution of

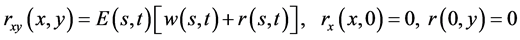
This completes the proof.

Application: As an application, let us consider the bound on the solution of a nonlinear hyperbolic partial differential equation of the form

(2.28)

with the given boundary conditions

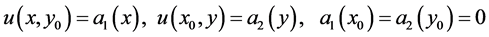(2.29)

where 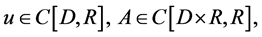and 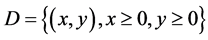such that

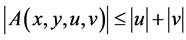(2.30)

(2.31)

where 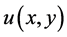and be nonnegative continuous functions defined on a domain D

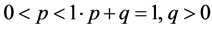. The Equation (2.28) with (2.29) is equivalent to the integral equation

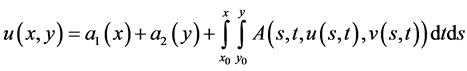(2.32)

Let be any solution of (2.28) with (2.29) and taking absolute values of both sides, we get

(2.33)

Using (2.30)-(2.32) in (2.33) and assuming that, where be a positive continuous and nondecreasing function defined in the respective domain, we have

Then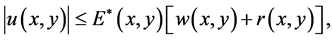

where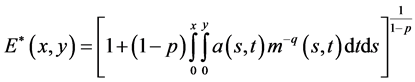, and is the maximal solution of

The remaining proof will be the same as the proof of Theorem 2.1 with suitable modifications.

We note that Theorem 2.1 can be used to study the stability, boundedness and continuous dependence of the solutions of (2.28).

References