Atmospheric and Climate Sciences
Vol.4 No.3(2014), Article ID:48253,10 pages
DOI:10.4236/acs.2014.43043
Analysis of the Homogeneity of Wind Roses' Groups Employing Andrews’ Curves
Ratto Gustavo1,2*, Videla Fabián1,3, Reyna Almandos Jorge3,4
1Optical Research Center, Gonnet, Argentina
2Faculty of Engineering, National University of La Plata, La Plata, Argentina
3Scientific Research Commission, La Plata, Argentina
4National Technological University, La Plata Regional Faculty, Berisso, Argentina
Email: *gustavratto@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 May 2014; revised 20 June 2014; accepted 22 July 2014
ABSTRACT
The homogeneity of groups of 16-dimensional wind direction roses (obtained by hierarchical clustering in a previous report) is discussed through the application of Andrews’ Curves. Principal Component Analysis (PCA) is employed to reduce dimensionality and to provide an ordering of the variables to compute Andrews’ Curves. Our results suggest that Andrews’ Curves greatly facilitate the visualization of homogeneity as well as reveal information that allows improving the clusters’ arrangement. A combined analysis employing Andrews’ Curves and Calinkski and Harabasz’ approach (a method for determining the optimal number of groups) helps to assess the strength of the group structure of the data as well as to detect anomalies such as misclassified objects or atypical values. Furthermore, it allows finding out that the 24 original seasonal hourly roses (representing the “day”) become better represented by 6 groups (rather than by 5 as proposed in the previous report). The new group arrangement was consistent with the dendogram for another cut-off distance. As a result the wind occurrences are now represented by a more detailed and smooth pattern: there is a decrease in northern wind between midday and twilight while eastern winds become more important towards the evening. The methodology proposed is a subject to be considered to become part of an automated system.
Keywords:Andrews’ Curves, Cluster, Group Homogeneity, Principal Component Analysis (PCA), Wind Roses

1. Introduction
In [1] wind roses at La Plata City and surroundings were studied employing hierarchical cluster analysis. This method allowed synthesizing information covering 1998-2003 as well as assisting the discussion of physical phenomena related to wind occurrences. Hierarchical clustering allowed us to reduce from 24 to 5, the number of representative wind roses characterizing the “day” for each season and monitoring site.
The goal of the present work is to evaluate the homogeneity of the groups obtained with cluster analysis by employing Andrews’ Curves [2] which are a type of graphical display to present and explore data [3] . To this end, the observed data for summer at site “J”—one of the monitoring sites referred in [1] —was taken as an example. This season was selected because it was the most variable one; site “J” was chosen because it had the most complete records (above 97% percent of completeness).
Each hourly averaged wind rose is represented by a 16-dimensional vector (the 16 directions of the compass) which can be well represented by Andrews’ Curves. These curves, often employed to visual data mining [4] , allow representing multidimensional data in two (or three) dimensional plots; its importance lies on the simplicity of the method and becomes very suitable in those cases in which the dimensionality reduction applied to the original data still yields more than three dimensions (in these cases the classic plots become complex).
Although in this paper Andrews’ Curves are employed to carry out a qualitative analysis concerning the homogeneity of the groups, it is important to point out that its validity [5] [6] is due to its mathematical properties [7] that are related with other methods [8] allowing therefore working in a less subjective manner. According to [9] these curves also help to visualize structures in high dimensional data. Andrews showed that the difference between two given curves is proportional to the Euclidean distance, i.e., close points in the multidimensional space will be observed as close Andrew’s Curves in the plane. This characteristic provides affinity with the clustering method that is the starting point of this work.
Principal Components Analysis (PCA) is used as a method to reduce dimensionality: its outputs are employed as inputs for the computation of Andrews’ Curves. Calinski and Harabasz’ index is employed to support the findings suggested by Andrews’ Curves.
In summary, this paper gathers four well-known approaches (hierarchical clustering, PCA, Andrews’s Curves and Calinski and Harabasz’s index) that are independent but that supply a powerful tool to allow gaining insight into data characteristics. The results discussed in the present paper were obtained applying to the interaction between a human user and the outcomes of different software packages (e.g., Excel, Ststistica, Matlab, etc.) but the authors considered that the whole methodology could become part of an automated system.
2. Methods
Each p-dimensional point
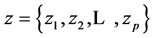 defines a periodic function given by:
defines a periodic function given by:
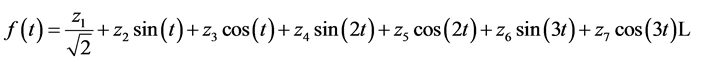 (1)
(1)
called Andrews’ curve where t is defined in the range [−180, 180] in sexagesimal degrees. The number of terms in the equation is given by the number of dimensions of the data. Then f(t) is a linear combination of orthonormal functions. Two consequences of this representation are that the mean of the observations equals the mean of the corresponding Andrews’ Curves, and the squared Euclidean distance between observations is the same that of the corresponding Andrews’ Curves. These properties allow working with a large number of variables. For these reasons, the f(t)’s plots in the mentioned range are very useful to detect group configurations of multivariate vectors. Given a data set where all the curves can be grouped (in two or more groups) showing different patterns, the curves help to find out the group structure in the data set. If the curves are much overlapping it is not possible to distinguish groups, then it may be considered that the data set has no well conformed groups.
As can be seen from Equation (1), f(t) depends on the order of the variables, the first coordinates in the equation emphasize low frequencies that tend to dominate the visual plot [10] . Nevertheless, this fact does not influence the application of the curves to detect group structure or atypical values [11] because any chosen order will allow detecting relative differences among curves (the inherent information is the same). Gnanadesikan [12] points out that when it is not possible to assign different importance to the variables in Equation (1), one may analyze the results of some permutations of them and, in this way, get a deeper insight on the nature of the data under study.
In the present study the order of the variables followed the “natural order” given by that of the principal components. This “implicit” order given by the application of PCA provides a solution to the variable order assignment [13] and gives a criterion for future comparisons among different data sets. Besides providing an order in the terms of Equation (1), the PCA method gives a sound approach to reduce the dimensionality [14] from the original 16 dimensions to a lower number but retaining a high proportion of the total variance.
It has been pointed out [11] [12] [15] that two possible drawbacks of Andrews’ Curves are their computing time and the cluttering effect in to the plots. In the present case none of them are relevant; PCA reduces the dimensionality from 16 to 5, which simplifies the computations while the size of the data set (24 vectors represented by 24 Andrews’ Curves) makes it easy to manage from the visual point of view.
The current use of Andrews’ Curves is reflected by the different degrees of sophistication of the software involved [9] [13] [16] -[18] that goes from simple graphing to interactive tools and animation models; most of them devoted as visualization and, in a less extent as exploration tools. As other visual data mining approaches [19] Andrews’ Curves recalls the use of the human visual perception system as part of the data processing task.
Calinski and Harabasz’ index [20] allows determining
the optimal number of groups in a given set of multivariate data. In this work it
is mainly employed to corroborate findings coming from the application of hierarchical
clustering and Andrews’ Curves. This index is defined as
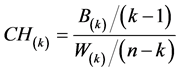 where B(k) indicates the degree of dispersion that exists between the
groups formed in the agglomeration process to get k-groups (i.e., the between-groups
sum of squares). B(k) is computed as the total sum of the squared distances
between the centroid of a group and the centroid of the original data (general centroid).
W(k) indicates the degree of dispersion that exists within a group (i.e.,
the within-group sum of squares). W(k) is computed as the total sum of
the squared distances between each individual data and the centroid of its group
for all the groups. A plot of W(k) versus k is employed traditionally
to show the degree in which additional groups give more “compact” groups. k indicates
a particular number of groups obtained from the original data set. n is the total
number of single p-dimensional vectors. CH(k) is defined for k > 1, when
there is a strong group structure CH(k) gives a unique maximum. When
this is not the fact (e.g., local extremes indicate there is moderate group structure)
the authors recommend to adopt the first local maximum. In the case CH(k)
increases as k increases the approach predicts there is no hierarchical structure.
This index was chosen due to its simplicity and high performance characteristics
as demonstrated by [21] and
[22] .
where B(k) indicates the degree of dispersion that exists between the
groups formed in the agglomeration process to get k-groups (i.e., the between-groups
sum of squares). B(k) is computed as the total sum of the squared distances
between the centroid of a group and the centroid of the original data (general centroid).
W(k) indicates the degree of dispersion that exists within a group (i.e.,
the within-group sum of squares). W(k) is computed as the total sum of
the squared distances between each individual data and the centroid of its group
for all the groups. A plot of W(k) versus k is employed traditionally
to show the degree in which additional groups give more “compact” groups. k indicates
a particular number of groups obtained from the original data set. n is the total
number of single p-dimensional vectors. CH(k) is defined for k > 1, when
there is a strong group structure CH(k) gives a unique maximum. When
this is not the fact (e.g., local extremes indicate there is moderate group structure)
the authors recommend to adopt the first local maximum. In the case CH(k)
increases as k increases the approach predicts there is no hierarchical structure.
This index was chosen due to its simplicity and high performance characteristics
as demonstrated by [21] and
[22] .
3. Results and Discussion
3.1. Generalities
Figure 1 shows the dendogram of the hourly wind roses for summer at site “J”. The “Y” axis refers to 16 hourly averaged wind direction roses covering 1998-2003, e.g., “Hour 0” covers observations during 00:00 - 00:59 h (Local Time). “X” axis correspond to the squared Euclidean distance expressed in percent. The linkage criteria for the clustering process were the mean squared Euclidean distance between groups. The dashed vertical line (located around 50% in the X scale) indicates the five groups provided by the cluster analysis according to [1] . These five groups of representative wind roses are shown in Figure 2. The wind rose named as Group 1 (assigned as such arbitrarily) is obtained by averaging the wind roses corresponding to Hour 0, Hour 1, Hour 2 and Hour 3; the same procedure was applied to obtain the rest of the groups.
Following [23] it is pertinent to explore the number of significant dimensions of the data (16 dimension wind roses) in order to simplify the computing process to build Andrews’ Curves. With this purpose, and considering the advantages exposed in Section 2, PCA was applied to the hourly wind direction roses of Figure 1. This method was carried out with Statistica’s software package Version 8.0 employing the covariance matrix of the variables as reference. With illustrative purposes Figure 3 shows the configuration of points obtained with the two first principal components (that explain 86.70% of the total variance). In this plot it is possible to see the existence of a group structure and the absence of atypical values (not conclusive).
Figure 4 show the scree plot corresponding to all principal components. It can be easily seen that after the first five or six eigenvalues the curve becomes flat. This implies that with a few components (4 or 5 of the new variables) it is possible to represent the original 16-dimensional objects (wind roses).
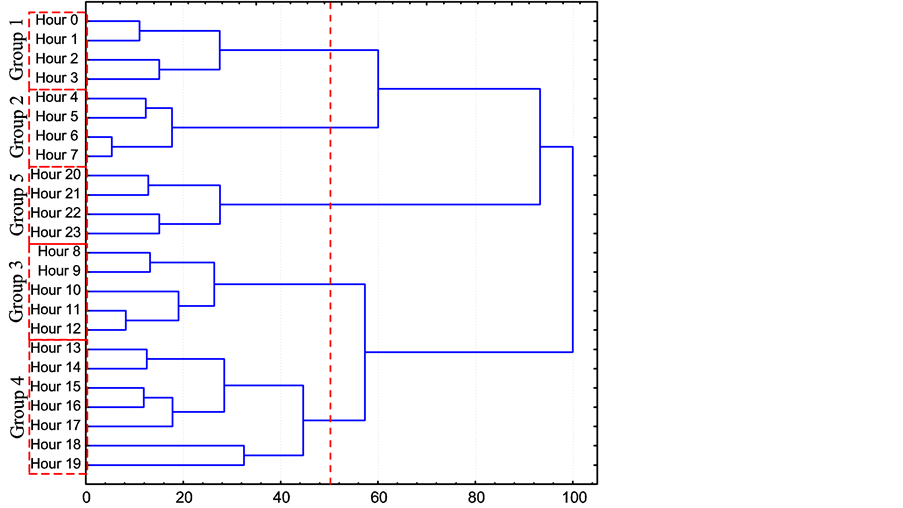
Figure 1. Dendogram for the 16 direction hourly wind roses observed in summer 1998-2003 at site “J” at La Plata City.
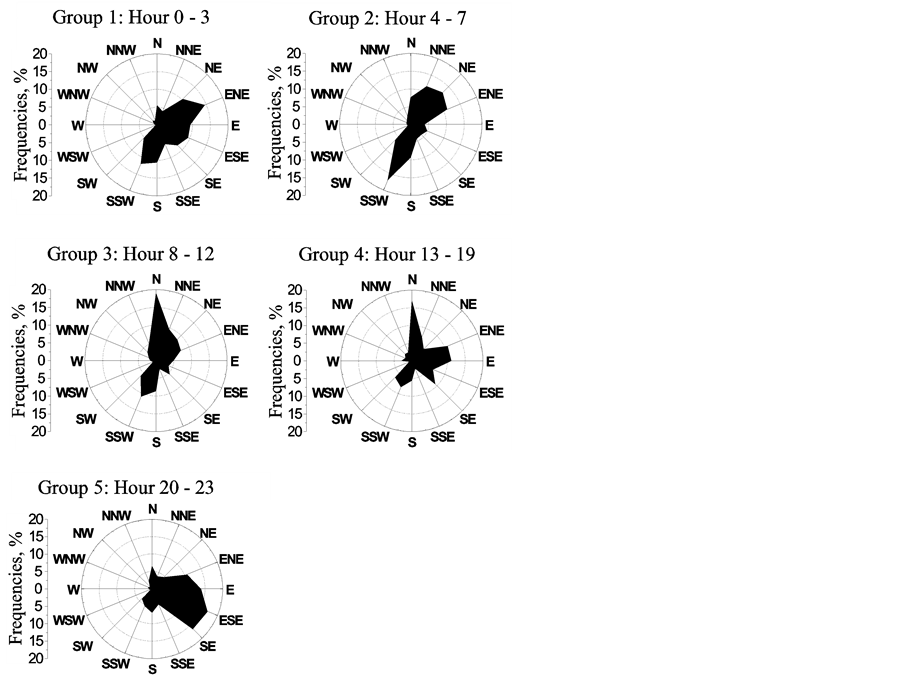
Figure 2. Wind direction roses representing “the day” as a result of the dendogram (Figure 1) for a cut distance around 50%.
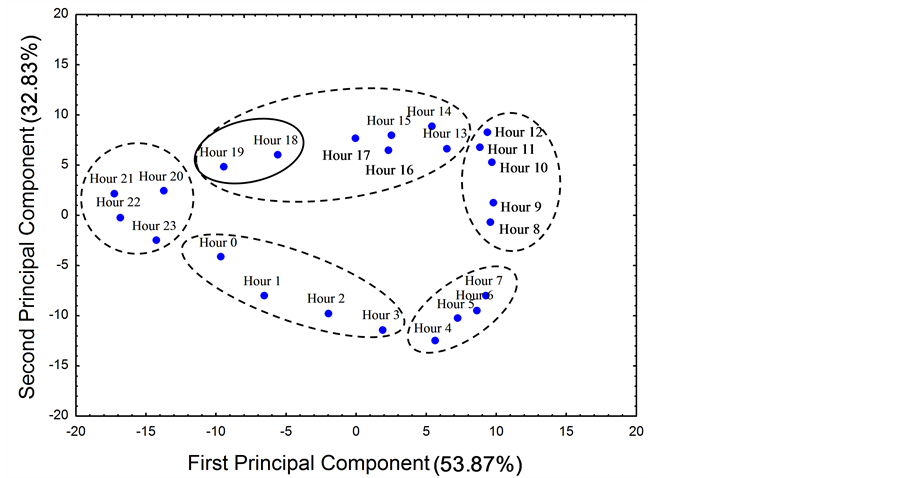
Figure 3.
The blue points show the wind roses of the dendogram (Figure
1) expressed by the first two principal components. The involving dashed
lines indicate the groups given by the dendogram for a cut distance around 50%.
The involving solid line comprising Hour 18 and 19 indicate a possible subgroup
(Section 3.3.2 and Section 3.3.3). Both lines do not reflect the shape of the groups;
they have been drawn just to illustrate the idea of group structure. X axis values
divided by
![]() constitute the first term of Equation (1) and the constant value for each of the
curves of Figure 5 from
(a1) to (e1).
constitute the first term of Equation (1) and the constant value for each of the
curves of Figure 5 from
(a1) to (e1).
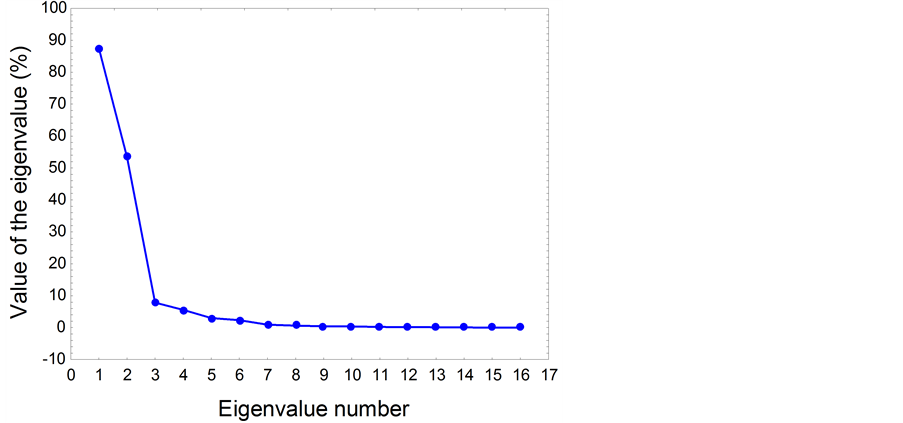
Figure 4. Scree plot. It helps to determine the optimal number of eigenvalues to retain.
As can be seen from Table 1 the accumulated variance regarding the first five principal components explains more than 95% of the total variation. So, Andrews’ Curves can be built using only these five components (instead of the original 16 variables).
Figure 5 shows Andrews’ Curves obtained for each of the members of the groups defined by the dendogram (Figure 1); besides, the group averages are shown.
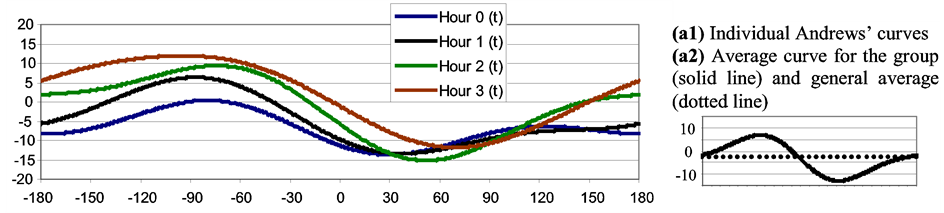 (a1) (a2)
(a1) (a2)
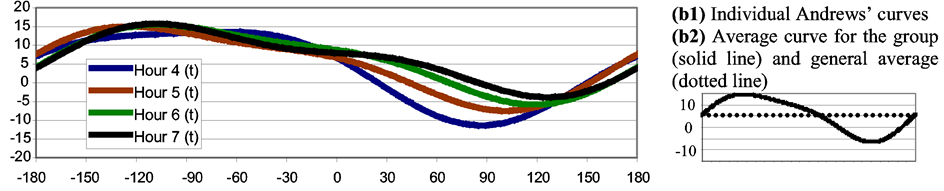 (b1) (b2)
(b1) (b2)
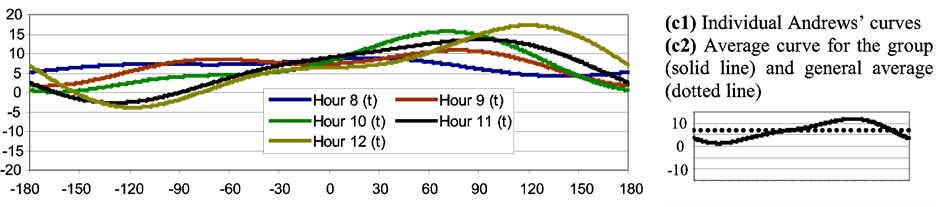 (c1) (c2)
(c1) (c2)
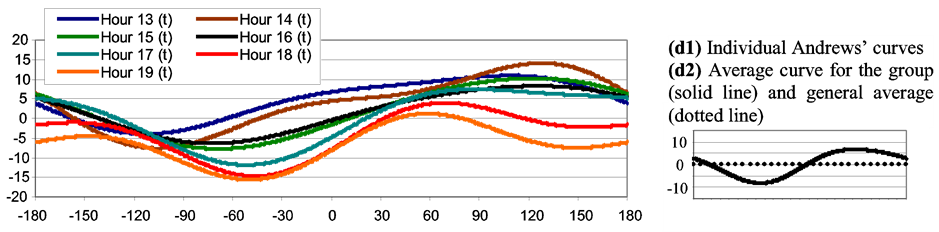 (d1) (d2)
(d1) (d2)
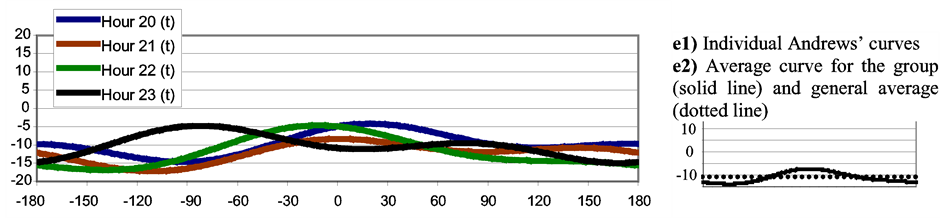 (e1) (e2)
(e1) (e2)
Figure 5. Andrews’ curves for the hourly wind roses involved in Figure 1. Each curve was built based on the first 5 principal components employed as variables in Equation (1). The X axis covers the interval t [−180, 180]. The Y axis corresponds to f(t) (see Equation (1)). (a): Group 1; (b): Group 2; (c): Group 3; (d): Group 4; (e): Group 5.
Table 1. Accumulated variance according to the eigenvalues order.
3.2. Visual Inspection of the Andrews’ Curves
A panoramic view of Figure 5 from (a1) to (e1) allows determining that there is a good homogeneity in each of the groups, i.e., the individual curves tend to stay close to each other and with a similar shape. In almost all the groups the curves that belong to the extremes of the interval (e.g., Hour 0 and Hour 3 in Group 1, Hour 13 and Hour 19 in Group 4, etc.) are the most different ones (considering distance and/or shape). Throughout the groups the occurrences of peaks and valleys (that give identity to the group) are different: Figure 5 from (a2) to (e2) –solid line—allows seeing this phenomenon on average. In the same figure the dotted lines indicate the general average for each of the group that corresponds to the first term in Andrews’ series (influenced by the first principal component). For Group 1 this average is –2.8, for Group 2 is 5, 4, for Group 3 is 6.6, for Group 4 is 0.1 and for Group 5 is –11. This means that, in some cases, it is possible to distinguish important differences among groups (e.g., between Group 3 and 4 or between Group 4 and 5) only with the first principal component. Some of the groups show few oscillations (e.g., Group 1) showing more influence of sin(t) and cos(t) (that correspond to the second and third principal component respectively) than sin(2t) and cos(2t) (that correspond to the fourth and fifth principal component respectively). The contrary occurs with Group 5 where the functions sin(2t) and cos(2t) associated with more oscillations are easy to notice.
In Group 4 (Figure 5(d1)) the curves corresponding to Hour 18 and 19 are somewhat different from the rest; besides, they don’t look very similar to curves of the adjacent groups (i.e., Group 3 and Group 5). Comparing neighbors (i.e., Hour 17 with Hour 18 and Hour 19 with Hour 20) there exist differences but they do not seem very strong. The general average was computed considering that there may exist two subgroups in Group 4. The obtained values were 2.3 for Hour 13 - Hour 17 while –5.3 for Hour 18 - Hour 19 what implies a relevant difference between subgroups.
In Group 5 (Figure 5(e1)) the curve for Hour 23 shows a different pattern than the rest. Comparing Hour 23 with Hour 0 (nearest neighbor of Group 1) and with Hour 22 (nearest neighbor within the group) it is not possible to conclude that Hour 23 constitutes a misclassified member. Although somewhat atypical it is not possible to consider that Hour 23 is an outlier.
In summary, on one hand it is pertinent to regroup the members of Group 4 into two “new” groups: Hour 13 - Hour 17 and Hour 18 - Hour 19. This is in accordance with the dendogram (Figure 1) if the cut off distance is carried towards 40%. So, the 24 original wind roses will be grouped into 6 groups (rather than into 5). On the other hand the presence of a potential outlier is rejected.
3.3. Calinski and Harabasz Index
Calinski and Harabasz’s index (see Section 2) is computed for nine possible ways of grouping the 24 original data following the dendogram of Figure 1. Table 2 shows the CH(k) index computed up to nine groups. The local maximum is the reference to consider that the optimal number of groups is six. To better visualize this result Figure 6 shows the values of W(k) for different numbers of groups. At the beginning the curve shows a steep descent slope indicating the segregation between groups for small values of k (between 1 and 3). Then the slope smoothes (when k is between 3 and 5) and for k = 6 it flattens. K = 6 can be considered as a critical value because higher values will not indicate the presence of real groups. So, it can be concluded that the Calinski and Harabasz’s approach reinforces the findings of previous sections determining that six averaged wind roses will be the best number to represent the original 24 ones.
As stated in Section 3.2 Andrews’ Curves allow revealing information regarding the group structure of the data. In some cases the wind roses that are neighbors but belong to different groups may look similar. So it can
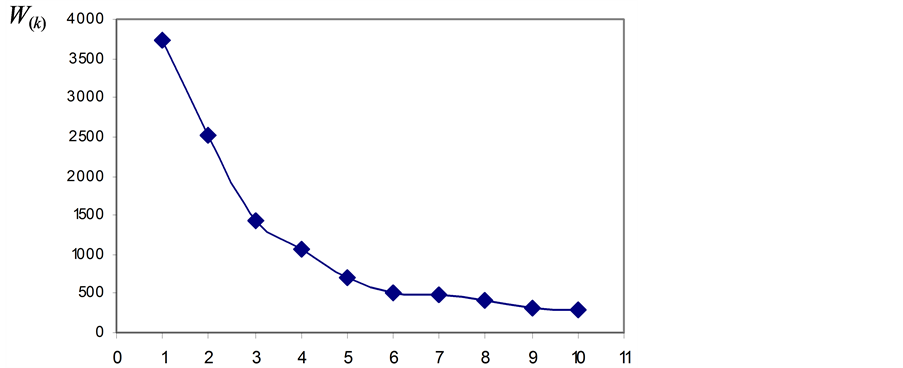
Figure 6. Extinction diagram for the within-group sum of squares. Note that W(k) is defined for k = 1.
be concluded, from a general point of view, that the original data have a moderate group structure. This is in accordance with the values of CH(k) that contain a local maximum (Section 2). An illustration of the moderate structure fact can be appreciated in Figure 3 that considers only the two first principal components (for example, compare the distance between Hour 19 and 18 to that between Hour 19 and 20).
3.4. Meteorological Implications
Figure 7 shows the new groups, namely Group 4* and Group 5*, that modifies Figure 2 as a result of the findings of the previous sections. Group 5 in Figure 2 is now called Group 6.
An advantage of Figure 7 (compared to Figure 2) is that allows appreciating a smoother change of the prevailing winds from midday to twilight. The Group 5* reveals the decrease in northern wind and the importance of eastern winds towards the evening (this effect was not caught by Group 4 in Figure 2).
4. Conclusions
Andrews’ Curves have been used to gain insight in the characteristics of wind roses groups obtained in a previous report with a hierarchical clustering method. PCA was employed to reduce dimensionality, and hence, to simplify computations. Five principal components (explaining more than 95% of the variance) were employed instead of the 16 original variables (wind directions); this method was also helpful in the order allocation of the variables in Andrews’ Curves equation.
Andrews’ Curves allowed visualizing in two dimensions, in a very simply and tangible manner, multidimensional vectors (wind roses). Therefore, the homogeneity of the groups merged from the dendogram was visually
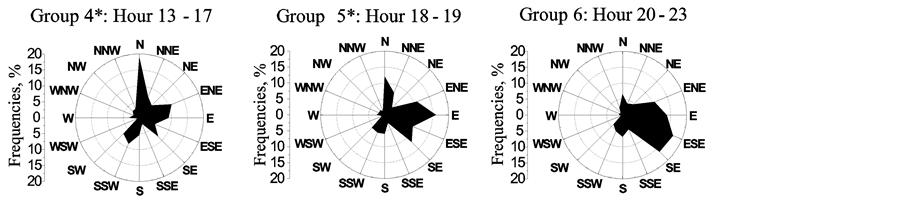
Figure 7. New groups of averaged wind roses in accordance with Figure 1 for a cut distance around 40%. Group 4 In Figure 2 was converted into Group 4* and Group 5*. The asterisk (*) indicates a new group.
inspected. These groups showed, in general, high degree of homogeneity; detected anomalies such as the presence of potential outliers and new subgroups were further discussed. As a result the presence of outliers was discarded and a new configuration of the groups was defined. This finding was supported by the Calinski and Harabasz’s index that gave 6 as the number of optimal groups. The combined analysis (Andrews’ Curves and Calinski and Harabasz approach) evidenced the degree of strength of the group structure indicating that the original data had a moderate structure. The consequences of these results in the description of wind occurrences were outlined: there was a decrease in northern wind between midday and twilight while eastern winds became more important towards the evening (this was not evidenced in the previous report).
The integration of the approaches employed (hierarchical clustering, principal component analysis, Andrews’ Curves and Calinski and Harabasz’s index) can be viewed as a guidance to be followed when finding homogeneous groups in high-dimensional data is required. Furthermore, this outlined guidance is capable to become part of an automated processing system which is very helpful when large data sets (in our case more seasons and monitoring sites) need to be assessed and compared.
Acknowledgments
The authors are grateful to Dr. Ricardo Maronna for his help in the revision of the manuscript.
References
- Ratto, G., Maronna, R. and Berri, G. (2010) Analysis of Wind Roses Using Hierarchical Cluster and Multidimensional Scaling Analysis at La Plata, Argentina. Boundary-Layer Meteorology, 137, 477-492. http://dx.doi.org/10.1007/s10546-010-9539-3
-
Andrews, D.F. (1972) Plots of High-Dimensional Data. Biometrics, 28, 125-136.
http://dx.doi.org/10.2307/2528964 - Unwin, A. (2008) Good Graphics? In: Chen, C., Hardle, W. and Unwin, A., Eds., Handbook of Data Visualization, Springer, Heidelberg, 57. http://dx.doi.org/10.1007/978-3-540-33037-0_3
- Moustafa, R.E. (2011) Andrews’
Curves. Computational Statistics, 3, 373-382.
http://dx.doi.org/10.1002/wics.160 - Fayyad, U., Grinstein, G. and Wierse, A. (2002) Information Visualization in Data Mining and Knowledge Discovery. Elsevier, London.
- Uddin, M., Hussain, M. and Fatmi, A.I. (2011) Visualizing Multivariate Data with Andrews’ Curves. Proceedings of the 8th International Conference on Recent Advances in Statistics: Statistics, Biostatistics and Econometrics, Lahore, 8-9 February 2011, 213-222.
- Cluff, E., Burton, R. and Barrett, W. (1991) A Survey and Characterization of Multidimensional Presentation Techniques. Journal of Imaging Technology, 47, 142-153.
- Embrechts, P., Herzbergb, A.M., Kalbfleischb, H.K., Travesc, W.N. and Whitlad, R. (1995) An Introduction to Wavelets with Applications to Andrews’ Plots. Journal of Computational and Applied Mathematics, 64, 41-56. http://dx.doi.org/10.1016/0377-0427(95)00005-4
- Garcia-Osorio, C. and Fyfe,
C. (2005) The Combined Use of Self-Organizing Maps and Andrews’ Cur-
ves. International Journal of Neural Systems, 15, 197-206. http://dx.doi.org/10.1142/S01290657050
00207 - Carr, D.B. (1998) Multivariate Graphics. In: Armitage, P. and Colton, T., Eds., Encyclopedia of Biostatistics, Wiley, Chichester, 2864-2886.
- Seber, G.A.F. (2004) Multivariate Observations. John Wiley and Sons, New Jersey.
- Gnanadesikan, R. (1997) Methods for Statistical Data Analysis of Multivariate Observations. John Wiley and Sons, New York. http://dx.doi.org/10.1002/9781118032671
- Spencer, N.H. (2003) Investigating Data with Andrews Plots. Social Science Computer Review, 21, 244-249. http://dx.doi.org/10.1177/0894439303021002010
- Wilks, D.S. (2006) Statistical Methods in the Atmospheric Sciences, 2nd Edition, Elsevier, New York.
- Chan, W.W.-Y. (2006) A Survey on Multivariate Data Visualization. Report of the Department of Computer Science and Engineering, Hong Kong University of Science and Technology, Kowloon, Hong Kong. http://www.cse.ust.hk/~wallacem/winchan/research/multivis-report-winnie.pdf
- Schmid, C. and Hinterberger, H. (1994) Comparative Multivariate Visualization across Conceptually Different Graphic Displays. Proceedings of SSDBM’94, Charlottesville, 28-30 September 1994, 42-51.
- Hinterberger, H. (2010) The VisuLab®: An Instrument for Interactive, Comparative Visualization. Technical Report Nr. 682, Department of Computer Science Information Technology and Education, Zurich.
- Martinez, W. and Martinez, A. (2002) Computational Statistics Handbook with MATLAB®. Chapman & Hall/CRC, Washington.
- Garcia, J.R.M., Monteiro, A.M.V. and dos Santos, R.D.C. (2012) Visual Data Mining for Identification of Patterns and Outliers in Weather Stations’ Data. Proceedings of the 13th International Conference on Intelligent Data Engineering and Automated Learning—IDEAL 2012, Natal, 29-31 August 2012, 7435, 245-252. http://dx.doi.org/10.1007/978-3-642-32639-4
- Calinkski, T. and Harabasz, J. (1974) A Dendrite Method for Cluster Analysis. Communications in Statistics, 3, 1-27.
- Milligan, G.W. and Cooper, M.C. (1985) An Examination of Procedures for Determining the Number of Clusters in a Data Set. Psychometrika, 50, 159-179.
-
Tibshirani, R., Walther G. and Hastie, T. (2001) Estimating the Number of Clusters
in a Dataset via the Gap Statistic. Journal of the Royal Statistical Society Series
B, 63, 411-423.
http://dx.doi.org/10.1111/1467-9868.00293 - Jolliffe, I.T., Jones, B. and Morgan, B.J.T. (1986) Comparison of Cluster Analyses of the English Personal Social Services Authorities. Journal of the Royal Statistical Society Series A, 149, 253-270. http://dx.doi.org/10.2307/2981557
NOTES

*Corresponding author.


