Advances in Nanoparticles
Vol.3 No.3(2014), Article ID:49329,11 pages DOI:10.4236/anp.2014.33017

Molecular Dynamic Study of Pull-In Instability of Nano-Switches

Sogand Hoshyarmanesh, Mohsen Bahrami*

Department of Mechanical Engineering, Amirkabir University of Technology, Tehran, Iran

Email: *mbahrami@aut.ac.ir

Copyright © 2014 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 24 May 2014; revised 30 June 2014; accepted 16 July 2014

ABSTRACT

Capacitive nano-switches have been of great interest as replacements for conventional semiconductor switches. Accurate determination of the pull-in voltage is critical in the design process. In the present investigation, pull-in instability of nano-switches made of two parallel plates subjected to electrostatic force is studied. For this purpose, two parallel rectangular nanoplates with opposite charges are modeled based on molecular dynamics (MD) technique. Different initial gaps between nanoplates and its effect on pull-in phenomena are studied in addition to taking different values of geometrical and physical parameters into account to evaluate pull-in voltages. Here molecular dynamic simulations as an atomic interaction approach are employed for modeling of nano-switches in order to study pull-in instability considering atomic interaction and surface tension. Boundary conditions and also the van der Waals force are considered as important parameters to investigate their effects on pull-in voltage values.

Keywords:Nanomechanics, Pull-In Instability, Electric Field, Molecular Dynamics Simulation, van der Waals Force

1. Introduction

The potential difference across the conductors develops an electric field across the dielectric, causing positive plate to come in contact with the ground plane. If the applied voltage exceeds this pull-in limit, the upper plate will snap down. Accurate determination of the pull-in voltage is critical in the design process of capacitive switches and in virtue of the electromechanical coupling effect and the nonlinearity of electrostatic force [1] [2] . To operate devices such as capacitors, they need to be biased with a DC voltage to form a surface charge [3] [4] . The aspects such as drive mode, temperature dependence and dielectric charging have been analyzed and their effects on the pulling-voltage are evaluated [5] . There are numerous investigations based on analytical modeling of the pull-in voltage for beams or diaphragms with the modified capacitance accounting to the fringing field and the equivalent spring constant to meet the emerging need for microelectromechanical systems (MEMS) process during both process development and manufacturing [6] -[11] . Distributed modeling based on well-known beam and plate theories [12] is also developed. Moreover, analytical approximate solutions for pull-in voltages are obtained via energy methods [13] , homotopy perturbation method [14] , modified couple stress theory [15] , and with elastic boundaries [16] . Parallel plate capacitors are modeled in the equations of motion based on classical elasticity theory and the orthodox theory of Coulomb blockade [17] Researchers have shown that there is a close match between analytical solution and numerical simulations of the nano-devises. For instance in [18] the continuum model’s accuracy is compared with atomistic simulation to compute the pull-in voltage of Nano-cantilever switches. Atomistic simulation is an applicable approach to studying nano system’s properties [19] -[21] . Hoshyarmanesh et al. applied molecular dynamics to investigate surface molecular interaction in micro-cantilever biosensors [22] . Molecular dynamics simulation of pull-in phenomena is also derived in carbon nanotubes to study Stone-Wales defects, different geometries and boundary conditions on the pull-in charges [23] [24] .

Different methods such as molecular mechanics and atomistic modeling are employed in order to investigate the mechanical behaviors of nanostructures. Ansari and Sahmani [25] studied biaxial buckling behavior of single-layered graphene sheets on the basis of two approaches including nonlocal continuum elasticity and MD simulation. Bahrami et al. used molecular dynamic to simulate the Interaction of Carbon Nanotubes and External Flow [26] .

Additionally, various investigations have been conducted to indicate the size effect on the pull-in phenomenon of microand nano-switches. Mohammadi et al. [27] investigated the size effect on the pull-in instability of hydrostatically and electrostatically actuated circular microplates. The research revealed that variation of dimensionless internal length scale parameter and hydrostatic pressure leads to different values of pull-in voltage. Mousavi et al. [28] studied the small scale effect on the pull-in instability of nano-switches subjected to electrostatic and intermolecular forces. The intermolecular and electrostatic attraction forces using Eringen’s nonlocal elasticity theory are solved numerically by differential quadrature method. Wang and Wang [29] studied the pull-in instability of a nano-switch under electrostatic and intermolecular Casimir forces with consideration of the surface energy. The analysis is based on the geometrically non-linear Euler-Bernoulli beam theory with consideration of the surface energy. The research has proved the effect of intermolecular Casimir force on the pullin voltage weakens as the initial gap has increases.

Many problems in the natural sciences and engineering are common with sources of uncertainty. There are various numerical and analytical methods to solve the static uncertain systems like fuzzy finite element analysis [30] and other trial and errors approaches, however these are not approximate solutions and lack of accuracy is observable. Computer simulations are the most common approach to studying problems in uncertainty quantification. Simulation-based methods like Monte Carlo simulations are one of the basic probabilistic approaches for uncertainty propagation. Plates uniformly loaded with electrical potential and fixed at both four edges and two edges are studied here and also the nano-switche with fixedplate at four sides as an uncertain static system is solved through molecular dynamic technique.

In the current investigation, the pull-in instability of electrostatically actuated nano-switches is studied with considering the small scale effect conducting molecular dynamic simulation. To study pull-in phenomena nanoswitches with different initial gaps and different boundary conditions are simulated and pull-in voltages are evaluated. In addition to investigate the effects of van der Waals force in the small-scale, the simulation is solved by both considering and neglecting van der Waals force, and the results are compared.

2. Molecular Dynamics Simulation

Two approaches have been used to obtain the solution of the maximum deflection for fixed thin rectangular plates under uniform load; these are the double cosine series and the superposition method as a generalization of Hencky’s solution [31] . The problem of the uniformly loaded rectangular plate with fixed at all sides has been solved by Hencky (1913) and independently by Boobnoff (1902). Boobnoff made exact calculations for several aspect ratios for the plate while Hencky made refined calculations only for the case of a square plat [32] . Hutchinson has used the solution from which was presented in [33] . However molecular dynamic investigate the atomic interaction of plates in nano-devices considering non-local view.

Due to the difficulties in manufacturing nanostructure, experiments on nano-switches have been costly. Computational design tools, when sufficiently precise and accurate, can be far more economical than trial-and-error design cycles based purely on experimentation. In this section, a molecular dynamic approach is proposed for analysis and design of capacitors. To this end, MD simulation of a nano-switch and it’s response to electrical field and estimation of mechanical deflection of capacitor is performed. Schematic of nanoplate-based switch is shown in Figure 1. The capacitor plates are constrained with two different boundary conditions as are displayed in Figure 2, clamped square diaphragm and fixed-fixed sides, while the lower plate is fixed in bottom side.

The necessary step that must be considered in MD simulation is equilibration of the capacitor, since it is the starting point of minimization process [34] . NAMD execution consists of three stages of equilibration and one stage under applied electrical field [35] . The stages are prevalent in most of simulations. First stage is energy minimization; second stage temperature is increased from zero to 295 Kelvin degree with constant volume. In the next stage pressure is constant and the Langevin thermostat is applied. The last stage the volume is adjusted constant and the desire voltage is applied to system. The constant pressure simulation let volume to alter. An equilibrate system can be find out by following conditions, volume should fluctuate smoothly around a constant value; also energy is approached to a certain value. If one draws the volume curve versus time, a noticeable reducing tangent would be observed in the volume.

In order to simulate the mechanical deflection of a capacitor, the electrical field with different values is applied to the system. In other words, potential difference applied to a system causes a certain value of voltage along z-axis. Electrostatic forces deflect the moveable nanoplate depending on the gap between the movable plate and the fixed one. van der Waals force also acts an important role in the nanoplate’s attraction. LennardJones potential has two attractive and repulsive terms. Forcefield potential energy function [36] consists of intermolecular or bonding interactions, Lennar-Jones potential for the vdW interaction and the Coulomb potential for electrostatic actuation are utilized to model the nano-switches as it is brought in Equation (1) and expanded in Equation (2).

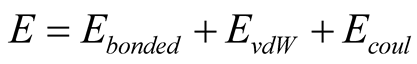(1)

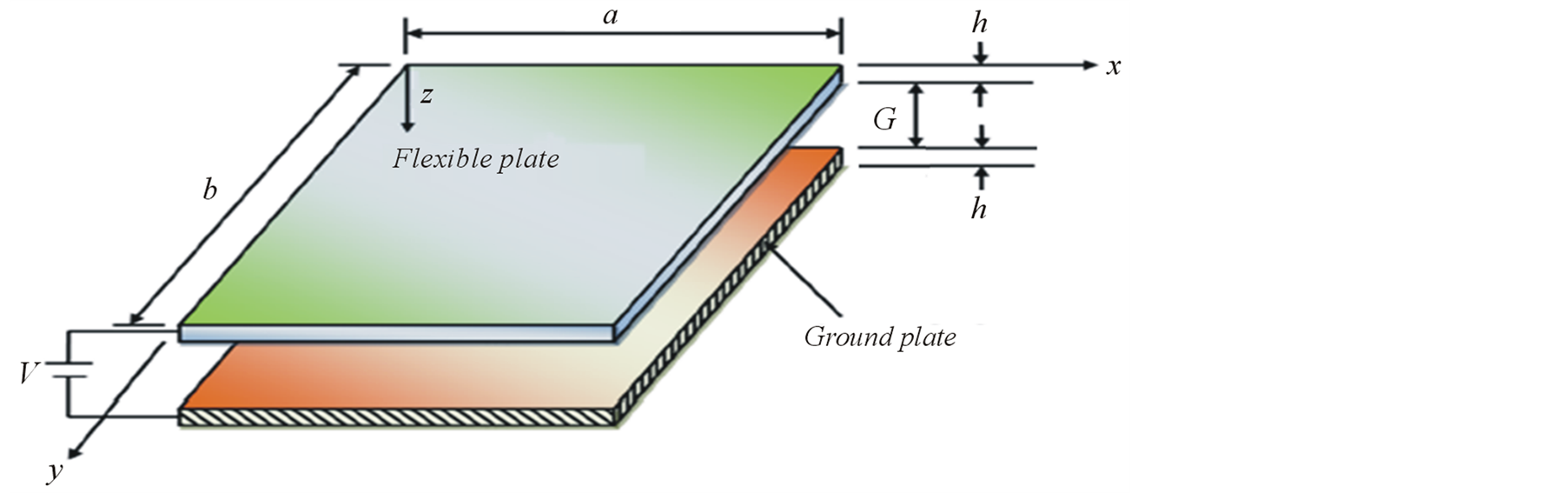
Figure 1. Schematic of nanoplate-based switch: kinematic parameters and coordinate system.

Figure 2. Boundary conditions (left) clamped-clamped (right) four sides fixed.

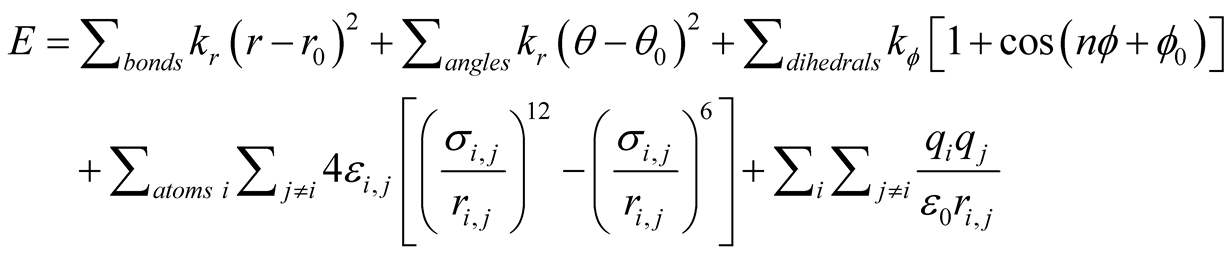(2)

where 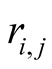is the distance between atoms i and j, the parameter ε denotes the strength of the interaction and σ defines a length scale. The attractive term proportional to dominates at large distances and it models the van der Waals dispersion forces caused by the dipole-dipole interactions due to fluctuating dipoles. The electrostatic interaction of two atoms with charges 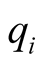and 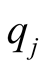separated by is given by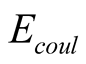, the dielectric contant ε0 in vacuum is equal to 1. When two plates contact with each other, the vdW repulsive force will make the collapse harder; the total van der Waals energy can be computed by a pairwise summation over all the atoms.

Plats are made of silicon which the upper plate is n-type silicon and the lower one is p-type silicon. This basically means n-type silicon is positively charged, and p-type silicon becomes negatively charged. Subsequently applying an uniform electric field across the z-axis enforce an attractive force between plats and voltage has a direct relation to electric field, which is electric field multiple the size of system along the z-axis, consequently the pull-in voltage will be determined.

When an electrical field is applied, the lines of pressure control will be absent. Inserting an electrical field with controlled pressure disturbs the system and led to incorrect answers. In addition the Langevin temperature controlled should be turning on. Applying Langevin forces to ions, their motions which supposed to be measured through applied electrical field, led to an infinitesimal deviation in the current. If a high electrical field was applied to system, the high ionic current would increase the temperature up to 450 Kelvin degree. The simulation leans to be invalid in such degree of heat, since this restriction limits us to work by smaller electrical field in real simulation. In the MD simulation, the atom’s interaction and the surface tension are considered that impose an ineligible force on nano-scale devices. Surface tension plays an important role in nano-devices function which is neglected in classic mechanic. It makes the simulation more accurate than analytical calculation such as continuum mechanics that is originated from classic mechanics.

Total number of atoms simulated to form plates is 66,304, and plates are made of silicon. Force field parameters of silicon for the covalent bonds between atoms including bond energy, bond radius, angle, dihedral, van der Waals radius and some other decisive factors are brought in the Appendix. Overall simulation time is determined based on reaching to a stable point in energy and volume, as it is seen in following graphs the simulation steps has exceeded 120,000 steps considering time step fixed at 2 fs/step. Fixed atom constraint facility made it possible to take the effects of boundary condition into account.

Simulation is adjusted as the coordinate of atoms be registered once in every 100 steps to find the pull-in voltage. As it is illustrated in the Figures 3-5 the applied electric field should be large enough to contact plates.

The capacitor with gap value of 2.719 nm was actuated by the electric field of 7 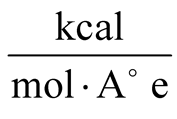and 5

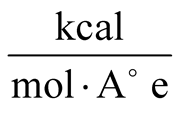
considering with and without vdW respectively. The electric field value is gradually augmenting for the gap values of 1.543, 4.3504 nm, respectively, in the case of c lamped-clamped boundary condition. Thus, absorption has happened over the time and plates have connected completely. Figure 5 demonstrates plate’s absorption in the case of four sides fixed boundary condition regarding gap value of 4.3504.

The Newtonian equations of motion are solved for the atoms which are consisting of following terms [37] :

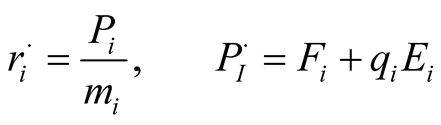(3)

where Ei is the electric field acting on atom i, mi the mass, qi the partial charge, and pi the laboratory momentum of atom i. Fi represents the total intermolecular force acting on atom i due to all other atoms. Silicon mass and partial charge are respectively equal to 28 u and +4 for n-type and −4 for p-type.

Simulation has been executed with and without van der Waals force to discover the exact effect of surface forces in the function nano-scale switches. Molecular dynamic results indicate that the der Waals force can play a significant role in determining the pull-in voltage of cantilever switches especially for smaller gaps. When the gap between the cantilevers plats is very small, vdW force acts as a repelling force to avoid the distance to

(a)(b)(c)(d)(e)(f)

Figure 3. MD simulation performed for pull-in phenomenon in a nano-switch, fixed at two sides, gap = 4.3504.

(a)(b)(c)(d)(e)(f)

Figure 4. MD simulation performed for pull-in phenomenon in a nano-switch, fixed at two sides, gap = 1.543.

(a)(b)(c)(d)

Figure 5. MD simulation performed for pull-in phenomenon in a nano-switch, fixed at four sides, gap = 4.3504.

exceed the atomic van der Waals radius. Under this circumstance system requires a bigger snap-down voltage to overcome the repulsive force.

3. Results and Discussion

The successful application of molecular dynamic simulations is using a nonlinear least square fitting procedure to minimize the equilibrate energy and obtain stabilize system results. The geometrical parameters of nanoswitches are considered in MD simulations, i.e. as are seen below. Capacitors with two different gaps are modeled in Figure 3, Figure 4 and plates are fixed at two sides; however, in Figure 5 upper plate is fixed at four sides. The figures show the transient absorption of plates under the electrical field so the whole parts are illustrating the snap-down phenomena. Although for pulling phenomenon just a small connection between the electrodes are enough, as shown in the Figures 3-5, the connection is not so small and a remarkable area of the upper electrode touches the lower electrode, this is due to gaps size designed in the vicinity of plats thickness value in addition to a potent atomic interaction. In the other word relatively small gaps, which are in the order of plats thickness, make a large area of plats surface to contact.

The values of pull-in voltages obtained by MD simulations are tabulated in Table 1 corresponding to nanoswitches with different initial gaps between the nanoplates. It is clearly seen that by increasing the value of initial gap of nano-switch, the pull-in instability occurs at higher applied voltages.

As a necessary condition for equilibration, the volume should be smoothly fluctuated around an average value and stabilized energy lean to a certain value. Figure 6 and Figure 7 demonstrate the system’s steady state energy versus time-step regarding four different initial capacitor’s gaps and fixed edges. As it is demonstrated the system’s total energy has remained constant during equalization. If the gap between the upper electrode and the ground plane is smaller than vdW radius, van der Waals force acts inversely, so applies an repelling force that inhibit plates from having contact; to obtain precious results vdW must be taken into account. Numerical value of vdW force during equalization is drawn distinguishingly in Figure 8. One can see that the graph reaches its peak in the plats distance of 0.22 nm before dropping and converting to a repellent force.

To have a better judgment, graphs of applied voltage in fourvarious gaps are drawn in one picture. Figure 9 illustrates the applied voltages versus deflection regarding different gap values; in addition pull-in voltages

Table 1 . The values of pull-in voltages predicted by MD simulations corresponding to various initial gaps and boundary conditions.

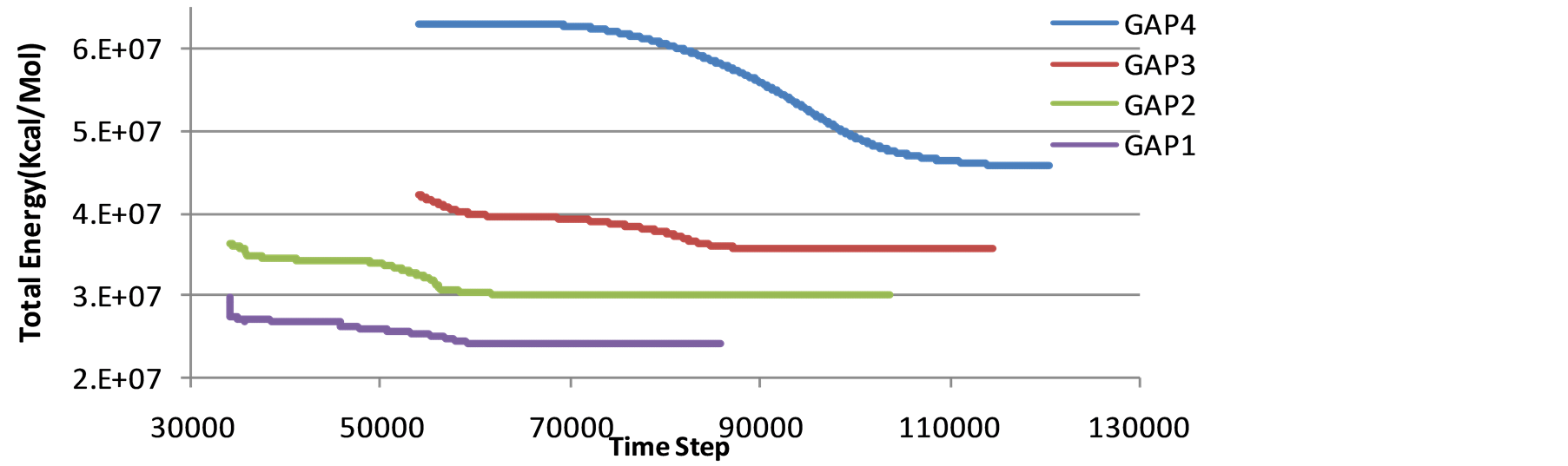
Figure 6. Variation of system’s total energy versus step time regarding various initial gaps, fixed at two sides, G1 = 0.514 nm, G2 = 1.08 nm, G3 = 2.72 nm, G4 = 4.3504 nm.

Figure 7. Variation of system’s total energy versus step number regarding various initial gaps, fixed at four sides.

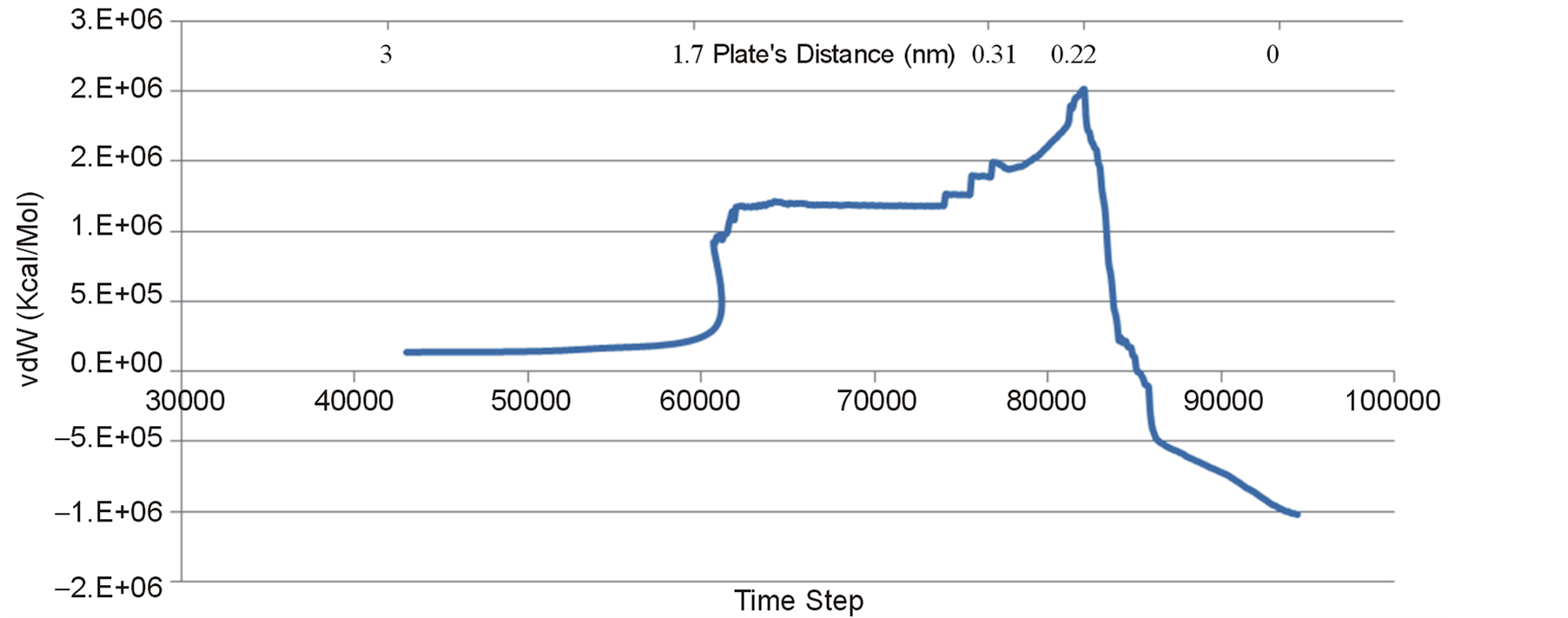
Figure 8. Variation of system’s van der Waals energy versus step number for silicon plats, fixed at two sides.

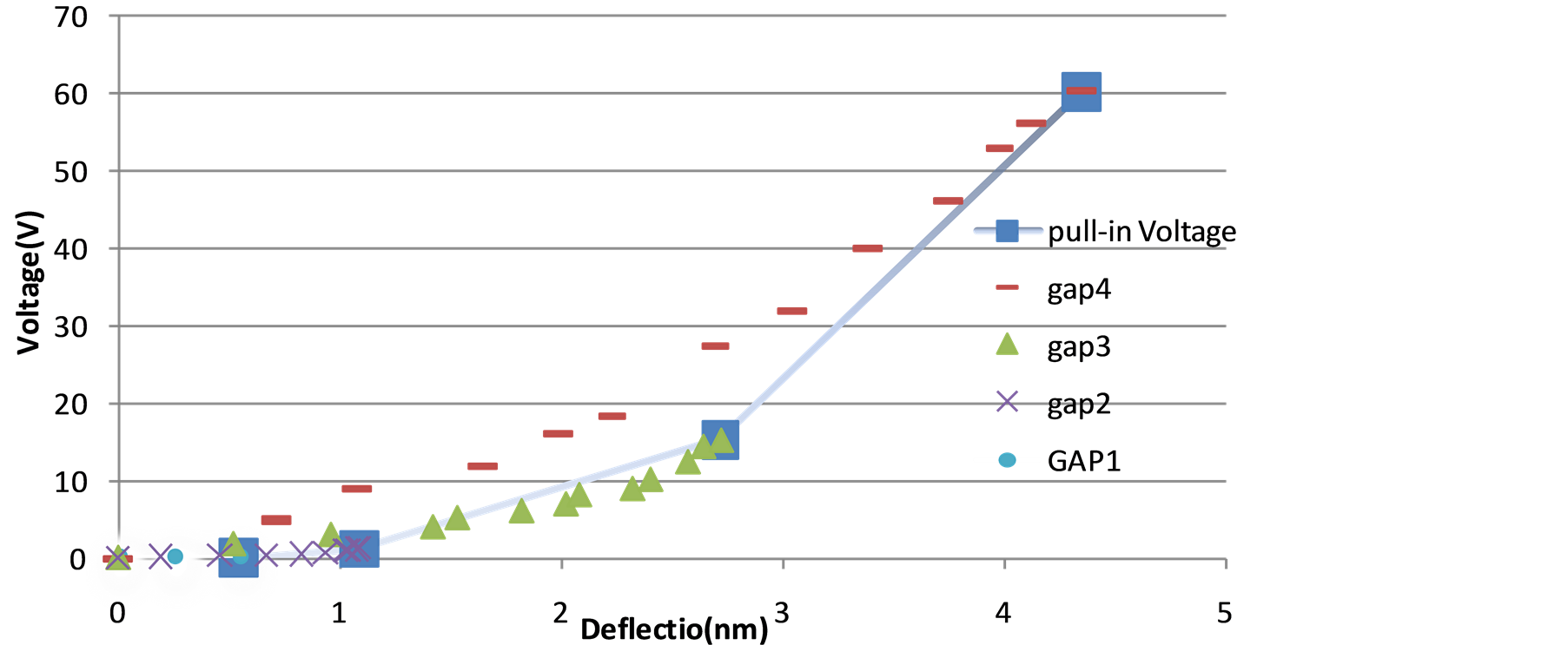
Figure 9. Variation of pull-in voltage versus deflection under clamped-clamped boundary condition regarding various gap values as: G1 = 0.514 nm, G2 = 1.08 nm, G3 = 2.27 nm, G4 = 4.3504 nm.

being obtained by the MD simulations versus their relevant gap value are drawn as a separated curve. It is indicated that the plats initial distance as a part of geometry plays an important role in the pull-in phenomenon of nano-switches.

The pull-in voltage versus gap values in case of investigation of boundary condition (fixed plates at two sides and four sides) and vdW effects are respectively illustrated in Figure 10 and Figure 11 which present a nonlinear relation of them. In the Figure 11 one can clearly perceive the obtained pull-in voltage is directly influenced by the van der Waals force; for a more intensive contact the repulsive force must be defeated, so the plats are so close, it requires a bigger electric field to frustrate vdW repulsive force. To emphasize this concept nano-switch sensitivity is calculated and shown in Figure 12 in two cases of considering and ignoring vdW based on following formula, output(deflection) divided input(actuation voltage), also the boundary condition is considered into sensitivity. To increase the sensitivity and decrease the pull-in voltage it is viable to increase the degree of freedom of plates in addition to decreasing the gap value.

4. Conclusion

In the present work, the pull-in phenomenon in nano-switches considering gap value and boundary condition is investigated. MD simulations as a unique view in simulation of pull-in phenomena are performed in capacitor switches with different boundary conditions and gap values. Pull-in voltages of nano-switches are predictedus-

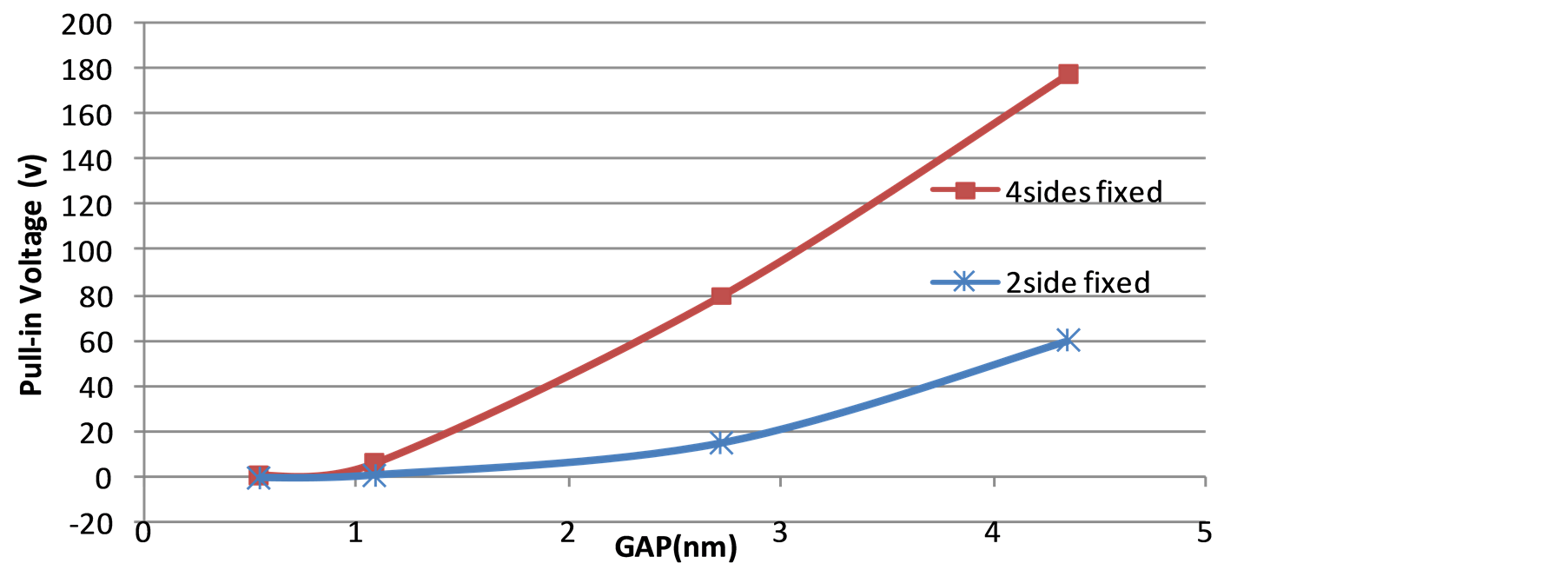
Figure 10. Variation of pull-in voltage versus gap value regarding boundary conditions.

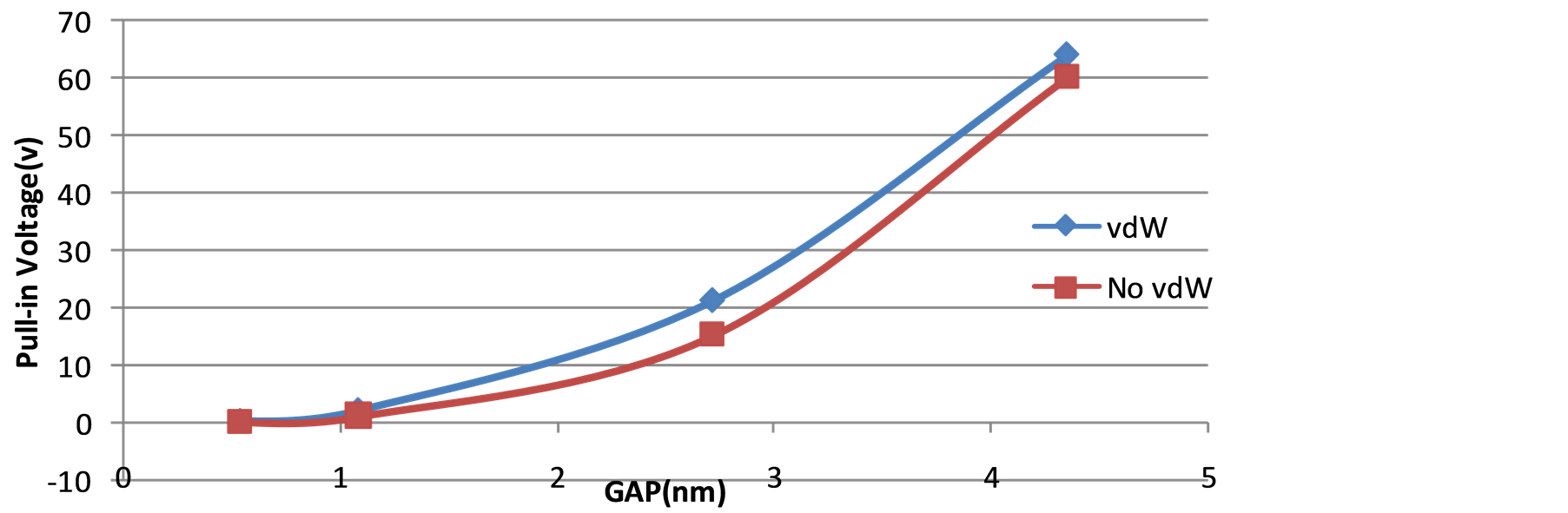
Figure 11. The pull-in voltage versus gap values considering vdW effects.

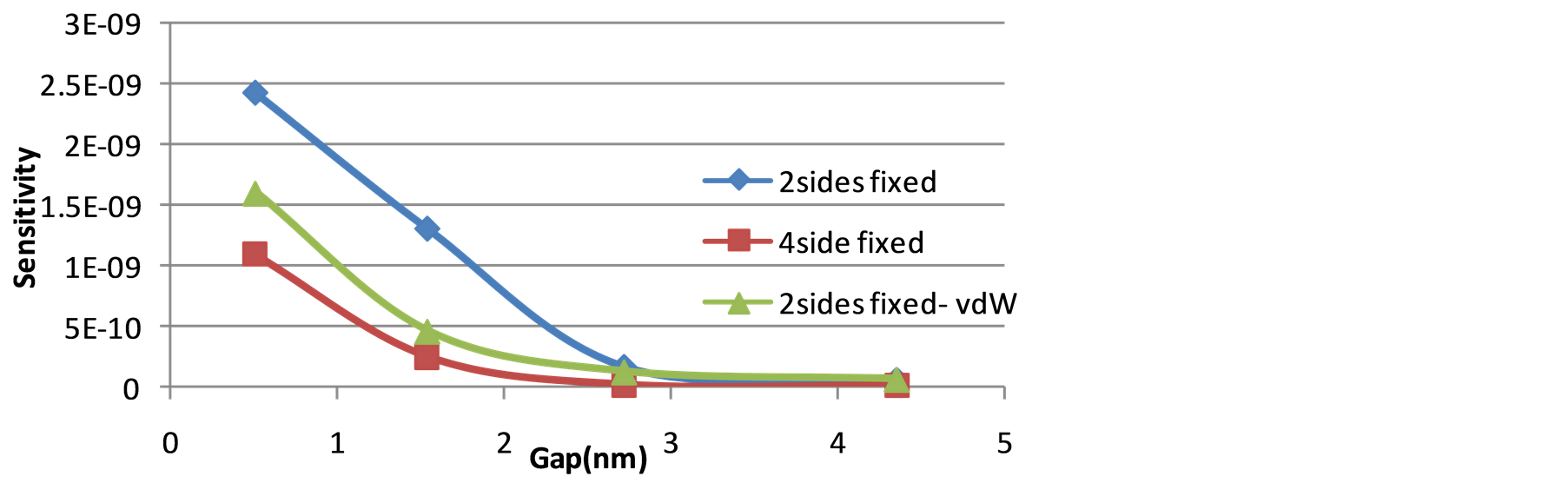
Figure 12. Variation of sensitivity versus gap value.

ing MD. It was revealed that plats’ initial gap has a considerable influence on the pull-in phenomenon in nanoswitches. van der Waals force plays a significant role in plate’s absorption especially in the case of smaller gaps, based on the results that the effects of van der Waals force have intensified in nano-scaled switches and played as an auxiliary force at first; however, for closer contact its role has changed to a repulsive force. Clamped edges compel a resisting force against electrical field which acquires system an extra load for plates contact, hence the pull-in voltage is much bigger in the case of four sides fixed plates in comparison to two sides fixed. Mechanism of pull-in phenomena is analyzed and studied without carrying out time-consuming and high cost experiments; through molecular dynamic it is workable to study each important parameter thoroughly. That is the reason that makes the MD a powerful technique to scrutinizenano-devices and their internal interaction like force field potential, electrostatic forces and van der Waals forces.

References

  1. Hu, Y.-C., Chang, C. and Huang, S. (2004) Some Design Considerations on the Electrostatically Actuated Microstructures. Sensors and Actuators A: Physical, 112, 155-161. http://dx.doi.org/10.1016/j.sna.2003.12.012
  2. Hu, Y.-C., Wang, Y.H. and Huang, S.C. (2004) On the Dynamic and Stability Analysis of Electrostatically Actuated Microstructures. Proceedings of the 1st International Symposium on Micro & Nano Technology (ISMNT-1), III, 2-01.
  3. Pappalardo, M. and Caronti, A. (2002) A New Alternative to Piezoelectric Transducer for NDE and Medical Applications: The Capacitive Ultrasonic Micromachined Transducer (cMUT). University Roma, Rome.
  4. Pappalardo, M. (2002) A New Approach to Ultrasound Generation: The Capacitive Micromachined Transducers. University Roma, Rome.
  5. Rocha, L., Cretu, E. and Wolffenbuttel, R. (2004) Full Characterisation of Pull-In in Single-Sided Clamped Beams. Sensors and Actuators A: Physical, 110, 301-309. http://dx.doi.org/10.1016/j.sna.2003.09.023
  6. Osterberg, P.M. and Senturia, S.D. (1997) M-TEST: A Test Chip for MEMS Material Property Measurement Using Electrostatically Actuated Test Structures. Journal of Microelectromechanical Systems, 6, 107-118. http://dx.doi.org/10.1109/84.585788
  7. Pamidighantam, S., et al. (2002) Pull-In Voltage Analysis of Electrostatically Actuated Beam Structures with FixedFixed and Fixed-Free end Conditions. Journal of Micromechanics and Microengineering, 12, 458-464. http://dx.doi.org/10.1088/0960-1317/12/4/319
  8. Gupta, R.K. (1998) Electrostatic Pull-In Test Structure Design for In-Situ Mechanical Property Measurements of Microelectromechanical Systems (MEMS), Citeseer.
  9. Wei, L.C., Mohammad, A.B. and Kassim, N.M. (2002) Analytical Modeling for Determination of Pull-In Voltage for an Electrostatic Actuated MEMS Cantilever Beam. IEEE International Conference in Semiconductor Electronics, 19-21 December 2002, 233-238.
  10. Ganji, B.A. (2012) Accurate Determination of Pull-In Voltage for MEMS Capacitive Devices with Clamped Square Diaphragm. International Journal of Engineering, 25, 161-166. http://dx.doi.org/10.5829/idosi.ije.2012.25.03b.02
  11. Rocha, L., Cretu, E. and Wolffenbuttel, R. (2003) Displacement Model for Dynamic Pull-In Analysis and Application in Large-Stroke Electrostatic Actuators. Proceedings of Eurosensors 17, 17th European Conference on Solid-State Transducers, Guimar, 20-21 September 2003, 448-451.
  12. Osterberg, P., Yie, H., Cai, X., White, J. and Senturia, S. (1994) Self-Consistent Simulation and Modelling of Electrostatically Deformed Diaphragms. IEEE Workshop on Micro Electro Mechanical Systems, MEMS’94, Oiso, 25-28 January 1994, 28-32.
  13. Hu, Y.C. and Lee, G.D. (2007) A Closed Form Solution for the Pull-In Voltage of the Micro Bridge Tamkang. Journal of Science and Engineering, 10, 147-150.
  14. Fakhrabadi, M.M.S., Rastgoo, A. and Ahmadian, M.T. (2013) Analysis of Pull-In Instability of Electrostatically Actuated Carbon Nanotubes Using the Homotopy Perturbation Method. Journal of Mechanics of Materials and Structures, 8, 385-401. http://dx.doi.org/10.2140/jomms.2013.8.385
  15. Fakhrabadi, M.M.S., Rastgoo, A., Ahmadian, M.T. and Mashhadi, M.M. (2014) Dynamic Analysis of Carbon Nanotubes under Electrostatic Actuation Using Modified Couple Stress Theory. Acta Mechanica, 225, 1523-1535.http://dx.doi.org/10.1007/s00707-013-1013-0
  16. Hu, Y.C., Chang, P.Z. and Chuang, W.C. (2007) An Approximate Analytical Solution to the Pull-In Voltage of a Micro Bridge with an Elastic Boundary. Journal of Micromechanics and Microengineering, 17, 1870-1877.
  17. Kinaret, J.M., Nord, T. and Viefers, S. (2003) A Carbon-Nanotube-Based Nanorelay. Applied Physics Letters, 82, 1287-1289. http://dx.doi.org/10.1063/1.1557324
  18. Dequesnes, M., Rotkin, S. and Aluru, N. (2002) Calculation of Pull-In Voltages for Carbon-Nanotube-Based Nanoelectromechanical Switches. Nanotechnology, 13, 120.
  19. Istadeh, K.H., Kalantarinejad, R., Aghaei, M.J. and Yazdi, M.R.S. (2013) Computational Investigation on H2S Adsorption on the CNT Channel of Conductometric Gas Sensor. Journal of Computational and Theoretical Nanoscience, 10, 2708-2713. http://dx.doi.org/10.1166/jctn.2013.3270
  20. Sarkisov, L. and Harrison, A. (2011) Computational Structure Characterisation Tools in Application to Ordered and Disordered Porous Materials. Molecular Simulation, 37, 1248-1257. http://dx.doi.org/10.1080/08927022.2011.592832
  21. Smith, W., Yong, C. and Rodger, P. (2002) DL_POLY: Application to Molecular Simulation. Molecular Simulation, 28, 385-471. http://dx.doi.org/10.1080/08927020290018769
  22. Hoshyarmanesh, S., Bahrami, M. and Kalantarinejad, R. (2014) A Multiscale Approach in the Computational Modeling of Bio-Physical Environment of Micro-Mechanical Biosensor towards the Prostate Specific Antigen Diagnosis. Journal of Computational and Theoretical Nanoscience, 11, 1374-1384. http://dx.doi.org/10.1166/jctn.2014.3507
  23. Fakhrabadi, M.M.S., Khorasani, P.K., Rastgoo, A. and Ahmadian, M.T. (2013) Molecular Dynamics Simulation of Pull-In Phenomena in Carbon Nanotubes with Stone-Wales Defects. Solid State Communications, 157, 38-44.http://dx.doi.org/10.1016/j.ssc.2012.12.016
  24. Fakhrabadi, M.M.S., Rastgoo, A. and Ahmadian, M.T. (2013) On the Pull-In Instability of Double-Walled Carbon Nanotube-Based Nano Electromechanical Systems with Cross-Linked Walls. Fullerenes, Nanotubes and Carbon Nanostructures.http://dx.doi.org/10.1080/1536383X.2013.787603
  25. Ansari, R. and Sahmani, S. (2013) Prediction of Biaxial Buckling Behavior of Single-Layered Graphene Sheets Based on Nonlocal Plate Models and Molecular Dynamics Simulations. Applied Mathematical Modelling, 37, 7338-7351.http://dx.doi.org/10.1016/j.apm.2013.03.004
  26. Bahrami, M., Kalantarinejad, R., Aghaei, M.J. and Azadi, N. (2011) Simulation of the Interaction of Carbon Nanotubes and External Flow. Journal of Computational and Theoretical Nanoscience, 8, 563-567. http://dx.doi.org/10.1166/jctn.2011.1723
  27. Mohammadi, V., Ansari, R., Shojaei, M.F., Gholami, R. and Sahmani, S. (2013) Size-Dependent Dynamic Pull-In Instability of Hydrostatically and Electrostatically Actuated Circular Microplates. Nonlinear Dynamics, 73, 1515-1526.http://dx.doi.org/10.1007/s11071-013-0882-z
  28. Mousavi, T., Bornassi, S. and Haddadpour, H. (2013) The Effect of Small Scale on the Pull-In Instability of NanoSwitches Using DQM. International Journal of Solids and Structures, 50, 1193-1202.http://dx.doi.org/10.1016/j.ijsolstr.2012.11.024
  29. Wang, K.F. and Wang, B.L. (2014) Influence of Surface Energy on the Non-Linear Pull-In Instability of NanoSwitches. International Journal of Non-Linear Mechanics, 59, 69-75. http://dx.doi.org/10.1016/j.ijnonlinmec.2013.11.004
  30. Behera, D. and Chakraverty, S. (2013) Fuzzy Finite Element Based Solution of Uncertain Static Problems of Structural Mechanics. International Journal of Computer Applications, 59, 69-75.
  31. Wojtaszak, I.A. (1937) The Calculation of Maximum Deflection, Moments, and Shear for Uniformly Loaded Rectangular Plate with Clamped Edge. Journal of Applied Mechanics, Transactions ASME, 4, A173-A176.
  32. Szilard, R. (1973) Theory and Analysis of Plates: Classical and Numerical Methods. Prentice-Hall, Upper Saddle River.
  33. Timoshenko, S., Woinowsky-Krieger, S. and Woinowsky, S. (1959) Theory of Plates and Shells. Vol. 2, McGraw-Hill, New York.
  34. Hansson, T., Oostenbrink, C. and van Gunsteren, W. (2002) Molecular Dynamics Simulations. Current Opinion in Structural Biology, 12, 190-196. http://dx.doi.org/10.1016/S0959-440X(02)00308-1
  35. Phillips, J.C., Braun, R., Wang, W., Gumbart, J., Tajkhorshid, E., Villa, E., et al. (2005) Scalable Molecular Dynamics with NAMD. Journal of Computational Chemistry, 26, 1781-1802. http://dx.doi.org/10.1002/jcc.20289
  36. Verlet, L. (1967) Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Physical Review, 159, 98. http://dx.doi.org/10.1103/PhysRev.159.98
  37. De Luca, S., Todd, B.D., Hansen, J.S. and Daivis, P.J. (2013) Electropumping of Water with Rotating Electric Fields. The Journal of Chemical Physics, 138, Article No. 154712. http://dx.doi.org/10.1063/1.4801033

Appendix

Applied force field parameters of silicon Table A1. Bond force field parameters.

Table A2. Angles force field parameters. 

Table A3. Dihedral force field parameters. 

Table A4. Non-bonded force fields parameters.

NOTES

*Corresponding author.

Journal Menu >>