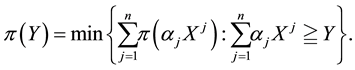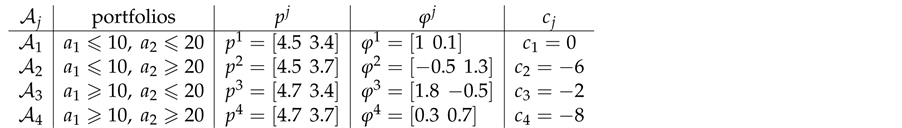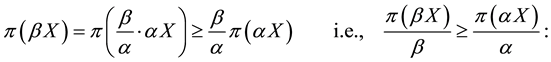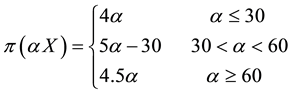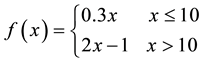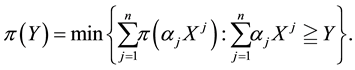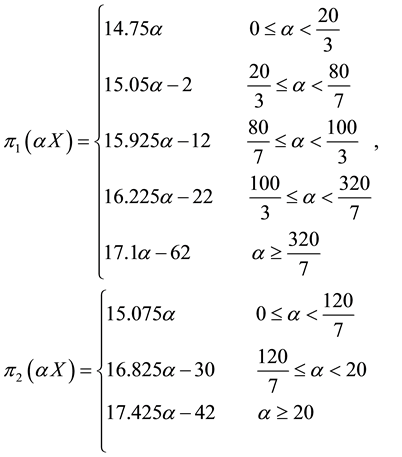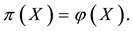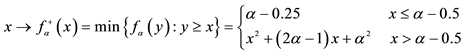Journal of Financial Risk Management
Vol.04 No.03(2015), Article ID:60111,22 pages
10.4236/jfrm.2015.43018
Granular and Star-Shaped Price Systems
Erio Castagnoli1, Marzia De Donno2, Gino Favero2, Paola Modesti2*
1Accademia Nazionale Virgiliana and Università Bocconi, Mantova and Milan, Italy
2Università degli Studi di Parma Dipartimento di Economia, Parma, Italy
Email: *paola.modesti@unipr.it
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2015; accepted 27 September 2015; published 30 September 2015
ABSTRACT
Linear price systems, typically used to model “perfect” markets, are widely known not to accommodate most of the typical frictions featured in “actual” ones. Since some years, “proportional” frictions (taxes, bid-ask spreads, and so on) are modeled by means of sublinear price functionals, which proved to give a more “realistic” description. In this paper, we want to introduce two more classes of functionals, not yet widely used in Mathematical Finance, which provide a further improvement and an even closer adherence to actual markets, namely the class of granular functionals, obtained when the unit prices of traded assets are increasing w.r.t. the traded amount; and the class of star-shaped functionals, obtained when the average unit prices of traded assets are increasing w.r.t. the traded amount. A characterisation of such functionals, together with their relationships with arbitrages and other (more significant) market inefficiencies, is explored.
Keywords:
Arbitrage, Asset Pricing, Super-Hedging, Granularity, Star-Shaped Prices

1. Introduction
One of the first and biggest concerns of Mathematical Finance is to study the prices of a suitable set of risky financial assets of any type, including stocks, indexed bonds, variable rate deposits, derivative securities, and so on. Usually, financial assets are modeled as random variables on some state sets, which are supposed to be the same for every asset in the considered market.
In earlier models, such as the one leading to the celebrated Black, Scholes, and Merton formula for option pricing ( Black & Scholes, 1973 ; Merton, 1973 ), the market is supposed to be a perfect one; in particular, no frictions are featured and no bid-ask spreads or commissions affect prices. Consequently, as it is clearly shown, for instance, in Dothan (1990) , Pliska (1997) , and Björk (1999) , asset prices turn out to be linear with respect to assets themselves, in the sense that the price of the sum of two positions exactly equals the sum of the two separated prices. In such a setting, a central result is found, called the Fundamental Theorem of Asset Pricing, of which dozens of variants are featured in the literature (besides the cited books see, for instance, Delbaen & Schachermayer, 1994 , for quite a general version), which essentially is a representation theorem: roughly speaking, the market prices do not allow for arbitrages (i.e., free gains without risks) if and only if there exist a probability measure called the risk neutral probability―and a discount factor such that prices themselves are (discounted) expected values of the future asset values.
The perfect market model, however, quickly proves to be unfit to provide a good description of realistic markets. For instance, it may be impossible to obtain the exact replication of a given pay-off, and therefore no linear price can be given for it. In such a case, as investigated by Davis & Clark (1994) , the investor may naturally aim at super-hedging it, i.e., at getting at least as much as needed (possibly more) at the minimum possible price. There are also cases when, due to market frictions, a dynamical strategy that exactly replicates the given pay-off may turn out to be more expensive than a super-hedging one: see, e.g., Hodges & Neuberger (1989) . El Karoui & Quenez (1995), Jouini & Kallal (1995), Jouini (1997), and Cvitanić et al. (1999) among others, had investigated such a setting and found a representation theorem: in any case, super-hedging prices turn out to be the maximum of a family of linear prices, which, for instance, Cvitanić et al. (1999) interpreted as prices in “shadow markets”. Moreover, Pham (2000) studied the properties of super-hedging price functionals to find them sublinear: additivity was replaced by subadditivity, meaning that the price of the sum of two positions might be cheaper than the sum of the two separated prices. Since sublinearity entails positive homogeneity besides subadditivity, it turns out to be perfectly fit to describe markets affected by proportional transaction costs (such as taxes or percentage commissions): see, e.g., Pham, Touzi, & Touzi (1999) . Furthermore, sublinearity turned out to be interesting for risk management purposes as well, being the foundational point for the celebrated paper by Artzner et al. (1999) on coherent risk measures.
A class of risk measures more general than the sublinear (i.e., coherent) ones of Artzner et al. (1999) is proposed by Föllmer & Schied (2002) , who replace sublinearity with the weaker convexity1. Inspired by their work, we started wondering whether convex price functions may sensibly be adapted to financial markets: we realized that this was naturally the case, for instance, if unit asset prices are supposed to increase with respect to the traded amount. A representation result can be found, stating that convex price functionals are the upper envelope of a family of affine prices, which admit an interpretation similar to the “shadow markets” of Cvitanić et al. (1999) .
Another, further generalisation, may require average unit asset prices to be increasing, instead of “marginal” ones. This may be the case, for instance, when an agent can choose to buy an asset on several different markets, featuring different increasing unit prices: of course, the purchase will be conducted in such a way that the overall price (or, which is the same, the average unit price) is as low as possible. This leads to a totally new class of price functions, which we name star-shaped because their epigraph turns out to be a star-shaped set with respect to the origin, in the sense of Stewart & Tall (1983) . A representation result can be given for this class of functionals as well, with an interesting economical interpretation.
In the remaining part of this section, the notation used throughout the entire paper is stated, and the current state of the literature about linear and sublinear prices is briefly summarized. Although in different notation, everything exposed here can be found, for instance, in Dothan (1990) , Pliska (1997) , and Björk (1999) for the linear setting, and in Jouini & Kallal (1995) and Koehl & Pham (2000) for the sublinear case. Some examples, in a simple discrete setting, are also given, in order to allow the reader for familiarising with the phenomena under study. Remarkably, we emphasise that, as soon as the price functional is no longer linear, market efficiency is no longer guaranteed by absence of arbitrages only, and that another class of inefficiencies, namely the convenient super-hedgings (roughly speaking, the opportunity to get a better pay-off at a lower price), have to be taken into account.
Section 2 is dedicated to introducing and examining the convex case. After observing that convex functions naturally pop out when pricing by super-hedging by means of assets whose unit price is increasing, we give a generalisation of the Fundamental Theorem of Asset Pricing, and give an interpretation of the representation in terms of market efficiency. It turns out that the market is fully efficient, i.e., that no convenient super-hedging is possible, if all of the “shadow markets” are efficient, whereas absence of arbitrage is guaranteed by a local, less restrictive property.
Star-shaped prices are analysed in Section 3. We show that such functionals are the result of pricing by super- hedging by means of assets whose average price is increasing, and show that such a requirement is actually a proper generalisation of the previous, convex case. We also introduce a new pricing technique, which we may call “super-hedging by chunks” and that mathematically corresponds to the inf-convolution of the price functionals of the “shadow markets”. We show that convexity and star-shape are in some sense “stable” under super-hedging, either in the classical sense or in the “by chunks” one, and analyse the representation of star-shaped functionals in terms of market efficiency.
Finally, Section 4 is dedicated to summarising and comparing the main properties and the efficiency conditions of the four analysed market types and Section 5 features some concluding remarks.
1.1. Notation
A state space
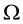 is supposed to be given, and the market
is supposed to be given, and the market
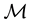 is a set of (real valued) random variables2
is a set of (real valued) random variables2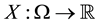 : every
: every
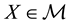 is identified with an asset, in the sense that the (random) value attained by X corresponds to the pay-off (or the market value) of the considered asset at a suitable maturity. We are supposing that the uncertainty is resolved in a single time period: in other words, the models we encompass are of a static, not dynamic, type. We write
is identified with an asset, in the sense that the (random) value attained by X corresponds to the pay-off (or the market value) of the considered asset at a suitable maturity. We are supposing that the uncertainty is resolved in a single time period: in other words, the models we encompass are of a static, not dynamic, type. We write
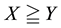 (respectively,
(respectively,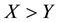 ) to intend that
) to intend that
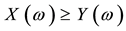 (respectively,
(respectively,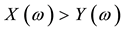 ) for every
) for every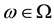 , where
, where
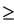 indicates the usual weak inequality between real numbers.
indicates the usual weak inequality between real numbers.
We shall suppose one of the classical “perfect market hypotheses” to hold, requiring every asset
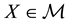 to be infinitely available (there is no “maximum tradable amount”) and divisible (it is possible to buy any fraction of it); furthermore, short sales are allowed. This translates into the fact that, for every
to be infinitely available (there is no “maximum tradable amount”) and divisible (it is possible to buy any fraction of it); furthermore, short sales are allowed. This translates into the fact that, for every
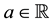 and every
and every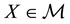 , the investor can hold the position
, the investor can hold the position
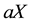 (where
(where
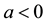 indicates short sale of
indicates short sale of
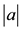 units of X). Of course, several assets
units of X). Of course, several assets
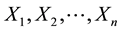
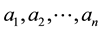

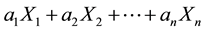
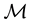
Giving a price to every traded asset
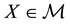
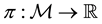

• An arbitrage (see, e.g.,
Björk, 1999
and
Pliska, 1997
) if there exist a


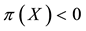
• A convenient super-hedging (quite a recent concept: see, e.g.,
Castagnoli et al., 2009
and
Castagnoli et al., 2011
, but also, for instance,
Hodges & Neuberger (1989)
, who observe the phenomenon although without specifically titling it) if there exist



Of course, the basic laws of supply and demand imply that neither of the above opportunities, which we shall jointly refer to as inefficiencies, should hold in a market: in both cases, the demand pressure on X would quickly lead its price
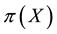
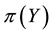
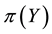
•
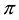
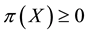

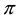
•



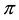
Generally speaking, absence of arbitrages has the nature of a local property, because it only involves the behaviour of the price functional


It is noteworthy as well that there are no general links between positivity and monotonicity. Take for instance,

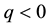


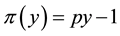
not positive (because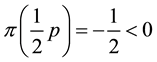

Note also that, for every
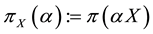
Remark 1. We purposefully decided to avoid measurability issues: in particular, we never mentioned the (

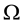
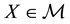

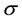
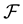


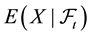
In the same way, the price functional




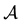

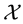
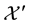
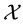
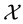
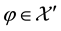

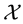
Remark 2. The arbitrage and convenient super-hedging opportunities defined above are often called strong in the literature, and their weak counterparts are defined as follows. Write
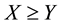
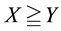

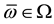
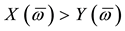
• A weak arbitrage (or an arbitrage of the second kind) if there exists a
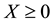
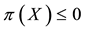

• A weak convenient super-hedging (or a convenient super-hedging of the second kind) if there exist
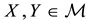
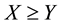
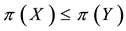

It is straightforward that:
•
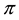
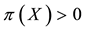
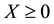

•
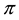

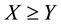
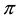
As a matter of fact, when the assets
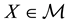
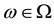
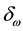
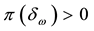

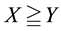
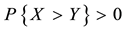
We decided not to take into consideration the weak arbitrages, both for the sake of simplicity and because we want to emphasize that there is no actual need for the a priori probability P to be given. It is nevertheless proper to cite this cases, both for compatibility with the existing literature and to remark that asking for weaker and weaker inefficiencies to be removed from the market translates into stronger and stronger regularity properties for the price functional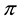
It is also noteworthy that, in order to define weak inefficiencies and to intend the inequalities “almost everywhere”, instead of an a priori probability P, any a priori measure
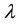

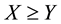
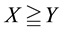

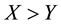
1.2. Perfect Markets: The Linear Case
Besides the infinite availability and divisibility hypotheses cited above, the classical models based on “perfect markets” (see the already cited Björk, 1999 , Pliska, 1997 , and Dothan, 1990 ) ask for three more requirements. First of all, all market agents are fully rational and they aim at maximising their profit; furthermore, all agents are equally informed, without “informational asymmetries”. Secondly, the agents are price takers: they have no possibility to negotiate the prices they see on the markets. Finally, in the market there are no taxes, no bid-ask spreads, no commissions: in a word, there are no frictions.
All of these hypotheses together could be simply summarised in a single property: a market is called perfect if the price functional

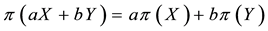

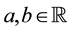

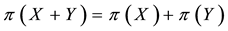
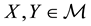
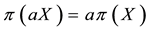





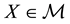

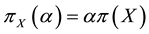
Every linear functional on a linear space attains null value at the “origin” (i.e., at the null vector): as an immediate consequence, an increasing linear functional turns out to be positive as well. Shortly said, for linear functionals, (increasing) monotonicity implies positivity. In the case of linear functionals, moreover, the converse is also true:
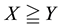

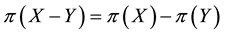
A classical duality result states that, given a linear space
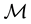



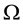
(Lebesgue integrals). Usually, it is said that
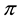
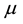
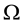
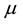
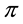
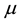
If the “constant” (degenerate) random variables

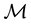




lisation factor”
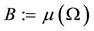

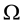
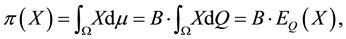
which is classically told by stating that, if no arbitrages are allowed, the current prices of financial assets are the discounted expected values of their final random pay-off. In such a case,
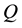
Example 1. Take into consideration the state space


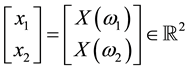
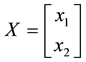
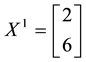

The decision to hold a portfolio obtained by buying (or short selling)


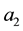
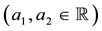
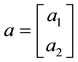
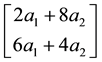
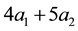

words,


We can simplify the notation by defining the pay-off matrix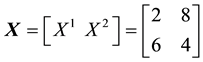


Note that every linear functional
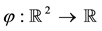

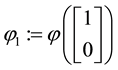
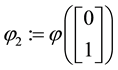
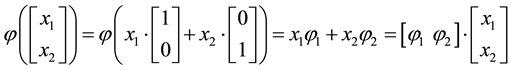
Let us now represent the price functional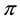


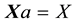
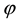
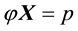
that
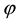
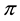

the unique solution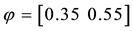

It is immediate to realise that, since both components of

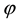
discount factor is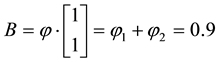
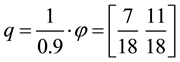
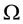
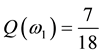
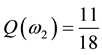
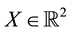
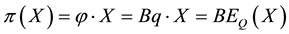
Just for the sake of completeness, suppose that the price of
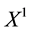
lution of the system
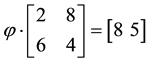
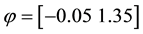



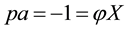
1.3. Proportional Frictions: The Sublinear Case
A natural generalisation of the linear model is to suppose that some frictions affect the market, in order to accommodate, for instance, taxes or commissions. By supposing such frictions to be proportional to the traded amount, it is possible to maintain “half” of the homogeneity property of the price functional: namely,
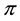

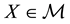


It is clear that such a price functional can no longer be expected to be additive: for instance, an agent buying both


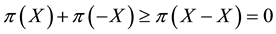
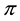
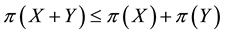
If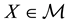
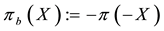
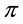
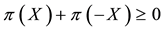
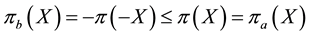

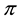
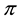
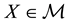

Every sublinear functional attains null value at the origin: therefore, every increasing sublinear functional is positive as well. The converse is not true, as already mentioned: the norm functional is positive, but not increasing. As a consequence, there may be sublinear price functionals that allow for convenient super-hedgings although not allowing for arbitrages. It is noteworthy, nevertheless, that
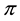

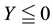

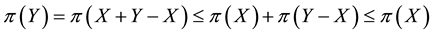

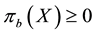

As an immediate consequence of the classical Hahn-Banach Theorem, a sublinear functional
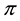
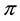
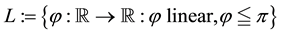


•
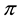

•
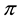
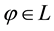
From a mathematical point of view, L is the subdifferential of

According to such a characterisation, if
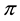
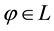
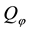
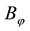
In other words, an efficient sublinear functional acts “as if” a whole set L of “plausible” scenarios

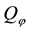

One final consideration is in order. A rational investor who aims at obtaining the pay-off
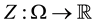
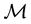

called the cheapest super-hedging price of Z. It is quite clear that, if
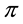

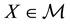
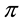
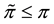

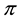
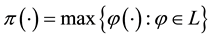

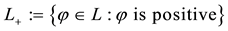
Roughly speaking,
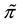
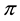
Example 2. Consider the same two assets of Example 1, with pay-off matrix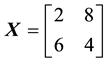
that two price vectors are given, namely that of the ask prices
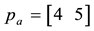
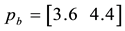
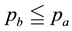

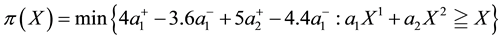

denote the positive and negative part of
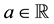


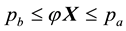


The solutions of the given parametric linear system is the set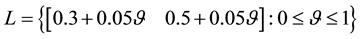

It is possible to build examples when the functional
2. Increasing Unit Prices
The Granular (Convex) Case
Although sublinear prices can indeed capture several features of prices in the “real world”, they still feature unit prices which do not depend on the traded amount. Who trades on actual markets, instead, knows well that unit prices tend to increase with respect to the amount bought, and to decrease with respect to the amount sold. Suppose, for instance, that we are set to buy 1000 units of some asset. Having a look at the offer prices, we see that someone is selling up to 100 units at 3?each, someone else up to 500 units at 3.1?each, someone else up to 600 units at 3.2?each, and so on. This way, we are facing increasing unit prices, and to buy all of the 1000 units we have to pay
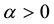
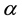
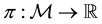
Suppose that, in an exchange list under consideration, the assets
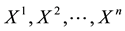
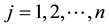
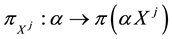
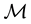

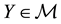
It is immediate to show that such functional



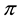
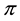
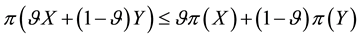

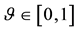
Fenchel’s Theorem ensures that a convex functional
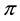
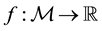
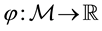
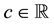
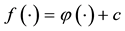
Proposition 1 (Fenchel’s Theorem). Let
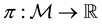
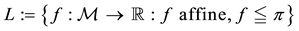
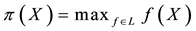
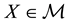
Since every
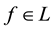

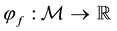
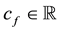

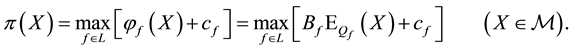
Note that

because
Example 3. Take into consideration the same two assets of Examples 1 and 2, with pay-off matrix,
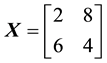
•
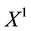
•
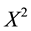
Such prices split the portfolio space into nine regions, identified by four vertices (see Figure 1).
Let
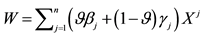
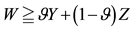
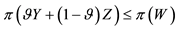
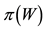
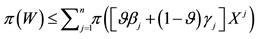
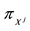
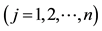
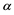
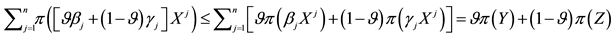

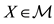
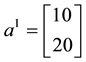
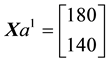
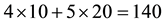
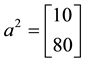
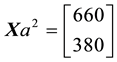
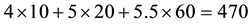



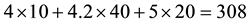
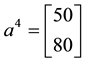
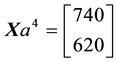
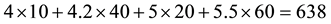
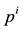
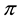
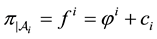
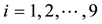
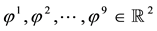
Figure 1. The portfolio space in Example 3.

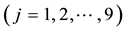
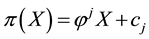
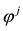

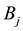
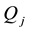
identifies at least nine risk-neutral measures; however, as already pointed out, the risk-neutral measures turn out not to be as important as the properties of the price functional in order to investigate market efficiency.
Note that, if both X and
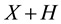
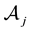

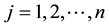

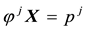

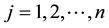
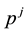
• In

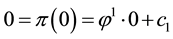
• In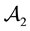

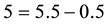
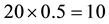
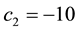
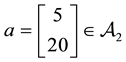
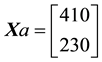
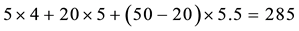
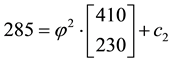
cisely yields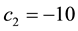
• In


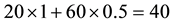

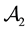


• In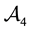
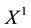
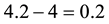


• In
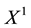
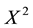
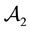
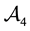

• In
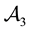
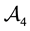
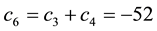
• In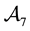
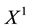
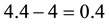



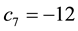
• In
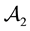
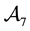
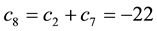
• Finally,
Now, the price of every pay-off
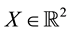
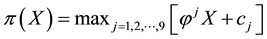

(the maximum price is emphasised). Note that, indeed, X is yielded by the portfolio
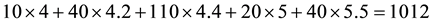
As already mentioned, the price functional

speaking, it is neither sub- nor superadditive: for instance, consider again the pay-off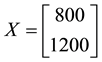

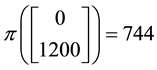
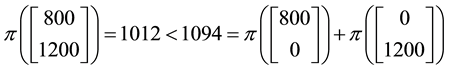


does not correspond to a convenient super-hedging: indeed, it is not possible to buy simultaneously two portfo-
lios yielding the claim
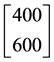
It is still possible to show that, if


convex. Mathematically speaking, the set
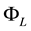


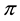

In perfect analogy to what happens for sublinear functionals,
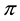

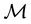
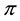
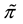
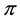
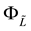



Example 4. On

•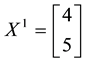
•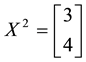
This way,

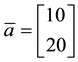
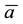

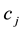
Table 1. The four regions of the portfolio space in Example 4.
previous Example 3, are also shown.
There are positive vectors in
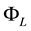
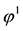
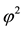
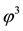
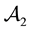
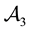
Consider, for instance, the portfolio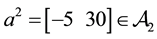

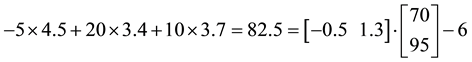
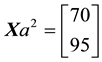
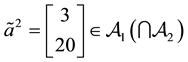



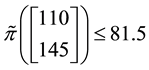
Analogously, the portfolio
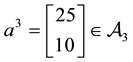
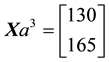


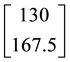

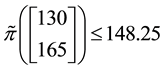
It is possible to prove7 that the “adjusted” functional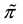
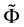

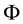


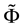



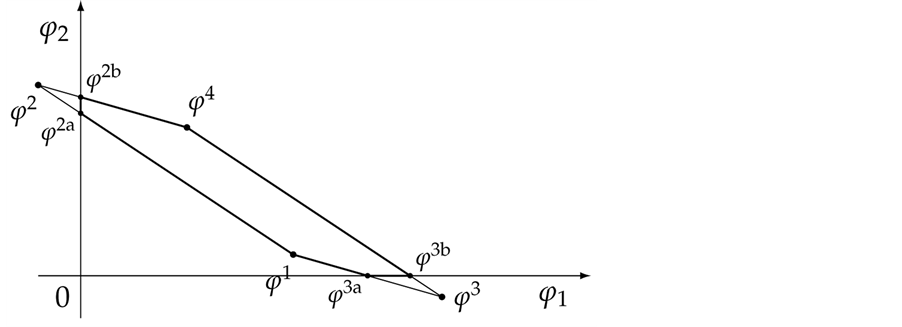
Figure 2. The sets


Table 2. The four regions of the portfolio space in Example 4 after taking advantage of the convenient super-hedging opportunities.
tor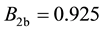
When it comes to positivity, things get a little more complicated: indeed, the fact that

Example 5. Again on

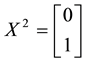
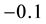


It is clear that arbitrages are possible, because buying
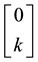

It is still possible to define the cheapest super-hedging price functional
to replace, in the region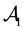
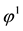
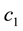
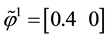
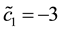
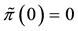
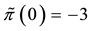
also worth pointing out that such an arbitrage is just “local” in the spirit of Castagnoli et al. (2011) , in the sense that there is an upper bound to the gains that can be obtained by means of arbitrages.
The point is that, as already mentioned, an arbitrage is nothing but a convenient super-hedging of the null vector. In the sublinear case, positive homogeneity ensures that such a convenient super-hedging (meaning both its positive pay-off and its negative price) can be multiplied by an arbitrary positive constant and still remain an arbitrage: this way, if arbitrages are possible, the region of the arbitrage portfolios is always unbounded. In the “granular” convex case, instead, positive homogeneity no longer holds, and therefore arbitrages may be confined to a bounded region, as it happens in Example 5.
As a matter of fact, it is possible to show that a linear functional
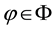

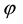
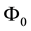

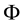
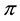
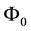

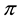
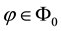
For sublinear functionals, it can be proven that the subdifferential at each point is by necessity a subset of the subdifferential at 0, or, in other words that
The results of this section can be summarized and formalized in the following
Theorem 1. Let

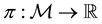

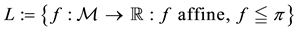
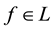


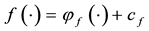
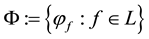

1. L is non-empty, closed and convex;
2. for every
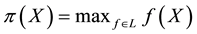
3. for every

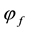
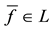
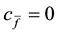
4.

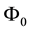

5.

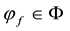
6.

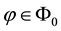
3. Increasing Average Prices
The Star-Shaped Case
Suppose that

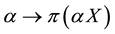
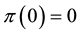
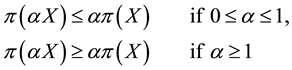
the first inequality comes from the convexity property, because (being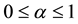

A possible reason why inequalities (3) are sensible in ordinary markets can be seen as follows. Take

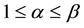
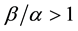
in other words, the supply and demand function of an
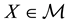
Suppose, for instance, that three agents sell the same asset X on the market. The first one sells it at 4 per unit, but can only provide up to 30 units. The second one sells it at 5 per unit (for any amount). The third one sells it at 4.5 per unit, but only for a minimum order of 50 units. It is clear that the best price that can be obtained to buy

for instance, to buy 50 units of X, the unit price of 4.5 may be obtained, but it is less expensive to buy 30 units from the first agent and 20 from the second, at a total price of
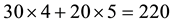

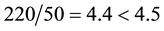
We shall call star-shaped a supply and demand function
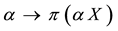

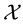
Example 6. The function

is star shaped, because (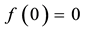

A geometrical interpretation of the star-shaped property is easily deduced from the monotonicity of average prices. Recall that, given any real linear space
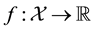

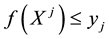
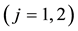


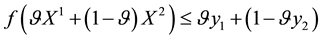
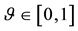
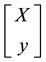

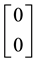



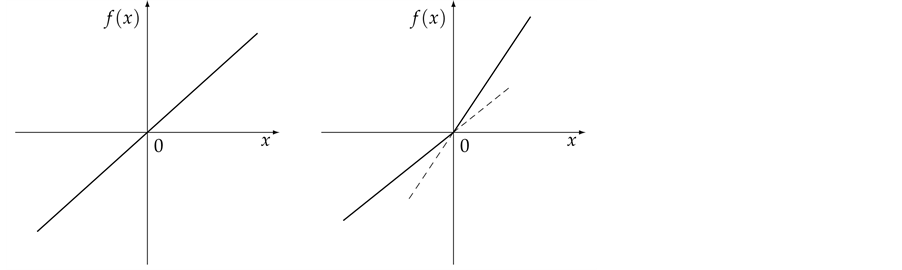

Figure 3. Typical graphs of (a) a linear function; (b) a sublinear (and not linear) function; (c) a convex (and not sublinear) function and (d) a star-shaped (and neither convex nor continuous) function.
Suppose that, in an exchange list under consideration, the assets
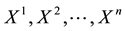

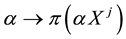


As usual, such a functional immediately turns out to be increasing (and therefore positive, because
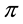
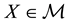
An adaptation of a result by
Chateauneuf & Aouani (2008)
, still unpublished (see
Castagnoli et al., 2009
), shows that a star-shaped functional
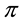
Proposition 2. Let

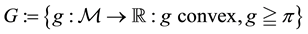
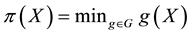
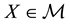
It is indeed possible to prove that only the convex functionals
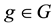
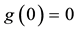


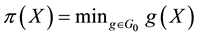
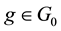
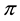

To give an economical interpretation of such a representation, think that several agents are available to sell X on the market. Each agent, corresponding to a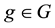
It is worth mentioning that the class of star-shaped functionals is closed under pointwise sup and inf, even for an infinite family of functionals; more explicitly, if
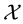
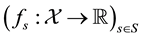
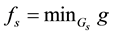
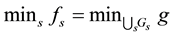

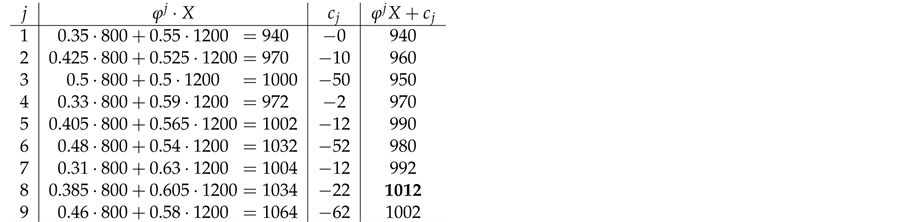
Example 7. Take into consideration the same two assets of Examples 1, 2, and 3, with pay-off matrix
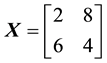


The second agents gives the granular price functional
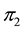

The third agent simply gives a linear price:
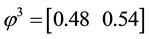
Let us take into consideration some random variables: the details of the calculations (which amount to see in which region the price of the given pay-offs is maximum) are left to the reader.
• For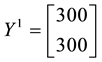
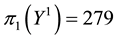
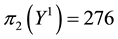
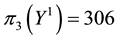

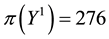
• For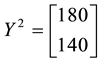
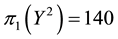
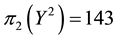
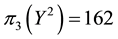
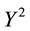
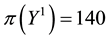
• For
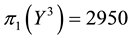

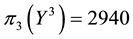
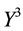
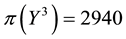
It is then clear that each of the three price systems has a chance to prove the cheapest one and, therefore, that it is effective in determining



single asset: for instance, the three demand functions
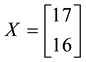
kets turn out to be:
and
note that the marginal price is not increasing (for instance, around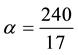
15.075), whereas the average one is.
It is still true that the star-shaped price functional
Notably, if this is the case, instead of the set
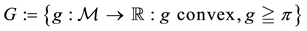

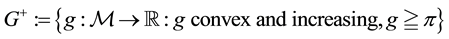
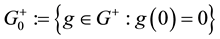
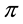
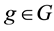
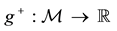


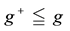
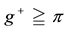
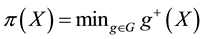


Since it is trivial that the minimum of a family of increasing functionals remains increasing, the above considerations allow us to conclude that a star-shaped functional does not allow for convenient super-hedgings if, and only if, it can be represented as the pointwise minimum of a family of increasing functionals. Note that this is quite analogous to what happened for convex and, before, for sublinear functionals:
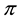
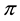
In order to deal with arbitrages, one more consideration is needed. Since, in the economical interpretation we gave, we are free to choose, among several agents, the best one to buy the pay-off X we want to detain, it is reasonable to think that we may prefer to buy several different portfolios from the different agents, in such a way that the overall position matches or, better, super-hedges X. Mathematically speaking, we are dealing with the following object:
Definition 1. Let
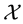
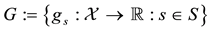
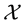
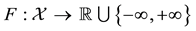
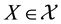
This way, if we are given a set

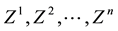
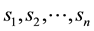
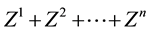
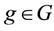
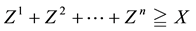

The following proposition holds true, with evident consequences from the financial point of view.
Proposition 3. Let

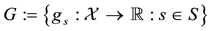

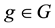
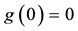
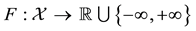
1. if every
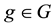
2. if every
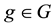
The fact is that, even if every
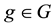
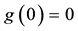
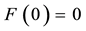
Example 8. Consider again the three markets of Example 7: we saw that
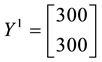
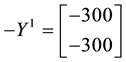
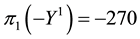

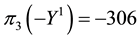
As a consequence, the inf-convolution

Proposition 3, but such that

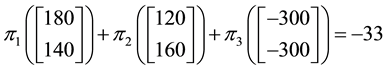
Although the technical details for a complete proof become too complex to be reported here, the key feature can be guessed from the following (and last) example.
Example 9. The function
is increasing, star-shaped and such that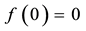



The point that can be proven is that, if a star-shaped price functional is the result of a “best price” over several markets, “cross-market” arbitrages are possible if and only if there are assets whose price around 0 behaves like the function of Example 9. Therefore, the same condition seen for convex functionals applies: a star-shaped price functional does not allow for arbitrages, not even cross-market ones, if and only if the subdifferential



Note that cross-market convenient super-hedgings may still be possible, as Example 8 itself makes clear12: as a consequence of Proposition 3, this is of course bound to happen every time that the price function is (star- shaped but) not convex.
We can summarise the results of this section in the following:
Theorem 2. Let


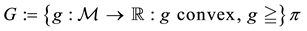
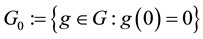

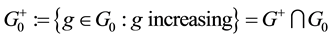

1. G and
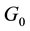
2. for every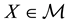
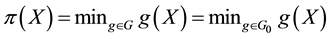
3.

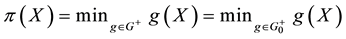
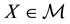
4.


Remark 3. In this section, we have seen two ways to build the overall supply and demand function of a given asset in the case when several “markets” are available.
1. In the first case, seen at the beginning of the section, we supposed that the agent simply chooses the “best market”: implicitly, we imposed that every single trade can only happen with a single agent. In such a case, the market is chosen where the total price, or (which is the same) the average price, is the minimum one.
2. In the second case, by using the “inf-convolution” technique, we supposed that the agent is free to split the desired position into “chunks” and buy the various “chunks” separately on the various markets. This way, for every single additional unit, the agent chooses the market where the marginal price is the minimum one.
Depending on the type of price functionals on the “original” market, we saw that:
1. In the first case, when all of the markets feature either a convex or a star-shaped price functional, the overall price functional turns out to be star-shaped: we pointed indeed out that an increasing average price is obtained;
2. In the second case, the overall price functionals inherit the convexity or the star-shape of the original functions (namely, it is convex if all of the original pricing functionals are, and star-shaped likewise): the minimum marginal price is chosen, and yet it need not be increasing unless it is in the original markets already.
In some sense, we have found that convexity and star-shape are quite “stable” properties in financial markets.
Of course, several other “rules” can be imagined: for instance, some markets may be only available for purchases, or for sales, or only some particular amounts can be bought (not just with a minimum or a maximum amount, as seen in the beginning of this section, but for instance for multiples of some “size” only), in such a way that the offer price function turns out not even to be star-shaped. Anyway, examining such cases goes beyond the scopes of the present paper.
4. Analysis
Four type of price systems, each a generalisation of the previous one, have been examined in this paper. From the last to the first, they are:
1. star-shaped prices:
2. convex (or granular) prices, obtained when G is a singleton:
3. sublinear prices, obtained when (G is a singleton and)

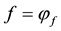
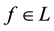
4. linear prices, obtained when (G is a singleton,
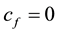

The mentioned fact that both the pointwise minimum and the inf-convolution of a family of star-shaped functionals still are star-shaped seems to suggest that no further generalisation of this type should be fruitful.
For each of the above types, the conditions for absence of arbitrages and of convenient super-hedgings can be examined by taking into consideration the behaviour of the price functionals on the indicator functions

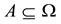
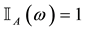

1. Linear prices:
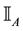


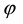
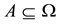

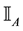
2. Sublinear prices:



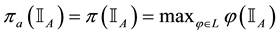
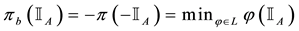
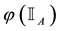
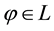
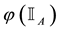
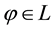

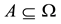
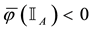
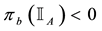
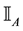

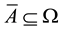
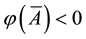
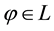

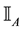
3. Convex prices:

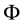
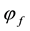

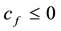
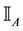
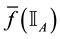

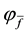
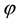
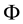
As for arbitrages, since
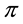
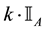
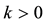

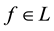




enough to take
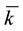
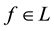

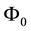
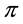
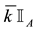
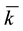

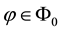
Intuitively, if there is a non-positive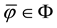
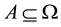
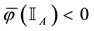
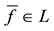
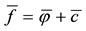
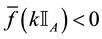
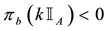
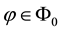

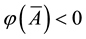
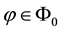
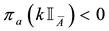
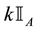
4. Star-shaped prices: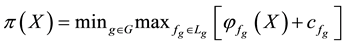
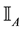
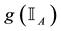
all
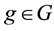
(for instance, it is possible to prove that, for every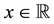
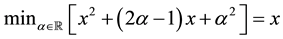
functional, i.e., the identity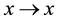
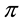
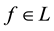
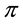
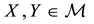
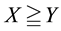
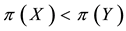
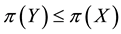
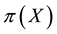
It is clear that moving from linear to star-shaped price systems yields price systems whose properties are closer and closer to what happens in “real” financial markets. Yet, because of the fact that such systems are each the generalisation of the previous one, the “efficiency” conditions for each family of functionals propagates on the further generalisations in a reasonable way. All in all, therefore, these four price systems altogether make quite a versatile toolbox for building financial models, in the sense that, when a financial model is needed, it is easy to “fine tune” the level of precision to suit the needs of the considered problem.
which are all convex and increasing.
5. Conclusion
A classical problem in Mathematical Finance is to study the prices of a suitable set of risky financial assets, modeled as random variables on some state sets, by means of suitable functionals defined on this set of random variables. The properties of the price functional reflect the assumptions on the market. In this paper, we analysed four types of price functionals. We first summarized the properties of the widely known linear functionals, obtained when the market was supposed to be perfect, and of sublinear functionals, which took into account the proportional frictions. Then, we introduced two more classes of functionals which accommodate a wider set of market frictions: granular (convex) functionals, obtained when the unit prices of traded assets were increasing w.r.t. the traded amount, and star-shaped functionals, obtained when the average unit prices of traded assets were increasing w.r.t. the traded amount. We explored some characterizations of such functionals, together with their relationships with arbitrages and market inefficiencies, and performed a final analysis on their effectiveness in allowing for versatile modelling.
Cite this paper
ErioCastagnoli,Marzia DeDonno,GinoFavero,PaolaModesti, (2015) Granular and Star-Shaped Price Systems. Journal of Financial Risk Management,04,227-249. doi: 10.4236/jfrm.2015.43018
References
- 1. Artzner, P., Delbaen, F., Eber, J. M., & Heath, D. (1999). Coherent Measures of Risk. Mathematical Finance, 9, 203-228.
http://dx.doi.org/10.1111/1467-9965.00068 - 2. Björk, T. (1999). Arbitrage Theory in Continuous Time. Oxford: Oxford University Press.
- 3. Black, F., & Scholes, M. (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637-654.
http://dx.doi.org/10.1086/260062 - 4. Castagnoli, E., Favero, G., & Maccheroni, F. (2009). Marchetto, il prezzatore perfetto. Elogio dell'internalità. Milan: Electronic Draft.
- 5. Castagnoli, E., Favero, G., & Modesti, P. (in print). Price Systems for Random Amounts: A Unified Approach. In D. Jakóbczak (Ed.), Analyzing Risk through Probabilistic Modeling in Operations Research. Hershey: IGI Global.
- 6. Castagnoli, E., Favero, G., & Tebaldi, C. (2011). One-Penny Arbitrages, or: A Free Snack without a Free Lunch. Journal of Applied Computer Science & Mathematics, 10, 20-21.
- 7. Cerreia-Vioglio, S., Maccheroni, F., Marinacci, M., & Montrucchio, F. (2011). Risk Measures: Rationality and Diversification. Mathematical Finance, 21, 743-774.
- 8. Chateauneuf, A., & Aouani, Z. (2008). Exact Capacities and Star-Shaped Distorted Probabilities. Mathematical Social Sciences, 56, 185-194.
http://dx.doi.org/10.1016/j.mathsocsci.2008.01.006 - 9. Cvitanic, J., Pham, H., & Touzi, N. (1999). A Closed-Form Solution for the Problem of Super-Replication under Transaction Costs. Finance and Stochastic, 3, 35-54.
http://dx.doi.org/10.1007/s007800050051 - 10. Davis, M. H. A., & Clark, J. M. C. (1994). A Note on Super-Replicating Strategies. Philosophical Transactions: Physical Sciences and Engineering, 347, 485-494.
- 11. de Finetti, B., & Obry, S. (1933). L’optimum nella misura del riscatto. Atti del Secondo Congresso Nazionale di Scienza delle Assicurazioni, 2, 99-123.
- 12. Delbaen, F., & Schachermayer, W. (1994). A General Version of the Fundamental Theorem of Asset Pricing. Mathematische Annalen, 300, 463-520.
http://dx.doi.org/10.1007/BF01450498 - 13. Dothan, M. U. (1990). Prices in Financial Markets. Oxford: Oxford University Press.
- 14. El Karoui, N., & Quenez, M. C. (1995). Dynamic Programming and Pricing of Contingent Claims in an Incomplete Market. SIAM Journal on Control and Optimization, 33, 29-66.
http://dx.doi.org/10.1137/S0363012992232579 - 15. El Karoui, N., & Ravanelli, C. (2009). Cash Sub-Additive Risk Measures and Interest Rate Ambiguity. Mathematical Finance, 19, 561-590.
http://dx.doi.org/10.1111/j.1467-9965.2009.00380.x - 16. Föllmer, H., & Schied, A. (2002). Convex Measures of Risk and Trading Constraints. Finance and Stochastic, 6, 429-447.
http://dx.doi.org/10.1007/s007800200072 - 17. Hodges, S. D., & Neuberger, A. (1989). Optimal Replication of Contingent Claims under Transaction Costs. The Review of Futures Markets, 8, 222-239.
- 18. Jouini, E. (1997). Market Imperfections, Equilibrium and Arbitrage. Lecture Notes in Mathematics, 1656, 247-307.
http://dx.doi.org/10.1007/BFb0092002 - 19. Jouini, E., & Kallal, H. (1995). Martingales and Arbitrage in Securities Markets with Transaction Costs. Journal of Economic Theory, 66, 178-197.
http://dx.doi.org/10.1006/jeth.1995.1037 - 20. Koehl, P. F., & Pham, H. (2000). Sublinear Price Functionals under Portfolio Constraints. Journal of Mathematical Economics, 33, 393-399.
http://dx.doi.org/10.1016/S0304-4068(99)00024-5 - 21. Merton, R. (1973). Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4, 141-183.
http://dx.doi.org/10.2307/3003143 - 22. Pham, H., & Touzi, N. (1999). The Fundamental Theorem of Asset Pricing with Cone Constraints. Annals of Mathematical Economics, 31, 265-279.
http://dx.doi.org/10.1016/s0304-4068(97)00059-1 - 23. Pliska, S. (1997). Introduction to Mathematical Finance: Discrete Time Models (2nd ed.). Malden: Blackwell.
- 24. Rockafellar, R. T. (1970). Convex Analysis. Princeton: Princeton University Press.
http://dx.doi.org/10.1515/9781400873173 - 25. Stewart, I., & Tall, D. (1983). Complex Analysis. Cambridge: Cambridge University Press.
NOTES
*Corresponding author.
1Further generalisations of convex risk measures have been proposed. El Karoui & Ravanelli (2009) remarked that cash additivity, which was a required property of coherent risk measures, should be replaced with cash subadditivity in several cases (e.g., with lack of liquidity for the “riskless” asset). Starting from this, Cerreia-Vioglio et al. (2011) proposed to replace convexity with quasi-convexity in order to better maintain the financial meaning of “diversification” originally connected with the subadditivity requirement. An interpretation of such generalisation in terms of financial prices, though, does not appear to be immediate, and is still under investigation.
2A puzzled reader, wondering about the measurability of such random variables, will find some clarifications in Remark 1 below.
3It is natural to wonder whether such a j always exists. It can be shown (see Pliska, 1997 and Castagnoli et al., 2009 ) that existence is guaranteed by a weaker condition than the absence of arbitrages, called the law of one price (roughly speaking, there is no way to obtain the same pay-off at two different prices): this always happens if, as in this example, the pay-off of the listed assets are linearly independent.
4The dual of the problem
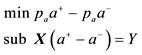

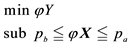


5Suppose that



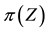


6To prove the inequality, suppose that the cheapest (super) hedges for

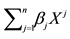
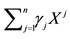

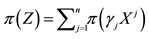
7We confine ourselves to a few hints, in order to help a reader possibly interested in finding a method into this madness. In the region


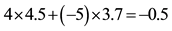
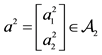
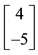
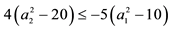



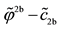
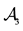
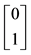
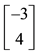
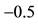
8In the case when
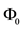
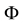
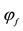

9Define, indeed
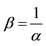
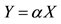
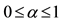
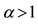


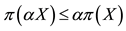

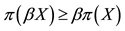
10We are supposing here that the three “markets” share the exchange list, i.e., that the same assets are exchanged on the three markets. This is just chosen in order to avoid further complications: indeed, on different markets, different assets could be quoted and exchanged.
11For every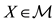

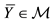
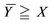
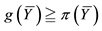


12In Example 8, buying
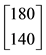

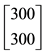
13In the spirit of Remark 1, we should write
14To conclude the short example: in computing