ABSTRACT

The techniques to find appropriate new models for data sets are very popular nowadays among the researchers of this area where existed models in the literature are not suitable. In this paper, a new distribution, generalized inverted Kumaraswamy (GIKum) distribution is introduced. The main aims of this research are to develop a general form of inverted Kumaraswamy (IKum) distribution which is flexible than the IKum distribution and all of its related and sub models. Some properties of GIKum distribution such as measures of central tendency and dispersion, models of stress-strength, limiting distributions, characterization of GIKum distribution and related probability distributions through some specific transformations are derived. The mathematical expressions of reliability function (r.f) and the hazard rate function (hrf) of the GIKum distribution are found and presented through their graphs. The parameters estimation through the maximum likelihood (ML) estimation method is used and the results are applied to the data set of prices of wooden toys of 31 children.

Keywords:

Generalized Inverted Kumaraswamy Distribution, Stress-Strength Models, Maximum Likelihood Estimation

1. Introduction

In the past years, several ways of generating inverted distributions from classic ones were developed and discussed. Calabria and Pulcini [1] defined the inverse Weibull distribution. AL-Dayian [2] introduced a family of distributions that arises naturally from the inverted Burr type XII distribution. Abed El-Kader et al. [3] proposed the inverted Pareto type I distribution and introduced some properties of this class of distributions.

A number of researchers studied the inverted distributions and its applications; for example, Prakash [4] studied the inverted exponential model and Aljuaid [5] presented exponentiated inverted Weibull distribution. The inverted distributions are important in problems related to econometrics, engineering sciences, life testing, financial literature and environmental studies.

Kumaraswamy [6] obtained a distribution, which is derived from beta distribution after fixing some parameters in beta distribution. But it has a closed-form cumulative distribution function which is invertible and for which the moments do exist. The distribution is appropriate to natural phenomena whose outcomes are bounded from both sides, such as the individuals’ heights, test scores, temperatures and hydrological daily data of rain fall (for more details, see Kumaraswamy [6] , Jones [7] , Golizadeh et al. [8] , Sindhu et al. [9] and Sharaf El-Deen et al. [10] ).

Abd Al-Fattah et al. [11] derived the inverted Kumaraswamy (IKum) distribution from Kumaraswamy (Kum) distribution using the transformation $T=x^{-1}-1$ . When $X\sim \text{Kum}\left(\alpha ,\beta \right)$ where $\alpha$ and $\beta$ are shape parameters, then the $T$ has a IKum distribution with probability density function (pdf)

$F\left(x;\alpha ,\beta \right)={\left(1-{\left(1+x\right)}^{-\alpha }\right)}^{\beta }\text{,}x>0;\alpha ,\beta >0$ (1)

Iqbal et al. generalized the some continuous distribution by using power transformation. Here we use the same technique to find the cdf of generalized inverted Kumaraswamy distribution (GIKum) and is derived by using transformation $t=x^{\gamma }$ which has closed form and is as under

$F\left(x\right)={\left(1-{\left(1+x^{\gamma }\right)}^{-\beta }\right)}^{\alpha },\alpha ,\beta ,\gamma >0$ (2)

Assuming X is a random variable with shape parameters, $\alpha >0$ , $\beta >0$ and $\gamma >0$ the pdf of GIKum is as

#Math_13# (3)

This model is flexible enough to accommodate both monotonic as well as non-monotonic failure rates.

From Figure 1, the GIKum pdf is positively skewed distribution for all parameters’ values and for $\beta =0.5$ , the GIKum pdf is monotonically decreasing. The asymptote of distribution occurs at $x\to \infty$ and is $\alpha \beta \gamma x^{\gamma -1}{\left(1+x^{\gamma }\right)}^{-\left(\alpha +1\right)}$ . The GIKum pdf has the higher peaked for larger $\alpha$ when other parameters values are fixed.

This paper is arranged as follows. In Section 2, some statistical properties of GIKum distribution such as measures of central tendency and dispersion, reliability function (rf) hazard rate functions (hrf) and reverse hazard function, models of stress-strength, mode, moment generating function, the asymptotic mean and variance, incomplete moments, quantile functions, mean deviation and

Renyi entropy are analyzed [12] . In Section 3, sub-models and limiting distributions of GIKum and the related probability distributions of GIKum are derived through some specific transformations. In Section 4, characterization of GIKum is presented. In Section 5, maximum likelihood estimation for the parameters is obtained with some useful remarks and a theorem. Finally, in Section 6, we have applied this on real data set of prices of wooden toys of 31 children.

2. The Main Properties of the Generalized Inverted Kumaraswamy Distribution

This section is devoted to illustrate some statistical properties of GIKum distribution, through rf, some models of the stress-strength, hrf and reversed hazard (rhrf), measures of central tendency and dispersion, graphical and order statistics (Figure 2).

2.1. Reliability Function

$R_1\left(x;\alpha ,\beta ,\gamma \right)=P\left(T>x\right)=1-{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\beta }\text{,}t>0,\alpha ,\beta ,\gamma >0$ (4)

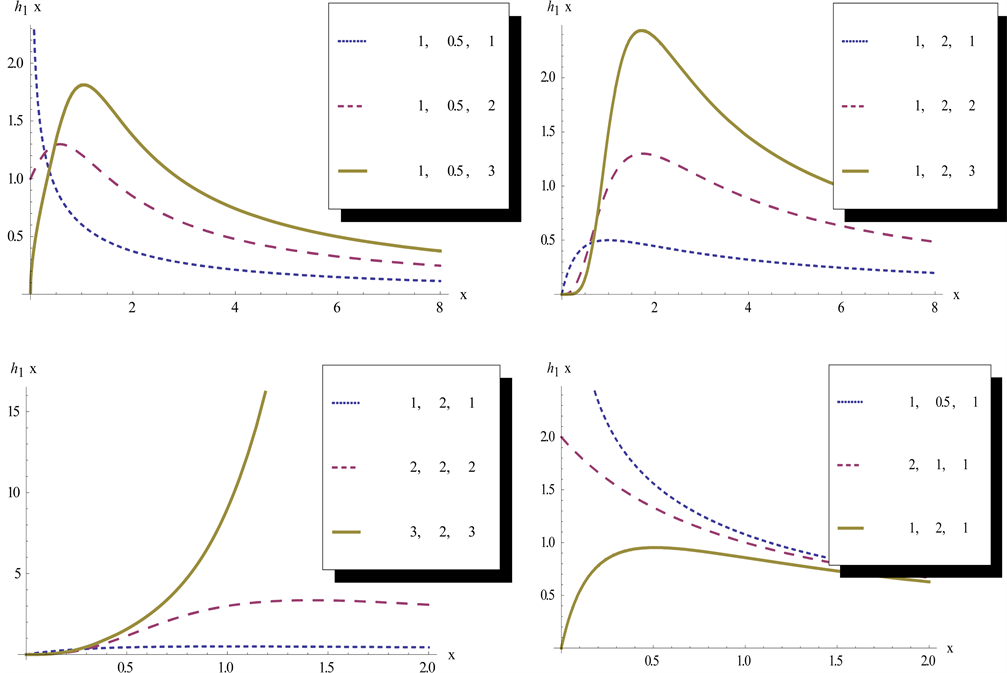
2.2. Hazard Function and Reverse Hazard Function of GIKum Distribution (Figure 3 & Figure 4)

Suppose if $G\left(x\right)$ the distribution function is defined as

$G\left(x\right)=1-{\left(1+x^{\gamma }\right)}^{-\alpha },\alpha ,\gamma >0$

then [2] written as

$F\left(x\right)={\left(G\left(x\right)\right)}^{\beta },\beta >0$

The hazard rate function (hrf) denoted by $\lambda \left(x\right)$ and reverse hrf denoted by ${\lambda }^{*}\left(x\right)$ are given, respectively, by

${\lambda }_F\left(x\right)=\frac{\alpha \beta \gamma x^{\gamma -1}{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\beta -1}}{{\left(1+x^{\gamma }\right)}^{\left(\alpha +1\right)}\left(1-{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\beta }\right)},x>0,\alpha ,\beta ,\gamma >0$

and

${\lambda }_F^{*}\left(x\right)=\frac{\alpha \beta \gamma x^{\gamma -1}{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{-1}}{{\left(1+x^{\gamma }\right)}^{\left(\alpha +1\right)}},x>0,\alpha ,\beta ,\gamma >0$

and their relations are shown as under

${\lambda }_F\left(x\right)=\beta \left(1-{\delta }_{\beta }\left(x\right)\right){\lambda }_G\left(x\right),\beta >0$

where

${\delta }_{\beta }\left(x\right)=\frac{1-{\left(G\left(x\right)\right)}^{\alpha -1}}{1-{\left(G\left(x\right)\right)}^{\alpha }}$

For $0<\alpha <1$ ${\lambda }_F\left(x\right)\ge {\lambda }_G\left(x\right)$

For $\alpha \ge 1$ $0\le {\lambda }_F\left(x\right)\le {\lambda }_G\left(x\right)$ .

and relation in reverse hrf of F and G as ${\lambda }_F^{*}\left(x\right)=\beta {\lambda }_G^{*}\left(x\right)$ and cdf can be expressed as

$F\left(x\right)=\frac{{\lambda }_F\left(x\right)}{{\lambda }_F\left(x\right)+{\lambda }_F^{*}\left(x\right)}$ .

2.3. Some Stress-Strength Models

1) Let T be the stress component subject strength Y, the random variables T and Y are independent distributions from GIKum (α, β, γ) respectively, then the reliability function is given by;

$R_2(t)=P(T<Y)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{y}{\int }}\alpha {\beta }_2\gamma t^{\gamma -1}\frac{{\left(1-{\left(1+t^{\gamma }\right)}^{-\alpha }\right)}^{{\beta }_1+{\beta }_2-1}}{{\left(1+t^{\gamma }\right)}^{\left(\alpha +1\right)}}}}\text{dtdy}=\frac{{\beta }_2}{{\beta }_1+{\beta }_2}$

Let T and Z be two independent random stress variables with known cdfs (𝑡), 𝐺(𝑧), and both follow $GIKum\left({\alpha }_1,{\beta }_1,\gamma \right)$ and $GIKum\left({\alpha }_2,{\beta }_2,\gamma \right)$ respectively, and let Y be, independent of T and Z, a random strength variable follow to $GIKum\left({\alpha }_2,{\beta }_2,\gamma \right)$

$\begin{array}{c}{R}_3\left(t\right)=P\left(T<Y<Z\right)\\ ={\displaystyle \underset{0}{\overset{\infty }{\int }}{H}_T\left(y\right)\text{d}{F}_Y\left(y\right)}-{\displaystyle \underset{0}{\overset{\infty }{\int }}{H}_T\left(y\right)G_z\left(y\right)\text{d}{F}_Y\left(y\right)}\\ ={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{y}{\int }}\alpha {\beta }_2\gamma t^{\gamma -1}{\left(1+t^{\gamma }\right)}^{-\left(\alpha +1\right)}\cdot {\left(1-{\left(1+t^{\gamma }\right)}^{-\alpha }\right)}^{{\beta }_1+{\beta }_2-1}}}\\ -{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{y}{\int }}\alpha {\beta }_2\gamma t^{\gamma -1}\cdot {\left(1+t^{\gamma }\right)}^{-\left(\alpha +1\right)}\cdot {\left(1-{\left(1+t^{\gamma }\right)}^{-\alpha }\right)}^{{\beta }_1+{\beta }_2+{\beta }_3-1}}}\\ =\frac{{\beta }_2{\beta }_3}{\left({\beta }_1+{\beta }_2\right)\left({\beta }_1+{\beta }_2+{\beta }_3\right)}\end{array}$

2.4. The Mode of the Generalized Inverted Kumaraswamy Distribution

The mode of the GIKum distribution is given by

$\frac{\partial \ln f}{\partial x}=\frac{\left(\gamma -1\right)}{x}-\frac{\left(\alpha +1\right)\cdot \gamma x^{\gamma -1}}{\left(1+x^{\gamma }\right)}+\frac{\alpha \cdot \gamma \left(\beta -1\right)\cdot x^{\gamma -1}}{\left(1+x^{\gamma }\right)\cdot \left({\left(1+x^{\gamma }\right)}^{\alpha }-1\right)}=0$

When $\gamma =1$ , $Mode={\left(\frac{\alpha +1}{\alpha \beta +1}\right)}^{-\frac{1}{\alpha }}-1$

The mode of the GIKum distribution is given by

When $\gamma =1$ , $Mode={\left(\frac{\alpha +1}{\alpha \beta +1}\right)}^{-\frac{1}{\alpha }}-1$

2.5. Quantiles of the Generalized Inverted Kumaraswamy Distribution

The quantile function of the GIKum is given by

$t_q={\left({\left(1-q^{\frac{1}{\beta }}\right)}^{-\frac{1}{\alpha }}-1\right)}^{\frac{1}{\gamma }},0<q<1$

$\text{for}\gamma =1,t_q={\left(1-q^{\frac{1}{\beta }}\right)}^{-\frac{1}{\alpha }}-1,0<q<1$

Special cases can be obtained using [10] such as the second quartile (median), when q = 0.5

2.6. The Central and Non-Central Moments

The r^th non central moment of the GIKum (α, β) distribution is given by

${{\mu }^{\prime }}_s={\displaystyle \sum _{j=0}^{\frac{s}{\gamma }}\left(\begin{array}{l}\frac{s}{\gamma }\\ j\end{array}\right)}{\left(-1\right)}^{\frac{s}{\gamma }-j}\beta B\left(i\alpha +1,\beta \right),\alpha ,\beta ,\gamma >0$

where $B\left(.,.\right)$ is the beta function.

The central moments can be obtained by applying the general relation in central and the non-central moments which as follows

${\mu }_r={\displaystyle \sum _{i=0}^r\left(\begin{array}{l}r\\ i\end{array}\right)}{\left(-1\right)}^{r-i}{\mu }^i{\widehat{\mu }}_{r-i},r=1,2,3,\cdots ,$

Thus the mean and variance of GIKum when $\gamma =1$ are given by

$\mu =\beta B\left(1-\frac{1}{\alpha },\beta \right)-1,\alpha \ge 1$ ,

and

${\mu }_2=\beta B\left(1-\frac{2}{\alpha },\beta \right)-{\left(\beta B\left(1-\frac{2}{\alpha },\beta \right)\right)}^2\text{,}\alpha \ge 1$

The Asymptotic Mean and Variance

If $W\sim \exp \left(\beta \right)$ with $\mu =\frac{1}{\beta }$ and ${\sigma }^2=\frac{1}{{\beta }^2}$ then the variable

$T=g\left(W\right)={\left({\left(1-{\text{e}}^{-w}\right)}^{-\frac{1}{\alpha }}-1\right)}^{\frac{1}{\gamma }}\sim \text{GIKum}\left(\alpha ,\beta ,\gamma \right)$ . This relation can be used to approximate the mean and variance

$E\left(T\right)\approx g\left(\mu \right)+\frac{1}{2}{\sigma }^2{g}^{\prime }\left(\mu \right)$

$V\left(T\right)\approx {\sigma }^2{\left(g^{\prime }\left(\mu \right)\right)}^2$

where

$g\left(\mu \right)={\left({\left(1-{\text{e}}^{-\mu }\right)}^{-\frac{1}{\alpha }}-1\right)}^{\frac{1}{\gamma }}$

$g^{\prime }\left(\mu \right)=\frac{1}{\gamma }{\left({\left(1-{\text{e}}^{-\mu }\right)}^{-\frac{1}{\alpha }}-1\right)}^{\frac{1}{\gamma }-1}\cdot \left(-\frac{1}{\alpha }{\left(1-{\text{e}}^{-\mu }\right)}^{-\left(\frac{1}{\alpha }+1\right)}{\text{e}}^{-\mu }\right)$

$V\left(T\right)\approx \frac{1}{{\beta }^2}\left(\frac{1}{{\alpha }^2{\gamma }^2}{\left({\left(1-{\text{e}}^{-\frac{1}{\beta }}\right)}^{-\frac{1}{\alpha }}-1\right)}^{\frac{2}{\gamma }-2}\left({\left(1-{\text{e}}^{-\frac{1}{\beta }}\right)}^{-\left(\frac{2}{\alpha }+2\right)}{\text{e}}^{-\frac{2}{\beta }}\right)\right)$

2.7. Moments and Moment Generating Function

$E\left(Y^r\right)=\alpha B\left(1+r/\gamma ,\alpha -r\right)\text{,}r/\gamma <\alpha$

$E\left(X^r\right)={\displaystyle \sum _{i=0}^{\infty }{q}_i\cdot \alpha \cdot \left(i+1\right)B\left(1+r/\gamma ,\alpha \left(i+1\right)-r/\gamma \right)}\text{,}r/\gamma <\alpha$

$M\left(t\right)={\displaystyle \sum _{s=0}^{\infty }{\displaystyle \sum _{i=0}^{\infty }{q}_i\alpha \left(i+1\right)B\left(1+s/\gamma ,\alpha \left(i+1\right)-s/\gamma \right)\frac{t^s}{s!}}}\text{,for}s/\gamma <\alpha$

where $q_i$ is defined as

$q_i={\displaystyle \sum _{j=0}^{\infty }\frac{\beta \cdot {\left(-1\right)}^{j+i}\Gamma \left(a+b\right)\cdot \Gamma \left(\beta \cdot \left(a+j\right)\right)}{i!\Gamma \left(a\right)j!\left(i+1\right)\Gamma \left(b-j\right)\Gamma \left(\beta \left(a+j\right)-i\right)}}$

2.8. Quantile Functions

$\begin{array}{l}x=Q\left(u\right)={\left[{\left[1-{\left(Q_{a,b}\left(u\right)\right)}^{1/\beta }\right]}^{-1/\alpha }-1\right]}^{1/\gamma },u\in \left(0,1\right)\\ X={\left[{\left[1-{\left(V\right)}^{1/\beta }\right]}^{-1/\alpha }-1\right]}^{1/\gamma }\\ SK=\frac{Q\left(3.0/4.0\right)+Q\left(1.0/4.0\right)-2.0Q\left(1.0/2.0\right)}{Q\left(3.0/4.0\right)-Q\left(1.0/4.0\right)},\\ KR=\frac{\left[Q\left(7.0/8.0\right)-Q\left(5.0/8.0\right)\right]+\left[Q\left(3.0/8.0\right)-Q\left(1.0/8.0\right)\right]}{\left[Q\left(6.0/8.0\right)-Q\left(2.0/8.0\right)\right]}\end{array}$

2.9. Incomplete Moments

The r^th incomplete moments $m_r\left(z\right)$ of GIKum distribution is

$\begin{array}{l}{m}_r\left(z\right)={\displaystyle \underset{0}{\overset{z}{\int }}{y}^{r}g\left(\gamma ,\alpha \right)\text{d}y}=k{B}_{z^{\gamma }}\left(1+r/\gamma ,\alpha -r/\gamma \right)\text{,}r/\gamma <\alpha \\ m_r\left(z\right)={\displaystyle \sum _{i=0}^{\infty }{q}_i\alpha \left(i+1\right)B_{z^{\gamma }}\left(1+r/\gamma ,\alpha \left(i+1\right)-r/\gamma \right)}\text{,}r/\gamma <\alpha \end{array}$

where

$q_i={\displaystyle \sum _{j=0}^{\infty }\frac{\beta {\left(-1\right)}^{j+i}\Gamma \left(a+b\right)\Gamma \left(\beta \left(a+j\right)\right)}{i!\Gamma \left(a\right)j!\left(i+1\right)\Gamma \left(b-j\right)\Gamma \left(\beta \left(a+j\right)-i\right)}}$

2.10. Mean Deviation

The mean deviation $D\left(\mu \right)$ of GIKum

$\begin{array}{c}D\left(\mu \right)=E\left|X-\mu \right|=2\mu F\left(\mu \right)-2m_1\left(\mu \right)\\ =2\beta B\left(1-\frac{1}{\alpha },\beta \right){\left(1-{\left(1+{\left(\beta B\left(1-\frac{1}{\alpha },\beta \right)-1\right)}^{\gamma }\right)}^{-\beta }\right)}^{\alpha }\\ -2{\displaystyle \sum _{i=0}^{\infty }{q}_i\alpha \left(i+1\right)}{B}_{{\left(\beta B\left(1-\frac{1}{\alpha },\beta \right)-1\right)}^{\gamma }}\left(1+1/\gamma ,\alpha \left(i+1\right)-1/\gamma \right)\end{array}$

2.11. Rényi Entropy

The Rényi entropy of an r.v X is defined as

$I_R\left(\delta \right)=\frac{1}{1.0-\delta }\log I\left(\delta \right),\delta >0,\delta \ne 1$

where $I\left(\delta \right)={\displaystyle \int f^{\delta }\left(x\right)\text{d}x}$ , $\delta >0$ and $\delta \ne 1$ using the pdf of GIKum

$\begin{array}{l}I\left(\delta \right)\\ =\frac{{\alpha }^{\delta }{\beta }^{\delta }{\gamma }^{\delta }}{B^{\delta }\left(a,b\right)}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^{\delta \left(\gamma -1\right)}{\left(1+x^{\gamma }\right)}^{-\delta \left(\alpha +1\right)}{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\delta \left(a\beta -1\right)}\times {\left({\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\beta }\right)}^{\delta \left(b-1\right)}}\text{d}x\end{array}$

expanding the last term of integrand through binomial expansion which simplifies as

Again, applying the same expansion we have

Using the transformation $y=x^{\gamma }$ in above expression and simplifying,

$\begin{array}{c}I\left(\delta \right)=\frac{{\alpha }^{\delta }{\beta }^{\delta }{\gamma }^{\delta -1}}{B^{\delta }\left(a,b\right)}{\displaystyle \sum _{i=0}^{\infty }{\displaystyle \sum _{j=0}^{\infty }\left(\begin{array}{c}\delta \left(b-1\right)\\ i\end{array}\right)}\left(\begin{array}{c}\beta \left(i+a\delta \right)-\delta \\ j\end{array}\right){\left(-1\right)}^{i+j}}\\ \times B\left[\left(\frac{\delta \left(\gamma -1\right)+1}{\gamma },\frac{\alpha \left(\delta +j\right)\gamma +\left(\delta -1\right)}{\gamma }\right)\right]\end{array}$

the Rényi entropy, hence, finally reduces to

$\begin{array}{c}{I}_R\left(\delta \right)=\left(\frac{1}{1-\delta }\right)[\delta \log \left(\frac{\alpha \cdot \beta }{B\left(a,b\right)}\right)+\log {\displaystyle \sum _{i=0}^{\infty }{\displaystyle \sum _{j=0}^{\infty }\left(\begin{array}{c}\delta \left(b-1\right)\\ i\end{array}\right)}\left(\begin{array}{c}\beta \left(i+a\delta \right)-\delta \\ j\end{array}\right){\left(-1\right)}^{i+j}}\\ \times B\left[\left(\frac{\delta \left(\gamma -1\right)+1}{\gamma },\frac{\alpha \left(\delta +j\right)\gamma +\left(\delta -1\right)}{\gamma }\right)\right]]\end{array}$

3. Related Distributions

This section discussed some sub-models of GIKum distribution, some relations of the GIKum distribution to other distributions, limiting and several IKum G families of distributions.

3.1. Some Sub-Models

3.1.1. Lomax (Pareto Type II) Distribution

The Lomax (Pareto type II) distribution is a special case from GIKum distribution, when $\beta =1,\gamma =1$ in (2) with the following pdf

$f\left(x\right)=\frac{\alpha }{{\left(1+x\right)}^{\alpha +1}},\alpha ,x>0$

3.1.2. Beta Type II (Inverted Beta) Distribution

The inverted beta type II (β, 1) is a special case from GIKum distribution, when $\alpha =1,\gamma =1$ in (2)

$f\left(x;\beta \right)=\frac{1}{B\left(\beta ,1\right)}\frac{x^{\beta -1}}{{\left(1+x\right)}^{\left(\beta +1\right)}},x,\beta >0$

Also when $Y={\left(k\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)\right)}^{-1}$ then $Y\sim \text{Pareto}\text{typeI}\left(\beta ,k\right)$

3.1.3. The Log-Logistic (Fisk) Distribution

The log-logistic (Fisk) distribution is a special case from IKum distribution, when $\alpha =\beta =\gamma =1$ in (2), with the following form

$f\left(x\right)=\frac{1}{{\left(1+x\right)}^2},x>0$

3.2. Some Relations between the Inverted Kumaraswamy Distribution and Other Distributions

The inverted distribution can be transformed to several distributions using appropriate transformations such as exponentiated Weibull (exponentiated exponential, Weibull, Burr type X, exponential, Rayleigh), generalized uniform (beta type I, inverted generalized Pareto type I, uniform (0, 1)), left truncated exponentiated exponential (left truncated exponential, exponential), exponentiated Burr type XII (Burr type XII, generalized Lomax, beta type II, F- distribution), Kumaraswamy-Dagum (Dagum, Kumaraswamy-Burr type III, Burr type III, log logistic) and Kumaraswamy-inverse Weibull (Kumaraswamy-inverse exponential, inverse exponential). Table 1 summarizes the transformations from IKum to other distributions.

Limiting Distributions

1) If $X\sim \text{GIkum}\left(\alpha ,\beta ,\gamma \right)$ and $Y={\beta }^{-\frac{1}{\alpha }}\left(1+X^{\gamma }\right)$ on $\left({\beta }^{-\frac{1}{\alpha }},\infty \right)$ then the PDF of y is

$f\left(y\right)=\alpha y^{-\left(\alpha +1\right)}{\left(1-\frac{y^{-\alpha }}{\beta }\right)}^{\beta -1},y>0$

If $\beta \to \infty$ then it is the pdf of the inverted Weibull distribution.

2) If $X\sim \text{GIkum}\left(\alpha ,\beta ,\gamma \right)$ and $Y=\alpha \left(1-{\left(1+X^{\gamma }\right)}^{-1}\right)$ then the pdf of y is $f\left(y;\alpha ,\beta \right)=\beta {\left(1-\frac{y}{\alpha }\right)}^{\alpha -1}{\left(1-{\left(1-\frac{y}{\alpha }\right)}^{\alpha }\right)}^{\beta -1},y>0$ and as $\alpha \to \infty$ the pdf of y tends to $f\left(y;\beta \right)=\beta {\text{e}}^{-y}{\left(\text{1}-{\text{e}}^{-y}\right)}^{\beta -1},y>0$ , which is the pdf of the generalized exponential distribution.

3) If $T\sim \text{GIKUM}\left(\alpha ,\beta ,\gamma \right)$ and $Y=\alpha \left(1-{\beta }^{\frac{1}{\alpha }}{\left(1+T^{\gamma }\right)}^{-1}\right)$ on $\left(\alpha \left(1-{\beta }^{\frac{1}{\alpha }}\right),\alpha \right)$ , then the pdf of y is $f\left(y;\alpha ,\beta \right)={\left(1-\frac{y}{\alpha }\right)}^{\alpha -1}{\left(1-{\left(1-\frac{\left(1-\frac{y}{\alpha }\right)}{\beta }\right)}^{\alpha }\right)}^{\beta -1},y>0.$ As

both $\beta \to \infty$ and $\alpha \to \infty$ the pdf of y tends to $f\left(y;\beta \right)={\text{e}}^{-y}\exp {\left(-{\text{e}}^{-y}\right)}^{\beta -1},y>0,$ which is the pdf of the standard extreme value distribution of the first type (Table 2).

4. Characterizations Based on Conditional Expectation

Characterization of a probability distribution for continuous r.v is important in several research areas and has recently involved many researchers attention. Here we characterize generalized inverted Kumaraswamy distribution based on 1) relationship of two moments based on truncation; 2) truncated moments of the statistic of n^th order with certain functions.

4.1. Characterizations Based on Two Truncated Moments

Following Hamedani [13] , we are going to mention here that the advantage of this characterization is twofold: it relates the cdf or pdf of a distribution to the solution of the differential equation of a first order type and further there is not necessary for simple format of cdf.

Theorem 4.1

Let probability space $\left(\Omega ,\wp ,P\right)$ and for a < b with $a=-\infty$ and $b=\infty$ ,

where as the interval H is defined as H = [a, b]. Suppose continuous r.v X with cdf F where X is such that $X\left(\Omega \right)=H$ and let both g, h be functions of real type on H satisfying the following expression

$E\left[g\left(X\right)|X\ge x\right]=E\left[h\left(X\right)|X\ge x\right]\eta \left(x\right),\text{with}x\in H,$

where $\eta$ is a real function. Furthermore, assuming that g, $h$ are continuous $\eta$ and F are differentiable twicely and F monotone function on H. Finally, assuming the equation $h\eta =g$ and it has never any solution in real belongs to H. and then F is determined uniquely from the following relation

$F\left(x\right)=c{\displaystyle \underset{0}{\overset{x}{\int }}\left|{\eta }^{\prime }\left(u\right)/\left(\eta \left(u\right)h\left(u\right)-g\left(u\right)\right)\right|\exp \left(-s\left(u\right)\right)\text{d}u},$

and the function $s\left(u\right)$ has a solution of $s^{\prime }\left(u\right)={\eta }^{\prime }\left(u\right)h\left(u\right)/\left(\eta \left(u\right)h\left(u\right)-g\left(u\right)\right)$ and C is chosen so that ${\displaystyle {\int }_H\text{d}F}=1$ .

The condition in which the both functions $g_n\left(X\right)$ and $h_n\left(X\right)$ are integrable uniformly and the cdf $\left\{F_n\right\}$ relatively compact form, and $\left\{X_n\right\}\to X$ in distribution if ${\eta }_n\to \eta$

$\eta \left(x\right)=\frac{E\left[g\left(X\right)|X\ge x\right]}{E\left[h\left(X\right)|X\ge x\right]}.$

Proposition 4.1

Let $X:\Omega \to \left(0,\infty \right)$ be an r.v and let $h\left(x\right)={\left\{1-{\left[1+x^{\gamma }\right]}^{-\alpha }\right\}}^{1-\beta }{\left[1+x^r\right]}^{-\alpha }$ and $g\left(x\right)={\left\{1-{\left[1+x^{\gamma }\right]}^{-\alpha }\right\}}^{1-\beta },x\in \left(0,\infty \right)$ . The pdf of X is (2) if $\eta$ defined in 2.1 theorem and has the following form $\eta \left(x\right)=2{\left[1+x^{\gamma }\right]}^{\alpha }$ for $x>0$ .

Proof. Let X has density (1.3), then

$E\left[g\left(X\right)|X\ge x\right]=\frac{1}{2B\left(\alpha ,\beta \right)\overline{F}\left(x\right)}{\left[1+x^{\gamma }\right]}^{-2\alpha },x>0$

and $E\left[h\left(X\right)|X\ge x\right]=\frac{1}{B\left(\alpha ,\beta \right)\overline{F}\left(x\right)}{\left[1+x^{\gamma }\right]}^{-2\alpha },x>0$ and finally $\eta \left(x\right)\cdot h\left(x\right)-g\left(x\right)={\left(1-{\left[1+x^{\gamma }\right]}^{-\alpha }\right)}^{1-\beta }>0$ for $x>0$

Conversely, when $\eta$ is defined earlier, then

$s^{\prime }\left(x\right)={\eta }^{\prime }\left(x\right)\cdot h\left(x\right)/\left(\eta \left(x\right)\cdot h\left(x\right)-g\left(x\right)\right)=2\alpha \gamma x^{\gamma -1}{\left[1+x^{\gamma }\right]}^{-1},x>0$

and finally hence $s\left(x\right)=\ln {\left[1+x^{\gamma }\right]}^{2\alpha },x>0$

Now, from 2.1 theorem, X has pdf (3)

Corollary 4.1

Let $X:\Omega \to \left(0,\infty \right)$ be an r.v with $h\left(x\right)$ proposition in 4.1. The pdf of X is (2) if there exist $g$ and $\eta$ functions given in 4.1 theorem with the following differential equation (DE)

$s^{\prime }\left(x\right)=\frac{{\eta }^{\prime }\left(x\right)h\left(x\right)}{\eta \left(x\right)h\left(x\right)-g\left(x\right)}=2\alpha \gamma x^{\gamma -1}{\left[1+x^{\gamma }\right]}^{-1},x>0$

Remark 4.1. (a) The DE has the general solution of 4.1 corollary of the form

$\eta \left(x\right)={\left[1+x^r\right]}^{2\alpha }\left[-{\displaystyle \int g\left(x\right)2\alpha \gamma x^{\gamma -1}}{\left[1+x^r\right]}^{-\left(\alpha +1\right)}\times {\left\{1-{\left[1+x^r\right]}^{-\alpha }\right\}}^{\beta -1}\text{d}x+D\right]$

for $x>0$ , where a new constant D is introduced and it may be in particular value $D=0$ according to proposition 4.1.

4.2. Characterization through the Statistic of n^th Ordered Truncated Moment

This section contains the characterizations of GIKum distribution based on function of the last order statistics. This characterization is derived through the consequence of the proposition 4.2, which is similar to the Hamedani [13] .

Proposition 4.2

Let $X:\Omega \to \left(0,\infty \right)$ be a r.v with cdf F. let $\psi \left(x\right)$ and $q\left(x\right)$ be two differentiable functions on $\left(0,\infty \right)$ such that $\underset{x\to 0}{\lim }\psi \left(x\right){\left[F\left(x\right)\right]}^n=0$ and ${\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{q^{\prime }\left(t\right)}{\left[\psi \left(t\right)-q\left(t\right)\right]}\text{d}t}$

Then

$E\left[\psi \left(X_{n:n}\right)|X_{n:n}<t\right]=q\left(t\right),t>0$

implies

$F\left(x\right)=\exp \left\{-{\displaystyle \underset{x}{\overset{\infty }{\int }}\frac{q^{\prime }\left(t\right)}{n\left[\psi \left(t\right)-q\left(t\right)\right]}\text{d}t}\right\},x\ge 0$

Taking, e.g. $\psi \left(x\right)=2\left\{{\displaystyle \underset{0}{\overset{1-{\left[1+x^r\right]}^{-\alpha }}{\int }}{\omega }^{\beta -1}\text{d}\omega }\right\}$ and $q\left(x\right)=\frac{1}{2}\psi \left(x\right)$ , $F\left(x\right)$ will be a result in (2).

5. Maximum Likelihood (ML) Estimators of GIKum Distribution’s Parameters

We present here a ML estimator of the parameters of GIKum distribution

$l\left(\alpha ,\beta ,\gamma ;x_{obs}\right)={\alpha }^n{\beta }^n{\gamma }^n{\displaystyle \prod _{j=1}^n{x}^{\gamma -1}{\left(1+x^{\gamma }\right)}^{-\left(\alpha +1\right)}{\left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}^{\beta -1}},$ (5)

and

$\begin{array}{c}\ln \left(l\left(\alpha ,\beta ,\gamma ,x_{obs}\right)\right)=n\text{ln}\alpha +n\ln \beta +n\ln \gamma +\left(\gamma -1\right){\displaystyle \sum \ln x}-\left(\alpha +1\right){\displaystyle \sum \ln \left(1+x^{\gamma }\right)}\\ +\left(\beta -1\right){\displaystyle \sum \ln \left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}\end{array}$ (6)

Taking partial derivatives with respect to $\alpha ,\beta$ and $\gamma$ respectively from (6), we have

$\frac{\partial \ln \left(l\left(\alpha ,\beta ,\gamma ,x_{obs}\right)\right)}{\partial \alpha }=\frac{n}{\alpha }-{\displaystyle \sum \ln \left(1+x^{\gamma }\right)+\left(\beta -1\right)}{\displaystyle \sum \frac{\ln \left(1+x^{\gamma }\right)}{\left({\left(1+x^{\gamma }\right)}^{\alpha }-1\right)}}$ (7)

$\frac{\partial \ln \left(l\left(\alpha ,\beta ,\gamma ,x_{obs}\right)\right)}{\partial \beta }=\frac{n}{\beta }+{\displaystyle \sum \ln \left(1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right)}$ (8)

$\frac{\partial \ln \left(l\left(\alpha ,\beta ,\gamma ,x_{obs}\right)\right)}{\partial \gamma }=\frac{n}{\gamma }+{\displaystyle \sum \ln x}-\left(\alpha +1\right){\displaystyle \sum \frac{x^{\gamma }\left(\ln x\right)}{\left[\left(1+x^{\gamma }\right)\right]}}+\alpha \left(\beta -1\right){\displaystyle \sum \frac{x^{\gamma }{\left(1+x^{\gamma }\right)}^{-1}\ln x}{\left({\left(1+x^{\gamma }\right)}^{\alpha }-1\right)}}$ (9)

The ML estimators say $\widehat{\Theta }$ of $\Theta$ , are found through solution of the nonlinear system. This system of nonlinear equations does not provide explicit functions of the estimators of the parameters of GIKum distribution. Therefore, for the solution of this system of equations using software can be estimated numerically with R.

For the inference about model parameters i.e. the point estimation and the testing of hypothesis we require the information matrix of order 3 × 3 which have partial derivatives of second order and they derived from Equations (7)-(9) with again differentiating. Assuming that the regularity conditions holds, the vector $\sqrt{n}\left(\widehat{\theta }-\theta \right)$ follows the multivariate normal distribution asymptotically i.e. $N_3\left(0,A^{-1}\left(\Theta \right)\right)$ , where $A^{-1}\left(\Theta \right)={\lim }_{n\to \infty }{I}_n\left(\Theta \right)$ and $I_n\left(\Theta \right)$ is an information matrix.

We conclude this section by expressing $\widehat{\beta }$ in terms of a random variable $T^{\prime }$ whose distribution will be derived in the next section.

$\widehat{\beta }=-\frac{n}{{\displaystyle \sum \ln \left[1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right]}}=-\frac{n}{T^{\prime }}$

where

$T^{\prime }=-{\displaystyle \sum \ln \left[1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right]}={{\displaystyle \sum \ln \left[1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right]}}^{-1}$

5.1. Distributions of $T_i$ and $T^{\prime }$

The following remarks and a theorem illustrate the distributions of $T_i$ and $T^{\prime }$ .

5.1.1. Remarks

The following conclusions can be obtained easily which we present them as remarks.

i) If $X~\text{GIKumdistribution}\left(\alpha ,\beta \right)$ with $\gamma$ known, then $T_i=-\ln \left[1-{\left(1+x^{\gamma }\right)}^{-\alpha }\right]$ follows $\text{Exp}\left(\beta \right)$ .

ii) $T^{\prime }~\text{Gamma}\left(\beta ,n\right)$ $T^{\prime }~\text{GIKumdistribution}\left(\alpha ,\beta \right)$

iii) $\overline{T}=\frac{{\displaystyle \sum T_i}}{n}~\text{Gamma}\left(\frac{\beta }{n},n\right).$

iv) In view of (2), $\frac{1}{T^{\prime }}~\text{InvertedGamma}$ .

v) If $X_1,X_2,\cdots ,X_n$ are i.i.d. Gamma (β, n), then the i^th transformed ordered failures are i.i.d. Exp(β).

vi) $Y=\frac{\stackrel{⌢}{\beta }}{n\beta }~\text{Gamma}$

5.1.2. Moments of $Y=\frac{\stackrel{⌢}{\beta }}{n\beta }$

The r^th moment of the statistic $Y=\frac{\stackrel{⌢}{\beta }}{n\beta }$ is

${{\mu }^{\prime }}_r=E\left(Y^r\right)=\frac{\Gamma \left(n-r\right)}{\Gamma n}$

and that of $\widehat{\beta }$ is

$E\left({\widehat{\beta }}^r\right)={\left(n\beta \right)}^r\frac{\Gamma \left(n-r\right)}{\Gamma n}$

Theorem 5.1

Let $X_1,X_2,\cdots ,X_n$ be i.i.d. random variable with cdf F and let $X_{\left(n\right)}$ be the n^th order statistic. Consider the sequence of random variables $Y_n=\left[1-F\left(X_n\right)\right]$ The limiting function of $Y_n\left(Y_n>0\right)$ is ${\text{e}}^{-Y_n}$ for $\alpha >0$ and $n\to \infty$ .

Proof:

The pdf of $u=X_{\left(n\right)}$ is

$g\left(u\right)=n{\left[F\left(u\right)\right]}^{n-1}f\left(u\right)$

$g\left(u\right)=n\alpha \gamma \beta {\left[1-{\left(1+u^{\gamma }\right)}^{-\alpha }\right]}^{\left(n-1\right)\beta +\beta -1}{u}^{\gamma -1}{\left(1+u^{\gamma }\right)}^{-\alpha -1}$

Let $\frac{Y_n}{n}=1-{\left[1-{\left(1+u^{\gamma }\right)}^{-\alpha }\right]}^{\beta }$

Differentiating it w.r.t $u$ , we have

$\frac{\text{d}{Y}_n}{n}=\alpha \beta \gamma {\left[1-{\left(1+u^{\gamma }\right)}^{-\alpha }\right]}^{\beta -1}{u}^{\gamma -1}{\left(1+u^{\gamma }\right)}^{-\alpha -1}\text{d}u.$

The pdf of $Y_n$ is $g\left(y_{\left(n\right)}\right)={\left(1-\frac{y_{\left(n\right)}}{n}\right)}^{\beta \left(n-1\right)}$ and its cdf is

$G\left(y_{\left(n\right)}\right)={\displaystyle \underset{0}{\overset{y_{\left(n\right)}}{\int }}{\left(1-\frac{t}{n}\right)}^{\beta \left(n-1\right)}\text{d}t}$

$G\left(y_{\left(n\right)}\right)=\frac{1}{\beta \left(1-\frac{1}{n}\right)+\frac{1}{n}}-\frac{{\left(1-\frac{y_{\left(n\right)}}{n}\right)}^{\beta \left(n-1\right)}}{\beta \left(1-\frac{1}{n}\right)+\frac{1}{n}}$

Letting $n\to \infty$ , we arrive at $G\left(y_{\left(n\right)}\right)=\frac{1-{\text{e}}^{-\beta y_{\left(n\right)}}}{\beta }$ and $g\left(y_{\left(n\right)}\right)={\text{e}}^{-\beta y_{\left(n\right)}}$

6. Applications of GIKum Distribution

In this section, the proposed distribution is fitted to the data set of prices of wooden toys of 31 children in April 1991 at Suffolk craft shop (Table 3):

The maximum likelihood estimates of unknown parameters of GIKUM, Lomax and Beta type-II distributions, $-2LL$ and information criteria are given in Table 4.As the values of $-2L$ , AIC, BIC and HQIC are smaller for GIKum distribution as compare to Lomax distribution and Beta type-II distribution, GIKumTable 3. Descriptive statistics.table_table_tableTable 4. Maximum likelihood estimates and information criteria.table_table_table

distribution fits better for given data set. The same thing can be confirmed after seeing Figure 5.

7. Concluding Remarks

In this paper, a new distribution called GIKum distribution is introduced. Some properties of GIKum distribution such as measures of central tendency and dispersion, models of stress-strength, limiting distributions, characterization of GIKum distribution and related probability distributions through some specific transformations are derived. The mathematical expressions of reliability function (r.f) and the hazard rate function (hrf) of the GIKum distribution are found and presented through their graphs. The parameters estimation through the technique of maximum likelihood estimation is used and the results are applied to the data set of prices of wooden toys of 31 children.

Cite this paper

Iqbal, Z., Tahir, M.M., Riaz, N., Ali, S.A. and Ahmad, M. (2017) Generalized Inverted Kumaraswamy Distribution: Properties and Application. Open Journal of Statistics, 7, 645-662. https://doi.org/10.4236/ojs.2017.74045

References