American Journal of Computational Mathematics
Vol.2 No.2(2012), Article ID:20121,5 pages DOI:10.4236/ajcm.2012.22017
The Appearance of Noise Terms in Modified Adomian Decomposition Method for Quadratic Integral Equations
Department of Mathematics, Sciences Faculty for Girls, King Abdulaziz University, Jeddah, Saudi Arabia
Email: h.o.bak@ hotmail.com, hbakodah@kau.edu.sa
Received January 10, 2012; revised February 12, 2012; accepted February 20, 2012
Keywords: Modified Adomian Decomposition method; Quadratic Integral Equation; The Noise Terms
ABSTRACT
In this paper, we apply the modified Adomian Decomposition Method to get the numerical solutions of Quadratic integral equations. The appearance of noise terms in Decomposition Method was investigated. The method was described along with several examples.
1. Introduction
The theory of integral equations plays an important role in the theory of nonlinear analysis; this is due to the various applications of integral equations in many branches of mathematical physics, such as neutron transportation, radiation and kinetic theory of gases (cf. [1-3], among others).
Quadratic integral equations (QIEs) are often applicable in the theory of radiative transfer, neutron transport and in the traffic theory. The quadratic integral equations can be very often encountered in many applications. Some treatments for solvability of (QIEs) are given in [4-6].
A quadratic integral equation of the form
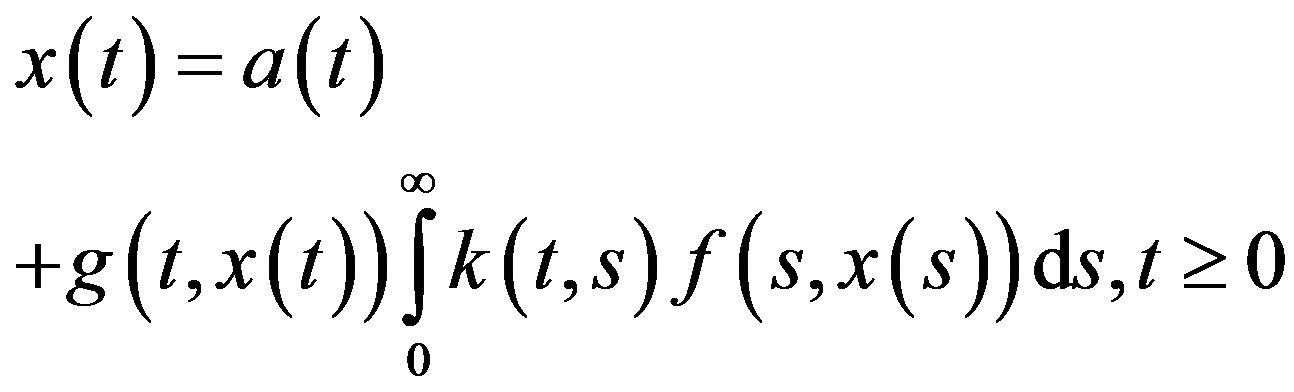 (1)
(1)
creates a generalization of several kinds of quadratic integral equations. In the case of a bounded interval this equation has the form
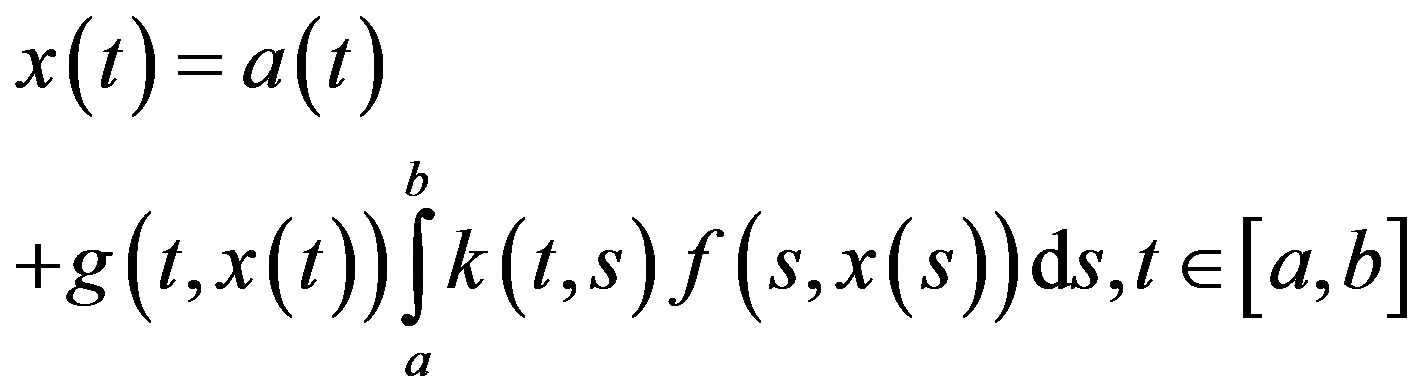 (2)
(2)
On the other hand, Equation (1) contains, as a special case, the classical Hammerstein integral equation on an unbounded interval having the form
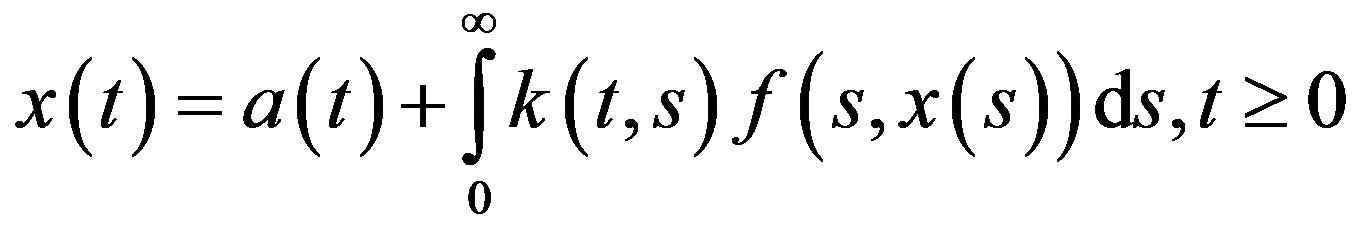 (3)
(3)
Indeed, putting 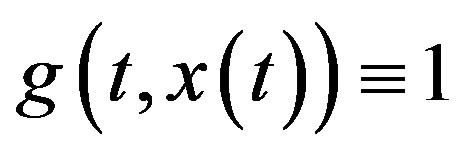 in Equation (1), we obtain Equation (3).
in Equation (1), we obtain Equation (3).
In the last 35 years or so, many authors have studied the existence of solutions for several classes of nonlinear quadratic integral equations. For example, see the papers by Argyros [7], Caballero et al. [8] and Darwish [9].
It is worth mentioning that up to now only few papers have dealt with the numerical solutions of quadratic integral equations. In [10] El-Sayed et al. concerned with the two methods; Picard method and Adomian method for solving quadratic integral equations. Adomian’s decomposition method (ADM) is useful and powerful method for solving linear and nonlinear functional equations [11- 13]. Recently a great deal of interest has been focused on the application of Adomian’s decomposition method to solve a wide variety of stochastic and terministic problems [14,15].
Since this method was first presented in the 1980’s, Adomian’s decomposition method has led to several modifications made by various researchers in attempt to improve the accuracy or expand the application of the original method. A reliable modification to the standard (ADM) was proposed by Wazwaz [16], the modification arises in the initial definition of the operator when applying the (ADM) to the differential or integral equations.
In the study of non-homogenous equations, the noise term phenomenon is rather useful because of the role it plays in the rapid convergence of solutions obtained by (ADM). In this work, we apply the modified Adomian decomposition method to quadratic integral equations. Also, we are considering the appearance of noise terms in the solution of non-homogenous quadratic integral equations.
2. The Modified Adomian Decomposition Method
2.1. The Standard Adomian Method
Consider the quadratic integral equation
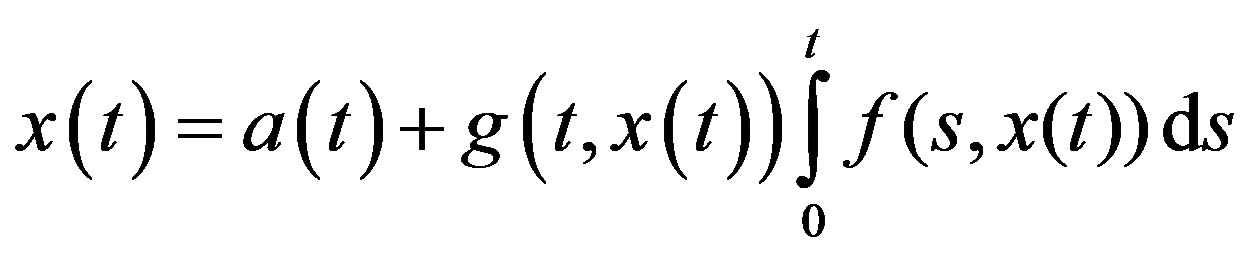 (4)
(4)
The existence of continuous solution on this nonlinear quadratic integral equations was proved in [10]. Applying (ADM) to Equation (4), the solution can be written as infinite series
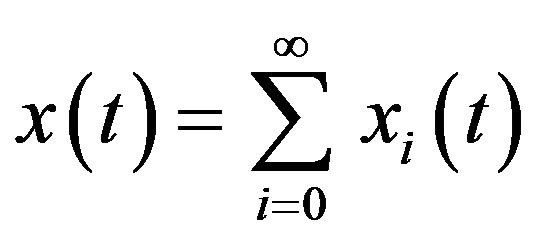 (5)
(5)
Theorem (1)
Let the solution of the quadratic integral equation (4) exist. If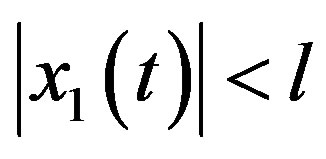 ,
, 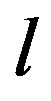 is a positive constant, then the series solution (5) of the quadratic integral equation (4) using (ADM) converges.
is a positive constant, then the series solution (5) of the quadratic integral equation (4) using (ADM) converges.
Theorem (2)
If the series of numerical implementation of Adomian decomposition method is convergent, then it converges to the exact solution.
We set
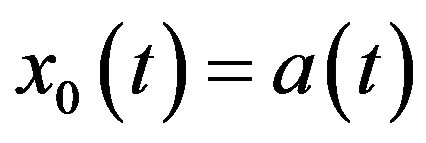 (6)
(6)
and remaining terms are to be determined by a recursive relationship
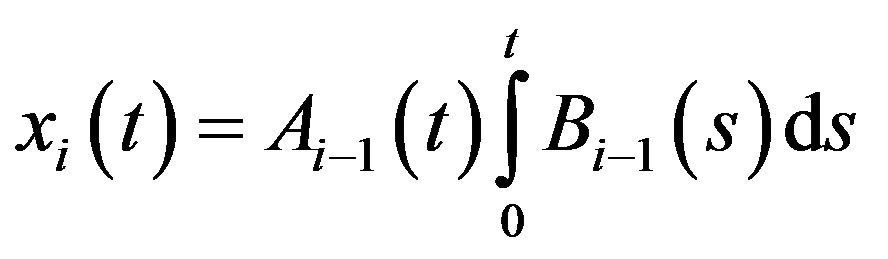 (7)
(7)
where 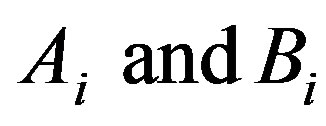 are Adomian polynomials of the nonlinear terms
are Adomian polynomials of the nonlinear terms 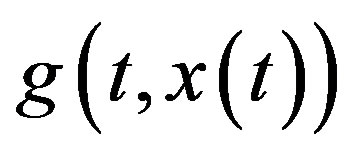 and
and 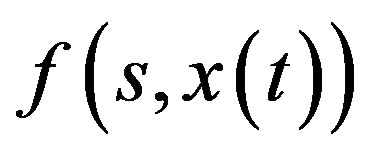 respectively, which have the form
respectively, which have the form
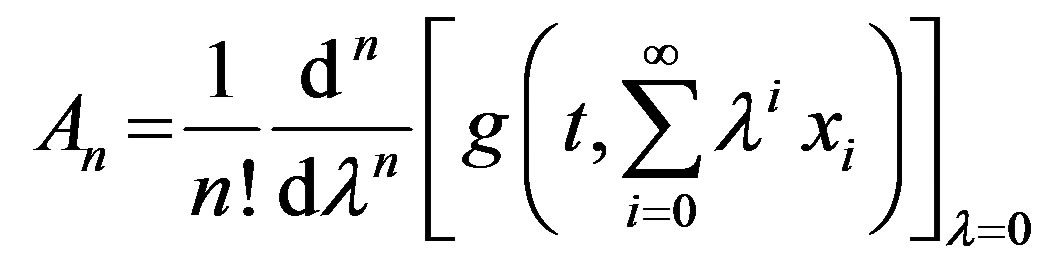 (8)
(8)
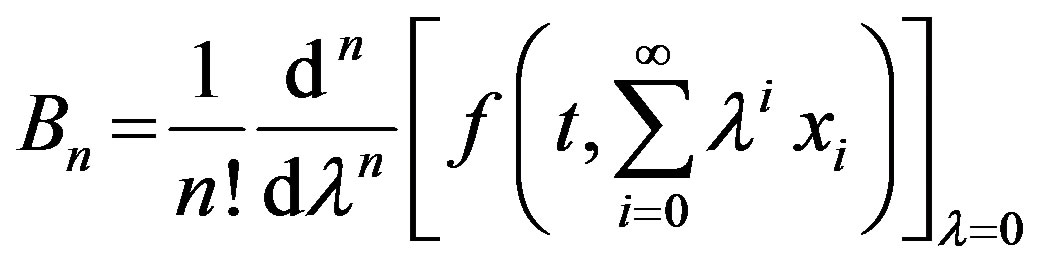 (9)
(9)
Substituting the decomposition (5) into both sides of (4) yields
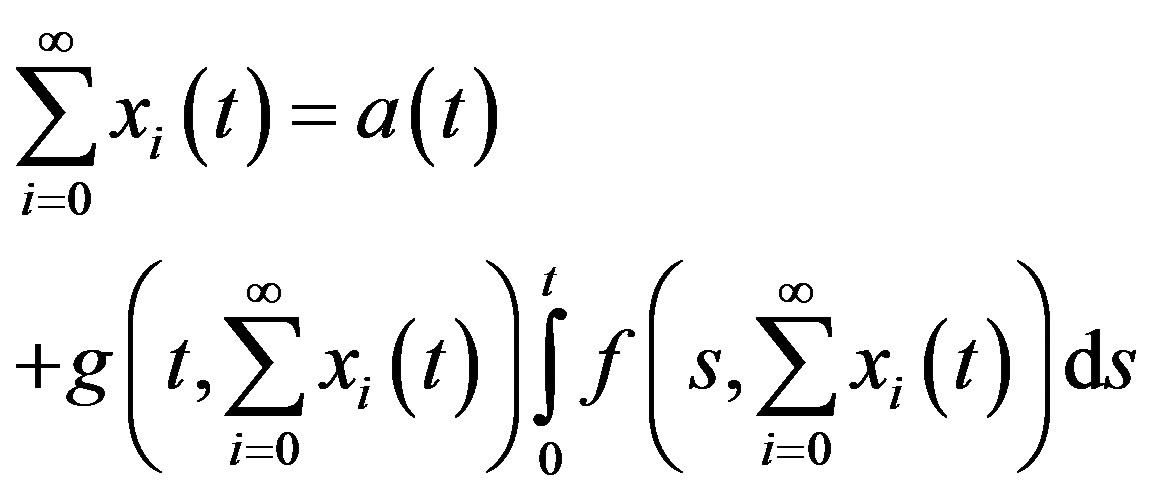 (10)
(10)
The components 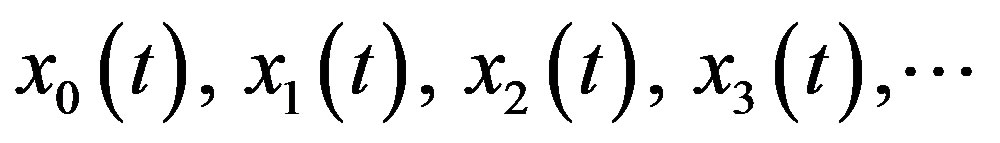 of the unknown function
of the unknown function 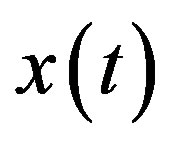 are completely determined in a recurrent manner if we set
are completely determined in a recurrent manner if we set
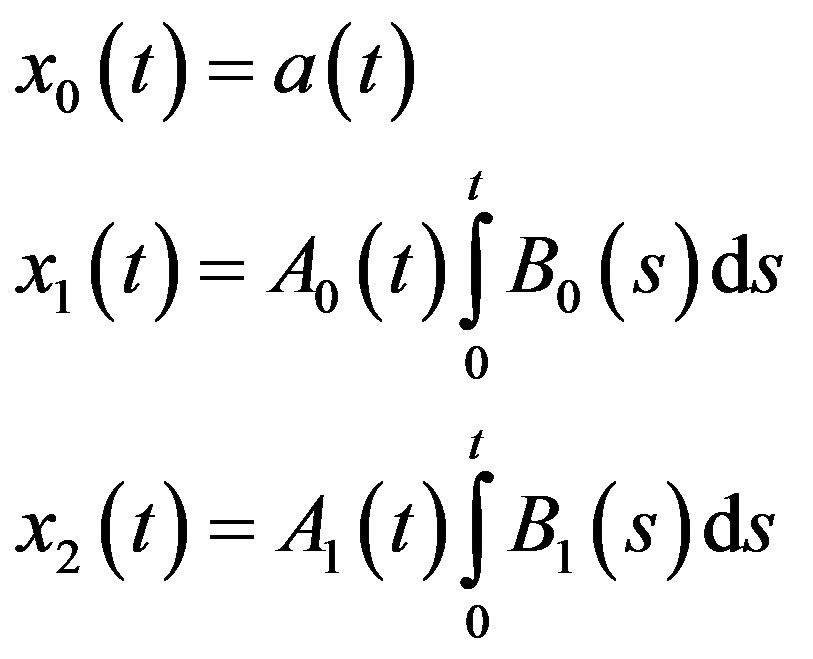
and so on.
The recursive relations (6) and (7) reduced the quadratic integral equation under consideration into an elegant determination of components. If an exact solution exists, then the series obtained by Equation (5) rapidly converges to the solution. If the case that a closed form solution cannot obtained, a truncated number of terms can be used to approximate the solution numerically. Research has shown that evaluating a few terms in the series gives an approximation of high degree of accuracy when compared with other numerical methods.
2.2. The Modified Decomposition Method
The modified decomposition method has been developed by Wazwaz [16], many work where have shown that this modification is efficient and minimizes the size of calculation if compared with the standard Adomian decomposition method. To apply this modification we assume that the function 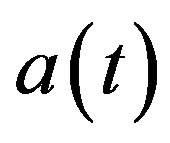 can be divided into the sum of two parts, namely
can be divided into the sum of two parts, namely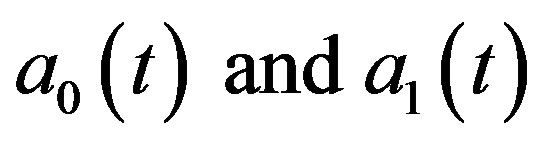 , therefore, we set
, therefore, we set
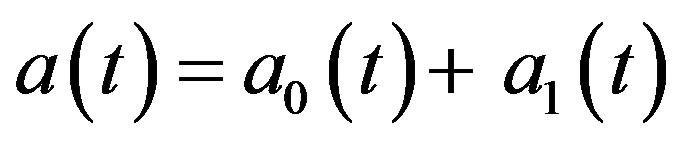 (11)
(11)
In view of this assumption, we propose a slight variation only on the components 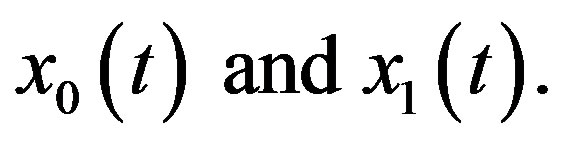 This slight change plays a major role in accelerating the convergence of the solution and minimizing the size of calculations. Based on these suggestions, we formulate the following modified decomposition method
This slight change plays a major role in accelerating the convergence of the solution and minimizing the size of calculations. Based on these suggestions, we formulate the following modified decomposition method
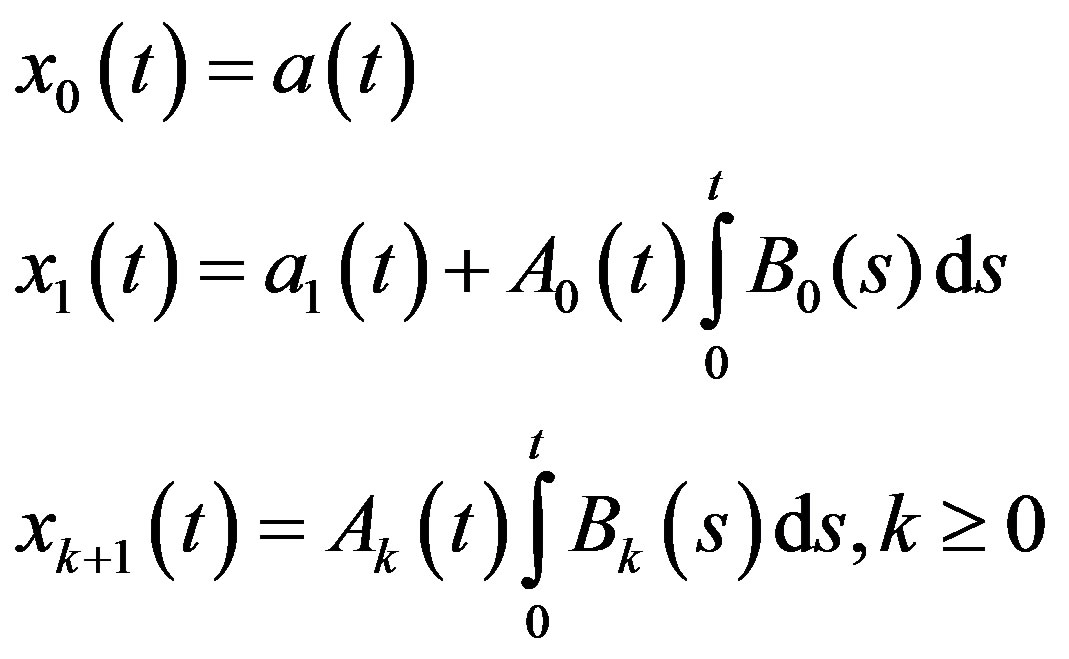 (12)
(12)
The success of this method depends mainly on the proper choice of the parts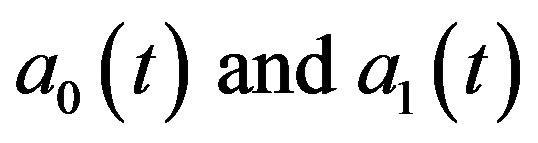 . We have been unable to establish any criterion to judge what forms of
. We have been unable to establish any criterion to judge what forms of 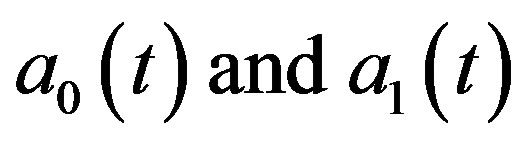 can be used to yield the acceleration demanded, but selecting a minimal number of terms for
can be used to yield the acceleration demanded, but selecting a minimal number of terms for 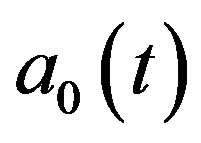 has been found to be effective.
has been found to be effective.
3. The Noise Terms Phenomenon
In applications solved by the Adomian decomposition method, the appearance of noise terms sometimes makes it necessary to compute more terms to observe the selfcancellations and separate solution terms from the terms whose sum vanishes in the limit. We investigate the phenomenon further in this section.
Adomian and Rach [17] were firstly discussed the appearance of noise terms, they concluded that, the inhomogeneity of the equation is the major and only reason. The appearance of these terms in the first two components of the solution series is considered by Adomian [13] as the first condition of demonstrating a fast convergence of the solution. Wazwaz [18,19] stated the inhomogeneity condition is not sufficient for occurring this phenomena and he added another necessary condition (if the exact solution explicitly appears in the zeroth component) to interpret this phenomena. Wazwaz [16] modified the Adomian decomposition method by dividing the initial approximation into two parts, and distribute these parts through the calculations. In [20] Wazwaz and Salah expand the same initial approximation using Taylor expansion and insert the terms of this expansion through the calculations, they succeed to avoid noise terms for some integral equations.
Definition (1)
The noise terms are the identical terms with opposite sign that appear within the components . They only exist in specific types of non-homogenous equations.
. They only exist in specific types of non-homogenous equations.
Remark
If noise terms indeed exist in the 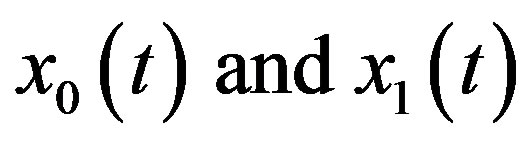 components, then, in general, it could be said that a closed form solution can be obtained after two successive iterations.
components, then, in general, it could be said that a closed form solution can be obtained after two successive iterations.
In canceling the noise terms from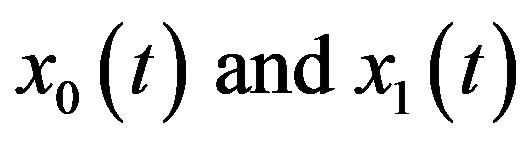 , even though
, even though 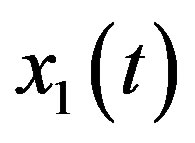 may contain more terms, the remaining non-canceled terms of
may contain more terms, the remaining non-canceled terms of 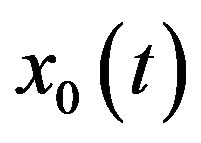 may give the exact solution of quadratic integral equation. Thus, it necessary to verify that the non-canceled terms of
may give the exact solution of quadratic integral equation. Thus, it necessary to verify that the non-canceled terms of 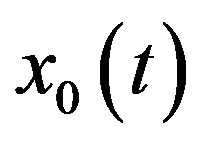 satisfy the quadratic integral equation.
satisfy the quadratic integral equation.
However, if these non-canceled terms do not satisfy the quadratic integral equation, or if the noise terms do not appear between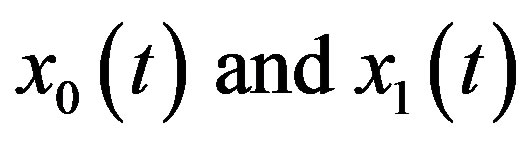 , then it is necessary to compute more components of
, then it is necessary to compute more components of 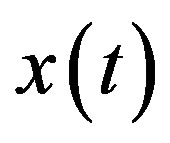 to determine the solution in series form. However, not all non-homogenous equations have the noise terms phenomenon.
to determine the solution in series form. However, not all non-homogenous equations have the noise terms phenomenon.
4. Illustrating Examples
To illustrate the use of modified decomposition method with the noise terms phenomenon we show the following examples.
Example (1)
Consider the following non-linear quadratic integral Equation [10]
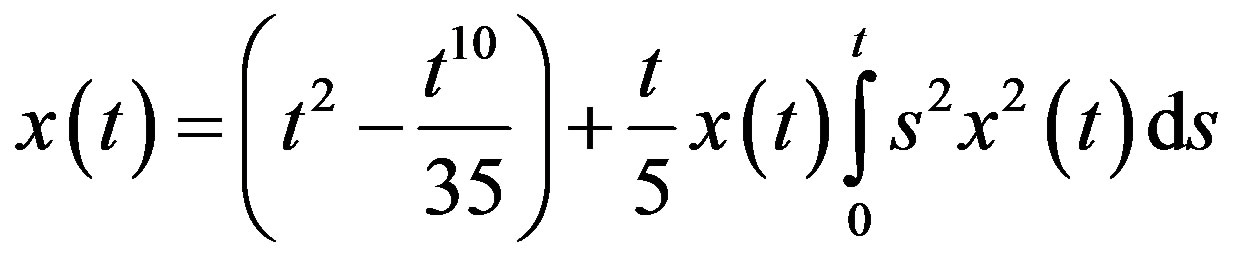 (13)
(13)
and has the exact solution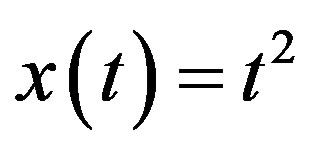 .
.
Applying modified decomposition method (12), we get
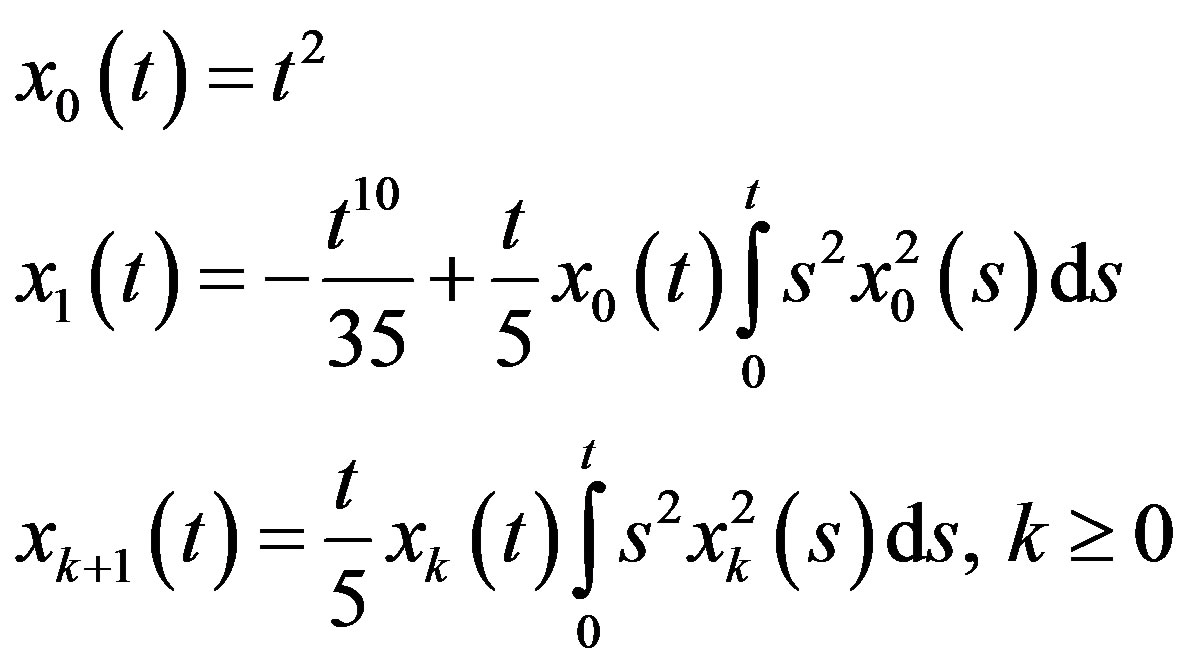 (14)
(14)
then
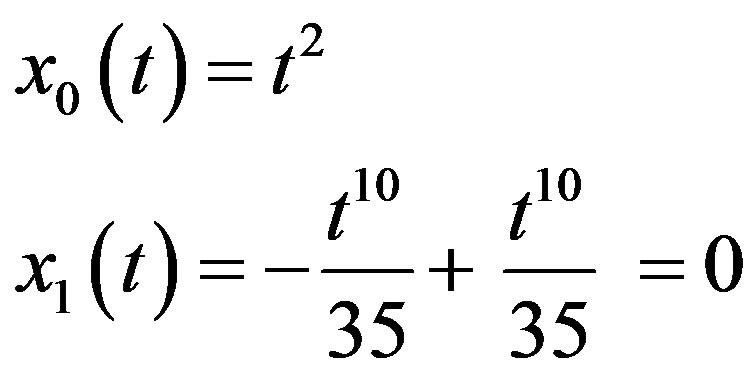
Based on the result we obtained for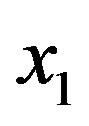 , other component of
, other component of  will vanish. Consequently, we find that
will vanish. Consequently, we find that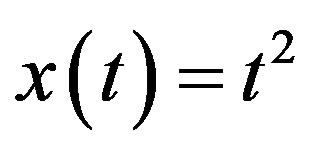 .
.
Example (2)
Consider the following non-linear quadratic integral equation [10]
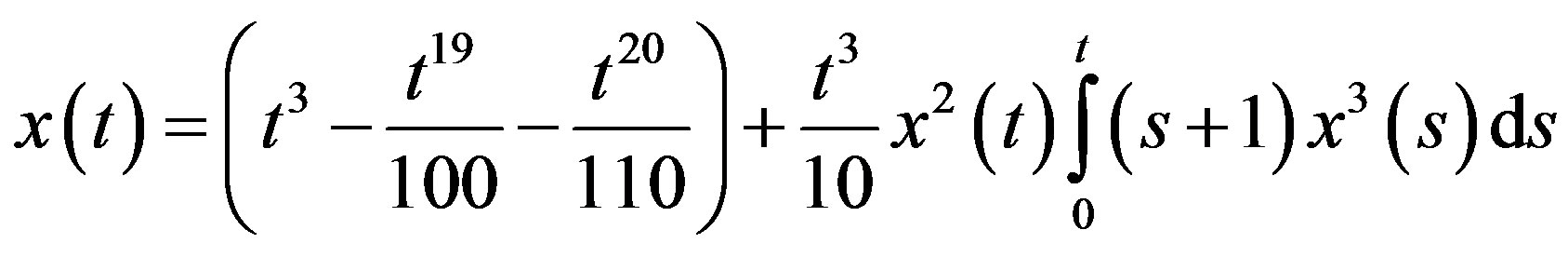 (15)
(15)
and has the exact solution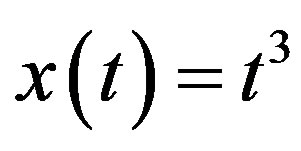 .
.
Applying modified decomposition method (12), we get
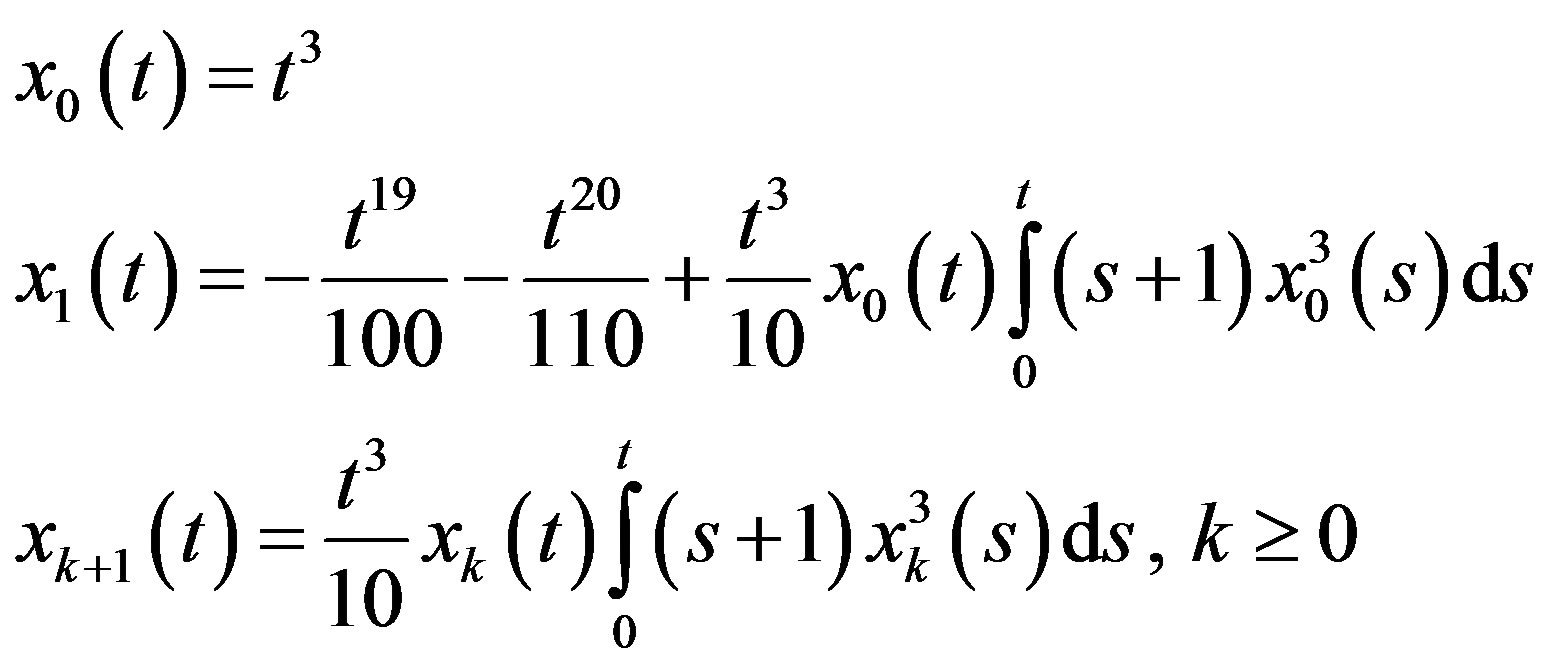 (16)
(16)
then
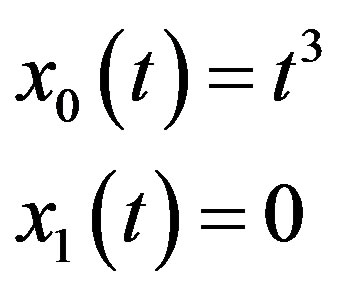
Based on the result we obtained for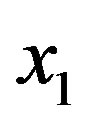 , other component of
, other component of 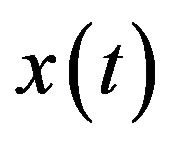 will vanish. Consequently, we find that
will vanish. Consequently, we find that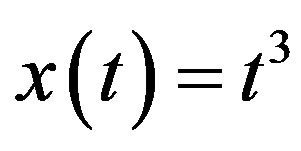 .
.
Example (3)
Consider the following non-linear quadratic integral equation [10]
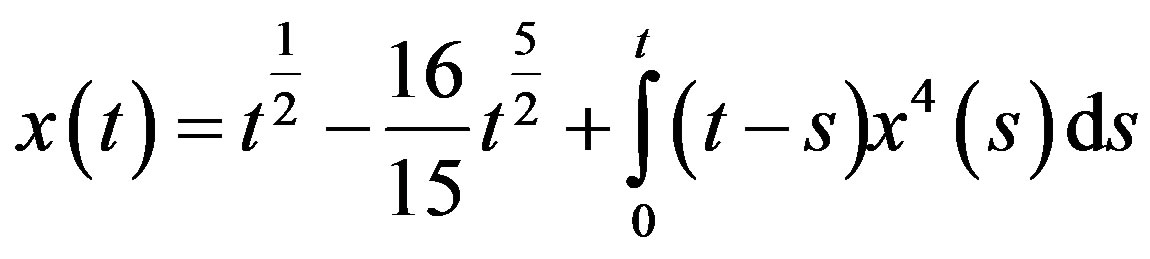 (17)
(17)
and has the exact solution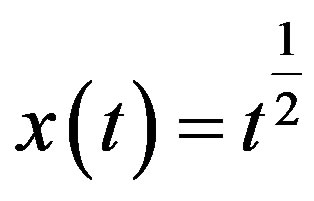 .
.
Applying modified decomposition method (12), we get
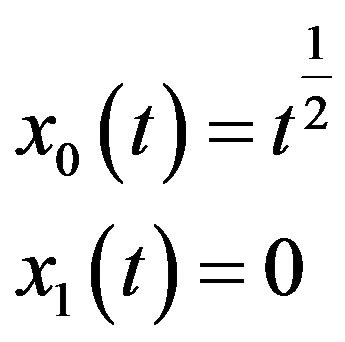

Table 1. the numerical solution for example (4) by standard ADM.
Based on the result we obtained for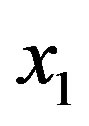 , other component of
, other component of 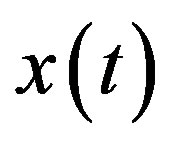 will vanish. Consequently, we find that
will vanish. Consequently, we find that
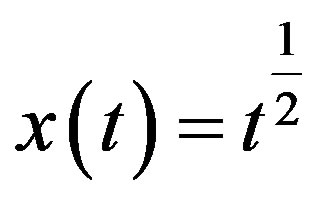 .
.
Example (4)
Consider the following non-linear quadratic integral equation [21]
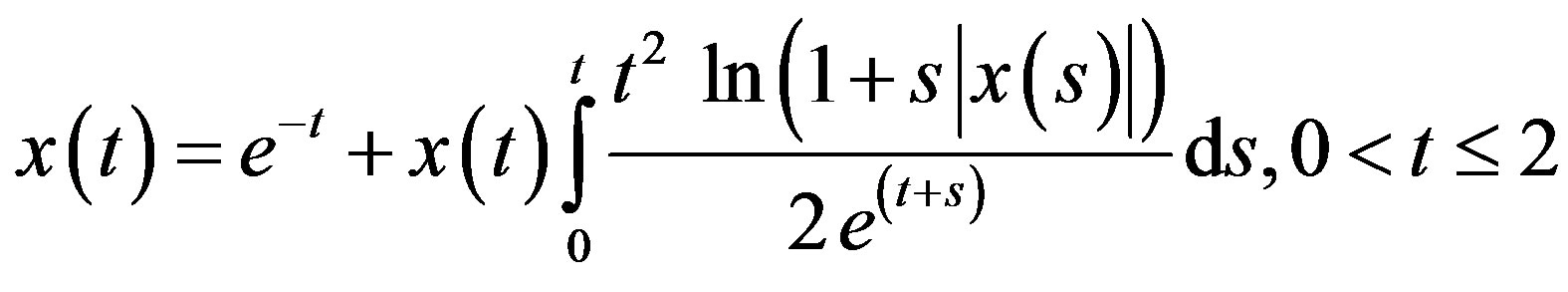 (18)
(18)
Applying Adomian decomposition method (7), we get
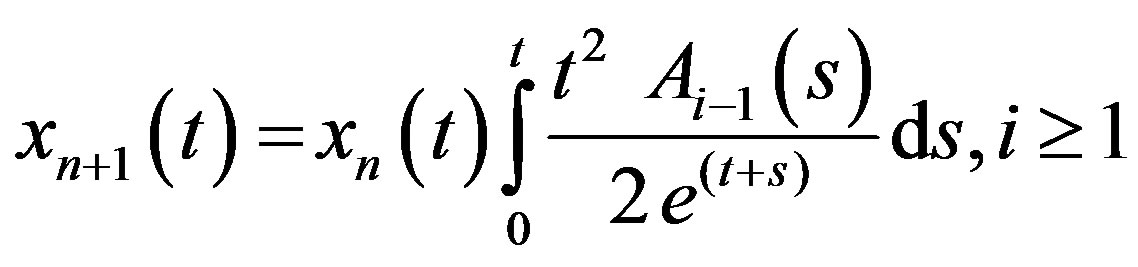 (19)
(19)
where 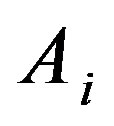 are Adomian polynomials of the nonlinear terms
are Adomian polynomials of the nonlinear terms 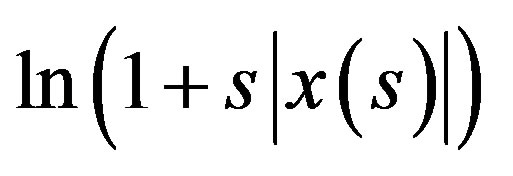 and the solution will be,
and the solution will be,
Table 1 shows a numerical solution for Equation (18) by standard Adomian decomposition method.
5. Conclusion
The appearance of noise terms in the approximate solution using Adomian decomposition method plays a major role in accelerating the convergence of the solution of quadratic integral equation and minimizing the size of calculations if an exact solution exists. If the case that a closed form solution cannot be obtained as in example (4), the solution determine in approximate form.
REFERENCES
- J. Appell, “On the solvability of Nonlinear Non-Compact Problems in Function Spaces with applications to integral and Differential Equations,” Bollettino della Unione Matematica Italiana, Vol. 6, No. 1B, 1982, pp. 1161-1177.
- J. Banas and K. Goebel, “Measures of Non-Compactness in Banach spaces,” Dekker, New York, 1980.
- L. W. Busbridge, “The Mathematics of Radiative Transfer,” Cambridge University Press, Cambridge, 1960.
- J. Banas, J. Rocha Mortin and K. sadarangani, “On the solution of a Quadratic Integral Equation of Hammerstein type,” Mathematical and Computer Modelling, Vol. 43, No. 1-2, 2006, pp. 97-104. doi:10.1016/j.mcm.2005.04.017
- W. G. El-Sayed and B. Rzepka, “Non decreasing solutions of a Quadratic Integral Equations of Uryshon type,” Computers & Mathematics with Applications, Vol. 51, No. 6-7, 2006, pp. 1065-1074. doi:10.1016/j.camwa.2005.08.033
- A. M. A. El-sayed and H. H. G. Hashem, “Solvability of Nonlinear Hammerstein Quadratic Integral Equations,” Journal of Nonlinear Sciences and its Applications, Vol. 2, No. 3, 2009, pp. 152-160.
- I. K. Argyros, “Quadratic equation and applications to chandrasckar’s and Related Equations,” Bulletin of the Australian Mathematical Society, Vol. 32, No. 2, 1985, pp. 275-292. doi:10.1017/S0004972700009953
- J. Caballero, B. Lopez and K. Sadaramgani, “Existence of Non Decreasing and Continuous Solutions for a Nonlinear Integral Equation with supremum in the kernel,” Zeitschrift für Analysis und ihre Anwendungen, Vol. 26, No. 2, 2007, pp. 195-205. doi:10.4171/ZAA/1318
- M. A. Darwish, “On solvability of Some Quadratic Functional Integral Equations in Banach algebra,” Communications in Applied Analysis, Vol. 11, 2007, pp. 441-450.
- A. M. El-Sayed, H. G. Hashem and E. A. Ziada, “Picard and Adomian methods for Quadratic Integral Equation,” Computational & Applied Mathematics, Vol. 29, No. 3, 2010, pp. 447-463. doi:10.1590/S1807-03022010000300007
- G. Adomian, R. C. Rach and R. E. Meyers, “An efficient methodology for Physical Sciences,” Kybernetes, Vol. 20, No. 7, 1991, pp. 24-34. doi:10.1108/eb005909
- G. Adomian, “A review of Decomposition Method and Some Recent Result for Nonlinear Equations,” Mathematical and Computer Modelling, Vol. 13, No. 7, 1992, pp. 17-43. doi:10.1016/0895-7177(90)90125-7
- G. Adomian, “Solving Frontier Problems of Physics: The Decomposition Method,” Springer, Berlin, 1994.
- G. Adomian, “Nonlinear Stochastic Systems: Theory and Applications to Physics,” Springer, Berlin, 1989.
- A. Wazwaz, “A Reliable Modification of Adomian decomposition method,” Applied Mathematics and Computation, Vol. 92, No. 1, 1998, pp. 1-7. doi:10.1016/S0096-3003(97)10037-6
- G. Adomian and R. Rach, “Noise terms in decomposition Series Solution,” Computers & Mathematics with Applications, Vol. 24, No. 11, 1992, pp. 61-64. doi:10.1016/0898-1221(92)90031-C
- A. Wazwaz, “Necessary conditions for the appearance of Noise Terms in Decomposition Solution Series,” Applied Mathematics and Computation, Vol. 81, No. 2-3, 1997, pp. 265-274. doi:10.1016/S0096-3003(95)00327-4
- A. Wazwaz, “The existence of Noise Terms for systems of Inhomogeneous Differential and Integral Equations,” Applied Mathematics and Computation, Vol. 146, No. 1, 2003, pp. 81-92. doi:10.1016/S0096-3003(02)00527-1
- A. Wazwaz and S. M. El-Syed, “A New Modification of the Adomian Decomposition Method for linear and Nonlinear Operators,” Applied Mathematics and Computation, Vol. 122, No. 3, 2001, pp. 393-405. doi:10.1016/S0096-3003(00)00060-6
- J. Banas and A. Martinon, “Monotonic solutions of a Quadratic Integral Equations of Volterra type,” Computers & Mathematics with Applications, Vol. 47, No. 2-3, 2004, pp. 271-279. doi:10.1016/S0898-1221(04)90024-7

