World Journal of Nuclear Science and Technology
Vol.04 No.04(2014), Article ID:51026,11 pages
10.4236/wjnst.2014.44031
Dynamic Interaction Confinement
Gabriel Barceló
Advanced Dynamics S.A., Madrid, Spain
Email: gestor@advanceddynamics.net
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 August 2014; revised 19 September 2014; accepted 30 September 2014
ABSTRACT
The importance of developing new technologies to obtain energy by means of nuclear fusion procedures is beyond question. There are several different and technically possible models for doing this, though to date none of these has been able to attain an industrial reactor with an end performance greater than unity. We still find ourselves at the initial phase, after many years, as a result of having failed as yet to come up with a commercially productive machine. Nuclear fusion research has defined a prototype reactor based on a fluid conductor, isolated materially in a physical container and confined by means of magnetic fields. In this fluid-plasma which interacts with magnetic fields, fusion reactions are caused that release energy, while at the same time a quantity of movement and angular momentum is moved or “rotated” and transported. However, turbulence is caused in these magnetic confinement fusion processes that reduces system efficiency and prevents the obtaining of sufficient net energy from the nuclear reactions. This paper aims to propose new dynamic hypotheses to enhance our understanding of the behaviour of the plasma in the reactor. In doing so, we put forward a profound revision of classical dynamics. After over thirty years studying rotational dynamics, we propose a new theory of dynamic interactions to better interpret nature in rotation. This new theory has been tested experimentally returning positive results, even by third parties. We suggest that these new dynamic hypotheses, which we hold applicable to particle systems accelerated by rotation, be used in the interpretation and design of fusion reactors. We believe that this proposal could, in addition to magnetic confinement, achieve confinement by simultaneous and compatible dynamic interaction. Accordingly, we are of the opinion that it would be possible to get better performance and results in the design of fusion reactors by way of simultaneous magnetic and dynamic interaction confinement.
Keywords:
Nuclear Fusion, Rotational Dynamics, Non-Coaxial Spins, Dynamic Interactions, Dynamic Interaction Confinement

1. Introduction
We are currently in the phase of developing new technologies to obtain energy by means of nuclear fusion procedures. There are several different, technically possible models for doing this, all of which are based on the simulation of fusion processes that we assume and occur in our universe, though to date none of these has been able to attain an industrial reactor with an end performance greater than unity.
It was recently published [1] that scientists from the Lawrence Livermore National Laboratory (LLNL) in the USA have carried out a series of experiments on the thermonuclear ignition of the reactor at the National Ignition Facility (NIF), which have confirmed an improvement in fusion reaction performance, releasing more energy than that absorbed by the fuel used in the process.
For any fusion reaction to occur between two atomic nuclei, these have to overcome the Coulomb repulsion force. This force refers to the inverse-square law between charges. An example of the Sun itself has been taken to achieve the desired result, by way of an attempt to simulate in a reactor the conditions that hold with respect to the Sun. Notwithstanding, the nuclear process that the design of these experimental nuclear fusion reactors is trying to achieve is different to that of the solar one. The aim is to get Helium, a neutron and fusion energy from Deuterium and Tritium in accordance with the following formula:
H2(D)+ H3 (T) → He4 + n + 18 MeV
Plasma confinement is the most difficult obstacle to solve in thermonuclear fusion reactions with the current technological prototypes. Plasma [2] is an aggregate state of matter in which thermal agitation is capable of overcoming the electrical attraction electrons feel for atom nuclei. The Sun’s content is one of the best examples of plasma as it is capable of causing nuclear fusion reactions that produce energy output.
As a result of the extremely high temperatures at which nuclear fusion occurs, hydrogen or helium isotopes that are used as fuel are not in a solid, or liquid or gaseous state, but rather in a “fourth state”, which has become known as plasma. Plasma is, therefore, an ionised fluid in which reactions can take place that could not occur, or would not be sufficiently effective, in solids, liquids or gases. Plasma as a reactive medium is the subject of numerous studies at both basic and applied levels. Most of the foundational articles on plasma physics first saw the light of day in the middle and second half of the 20th century [3] , however, since then, theory and laboratory techniques have struck out into diverse branches.
Given that plasma, under its pressure and temperature conditions, can modify the structure of that which contains it, nuclear fusion reactor fuel “containers” cannot be exclusively physical, but rather require confinement procedures to avoid the content damaging the container. Magnetic confinement, and more recently, inertial confinement, techniques have been used to deal with this problem. However, great quantities of energy are required for these technological solutions to work. Indeed, to date, more energy has been required to ignite the reactor than it is capable of producing, and thus the end balance is still negative, given that these nuclear fusion reactors generate energy amounts below that which is required to start up and maintain the fusion process.
Consequently, the current goal is to achieve plasma ignition with a positive energy balance to enable its industrial use. This goal could be achieved, either by means of a new confinement procedure, based on other principles of physics, or by improving the performance of known procedures.
This paper proposes a revision of the grounds of classical dynamics that apply to these reactors, particularly when using fluids accelerated by rotation. Indeed, new specific dynamic hypotheses are put forward.
2. Methods for Achieving Fusion
Confinement enables us to avail of matter at a very high temperature without the containing recipient losing any of its initial structural characteristics or becoming contaminated. As indicated above, the two main technological procedures to isolate the plasma within its container are magnetic and inertial confinement. Other confinement systems have been proposed and studied, albeit without success.
Magnetic confinement consists of containing material in a state of plasma inside an enclosure inside which, in turn, a magnetic field has been created, in accordance with a preconceived design, so that the positive and negative particles that go to make up the plasma do not enter into contact with the inner walls of the enclosure. This procedure is based on the Lorentz force, which acts on any charged particle in motion in a magnetic field, by virtue of which it experiences a force perpendicular to the magnetic field vector and the displacement vector.
Inertial confinement consists of achieving the conditions required to produce nuclear fusion by endowing the fuel particles with an amount of movement such that with the colliding of these the Coulomb barrier is overcome, thus making it possible for the nuclear fusion reaction to occur.
Inertial confinement can be achieved by means of an electromagnetic system made up of laser rays focused on a target, or accelerated heavy ions focused on a small, spherical deuterium-tritium target. Indeed, even a direct or indirect approach can be designed.
In the cosmos we have gravitational confinement [4] , which occurs at the core of stars by means of fusion reactions, owing to the powerful gravitational field. However, it is not technologically possible to imitate this process on Earth.
To sum up, we can define the conditions required for controlled nuclear fusion in a reactor:
· Create a fuel and raise its temperature to values high enough to overcome Coulomb repulsion.
· Design a material and non-material container to confine plasma for long enough for the energy that is generated in the fusion to exceed the losses caused by radiation.
· Design a continuously and repeatedly operating reactor for commercial use at an acceptable maintenance cost and that exercises a feasible environmental impact.
To date, work has been done on developing the prototype of a reactor in Europe based on a conductor fluid interacting with magnetic fields, which is isolated materially in a physical container and confined therein by means of magnetic fields. Fusion reactions are caused in this fluid-plasma that release energy, while at the same time a quantity of movement and angular momentum is moved or “rotated” and transported.
3. Models of Experimental Reactors
The I. V. Kurchatov Institute of Atomic Energy of the ex-URSS Academy of Sciences developed the first Tokamak fusion reactor in the 1950s, designed by the Russian physicists Igor Tamm and Andrei Sakharov.
Other reactor models were built thereafter, such as the Joint European Torus (JET) (Figure 1) in England,
Figure 1. Joint European torus (European fusion development agreement—EFDA).
which is also a fusion reactor of the same type. Funded by the European Commission, it has been in operation since 1983 and is the biggest magnetic confinement fusion reactor in the world today.
In 1991 it achieved a performance of 0.7, the coefficient between the system’s input energy and the energy obtained from the reactor. Therefore, even though it is an efficient prototype that confirms the physics on which it is based, as well as its technological possibilities, it is still not a commercially viable reactor.
This round furnace is capable of handling a fuel mixture of deuterium and tritium which is supposedly to be used in future commercial fusion energy power plants and which is to be tested beforehand at the International Thermonuclear Experimental Reactor (ITER). ITER is an international experiment designed to show the scientific and technological feasibility of a full-scale fusion power reactor.
ITER is also based on the Tokamak magnetic confinement concept, in which plasma is contained in a toroidal-shaped vacuum chamber. It is, therefore, a cylindrical, ring-shaped fusion reactor, which explains why those of this type are also known as “torus” reactors. The fuel is heated to temperatures in excess of 150 million ˚C thus forming hot plasma. The strong magnetic fields that are used to keep the plasma away from the walls are created by superconducting coils that surround the container and by an electric current sent through the plasma. The problem lies in the enormous difficulty of compressing the fuel uniformly. In stars, gravity compresses the hydrogen into a perfect sphere thus the gas is heated uniformly and homogeneously. Such uniformity and homogeneity is very difficult to achieve under the reactor’s current technical conditions.
4. Plasma Dynamics
The dynamics of a conducting fluid that is interacting with intense magnetic fields created by sets of external coils are complex. Consequently, a lot of research being done into nuclear fusion as an energy source focuses on this issue.
Plasma movement is a complex variable in magnetic confinement that affects the capacity to confine it for long enough to obtain net energy from the fusion reactions. Plasma must be kept in constant circular motion within the reactor. Nevertheless, it is thought that each plasma particle following that circular path is at the same time exercising an orbital movement, as is shown in Figure 2.
The velocity fields that affect each particle generate this complex path, though the behaviour of the plasma in the reactor does not depend on dynamic laws alone, given that its very nature determines the influence of other physical variables. As plasma is a charged particle fluid, electrodynamics also affects its behaviour.
We recommend Enrique Larrea’s treatise [6] for an analysis and study of the different theories and meanings of the classical electromagnetic field from the perspective of the theoretical and philosophical models developed, and of classical electrodynamics.
The electrical charges form stable links in matter in the form of atoms, molecules, crystalline networks, etc. The electrodynamic nature of these links is expressed on an atomic scale, in such a way that the matter normally manifests itself as neutral.
Nevertheless, if the temperature of the neutral matter is raised to values comparable to those of the link energies, these links break in such a way that their constituent parts, the electrons and the ions in the case of atoms, are no longer linked to each other, but rather each charged particle moves independently in the electromagnetic fields created by the particles themselves, or by input from without.
Plasmas formed by ionisation from initially neutral constituents tend to contain the same number of positive and negative charges in terms of volume and have a strong tendency to remain quasi-neutral. Consequently,
Figure 2. Exact and reduced single-particle orbits in a magnetic field. [5] [7] .
small deviations in neutrality give rise to intense electric fields that are rapidly compensated by the free charges in the plasma.
Moreover, in the experiments carried out in magnetic confinement fusion reactors, turbulence has been seen to be generated that reduces system efficiency and prevents the obtaining of sufficient net energy from the process.
5. Gyrokinetic Theory
The study of magnetised plasma dynamics has come to form a new scientific discipline known as gyrokinetic theory. This theory is based on Maxwell and Fokker-Planck system of equations, consequently the resulting distribution functions and fields are in constant development [7] . Nevertheless, the theory is evolving in parallel with technological developments, while its analytical and computational resolution is proving to be extremely complex [8] . The theory has been gradually developed from its beginnings, with the following representing a historical summary of this evolution:
Brief History of Reduced Plasma Dynamics [9] .
· Adiabatic motion of charged-particle motion
Alfven (1940)
Northrop & Teller (1960)
Kruskal (1962)
Northrop (1963)
Littlejohn (1979-1983)
Cary & Littlejohn (1983)
Review: Cary & Brizard (2009)
· Oscillation-center dynamics & Ponderomotive Hamiltonian
Dewar (1973-1978)
Cary & Kaufman (1977)
· Reduced fluid dynamics
Strauss (1976)
Hasegawa & Mima (1977)
Hazeltine (1983) + Morrison & Hazeltine (1983)
· Linear gyrokinetic theory
Taylor (1967)
Rutherford & Frieman (1968)
Catto (1978)
Catto, Tang & Baldwin (1981)
· Nonlinear gyrokinetic theory
Frieman & Chen (1982)
Dubin, Krommes, Oberman & Lee (1983)
Hahm, Lee & Brizard (1988)
Brizard (1989)
Hahm (1996)
Sugama (2000) & Brizard (2000)
Qin & Tang (2004)
Review: Brizard & Hahm (2007)
In a lot of cases, possible concomitance has been sought with astrophysical plasmas [10] which are supposedly to be found in the universe. The inspiration for such theories is to be found in the studies carried out by H. Alfvén [11] .
The rotational nature of astrophysical plasmas has been taken into account in its development [12] , an issue that is reiterated and studied in fusion reactor plasmas. Accordingly, the idea is to have a model constituted by a continuous process, which is what is required for its industrial development. Current developments in our knowledge concerning the magnetic confinement of plasma for fusion defines a toroidal design of magnetic field force lines, which in successive toroidal transits travel over a surface topologically equivalent, in geometrical terms, to a torus, as is shown in Figure 3. Indeed, this is the basis of the JET Tokamak design and that of later reactors.
Figure 3. Gyrokinetic particle simulation. Implementation of Mixed-Mode Parallelism© Princeton plasma physics laboratory. http://w3.pppl.gov/theory/proj_gksim.html
Notwithstanding, it has been confirmed that circulation in the experimental reactors is more turbulent than that which is supposed in stellar dynamic systems and, as we have pointed out above, this reduction of fluid uniformity can cause undesired losses in the system’s power of confinement, or even, the possible cavitation of the physical container.
The speed of the plasma is an important physical field in the study of current laboratory systems, and particularly, in the improvement of its material isolation. The rotation profile can exercise considerable influence in the confinement time of the magnetically confined fluid. Profiles with a sharp radial velocity variation can cause a reduction of the turbulent transport and, therefore, could lead to improved confinement.
The study of plasma microturbulence caused by the electromagnetic interactions of its particles is one of the current goals in an attempt to improve the performance of these reactors. Understanding this microturbulence in plasma would enable its control and thus have a direct favourable impact on the building of more efficient fusion reactors.
Simulations conducted for numerous situations, and their comparison, as suggested in Figure 4, can be found in the bibliography. It has been confirmed that the existing gyrokinetic models are sufficiently valid for shorter times than the real time scales of the evolution of the reactor’s dynamic profiles, thus it is thought that the effect of turbulence on the electric field and plasma velocity provide incorrect values for the electric field. Consequently more precise mathematical models are needed to represent the real behaviour of plasma at a longer time scale, called the transport scale.
This was in fact just the approach taken by the Spanish aeronautical engineer and physicist, Félix Parra, in his doctoral thesis written at the Massachusetts Institute of Technology (MIT) under the supervision of Dr. Peter J. Catto. This thesis won him the 2011 prize awarded each year by the American Physical Society (APS): For demonstrating limitations in the gyrokinetic theory of the radial electric field for plasmas in an axisymmetric magnetic field and formulating an alternative procedure—insights that have inspired research around the world [13] .
As we have already pointed out above, plasma rotation is another essential factor in this analysis of the turbulent transport of momentum in axisymmetric systems. In magnetic confinement fusion systems such as the aforementioned ITER [14] , the plasma circulates in the container at a constant movement, which we could define as rotation with respect to its walls. Notwithstanding, it has been shown [15] that the plasma in the reactor can initiate spontaneous circular movement or rotation, without the need for any external dynamic momentum input. The theoretical development of this behaviour is still under study [16] . According to Parra: The origin of the intrinsic rotation is still unclear [17] .
There has been some theoretical work in turbulent transport of momentum using gyrokinetic simulations [18] - [23] and different mechanisms have been proposed as candidates to explain intrinsic rotation [24] .
The presence of an external magnetic field introduces a source of plasma anisotropy. Variations or fluctuations in the thermodynamic fields are much greater perpendicularly to the field than parallel to it.
According to recent investigations by Dr. Parra: The ion toroidal rotation in a Tokamak consists of an E × B flow due to the radial electric field and a diamagnetic flow due to the radial pressure gradient… the momentum
Figure 4. Comparison of nonlinear mode structure: effects of zonal flows. GTC simulations, Gyrokinetic Toroidal Code (GTC)© Princeton plasma physics laboratory. http://w3.pppl.gov/theory/bin/zonal-flow.jpg
pinch for the rotation generated by the radial pressure gradient is calculated and is compared with the Coriolis pinch. This distinction is important for subsonic flows or the flow in the pedestal where the two types of flows are similar in size and opposite in direction. At the edge, the different pinches due to the opposite rotations can result in intrinsic momentum transport that gives significant rotation peaking [25] .
In recent articles, Dr. Parra also puts forward intrinsic rotation evolution equations in conventional Tokamak reactors [26] [27] .
6. Theory of Dynamic Interactions
Against this background of study and constant advancement in unravelling the physical behaviour of Tokamak- type nuclear reactors, we suggest a revision of the dynamic criteria being applied, given that we believe there may well be inappropriate interpretations in the principles of classical rotational dynamics at play.
We propose a dynamic model for confined plasma equivalent to the flight of the boomerang, which enables its return to its point of departure and, therefore, a natural dynamic confinement. We advise the study of boomerang dynamics, given that it would afford us a better understanding of the dynamics of confined plasma by dynamic interaction, along with an improved reactor result.
Nevertheless, we believe that the boomerang is nothing more than an illustrative example of the true behaviour of nature when mass is subjected to simultaneous non-coaxial rotations. We hold that its theoretical dynamic principles can be applied in general to bodies or particles with mass, thus we suggest that the classical rotational dynamics theory be rigorously tested and verified.
Over the last thirty years we have been analyzing the behaviour of bodies subjected to accelerations by non- coaxial rotations. We propose a new interpretation of the dynamic behaviour of the boomerang and, in general, of rigid bodies exposed to simultaneous non-coaxial rotations. We have developed a new rotational, non-inertial dynamics hypothesis, which can be applied to understand both, the flight of the boomerang, as well as celestial mechanics. […]
The Theory of Dynamic Interactions (TDI) claims that the boomerang returns to its origin as a result of being a body that is subject to two simultaneous rotations on different axes (Figure 5). As of the moment it is first released into the air, in addition to the impulse driving it forward, it is made to revolve around an axis that is perpendicular to its plane [28] .
In accordance with the Theory of Dynamic Interaction: The anisotropic distribution of the velocities (Vc) generated by the torque shall be compounded with the initial linear velocity (VT), enabling a curved path… The velocity VR = (vx, vy, vz) of the new path of its center of mass will be defined by the matrix multiplication of the ro-
tating operator  by the velocity vector V0 = (0, V0, 0) [29] :
by the velocity vector V0 = (0, V0, 0) [29] :
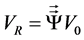 (1)
(1)
This is the equation for movement that we have deduced for bodies with intrinsic rotation and translation when they are subjected to momenta that are non-coaxial with their rotation. In our opinion, this applies to the flight of the boomerang, but we also suggest that it would enable the definition of the path of each plasma particle, as long as the established baseline hypotheses are met.
We have conducted several test experiments on the theory under proposal e.g. moving objects with intrinsic rotation on their main axis semi-submerged in water and subject to a righting torque, consisting of the weight and force of floatation, the relative positions of which do not coincide [30] . This righting torque was not coaxial with the intrinsic rotation. The moving object was, therefore, subject to two non-coaxial rotations, as is the case with the boomerang, but we noticed how the rotation caused by the righting torque did not generate any new moving rotations, but rather was transformed into a change of path of the center of mass [31] . Experiments were also conducted on terra firme [32] , which can also be seen in video [30] [33] [34] .
In accordance with the theory being put forward, and as can be appreciated in Figure 6, we suggest that each particle, instead of following a linear path, as would be expected from the classical mechanics equations of Newton-Euler, it would follow a closed path owing to the coupling of the velocities’ fields that are caused on every point of each particle.
Figure 5. Rotations that generate changes in the boomerang’s path as a result of the coupling of the velocity fields that act on its center of mass [28] .
Figure 6. The position of the center of mass varies depending on the coupling between the field of the linear velocity and the velocity field caused by the non- coaxial torque [35] . (Figure Alejandro Alvarez).
The issue can be summed up as follows: If we apply this dynamic theory to a Tokamak reactor, every plasma particle with intrinsic rotation will follow a closed path like that of the boomerang when it is subjected to a non-coaxial momentum in addition to its intrinsic angular momentum. Consequently, there are different authors [32] [36] who share these same hypotheses with a view to understanding the dynamic behaviour of bodies or particles in those circumstances in which they have translational velocity, intrinsic rotation and are simultaneously subjected to a non-coaxial momentum with its own rotation [37] . Notwithstanding, in our hypothesis, based on a possible analogy, we are extrapolating the observed behaviour in macroscopic moving bodies to the reactor’s plasma particles.
In our opinion, this dynamic model also coincides with the behaviour of hurricanes on the Earth and also resembles atmospheric toroidal vortex rings.
It must be pointed out that in our investigations we have come to a rational deduction to the effect that in such circumstances, the kinetic translational energy can be transformed into kinetic rotational energy, and vice versa, and in general, energy transfers can occur at the core of particles endowed with intrinsic angular momentum: […] kinetic energy can be transferred, increasing its rotation velocity, its linear velocity or modifying its state of potential [38] .
At the beginning of this paper we stated that magnetic confinement is based on the Lorentz force. This force manifests itself when an electric charge in movement moves in a magnetic field. We have stated in other works that, in our opinion, the origin of this force is analogous to that of the inertial forces that manifest themselves in TDI circumstances [39] and which oblige particles to follow a closed path. Therefore, and in accordance with our hypothesis, the same dynamic effect and the same effective confinement could be obtained doubly, by the magnetic effect and by the dynamic effect.
Both ideas being proposed should, we feel, be further explored and, where appropriate, confirmed experimentally; on the one hand, that the Lorentz force is analogous to an inertial dynamic force, similar to TDI ones, and on the other hand, that this theory be applied to the reactor’s plasma.
7. Conclusions
Nuclear fusion is a necessary energy alternative into which countries are researching and in which they trust. However, investment is still needed to develop the requisite technology, or even, to conceive the new physical ideas involved in obtaining the energy.
It does not seem likely in the short term that it will be possible to come up with new continuous nuclear fusion procedures and technology without using plasma, which represents another great research challenge in physics.
Even though over fifty years of theoretical and technological developments have passed, the road yet to be travelled to develop industrial fusion reactors is still a long one, both in terms of physics, as well as the engineering required.
As far as magnetic confinement reactors are concerned, plasma dynamics is still a work in progress. We are as yet ignorant of the exact dynamic behaviour of plasma and, moreover, when designing these generators it is still necessary to reduce their turbulent tendency and improve their momentum transport capacity.
We propose a profound revision of the principles of classical rotational mechanics, especially as regards particles subjected to accelerations by simultaneous and non-coaxial rotations. After conducting our research, we put forward certain specific, alternative dynamic hypotheses.
In addition to the plasma’s material container, we can envisage another simultaneous, non-material container, along with the use of magnetic confinement techniques. We suggest the exploring of a new type of dynamic confinement based on the TDI and one that is compatible with magnetic confinement.
Gyrokinetics is the workhorse for modern research on low-frequency microturbulence in magnetised plasmas. It is a very powerful tool that has been used successfully in many different applications in both fusion and astrophysics:
Analytical theory of drift waves and related modes.
Statistical mechanics of magnetised systems.
Simulations of turbulent transport.
Interpretation of solar-wind data.
Theory of momentum transport.
Simulations of intrinsic rotation [40] .
Moreover, in our opinion, the TDI could also be employed as a complementary theoretical instrument that would lead to greater reactor efficiency. Consequently, its dynamic hypotheses ought to be studied in the field of gyrokinetic theory.
The equation for movement that we are proposing in the Theory of Dynamic Interactions for these non-iner- tial situations is very simple (1) […]. It becomes possible to determine the path of [28] plasma particles in translation, when these particles are endowed with intrinsic rotation and are subjected to rotation actions on another, different axis. […]
The Theory of Dynamic Interactions on which this proposal is based is fully described in different texts and articles, in which it is possible to see how this theory affects, in a far reaching way, the basic principles of dynamics [41] , not to mention astrophysics [42] , cosmology [43] , atomic physics and technology. An analysis of this theory reveals its capacity to answer numerous unknowns in dynamics and celestial mechanics and, moreover, explains the behaviour of rotating bodies [31] .
These new dynamic hypotheses we are putting forward and which we hold applicable to particle systems accelerated by rotation can, we suggest, be used in the interpretation and design of fusion reactors. Accordingly, we persist in our belief that magnetic confinement in a reactor can be likened to confinement by dynamic interactions based on the Theory of Dynamic Interactions. Applying this criterion we are proposing would enable a twin physical-theoretical principle to isolate plasma and try to minimize its turbulence: each plasma particle should have spin and be subjected to a non-coaxial magnetic momentum from without and another gravimetric one. Accordingly, plasma confinement will be based on two different, albeit analogous, physical principles, generating double intransigence in its path.
The dynamic model based on boomerang dynamics could improve the performance of these energy power plants, minimize turbulence and improve momentum transport. Consequently, we insist on the exploration of the ideas expounded in this paper with respect to the origin of the Lorentz force and the true, dynamic nature of plasma made up of particles with intrinsic rotation when they are subjected to new, non-coaxial momenta.
References
- Hurricane, O.A., et al. (2014) Fuel Gain Exceeding Unity in an Inertially Confined Fusion Implosion. Nature, 506, 343-348. http://dx.doi.org/10.1038/nature13008
- Bittencourt, J.A. (2004) Fundamentals of Plasma Physics. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4757-4030-1
- Chen, F.F. (1984) Introduction to Plasma Physics and Controlled Fusion: Plasma Physics. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4757-5595-4
- Clayton, D.D. (1983) Principles of Stellar Evolution and Nucleosynthesis. McGraw-Hill, New York; Reissued by University of Chicago Press, Chicago.
- Brizard, A.J. and Hahm, T.S. (2007) Foundations of Nonlinear Gyrokinetic Theory. Reviews of Modern Physics, 79, 421.
- Larrea Bellod, E. (2010) Los significados del campo electromagnético y sus transformaciones históricas. Bubok. C/ Belén 13, Madrid. Also: Larrea Bellod, E. (2008) Teorías sobre el origen de la luz y el campo electromagnetic. Bubok. C/Belén 13, Madrid.
- Alonso de Pablo, J.A. and Almeida, J.S. (2013) La rotación y el transporte de momento en plasmas astrofísicos y de laboratorio.
- Abel, I.G., Plunk, G.G., Wang, E., Barnes, M., Cowley, S.C., Dorland, W. and Schekochihin, A.A. (2013) Multiscale Gyrokinetics for Rotating Tokamak Plasmas: Fluctuations, Transport and Energy Flows. iv: 1209.4782v4 [physics.plasm-ph]
- Brizard, A.J. (2010) Lectures on Gyrokinetic Theory. Part I: Physical and Mathematical Foundations of Gyrokinetic Theory. Summer School on Self-Organization in Turbulent Plasmas and Fluids. Max-Planck-Institut für Physik Kom- plexer Systeme. Dresden.
- Howes, G.G., et al. (2006) Astrophysical Gyrokinetics: Basic Equations and Linear Theory. The Astrophysical Journal, 651, 590-614. http://stacks.iop.org/0004-637X/651/i=1/a=590
- Alfvén, H. (1950) Cosmical Eletrodynamics (The International Series of Monographs on Physics). Clarendon Press. http://ia600703.us.archive.org/23/items/CosmicalElectrodynamics/Alfven-CosmicalElectrodynamics.pdf
- Parra, F.I. and Calvo, I. (2011) Phase-Space Lagrangian Derivation of Electrostatic Gyrokinetics in General Geometry. Plasma Physics and Controlled Fusion, 53, Article ID: 045001. http://stacks.iop.org/0741-3335/53/i=4/a=045001
- Text of the Declaration of the Jury of the American Physical Society (APS) on Awarding Félix Parra Díaz, Aeronauti cal Engineer from the Universidad Politécnica de Madrid, with the 2011 Marshall N. Rosenbluth Award for His Thesis: Extension of Gyrokinetics to Transport Time Scales, Massachusetts Institute of Technology (MIT).
- Ikeda, K. (2007) Progress in the ITER Physics Basis. Nuclear Fusion, 47, S203. http://stacks.iop.org/0029-5515/47/i=6/a=E01
- Rice, J.E., Ince-Cushman, A.C., Reinke, M.L., Podpaly, Y., Greenwald, M.J., LaBombard, B. and Marmar, E.S. (2008) Spontaneous Core Toroidal Rotation in Alcator C-Mod L-Mode, H-Mode and ITB Plasmas. Nuclear Fusion, 50, Artcle ID: 124042. http://dx.doi.org/10.1088/0741-3335/50/12/124042
- Parra, F.I., Barnes, M., Calvo, I. and Catto, P.J. (2012) Intrinsic Rotation with Gyrokinetic Models. Physics of Plasmas, 19, Article ID: 056116. http://link.aip.org/link/?PHP/19/056116/1
- Parra, F.I., Barnes, M., Peierls, R. and Catto, P.J. Sources of Intrinsic Rotation in the Low Flow Ordering. Centre for Theoretical Physics, University of Oxford, Oxford, Plasma Science and Fusion Center, Massachusetts Institute of Technology.
- Peeters, A.G., Angioni, C. and Strinzi, D. (2007) Toroidal Momentum Pinch Velocity due to the Coriolis Drift Effect on Small Scale Instabilities in a Toroidal Plasma. Physical Review Letters, 98, Article ID: 265003. http://dx.doi.org/10.1103/PhysRevLett.98.265003
- Waltz, R.E., Staebler, G.M., Candy, J. and Hinton, F.L. (2007) Gyrokinetic Theory and Simulation of Momentum Transport and Energy Exchange. Physics of Plasmas, 14.
- Roach, C.M., Abel, I.G., Akers, R.J., Arter, W., Barnes, M., et al. (2009) Gyrokinetic Simulations of Spherical Tokamaks. Plasma Physics and Controlled Fusion, 51, Article ID: 124020. http://dx.doi.org/10.1088/0741-3335/51/12/124020
- Camenen, Y., Peeters, A.G., Angioni, C., Casson, F.J., Hornsby, W.A., Snodin, A.P. and Strintzi, D. (2009) Transport of Parallel Momentum Induced by Current-Symmetry Breaking in Toroidal Plasmas. Physical Review Letters, 102, Article ID: 125001. http://dx.doi.org/10.1103/PhysRevLett.102.125001
- Casson, F.J., Peeters, A.G., Camenen, Y., Angioni, C., Hornsby, W.A., Snodin, A.P., Strintzi, D. and Szepesi, G. (2009) Anomalous Parallel Momentum Transport Due to E × B Flow Shear in a Tokamak Plasma. Physics of Plasmas, 16, Article ID: 092303. http://dx.doi.org/10.1063/1.3227650
- Highcock, E.G., Barnes, M., Schekochihin, A.A., Parra, F.I., Roach, C.M. and Cowley, S.C. (2010) Transport Bifurcation in a Rotating Tokamak Plasma. Physical Review Letters, 105, Article ID: 215003. http://dx.doi.org/10.1103/PhysRevLett.105.215003
- Wang, L. and Diamond, P.H. (2013) Gyrokinetic Theory of Turbulent Acceleration of Parallel Rotation in Tokamak Plasmas. Physical Review Letters, 110, Article ID: 265006.
- Lee, J.P., Parra, F.I. and Barnes, M. (2013) Turbulent Momentum Pinch of Diamagnetic Flows in a Tokamak. Nuclear Fusion, 54, Article ID: 022002.
- Parra, F.I. and Barnes, M. (2014) Intrinsic Rotation in Tokamaks. Theory. arXiv: 1407.1286v1
- Parra, F.I., Calvo, I., Burby, J.W., Squire, J. and Qin, H. (2014) Equivalence of Two Independent Calculations of the Higher Order Guiding Center Lagrangian. Physics of Plasmas, 21, Article ID: 104506.
- Barceló, G. (2014) Theory of Dynamic Interactions: The Flight of the Boomerang. Journal of Applied Mathematics and Physics, 2, 569-580. http://dx.doi.org/10.4236/jamp.2014.27063
- Barceló, G. (2005) The Flight of the Boomerang. El Vuelo del Bumerán, Marcombo, Barcelona. http://www.dinamicafundacion.com/
- Theory of Dynamic Interactions. http://www.youtube.com/watch?v=P9hGgoL5ZGk&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=XzTrGEtJGXU&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=dtMqGSU9gV4&list=PL3E50CF6AEBEED47B http://www.youtube.com/watch?v=qK5mW2j2nzU&list=PL3E50CF6AEBEED47B
- Rico-Avello, G.B. Analysis of Dynamic Field Systems Accelerated by Rotation. Dynamics of Non-Inertial Systems. DeMSET-2011 Congress, Miami. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/DeMSET_2011_GBarcelo.pdf
- Pérez, L. (2013) New Evidence on Rotational Dynamics. World Journal of Mechanics, 3, 174-177. http://www.scirp.org/journal/wjm http://dx.doi.org/10.4236/wjm.2013.33016
- Pérez, L.A. (2013) Reflecting New Evidence on Rotational Dynamics. http://vimeo.com/68763196
- Bauluz, E. New Dynamic Hypotheses. This Video Showed the Experimental Tests Carried out by Advanced Dynamics S. A. to Proof and Justify the Theory of Dynamic Interactions. http://www.advanceddynamics.net/
- Barceló, G. (2013) Technological Applications of the New Theory of Dynamic Interactions. Global Journal of Researches in Engineering: Mechanical and Mechanics Engineering-G, 13, Version 1.0. https://globaljournals.org/GJRE_Volume13/E-Journal_GJRE_(G)_Vol_13_Issue_5.pdf
- González, M.D. (2013) Dinámica de sistemas con spin: Un nuevo enfoque. Fundamentos y aplicaciones. ADI Ser, Ma- drid.
- González, M.D. Equation of Motion of Systems with Internal Angular Momentum-II. arXiv:physics/0603207.
- Barceló, G. (2013) Theory of Dynamic Interactions: Laws of Motion. World Journal of Mechanics, 3, 328-338. http://dx.doi.org/10.4236/wjm.2013.39036
- Barceló, G. (2008) A Rotating World (Un mundo en rotación). Editorial Marcombo: Barcelona. http://www.dinamicafundacion.com/
- Krommes, J.A. (2011) The History and Present Status of Gyrokinetic Theory. International Sherwood Fusion Theory Conference, Austin, 4 May 2011.
- Barceló, G. (2010) On the Equivalence Principle. 61st International Astronautical Congress, American Institute of Ae- ronautics and Astronautics, Prague. http://www.coiim.es/forocientifico/FORO%20CIENTFICO/Documentos/ON_THE_EQUIVALENCE_PRINCIPLE.pdf
- Barceló, G. (2013) Proposal of New Criteria for Celestial Mechanics. International Journal of Astronomy and Astrophysics, 3, 385-391. http://dx.doi/org/10.4236/ijaa.2013.34044
- Barceló, G. (2013) Imago Universi: A Story of the Human Conception of the Cosmos. Arpegio, Barcelona. http://www.editorialarpegio.com/ http://imagouniversi.com/








