Comparative analysis of internal and external-
hex crown connection systems - a finite element
study
Comparative analysis of internal and external-
hex crown connection systems - a finite element
study
1111 2
Rudi C. Van Staden, Hong Guan , Yew-Chaye Loo, Newell W. Johnson& Meredith Nell
12
Griffith School of Engineering/Dentistry and Oral Health, Griffith University, Gold Coast Campus, Queensland 4222, Australia. Neoss Pty
Ltd,Harrogate HG1 2PW, United Kingdom.* Correspondence should be addressed to Rudi C. Van Staden ([e-mail]).
has reduced stress concentrations in the
ABSTRACT crown. However, because the torque is trans-
ferred through the abutment screw to the abut-
Objectives: The abutment connection with
ment contact, changing the torque has greater
the crown is fundamental to the structural
effect on this hex system than the masticatory
stability of the implant system and to the pre-
force. Overall the masticatory force is more
vention of mechanical exertion that can com-
influential on the stress within the crown for
promise the success of the implant treatment.
the external-hex system and the torque is more
The aim of this study is to clarify the difference
influential on the internal-hex system.
in the stress distribution patterns between
implants with internal and external-hex con-
nections with the crown using the Finite Ele-
ment Method (FEM). Material and Methods: The
internal and external-hex connections of the
Neoss and 3i implant systems respectively, are1. INTRODUCTION
considered. The geometrical properties of theDental implants are a consistently accepted form of
implant systems are modeled using three-dental treatment. Clinical research in oral implantology
dimensional (3D) brick elements. Loading con-has led to advancements in the biomechanical aspects
ditions include a masticatory force of 200, 500of implants, implant surface features and implant
and 1000N applied to the occlusal surface ofcomponentry. These advancements in implant
the crown along with an abutment screw torquecomponentry include the modification of the exter-
of 110, 320 and 550Nmm. The von Mises stressnal-hex connection between the abutment and crown
distribution in the crown is examined for allto the currently used internal-hex ()).
loading conditions. Assumptions made in theAlthough both internal and external-hex connected
modeling include: 1. half of the implant systemimplant systems are extensively used, distinctly dif-
is modeled and symmetrical boundary condi-ferent performances are on offer in terms of the stress
tions applied; 2. temperature sensitive ele-characteristics produced within the crown. Observa-
ments are used to replicate the torque withintions by practitioners have aided the identification of
the abutment screw. Results: The connectionimplant components which lead to mechanical failure
type strongly influences the resulting stressof the crown and implant [1-3]. Failure may be
defined as the point at which the material exceeds the characteristics within the crown. The magni-
fracture stress, as indicated by its stress strain rela- tude of stress produced by the internal-hex
tionship. There are two major factors which can implant system is generally lower than that of
cause the crown and implant to fail. These are
the external-hex system. The internal-hex sys-
described below;
tem held an advantage by including the use of
- typically, over tightening of the abutment screw
an abutment between the abutment screw and
causes failure of the crown for internal and external-
the crown. Conclusions: The geometrical
hex systems.
design of the external-hex system tends to
- failure of the implant may also be a result of over
induce stress concentrations in the crown at a
tightening of the abutment screw or excessive
distance of 2.89mm from the apex. At this loca-
masticatory loads being transferred from the occlusal
tion the torque applied to the abutment screw
plane of the crown to an area of stress concentration
also affects the stresses, so that the compres-
at the interface between the abutment and implant
sive stresses on the right hand side of the
body.
crown are increased. The internal-hex system
Keywords: Component; Biomedical modelling;
Dental implant; Finite element technique
Figure 1b
J. Biomedical Science and Engineering, 2008, 1, 10-14Scientific
Research
Publishing
JBiSE
Published Online May 2008 in SciRes.http://www.srpublishing.org/journal/jbise
SciRes Copyright ©2008

Using theoretical techniques, such as the FEM, all
mechanical aspects that could affect the implant suc-
cess can be evaluated. FEM has been used exten-
sively to evaluate the performance of dental implant
prosthesis [4-15]. Studies by Maeda et al. (2006),
Merz et al. (2000) and Khraisat et al. (2002) have all
considered the behavior of the stress within the abut-
ment screw however disregarding the stress within
the crown. To date no published research appears to
have investigated the stress characteristics in the
crown due to an internal or external-hex system. Ulti-
mately, the outcome of this study will facilitate den-
tal practitioners to identify locations within the
implant system that are susceptible to stress concen-
trations.
2. METHODOLOGY
The modeling and simulation herein are performed
using the Strand7 Finite Element Analysis (FEA) Sys-
tem (2004). The first step of the modeling is to define
the geometry of the implant system. This is then fol-
lowed by specifying the material behavior in terms of
the Young's modulus, Poisson's ratio and density for
the implant and componentry.After applying the
appropriate loading and restraint conditions, the
c) Locations for measuring stress profile and contour
a) Loading and restraint conditions
(with detailed variables)
Figure 1. Finite element model of internal and external-hex systems.
internal and external-hex systems can be evaluated
for their contributions to the stress characteristics
within the crown.
2.1. Modelling
Data acquisition for the internal and external-hex sys-
tems are obtained from the manufacturer's data.
Shown in ) are details of the Neoss (2006)
and 3i (2006) systems.
Shown in ) are the detailed variables con-
sidered in this study. The implant is conical with 2
degrees of taperage, a helical thread, diameter of
4.5mm, and length of 11mm. Different fixed
restraints are applied to the symmetrical edge of the
implant system as compared to the outer edge of
implant thread. The symmetrical edge is restrained
from rotating around the z-axis and translating
through the x- and y-axis. The outer edge of the
implant thread is restrained from deforming in any
direction. Note that these loading and restraint condi-
tions are the same for both internal and external-hex
systems.
For the Neoss and 3i finite element models, the
total numbers of elements are respectively 13464 and
30420 for the implant, 3564 and 9108 for the abut-
ment, 17424 and 25956 for the abutment screw,
38484 and 47052 for the crown. The total number of
nodal points for the entire Neoss and 3i models are
82547 and 122688 respectively.
2.2. Stress Measuring
As indicated in) the von Mises stresses
along the lines NN (NN, NNand NN) and II
1-22-3 3-4
(II, II, II, II, IIand II) for the Neoss
1-2 2-3 3-4 4-5 5-66-7
and 3i systems respectively, are measured for all pos-
sible combinations of loading. Note that, for example,
along the line IIthe beginning location of the line
1-2
is identified as II and the end as II. These locations
12
are believed by clinicians to be critical for examining
the stress levels in the crown. Note that both lines NN
and II are chosen on Section AA because the highest
stress magnitudes (compressive is prominent over ten-
Figure 1b
Figure 1a
Figure 1c
SciRes JBiSE Copyright ©2008
11
R.C. Van Staden et al./J. Biomedical Science and Engineering 1 (2008) 10-14
b) Implant systems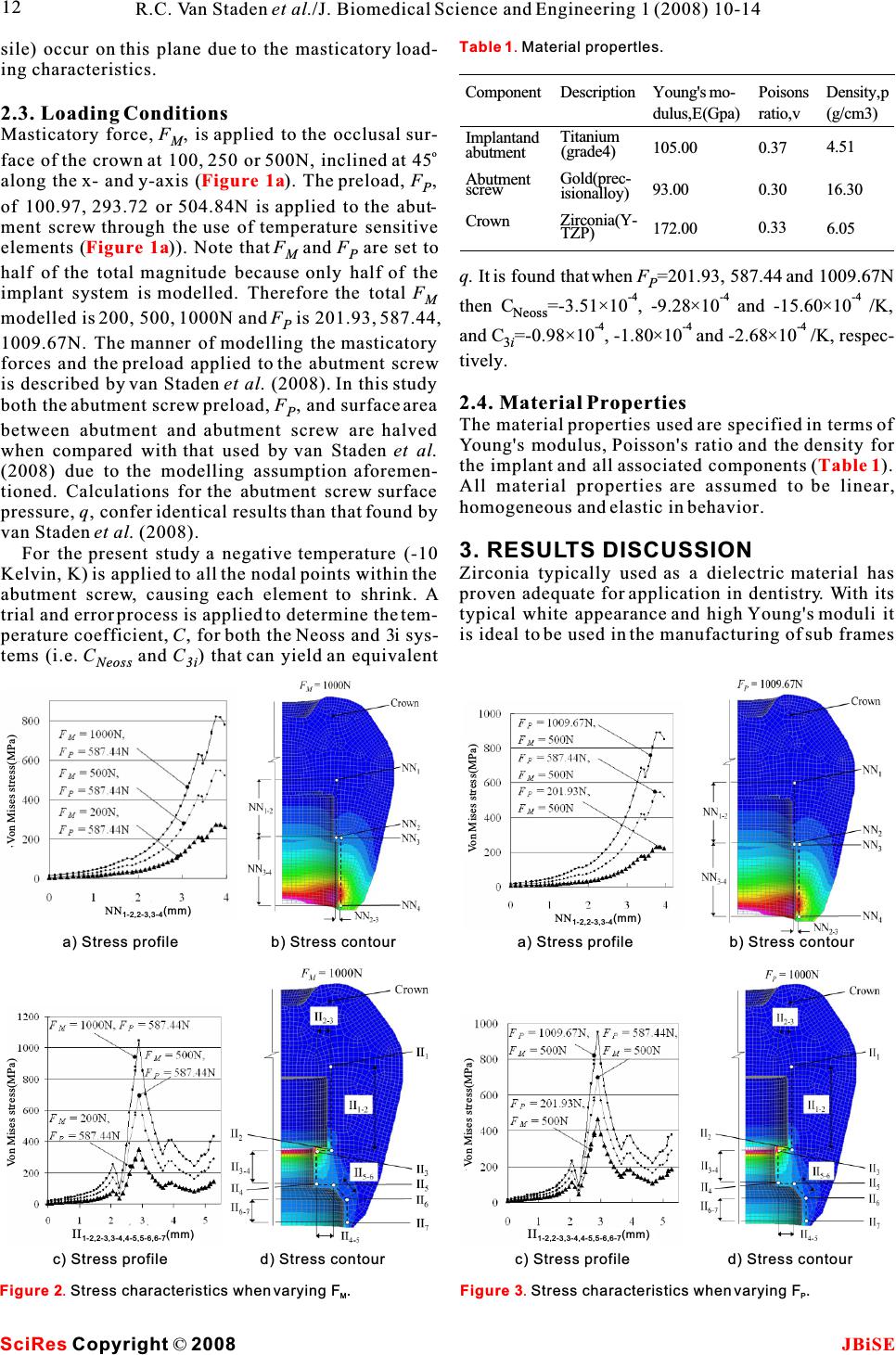

sile) occur on this plane due to the masticatory load-
ing characteristics.
2.3. Loading Conditions
Masticatory force, F, is applied to the occlusal sur-
M
o
face of the crown at 100, 250 or 500N, inclined at 45
along the x- and y-axis (). The preload, F,
P
of 100.97, 293.72 or 504.84N is applied to the abut-
ment screw through the use of temperature sensitive
elements ()). Note thatF and F are set to
MP
half of the total magnitude because only half of the
implant system is modelled. Therefore the total FM
modelled is 200, 500, 1000N andF is 201.93, 587.44,
P
1009.67N. The manner of modelling the masticatory
forces and the preload applied to the abutment screw
is described by van Staden et al. (2008). In this study
both the abutment screw preload, F, and surface area
P
between abutment and abutment screw are halved
when compared with that used by van Staden et al.
(2008) due to the modelling assumption aforemen-
tioned. Calculations for the abutment screw surface
pressure, q, confer identical results than that found by
van Staden et al. (2008).
For the present study a negative temperature (-10
Kelvin, K) is applied to all the nodal points within the
abutment screw, causing each element to shrink. A
trial and error process is applied to determine the tem-
perature coefficient,C, for both the Neoss and 3i sys-
tems (i.e. C and C) that can yield an equivalent
Neoss 3i
Figure 1a
Figure 1a
Figure 2. Stress characteristics when varying F.
MFigure 3.Stress characteristics when varying F. P
a) Stress profileb) Stress contour
c) Stress profiled) Stress contour
a) Stress profileb) Stress contour
c) Stress profiled) Stress contour
q. It is found that when F=201.93, 587.44 and 1009.67N
P
-4 -4-4
then C=-3.51×10 , -9.28×10 and -15.60×10 /K,
Neoss
-4 -4-4
and C=-0.98×10, -1.80×10 and -2.68×10 /K, respec-
3i
tively.
2.4. Material Properties
The material properties used are specified in terms of
Young's modulus, Poisson's ratio and the density for
the implant and all associated components ().
All material properties are assumed to be linear,
homogeneous and elastic in behavior.
3. RESULTS DISCUSSION
Zirconia typically used as a dielectric material has
proven adequate for application in dentistry. With its
typical white appearance and high Young's moduli it
is ideal to be used in the manufacturing of sub frames
Table 1
Table 1. Material propertles.
Component
Implantand
abutment
Abutment
screw
Crown
Description
Titanium
(grade4)
Gold(prec-
isionalloy)
Zirconia(Y-
TZP)
Young's mo-
dulus, E (Gpa)
105.00
93.00
172.00
Poisons
ratio, v
0.37
0.30
0.33
Density, p
(g/cm3)
4.51
16.30
6.05
SciRes JBiSE Copyright ©2008
12 R.C. Van Staden et al./J. Biomedical Science and Engineering 1 (2008) 10-14
Von Mises stress(MPa)Von Mises stress(MPa)
Von Mises stress(MPa)
Von Mises stress(MPa)
NN (mm)
1-2,2-3,3-4
II (mm)
1-2,2-3,3-4,4-5,5-6,6-7 II (mm)
1-2,2-3,3-4,4-5,5-6,6-7
NN (mm)
1-2,2-3,3-4

stresses along the lines NN and II for all values ofFP
for the construction of dental restorations such as are shown in.
crowns and bridges, which are then veneered with As found forF, when F increases the stresses
conventional feldspathic porcelain. Zirconia has aMP
fracture strength that exceeds that of Titanium there-calculated along the line NN increase, showing two
fore it may be considered as a high strength material. peaks along the line NN(refer to) and
3-4
However with cyclic preload and masticatory loads )).Also, as found for F, elevated stress
M
the compressive strength of 2.1GPa (Curtiset al.peaks are identified at the beginning of the line II3-4
2005) can easily be exceeded especially for implant() and)). Overall, all values of
systems with external-hex connections, as confirmedF cause greater stresses along lines NN and II, than
M during this study.
do varying values ofF.
The distribution of von Mises stresses in the crownP
is discussed for both the internal and external-hex sys-
tems for all combinations of masticatory and preload 4. DISCUSSION
forces. Shown in), are the von Mises FEA has been used extensively to predict the
stresses measured between locations NN (0-
1-2 biomechanical performance of the jawbone sur-
1.76mm), NN (1.76-1.87mm) and NN(1.87-rounding a dental implant [21, 22]. Previous research
2-3 3-4
considered the influence of the implant dimensions
3.96mm) for the Neoss system. For the 3i system the
and the bone-implant bond on the stress in the sur-
von Mises stresses are measured between locations
rounding bone. However, to date no research has
II(0-2.38mm), II(2.38-2.78mm), II(2.78-
1-22-33-4 been conducted to evaluate the stress produced by dif-
3.67mm), II(3.67-4.06mm), II(4.06-4.65mm)
4-55-6 ferent implant to crown connections (i.e. internal and
and II(4.65-5.27mm), as shown in ).
6-7 external-hex). The analysis completed in this paper
uses the FEM to replicate internal and external-hex
systems when subjected to both Fand F loading
MP
3.1. Masticatory Force, FMconditions.As shown in, two stress peaks
The distributions of von Mises stresses along thewere revealed along the lines NN and II at locations
lines NN and II for all values ofF are shown in
M3.76 and 2.89mm from the top. The stress values
Note that the preload,F, is set at its medium
pshown were calculated with the other variables (i.e.
value, i.e. 587.44N. F or F) set to its average.
MP
In general, when the applied masticatory force, F,
MThe mastication forceF is applied on the
M
is increased, the von Mises stresses also increase pro-occlusal surface of the crown, evenly distributed
portionally, because the system being analysed is lin-along 378 nodal locations (), and orien-
o
ear elastic. WhenF increases the stress along the
Mtated at 45 in the x-y plane. This induces compres-
line NN increases showing two peaks along the line sive stresses in the right hand side of the crown and
NN(refer to )). The larger of these two tensile in the left. VaryingFfrom 200 to 1000N for
3-4 M
peaks occurs at a distance of±3.8mm in length fromthe internal and external-hex systems results in a
NN. This stress peak (as can be identified in change in von Mises stress of 545.64 (818.47-
1
272.82MPa) and 698.09MPa (1047.14-349.05MPa)
)) is caused by a sharp corner and sudden change in
respectively. The geometrical design of the external-
section at this point.
hex system tends to induce stress concentrations,
Elevated stress concentrations are identified at the
located 2.89mm from the apex in this study. For this
beginning of the line II () and)).
3-4 system, a stress concentration at this point is also
This stress peak, as can be identified in ), is induced byF, increasing the compressive stresses
P caused by a sharp corner at this point. For the 3i sys-
on the right hand side of the crown. Increasing F
tem, the volume of the crown exceeds that of theP
Neoss system, thereby suggesting that the 3i crownfrom its minimum to maximum values, for the exter-
may endeavor greater resistance to the applied nal-hex system, increases the stress by 485.46MPa
masticatory forces. However, even though the Neoss (951.67-466.21MPa).
crown has a thinner wall thickness along the line The internal-hex system has reduced stress concen-
NN, reduced stresses are still evident due to the
3-4
abutments high Young's modulus. Overall, the design
differences between the Neoss and 3i systems ulti-
mately results in the 3i system having higher stresses
when F is increased.
M
3.2. Preload Force, FP
To investigate the effect of different preload F,F
PM
is kept as a constant and its medium value, i.e. 500N
is considered herein. The distributions of von Mises
Figure 3
Figure 3a
Figure 3b
Figure 3cFigure 3d
Figure 1c
Figure 1c
Table 2
Fig-
ure 2.
Figure 1a
Figure 2a
Figure
2b
Figure 2cFigure 2d
Figure 2c
SciRes JBiSE Copyright ©2008
Table 2. Von Mises stress (MPa) in crown (location of stress
recording in brackets).
Variables
Line
NN
(3.76mm)
II
(2.89mm)
F(N) F(N)
MP
200
272.82
349.05
500
545.64
698.09
1000
818.47
1047.14
201.93
231.55
466.21
587.44
545.64
698.09
1009.67
891.83
951.67
13
R.C. Van Staden et al./J. Biomedical Science and Engineering 1 (2008) 10-14

Clinical Implant Dentistry and Related Research 2005,
trations, demonstrating that this design is less sus-7(4):221-228.
ceptible to stress concentrations within the crown. [7]F. H. G. Butz, M. Okutan & J. R. Strub. Survival rate, fracture
However, because of the transfer of the preloadstrength and failure mode of ceramic implant abutments after
through the abutment screw to abutment contact, chewing simulation. Journal of Oral Rehabilitation 2005,
32(11):838-843.
changing F is more influential on this hex system
P[8]K. J. Anusavice & P. H. Dehoff. Influence of metal thickness on
than F. Overall Fis more influential on the stressstress distribution in metal-ceramic crowns. Journal of Dental
MM
Research 1986, 65(9):1173-1178.
within the crown for the external-hex system andFP[9]K. J. Anusavice. Stress distribution in metal-ceramic crowns
is more influential on the internal-hex system.with a facial porcelain margin. Journal of Dental Research
1987, 66(9):1493-1498.
[10]K. J. Anusavice. Influence of incisal length of ceramic and
5. CONCLUSIONloading orientation on stress distribution in ceramic crowns.
Journal of Dental Research 1988, 67(11):1371-1375.
This research is a pilot study aimed at offering an ini-
[11]H.Y. Suzuki. Finite element stress analysis of ceramics crown
tial understanding of the stress distribution charac-on premolar. Relation between ceramics materials and abut-
teristics in the crown under different loading condi-ment materials. Nippon Hotetsu Shika Gakkai Zasshi 1989,
tions. Realistic geometries, material properties, load-33(2):283-293.
[12]T. Hino. A mechanical study on new ceramic crowns and ing and support conditions for the implant system
bridges for clinical use. Osaka Daigaku Shigaku Zasshi 1990,
were considered in this study. The geometrical design 35(1):240-267.
of the external-hex system tends to induce stress con-[13]Zhang, B. & Wang , H. Three-dimensional finite element anal-
centrations in the crown at a distance of 2.89mm fromysis of all-ceramic crowns of the posterior teeth. Hua Xi Yi Ke
Da Xue Xue Bao 2000, 31(2):147-148. the apex. At this location,F also affects the stresses,
P[14]K. A. Proos, J. Ironside & G. P. Steven. Finite element analysis
so that the compressive stresses on the right hand sidestudies of an all-ceramic crown on a first premolar. Interna-
of the crown are increased. The internal-hex systemtionalJournal of Prosthodontics2002, 15(4):404-412.
[15]A. Imanishi, T. Ohyama & T. Nakamura. 3-D Finite element
has reduced stress concentrations in the crown. How-
analysis of all-ceramic posterior crowns. Journal of Oral
ever, because the preload is transferred through theRehabilitation 2003, 30(8):818-822.
abutment screw to the abutment contact, changing FP[16]Strand7 Pty Ltd.Strand7 Theoretical Manual 2004. Sydney,
Australia.
has greater effect on this hex system thanF. Overall
M[17]Neoss Pty Ltd,Neoss Implant System Surgical Guidelines
Fis more influential on the stress within the crown
M2006. United Kingdom.
th
[18]http://www.3i-online.com.htm (accessed 12 July 2006).
for the external-hex system and Fis more influen-
P[19]R. C. van Staden, H. Guan, Y. C. Loo, N. W. Johnson & N.
tial on the internal-hex system.Meredith. Stress Evaluation of Dental Implant Wall Thickness
Future recommendations include the evaluation using Numerical Techniques.Applied Osseointegration
Research 2008, (In Press).
of other implant variables such as the implant wall[20]A. R. Curtis, A. J. Wright & G. J. Fleming. The influence of
thickness and thread design. Ultimately, all implantsimulated masticatory loading regimes on the bi-axial flexure
components can be understood in terms of their influ-strength and reliability of a Y-TZP dental ceramic. Journal of
ence on the stress produced within the implant itself.Dentistry 2005, 34(5):317-325.
[21]D. H. DeTolla, S. Andreana, A. Patra, R. Buhite & B. Comella.
Role of the finite element model in dental implants.Journal of
Oral Implantology 2000, 26(2):77-81.
[22]J. P. Geng, K. B. Tan & G. R. Liu. Application of finite element
ACKNOWLEDGEMENTS
analysis in implant dentistry: a review of the literature.Jour-
This work was made possible by the collaborative support from nal of Prosthetic Dentistry 2001, 85(6):585-598.
griffith's school of engineering and school of dentistry and oral
health. A special thank you goes to messer john divitini and fredrik
engman from neoss pty ltd for their continual contribution.
REFERENCE
[1]Y. Maeda, T. Satoh & M. Sogo. In vitro differences of stress con-
centrations for internal and external hex implantabutment con-
nections: a short communication. Journal of Oral Rehabilita-
tion 2006, 33:75-78.
[2]B. R. Merz, S. Hunenbart & U. C. Belser. Mechanics of the
implantabutment connection: an 8-degree taper compared to a
butt joint connection.International Journal of Oral and
Maxillofacial Implants 2000, 15:519-526.
[3]A. Khraisat, R. Stegaroiu, S. Nomura & O. Miyakawa. Fatigue
resistance of two implant/abutment joint designs.Journal of
Prosthetic Dentistry2002, 88:604-610.
[4]S. Capodiferro, G. Favia, M. Scivetti, G. De Frenza & R. Grassi.
Clinical management and microscopic characterisation of
fatique-induced failure of a dental implant.Case report. Head
and Face Medicine 2006, 22, 2:18.
[5]P. Gehrke, G. Dhom, J. Brunner, D. Wolf, M. Degidi & A.
Piattelli. Zirconium implant abutments: fracture strength and
influence of cyclic loading on retaining-screw loosening.Quin-
tessence International 2006, 37, 1:19-26.
[6]A. Khraisat. Stability of implant-abutment interface with a hexa-
gon-mediated butt joint: failure mode and bending resistance.
SciRes JBiSE Copyright ©2008
14 R.C. Van Staden et al./J. Biomedical Science and Engineering 1 (2008) 10-14