Received 12 December 2014; accepted 13 February 2015; published 16 February 2015

ABSTRACT

We consider a multiproduct incumbent which monopolizes one market but faces a potential entrant in another market. In a two dimensional Hotelling model, when consumers’ reservation value is relatively high, we show that the incumbent has an incentive to use bundling to deter entry only if a prior commitment is applicable. However, when consumers’ reservation value is low, the multiproduct firm even has no incentive to use bundling and bundling has no effect on entry deterrence.

Keywords:

Bundling, Entry Deterrence, Multiproduct firm, Product-Specific Preferences

1. Introduction

Suppose a multiproduct incumbent monopolizes one market but faces a potential entrant in another market. Whinston (1990) considered such a situation and, using a simple Hotelling model, argued that the incumbent could deter entry by bundling but only if it makes a prior commitment [1] . Nalebuff (2004) showed that in a modified Hotelling model, if the incumbent chooses prices before the entrant, it could deter entry by bundling even without any commitment [2] . Peitz (2008) showed that bundling may block entry in a two-dimensional Hotelling model [3] . However, there is a lack of research on this question by considering consumers’ reservation value.

In reality, consumers hold different reservation value to different products. A consumer’s reservation value is the highest price she is willing to pay. A product may be very welcomed thus consumers’ reservation value is very high and consumers are willing to pay high price. One example may be Apple Company’s products, saying IPhone. When the firm launches a new version of IPhone, consumers rush into the store to buy at a high price. At the same time, there are goods that are not popular for consumers, thus many people do not want to afford. We can say that consumers’ reservation value is relatively low in this case. Therefore, it is closer to the reality if we consider the entry deterrence problem by considering consumer’s reservation value. In opposite to previous work [1] - [3] where deterring entry by bundling (monopoly under bundling) is always more profitable than letting the entry occur, we find that when consumer’s reservation value is low, the incumbent even has no incentive to use bundling to deter entry. But when consumer’s reservation value is relatively high, it is not the case.

Bundling has attracted significant research attention, and most studies in this field consider symmetric competition. Matutes and Regibeau (1988) examined the incentive of pure bundling for two symmetric, multiproduct firms by building a two-dimensional Hotelling unit square [4] . They found that pure bundling selling strategies were always dominated by independent pricing strategy, regardless of the level of consumers’ reservation value. Gans and King (2006) extended Matutes and Regibeau’s (1992) model to analyze the incentives associated with mixed bundling [5] [6] . Thanassoulis (2007) and Armstrong and Vickers (2010) analyzed the case of mixed bundling in a fully served market [7] [8] .

The remainder of this paper is arranged as follows. In Section 2, the model is introduced. In Section 3, we analyze equilibriums and results. In Section 4, we present our conclusion.

2. The Model

Suppose there are two products, products 1 and 2. Product 1 is only provided by firm A, while product 2 may also be provided by firm B. We assume the marginal cost of either product for both firms is zero. Firm A has two strategies to select from, that is, pure bundling and independent pricing. Consumers purchase at most one unit of each product. Therefore, consumers are able to select at most six consumption combinations if firm A does not bundle, namely AA, AB, A1, A2, B2, and purchasing nothing. AA means buying products 1 and 2 from firm A; AB means buying product 1 from firm A and product 2 from firm B; and A1, A2, and B2 mean purchasing only a single product 1 from firm A, a single product 2 from firm A, and a single product 2 from firm B, respectively. A consumer purchasing one product will have a reservation value of C. Therefore, a consumer will have 2C if she purchases two products. We engage in a three-stage game. At the first stage, firm B decides whether to enter. If it enters, it pays a cost of F. At the second stage, firm A decides whether to bundle. At stage three, firms simultaneously set prices. We consider four situations: (1) independent pricing by monopolist A, (2) bundling by monopolist A, (3) competitive independent pricing, and (4) competitive bundling.

Consumers should be uniformly located in a Hotelling unit square with firm A located at (0, 0) and firm B located at (1, 1). The horizontal interval represents product 1 and as a consumer located further away from firm A horizontally, she holds less taste preference towards firm A’s product 1 and more prefers to firm B’s product 1. The vertical interval represents product 2. Under an independent pricing scheme, a consumer located at

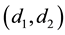
buying AB will get a surplus of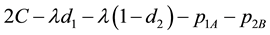, where 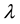is the strength parameter of differentiation. Similarly, the consumer purchasing only a single product will get a surplus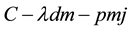, , 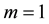2, 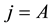, B. When firm A bundles, the consumer buying the bundle will earn a surplus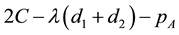, where 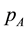is the bundle price.

We denote the profit of firms A and B as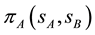, , 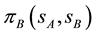respectively.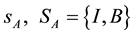, where I

stands for independent pricing and B stands for bundling. In addition, 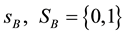, where 0 means does not enter and 1 means enter.

3. The Equilibrium Prices and Results

We extend the model of Matutes and Regibeau (1988) [4] by adding the single consumption. For simplicity of calculation, we set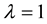. We show the market configurations according to different levels of consumers’ reservation value in Figure 1. Concerning the situation where firm A bundles in a competitive market (situation 4), we demonstrate an example for the calculation in the situation where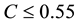. The demand of AA on the horizontal and vertical axes are the same, and we denote demand as, , 2, and

(i.e.,). Then, the area of the triangle is, and this is the demand for firm A. Therefore, profit is. Maximizing firm A’s profit with respect to p_A gives us maximized and.

Independent pricing selling by a monopolist A

When, the market of competitive independent pricing is an adjacent market. In an adjacent market, according to Matutes and Regibeau (1992, p. 52, line 36) [6] , “both firms set prices for their complete systems so as to leave consumers located at the common market boundary with exactly zero surplus.” The market boundary of AA and AB just touches. And the market boundary of A2 and B2 just touches. In market 2, A2, B2 are symmetric. Therefore, for the consumer located in the boundary, and are satisfied. and. The profit in market one is still monopoly profit. Then the total profit is.

When, all consumers can buy product 1 in the market of competitive independent pricing. Therefore firm A sets a price to ensure all consumers to buy product 1 thus, and we have,. And we can find the demand for product 2 of each firm by finding the critical point (0, d₂) where buying AA is indifferent with buying AB:, then we have . Therefore, ,). Maximizing the profits with respect to, , we get, , so. For more calculations, please refer to Appendix.

We find if firm A monopolizes the market, when, , otherwise . In addition, always. Therefore when, firm A never uses bundling and firm A must enter the market on a certain range of entry costs. We show an example in Table 1.

We can easily see if, firm B must enter the market. in this case, therefore firm A has no incentive to bundle and deter entry. And we find that the profit of firm A has no change whatever the entry happens or not. This is because in this range of C, even entry has occurred, under independent pricing scheme, there is no competition.

However, if, firm A can use bundling to deter entry only if it commits to bundle. We give an example in Table 2.

We can see if, firm A can use bundling to deter entry only if it commits to bundling( in the game, stage1 and stage2 are in reverse order so that firm A can commit to bundle). In this case, firm A optimally engages in bundling to deter entry for a higher profit. This outcome and profit ranking are similar to the model by Whinston (1990) [1] .

In a monopoly market, the bundle price is always lower than the total price of the two products under independent pricing. However, when consumers’ reservation value is small, consumers who cannot buy the bundle can buy single product under independent pricing. Independent pricing provides more selections and the demand under this situation is larger. Thus when. As consumers’ reservation value increases, more and more consumers can afford two products and the lower price of the bundle attracts more demands. Therefore bundling makes more profits. Then in a competitive market, the competition under bundling is more intensified thus harms firms’ profits. Independent pricing is preferred in a competitive market.

4. Conclusion

When, we consider a competitive bundling market. First, we can find the critical point where buying AA is indifferent from buying B2 for it to analyze the effect of bundling to deter entry by considering consumers’ reservation value and this makes the result differ from the previous research. In Whinston (1990) [1] , bundling deter entry only if the incumbent makes a prior commit. We show that when consumers’ reservation value is low, the incumbent even has no incentive to deter entry by using bundling because the profit, if the entry happened under independent pricing, is even higher than it is in a monopoly bundling market. As consumers’ reservation value increases, we find the outcome is similar to Whinston (1990) [1] . In reality, we can imagine that consumers obtain different level of value on different goods. If we consider a multiproduct firm’s products

which are not that popular for consumers so that there are many consumers that even do not want or just want one rather than both, we see that bundling cannot deter entry. If the products are very welcomed, bundling may deter entry only if the incumbent makes a prior commit. Therefore, we can see that by considering consumers’ reservation value in a two dimensional Hotelling model, bundling is not easy to happen because prior commitment to bundling is also difficult sometimes.

References

Appendix

Because there are a great number of market configurations and the ways of calculations are similar, we show one example of how we derived the outcomes. For more calculations, please contact with the author for the calculation paper.

When, we consider a competitive bundling market. First, we can find the critical point where buying AA is indifferent from buying B2 for the consumer:, so. Then we can find the line where AA is indifferent from B2, where

, so., stand for the consumers located on the line in the unit square horizontally and vertically, respectively. We find the demand for each firm by using the critical points and indifference lines. The first order conditions are:

(A)

(B)

The Equations of (A) and (B) can be solved by computer for several values of.