Received 27 July 2015; accepted 15 September 2015; published 18 September 2015

ABSTRACT

Precessing ball solitons (PBS) in a ferromagnet during the first order phase transition induced by a magnetic field directed along the axis of anisotropy, while the additional action of high-frequency field perpendicular to the main magnetic field, are analyzed. It is shown that the spatial motion of solitons, associated with thermal fluctuations in the crystal, does not destroy the equilibrium of self-organized PBS.

Keywords:

Ferromagnet, First-Order Phase Transition, Magnetic Field, High-Frequency Magnetic Field, Precessing Ball Soliton, Self-Organizing State, Equilibrium, Spatial Motion of Solitons

1. Introduction

Precessing ball solitons (PBS) that may occur at the first order phase transition in a uni-axis ferromagnet under the action of a magnetic field along the easy axis has been considered in several papers [1] -[11] . The main characteristics of PBS have been investigated in articles [10] [11] . In [12] it was shown that with the additional effect of high-frequency magnetic field perpendicular to the main field, there may be of self-organizing state of PBS, when the decrease of the energy associated with dissipation, fully offset by the influx of energy from the source of the high-frequency field. But in this case, only immobile PBS were considered, i.e. without three-dimensional motion. The question of the existence of equilibrium self-organizing states of moving PBS remained open.

In this paper, an analysis was conducted and it was shown that the existence of self-organizing state for PBS had a dynamic character, in which strict observance of the equilibrium was disrupted, but immediately the movement was damped, and thereby the equilibrium state of self-organized PBS restored. i.e. actually self- organizing state for PBS exists even at three-dimensional motion.

2. Analysis of PBS Movement

To analyze magnetic solitons in a ferromagnet at the first-order transition in the presence of periodic magnetic field, as in [12] , we use the Landau-Lifshitz equation with a Gilbert form of dissipative term [13] :

(1)

and corresponding expression for the density of thermodynamic potential (as in [12] )

. (2)

Here H_z > 0, 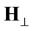is the periodic field directed perpendicular to the Z-axis and to the main field H_z, ,; m is a non-dimensional vector of ferromagnetism equal in the absolute value to 1;, in initial state:.

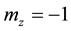We consider the PBS in a flat plate perpendicular to the Z-axis, use the following dimensionless values: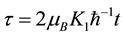, , ,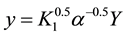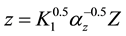; and note:,

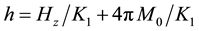. The change of sign of the self-demagnetizing field for PBS, 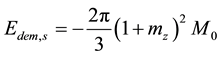in

Equation (2), in comparison with article [12] , does not lead to a qualitative change in results, but is logically more correct.

If added periodic field is

, (3)

the Equation (1) can be present in form

. (4)

In the case if the movement of PBS is directed along Z-axis, i.e., the expression for magnetic component is

(5)

In this paper, the PBS is considered in a spherical coordinate system, when its beginning coincides with the center of the soliton:

. (6)

In this case, the phase shift associated with moving becomes zero in the center of the PBS, and phase shift for other parts of the soliton is determined by the values of and the angle between vector and Z-axis: if, and if.

The phase of precession of magnetic moments for localized excitation depends on a radius, i.e.. From (4) equation, we have the next two equations that describe the configuration of the soliton and the time dependence of the parameter:

(7)

(8)

(In these equation, are the unit vectors of spherical coordinate system.)

The (7) and (8) equations correspond to the expressions describing the time dependencies of the density parameter and energy e:

, (9)

(10)

(It does not show here the gradient of these expressions related to “domestic” parts of these parameters, which are vanish when integrated over the volume of the soliton.)

We see that for unmoving PBS, i.e. if k_z = 0 and, these equations corresponds to a solution for self- organizing state, when and (see [12] ). In this case.

For spherical solitons (PBS) at, the (7) equation for equilibrium state takes the form:

(11)

here

(12)

(In (11): for, and for.)

However if, , this equilibrium state of PBS disappears. Let us consider this situation quanti-

tatively. Kinetic energy of PBS

, (13)

where. For example, at the average energy of motion of PBS is

. This corresponds for PBS at h = 0.998, , (,

, , see Figure 1 and Figure 2) to the average value of the wave vector

. Consider how parameters of and e of equilibrium PBS are changed at occurrence and decreasing

of movement. We expand the expression (9) and (10) in powers of the quantities and,

leave only the first degree of decomposition, and believing that at the initial time, at, all the conditions for equilibrium are fulfilled, we obtain the expression for the change of parameters directly related to the pres-

ence of and at:

(14)

(15)

There expressions can be split to two parts, proportional to and correspondingly. Here is important dependence on the.

Excitation of PBS movement due to thermal fluctuations in a crystal are random and chaotic. Evolution of PBS can be presented in two stages. In the first stage, movement due to fluctuations of the kinetic energy arises.

In this case and. For example at, in correspondingly with (14) and (15), there is a de-

formation of the soliton and redistribution of and e densities between the front and the back parts of PBS: at there are decreasing of but increasing of e―on the front part of PBS, and contrary, increasing of but decreasing of e―on the back part of PBS. Of course, strictly speaking, PBS ceases be in equilibrium in this stage. However further, in the second stage of process, restoration of the initial configuration of PBS is carried out, also in accordance with (14) and (15) expressions. In this case, and as a consequence,

and, i.e. accurate to linear values by and, equilibrium state of PBS is restored.

(16)

(17)

Note that during the deformation of PBS due moving, and magnetic moment

(18)

and energy where

(19)

without taking into account the kinetic energy (see [12] ), do not change.

For at, the value, i.e. (see Figure 2). In accordance with the

expression in Equation (14), the change causes a change, i.e. only to

part of the initial value. Can be estimated the time during which this change is carried out at return

to the initial state. In accordance with the expression in Equation (14), taking into account that

, , we receive for:.

For at, the value, i.e. (see Figure 3). The change causes a change, i.e. only to part of the initial value. Taking into account that in this case, we receive.

3. Angle Parameter as Invariant of Landau-Lifshitz Equation for Equilibrium PBS

Let us consider one more invariant of (4) equation, namely density of a momentum:

. (20)

Using (6) expression, we obtain for the density of momentum in spherical coordinate system:

. (21)

This expression refers to the case of moving precessing ball soliton at the presence of high-frequency field when the energy dissipation is almost completely offset by the influx of energy from the source of the high- frequency field. Note that if:

(22)

Integrating the expression (21) on the values of the angle, we obtain the expression for total momentum of PBS:

(23)

Differentiating (21) and using (9), we have

, (24)

where

(25)

Note that (24) equation also satisfies all the conditions for equilibrium of PBS in self-organizing state, if

.

It is believed that similar to momentum (21), the value is invariant for the PBS, moving along the axis z:

. (26)

To evaluate the effect of motion on the PBS, we consider value obtained from (9) and (12). We are

using (9) where there is the most direct connection between and. From here, the change in the angular parameter near equilibrium is equal to

(27)

This expression can be split into two parts:

(28)

• quantity related with, and

(29)

• quantity related with. Here values and relate to initial equilibrium state, at.

We see that the changes of, as for, is proportional to. With an increase in, if

, i.e. on front part (fore-part) of soliton, the values are increasing, but decreasing with the identical value on back part of soliton, i.e. for condition. There is contrary change of (see the sign in (14)). Thus, we have:

. (30)

Note that

. (31)

Moreover, integral value

(32)

(here is amplitude of PBS) in equilibrium state of PBS does not change.

Therefore, self-organizing state of PBS does not disappear, but continues to live, in spite of the thermal vibrations in the crystal.

Like to consideration for and, we calculate the estimate for. For

at, where, in accordance with Equation (28), the change causes a change. Note that in this case initial value is. The time required to return from to the initial value, in accordance with Equation (29), equals.

For at, where, the change causes a change. Taking into account that in this case, we receive for:.

4. Conclusions

The analysis of moving precessing ball solitons, arising at the first-order phase transition in ferromagnet at the combined action of main field, causes the transition, and transverse high-frequency magnetic field.

It is shown that the movement caused by thermal fluctuations in a crystal causes a small change in the parameters of solitons and thereby to a very small distortion of equilibrium self-organizing state of PBS. However, this distortion is eliminated very quickly and verily equilibrium state is restored. In practice, equilibrium self- organizing PBS, when dissipative losses of energy are compensated by the influx of energy from the high- frequency field, continues to exist at mechanical motion of PBS inside the crystal.

Cite this paper

V. V.Nietz, (2015) Movement of Self-Organizing Solitons in Ferromagnet. Applied Mathematics,06,1747-1754. doi: 10.4236/am.2015.610155

References