Modern Economy
Vol.4 No.4(2013), Article ID:30762,15 pages DOI:10.4236/me.2013.44034
The Breakdown of the Traditional Mechanistic Worldview, the Development of Complexity Sciences and the Pretence of Knowledge in Economics
Faculty of Economics, Business Administration and Social Sciences, University of Dortmund, Dortmund, Germany
Email: andreas.liening@tu-dortmund.de
Copyright © 2013 Andreas Liening. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 11, 2013; revised February 14, 2013; accepted March 10, 2013
Keywords: Bifurcation; Butterfly Effect; Chaos Theory; Complexity Theory; Nonlinear Systems
ABSTRACT
This article is an introduction to complexity theory, which will be discussed using the example of economic science. In this context, a short historical overview is intended to demonstrate why the traditional mechanistic worldview persistently remains a part of economic science and how it led to the development of the theory of complex systems, which, for example, can be subsumed under chaos theory. Furthermore, a simple supply and demand model is employed as an example to discuss this new theory and to describe the characteristics of complexity in comparison with the general mechanistic principle. For this purpose, specially designed software is used for the simulation and analysis of selected complex systems.
1. “Run Through” and Introduction
Because the economy is characterized by increasing complexity, many traditional economic explanatory models have increasingly lost their persuasive power. As suggested by numerous traditional models, the economic development of the system as a whole and in specific domains, such as the business sector, are not always characterized by fluent transitions. In fact, discontinuities, jump discontinuities and turbulence occur. Thus, the economy and economy related subareas can be understood as nonlinear, dynamic systems. In this context, complex systems are discussed.
Therefore, it is particularly important to conduct research on new concepts and methods in the field of complex dynamical systems. The research approaches within this domain are increasingly being used in the field of economic science; for example, such an approach may be employed to better understand complex order structures, which are generated by market-based systems.
For example, an examination of the works of the Nobel Prize winner in economics von Hayek reveals that order is not necessarily a result of planning. In this connection, he even postulates a constructivist error [1]. In this context, von Hayek writes as follows:
“It is thus a paradox, based on a complete misunderstanding of these connections, when it is sometimes contended that we must deliberately plan modern society because it has grown so complex. The fact is rather that we can preserve an order of such complexity only of we control it not by the method of “planning”, i.e., by direct orders, but on the contrary aim at the formation of a spontaneous order based on general rules” [2].
Following von Hayek, such an order cannot be analyzed adequately with the assistance of mechanistic models that are still frequently applied1 and are based on lineal2 cause-and-effect chains and which are thus predictable.
To model complex developments based on realistic scenarios, one must utilize traditional exogenic dysfunctions or random variables. Eventually, abnormal and noncontinuous developments are analyzed through the use of methods that seem to be applicable only to linear and lineal conditions or continuous processes, respectively. For a long time, economics was subordinate to the influence of a mechanistic worldview, which, for example, applied to models whose trajectories3 tended toward equilibrium and seemed to be predictable and tangible with the assistance of partial analyses.
However, the economic reality is often much more difficult and complex than suggested, for example, by linear models. For instance, it is not possible to explain self-organizing processes separately from equilibrium with the use of linear views. Therefore, Nijkamp and Poot assert the following:
“Our economic world is highly dynamic and exhibits a wide variety of fluctuating patterns. This forms a sharp contrast with our current economic toolbox, which is largely filled with linear and comparative static instruments” [4, p. 25].
Consequently, if you look at economic theory one can say:
“The assumptions of mainstream economics are totally changing” [5, p. 7].
So, the engagement with nonlinear, complex systems may have a decisive role in searching for an expansion of the “economic toolbox.” With this approach, it is possible to represent a wide range of economic behavioral patterns and explanatory approaches. Using this method, complexity can be described, analyzed and understood in a manner in which traditional statistical methods would fail4.
In addition to the theory of self-organization (synergetics) or the theory of thermodynamics, fractal geometry or catastrophe theory, chaos theory in particular must be mentioned [7]. Although these approaches seem to differ greatly from each other, they are all primarily concerned with questions related to the origination and analysis of complex order patterns. Therefore, they can properly be subsumed as a subdiscipline of a theoretical superstructure, which is referred to as a “theory of complex systems” in this context.
Within the scope of its popular scientific upswing in the 1990s, chaos theory became a theory of a new, homogeneous world explanation for the one part—or rather a world transfiguration5—whereas the others insulted the representatives of chaos theory as shamans6. Today, these advocates of chaos theory continue to search in the structures of remote galaxies or in the ascending wads of the smoke from a cigarette for the power of chaos. The opponents repeatedly question why chaos exists exclusively in the computer and why the “spook” disappears as soon as the computer is shut down.
Consequently, there have been many misunderstandings. It is widely believed that chaos theory is a theory of disorder. As this essay will demonstrate, this belief is entirely misleading. Chaos theory neither disproves determinism nor considers ordered systems impossible. Although chaos theory suggests that the current state of a system may not be predictable, it nevertheless demonstrates that it is generally possible to model the overall characteristics of such a system. Consequently, chaos theory does not emphasize disorder, which is the inherent unpredictability of a system’s status; rather, this theory emphasizes the order structures that are inherent to a system—the universal characteristics of homogeneous systems. Nijkamp and Reggiani explain as follows:
“There is ‘order in chaos’” [4, p. 12].
The possibility of researching “chaos” and the connected order patterns in complex systems was not imaginable prior to the development of modern computer technology. The multitude of calculations and the different types of visualizations of complex structures were previously unrealizable. Therefore, it is not surprising that this theory gained importance especially at the beginning of the 1990s.
Meanwhile, the euphoria that accompanied chaos theory has again receded, and the number of new popular scientific publications has decreased. However, the number of scientific publications attempting to transfer important aspects of chaos theory to other areas of science has increased. In this regard, economics is not excluded because one expects a better approach to economic reality from chaos theory than, for example, the neoclassical paradigm can render7.
Regarding these considerations, this article is titled “Econoplexity,” which refers to the application of the theory of complex systems to economics. In this article, Section 1 presents a short historical overview to demonstrate why the traditional linear causal mechanistic worldview persistently remains a part of economic science, and Section 2 explains how this worldview led to the development of the “theory of complex systems”. Section 3 explains the new theory with the assistance of software that was specifically designed to simulate a supply and demand model. Thus, the characteristics of complexity are described briefly.
2. Economic Science Under the Mechanistic Counterbalance, or Economia Non Facit Saltum
2.1. A Short History
The question of what effect natural sciences, particularly the findings of classical mechanics, had on the development of economics is of great relevance for the understanding of economic science because the past influence of mechanistic thinking on economic science continues today. However, it must be critically analyzed with respect to the subject matter and this is done [21].
To enable readers to understand the influence of classical mechanics—and thus of Newtonian Physics—on economic science, this section provides a brief historical review.
An examination of the history of economics reveals that a wide range of economic schools of thought have developed over time and had—or rather have—a more or less important position in the discussion of the development of economic science.
By the middle of the 18th century, Quesnay, one of the forerunners of the classical economic school, developed his “Tableau économique”, which graphically illustrates the national economy as a whole. Initially, it was thought that Quesnay was inspired by the process of blood circulation when creating his “Tableau” (see Figure 1). However, more recent research has shown that the work of Qu-

Figure 1. Tableau Economique, visualization of the physiocratic concept [26].
esnay is rather a mechanistic analogy and that Quesnay intended to apply the physical findings of Descartes to political economics [21]. In later comments regarding his Tableau, Quesnay underlined the mechanistic and mathematic character of his illustration because he wanted to prove that the functioning of the economic system is similar to that of a machine [22].
Mainzer argues that the school of physiocracy, which was represented by Quesnay, modeled economic development on the natural science-based course of a ball in the firm chutes of a clock; this analogy was commonly used at that time [23]. Thus, Quesnay was among the first economists to apply natural scientific thinking to the economy, and he argued for the self-regulation of the market, which is consistent with findings from this field [24]. The “laissez faire, laissez passé” motto of the physiocrats became well known.
Classical economics, which emerged with Adam Smith, John Stuart Mill and others in the 1770s, replaced physiocracy. Indeed, Smith also advocated for the selfregulation of the market, but he differed from his predecessors in some aspects [25]; particularly, he did not argue in favor of an unlimited “laissez-faire economy”8. According to Bürgin, Smith’s work, in which the physiocratic motto has been developed into a closed economic concept, can be considered an application of Newtonian physics [26]. However, especially in the case of Smith, economists were at least slightly hesitant to subscribe to the mechanistic view9. Nevertheless, similar to that described in Newtonian gravitation theory (which provides for actions at a distance, according to which levitating astronomical objects move into a condition of equilibrium when they interact), Smith claimed that an “invisible hand” [28] coordinates millions of individual plans in such a way that an equilibrium of supply and demand is achieved.
“By preferring the support of domestic to that of foreign industry he [the individual person; the author] intends only his own security; and by directing that industry in such a manner as its produce may be of the greatest value, he intends only his own gain, and he is in this, as in many other cases, led by an invisible hand [emphasis added; the author] to promote an end which was no part of his intention [ ]. By pursuing his own interest he frequently promotes that of the society more effectually than when he really intends to promote it” [28, p. 485].
]. By pursuing his own interest he frequently promotes that of the society more effectually than when he really intends to promote it” [28, p. 485].
The physiocrats and later the classics restricted themselves to the formation of analogies between mechanics and economic science, whereas neoclassical economics, which was initiated by Alfred Marshall and Leon Walras in the middle of the 19th century and continued by Kenneth Arrow, Gérard Debreu and Frank Hahn in this century, effected the concrete formalization of these ideas [30]. Thus, mechanics became more than merely the basis of an analogy with economic science, whose tertium comparationis was the mechanistic functioning of the physical world. Rather, in neoclassical economics, the economic science got under the regulative ideas of mechanics or, as Söllner writes with reference to Mirowski, a revaluation of economic science to the physics of social science occurred [31].
Röpke notes that classical mechanics (and the constructivist form of rationality that explains it) presents the living world as something that consists of rationally determined beings. These beings are controlled by a superior rationality from the outside, and thus, they are beings without an “internal principle of action” (Kant) and are only able to pass on a movement which once has been got from the outside (in the case of Descartes from the creator god). This basic mechanistic-constructivist element of the early enlightenment period has paradigmatically become fundamental to one part of modern economics [32]. Röpke divides this basic mechanistic principle into three areas of economic theory:
• First, on the individual level, the mechanistically influenced theory type can be found in the concept of humankind in economics. The neoclassical homo oeconomicus, with its implicitly used psychology, must be assigned to the field of behaviorism, which is based on the stimulus-response intensification principle10. The homo oeconomicus systematically reacts to given action restrictions and their changes. His preferences (wishes, objectives, and motives) are constant. Thus, the action of the homo oeconomicus is considered a reaction that is determined by the environment (i.e., that is externally controlled). It is not considered a spontaneous, self-organizing activity11.
• Second, the “machine-command-organization” [36], or the “mechanistic organization” [37], is found at the level of businesses. The inner life of businesses and their internal organization, production and contract problems are not of interest in this context. Rather, their members are able to reproduce optimal adaptation reactions according to particular circumstances [37].
• Finally, on the level of the market, one finds clearly definable market structures that are supposed to be historically given and that assign certain behavioral patterns to individual market participants; their change and their evolution remain unconsidered; and their particular macroeconomic efficiency and optimality (with regard to the allocation of scarce resources or other supra-individual objectives) can be shown theoretically and achieved socio-technologically, at least by tendency [37].
Based on the economic principle that the highest possible output must be achieved with the means that are available (or that a given yield target must be achieved with the least possible input), optimal circumstances on the level of individuals, businesses and the market can be achieved or can be assumed to exist with neoclassical assumptions. One may share the opinion of Schlösser, who consistently remarks that a theory of spontaneous social order is not achievable with the neoclassical fiction [35].
In this context, it is interesting that some advocates of neoclassical economics had a technical, natural scientific or mathematic education12. For example, Pareto was a trained engineer13; Marshall was a mathematician [38], and Jevons studied natural sciences [25]. However, this education alone cannot explain a formalized assumption of the ideas of mechanics applied to neoclassical economics. To answer this question with regard to specific reasons, this paper will offer some comments regarding classical mechanics and its philosophy.
2.2. Regarding Classical Mechanics and Newtonian Physics
The most important principles of mechanics were founded through the use of Newton’s “Philosophiae Naturalis Principia Mathematica”14 (1687) and the principle of continuity by Leibniz15 (1700), which can be circumscribed by the famous sentence “natura non facit saltus”16. These principles, which will be described subsequently, are as follows:
• determinism
• reversibility
• (strong) causality
• the assumption that the whole consists of the sums of its parts
• the assumption that complex elements are composed of a multitude of basic elements With the help of the Newtonian laws, the relationships between factors such as velocity, acceleration, force and mass can be established. For example, one can calculate how long it takes for an apple falling from a tree to touch the ground. Based on these laws, it is also possible to describe the courses of the planets around the sun or the path of a space shuttle back into orbit.
Among other things, the given examples show that classical mechanics can illustrate the time development of physical systems. Newton was the first scientist to be proficient in this art. Based on his work, it is known that any state at any time can be derived if the initial state of a system is known. Consequently, the result is an entirely deterministic worldview. The mathematician Poincaré expresses this result as follows:
“Every phenomenon, however minute, has a cause; and a mind infinitely powerful, infinitely well-informed about the laws of nature, could have foreseen it from the beginning of the centuries”17.
Laplace’s (fictional) demon is regarded as a symbol for this determinism of classical mechanics [42]. Laplace’s demon is the institution that has all of the data of the universe at its disposal such that it can predict future developments at any point in time. However, it can also recalculate past developments from the earliest times. Thus, Laplace writes as follows:
“Given for one instant an intelligence which could comprehend all the forces by which nature is animated and the respective positions of the beings which compose it, if moreover this intelligence were vast enough to submit these data to analysis, it would embrace in the same formula both the movements of the largest bodies in the universe and those of the lightest atom; to it nothing would be uncertain, and the future as the past would be present to its eyes” [43, Chapter II].
Thus, determinism and reversibility, or time reversibility, predominate in classical mechanics18. Because mechanistic sequences are identically reproducible, time is only the duration of an event that occurs between the beginning and the end of mechanistic processes (thus, until the new equilibrium is reached).
In addition to the abovementioned points, the apparent weak law of causality, according to which the same causes incur the same effects (and thus causality is invariant), is not the only important concept in classical mechanics. In fact, strong causality, which means that similar initial conditions always lead to similar results, is also important.
Descartes, who certainly would not have accepted every aspect of the later Newtonian mechanics19, is regarded as one of the most important representatives of this mechanistic school of thought. It is not an exaggeration to state that the basic concept of classical mechanics can be traced back to Descartes. In particular, Descartes was interested in the methods that allowed for reliable scientific findings. He applied logic for this purpose, and among numerous rules, he selected four rules that he believed are especially relevant for logic. In this context, the second rule is particularly important. In 1637, Descartes wrote as follows:
“Le second, de diviser chacune des difficultés que j’examinerais, en autant de parcelles qu’il se pourrait, et qu’il serait requis pour les mieux résoudre” [45, p. 30].
In other words, if a problem is too complex to be solved in one step, it should be divided into many subproblems that are sufficiently small to be solved separately. Thus, it is assumed with this analytical notion that the whole consists of the sum of its parts.
Descartes’s third rule illustrates that the purpose of scientific thinking is to consistently organize all thoughts in a certain way when researching the truth: the process should begin with the easiest and most comprehensible ideas and gradually progress to obtaining an awareness of more difficult and sophisticated issues. Furthermore, such things that do not automatically form a sequential relationship should be organized in a certain order [45]20. In principle, Descartes considers it possible to subdivide complex matters into a multitude of basic elements and to recompose them. As a basic principle, scientists since Demokrit and Aristoteles have believed that there is a multitude of simple objects and forces behind the complexity of the world [46]. The entire worldview of classical mechanics is affected by concentration on closed, simple, and frequently linear systems [25]. These systems comprise exactly those characteristics that have been described: the characteristics of determinism, reversibility, and (strong) causality; the assumption that the whole consists of the sum of its parts; and the assumption that complex elements are composed of a multitude of basic elements.
2.3. Analogy between Classical Mechanics and Economic Science
With regard to discovering the reasons for the analogy between classical mechanics and economic science, the following should be noted: economic science is often said to be inexact, or rather unreliable. It is not reliable science in the sense that economic findings have no objective validity. In this regard, the lack of reliable findings in economics was problematic, particularly because during that period economic science belonged to the field of humanities, which was not always viewed positively from a natural scientific point of view.
However, the concepts of mechanics spread quickly due to its practical utility. The fascinating aspect of classical mechanics is that everything is definitely describable, mathematically deducible and predictable when all initial parameters are known. Thus, it is not surprising that the optimism that spread with classical mechanics also influenced other disciplines, including economic science. Thus, classical mechanics could support the endeavor of economists to successfully develop economics into an “exact” science.
According to Dopfer, three fundamental assumptions of classical mechanics found their way into economics:
• A mechanistic whole can be subdivided into its basic elements. These elements can be analyzed individually and recomposed.
• The causalities are invariant, and the relations between the elements can be described by linear functions.
• The same or similar conditions lead to the same or similar dynamic paths of a system [47].
As mentioned above, the classics had already established analogies between economics and mechanics. On the basis of the first assumption, for example, John Stuart Mill writes impressively as follows:
“The order of nature, as perceived at first glance, presents at every instant a chaos followed by another chaos. We must decompose each chaos into single facts. We must learn to see in the chaotic antecedent a multiple of distinct antecedents, in the chaotic consequent a multitude of distinct consequents”21.
Beyond this analogy, neoclassical economics, which emerged from the “marginalist revolution,” applied the ideas of mechanics to mathematical-economic models. This borrowing facilitated the development of the neoclassical equilibrium theory.
Another typical example reflecting the assumption of ideas from mechanics is Marshall’s partial analysis. To better analyze complex reality, economists rely on the study of the partial aspects of economic events. This approach corresponds to the first mentioned fundamental assumption of classical mechanics, according to which a whole can be subdivided into its basic elements. These elements can be analyzed individually to obtain an impression of the whole. This concept is also reflected in Marshall’s ceteris paribus assumption, according to which one variable is changed whose effects can be examined in a model by holding all of the other relevant factors constant.
Marshall’s successor Pareto, after whom the wellknown pareto optimum22 is named, employed many mathematic principles in his economic models. His thoughts also revealed a great affinity for mechanics, as the following sentences demonstrate. With regard to the immediate benefit, for example, the analysis of the exchange in the pure economy corresponds to the analysis of freefalling bodies in physics textbooks. A falling feather does not act more upon the laws of falling bodies than certain acts of exchange act upon the laws of exchange [38].
Dopfer extends this idea further, perhaps even too far, when he quotes Frank Knight, who claims that economic science is a “sister science” of classical mechanics [49].
However, one can follow Dopfer when he states that neoclassical works missed few opportunities to emphasize mechanics as a role model for economics.
3. The Breakdown of Laplace’s World View
As demonstrated in the previous chapter, the influence of classical mechanics on economic science, which underwent a concrete formalization in neoclassical economics for the first time, was not insignificant. Even today, the general principle of mechanics influences many economic approaches. These approaches are based on comparative statics—which facilitates the comparison of equilibrium states (e. g. on the basis of different constellations of demand and supply curves)—or in some cases, they are based on linear-dynamical systems, which enable a process-related analysis.
3.1. First Doubts
However, the mechanistic worldview was destabilized at the end of the 19th century and at the beginning of the 20th century. At that time, the French mathematician Henri Poincaré confronted the physical worldview, which had been widely accepted until then, with entirely new findings based on his questions regarding the stability of the solar system.
According to Newtonian physics, few interacting bodies demonstrate predictable behavior. However, Poincaré knew that the Newtonian equations could be solved only approximately and that these equations—also in the case of very minor alterations of the initial conditions—to some extent, bring forward very irregular, chaotic developments.
With respect to the solar system, in the context of observing more than two planets, entirely eccentric orbits, which call the stability of the solar system into question, are possible23. In this regard, Poincaré showed that systems that have been stable for a long period of time can become instable without an extraneous cause. At this point, the concept of disorder—chaos—became relevant because it could be initiated by any small interference.
Until this time, chaos was considered as a type of infection that could affect a system from the outside. However, it became clear that a closed system could be described with few equations and could feature unpredictable, chaotic characteristics [46]. Apparently, determinism was questioned because Poincaré aligns coincidence with determinism via long-term unpredictability. He writes as follows:
“A very small cause which escapes our notice determines a considerable effect that we cannot fail to see, and then we say that the effect is due to chance”24.
However, at this time, few scientists anticipated the importance of his research results; many economists either ignored his results or were simply unaware of them25. Despite some subsequent important findings, such as the findings of Birkhoff (USA) in the 1920s or Cartwright and Littlewood (GB) in the 1940s, which were provided by mathematical works in the field of dynamic systems, Poincaré’s discoveries were ignored for decades26.
3.2. The Weather Forecast and the Butterfly Effect
At the beginning of the 1960s, the meteorologist Edward Lorenz made an interesting discovery, which can be considered a practical consequence of Poincaré’s findings27.
Lorenz used his computer to solve non-linear equations for modeling the earth’s atmosphere. To verify the result, he repeated the computer calculations. Howeverin the second instance, he reduced the accuracy of the computer from six to three decimal places. The result was fundamentally different from that obtained in the first instance. Lorenz discovered that non-linear dynamical systems, such as the weather, react very sensitively to very minimal changes. Thus, he confirmed Poincaré’s assumption.
This finding, which became known as the butterfly effect, is expressed as follows: the flapping of a butterfly wing in Hong Kong can cause a hurricane in New York.
Lorenz’s investigations demonstrate that unpredictable nature of dynamical systems cannot be observed because some details are not known. Even the most detailed knowledge does not necessarily allow for exact projections in the case of dynamical systems.
However, if this notion is correct, then Laplace’s demon (the hypothetical construct that can theoretically predict the future if it knows all initial conditions) is an absurd figure, and the mechanistic worldview must be denied or at least qualified.
In the following section, some aspects of the new approach will be considered in greater detail.
4. Criteria of the New Approach
4.1. Paradigm Shift in Economic Science
Schefold states that new economic ideas are often old ideas that quasi-recur periodically: a mercantilist theory of interest is part of Keynesianism, and the monetary theoretical nominalism of antiquity recurs in this century—not for the first time—due to the rejection of metallism [56].
Moreover, Schmalensee opines that the majority of scientists work on existing theories and approaches develop them further and apply them. Only rarely, Schmalensee writes, do erratic changes occur when seemingly unsolvable anomalies or other problems are overcome by “scientific revolutions”. Such revolutions are accompanied by a development that Thomas Kuhn described as a “paradigm shift”—fundamental changes in the worldview that radically converted the entire discipline and its research agenda [57].
In the history of economics, such paradigm shifts have occurred frequently. Examples of these shifts are the methodological triumph of mathematical analysis or the neoclassical subjective theory of values, which radically changed the objective view. In today’s world, economists such as Schmalensee lament that a large portion of today’s economic research is merely concerned with the reworking and improving of concepts, such as those of rational behavior and competitive markets, which were already known by Marshall and even Smith [57].
The analogy with Newtonian mechanics by classical economics and the further integration of the general principles of mechanics by neoclassical economics have influenced many fields of economic science in a sustainable manner. Furthermore, this analogy reflected in the static, statically comparative or linear-dynamic model analyses rather than merely in neoclassical economics. Thus, this analogy also provides the foundation for economic approaches that contrast with neoclassical economics. For example, the Keynesian, mechanistic overall model suggests that the state can (e.g., by means of countercyclical fiscal policy and global regulation) affect the economic process of an entire national economy in a sustainable, positive manner. However, the stagflation problems in the 1970s demonstrated that these mechanistic concepts do not work or they only work for a short time. The failure of the mechanistic regulation approach in the former Eastern bloc countries, whose centrally controlled economic systems collapsed in the 1990s, proved to be significantly more serious. Thus, the theoretically justified breakdown of Laplace’s worldview and the empirical findings in economics call the mathematical-mechanistic way of thinking as well as economic sciences in general into question.
When a shift in perspective proceeds rapidly, economic development proceeds more rapidly in highly industrialized states, and permanent change begins. Static theories, which are based on linear systems, are a good approximation for an economy with an unchanging structure. However, these theories do not help to explain evolutionary, nonlinear dynamical phenomena [25]. Therefore, some economists have abandoned mathematics in economics28. However, this complete abandonment is unnecessary. The poet Hölderlin writes that in situations in which there is danger, a rescuing element also grows [58]; thus, in particular, the mathematically influenced “theory of complex systems” initiates a rethinking in economic science29.
The first indications of a paradigm shift have arisen because numerous recent publications have deliberately transitioned from the traditional economic models to a “theory of complex systems”. For Instance, deterministic, market-oriented growth models to explain irregular business developments are developed in business economics. In the theory of business development, there are, for example, non-mechanistic explanatory approaches to determining why many processes are not predictable in the long term. The new concepts can be found in the organizational and process structures of businesses, human resource development, marketing, knowledge management and strategic management, especially in “change management”30.
Especially in the fields of human resource development and career research, the most recent works have abandoned the traditional linear-mechanistic approach with the emergence of numerous new empirical findings resulting from the use of innovative empirical methods beyond the traditional statistical methods [64].
Interesting research, which is not centered on general principles of mechanics, can be found in economics, for example, in the field of business cycles and growth models, particularly in the area of endogenous growth theory, consumption choice models and overlapping generation models. Additional economic topics that indicate a paradigm shift include research and model formation in subject areas that address exchange rate fluctuations, the development of share prices, the development of the gross national product and related time series analyses31.
In the following discussion, the basic characteristics of the new approach are explained.
4.2. Simulation of a Complex System Using the Example of a Supply and Demand Model
Scientists from non-natural scientific disciplines are increasingly acknowledging that even experiences from everyday life are opposed to the beloved image of a wellregulated, clearly arranged and predictable world [66]. The “butterfly effect” can be found in many fields in which feedback affects and intensify irregularities. Any small change in the cause can result in an enormous change in the effects.
For the purposes of describing irregularities through the use of linear equations, a system must be “disturbed” exogenously (i.e., from the outside). None of the known patterns of dynamic-linear systems are able to create such behaviors by themselves32. If linear models are considered, then there are only three possibilities in terms of how a system can develop.
A linear dynamic system can engage in any of the following actions:
• converge to a fixed point
• feature a cyclical movement, i.e., “circle” around a fixed point in constant distance (thus, it has two accumulation points)
• diverge, i.e., remove itself from a fixed point33
Thus, in principle, nothing unpredictable, new or surprising is possible in linear systems. Considered from a historical point of view, economic events remain timeless. Röpke explicitly mentions this fact when he states that the closed models of equilibrium economics cannot— even if they are “dynamized”—have explanatory relevance beyond the processes that occur in a determinate-mechanical manner [32].
As previously mentioned, only three types of courses of movements can be simulated through the use of linear, discrete and dynamic recurrence relations. However, if non-linear equations are considered, then those courses of movement become simulatable, which thus far might be integrated into the system only as exogenous disturbance variables.
The following supply and demand model, whose equations result in a non-linear price function and which has been implemented using object-oriented simulation software [67], is intended to demonstrate that even simple non-linear equations can exhibit irregular behavior.
For this, the following price function will be considered:
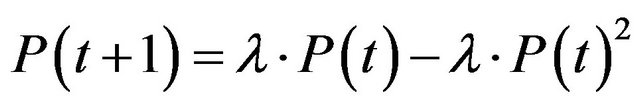 (1)
(1)
The function is then formulated differently:
 (2)
(2)
This function is also referred to as a logistic function and is a fundamental discrete function in the theory of complex systems.
This mapping is a recursive function (i.e., the respective price is dependent on the previous price). In this context, this dependency is quadratic and thus non-linear. In the simulation, the calculations of the market are conducted by means of iterations (i.e., in which the calculated value is reinserted into the same equation as the initial value). This process can be repeated as frequently as necessary. For the considered market model, a number of basic conditions apply. There are many demanders and suppliers, who rationally behave as price takers and who can enter and leave the market without restrictions. Thus, none of the people involved is so important that he or she might influence the price individually. Furthermore, there are no transaction costs or taxes, and there is only one homogeneous good. In situations with a high degree of market transparency34, this economic model largely corresponds to the model of “pure competition.” It is assumed that the good that is traded on the market is the low-priced ballpoint pen, “Chaoswriter” (but, nevertheless, it is regarded as a trendsetter). At a price of 0.00, no supplier would be willing to offer only a single ballpoint pen. At a price of 1.00 or higher, no one would demand the good (prohibitive price); thus, the market price must be between 0.00 and 1.00.
In this model, the value λ reflects the market transparency. Here, a value of 1 denotes a very high degree of market transparency, and a value of 5 denotes a very low degree of market transparency35.
The first simulation begins with a rather high degree of market transparency, λ = 2.75. With an arbitrary initial price, we obtain a converging development of the systems with one fixed point.
Price “P”, which, in the initial situation, has been arbitrarily set very low relatively, is initially still comparatively far away from the actually higher equilibrium price. Already in the fifth period, the price reaches a peak value, and numerous suppliers are willing to offer many “Chaoswriters” at that high price. Due to high expectations of profits, new suppliers enter the market. However, the price has risen so high that, henceforth, the demanders react reluctantly, and the demand decreases. Consequently, the price decreases because the suppliers are apparently unable to sell the desired quantity of ballpoint pens when the price is excessively high. The price decreases but does not become as low as it was in the fourth period because this price was apparently too low. However, because of the fallen price, the demand for “Chaoswriters” increases. The increasing demand results in increasing prices because the suppliers are unable to immediately meet the increased demand. A smaller supply is associated with a higher price. This time, however, the suppliers raise the prices more cautiously to ensure that they do not frighten the demanders as they had when they previously raised the prices.
Nevertheless, demanders again withdraw after the price increase. The decline of demand with unchanging supply results in falling prices. Thus, the price amplitudes become smaller each time, and the price relatively quickly settles into an equilibrium, as shown in Figure 2. This cycle corresponds to the traditional pork cycle or a cobweb model.
If the market transparency is reduced (by setting the value at, for example, λ = 3.2), the system initially seems to diverge because of the insufficient market knowledge of all persons involved, but after some time, it stabilizes. As in the first situation, an equilibrium price is not achieved. At least two fixed points (or rather, accumulation points) are obtained, as shown in Figure 3.
In this case, the price fluctuates between two points.
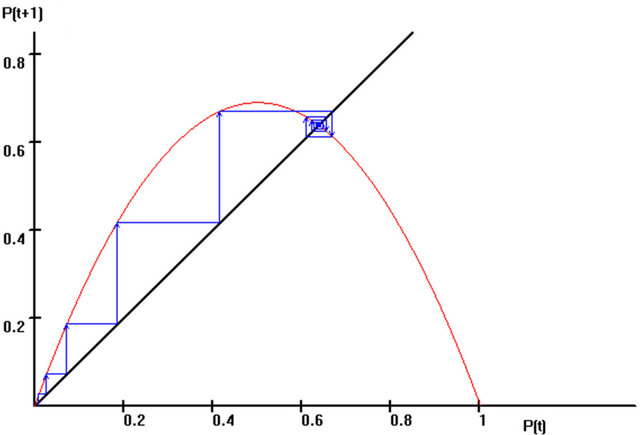
Figure 2. Fixed point attractor in the price system for the function , with λ = 2.75 and the initial value P(0) = 0.01 and 2000 iterations [67].
, with λ = 2.75 and the initial value P(0) = 0.01 and 2000 iterations [67].
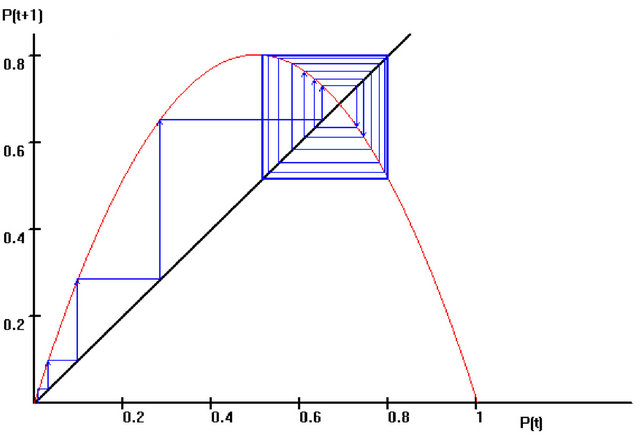
Figure 3. Double cycle attractor in the price system for the function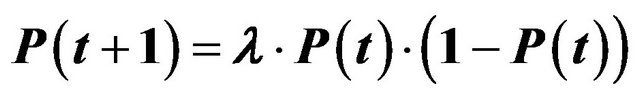 , with λ = 3.2 and the initial value P(0) = 0.01 and 2000 iterations [67].
, with λ = 3.2 and the initial value P(0) = 0.01 and 2000 iterations [67].
At a higher price, the suppliers will be inclined to offer more products. However, many demanders consider the price to be excessively high; thus, they are unwilling to buy all of the goods offered for purchase. The price then decreases. However, when the price decreases, the demand increases again. Because the suppliers cannot entirely meet the increased demand, the prices increase.
Because there is a lack of market transparency, the businessmen ultimately set a price that is so high that the demand and consequently the price again decrease. Thus, the price ultimately fluctuates due to the low level of market transparency and does not achieve an equilibrium value.
If the system is modified in such a way that, for example, λ = 4.0, (whereby the market transparency worsens again), an unexpected result occurs: suddenly, the system is literally “thrown off joint” because suppliers and demanders no longer possess knowledge regarding the market. Irregular fluctuations occur.
Prices that are too high result in decreased demand and increased supply, whereas decreasing prices cause increased demand and decreased supply. Due to the lack of market transparency, the prices do not develop toward an equilibrium point or a cycle.
The values seem to jump completely randomly. In short, the system reacts chaotically. As a consequence, an extremely complex structure develops, as shown in Figure 4.
Remarkably, the irregular price developments are neither caused by exogenous shocks—and thus can be explained endogenously by the system itself—nor a stochastic process. The apparently arbitrary price trends are not random; rather, they are deterministic.
The price development over the course of time changes fundamentally in the system as soon as it is apparently calculated more accurately.
Figure 5 demonstrates what occurs if the accuracy of the result is increased (at a given (low) market transparency of λ = 4.0) by one decimal place at a time after 2000 iterations of the price function.
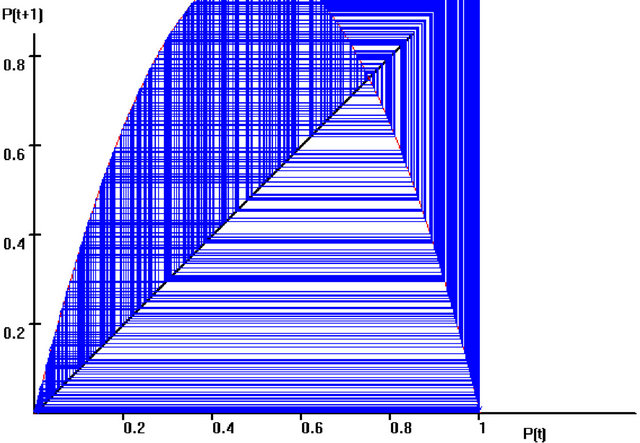
Figure 4. Chaos in the price system system for the function , with λ = 4.0 and the initial value P(0) = 0.01 and 2000 iterations [67].
, with λ = 4.0 and the initial value P(0) = 0.01 and 2000 iterations [67].
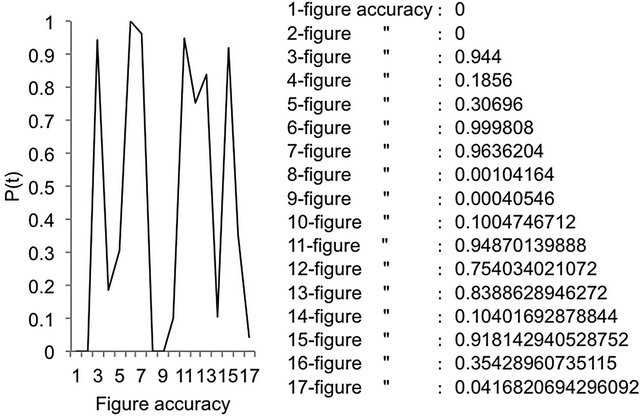
Figure 5. Butterfly effect in a price system. [67] P(t) after 2000 iterations of the function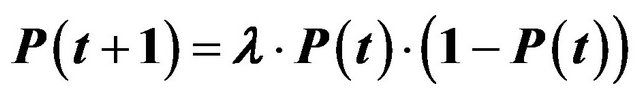 , with λ = 4.0 and the initial value P(0) = 0.01.
, with λ = 4.0 and the initial value P(0) = 0.01.
As can be observed, the result does not “improve” as might be expected; each time, the calculated price is fundamentally different than the previous instance of increasing the accuracy of the decimal places. In the case of three-figure accuracy, the price is almost 0.94; in the case of five-figure accuracy, it is approximately 0.31; at six-figure accuracy, it is almost 1.00; in the case of fifteen-figure accuracy, we obtain a price of almost 0.92; and in the case of, for example, seventeen-figure accuracy, the price of the “Chaoswriter” is nearly 0.0436.
Thus, any small change in the initial conditions (here, the increase of the exactness of the decimal places when calculating the price) leads to fundamentally different results. What is the correct result? This question cannot be answered because the results seem to be stochastically independent from one another. One might have a maximal amount of information regarding a complex system but will never successfully obtain an exact calculation or prediction of the system behavior. The reason can be observed in the complexity of the system and not in the lack of information. This idea is the butterfly effect that was described above.
If the state were to regulate this seemingly chaotic market (e.g., by means of a direct intervention by establishing minimum or maximum prices37), then this attempt would not be very successful because such efforts would result in a disruption of the price mechanism. Thus, the signal function of the prices (on the basis of which a market can function), which is so important for the market, would be further reduced. The only reasonable possibility of an intervention by the state would be to establish the general framework for the functioning of the market (in the sense of periodical price cycles); in our model, it must be initially discovered how high the market transparency must be to enable the chaos of the price development to evolve into a cyclical price development. Subsequently, the market transparency has to be supported according to this. To determine how high the market transparency must be to ensure that market prices stabilize, one would traditionally utilize a breakdown or reduction of the system to analyze it. However, due to the butterfly effect, a reductive breakdown for the purpose of comprehension does not assist any further. Many systems, including economic systems, fall into this category and cannot be simplified or broken down without considerable problems. In particular, complex systems cannot be disassembled and reassembled as a mechanical clock can. Continuing with the clock analogy, it can be stated that, in particular, economic processes rather function like a quartz clock, whose connections between the single parts are not mechanical and which is irrevocably - and thus irreversibly-destructed when it is disassembled. Consequently, one must agree with Wesson, who states that the world of simplicity exists only in the imagination. According to Wesson, the world is a nirvana, in which science is treated in the same manner as a wish [68]. Thus, methods that differ from the traditional methods are necessary to research complex systems38.
One possibility would be the execution of a bifurcation analysis39. For the purpose of this model, the market price is entered in a diagram after, for example, 2500 iterations of the model in the face of a gradual increase in market transparency. A bifurcation diagram is produced, and this diagram illustrates how the structure of the system changes at certain parameter values, under which the conditions (e.g., regular price fluctuations) become chaotic. Figure 6 represents the bifurcation diagram.
At a market transparency of λ < 3.68, regular price fluctuations occur, whereas at λ = 3.68, the first aperiodic, chaotic price cycles appear.
Even at a lower level of market transparency, phases of regular price developments are possible. For example, at a value of λ = 3.83, a three-period price cycle occurs. Such “islands” in the chaos are also referred to as intermittence, and they are visible in the illustration as white, vertical stripes in the midst of the black area of chaos.
After all, the complexity can only have developed due to the feedback of the system as a result of the iteration.

Figure 6. Bifurcation Diagram for the function 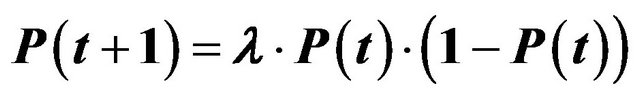 [67].
[67].
However, if complex systems develop due to the feedback and iteration of the dynamics, then they are not reducible to single elements because these elements do not create complexity until there is a permanent feedback effect on them—recursion. The whole is greater and different than the sum of its parts.
The model described above demonstrates that by means of a mathematically simple, non-linear, recursive function, a much wider spectrum of possible system developments can be illustrated, as is the case for linear functions. Due to the non-linear feedback of the system, the irreversibility of the system becomes apparent. Here, in contrast with an unobstructed oscillating movement, it is important to consider whether time goes backward or forward. This irreversibility is the precondition for selforganization. With regard to this irreversibility, Ebeling states that self-organization can be viewed as the counterpart to the generally observed tendency of a spontaneous “drifting apart of sand dunes”. However, in any case, this process is an irreversible process.
Because the irreversibility is a consequence of the “creative character” of mechanical movements (namely, its tendency for drifting apart, for divergence, and for diversity), self-organization establishes a new form of the creative potencies of matter [70].
The principle of self-organization states that order patterns do not develop as a result of determination from “outside”; rather, these patterns develop from the system itself40. This development process results in self-reproducing dynamic structures. Thus, self-organization is considered to be a process whose beginning is far from equilibrium and that causes complex order patterns by means of forces that are inherent to a system [70]. Therefore, self-organization is an attribute of systems—more precisely, an attribute of non-linear complex systems—that produce effects under certain conditions. However, it is both a “surplus” of these systems and an inseparable characteristic. Self-organization is one component, or as Ebeling indicates, perhaps even the crucial component of the evolution of complexity [70].
Thus, irreversibility and self-organization are two further important characteristics of complex systems in addition to non-linearity and the recursive connection of the system elements.
5. Conclusions—A Short Closing Argument for a (Free) Market Economy Rosser remarks that there are 45 definitions of complexity and this complexity is undoubtedly “a serious problem” [7, p. 170]. However, upon consideration of our former suggestions, it can be stated that complex systems reveal principles that cannot be derived from a high number of simple components or, perhaps, a high number of connections. Complex systems can also be composed of subsystems, but the type of connection, which becomes visible as a result of the dynamization of the system, seems to be decisive. Thus, the complexity of a system is not entirely determined by the number of elements of a system alone and the number of connections among these elements; this complexity is also determined by the following:
• the recursive type of connection
• the non-linear dynamics of the system Recursion and non-linearity dynamics are generated in a self-organizing and irreversible manner. If complexity develops in the manner that has been described in the above explanations, then a new type of view is necessary to obtain a better understanding; in this view, the complex and simple elements are closely linked to one another, and by means of simple iterations, the complexity (which is hidden in seemingly simple things) is revealed and—as stated by Briggs and Peat—an approach to creative potential [46] is created. Therefore, the equations and parameters of a model do not represent the construction plan; rather, they represent only the initial point for the evolution of a figure, which, as a type of “creatio ex nihilo”, gradually emerges [46] as a result of the feedback of the equations.
Even without knowledge of the theoretical approaches that have been presented in this essay (because of the increased use of computers, the mathematical findings did not become possible until the 1990s), von Hayek, in this context, appropriately discusses the pretension of knowledge41 [1] when writing his work of the same title.
Baumol and Benhabib indicated that chaos theory has the power to provide “caveats” for economic analysts and policy designers:
The chaos theory “warns us that apparently random behavior may not be random at all. It demonstrates dramatically the dangers of extrapolation and the difficulties that can beset economic forecasting generally. It shows that negotiation processes may elicit erratic behavior patterns which no one intends and which can occur even if the positions taken by both parties are inherently simple and straightforward” [20].
The initial findings from the “theory of complex systems”, which have been presented in this essay, need not result in—as may be assumed—an irreconcilability of “social justice” and “freedom” with regard to the market system. Nevertheless, these results can assist us in considering the profitable use of the self-organizing forces of freedom, which are inherent to the concept of a free market economy, but which, as a result of excessive interventions by the state, are decreased to the disadvantage of everyone.
However, the analysis of “complex systems” is far from complete. On the contrary, in this essay it was possible only to offer an introduction to this topic. A significant amount of research has yet to be conducted to better understand and evaluate complex systems and to identify options for action.
REFERENCES
- F. A. V. Hayek, “Die Anmaßung von Wissen,” Mohr Siebeck Verlag, Thübingen, 1996.
- F. A. V. Hayek, “Kinds of Order in Society,” In: R. Raico, Ed., New Individualist Review, Liberty Fund, Indianapolis, 1961, pp. 495-504.
- G. Niemeyer, “Kybernetische System-Und Modelltheorie,” Vahlen, München, 1977.
- P. Nijkamp, A. Reggiani, “Nonlinear Evolution of Spatial Economic Systems,” Springer-Verlag, Berlin, 1993. doi:10.1007/978-3-642-78463-7
- M. Faggini and A. Parziale, “The Failure of Economic Theory. Lessons from Chaos Theory,” Modern Economy, Vol. 3, No. 1, 2012, pp. 1-10.
- G. Strunk and G. Schiepek, “Systemische Psychologie: Eine Einführung in die Komplexen Grundlagen Menschlichen Verhaltens,” Spektrum-Akademischer-Verlag, Mü- nchen, 2006.
- B. J. Rosser, “On the Complexities of Complex Economic Dynamics,” Journal of Economic Perspectives, Vol. 13, No. 4, 1999, pp. 169-192. doi:10.1257/jep.13.4.169
- F. Bestenreiner, “Der Phantastische Spiegel: Quanten, Quarks, Chaos-Oder vom Trost, der aus der Formel kommt,” Fischer-Taschenbuch-Verlag, Frankfurt am Main, 1991.
- P. Brügge, “Mythos aus dem Computer. Über Ausbreitung und Mißbrauch der Chaostheorie,” SPIEGEL, No. 39, 1993, pp. 156-164.
- P. Brügge, “Mythos aus dem Computer. Über Ausbreitung und Mißbrauch der Chaostheorie,” SPIEGEL, Vol. 47, No. 40, 1993, pp. 232-241.
- P. Brügge, “Mythos aus dem Computer. Über Ausbreitung und Mißbrauch der Chaostheorie,” SPIEGEL, Vol. 47, No. 41, 1993, pp. 240-252.
- A. Liening, “Ökonomische Chaostheorie,” In: H. May, Ed., Lexikon der ökonomischen Bildung, Oldenbourg Wissenschaftsverlag, München, 2007.
- M. Faggini and C. P. Vinci, “Decision Theory and Choices: A Complexity Approach,” Springer-Verlag, Berlin, 2010. doi:10.1007/978-88-470-1778-8
- J. S. Metcalfe and J. Foster, “Evolution and Economic Complexity,” Edward Elgar Publishers, Northampton, 2007.
- F. Trosky, “Heterogene Erwartungen auf dem Geldmarkt,” Duncker & Humblot, Berlin, 2006.
- B. B. Mandelbrot and R. L. Hudson, “The Behavior of Markets: A Fractal View of Risk, Ruin and Reward,” Basic Books, New York, 2004.
- W. A. Barnett, C. Deissenberg and G. Feichtinger, “Economic Complexity: Non-linear Dynamics, Multi-Agents Economies, and Learning,” Emerald Group Publishing, Bingley, 2004.
- G. Zehetner, “Anwendungen der Chaostheorie in der Betriebswirtschaftslehre,” Facultas Verlag, Wien, 2003.
- T. Puu, “Attractors, Bifurcations and Chaos: Nonlinear Phenomena in Economics,” Springer-Verlag, Berlin, 2003. doi:10.1007/978-3-540-24699-2
- W. J. Baumol and J. Benhabib, “Chaos: Significance, Mechanism and Economic Applications,” Journal of Economic Perspectives, Vol. 3, No. 1, 1989, pp. 77-105. doi:10.1257/jep.3.1.77
- A. Liening, “Komplexe Systeme Zwischen Ordnung und Chaos,” Lit Verlag, Münster, 1999.
- H. Denis, “Geschichte der Wirtschaftstheorien. 1. Von Platon bis Marx,” Schäuble, Rheinfelden, 1985.
- K. Mainzer, “Zeit-Von der Uhrzeit zur Computerzeit,” Verlag C. H. Beck, München, 1995.
- G. Stavenhagen, “Geschichte der Wirtschaftstheorie,” Vandenhoeck & Ruprecht, Göttingen, 1969.
- W. Lentz, “Neuere Entwicklungen der Theorie Dynamischer Systeme und Ihre Bedeutung für Die Agrarökonomie,” Duncker & Humblot, Berlin, 1993.
- K.-H. Schmidt, “Merkantilismus, Kameralismus, Physiokratie,” In: O. Issing, Ed., Geschichte der Nationalökonomie, Vahlen, München, 1994, pp. 43-45.
- H. Frank, “Geschichte der Wirtschaftspolitik,” Oldenbourg Verlag, München, 1993.
- A. Smith, “Wealth of Nations: An Inquiry into the Nature and Causes of the Wealth of Nations,” Modern Library, New York, 1994.
- A. Smith, “The Theory of Moral Sentiments,” Liberty Fund, Indianapolis, 1976.
- K. J. Arrow and F. H. Hahn, “General Competitive Analysis,” Holden-Day, Amsterdam, 1971.
- F. Söllner, “Neoklassik und Umweltökonomie,” 1993.
- J. Röpke, “Die Strategie der Innovation: Eine SystemTheoretische Untersuchung der Interaktion von Individuum, Organisation und Markt im Neuerungsprozess,” Mohr Siebeck Verlag, Thybingen, 1977.
- B. F. Skinner and E. Ortmann, “Die Funktion der Verstärkung in der Verhaltenswissenschaft: Contigencies of Reinforcement,” Kindler, München, 1974.
- J. B. Watson, “Behaviorismus,” 1984.
- H. J. Schlösser, “Das Menschenbild in der Ökonomie,” Wirtschaftsverlag Bachem, Köln, 1992.
- N. Luhmann, “Zweckbegriff und Systemrationalität,” Mohr Siebeck Verlag, Tübingen, 1968.
- T. Burns and G. M. Stalker, “The Management of Innovation,” Tavistock Publications, London, 1966.
- R.-D. Graß, “Vilfredo Pareto—Marx der Bourgeoisie,” Schäffer-Poeschel Verlag, Stuttgart, 1994.
- S. Hawking, “Eine kurze Geschichte der Zeit,” Rowohlt Verlag, Düsseldorf, 1988.
- I. Kant, “Immanuel Kant. Werke in Sechs Bänden,” Wissenschaftliche Buchgemeinschaft, Darmstadt, 1983.
- U. Leonhardt, “Measuring the Quantum State of Light,” Cambridge University Press, Cambridge, 1997.
- R. Worg, “Deterministisches Chaos—Wege in Die Nichtlineare Dynamik,” BI Wissenschaftsverlag, Mannheim, 1993.
- P. S. Laplace, “Essai Philosophique sur les Probabilités,” 1819.
- D. Ruelle, “Zufall und Chaos,” Springer Verlag, Berlin, 1993.
- R. Descartes, “Discours de la Méthode,” Meiner Verlag, Hamburg, 1990.
- J. Briggs and F. D. Peat, “Die Entdechung des Chaos. Eine Reise durch die Chaos-Theorie,” Deutscher Taschenbuch Verlag, München, 1993.
- K. Dopfer, “Classical Mechanics with an Ethical Dimension: Professor Tinbergen’s Economics,” Journal of Economic Issues, Vol. 22, No. 3, 1988, pp. 675-706.
- A. Ryan, “The Philosophy of John Stuart Mill,” Macmillan, London, 1987.
- K. Dopfer, “Evolutionsökonomie in der Zukunft: Programmatik und Theorieentwicklungen,” In: H. R. Hanusch and C. Horst, Eds., Ökonomische Wissenschaft in der Zukunft: Ansichten Führender Ökonomen, Wirtschaft und Finanzen, Düsseldorf, 1992, pp. 1-28.
- H. Poincaré, “Les méthodes nouvelles de la mécanique céleste,” Gauthier-Villars, Paris, 1899.
- J. P. Crutchfield, J. D. Farmer, N. H. Packard and R. S. Shaw, “Non-Linear Physics for Beginners: Fractals, Chaos, Pattern Formation, Solutions, Cellular Automata and Complex Systems,” World Scientific, New Jersey, 1998.
- C. Chiarella, “Entwicklungen der Nichtlinearen, Dynamischen Ökonomischen Theorie: Vergangenheit, Gegenwart und Zukunft,” In: H. R. Hanusch and C. Horst, Eds., Ökonomische Wissenschaft in der Zukunft: Ansichten Führender Ökonomen, Wirtschaft und Finanzen, Düsseldorf, 1992, pp. 74-91.
- A. Medio, “Chaotic Dynamics: Theory and Applications to Economics,” Camebridge University Press, Cambridge, 1992.
- A. N. Kolmogorow, “Über die Entropie der Zeit. Eins als metrische Invariante von Automorphismen,” Dokladyi Akademii Nauk (UDSSR), Vol. 119, No. 5, 1958, pp. 861- 864.
- S. Smale, “Differentiable Dynamical Systems,” Bulletin of the American Mathematical Society, Vol. 73, No. 6, 1967, pp. 747-817. doi:10.1090/S0002-9904-1967-11798-1
- B. Schefold, “Wenn Du den Hals überschreitest : Gedanken zur Zukunft ökonomischer Wissenschaft,” In: H. R. Hanusch and C. Horst, Eds., Ökonomische Wissenschaft in der Zukunft: Ansichten Führender Ökonomen, Wirtschaft und Finanzen, Düsseldorf, 1992, pp. 346-360.
- R. Schmalensee, “Kontinuität und Wandel in der Wirtschaftswissenschaft,” In: H. R. Hanusch and C. Horst Eds., Ökonomische Wissenschaft in der Zukunft: Ansichten Fü- hrender Ökonomen, Wirtschaft und Finanzen, Düsseldorf, 1992, pp. 331-370.
- F. Hölderlin, “Sämtliche Gedichte und Hyperion,” Insel Verlag, Leipzig, 2001.
- H. J. Warnecke, “Die Fraktale Fabrik: Revolution der Unternehmenskultur,” Rowohlt, Reinbek, 1996.
- [61] G. Gerken, “Die fraktale Marke,” Econ Verlag, Wien, 1994.
- [62] A. Liening and E. Mittelstädt, “Intellectual Capital Reporting in Schools: A Complexity-Scientific Approach to Educational Management,” The International Journal Learning, Vol. 16, No. 7, 2009, p. 15.
- [63] A. Liening and E. Mittelstädt, “Innovative Instrumente zur Anreizkompatiblen Selbstorganisation von Wissenschaft—Die Wissensbilanzierung,” In: E. Brunner, Ed., Selbstorganisation in der Wissenschaft, Frege Centre for Structural Sciences, Jena, 2011.
- [64] B. Glazinski, “Innovatives Change Management,” Wiley- vch, Weinheim, 2007.
- [65] G. Strunk, “Die Komplexitätshypothese der Karriereforschung,” Frankfurt am Main, Wien, 2009.
- [66] M. Thiemann, “Chaostheorie auf Kapitalmärkten: Untersuchung des DAX, DOW und FTSE anhand modernerer Verfahren auf deterministisches Chaos,” WiKu-Verlag, Stuttgart, 2004.
- [67] O. Loistl and B. Iro, “Chaostheorie: Zur Theorie Nichtlinearer Dynamischer Systeme,” Oldenbourg Wissenschaftsverlag, München, 1993.
- [68] A. Liening, “Komplexe Systeme—Eine Software zur Simulation und Analyse,” 2010.
- [69] R. Wesson, “Chaos, Zufall und Auslese der Natur,” Insel-Verlag, Leipzig, 1995.
- [70] G. Strunk, et al., “Lost in Transition? Complexity in Organisational Behaviour—The Contributions of Systems Theories,” Management Revue, Vol. 15, No. 4, 2004, pp. 481-509.
- [71] W. Ebeling, “Selbstorganisation und Entropie in Ökologischen und Ökonomischen Prozessen,” In: F. B. A. H. Diefenbacher, Ed., Zwischen Entropie und Selbstorganisation—Perspektiven Einer Ökologischen Ökonomie, Metropolis-Verlag, Marburg, 1994, pp. 29-45.
- [72] M. Pasche, “Ansätze Einer Evolutorischen Umweltökonomik,” In: F. B. A. H. Diefenbacher, Ed., Zwischen Entropie und Selbstorganisation—Perspektiven einer ökologischen Ökonomie, Metropolis-Verlag, Marburg, 1994, p. 75.
NOTES
1Models can be interpreted as material or immaterial systems, which illustrate other systems such that experimental manipulations of the depicted structures and conditions become possible [3].
2Lineal systems are conceptions in which the elements of a system are arranged consecutively as a chain. Because feedback loops are missing in this structure, in contrast to non-lineal systems, a predefined performance is executed without reacting to endogenous or exogenous events. Frequently, lineal systems are mathematically linear, whereas non-lineal systems are often non-linear. Therefore, linear systems should be distinguished from lineal systems.
3A trajectory is the development line of a dynamic system. It depicts the course, which begins from a certain starting point and is conducted by a system in the course of its dynamical development in the phase space. Here, the phase space is a space spanned by the time-variant variables of a dynamical system. If the trajectory moves in an “attractive” dynamical state, it is referred to as an attractor, which is a subset of a phase space. There are four types of attractors: fixed point, limit-cycle, limit-tori, chaotic resp. strange attractors.
4For more information, cp. e. g. the comment on Grammar Complexity [6].
5With regard to popular scientific literature, refer to Bestenreiner [8]. Rosser, for instance, notices: “Chaos theory has no single inventor, but a fad for it followed publication of the best-selling book by the journalist, Gleick (1987), a fad further fueled in the popular mind by Goldblums’s portrayal of a ‘chaotician’ in the film Jurassic Park” [7, p. 173].
6At this point, an example from an article series in the German SPIEGEL magazine should be mentioned; this magazine is a popular scientific publication along the lines of “cult about chaos—superstition or world explanation” (“Kult um das Chaos—Aberglaube oder Welterklärung”) [9-11].
7For more information, cp. the comments and bibliographical references in Liening [12]. Especially in the recent past, numerous interesting publications addressing chaos theory and economics have been published. For example, the following monographs are cited: Faggini & Vinci [13], Metcalfe & Foster [14], Trosky [15], Mandelbrot & Hudson [16], Barnett, Deissenberg & Feichtinger [17], Zehetner [18], and Puu [19]. An introduction to chaos theory and some economic applications can be found, for instance, in the work by Baumol & Benhabib [20].
8In the areas in which the market fails, as in the cases of the allocation of public goods and the tendency to form monopolies, Smith definitely considers state interventions as justifiable. From the regulation of the banking business to the raising of taxes to reduce the consumption of alcohol, the moral philosopher Smith views many possibilities for governmental intervention. However, for the first time in history, Smith succeeded in illustrating that only by means of individual freedom of action in the economic system is it possible to achieve maximal economic growth and standards of wealth under the prevailing circumstances [27]. For more information, also cp. [28].
9The reasons for this hesitation are mentioned in Smith’s theory of moral sentiments [29]. Cp. also the explanations by Denis [22].
10For more information regarding (traditional) behaviorism, cp. [33,34].
11For a detailed illustration of the neoclassical image of humanity, cp. the critical analysis in [35].
12Lentz also indicates that a number of the most prominent advocates initially underwent a technical-natural scientific education [25].
13Oltmanns, cited according to [38].
14Hawking considers Newton’s contributions to be presumably the most important physical publication written by one person alone [39].
15Note that Kant characterized Leibniz as a mechanic [40].
16Leibniz and Newton were not actually friends and Newton’s realism conflicted with Leibniz’s realism. Nevertheless, the importance of both scholars for physics and mathematics is indisputable (consider infinitesimal calculus).
17Poincaré, cited according to [41].
18A system can be considered reversible if it can also proceed in a backward fashion. For instance, Newton’s first law states that the law of inertia is reversible such that if there is an equation of a force-free movement at time point t, then a solution at time point-t also exists. Here, the time reversal is expressed by a change of sign in the direction of movement.
19For example, according to Newton, the gravitational force of two astronomical objects is inversely proportional to the square of the distance of both bodies. Descartes would have been suspicious of this conception of “action at a distance.” He would have preferred a mechanistic explanation such as that which describes contact forces that cause one gear wheel to affect another rather than actions at a distance [44].
20Descartes resisted the term “treatise” and insisted on the original title “Discours” because he did not want to teach the method but only wanted to discuss it.
21Mill, cited according to [48].
22According to Pareto, goods and services in an economy are optimally distributed in situations in which a person can only improve his/her position if he/she takes something from another person. However, until today, it has been questionable whether this idea is actually positive because the optimum situation can be achieved irrespective of how the goods are distributed among the poor and the rich [38].
23This paper is not the appropriate context in which to comment on all of the details of Poincaré’s results. Therefore, interested readers are referred to [50].
24Poincaré, cited according to [51].
25Chiarella states that most of the early authors who wrote about the dynamical, time-dependent cycle theory were not aware of Poincaré’s work [52].
26For more information, cp., for example, [53].
27In addition to Lorenz, other scientists, such as Kolmogorow et al. and Smale, should be mentioned because these scientists also successfully researched the field of non-linear dynamics in the 1960s or perhaps as early as the 1950s. Interested readers are referred to, for example, [54] or [55].
28For instance, von Hayek developed a theory of complex phenomena without any recourse to mathematical concepts [1].
29As a supply and demand schema, static modeling can be traced back to Marshall. This schema shows that there is a tendency toward equilibrium in the case of functioning competition. For example, when examining it through the use of statically comparative analyses, a change of demand or supply would be illustrated by a shift in the curves in the graphical representation.
30With regard to organizational and process structures, see, e.g., [59]; with regard to marketing, see [60]; with regard to knowledge management, see, e.g., [61,62]; and with regard to change management, see, e.g., [63].
31Recently, numerous interesting publications addressing chaos theory and economics have been published. For example, the following monographs are cited: [15,16,19,65].
32For this, cp. the explanation by [66].
33Cp. in more detail [21].
34Market transparency indicates that suppliers and demanders know all of the development factors that are important to them. Examples of this transparency are knowledge regarding a particular good and its characteristics and the offered and demanded amount of goods and their prices.
35Lower values indicate that demanders and suppliers have more information regarding the market. Thus, the values mirror evaluation figures in the known grading system (Germany): 1 = excellent (sehr gut),..., 5 = inadequate (mangelhaft).
36According to Voltaire, “Donnez-moi un ordinateur, et je vais faire une monde”, as if the butterfly effect were computer-induced. This assessment is far from the truth. The world with its butterfly effect, which is illustrated here, does not correspond to its representation by a computer. Thus, it does not relate to inexact computer calculations, which are possible and occur absolutely algebraically. For a detailed explanatory statement and mathematical proof, cp [21].
37Even if the market featured a convergent cyclical movement and the state concluded that the equilibrium price was, for example, too high, intervention by means of an agreement regarding maximum prices would be rather problematic from an economic point of view. To have an effect, the maximum price would have to be considerably below the equilibrium price. However, the result of this price would be that the supply would decrease and ultimately be considerably lower than the demand, which would then increase due to the low maximum price. This maximum price-induced excess demand would be the consequence of the intervention by the state.
38Unfortunately, there is insufficient space in which to present such methods for the analysis of complex systems exhaustively. In addition to the method of bifurcation analysis, the calculation of Lyapunov exponents, the Li/Yorke theorem or the calculation of dimensions (e.g., box-counting dimension, Hausdorff dimension) are among the simplest methods of chaos theory. A detailed illustration, explanation and application can be found, for example, in [21]. Especially in the context of empirical studies, it has always been difficult to prove chaos on the sole basis of, for example, the calculation of Lyapunov exponents. It can be assumed that, in particular, the noise in the data, caused by incidental influences and exogenous shocks, complicates the proof cited by [21]. However, other methods, which to some extent must be considered in combination with one another, provide the opportunity to compensate for this deficit. Examples include methods that can be circumscribed with the keywords grammar complexity, recurrence plots, Kolmogorov-Sinai entropy or permutation entropy. Cp., e.g., [61,62,69].
39This term has been borrowed from Latin. In this language, the word “furca” refers to a fork with two tines. It is referred to as a bifurcation if, in the case of the continuous alteration of the parameters of a system, an abrupt structural change occurs (for example, when a convergent behavior to a point attractor abruptly “turns into” a double cycle from a certain parameter value).
40For more information, cp. the comments by [71].
41The included essay on the theory of complex phenomena was first published in 1967.

